Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-21T21:08:07.718Z Has data issue: false hasContentIssue false
  • English
  • Français

Range inclusion and diagonalization of complex symmetric operators

Part of: Selfadjoint operator algebras Special classes of linear operators General theory of linear operators

Published online by Cambridge University Press:  04 April 2024

Cun Wang ,
Jiayi Zhao  and
Sen Zhu Open the ORCID record for Sen Zhu [Opens in a new window]
Cun Wang
Affiliation:
School of Mathematics and Statistics, Beijing Institute of Technology, Beijing 102488, P. R. China e-mail: wangcun@bit.edu.cn
Jiayi Zhao
Affiliation:
Department of Mathematics, Jilin University, Changchun 130012, P. R. China e-mail: jiayi.zhau@gmail.com
Sen Zhu*
Affiliation:
Department of Mathematics, Jilin University, Changchun 130012, P. R. China e-mail: jiayi.zhau@gmail.com
*
e-mail: zhusen@jlu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the range inclusion and the diagonalization in the Jordan algebra 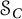$\mathcal {S}_C$ of C-symmetric operators, that are, bounded linear operators T satisfying 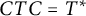$CTC =T^{*}$, where C is a conjugation on a separable complex Hilbert space 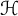$\mathcal H$. For 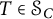$T\in \mathcal {S}_C$, we aim to describe the set 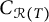$C_{\mathcal {R}(T)}$ of those operators 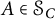$A\in \mathcal {S}_C$ satisfying the range inclusion 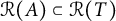$\mathcal {R}(A)\subset \mathcal {R}(T)$. It is proved that (i) 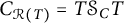$C_{\mathcal {R}(T)}=T\mathcal {S}_C T$ if and only if 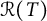$\mathcal {R}(T)$ is closed, (ii) 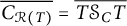$\overline {C_{\mathcal {R}(T)}}=\overline {T\mathcal {S}_C T}$, and (iii) 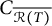$C_{\overline {\mathcal {R}(T)}}$ is the closure of 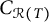$C_{\mathcal {R}(T)}$ in the strong operator topology. Also, we extend the classical Weyl–von Neumann Theorem to 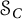$\mathcal {S}_C$, showing that every self-adjoint operator in 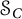$\mathcal {S}_C$ is the sum of a diagonal operator in 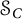$\mathcal {S}_C$ and a compact operator with arbitrarily small Schatten p-norm for 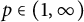$p\in (1,\infty )$.

Keywords

Complex symmetric operatorsrange inclusionthe Weyl–von Neumann Theoremdiagonal operators

MSC classification

Primary: 47B99: None of the above, but in this section 47A05: General (adjoints, conjugates, products, inverses, domains, ranges, etc.)
Secondary: 47A55: Perturbation theory 46L70: Nonassociative selfadjoint operator algebras
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 21
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The third author is the corresponding author and was partially supported by the National Natural Science Foundation of China (Grant No. 12171195)

References

Berg, I. D., An extension of the Weyl–von Neumann theorem to normal operators. Trans. Amer. Math. Soc. 160(1971), 365–371.CrossRefGoogle Scholar
Cartan, É., Sur les domaines bornés homog‘enes de l’espace de $n$ variables complexes. Abh. Math. Semin. Univ. Hamburg 11(1935), 116–162.CrossRefGoogle Scholar
Chu, C.-H., Jordan structures in geometry and analysis, Cambridge Tracts in Mathematics, 190, Cambridge University Press, Cambridge, 2012.Google Scholar
Conway, J. B., A course in operator theory, Graduate Studies in Mathematics, 21, American Mathematical Society, Providence, RI, 2000.Google Scholar
Davidson, K. R., ${C}^{\ast }$ -algebras by example, Fields Institute Monographs, 6, American Mathematical Society, Providence, RI, 1996.Google Scholar
Douglas, R. G., On majorization, factorization, and range inclusion of operators on Hilbert space. Proc. Amer. Math. Soc. 17(1966), 413–415.CrossRefGoogle Scholar
Embry, M. R., Factorization of operators on Banach space. Proc. Amer. Math. Soc. 38(1973), 587–590.CrossRefGoogle Scholar
Fillmore, P. A. and Williams, J. P., On operator ranges. Adv. Math. 7(1971), 254–281.CrossRefGoogle Scholar
Friedman, Y. and Russo, B., The Gelfand–Naimark theorem for JB ${}^{\ast }$ -triples. Duke Math. J. 53(1986), no. 1, 139–148.CrossRefGoogle Scholar
Garcia, S. R., Conjugation and Clark operators , In: A. L. Matheson, M. I. Stessin and R. M. Timoney (eds.), Recent advances in operator-related function theory, Proceedings of the conference held at Trinity College, Dublin, Ireland, August 4–6, 2004, Contemporary Mathematics, 393, American Mathematical Society, Providence, RI, 2006, pp. 67–111.Google Scholar
Garcia, S. R., Means of unitaries, conjugations, and the Friedrichs operator. J. Math. Anal. Appl. 335(2007), 941–947.CrossRefGoogle Scholar
Garcia, S. R., The norm and modulus of a Foguel operator. Indiana Univ. Math. J. 58(2009), no. 5, 2305–2315.CrossRefGoogle Scholar
Garcia, S. R., Prodan, E., and Putinar, M., Mathematical and physical aspects of complex symmetric operators. J. Phys. A.: Math. Gen. 47(2014), 353001.CrossRefGoogle Scholar
Garcia, S. R. and Putinar, M., Complex symmetric operators and applications. Trans. Amer. Math. Soc. 358(2006), 1285–1315.CrossRefGoogle Scholar
Garcia, S. R. and Putinar, M., Complex symmetric operators and applications, II. Trans. Amer. Math. Soc. 359(2007), 3913–3931.CrossRefGoogle Scholar
Garcia, S. R. and Wogen, W. R., Complex symmetric partial isometries. J. Funct. Anal. 257(2009), 1251–1260.CrossRefGoogle Scholar
Gilbreath, T. M. and Wogen, W. R., Remarks on the structure of complex symmetric operators. Integral Equations Operator Theory 59(2007), no. 4, 585–590.CrossRefGoogle Scholar
Glazman, I. M., An analogue of the extension theory of Hermitian operators and a non-symmetric one-dimensional boundary problem on a half-axis. Dokl. Akad. Nauk SSSR 115(1957), 214–216.Google Scholar
Glazman, I. M., Direct methods of qualitative spectral analysis of singular differential operators . In: Israel program for scientific translations, Jerusalem, 1965, Daniel Davey, New York, 1966, Translated from the Russian by the IPST staff.Google Scholar
Hai, P. V. and Putinar, M., Complex symmetric evolution equations. Anal. Math. Phys. 10(2020), no. 1, Article no. 14, 36 pp.CrossRefGoogle Scholar
Halmos, P. R., Irreducible operators. Michigan Math. J. 15(1968), 215–223.CrossRefGoogle Scholar
Halmos, P. R., Continuous functions of Hermitian operators. Proc. Amer. Math. Soc. 31(1972), 130–132.CrossRefGoogle Scholar
Herrero, D. A., Approximation of Hilbert space operators. Vol. 1, 2nd ed., Pitman Research Notes in Mathematics Series, 224, Longman Scientific & Technical, Harlow, 1989.Google Scholar
Hua, L.-K., On the theory of automorphic functions of a matrix level I. Geometrical basis. Amer. J. Math. 66(1944), 470–488.CrossRefGoogle Scholar
Jacobson, N., Normal semi-linear transformations. Amer. J. Math. 61(1939), 45–58.CrossRefGoogle Scholar
Kalinina, T. B., On the theory of extensions of $K$ -symmetric operators. Funkcionalniy analiz (Ulyanovsk) 7(1976), 78–85 (Russian).Google Scholar
Kato, T., Perturbation of continuous spectra by trace class operators. Proc. Japan Acad. 33(1957), 260–264.Google Scholar
Knowles, I., On the boundary conditions characterizing $J$ -selfadjoint extensions of $J$ -symmetric operators. J. Differential Equations 40(1981), 193–216.CrossRefGoogle Scholar
Kuroda, S. T., On a theorem of Weyl-von Neumann. Proc. Japan Acad. 34(1958), 11–15.Google Scholar
Li, V. P., On the theory of J-symmetric operators. Funkcionalniy analiz (Ulyanovsk) 3(1974), 84–91 (Russian).Google Scholar
Liu, T., Zhao, J. Y., and Zhu, S., Reducible and irreducible approximation of complex symmetric operators. J. Lond. Math. Soc. 100(2019), 341–360.CrossRefGoogle Scholar
Makarova, A. D., Extensions of $J$ -symmetric operators with a non-dense domain. Funkcionalniy analiz (Ulyanovsk), 8(1977), 102–112 (Russian).Google Scholar
von Neumann, J., Charakterisierung des Spektrums eines Integraloperators. Actualités Sci. Indust. 229(1935), 1–20.Google Scholar
Prodan, E., Garcia, S. R., and Putinar, M., Norm estimates of complex symmetric operators applied to quantum systems. J. Phys. A 39(2006), 389–400.CrossRefGoogle Scholar
Race, D., The theory of $J$ -selfadjoint extensions of $J$ -symmetric operators. J. Differential Equations 57(1985), 258–274.CrossRefGoogle Scholar
Radjavi, H. and Rosenthal, P., The set of irreducible operators is dense. Proc. Amer. Math. Soc. 21(1969), 256.Google Scholar
Rayh, L. M. and Tsekanovskii, E. R., Biinvolutive self-adjoint biextensions of $J$ -symmetric operators. Teoriya funkciy, funcionalniy analiz i ih prilozheniya (Kharkov) 23(1975), 79–93.Google Scholar
Sarason, D., Algebraic properties of truncated Toeplitz operators. Oper. Matrices 1(2007), 491–526.CrossRefGoogle Scholar
Schur, I., Ein Satz ueber quadratische Formen mit komplexen Koeffizienten. Amer. J. Math. 67(1945), 472–480.CrossRefGoogle Scholar
Siegel, C. L., Symplectic geometry. Amer. J. Math. 65(1943), 1–86.CrossRefGoogle Scholar
Sikonia, W., Essential, singular, and absolutely continuous spectra. Ph.D. thesis, University of Colorado at Boulder, 1970.Google Scholar
Takagi, T., On an algebraic problem related to an analytic theorem of Carathéodory and Fejér and on an allied theorem of Landau. Jpn. J. Math. 1(1925), 83–93.CrossRefGoogle Scholar
Voiculescu, D., Some results on norm-ideal perturbations of Hilbert space operators. J. Operator Theory 2(1979), 3–37.Google Scholar
Wang, C. and Zhu, S., The Jordan algebra of complex symmetric operators. To appear in Chinese Annals of Mathematics (Series B). arXiv:1912.10391v2 Google Scholar
Wang, P. H. and Zhang, X., Range inclusion of operators on non-archimedean Banach space. Sci. China Math. 53(2010), no. 12, 3215–3224.CrossRefGoogle Scholar
Weyl, H., Über beschränkte quadratische formen deren differenz vollstetig ist. Rend. Circ. Mat. Palermo 27(1909), 373–392.CrossRefGoogle Scholar
Zagorodnyuk, S. M., On a $J$ -polar decomposition of a bounded operator and matrices of $J$ -symmetric and $J$ -skew-symmetric operators. Banach J. Math. Anal. 4(2010), no. 2, 11–36.CrossRefGoogle Scholar