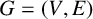1 Introduction
Partial differential equations play an important role in dynamics, mathematical physics, engineering, geometry and the other sciences. For examples, readers are referred to [Reference Che, Chen and Shi1, Reference Corra Corrêa, dos Santos, Tavares and Muhassua2, Reference Kang and Robertson8, Reference Yang12] and the references therein. As they model discrete systems, it is important to study such equations on graphs.
In recent years, Grigor’yan, Lin and Yang systematically raised and studied several partial differential equations involving Yamabe equations, Kazdan–Warner equations and Schrödinger equations on graphs [Reference Grigor’yan, Lin and Yang4–Reference Grigor’yan, Lin and Yang6]. They first established the Sobolev spaces and the functional framework on graphs. As a consequence, variational methods are applied to solve partial differential equations on graphs, that is, to find critical points of various functionals. In particular, in [Reference Grigor’yan, Lin and Yang4], they derived the Sobolev embedding theorems on graphs, that is, if
![]() $G=(V,E)$
is a locally finite graph and
$G=(V,E)$
is a locally finite graph and
![]() $\Omega \subset V$
is a bounded domain, then
$\Omega \subset V$
is a bounded domain, then
while if
![]() $G=(V,E)$
is a finite graph, then
$G=(V,E)$
is a finite graph, then
They observed that the Sobolev embedding theorems on graphs are quite different from those on Euclidean space, and thus they could assume different growth conditions on the nonlinear terms f and g on graphs. They also observed that the Sobolev space they established is pre-compact. By these crucial observations, they studied the following p-Laplacian equation:
 $$ \begin{align} \begin{cases} -\Delta_{p} u=f(x,u) &\mathrm{ in}~\Omega^{\circ},\\ u\geq 0 ~~\mathrm{ in} ~~ \Omega^{\circ}, u= 0 &\mathrm{ on}~\partial \Omega, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} -\Delta_{p} u=f(x,u) &\mathrm{ in}~\Omega^{\circ},\\ u\geq 0 ~~\mathrm{ in} ~~ \Omega^{\circ}, u= 0 &\mathrm{ on}~\partial \Omega, \end{cases} \end{align} $$
on a locally finite graph and obtained a local solution. They also studied the following equation on a locally finite graph:
 $$ \begin{align} \begin{cases} \mathcal{ L}_{m.p} u=f(x,u) &\mathrm{ in }~\Omega^{\circ},\\ |\nabla^{j} u|= 0, 0\leq j\leq m-1 &\mathrm{ on }~\partial \Omega, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \mathcal{ L}_{m.p} u=f(x,u) &\mathrm{ in }~\Omega^{\circ},\\ |\nabla^{j} u|= 0, 0\leq j\leq m-1 &\mathrm{ on }~\partial \Omega, \end{cases} \end{align} $$
and obtained a nontrivial local solution. In addition, they studied several equations on a finite graph and obtained global solutions. For more details, we refer readers to [Reference Grigor’yan, Lin and Yang4]. In [Reference Lin and Yang11], Lin and Yang studied several Laplacian equations involving the Schrödinger equation, the mean field equation and the Yamabe equation on a locally finite graph
![]() $G=(V,E)$
, and obtained global solutions in Sobolev space
$G=(V,E)$
, and obtained global solutions in Sobolev space
![]() $W^{1,2}(V)$
or its subspace
$W^{1,2}(V)$
or its subspace
![]() $\mathcal {H}$
by using calculus of variations, where
$\mathcal {H}$
by using calculus of variations, where
 $$ \begin{align*} \mathcal{H}=\bigg\{u\in W^{1,2}(V):\int_{V}(|\nabla u|^{2}+hu^{2})\,d\mu<\infty\bigg\}. \end{align*} $$
$$ \begin{align*} \mathcal{H}=\bigg\{u\in W^{1,2}(V):\int_{V}(|\nabla u|^{2}+hu^{2})\,d\mu<\infty\bigg\}. \end{align*} $$
For more results about differential equations on graphs, we refer readers to [Reference Ge3, Reference Hua and Keller7, Reference Lin, Ngai and Yau9, Reference Lin and Wu10], for example.
In this paper, we give a different division of graph
![]() $G =(V,E)$
from that in [Reference Lin and Yang11]. We divide the locally finite graph
$G =(V,E)$
from that in [Reference Lin and Yang11]. We divide the locally finite graph
![]() $G =(V,E)$
into a sequence of finite subgraphs
$G =(V,E)$
into a sequence of finite subgraphs
 $$ \begin{align*} G_{k} =(V_{k},E_{k})\quad \mathrm{ where}~k=1,2,3,\ldots,~\mathrm{ and}~ V=\bigcup^{\infty}_{k=1}(V_{k}\cup \partial V_{k}) \end{align*} $$
$$ \begin{align*} G_{k} =(V_{k},E_{k})\quad \mathrm{ where}~k=1,2,3,\ldots,~\mathrm{ and}~ V=\bigcup^{\infty}_{k=1}(V_{k}\cup \partial V_{k}) \end{align*} $$
(please see (2-3) for details), while in [Reference Lin and Yang11], the graph
![]() $G $
is divided into a sequence of balls centred at a fixed point O in V. We investigate several equations on each subgraph, and obtain a sequence of local solutions to each equation. At last, we derive the global existence of nontrivial solutions to each equation on graph G through the convergence of these local solutions. We extend the local existence results of [Reference Grigor’yan, Lin and Yang4, Problems 1 and 2] to global existence results on locally finite graphs, and also extend the results for
$G $
is divided into a sequence of balls centred at a fixed point O in V. We investigate several equations on each subgraph, and obtain a sequence of local solutions to each equation. At last, we derive the global existence of nontrivial solutions to each equation on graph G through the convergence of these local solutions. We extend the local existence results of [Reference Grigor’yan, Lin and Yang4, Problems 1 and 2] to global existence results on locally finite graphs, and also extend the results for
![]() $W^{1,2}(V)$
in [Reference Lin and Yang11] to space
$W^{1,2}(V)$
in [Reference Lin and Yang11] to space
![]() $W^{m,p}(V)$
, where
$W^{m,p}(V)$
, where
![]() $p\geq2$
,
$p\geq2$
,
![]() $p\in \mathbb{R}$
,
$p\in \mathbb{R}$
,
![]() $m\geq 1$
and
$m\geq 1$
and
![]() $m$
is an integer.
$m$
is an integer.
This paper is organized as follows. In Section 2, we give some preliminary results on graphs and state our main results. In Section 3, we prove our main results.
2 Preliminaries and main results
Let
![]() $G = (V, E)$
denote a graph where V is the vertex set and E is the edge set. Let
$G = (V, E)$
denote a graph where V is the vertex set and E is the edge set. Let
![]() $x\sim y$
represent that vertex x is adjacent to vertex y, and
$x\sim y$
represent that vertex x is adjacent to vertex y, and
![]() $(x,y)$
denote an edge in E connecting vertices x and y. Assume that
$(x,y)$
denote an edge in E connecting vertices x and y. Assume that
![]() $\chi _{xy}=\chi _{yx}>0$
, where
$\chi _{xy}=\chi _{yx}>0$
, where
![]() $\chi _{xy}$
is the edge weight. A graph G is called connected if for any vertices
$\chi _{xy}$
is the edge weight. A graph G is called connected if for any vertices
![]() $x,y\in V$
, there exists a sequence
$x,y\in V$
, there exists a sequence
![]() $\{x_{i}\}_{i=0}^{n}$
that satisfies
$\{x_{i}\}_{i=0}^{n}$
that satisfies
The degree of vertex x, denoted by
![]() $\vartheta (x)$
, is the number of edges connected to x. If for every vertex x of V the number of edges connected to x is finite, we say that G is a locally finite graph. The finite measure
$\vartheta (x)$
, is the number of edges connected to x. If for every vertex x of V the number of edges connected to x is finite, we say that G is a locally finite graph. The finite measure
![]() $\vartheta (x)=\sum _{y\sim x}\chi _{xy}$
.
$\vartheta (x)=\sum _{y\sim x}\chi _{xy}$
.
In this paper, let
![]() $G=(V,E)$
denote a connected graph. Thus, graph
$G=(V,E)$
denote a connected graph. Thus, graph
![]() $G = (V,E)$
has no isolated vertices.
$G = (V,E)$
has no isolated vertices.
From [Reference Grigor’yan, Lin and Yang4], for any function
![]() $u:V\rightarrow \mathbb {R}$
, the
$u:V\rightarrow \mathbb {R}$
, the
![]() $\vartheta (x)$
-Laplacian of u is defined as
$\vartheta (x)$
-Laplacian of u is defined as
 $$ \begin{align*} \Delta u(x)=\frac{1}{\vartheta(x)}\sum_{y\sim x}\chi_{xy}\big{(}u(y)-u(x)\big{)}. \end{align*} $$
$$ \begin{align*} \Delta u(x)=\frac{1}{\vartheta(x)}\sum_{y\sim x}\chi_{xy}\big{(}u(y)-u(x)\big{)}. \end{align*} $$
The associated gradient form is written as
 $$ \begin{align*} \Gamma(u,v)(x)&=\frac{1}{2}{\{}\Delta{(}u(x)v(x){)}-u(x)\Delta v(x)-v(x)\Delta u(x){\}} \\ &=\frac{1}{2\vartheta(x)}\sum_{y\sim x} \chi_{xy}{(}u(y)-u(x){)}{(}v(y)-v(x){)}. \end{align*} $$
$$ \begin{align*} \Gamma(u,v)(x)&=\frac{1}{2}{\{}\Delta{(}u(x)v(x){)}-u(x)\Delta v(x)-v(x)\Delta u(x){\}} \\ &=\frac{1}{2\vartheta(x)}\sum_{y\sim x} \chi_{xy}{(}u(y)-u(x){)}{(}v(y)-v(x){)}. \end{align*} $$
The length of the gradient for u is denoted by
 $$ \begin{align*} |\nabla u|(x)=\!\sqrt{\Gamma(u,u)(x)}=\bigg{(}\frac{1}{2\vartheta(x)}\sum_{y\sim x} \chi_{xy}{(}u(y)-u(x){)}^{2}\bigg{)}^{1/2}. \end{align*} $$
$$ \begin{align*} |\nabla u|(x)=\!\sqrt{\Gamma(u,u)(x)}=\bigg{(}\frac{1}{2\vartheta(x)}\sum_{y\sim x} \chi_{xy}{(}u(y)-u(x){)}^{2}\bigg{)}^{1/2}. \end{align*} $$
The length of the m-order gradient of u is written as
 $$ \begin{align*} |\nabla^{m} u|(x)= \begin{cases} |\nabla \Delta^{({m-1})/{2}} u| &\mathrm{{when }}\ m\ \mathrm{{ is\ odd}},\\ |\Delta^{{m}/{2}} u| &\mathrm{{when }} \ m\ \mathrm{{ is\ even}},\\ \end{cases} \end{align*} $$
$$ \begin{align*} |\nabla^{m} u|(x)= \begin{cases} |\nabla \Delta^{({m-1})/{2}} u| &\mathrm{{when }}\ m\ \mathrm{{ is\ odd}},\\ |\Delta^{{m}/{2}} u| &\mathrm{{when }} \ m\ \mathrm{{ is\ even}},\\ \end{cases} \end{align*} $$
where
![]() $|\Delta ^{{m}/{2}} u|$
is the usual absolute value of the function
$|\Delta ^{{m}/{2}} u|$
is the usual absolute value of the function
![]() $\Delta ^{{m}/{2}} u$
. To compare with the Euclidean setting, the integral of a function
$\Delta ^{{m}/{2}} u$
. To compare with the Euclidean setting, the integral of a function
![]() $u: V\rightarrow \mathbb {R}$
is defined as
$u: V\rightarrow \mathbb {R}$
is defined as
 $$ \begin{align*} \int_{V}u\,d\vartheta=\sum_{x\in V}\vartheta(x)u(x). \end{align*} $$
$$ \begin{align*} \int_{V}u\,d\vartheta=\sum_{x\in V}\vartheta(x)u(x). \end{align*} $$
Let
![]() $\mathcal {L}_{m,p}u$
be defined in the distributional sense: for any function
$\mathcal {L}_{m,p}u$
be defined in the distributional sense: for any function
![]() $\phi $
, there holds
$\phi $
, there holds
 $$ \begin{align*} \int_{V}(\mathcal{L}_{m,p}u)\phi \,d\vartheta= \begin{cases} \int_{V}|\nabla^{m}u|^{p-2} \Gamma(\Delta^{({m-1})/{2}}u, \Delta^{({m-1})/{2}}\phi)\,d\vartheta &\mathrm{when } \ m \ \mathrm{ is} \ \mathrm{ odd},\\ \int_{V}|\nabla^{m}u|^{p-2} \Delta^{{m}/{2}}u\Delta^{{m}/{2}}\phi \,d\vartheta &\mathrm{when } \ m \ \mathrm{ is} \ \mathrm{ even}.\notag \end{cases} \end{align*} $$
$$ \begin{align*} \int_{V}(\mathcal{L}_{m,p}u)\phi \,d\vartheta= \begin{cases} \int_{V}|\nabla^{m}u|^{p-2} \Gamma(\Delta^{({m-1})/{2}}u, \Delta^{({m-1})/{2}}\phi)\,d\vartheta &\mathrm{when } \ m \ \mathrm{ is} \ \mathrm{ odd},\\ \int_{V}|\nabla^{m}u|^{p-2} \Delta^{{m}/{2}}u\Delta^{{m}/{2}}\phi \,d\vartheta &\mathrm{when } \ m \ \mathrm{ is} \ \mathrm{ even}.\notag \end{cases} \end{align*} $$
In particular, the poly-Laplacian
![]() $(-\Delta )^{m}u$
can be defined as
$(-\Delta )^{m}u$
can be defined as
The p-Laplacian of
![]() $u:V\rightarrow \mathbb {R}$
, namely
$u:V\rightarrow \mathbb {R}$
, namely
![]() $\Delta _{p}u$
, is defined in the distributional sense as
$\Delta _{p}u$
, is defined in the distributional sense as
 $$ \begin{align} \Delta_{p} u(x)=\frac{1}{2\vartheta(x)}\sum_{y\sim x}\chi_{xy}\big{(}|\nabla u|^{p-2}(y)+|\nabla u|^{p-2}(x)\big{)}\big{(}u(y)-u(x)\big{)}. \end{align} $$
$$ \begin{align} \Delta_{p} u(x)=\frac{1}{2\vartheta(x)}\sum_{y\sim x}\chi_{xy}\big{(}|\nabla u|^{p-2}(y)+|\nabla u|^{p-2}(x)\big{)}\big{(}u(y)-u(x)\big{)}. \end{align} $$
Let
![]() $G = (V, E)$
denote a locally finite graph and
$G = (V, E)$
denote a locally finite graph and
![]() $\Omega \subset V$
. For any integer
$\Omega \subset V$
. For any integer
![]() $m\geq 1$
and any
$m\geq 1$
and any
![]() $p>1$
,
$p>1$
,
![]() $W^{m,p}(\Omega )$
is defined as a space of all functions
$W^{m,p}(\Omega )$
is defined as a space of all functions
![]() $u: \Omega \rightarrow \mathbb {R}$
with the norm
$u: \Omega \rightarrow \mathbb {R}$
with the norm
 $$ \begin{align*} \|u\|_{W^{m,p}(\Omega)}=\bigg(\sum^{m}_{k=0}\int_{\Omega}|\nabla^{k}u|^{p}\,d\vartheta\bigg)^{{1}/{p}}<+\infty. \end{align*} $$
$$ \begin{align*} \|u\|_{W^{m,p}(\Omega)}=\bigg(\sum^{m}_{k=0}\int_{\Omega}|\nabla^{k}u|^{p}\,d\vartheta\bigg)^{{1}/{p}}<+\infty. \end{align*} $$
Denote
![]() $C^{m}_{0}(\Omega )$
as a set of all functions
$C^{m}_{0}(\Omega )$
as a set of all functions
![]() $u:\Omega \rightarrow \mathbb {R}$
with
$u:\Omega \rightarrow \mathbb {R}$
with
![]() $u=|\nabla u|=\cdots =|\nabla ^{m-1}u|=0$
on
$u=|\nabla u|=\cdots =|\nabla ^{m-1}u|=0$
on
![]() $\partial \Omega $
. Here,
$\partial \Omega $
. Here,
![]() $W^{m,p}_{0} (\Omega )$
is denoted as the completion of
$W^{m,p}_{0} (\Omega )$
is denoted as the completion of
![]() $C^{m}_{0}(\Omega )$
with the norm
$C^{m}_{0}(\Omega )$
with the norm
 $$ \begin{align*} \|u\|_{W_{0}^{m,p}(\Omega)}=\bigg(\int_{\Omega}|\nabla^{m} u|^{p}\,d\vartheta\bigg)^{{1}/{p}}. \end{align*} $$
$$ \begin{align*} \|u\|_{W_{0}^{m,p}(\Omega)}=\bigg(\int_{\Omega}|\nabla^{m} u|^{p}\,d\vartheta\bigg)^{{1}/{p}}. \end{align*} $$
Moreover, for any
![]() $s>0$
,
$s>0$
,
![]() $L^{s}(\Omega )$
denotes a linear space with the norm
$L^{s}(\Omega )$
denotes a linear space with the norm
 $$ \begin{align*} \|u\|_{L^{s}(\Omega)}=\bigg(\int_{\Omega}|u|^{s}\,d\vartheta\bigg)^{1/s}. \end{align*} $$
$$ \begin{align*} \|u\|_{L^{s}(\Omega)}=\bigg(\int_{\Omega}|u|^{s}\,d\vartheta\bigg)^{1/s}. \end{align*} $$
Additionally,
![]() $L^{\infty }(\Omega )$
means
$L^{\infty }(\Omega )$
means
Obviously,
![]() $W_{0}^{m,p}(\Omega )$
and
$W_{0}^{m,p}(\Omega )$
and
![]() $L^{s}(\Omega )$
are two Banach spaces, and we have the following famous Sobolev embedding theorem derived by Grigor’yan, Lin and Yang.
$L^{s}(\Omega )$
are two Banach spaces, and we have the following famous Sobolev embedding theorem derived by Grigor’yan, Lin and Yang.
Theorem A [Reference Grigor’yan, Lin and Yang4, Theorem 7].
Let
![]() $G =(V,E)$
be a locally finite graph and
$G =(V,E)$
be a locally finite graph and
![]() $\Omega $
be a bounded domain of V with
$\Omega $
be a bounded domain of V with
![]() $\Omega ^{0}\neq \emptyset $
. Let m be any positive integer and
$\Omega ^{0}\neq \emptyset $
. Let m be any positive integer and
![]() $p> 1$
. Then,
$p> 1$
. Then,
![]() $W_{0}^{m,p}(\Omega )$
is embedded in
$W_{0}^{m,p}(\Omega )$
is embedded in
![]() $ L^{q}(\Omega )$
for all
$ L^{q}(\Omega )$
for all
![]() $1\leq q \leq +\infty $
, that is, there exists a constant
$1\leq q \leq +\infty $
, that is, there exists a constant
![]() $C_{0}$
depending only on p, m and
$C_{0}$
depending only on p, m and
![]() $\Omega $
such that for all
$\Omega $
such that for all
![]() $u\in W_{0}^{m,p}(\Omega )$
,
$u\in W_{0}^{m,p}(\Omega )$
,
 $$ \begin{align*}\bigg(\int_{\Omega}|u|^{q}\,d\vartheta\bigg)^{1/q}\leq C_{0}\bigg(\int_{\Omega}|\nabla^{m} u|^{p}\,d\vartheta\bigg)^{1/p}.\end{align*} $$
$$ \begin{align*}\bigg(\int_{\Omega}|u|^{q}\,d\vartheta\bigg)^{1/q}\leq C_{0}\bigg(\int_{\Omega}|\nabla^{m} u|^{p}\,d\vartheta\bigg)^{1/p}.\end{align*} $$
In particular, denoting
![]() $\vartheta _{0}=\min _{x\in \Omega }\vartheta (x)$
, there holds
$\vartheta _{0}=\min _{x\in \Omega }\vartheta (x)$
, there holds
Moreover,
![]() $W_{0}^{m,p}(\Omega )$
is pre-compact, namely, if
$W_{0}^{m,p}(\Omega )$
is pre-compact, namely, if
![]() $\{u_{k}\}$
is bounded in
$\{u_{k}\}$
is bounded in
![]() $W_{0}^{m,p}(\Omega )$
, then up to a subsequence, still denoted by
$W_{0}^{m,p}(\Omega )$
, then up to a subsequence, still denoted by
![]() $\{u_{k}\}$
, there exists some
$\{u_{k}\}$
, there exists some
![]() $u\in W_{0}^{m,p}(\Omega )$
such that
$u\in W_{0}^{m,p}(\Omega )$
such that
![]() $u_{k}\rightarrow u$
in
$u_{k}\rightarrow u$
in
![]() $ W_{0}^{m,p}(\Omega )$
.
$ W_{0}^{m,p}(\Omega )$
.
Now, we state our main results.
First, we define a sequence of subgraphs of
![]() $G=(V,E)$
denoted by
$G=(V,E)$
denoted by
where
![]() $k=1,2,3,\ldots\, $
,
$k=1,2,3,\ldots\, $
,
![]() $V_{k}$
is a finite vertex set,
$V_{k}$
is a finite vertex set,
![]() $E_{k}$
is a finite edge set,
$E_{k}$
is a finite edge set,
![]() $ V_{k}\subset V $
and
$ V_{k}\subset V $
and
![]() $E_{k}\subset E$
, such that
$E_{k}\subset E$
, such that
 $$ \begin{align*} V_{i}\cap V_{j}=\emptyset\quad \mathrm{ when}\ i\neq j~\mathrm{ and}~ V=\bigcup^{\infty}_{i=1}(V_{i}\cup \partial V_{i}). \end{align*} $$
$$ \begin{align*} V_{i}\cap V_{j}=\emptyset\quad \mathrm{ when}\ i\neq j~\mathrm{ and}~ V=\bigcup^{\infty}_{i=1}(V_{i}\cup \partial V_{i}). \end{align*} $$
For any finite set
![]() $\Re \subset V$
,
$\Re \subset V$
,
![]() $W^{m,p}(\Re )$
is a Sobolev space including all functions
$W^{m,p}(\Re )$
is a Sobolev space including all functions
![]() $u:\Re \rightarrow ~\mathbb {R}$
with the norm
$u:\Re \rightarrow ~\mathbb {R}$
with the norm
 $$ \begin{align*} \|u\|_{W^{m,p}(\Re)}=\bigg{(}\int_{\Re}(|\nabla^{m} u|^{p}+|u|^{p})\,d\vartheta\bigg{)}^{{1}/{p}}. \end{align*} $$
$$ \begin{align*} \|u\|_{W^{m,p}(\Re)}=\bigg{(}\int_{\Re}(|\nabla^{m} u|^{p}+|u|^{p})\,d\vartheta\bigg{)}^{{1}/{p}}. \end{align*} $$
For any
![]() $q>0$
,
$q>0$
,
![]() $p>1$
and integer
$p>1$
and integer
![]() $m\geq 1$
, we have the below Sobolev embedding theorem involving the two spaces
$m\geq 1$
, we have the below Sobolev embedding theorem involving the two spaces
![]() $W^{m,p}(\Re )$
and
$W^{m,p}(\Re )$
and
![]() $L^{q}(\Re )$
.
$L^{q}(\Re )$
.
Theorem 1. Let
![]() $G = (V,E)$
be a connected and locally finite graph. Suppose that the measure
$G = (V,E)$
be a connected and locally finite graph. Suppose that the measure
![]() $\vartheta (x)\geq \vartheta _{0}>0$
for all
$\vartheta (x)\geq \vartheta _{0}>0$
for all
![]() $x\in V$
, where
$x\in V$
, where
![]() $\vartheta _{0}$
is a constant. Let
$\vartheta _{0}$
is a constant. Let
![]() $m\geq 1$
be any integer,
$m\geq 1$
be any integer,
![]() $p>1$
and
$p>1$
and
![]() $q>0$
. Then, for any finite set
$q>0$
. Then, for any finite set
![]() $\Re \subset V$
,
$\Re \subset V$
,
where
In particular,
Moreover, by [Reference Grigor’yan, Lin and Yang4, Theorem 8],
![]() $W^{m,p}(\Re )$
is pre-compact, namely, if
$W^{m,p}(\Re )$
is pre-compact, namely, if
![]() $\{u_{k}\}$
is bounded in
$\{u_{k}\}$
is bounded in
![]() $W^{m,p}(\Re )$
, then up to a subsequence, still denoted by
$W^{m,p}(\Re )$
, then up to a subsequence, still denoted by
![]() $\{u_{k}\}$
, there exists some
$\{u_{k}\}$
, there exists some
![]() ${u\in W^{m,p}(\Re )}$
such that
${u\in W^{m,p}(\Re )}$
such that
![]() $u_{k}\rightarrow u$
in
$u_{k}\rightarrow u$
in
![]() $W^{m,p}(\Re )$
.
$W^{m,p}(\Re )$
.
Remark 2. Let
![]() $\mathbb {D}_{k}=W^{m,2}_{0}(V_{k})\cap W^{n,2}_{0}(V_{k})$
be the space with the norm
$\mathbb {D}_{k}=W^{m,2}_{0}(V_{k})\cap W^{n,2}_{0}(V_{k})$
be the space with the norm
Take a sequence of functions
![]() $(\hat {u}_{j})\in \mathbb {D}_{k}$
. If there exist
$(\hat {u}_{j})\in \mathbb {D}_{k}$
. If there exist
such that
we can easily get that
and thus
![]() $\hat {u}_{j}\rightarrow u_{k}$
in
$\hat {u}_{j}\rightarrow u_{k}$
in
![]() $\mathbb {D}_{k}$
as
$\mathbb {D}_{k}$
as
![]() $j\rightarrow \infty $
. In addition, if we use
$j\rightarrow \infty $
. In addition, if we use
![]() $\Re $
instead of
$\Re $
instead of
![]() $V_{k}$
and set
$V_{k}$
and set
![]() ${\mathbb {D}_{k}=W^{m,2}(\Re )\cap W^{n,2}(\Re )}$
, we can get a similar result.
${\mathbb {D}_{k}=W^{m,2}(\Re )\cap W^{n,2}(\Re )}$
, we can get a similar result.
Now, we obtain the following global existence result for a class of semi-linear elliptic equations involving the p-Laplacian, which can be used in wavelets and dimension reductions for high-dimensional data because p is a tunable parameter.
Theorem 3. Let
![]() $G = (V,E)$
be a connected and locally finite graph. Suppose that
$G = (V,E)$
be a connected and locally finite graph. Suppose that
![]() $\vartheta (x)\geq \vartheta _{0}>0$
for all
$\vartheta (x)\geq \vartheta _{0}>0$
for all
![]() $x\in V$
, where
$x\in V$
, where
![]() $\vartheta _{0}$
is a positive constant. Assume
$\vartheta _{0}$
is a positive constant. Assume
![]() $K(x)\in L^{{s}/({s-1})}(V)$
, where
$K(x)\in L^{{s}/({s-1})}(V)$
, where
![]() $s>1$
. The function
$s>1$
. The function
![]() $f(x,u)\in C(V\times \mathbb {R},\mathbb {R})$
satisfies
$f(x,u)\in C(V\times \mathbb {R},\mathbb {R})$
satisfies
and
where
![]() $a(x)\in L^{{s}/({s-1})}(V), b>0$
and
$a(x)\in L^{{s}/({s-1})}(V), b>0$
and
![]() $s>1$
. Then, for any
$s>1$
. Then, for any
![]() $p>2$
, there exists a nontrivial solution to the following problem:
$p>2$
, there exists a nontrivial solution to the following problem:
Moreover, if
there exists a positive solution to (2-6).
Now, we extend the global existence result for p-Laplacian to Laplacian systems. The next result is about a poly-Laplacian system on a locally finite graph G.
Theorem 4. Let
![]() $G = (V,E)$
be a connected and locally finite graph. Suppose that
$G = (V,E)$
be a connected and locally finite graph. Suppose that
![]() $\vartheta (x)\geq \vartheta _{0}>0$
for all
$\vartheta (x)\geq \vartheta _{0}>0$
for all
![]() $x\in V$
, where
$x\in V$
, where
![]() $\vartheta _{0}$
is a positive constant. For
$\vartheta _{0}$
is a positive constant. For
![]() $i=1,2$
, assume that
$i=1,2$
, assume that
Then for any integers
![]() $m,n>1$
, there exists a solution to the following problem:
$m,n>1$
, there exists a solution to the following problem:
 $$ \begin{align} (-\Delta)^{m} u+ (-\Delta)^{n}u= -\lambda_{1} \frac{\varphi_{1}(x)e^{-u}}{\int_{V}\varphi_{1}(x)e^{-u}\,d\vartheta} +\lambda_{2} \frac{\varphi_{2}(x)e^{u}}{\int_{V}\varphi_{2}(x)e^{u}\,d\vartheta}\end{align} $$
$$ \begin{align} (-\Delta)^{m} u+ (-\Delta)^{n}u= -\lambda_{1} \frac{\varphi_{1}(x)e^{-u}}{\int_{V}\varphi_{1}(x)e^{-u}\,d\vartheta} +\lambda_{2} \frac{\varphi_{2}(x)e^{u}}{\int_{V}\varphi_{2}(x)e^{u}\,d\vartheta}\end{align} $$
in V. Moreover, if
 $$ \begin{align*} \lambda_{1} \frac{\varphi_{1}(x)}{\int_{V}\varphi_{1}(x)\,d\vartheta} -\lambda_{2} \frac{\varphi_{2}(x)}{\int_{V}\varphi_{2}(x)\,d\vartheta} \not\equiv 0\quad\text{for all } x\in V, \end{align*} $$
$$ \begin{align*} \lambda_{1} \frac{\varphi_{1}(x)}{\int_{V}\varphi_{1}(x)\,d\vartheta} -\lambda_{2} \frac{\varphi_{2}(x)}{\int_{V}\varphi_{2}(x)\,d\vartheta} \not\equiv 0\quad\text{for all } x\in V, \end{align*} $$
there exists a nontrivial solution to problem (2-8).
Now, we consider another division of graph
![]() $G=(V,E)$
. By [Reference Lin and Yang11], for any fixed
$G=(V,E)$
. By [Reference Lin and Yang11], for any fixed
![]() ${O\in V}$
, the distance between x and O, denoted by
${O\in V}$
, the distance between x and O, denoted by
![]() $\rho (x)=\rho (x,O)$
, is the minimum number of edges connecting them. Thus, for any integer
$\rho (x)=\rho (x,O)$
, is the minimum number of edges connecting them. Thus, for any integer
![]() $k\geq 1$
, we define a ball centred at O with radius k by
$k\geq 1$
, we define a ball centred at O with radius k by
The boundary of
![]() $B_{k}$
can be defined as
$B_{k}$
can be defined as
Remark 5. Set
![]() $\mathbb {X}_{k}=W^{m,p}_{0}(B_{k})\times W^{n,q}_{0}(B_{k})$
and define the norm on
$\mathbb {X}_{k}=W^{m,p}_{0}(B_{k})\times W^{n,q}_{0}(B_{k})$
and define the norm on
![]() $\mathbb {X}_{k}$
as
$\mathbb {X}_{k}$
as
Take a sequence of functions
![]() $(\hat {u}_{j}, \hat {v}_{j})\in \mathbb {X}_{k}$
. If there exist
$(\hat {u}_{j}, \hat {v}_{j})\in \mathbb {X}_{k}$
. If there exist
such that
we can easily get that
Thus,
In addition, if we use
![]() $\Re $
instead of
$\Re $
instead of
![]() $B_{k}$
and set
$B_{k}$
and set
![]() $\mathbb {X}_{k}=W^{m,p}(\Re )\times W^{n,q}(\Re )$
, we can get a similar result.
$\mathbb {X}_{k}=W^{m,p}(\Re )\times W^{n,q}(\Re )$
, we can get a similar result.
Next, we study the system (2-10), where each equation can be viewed as one type of Kazdan–Warner equation when
![]() $u=v$
. The Kazdan–Warner equation has very important applications in geometry. By the division of graph G, we can obtain a global solution to the system on graph G.
$u=v$
. The Kazdan–Warner equation has very important applications in geometry. By the division of graph G, we can obtain a global solution to the system on graph G.
Theorem 6. Let
![]() $G = (V,E)$
be a connected and locally finite graph. Suppose that
$G = (V,E)$
be a connected and locally finite graph. Suppose that
![]() $\vartheta (x)\geq \vartheta _{0}>0$
for all
$\vartheta (x)\geq \vartheta _{0}>0$
for all
![]() $x\in V$
, where
$x\in V$
, where
![]() $\vartheta _{0}$
is a positive constant. Assume that
$\vartheta _{0}$
is a positive constant. Assume that
and
Then, for any integer
![]() $m,n\geq 2$
and
$m,n\geq 2$
and
![]() $p,q>2$
, there exists a nontrivial solution to the following problem:
$p,q>2$
, there exists a nontrivial solution to the following problem:
 $$ \begin{align} \begin{cases} \mathcal{L}_{m,p} u= K(x)e^{-u-v}-\kappa(x)&\mathrm{ in}~V,\\ \mathcal{L}_{n,q} v=\kappa(x)e^{-u-v}-K(x)&\mathrm{ in}~V. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \mathcal{L}_{m,p} u= K(x)e^{-u-v}-\kappa(x)&\mathrm{ in}~V,\\ \mathcal{L}_{n,q} v=\kappa(x)e^{-u-v}-K(x)&\mathrm{ in}~V. \end{cases} \end{align} $$
3 Proof of main results
First, we prove the Sobolev embedding theorem in Theorem 1. For the proof in the case of
![]() $W^{1,2}_{0}(V)$
and
$W^{1,2}_{0}(V)$
and
![]() $L^{p}(V)$
, where
$L^{p}(V)$
, where
![]() $p>0$
.
$p>0$
.
Proof of Theorem 1.
Since for all
![]() $x\in \Re $
,
$x\in \Re $
,
 $$ \begin{align*} \|u(x)\|^{p}_{W^{m,p}(\Re)}&=\int_{\Re}{(}|\nabla^{m} u(x)|^{p}+|u(x)|^{p}{)}\,d\vartheta \\ &\geq \sum_{x\in \Re} \vartheta(x)|u(x)|^{p}\\ &\geq \sum_{x\in \Re} \vartheta_{0}|u(x)|^{p}, \end{align*} $$
$$ \begin{align*} \|u(x)\|^{p}_{W^{m,p}(\Re)}&=\int_{\Re}{(}|\nabla^{m} u(x)|^{p}+|u(x)|^{p}{)}\,d\vartheta \\ &\geq \sum_{x\in \Re} \vartheta(x)|u(x)|^{p}\\ &\geq \sum_{x\in \Re} \vartheta_{0}|u(x)|^{p}, \end{align*} $$
we get
It is easy to see that (3-1) implies
For all
![]() $1\leq q <+\infty $
, by (3-2),
$1\leq q <+\infty $
, by (3-2),
 $$ \begin{align*} \|u(x)\|_{L^{q}(\Re)}&= \bigg{(}\sum_{x\in \Re}\vartheta(x)|u(x)|^{q}\bigg{)}^{{1}/{q}}\\&\leq \vartheta_{0}^{-{1}/{p}}(\operatorname{vol}(\Re))^{{1}/{q}} \|u(x)\|_{W^{m,p}(\Re)}, \end{align*} $$
$$ \begin{align*} \|u(x)\|_{L^{q}(\Re)}&= \bigg{(}\sum_{x\in \Re}\vartheta(x)|u(x)|^{q}\bigg{)}^{{1}/{q}}\\&\leq \vartheta_{0}^{-{1}/{p}}(\operatorname{vol}(\Re))^{{1}/{q}} \|u(x)\|_{W^{m,p}(\Re)}, \end{align*} $$
where
![]() $\mathrm{vol}(\Re)=\sum _{x\in \Re }\vartheta (x)$
.
$\mathrm{vol}(\Re)=\sum _{x\in \Re }\vartheta (x)$
.
Thus, we complete this proof.
Now, we prove the existence results. The method can be viewed as a variational method from local existence to global existence.
Proof of Theorem 3.
Let
![]() $G_{k}=(V_{k},E_{k})$
be a subgraph defined as in (2-3). Define the functional
$G_{k}=(V_{k},E_{k})$
be a subgraph defined as in (2-3). Define the functional
![]() $J_{k(K)}:W^{1,p}_{0}(V_{k})\rightarrow \mathbb {R}$
by
$J_{k(K)}:W^{1,p}_{0}(V_{k})\rightarrow \mathbb {R}$
by
 $$ \begin{align} J_{k(K)}(u)=\frac{1}{p}\int_{V_{k}}|\nabla u|^{p}\,d\vartheta-\int_{V_{k}}K(x)u\,d\vartheta+\int_{V_{k}}F(x,u)\,d\vartheta, \end{align} $$
$$ \begin{align} J_{k(K)}(u)=\frac{1}{p}\int_{V_{k}}|\nabla u|^{p}\,d\vartheta-\int_{V_{k}}K(x)u\,d\vartheta+\int_{V_{k}}F(x,u)\,d\vartheta, \end{align} $$
where
 $$ \begin{align*} F(x,u)=\int^{u}_{0}f(x,t)\,dt\quad \mathrm{ and}\quad F(x,0)=0. \end{align*} $$
$$ \begin{align*} F(x,u)=\int^{u}_{0}f(x,t)\,dt\quad \mathrm{ and}\quad F(x,0)=0. \end{align*} $$
From (2-5),
It is easy to see that
Set
Obviously,
To proceed, the proof is divided into three steps.
Step 1. For any integer
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $J_{k(K)}(u)$
is bounded from below in
$J_{k(K)}(u)$
is bounded from below in
![]() $ W^{1,p}_{0}(V_{k})$
.
$ W^{1,p}_{0}(V_{k})$
.
By the Hölder inequality, Theorem A and the Young inequality, for any
![]() $s>1$
,
$s>1$
,
 $$ \begin{align} \int_{V_{k}} Ku \,d\vartheta&\leq \|u\|_{L^{s}(V_{k})} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &\leq C_{0}\|u\|_{W^{1,p}_{0}(V_{k})} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &= \frac{1}{2}\|u\|_{W^{1,p}_{0}(V_{k})}\cdot2 C_{0} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &\leq \frac{1}{2p}\|u\|^{p}_{W^{1,p}_{0}(V_{k})}+\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}. \end{align} $$
$$ \begin{align} \int_{V_{k}} Ku \,d\vartheta&\leq \|u\|_{L^{s}(V_{k})} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &\leq C_{0}\|u\|_{W^{1,p}_{0}(V_{k})} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &= \frac{1}{2}\|u\|_{W^{1,p}_{0}(V_{k})}\cdot2 C_{0} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &\leq \frac{1}{2p}\|u\|^{p}_{W^{1,p}_{0}(V_{k})}+\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}. \end{align} $$
 $$ \begin{align} J_{k(K)}(u)&\geq \frac{1}{2p}\|u\|^{p}_{W^{1,p}_{0}(V_{k})}-\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)} \end{align} $$
$$ \begin{align} J_{k(K)}(u)&\geq \frac{1}{2p}\|u\|^{p}_{W^{1,p}_{0}(V_{k})}-\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)} \end{align} $$
 $$ \begin{align} &\geq -\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}.\ \qquad \end{align} $$
$$ \begin{align} &\geq -\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}.\ \qquad \end{align} $$
Therefore, we have that
![]() $J_{k(K)}(u)$
is bounded from below in
$J_{k(K)}(u)$
is bounded from below in
![]() $ W^{1,p}_{0}(V_{k})$
.
$ W^{1,p}_{0}(V_{k})$
.
Step 2. For any integer
![]() $k\geq 1$
, there exists a function
$k\geq 1$
, there exists a function
![]() $u_{k}\in W^{1,p}_{0}(V_{k})$
such that
$u_{k}\in W^{1,p}_{0}(V_{k})$
such that
Moreover,
![]() $u_{k}$
satisfies the Euler–Lagrange equation
$u_{k}$
satisfies the Euler–Lagrange equation
 $$ \begin{align} \left \{ \begin{array}{@{}lcr} -\Delta_{p} u_{k}=K(x)-f(x,u_{k}) & \mathrm{in}~ V_{k},\\u_{k}=0 & \kern6pt\mathrm{on}~\partial V_{k}. \end{array} \right. \end{align} $$
$$ \begin{align} \left \{ \begin{array}{@{}lcr} -\Delta_{p} u_{k}=K(x)-f(x,u_{k}) & \mathrm{in}~ V_{k},\\u_{k}=0 & \kern6pt\mathrm{on}~\partial V_{k}. \end{array} \right. \end{align} $$
Obviously, by (3-5) and (3-8),
 $$ \begin{align} -\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}\leq\Theta_{k}\leq 0. \end{align} $$
$$ \begin{align} -\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}\leq\Theta_{k}\leq 0. \end{align} $$
By (3-10), we get that
![]() $\Theta _{k}$
is a bounded sequence of numbers.
$\Theta _{k}$
is a bounded sequence of numbers.
Now fix a positive integer k. We take a sequence of functions
![]() $(\hat {u}_{j})\in W^{1,p}_{0}(V_{k})$
such that
$(\hat {u}_{j})\in W^{1,p}_{0}(V_{k})$
such that
Thus, by (3-7),
where M is a positive constant. Therefore, we get that
![]() $\{\hat {u}_{j}\}$
is bounded in
$\{\hat {u}_{j}\}$
is bounded in
![]() $W^{1,p}_{0}(V_{k})$
. By Theorem A, we have that up to a subsequence,
$W^{1,p}_{0}(V_{k})$
. By Theorem A, we have that up to a subsequence,
![]() $\hat {u}_{j}$
converges to some function
$\hat {u}_{j}$
converges to some function
![]() $u_{k}\in W^{1,p}_{0}(V_{k})$
. Clearly,
$u_{k}\in W^{1,p}_{0}(V_{k})$
. Clearly,
Thus,
![]() $u_{k}$
satisfies the Euler–Lagrange equation (3-9).
$u_{k}$
satisfies the Euler–Lagrange equation (3-9).
Step 3. There exist
![]() $\tilde {u}:V\rightarrow \mathbb {R}$
and a subsequence of
$\tilde {u}:V\rightarrow \mathbb {R}$
and a subsequence of
![]() $\{u_{k}\}$
, still denoted by
$\{u_{k}\}$
, still denoted by
![]() $\{u_{k}\}$
, such that
$\{u_{k}\}$
, such that
![]() $\{u_{k}\}$
converges to
$\{u_{k}\}$
converges to
![]() $\tilde {u}$
uniformly in V, that is,
$\tilde {u}$
uniformly in V, that is,
![]() $\tilde {u}$
is a solution to (2-6). Moreover,
$\tilde {u}$
is a solution to (2-6). Moreover,
![]() $\tilde {u}>0$
for all
$\tilde {u}>0$
for all
![]() $x\in V$
.
$x\in V$
.
where
![]() $M_{1}$
is a positive constant independent of k. By Theorem A and (3-11),
$M_{1}$
is a positive constant independent of k. By Theorem A and (3-11),
where
![]() $M_{2}$
is a positive constant independent of k.
$M_{2}$
is a positive constant independent of k.
It is easy to see that
![]() $\{u_{k}\}$
can be viewed as a sequence defined on V with
$\{u_{k}\}$
can be viewed as a sequence defined on V with
![]() $u_{k}=0$
on
$u_{k}=0$
on
![]() $ V\setminus V_{k}$
, that is,
$ V\setminus V_{k}$
, that is,
 $$ \begin{align} u_{k}(x)= \begin{cases} u_{k}(x)&\mathrm{for}\ x\in V_{k},\\ 0 &\mathrm{for}\ x\in V \setminus V_{k}. \end{cases} \end{align} $$
$$ \begin{align} u_{k}(x)= \begin{cases} u_{k}(x)&\mathrm{for}\ x\in V_{k},\\ 0 &\mathrm{for}\ x\in V \setminus V_{k}. \end{cases} \end{align} $$
Therefore, by (3-12) and (3-13), we get that
![]() $\{u_{k}\}$
is uniformly bounded in V. Thus, there exists a subsequence of
$\{u_{k}\}$
is uniformly bounded in V. Thus, there exists a subsequence of
![]() $\{u_{k}\}$
, still denoted by
$\{u_{k}\}$
, still denoted by
![]() $\{u_{k}\}$
, such that
$\{u_{k}\}$
, such that
![]() $\{u_{k}\}$
converges to
$\{u_{k}\}$
converges to
![]() $\tilde {u}$
uniformly in V, that is,
$\tilde {u}$
uniformly in V, that is,
For any fixed
![]() $x\in V$
, letting
$x\in V$
, letting
![]() $k\rightarrow \infty $
in (3-9),
$k\rightarrow \infty $
in (3-9),
Thus,
![]() $\tilde {u}(x)$
is a solution to (2-6). Since
$\tilde {u}(x)$
is a solution to (2-6). Since
![]() $K(x)-f(x,u)\not \equiv 0$
, we get
$K(x)-f(x,u)\not \equiv 0$
, we get
![]() $\tilde {u} \not \equiv 0$
.
$\tilde {u} \not \equiv 0$
.
Now, we prove that
![]() $\tilde {u}>0$
if (2-7) holds. We set
$\tilde {u}>0$
if (2-7) holds. We set
It is easy to see that
![]() $\tilde {u}=\tilde {u}^{+}+\tilde {u}^{-}$
. Noting that
$\tilde {u}=\tilde {u}^{+}+\tilde {u}^{-}$
. Noting that
since
![]() $K(x)-f(x,u)\geq 0$
,
$K(x)-f(x,u)\geq 0$
,
 $$ \begin{align*} \int_{V}|\nabla \tilde{u}^{-}|^{p}\,d\vartheta\leq& -\int_{V}\tilde{u}^{-}\Delta_{p}\tilde{u}\,d\vartheta =\int_{V}\tilde{u}^{-}\big{(}K(x)-f(x,\tilde{u})\big{)}\,d\vartheta\leq0. \end{align*} $$
$$ \begin{align*} \int_{V}|\nabla \tilde{u}^{-}|^{p}\,d\vartheta\leq& -\int_{V}\tilde{u}^{-}\Delta_{p}\tilde{u}\,d\vartheta =\int_{V}\tilde{u}^{-}\big{(}K(x)-f(x,\tilde{u})\big{)}\,d\vartheta\leq0. \end{align*} $$
So,
Next, we prove that
![]() $\tilde {u}>0$
for all
$\tilde {u}>0$
for all
![]() $x\in V$
. Suppose not. Then there would exist a point
$x\in V$
. Suppose not. Then there would exist a point
![]() $x^{*}\in V$
such that
$x^{*}\in V$
such that
Thus, by (2-1), we get
![]() $\Delta _{p}\tilde {u}(x^{*})>0$
. Then, by (3-14),
$\Delta _{p}\tilde {u}(x^{*})>0$
. Then, by (3-14),
which contradicts (2-7). Therefore, we have that
![]() $\tilde {u}(x)>0$
for all
$\tilde {u}(x)>0$
for all
![]() $x\in V$
, and the proof is completed.
$x\in V$
, and the proof is completed.
Proof of Theorem 4.
Let
![]() $G_{k}=(V_{k},E_{k})$
be a subgraph defined as in (2-3). By Remark 2, set
$G_{k}=(V_{k},E_{k})$
be a subgraph defined as in (2-3). By Remark 2, set
![]() $\mathbb {D}_{k}=W^{m,2}_{0}(V_{k})\cap W^{n,2}_{0}(V_{k})$
with the norm
$\mathbb {D}_{k}=W^{m,2}_{0}(V_{k})\cap W^{n,2}_{0}(V_{k})$
with the norm
Define the functional
![]() $J_{k(Q)}:\mathbb {D}_{k}\rightarrow \mathbb {R}$
by
$J_{k(Q)}:\mathbb {D}_{k}\rightarrow \mathbb {R}$
by
 $$ \begin{align} &J_{k(Q)}(u)=\frac{1}{2}\int_{V_{k}}|\nabla^{m} u|^{2}\,d\vartheta +\frac{1}{2}\int_{V_{k}}|\nabla^{n} u|^{2}\,d\vartheta \notag \\&\qquad -\lambda_{1}\log \int_{V_{k}}\varphi_{1}(x)e^{-u}\,d\vartheta-\lambda_{2}\log \int_{V_{k}}\varphi_{2}(x)e^{u}\,d\vartheta. \end{align} $$
$$ \begin{align} &J_{k(Q)}(u)=\frac{1}{2}\int_{V_{k}}|\nabla^{m} u|^{2}\,d\vartheta +\frac{1}{2}\int_{V_{k}}|\nabla^{n} u|^{2}\,d\vartheta \notag \\&\qquad -\lambda_{1}\log \int_{V_{k}}\varphi_{1}(x)e^{-u}\,d\vartheta-\lambda_{2}\log \int_{V_{k}}\varphi_{2}(x)e^{u}\,d\vartheta. \end{align} $$
Obviously,
![]() $J_{k(Q)}\in C^{1}\big {(}\mathbb {D}_{k},\mathbb {R}\big {)}$
.
$J_{k(Q)}\in C^{1}\big {(}\mathbb {D}_{k},\mathbb {R}\big {)}$
.
Since
![]() $\varphi _{1}(x)> 0$
for all
$\varphi _{1}(x)> 0$
for all
![]() $x\in V$
, there exists some
$x\in V$
, there exists some
![]() $x_{0}\in V_{k}$
such that
$x_{0}\in V_{k}$
such that
 $$ \begin{align} \vartheta_{0}\varphi_{1}(x_{0}) \leq \vartheta(x_{0})\varphi_{1}(x_{0})\leq\int_{V_{k}}\varphi_{1}(x)\,d\vartheta= \sum_{x\in V_{_{k}}} \vartheta(x)\varphi_{1}(x). \end{align} $$
$$ \begin{align} \vartheta_{0}\varphi_{1}(x_{0}) \leq \vartheta(x_{0})\varphi_{1}(x_{0})\leq\int_{V_{k}}\varphi_{1}(x)\,d\vartheta= \sum_{x\in V_{_{k}}} \vartheta(x)\varphi_{1}(x). \end{align} $$
Similarly,
 $$ \begin{align} & \vartheta_{0}\varphi_{2}(x_{0})\leq\int_{V_{k}}\varphi_{2}(x)\,d\vartheta. \end{align} $$
$$ \begin{align} & \vartheta_{0}\varphi_{2}(x_{0})\leq\int_{V_{k}}\varphi_{2}(x)\,d\vartheta. \end{align} $$
Set
![]() $\Theta _{k}=\inf _{u\in \mathbb {D}_{k} }J_{k(Q)}(u)$
. By (3-16) and (3-17),
$\Theta _{k}=\inf _{u\in \mathbb {D}_{k} }J_{k(Q)}(u)$
. By (3-16) and (3-17),
To proceed, the proof is divided into three steps.
Step 1. For any integer
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $J_{k(Q)}(u)$
is bounded from below in
$J_{k(Q)}(u)$
is bounded from below in
![]() $ \mathbb {D}_{k}$
.
$ \mathbb {D}_{k}$
.
By Cauchy’s inequality and (2-2), for any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
 $$ \begin{align*} &e^{u}\leq e^{{u^{2}}/{4\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}}+\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}}\leq e^{{C^{2}_{0}}/{4\varepsilon\vartheta^{2}_{0}}+\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}}, \\ &\!\!\!\! e^{-u}\leq e^{{(-u)^{2}}/{4\varepsilon\|u\|_{\mathbb{D}_{k}}^{p}}+\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}} \leq e^{{C^{2}_{0}}/{4\varepsilon\vartheta^{2}_{0}}+\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}}. \end{align*} $$
$$ \begin{align*} &e^{u}\leq e^{{u^{2}}/{4\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}}+\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}}\leq e^{{C^{2}_{0}}/{4\varepsilon\vartheta^{2}_{0}}+\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}}, \\ &\!\!\!\! e^{-u}\leq e^{{(-u)^{2}}/{4\varepsilon\|u\|_{\mathbb{D}_{k}}^{p}}+\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}} \leq e^{{C^{2}_{0}}/{4\varepsilon\vartheta^{2}_{0}}+\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}}. \end{align*} $$
Thus,
 $$ \begin{align} \log \int_{V_{k}}\varphi_{1}(x)e^{-u}\,d\vartheta\leq \log\|\varphi_{1}\|_{L^{1}(V)}+\frac{C^{2}_{0}}{4\varepsilon\vartheta^{2}_{0}} +\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}, \end{align} $$
$$ \begin{align} \log \int_{V_{k}}\varphi_{1}(x)e^{-u}\,d\vartheta\leq \log\|\varphi_{1}\|_{L^{1}(V)}+\frac{C^{2}_{0}}{4\varepsilon\vartheta^{2}_{0}} +\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}, \end{align} $$
 $$ \begin{align} \log \int_{V_{k}}\varphi_{2}(x)e^{u}\,d\vartheta\leq \log\|\varphi_{2}\|_{L^{1}(V)}+\frac{C^{2}_{0}}{4\varepsilon\vartheta^{2}_{0}} +\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}. \end{align} $$
$$ \begin{align} \log \int_{V_{k}}\varphi_{2}(x)e^{u}\,d\vartheta\leq \log\|\varphi_{2}\|_{L^{1}(V)}+\frac{C^{2}_{0}}{4\varepsilon\vartheta^{2}_{0}} +\varepsilon\|u\|_{\mathbb{D}_{k}}^{2}. \end{align} $$
 $$ \begin{align*} J_{k(Q)}(u)\geq \bigg(\frac{1}{2}-\varepsilon\bigg)\|u\|_{\mathbb{D}_{k}}^{2}-\log(\|\varphi_{1}\|_{L^{1}(V)}\cdot \|\varphi_{2}\|_{L^{1}(V)})-\frac{C^{2}_{0}}{2\varepsilon\vartheta^{2}_{0}}. \end{align*} $$
$$ \begin{align*} J_{k(Q)}(u)\geq \bigg(\frac{1}{2}-\varepsilon\bigg)\|u\|_{\mathbb{D}_{k}}^{2}-\log(\|\varphi_{1}\|_{L^{1}(V)}\cdot \|\varphi_{2}\|_{L^{1}(V)})-\frac{C^{2}_{0}}{2\varepsilon\vartheta^{2}_{0}}. \end{align*} $$
Choosing
![]() $\varepsilon =\tfrac 14$
, for any
$\varepsilon =\tfrac 14$
, for any
![]() $u\in \mathbb {D}_{k} $
,
$u\in \mathbb {D}_{k} $
,
 $$ \begin{align} J_{k(Q)}(u)&\geq \frac{1}{4}\|u\|_{\mathbb{D}_{k}}^{2}-\log(\|\varphi_{1}\|_{L^{1}(V)}\cdot \|\varphi_{2}\|_{L^{1}(V)}) -\frac{C^{2}_{0}}{2\varepsilon\vartheta^{2}_{0}} \end{align} $$
$$ \begin{align} J_{k(Q)}(u)&\geq \frac{1}{4}\|u\|_{\mathbb{D}_{k}}^{2}-\log(\|\varphi_{1}\|_{L^{1}(V)}\cdot \|\varphi_{2}\|_{L^{1}(V)}) -\frac{C^{2}_{0}}{2\varepsilon\vartheta^{2}_{0}} \end{align} $$
 $$ \begin{align} &\geq -\log(\|\varphi_{1}\|_{L^{1}(V)}\cdot \|\varphi_{2}\|_{L^{1}(V)}) -\frac{C^{2}_{0}}{2\varepsilon\vartheta^{2}_{0}}. \end{align} $$
$$ \begin{align} &\geq -\log(\|\varphi_{1}\|_{L^{1}(V)}\cdot \|\varphi_{2}\|_{L^{1}(V)}) -\frac{C^{2}_{0}}{2\varepsilon\vartheta^{2}_{0}}. \end{align} $$
Therefore, we have that
![]() $J_{k(Q)}(u)$
is bounded from below in
$J_{k(Q)}(u)$
is bounded from below in
![]() $ \mathbb {D}_{k}$
.
$ \mathbb {D}_{k}$
.
Step 2. For any integer
![]() $k\geq 1$
, there exists a function
$k\geq 1$
, there exists a function
![]() $u_{k}\in \mathbb {D}_{k}$
such that
$u_{k}\in \mathbb {D}_{k}$
such that
Moreover,
![]() $u_{k}$
satisfies the Euler–Lagrange equation:
$u_{k}$
satisfies the Euler–Lagrange equation:
 $$ \begin{align} (-\Delta)^{m} u_{k}+ (-\Delta)^{n}u_{k} = -\lambda_{1} \frac{\varphi_{1}(x)e^{-u_{k}}}{\int_{V}\varphi_{1}(x)e^{-u_{k}}\,d\vartheta} +\lambda_{2} \frac{\varphi_{2}(x)e^{u_{k}}}{\int_{V}\varphi_{2}(x)e^{u_{k}}\,d\vartheta}\quad \mathrm{ in}\ V. \end{align} $$
$$ \begin{align} (-\Delta)^{m} u_{k}+ (-\Delta)^{n}u_{k} = -\lambda_{1} \frac{\varphi_{1}(x)e^{-u_{k}}}{\int_{V}\varphi_{1}(x)e^{-u_{k}}\,d\vartheta} +\lambda_{2} \frac{\varphi_{2}(x)e^{u_{k}}}{\int_{V}\varphi_{2}(x)e^{u_{k}}\,d\vartheta}\quad \mathrm{ in}\ V. \end{align} $$
Obviously, by (3-18) and (3-22),
 $$ \begin{align} -\log(\|\varphi_{1}\|_{L^{1}(V)}\cdot \|\varphi_{2}\|_{L^{1}(V)}) -\frac{C^{2}_{0}}{2\varepsilon\vartheta^{2}_{0}}\leq\Theta_{k}\leq - \lambda_{1}\log\big{(}\vartheta_{0}\varphi_{1}(x_{0})\big{)}- \lambda_{2}\log\big{(}\vartheta_{0}\varphi_{2}(x_{0})\big{)}. \end{align} $$
$$ \begin{align} -\log(\|\varphi_{1}\|_{L^{1}(V)}\cdot \|\varphi_{2}\|_{L^{1}(V)}) -\frac{C^{2}_{0}}{2\varepsilon\vartheta^{2}_{0}}\leq\Theta_{k}\leq - \lambda_{1}\log\big{(}\vartheta_{0}\varphi_{1}(x_{0})\big{)}- \lambda_{2}\log\big{(}\vartheta_{0}\varphi_{2}(x_{0})\big{)}. \end{align} $$
By (3-24), we get that
![]() $\Theta _{k}$
is a bounded sequence of numbers.
$\Theta _{k}$
is a bounded sequence of numbers.
Now fix a positive integer k. We take a sequence of functions
![]() $\hat {u}_{j}\in \mathbb {D}_{k}$
such that
$\hat {u}_{j}\in \mathbb {D}_{k}$
such that
Thus,
where M is a positive constant. Therefore, we get that
![]() $\{\hat {u}_{j}\}$
is bounded in
$\{\hat {u}_{j}\}$
is bounded in
![]() $\mathbb {D}_{k}$
. By Theorem A and Remark 2, we have that up to a subsequence,
$\mathbb {D}_{k}$
. By Theorem A and Remark 2, we have that up to a subsequence,
![]() $\hat {u}_{j}$
converges to some function
$\hat {u}_{j}$
converges to some function
![]() $u_{k}\in \mathbb {D}_{k}$
. Clearly,
$u_{k}\in \mathbb {D}_{k}$
. Clearly,
Thus,
![]() $u_{k}$
satisfies the Euler–Lagrange system (3-23).
$u_{k}$
satisfies the Euler–Lagrange system (3-23).
Step 3. There exist
![]() $\acute {u}:V\rightarrow \mathbb {R}$
and a subsequence of
$\acute {u}:V\rightarrow \mathbb {R}$
and a subsequence of
![]() $\{u_{k}\}$
, still denoted by
$\{u_{k}\}$
, still denoted by
![]() $\{u_{k}\}$
, such that
$\{u_{k}\}$
, such that
![]() $\{u_{k}\}$
converges to
$\{u_{k}\}$
converges to
![]() $\acute {u}$
, that is,
$\acute {u}$
, that is,
![]() $\acute {u}$
is a solution to (2-8).
$\acute {u}$
is a solution to (2-8).
Since
![]() $\Theta _{k}$
is bounded, by (3-21),
$\Theta _{k}$
is bounded, by (3-21),
where
![]() $M_{1}$
is a positive constant independent of k.
$M_{1}$
is a positive constant independent of k.
By Theorem A and (3-25), for any
![]() $u_{k}\in \mathbb {D}_{k}$
,
$u_{k}\in \mathbb {D}_{k}$
,
where
![]() $M_{2}$
is a positive constant independent of k.
$M_{2}$
is a positive constant independent of k.
Let
![]() $\{u_{k}\}$
be extended as a sequence defined on V with
$\{u_{k}\}$
be extended as a sequence defined on V with
![]() $u_{k}=0$
on
$u_{k}=0$
on
![]() $ V\setminus V_{k}$
, that is,
$ V\setminus V_{k}$
, that is,
 $$ \begin{align} u_{k}(x)= \begin{cases} u_{k}(x)& \mathrm{{for }}\ x\in V_{k},\\ 0 \quad & \mathrm{{for }}\ x\in V \setminus V_{k}. \end{cases} \end{align} $$
$$ \begin{align} u_{k}(x)= \begin{cases} u_{k}(x)& \mathrm{{for }}\ x\in V_{k},\\ 0 \quad & \mathrm{{for }}\ x\in V \setminus V_{k}. \end{cases} \end{align} $$
Therefore, by (3-26) and (3-27), we get that
![]() $\{u_{k}\}$
is uniformly bounded in V. Thus, there exists a subsequence of
$\{u_{k}\}$
is uniformly bounded in V. Thus, there exists a subsequence of
![]() $\{u_{k}\}$
, still denoted by
$\{u_{k}\}$
, still denoted by
![]() $\{u_{k}\}$
, such that
$\{u_{k}\}$
, such that
![]() $\{u_{k}\}$
converges to
$\{u_{k}\}$
converges to
![]() $\acute {u}$
uniformly in V, that is,
$\acute {u}$
uniformly in V, that is,
For any fixed
![]() $x\in V$
, letting
$x\in V$
, letting
![]() $k\rightarrow \infty $
in (3-23),
$k\rightarrow \infty $
in (3-23),
 $$ \begin{align} (-\Delta)^{m} \acute{u}+ (-\Delta)^{n}\acute{u}= -\lambda_{1} \frac{\varphi_{1}(x)e^{-\acute{u}}}{\int_{V}\varphi_{1}(x)e^{-\acute{u}}\,d\vartheta} +\lambda_{2} \frac{\varphi_{2}(x)e^{\acute{u}}}{\int_{V}\varphi_{2}(x)e^{\acute{u}}\,d\vartheta}\quad\mathrm{ in}~V. \end{align} $$
$$ \begin{align} (-\Delta)^{m} \acute{u}+ (-\Delta)^{n}\acute{u}= -\lambda_{1} \frac{\varphi_{1}(x)e^{-\acute{u}}}{\int_{V}\varphi_{1}(x)e^{-\acute{u}}\,d\vartheta} +\lambda_{2} \frac{\varphi_{2}(x)e^{\acute{u}}}{\int_{V}\varphi_{2}(x)e^{\acute{u}}\,d\vartheta}\quad\mathrm{ in}~V. \end{align} $$
Thus,
![]() $\acute {u}(x)$
is a solution to (2-8).
$\acute {u}(x)$
is a solution to (2-8).
Moreover, if
 $$ \begin{align*} \lambda_{1} \frac{\varphi_{1}(x)}{\int_{V}\varphi_{1}(x)\,d\vartheta} -\lambda_{2} \frac{\varphi_{2}(x)}{\int_{V}\varphi_{2}(x)\,d\vartheta} \not\equiv 0\quad \mathrm{ for \ all}~ x\in V, \end{align*} $$
$$ \begin{align*} \lambda_{1} \frac{\varphi_{1}(x)}{\int_{V}\varphi_{1}(x)\,d\vartheta} -\lambda_{2} \frac{\varphi_{2}(x)}{\int_{V}\varphi_{2}(x)\,d\vartheta} \not\equiv 0\quad \mathrm{ for \ all}~ x\in V, \end{align*} $$
by (3-28), we get that
![]() $\acute {u}(x)\not \equiv 0$
. Therefore,
$\acute {u}(x)\not \equiv 0$
. Therefore,
![]() $\acute {u}(x)$
is a nontrivial solution to (2-8).
$\acute {u}(x)$
is a nontrivial solution to (2-8).
Proof of Theorem 6.
Let
![]() $B_{k}$
be defined as in (2-9). Set
$B_{k}$
be defined as in (2-9). Set
with the norm
Define the functional
![]() $J_{k(\kappa )}:\mathbb {X}_{k}\rightarrow \mathbb {R}$
by
$J_{k(\kappa )}:\mathbb {X}_{k}\rightarrow \mathbb {R}$
by
 $$ \begin{align} J_{k(\kappa)}(u,v)=&\frac{1}{p}\int_{B_{k}}|\nabla^{m} u|^{p}\,d\vartheta +\frac{1}{q}\int_{B_{k}}|\nabla^{n} v|^{q}\,d\vartheta +\int_{B_{k}}K(x)e^{-u-v}\,d\vartheta \notag \\ &+\int_{B_{k}}\kappa(x)e^{-u-v}\,d\vartheta +\int_{B_{k}}\kappa(x)u\,d\vartheta+\int_{B_{k}}K(x)v\,d\vartheta. \end{align} $$
$$ \begin{align} J_{k(\kappa)}(u,v)=&\frac{1}{p}\int_{B_{k}}|\nabla^{m} u|^{p}\,d\vartheta +\frac{1}{q}\int_{B_{k}}|\nabla^{n} v|^{q}\,d\vartheta +\int_{B_{k}}K(x)e^{-u-v}\,d\vartheta \notag \\ &+\int_{B_{k}}\kappa(x)e^{-u-v}\,d\vartheta +\int_{B_{k}}\kappa(x)u\,d\vartheta+\int_{B_{k}}K(x)v\,d\vartheta. \end{align} $$
Set
Obviously,
 $$ \begin{align} \Theta_{k}\leq J_{k(\kappa)}(0,0)=\int_{B_{k}}K(x)\,d\vartheta+\int_{B_{k}}\kappa(x)\,d\vartheta\leq \int_{V}K(x)\,d\vartheta+\int_{V}\kappa(x)\,d\vartheta. \end{align} $$
$$ \begin{align} \Theta_{k}\leq J_{k(\kappa)}(0,0)=\int_{B_{k}}K(x)\,d\vartheta+\int_{B_{k}}\kappa(x)\,d\vartheta\leq \int_{V}K(x)\,d\vartheta+\int_{V}\kappa(x)\,d\vartheta. \end{align} $$
To proceed, the proof is divided into four steps.
Step 1. For any positive integer k,
![]() $J_{k(\kappa )}$
is bounded from below in
$J_{k(\kappa )}$
is bounded from below in
![]() $\mathbb {X}_{k}$
.
$\mathbb {X}_{k}$
.
Noting the fact that
![]() $e^{-t}>-t+1$
for all
$e^{-t}>-t+1$
for all
![]() $t\in \mathbb {R}$
, since
$t\in \mathbb {R}$
, since
![]() $K(x),\kappa (x)>0$
, by (3-29),
$K(x),\kappa (x)>0$
, by (3-29),
 $$ \begin{align} J_{k(\kappa)}(u,v)\geq &\frac{1}{p}\int_{B_{k}}|\nabla^{m} u|^{p}\,d\vartheta +\frac{1}{q}\int_{B_{k}}|\nabla^{n} v|^{q}\,d\vartheta \notag \\ &-\int_{B_{k}}Ku\,d\vartheta-\int_{B_{k}}\kappa v\,d\vartheta+\int_{B_{k}}(K+\kappa)\,d\vartheta. \end{align} $$
$$ \begin{align} J_{k(\kappa)}(u,v)\geq &\frac{1}{p}\int_{B_{k}}|\nabla^{m} u|^{p}\,d\vartheta +\frac{1}{q}\int_{B_{k}}|\nabla^{n} v|^{q}\,d\vartheta \notag \\ &-\int_{B_{k}}Ku\,d\vartheta-\int_{B_{k}}\kappa v\,d\vartheta+\int_{B_{k}}(K+\kappa)\,d\vartheta. \end{align} $$
By the Hölder inequality, Theorem A and the Young inequality,
 $$ \begin{align} \int_{B_{k}} Ku \,d\vartheta&\leq \|u\|_{L^{s}(B_{k})} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &\leq C_{0}\|u\|_{W_{0}^{m,p}(B_{k})} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &= \frac{1}{2}\|u\|_{W_{0}^{m,p}(B_{k})}\cdot2 C_{0} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &\leq \frac{1}{2p}\|u\|^{p}_{W_{0}^{m,p}(B_{k})}+\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}. \end{align} $$
$$ \begin{align} \int_{B_{k}} Ku \,d\vartheta&\leq \|u\|_{L^{s}(B_{k})} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &\leq C_{0}\|u\|_{W_{0}^{m,p}(B_{k})} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &= \frac{1}{2}\|u\|_{W_{0}^{m,p}(B_{k})}\cdot2 C_{0} \|K\|_{L^{{s}/({s-1})}(V)} \notag \\ &\leq \frac{1}{2p}\|u\|^{p}_{W_{0}^{m,p}(B_{k})}+\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}. \end{align} $$
Similarly,
 $$ \begin{align} \int_{B_{k}} \kappa v\,d\vartheta\leq \frac{1}{2q}\|v\|^{q}_{W_{0}^{n,q} (B_{k})}+\frac{q-1}{2q}(2C_{0})^{{q}/({q-1})} \|\kappa\|^{{q}/({q-1})}_{L^{{\gamma}/({\gamma-1})}(V)}. \end{align} $$
$$ \begin{align} \int_{B_{k}} \kappa v\,d\vartheta\leq \frac{1}{2q}\|v\|^{q}_{W_{0}^{n,q} (B_{k})}+\frac{q-1}{2q}(2C_{0})^{{q}/({q-1})} \|\kappa\|^{{q}/({q-1})}_{L^{{\gamma}/({\gamma-1})}(V)}. \end{align} $$
 $$ \begin{align} \!\!\!J_{k(\kappa)}(u,v)&\geq \frac{1}{2p}\|u\|^{p}_{W_{0}^{m,p}(B_{k})}+\frac{1}{2q}\|v\|^{q}_{W_{0}^{n,q} (B_{k})}-\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)} \notag\qquad\qquad \\ &\quad-\frac{q-1}{2q}(2C_{0})^{{q}/({q-1})} \|\kappa\|^{{q}/({q-1})}_{L^{{\gamma}/({\gamma-1})}(V)} \quad\qquad\end{align} $$
$$ \begin{align} \!\!\!J_{k(\kappa)}(u,v)&\geq \frac{1}{2p}\|u\|^{p}_{W_{0}^{m,p}(B_{k})}+\frac{1}{2q}\|v\|^{q}_{W_{0}^{n,q} (B_{k})}-\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)} \notag\qquad\qquad \\ &\quad-\frac{q-1}{2q}(2C_{0})^{{q}/({q-1})} \|\kappa\|^{{q}/({q-1})}_{L^{{\gamma}/({\gamma-1})}(V)} \quad\qquad\end{align} $$
 $$ \begin{align} &\qquad\geq -\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}-\frac{q-1}{2q}(2C_{0})^{{q}/({q-1})} \|\kappa\|^{{q}/({q-1})}_{L^{{\gamma}/({\gamma-1})}(V)}. \end{align} $$
$$ \begin{align} &\qquad\geq -\frac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}-\frac{q-1}{2q}(2C_{0})^{{q}/({q-1})} \|\kappa\|^{{q}/({q-1})}_{L^{{\gamma}/({\gamma-1})}(V)}. \end{align} $$
Therefore, for any positive integer k,
![]() $J_{k(\kappa )}$
is bounded from below in
$J_{k(\kappa )}$
is bounded from below in
![]() $\mathbb {X}_{k}$
.
$\mathbb {X}_{k}$
.
Step 2. For any positive integer k, there exists
![]() $(u_{k},v_{k})\in \mathbb {X}_{k}$
such that
$(u_{k},v_{k})\in \mathbb {X}_{k}$
such that
Moreover,
![]() $(u_{k},v_{k})$
satisfies the Euler–Lagrange system:
$(u_{k},v_{k})$
satisfies the Euler–Lagrange system:
 $$ \begin{align} \begin{cases} \mathcal{L}_{m,p} u_{k}= K(x)e^{-u_{k}-v_{k}}-\kappa(x)&\mathrm{ in }~V_{k},\\ \mathcal{L}_{n,q} v_{k}=\kappa(x)e^{-u_{k}-v_{k}}-K(x)&\mathrm{ in }~V_{k},\\ u_{k}=v_{k}=0 &\mathrm{ on}~\partial V_{k}. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \mathcal{L}_{m,p} u_{k}= K(x)e^{-u_{k}-v_{k}}-\kappa(x)&\mathrm{ in }~V_{k},\\ \mathcal{L}_{n,q} v_{k}=\kappa(x)e^{-u_{k}-v_{k}}-K(x)&\mathrm{ in }~V_{k},\\ u_{k}=v_{k}=0 &\mathrm{ on}~\partial V_{k}. \end{cases} \end{align} $$
Obviously, by (3-30) and (3-35), there holds
 $$ \begin{align} \begin{cases} \Theta_{k}\geq-\dfrac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}-\dfrac{q-1}{2q}(2C_{0})^{{q}/({q-1})} \|\kappa\|^{{q}/({q-1})}_{L^{{\gamma}/({\gamma-1})}(V)}, \\[6pt] \Theta_{k}\leq\int_{V}K(x)\,d\vartheta+\int_{V}\kappa(x)\,d\vartheta. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Theta_{k}\geq-\dfrac{p-1}{2p}(2C_{0})^{{p}/({p-1})} \|K\|^{{p}/({p-1})}_{L^{{s}/({s-1})}(V)}-\dfrac{q-1}{2q}(2C_{0})^{{q}/({q-1})} \|\kappa\|^{{q}/({q-1})}_{L^{{\gamma}/({\gamma-1})}(V)}, \\[6pt] \Theta_{k}\leq\int_{V}K(x)\,d\vartheta+\int_{V}\kappa(x)\,d\vartheta. \end{cases} \end{align} $$
By (3-37), we know that
![]() $\Theta _{k}$
is a bounded sequence of numbers.
$\Theta _{k}$
is a bounded sequence of numbers.
Now we fix a positive integer k and take a sequence of functions
![]() $\{(\hat {u}_{j},\hat {v}_{j})\}\subset \mathbb {X}_{k}$
satisfying
$\{(\hat {u}_{j},\hat {v}_{j})\}\subset \mathbb {X}_{k}$
satisfying
It follows from (3-34) and (3-38) that
![]() $\{\hat {u}_{j}\}$
and
$\{\hat {u}_{j}\}$
and
![]() $\{\hat {v}_{j}\}$
are bounded in
$\{\hat {v}_{j}\}$
are bounded in
![]() $W_{0}^{m,p}(B_{k})$
and
$W_{0}^{m,p}(B_{k})$
and
![]() $W_{0}^{n,q}(B_{k})$
, respectively. By Theorem A, we get that there exist
$W_{0}^{n,q}(B_{k})$
, respectively. By Theorem A, we get that there exist
such that
By Remark 5, for
![]() $(u_{k},v_{k} )\in \mathbb {X}_{k}$
, up to a subsequence,
$(u_{k},v_{k} )\in \mathbb {X}_{k}$
, up to a subsequence,
![]() $\{(\hat {u}_{j},\hat {v}_{j} )\}$
converges to
$\{(\hat {u}_{j},\hat {v}_{j} )\}$
converges to
![]() $(u_{k},v_{k} )$
. Clearly,
$(u_{k},v_{k} )$
. Clearly,
Thus,
![]() $(u_{k},v_{k} )$
satisfies the Euler–Lagrange system (3-36).
$(u_{k},v_{k} )$
satisfies the Euler–Lagrange system (3-36).
Step 3. For any finite set
![]() $\Re \subset V$
,
$\Re \subset V$
,
![]() $(u_{k},v_{k})$
is uniformly bounded in
$(u_{k},v_{k})$
is uniformly bounded in
![]() $ W_{0}^{m,p}(\Re )\times W_{0}^{n,q}(\Re )$
.
$ W_{0}^{m,p}(\Re )\times W_{0}^{n,q}(\Re )$
.
where
![]() $M_{1}$
is a positive constant independent of k. When k is large enough, we get that
$M_{1}$
is a positive constant independent of k. When k is large enough, we get that
![]() $\Re \subset V_{k}$
. By (2-4), (3-39) and (3-40),
$\Re \subset V_{k}$
. By (2-4), (3-39) and (3-40),
where
![]() $M_{2}$
is a positive constant independent of k. Therefore,
$M_{2}$
is a positive constant independent of k. Therefore,
![]() $\{(u_{k},v_{k} )\}$
is uniformly bounded in
$\{(u_{k},v_{k} )\}$
is uniformly bounded in
![]() $ W_{0}^{m,p}(\Re )\times W_{0}^{n,q}(\Re )$
.
$ W_{0}^{m,p}(\Re )\times W_{0}^{n,q}(\Re )$
.
Step 4. There exist
![]() $(u^{*},v^{*}):V\times V\rightarrow \mathbb {R}$
and a subsequence of
$(u^{*},v^{*}):V\times V\rightarrow \mathbb {R}$
and a subsequence of
![]() $\{(u_{k},v_{k} )\}$
, still denoted by
$\{(u_{k},v_{k} )\}$
, still denoted by
![]() $\{(u_{k},v_{k} )\}$
, such that
$\{(u_{k},v_{k} )\}$
, such that
![]() $\{(u_{k},v_{k} )\}$
converges to
$\{(u_{k},v_{k} )\}$
converges to
![]() $(u^{*},v^{*})$
, that is,
$(u^{*},v^{*})$
, that is,
![]() $(u^{*},v^{*})$
is a solution to (2-10).
$(u^{*},v^{*})$
is a solution to (2-10).
By Step 3, we have that
![]() $\{(u_{k},v_{k} )\}$
is uniformly bounded in
$\{(u_{k},v_{k} )\}$
is uniformly bounded in
![]() $B_{1}$
. Thus, there exists a subsequence of
$B_{1}$
. Thus, there exists a subsequence of
![]() $\{(u_{k},v_{k} )\}$
, denoted by
$\{(u_{k},v_{k} )\}$
, denoted by
![]() $\{(u_{1k},v_{1k} )\}$
, and functions
$\{(u_{1k},v_{1k} )\}$
, and functions
![]() $(u^{*}_{1},v^{*}_{1} )$
such that
$(u^{*}_{1},v^{*}_{1} )$
such that
![]() $(u_{1k},v_{1k} )\rightarrow (u^{*}_{1},v^{*}_{1} )$
in
$(u_{1k},v_{1k} )\rightarrow (u^{*}_{1},v^{*}_{1} )$
in
![]() $B_{1}$
. By Step 3 again,
$B_{1}$
. By Step 3 again,
![]() $\{(u_{1k},v_{1k} )\}$
is uniformly bounded in
$\{(u_{1k},v_{1k} )\}$
is uniformly bounded in
![]() $B_{2}$
. Then there exists a subsequence of
$B_{2}$
. Then there exists a subsequence of
![]() $\{(u_{1k},v_{1k} )\}$
, denoted by
$\{(u_{1k},v_{1k} )\}$
, denoted by
![]() $\{(u_{2k},v_{2k} )\}$
, and functions
$\{(u_{2k},v_{2k} )\}$
, and functions
![]() $(u^{*}_{2},v^{*}_{2} )$
such that
$(u^{*}_{2},v^{*}_{2} )$
such that
![]() $(u_{2k},v_{2k} )\rightarrow (u^{*}_{2},v^{*}_{2} )$
in
$(u_{2k},v_{2k} )\rightarrow (u^{*}_{2},v^{*}_{2} )$
in
![]() $B_{2}$
. Obviously,
$B_{2}$
. Obviously,
![]() $(u^{*}_{1},v^{*}_{1} )=(u^{*}_{2},v^{*}_{2})$
in
$(u^{*}_{1},v^{*}_{1} )=(u^{*}_{2},v^{*}_{2})$
in
![]() $B_{1}$
. Repeating this process, we can find a diagonal subsequence
$B_{1}$
. Repeating this process, we can find a diagonal subsequence
![]() $\{(u_{kk},v_{kk} )\}$
, which is still denoted by
$\{(u_{kk},v_{kk} )\}$
, which is still denoted by
![]() $\{(u_{k},v_{k} )\}$
, and functions
$\{(u_{k},v_{k} )\}$
, and functions
![]() $(u^{*},v^{*}):V\times V\rightarrow \mathbb {R}$
such that for any finite set
$(u^{*},v^{*}):V\times V\rightarrow \mathbb {R}$
such that for any finite set
![]() $\Re \subset V$
,
$\Re \subset V$
,
![]() $(u_{k},v_{k})\rightarrow (u^{*},v^{*})$
in
$(u_{k},v_{k})\rightarrow (u^{*},v^{*})$
in
![]() $\Re $
. For any fixed
$\Re $
. For any fixed
![]() $x \in V$
, let
$x \in V$
, let
![]() $k \rightarrow \infty $
in (3-36), so
$k \rightarrow \infty $
in (3-36), so
 $$ \begin{align*} \begin{cases} \mathcal{L}_{m,p} u^{*}= K(x)e^{-u^{*}-v^{*}}-\kappa(x)&\mathrm{ in }~V,\\ \mathcal{L}_{n,q} v^{*}=\kappa(x)e^{-u^{*}-v^{*}}-K(x)&\mathrm{ in }~V. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \mathcal{L}_{m,p} u^{*}= K(x)e^{-u^{*}-v^{*}}-\kappa(x)&\mathrm{ in }~V,\\ \mathcal{L}_{n,q} v^{*}=\kappa(x)e^{-u^{*}-v^{*}}-K(x)&\mathrm{ in }~V. \end{cases} \end{align*} $$
Since
![]() $K(x)\not \equiv \kappa (x)$
, we get
$K(x)\not \equiv \kappa (x)$
, we get
![]() $(u^{*},v^{*})\not \equiv (0,0)$
. Therefore,
$(u^{*},v^{*})\not \equiv (0,0)$
. Therefore,
![]() $(u^{*},v^{*})$
is a nontrivial solution to (2-10).
$(u^{*},v^{*})$
is a nontrivial solution to (2-10).