1. Introduction
Taylor–Couette flow (TCF), the flow between two coaxial, independently rotating cylinders, is one of the paradigmatic systems in fluid dynamics. Taylor's seminal work (Taylor Reference Taylor1923) established the correctness of the Navier–Stokes equations and the no-slip condition through linear stability analysis, predicting the instability thresholds of the system and confirming them experimentally. Since then, TCF has become a highly productive laboratory for studying not only instabilities but also topics such as nonlinear dynamics, pattern formation and turbulence (Grossmann, Lohse & Sun Reference Grossmann, Lohse and Sun2016). For example, the toroidal cells (known as Taylor rolls) in TCF flow resemble Bénard convection cells, while the waves in spiral turbulence resemble flow structures in binary-fluid convection (Cross & Hohenberg Reference Cross and Hohenberg1993). Insights into one system have often been gained by analysing the other.
The work of Lin et al. (Reference Lin, Song, Liu, Liu, Lu and Khomami2024) builds on this tradition, using TCF with viscous polymers to study solar system formation. The connection between these two systems lies in an unresolved problem in astrophysics: stars and planets cannot form unless they shed most of their original angular momentum, and only turbulent diffusion provides enough mixing for this to happen. However, the origin of turbulence remains elusive. The fact that the magnetic Reynolds number seems insufficient to trigger turbulence (Armitage Reference Armitage2011) led to the suggestion that hydrodynamic instabilities could serve as an alternative. Taylor–Couette flow was proposed as a model system to probe this path to turbulence as the independent rotation of the cylinders can be set to resemble a Keplerian-like law, i.e. that the square of a planet's orbital period is proportional to the cube of the semi-major axis of its orbit (Zeldovich Reference Zeldovich1981; Richard & Zahn Reference Richard and Zahn1999). This configuration is termed quasi-Keplerian, as it mimics Kepler's third law by setting the cylinder velocities, but not the entire fluid, to follow this relationship.
Despite this analogy, the behaviour of quasi-Keplerian TCF deviates from expectations. While nonlinear transitions to turbulence are present in pipe or channel flows, they were not observed in quasi-Keplerian TCF, even at high Reynolds numbers. The initial experiments by Ji et al. (Reference Ji, Burin, Schartman and Goodman2006) with carefully controlled boundary conditions showed an absence of significant turbulence, which led to renewed interest in the problem, with some experiments showing increased mixing and others showing none (Ji & Goodman Reference Ji and Goodman2023). It is now well established that, in the quasi-Keplerian regime, TCF does not exhibit a nonlinear transition to turbulence at high Reynolds numbers. Any observed turbulence is attributed to the presence of end plates required to physically close the experiment (Lopez & Avila Reference Lopez and Avila2017; Ji & Goodman Reference Ji and Goodman2023). This surprising result prompted a return to an earlier idea: a magneto-hydrodynamic origin for the turbulence.
In the presence of a magnetic field, cylinders rotating in a quasi-Keplerian manner become linearly unstable through the magneto-rotational instability (MRI) (Chandrasekhar Reference Chandrasekhar2013). However, this instability was only expected to occur at very large magnetic Reynolds numbers, which are difficult to achieve experimentally. The work of Lin et al. (Reference Lin, Song, Liu, Liu, Lu and Khomami2024) seeks to bridge this gap by studying the MRI through its analogy with the elasto-rotational instability in non-Newtonian TCF, based on the ideas of Ogilvie & Proctor (Reference Ogilvie and Proctor2003) and Ogilvie & Potter (Reference Ogilvie and Potter2008). As they explain, the viscoelastic stresses in dilute polymeric fluids, modelled by dumbbells, and the Maxwell stresses in electrically conducting fluids, governed by magnetohydrodynamics, have mathematically similar terms (Vieu & Mutabazi Reference Vieu and Mutabazi2019). This similarity allows the use of direct numerical simulations (DNS) of polymeric fluids to study quasi-Keplerian TCF and gain insights into stellar formation. Additionally, the Reynolds numbers required for this analysis can be achieved (and likely exceeded) in laboratory settings.
2. Results
Lin et al. (Reference Lin, Song, Liu, Liu, Lu and Khomami2024) conduct a series of DNS of a Taylor–Couette system using a polymeric fluid modelled with the finite extensible nonlinear elastic-Peterlin (FENE-P) model. They vary the Reynolds number (
$Re$) between $10^2$ and $10^4$, and fix the Weissenberg number at $Wi=30$. While this configuration results in laminar flow for a Newtonian fluid, all simulations with the polymeric fluid show turbulence, even at the lowest Reynolds number examined. This has some immediate consequences: since the turbulence is sustained by the energy input from the torque on the cylinders, the system's torque must exceed that of the laminar state. This implies that angular momentum is transported from the inner to the outer cylinder through mechanisms other than viscosity. Remarkably, the authors demonstrate that this transport is primarily due to elastic stresses, rather than hydrodynamic or convective transport (cf. figure 1a). This finding emphasizes that even in turbulent quasi-Keplerian TCF, hydrodynamic turbulence does not contribute to angular momentum mixing.
The authors also analyse the structures present in the flow, finding that they differ significantly from the large-scale rolls commonly observed in TCF. These structures decrease in axial size as the Reynolds number increases. They examine the boundary layer scaling, showing that the extent of the boundary layers diminishes approximately as $\sim Re^{-1/2}$, which is consistent with the behaviour of a Prandtl–Blasius boundary layer. The authors then elucidate scaling laws for the torque, non-dimensionalized as a Nusselt number ($Nu_\omega = T / T_{pa}$, where $T$ is the torque and $T_{pa}$ is the torque for the purely azimuthal state). They compare these scaling laws with those found in Newtonian TCF and magnetized TCF, noting that the results closely match those obtained by Mishra, Mamatsashvili & Stefani (Reference Mishra, Mamatsashvili and Stefani2023) for TCF destabilized by the standard MRI, with a scaling of $Re^{0.4-0.5}$. In addition, they note that these scaling laws are less steep than those observed in Newtonian TCF (Grossmann et al. Reference Grossmann, Lohse and Sun2016). Finally, the authors break down the contributions to the torque, distinguishing between those arising from viscous dissipation and those from elastic dissipation. They show that the scaling laws hold quite well across the examined parameter space, and that elastic dissipation scales more steeply with Reynolds number than viscous contributions (cf. figure 1b). However, they note that the full range of applicability of these scaling laws and their origins are still unclear.
3. Outlook
Research on viscoelastic TCF dates back to the early 1990s, but DNS and experimental studies in the turbulent regime have primarily emerged in the last decade (Song et al. Reference Song, Zhu, Lin, Liu and Khomami2023). The work by Lin et al. (Reference Lin, Song, Liu, Liu, Lu and Khomami2024) serves as an important complement to an earlier study by the same research group (Song et al. Reference Song, Lin, Liu, Lu and Khomami2021), which investigated viscoelastic turbulent TCF with pure inner cylinder rotation. In this configuration, transport occurs through both elastic and hydrodynamic mechanisms with the latter predominating at high $Re$. Future experiments and simulations across a broader range of Reynolds numbers and cylinder rotation configurations will provide valuable insights into how the scaling laws for torque evolve, and in particular, what exponents will be obtained for the viscous, hydrodynamic and elastic contributions across the large parameter space of TCF. Additionally, it will be important to explore the dominant flow structures for different driving parameters, the behaviour of boundary layers as they become turbulent and other intriguing questions, such as the nature of pure ‘viscoelastic’ TCF.
Meanwhile, the astrophysical community continues to explore the nonlinear dynamics beyond the onset of the MRI in accretion-disk-like systems. This research is ongoing, both through magnetic TCF realizations (Wang et al. Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022) and simulations (Chan, Piran & Krolik Reference Chan, Piran and Krolik2024). Other mechanisms, such as stratification, are also being studied to address the challenges posed by low magnetic Reynolds numbers (Sandoval et al. Reference Sandoval, Riquelme, Spitkovsky and Bacchini2024). Further exploration of viscoelastic TCF may lead to more discoveries by analogy, as suggested by the authors’ comparison with Mishra et al. (Reference Mishra, Mamatsashvili and Stefani2023). A persistent challenge, however, remains the need for fluid dynamicists and astrophysicists to speak a common language. While TCF has at times served as a bridge between these fields, continued effort from both communities is needed to maintain and expand this tradition.
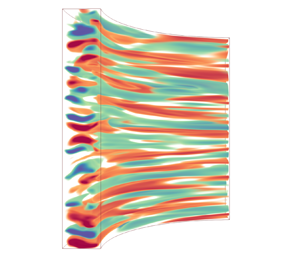
$J^\omega$ (analogous to the torque) for 
$Re=10^4$, 
$Wi=30$ across the cylinder gap: 
$J^\omega _d$, viscous; 
$J^\omega _p$, elastic; and 
$J^\omega _c$, convective. The viscous contribution dominates close to the cylinders, while the elastic contribution dominates the bulk. (b) Viscous (
$\epsilon _\nu$) and elastic (
$\epsilon _e$) contributions to the total dissipation (shown in purple) as a function of Reynolds number. The elastic component can be seen to be much larger than the viscous one, and to follow a 
$Re^{0.48}$ scaling law.
You have
Access
Open access
1. Introduction
Taylor–Couette flow (TCF), the flow between two coaxial, independently rotating cylinders, is one of the paradigmatic systems in fluid dynamics. Taylor's seminal work (Taylor Reference Taylor1923) established the correctness of the Navier–Stokes equations and the no-slip condition through linear stability analysis, predicting the instability thresholds of the system and confirming them experimentally. Since then, TCF has become a highly productive laboratory for studying not only instabilities but also topics such as nonlinear dynamics, pattern formation and turbulence (Grossmann, Lohse & Sun Reference Grossmann, Lohse and Sun2016). For example, the toroidal cells (known as Taylor rolls) in TCF flow resemble Bénard convection cells, while the waves in spiral turbulence resemble flow structures in binary-fluid convection (Cross & Hohenberg Reference Cross and Hohenberg1993). Insights into one system have often been gained by analysing the other.
The work of Lin et al. (Reference Lin, Song, Liu, Liu, Lu and Khomami2024) builds on this tradition, using TCF with viscous polymers to study solar system formation. The connection between these two systems lies in an unresolved problem in astrophysics: stars and planets cannot form unless they shed most of their original angular momentum, and only turbulent diffusion provides enough mixing for this to happen. However, the origin of turbulence remains elusive. The fact that the magnetic Reynolds number seems insufficient to trigger turbulence (Armitage Reference Armitage2011) led to the suggestion that hydrodynamic instabilities could serve as an alternative. Taylor–Couette flow was proposed as a model system to probe this path to turbulence as the independent rotation of the cylinders can be set to resemble a Keplerian-like law, i.e. that the square of a planet's orbital period is proportional to the cube of the semi-major axis of its orbit (Zeldovich Reference Zeldovich1981; Richard & Zahn Reference Richard and Zahn1999). This configuration is termed quasi-Keplerian, as it mimics Kepler's third law by setting the cylinder velocities, but not the entire fluid, to follow this relationship.
Despite this analogy, the behaviour of quasi-Keplerian TCF deviates from expectations. While nonlinear transitions to turbulence are present in pipe or channel flows, they were not observed in quasi-Keplerian TCF, even at high Reynolds numbers. The initial experiments by Ji et al. (Reference Ji, Burin, Schartman and Goodman2006) with carefully controlled boundary conditions showed an absence of significant turbulence, which led to renewed interest in the problem, with some experiments showing increased mixing and others showing none (Ji & Goodman Reference Ji and Goodman2023). It is now well established that, in the quasi-Keplerian regime, TCF does not exhibit a nonlinear transition to turbulence at high Reynolds numbers. Any observed turbulence is attributed to the presence of end plates required to physically close the experiment (Lopez & Avila Reference Lopez and Avila2017; Ji & Goodman Reference Ji and Goodman2023). This surprising result prompted a return to an earlier idea: a magneto-hydrodynamic origin for the turbulence.
In the presence of a magnetic field, cylinders rotating in a quasi-Keplerian manner become linearly unstable through the magneto-rotational instability (MRI) (Chandrasekhar Reference Chandrasekhar2013). However, this instability was only expected to occur at very large magnetic Reynolds numbers, which are difficult to achieve experimentally. The work of Lin et al. (Reference Lin, Song, Liu, Liu, Lu and Khomami2024) seeks to bridge this gap by studying the MRI through its analogy with the elasto-rotational instability in non-Newtonian TCF, based on the ideas of Ogilvie & Proctor (Reference Ogilvie and Proctor2003) and Ogilvie & Potter (Reference Ogilvie and Potter2008). As they explain, the viscoelastic stresses in dilute polymeric fluids, modelled by dumbbells, and the Maxwell stresses in electrically conducting fluids, governed by magnetohydrodynamics, have mathematically similar terms (Vieu & Mutabazi Reference Vieu and Mutabazi2019). This similarity allows the use of direct numerical simulations (DNS) of polymeric fluids to study quasi-Keplerian TCF and gain insights into stellar formation. Additionally, the Reynolds numbers required for this analysis can be achieved (and likely exceeded) in laboratory settings.
2. Results
Lin et al. (Reference Lin, Song, Liu, Liu, Lu and Khomami2024) conduct a series of DNS of a Taylor–Couette system using a polymeric fluid modelled with the finite extensible nonlinear elastic-Peterlin (FENE-P) model. They vary the Reynolds number (
$Re$) between 
$10^2$ and 
$10^4$, and fix the Weissenberg number at 
$Wi=30$. While this configuration results in laminar flow for a Newtonian fluid, all simulations with the polymeric fluid show turbulence, even at the lowest Reynolds number examined. This has some immediate consequences: since the turbulence is sustained by the energy input from the torque on the cylinders, the system's torque must exceed that of the laminar state. This implies that angular momentum is transported from the inner to the outer cylinder through mechanisms other than viscosity. Remarkably, the authors demonstrate that this transport is primarily due to elastic stresses, rather than hydrodynamic or convective transport (cf. figure 1a). This finding emphasizes that even in turbulent quasi-Keplerian TCF, hydrodynamic turbulence does not contribute to angular momentum mixing.
Figure 1. (a) Different contributions to angular velocity transport
$J^\omega$ (analogous to the torque) for 
$Re=10^4$, 
$Wi=30$ across the cylinder gap: 
$J^\omega _d$, viscous; 
$J^\omega _p$, elastic; and 
$J^\omega _c$, convective. The viscous contribution dominates close to the cylinders, while the elastic contribution dominates the bulk. (b) Viscous (
$\epsilon _\nu$) and elastic (
$\epsilon _e$) contributions to the total dissipation (shown in purple) as a function of Reynolds number. The elastic component can be seen to be much larger than the viscous one, and to follow a 
$Re^{0.48}$ scaling law.
The authors also analyse the structures present in the flow, finding that they differ significantly from the large-scale rolls commonly observed in TCF. These structures decrease in axial size as the Reynolds number increases. They examine the boundary layer scaling, showing that the extent of the boundary layers diminishes approximately as
$\sim Re^{-1/2}$, which is consistent with the behaviour of a Prandtl–Blasius boundary layer. The authors then elucidate scaling laws for the torque, non-dimensionalized as a Nusselt number (
$Nu_\omega = T / T_{pa}$, where 
$T$ is the torque and 
$T_{pa}$ is the torque for the purely azimuthal state). They compare these scaling laws with those found in Newtonian TCF and magnetized TCF, noting that the results closely match those obtained by Mishra, Mamatsashvili & Stefani (Reference Mishra, Mamatsashvili and Stefani2023) for TCF destabilized by the standard MRI, with a scaling of 
$Re^{0.4-0.5}$. In addition, they note that these scaling laws are less steep than those observed in Newtonian TCF (Grossmann et al. Reference Grossmann, Lohse and Sun2016). Finally, the authors break down the contributions to the torque, distinguishing between those arising from viscous dissipation and those from elastic dissipation. They show that the scaling laws hold quite well across the examined parameter space, and that elastic dissipation scales more steeply with Reynolds number than viscous contributions (cf. figure 1b). However, they note that the full range of applicability of these scaling laws and their origins are still unclear.
3. Outlook
Research on viscoelastic TCF dates back to the early 1990s, but DNS and experimental studies in the turbulent regime have primarily emerged in the last decade (Song et al. Reference Song, Zhu, Lin, Liu and Khomami2023). The work by Lin et al. (Reference Lin, Song, Liu, Liu, Lu and Khomami2024) serves as an important complement to an earlier study by the same research group (Song et al. Reference Song, Lin, Liu, Lu and Khomami2021), which investigated viscoelastic turbulent TCF with pure inner cylinder rotation. In this configuration, transport occurs through both elastic and hydrodynamic mechanisms with the latter predominating at high
$Re$. Future experiments and simulations across a broader range of Reynolds numbers and cylinder rotation configurations will provide valuable insights into how the scaling laws for torque evolve, and in particular, what exponents will be obtained for the viscous, hydrodynamic and elastic contributions across the large parameter space of TCF. Additionally, it will be important to explore the dominant flow structures for different driving parameters, the behaviour of boundary layers as they become turbulent and other intriguing questions, such as the nature of pure ‘viscoelastic’ TCF.
Meanwhile, the astrophysical community continues to explore the nonlinear dynamics beyond the onset of the MRI in accretion-disk-like systems. This research is ongoing, both through magnetic TCF realizations (Wang et al. Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022) and simulations (Chan, Piran & Krolik Reference Chan, Piran and Krolik2024). Other mechanisms, such as stratification, are also being studied to address the challenges posed by low magnetic Reynolds numbers (Sandoval et al. Reference Sandoval, Riquelme, Spitkovsky and Bacchini2024). Further exploration of viscoelastic TCF may lead to more discoveries by analogy, as suggested by the authors’ comparison with Mishra et al. (Reference Mishra, Mamatsashvili and Stefani2023). A persistent challenge, however, remains the need for fluid dynamicists and astrophysicists to speak a common language. While TCF has at times served as a bridge between these fields, continued effort from both communities is needed to maintain and expand this tradition.
Declaration of interests
The author reports no conflict of interest.