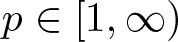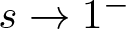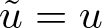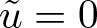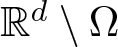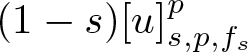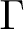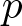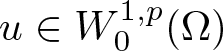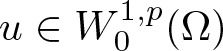1. Introduction
1.1. Framework
We let ![]() $d \in \mathbb{N}$,
$d \in \mathbb{N}$, ![]() $s \in (0,1)$, and
$s \in (0,1)$, and ![]() $p\in[1,\infty)$. Given a nonnegative weight
$p\in[1,\infty)$. Given a nonnegative weight ![]() $f \in L^\infty(\mathbb{R}^d;[0,\infty))$, our aim is to study the
$f \in L^\infty(\mathbb{R}^d;[0,\infty))$, our aim is to study the ![]() $\Gamma$-convergence as
$\Gamma$-convergence as ![]() $s\to1^-$ of the non-homogeneous (or weighted by
$s\to1^-$ of the non-homogeneous (or weighted by ![]() $f$)
$f$) ![]() $s$-fractional
$s$-fractional ![]() $p$-seminorm
$p$-seminorm
 \begin{equation}
[u]_{s,p,f}^p
=
\int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{| u(x)- u(y)|^p}{\|x-y\|^{d+sp}}\, f(x)\,f(y)\,\mathrm{d} x\,\mathrm{d} y,
\end{equation}
\begin{equation}
[u]_{s,p,f}^p
=
\int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{| u(x)- u(y)|^p}{\|x-y\|^{d+sp}}\, f(x)\,f(y)\,\mathrm{d} x\,\mathrm{d} y,
\end{equation} for ![]() $u\in L^p(\mathbb{R}^d)$.
$u\in L^p(\mathbb{R}^d)$.
The convergence as ![]() $s\to1^-$ of (1.1) in the case
$s\to1^-$ of (1.1) in the case ![]() $f\equiv 1$—for which we use the shorthand
$f\equiv 1$—for which we use the shorthand 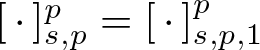 $[\,\cdot\,]_{s,p}^p=[\,\cdot\,]_{s,p,1}^p$—has been deeply studied in recent years, both in the pointwise and in the
$[\,\cdot\,]_{s,p}^p=[\,\cdot\,]_{s,p,1}^p$—has been deeply studied in recent years, both in the pointwise and in the ![]() $\Gamma$-sense. Since the literature is very vast, here we limit ourselves to a non-comprehensive list of results which are closer to the spirit of the present work.
$\Gamma$-sense. Since the literature is very vast, here we limit ourselves to a non-comprehensive list of results which are closer to the spirit of the present work.
The pointwise limit of the seminorm ![]() $[\,\cdot\,]^p_{s,p}$ as
$[\,\cdot\,]^p_{s,p}$ as ![]() $s\to1^-$ is a notable instance of the celebrated Bourgain–Brezis–Mironescu (BBM, for short) formula [Reference Bourgain, Brezis and Mironescu4, Reference Dávila10], yielding that
$s\to1^-$ is a notable instance of the celebrated Bourgain–Brezis–Mironescu (BBM, for short) formula [Reference Bourgain, Brezis and Mironescu4, Reference Dávila10], yielding that ![]() $(1-s)[\,\cdot\,]_{s,p}$ converges to the Dirichlet
$(1-s)[\,\cdot\,]_{s,p}$ converges to the Dirichlet ![]() $p$-energy up to a multiplicative constant. After the seminal contributions [Reference Bourgain, Brezis and Mironescu4, Reference Dávila10], the BBM formula has been extensively studied in several directions, see [Reference Davoli, Di Fratta and Giorgio11, Reference Ponce26, Reference Ponce27] for more general results and [Reference Leoni and Spector20, Reference Leoni and Spector21] for extensions to arbitrary domains. We also refer to [Reference Fanizza15, Reference Ludwig23, Reference Ludwig24] for anisotropic fractional energies and to [Reference Davoli, Di Fratta and Pagliari12, Reference Gennaioli and Stefani16] for sharp conditions for the validity of the BBM formula.
$p$-energy up to a multiplicative constant. After the seminal contributions [Reference Bourgain, Brezis and Mironescu4, Reference Dávila10], the BBM formula has been extensively studied in several directions, see [Reference Davoli, Di Fratta and Giorgio11, Reference Ponce26, Reference Ponce27] for more general results and [Reference Leoni and Spector20, Reference Leoni and Spector21] for extensions to arbitrary domains. We also refer to [Reference Fanizza15, Reference Ludwig23, Reference Ludwig24] for anisotropic fractional energies and to [Reference Davoli, Di Fratta and Pagliari12, Reference Gennaioli and Stefani16] for sharp conditions for the validity of the BBM formula.
The ![]() $\Gamma$-convergence of
$\Gamma$-convergence of ![]() $(1-s)[\,\cdot\,]_{s,p}^p$ to the Dirichlet
$(1-s)[\,\cdot\,]_{s,p}^p$ to the Dirichlet ![]() $p$-energy as
$p$-energy as ![]() $s\to1^-$ has been established in [Reference Brasco, Parini and Squassina5] for every
$s\to1^-$ has been established in [Reference Brasco, Parini and Squassina5] for every ![]() $p\in(1,\infty)$, in [Reference Crismale, De Luca, Kubin, Ninno and Ponsiglione9] only for
$p\in(1,\infty)$, in [Reference Crismale, De Luca, Kubin, Ninno and Ponsiglione9] only for ![]() $p=2$, and in [Reference Gennaioli and Stefani16] for every
$p=2$, and in [Reference Gennaioli and Stefani16] for every ![]() $p\in[1,\infty)$. We also refer to [Reference Bourgain, Brezis and Mironescu4, Reference Ponce26] for similar results on bounded open sets.
$p\in[1,\infty)$. We also refer to [Reference Bourgain, Brezis and Mironescu4, Reference Ponce26] for similar results on bounded open sets.
The geometric case ![]() $p=1$ deserves special mention, due to the link with the (relative) fractional perimeter, see [Reference Ambrosio, De Philippis and Martinazzi1, Reference Berendsen and Pagliari2, Reference Gennaioli and Stefani16, Reference Kubin and La Manna18, Reference Lombardini22, Reference Pagliari25] for closely related results in this direction. We also refer to [Reference Cesaroni and Novaga8, Reference De Luca, Kubin and Ponsiglione13, Reference Kubin, Pagliari and Tribuzio19] for higher-order convergence results.
$p=1$ deserves special mention, due to the link with the (relative) fractional perimeter, see [Reference Ambrosio, De Philippis and Martinazzi1, Reference Berendsen and Pagliari2, Reference Gennaioli and Stefani16, Reference Kubin and La Manna18, Reference Lombardini22, Reference Pagliari25] for closely related results in this direction. We also refer to [Reference Cesaroni and Novaga8, Reference De Luca, Kubin and Ponsiglione13, Reference Kubin, Pagliari and Tribuzio19] for higher-order convergence results.
Beyond the case ![]() $f\equiv1$, the asymptotic behavior of (1.1) and of similarly-defined energies has been studied for some particular weights, see [Reference Carbotti, Cito, La Manna and Pallara7, Reference De Rosa and La Manna14] for the Gaussian framework and [Reference Kijaczko17] for weights depending on negative powers of the distance from the boundary.
$f\equiv1$, the asymptotic behavior of (1.1) and of similarly-defined energies has been studied for some particular weights, see [Reference Carbotti, Cito, La Manna and Pallara7, Reference De Rosa and La Manna14] for the Gaussian framework and [Reference Kijaczko17] for weights depending on negative powers of the distance from the boundary.
The aim of the present paper is to investigate the asymptotic behavior of the weighted seminorm (1.1) as ![]() $s\to1^-$ as the weight
$s\to1^-$ as the weight ![]() $f$ is also allowed to vary with respect to the parameter
$f$ is also allowed to vary with respect to the parameter ![]() $s$. This is motivated by the recent interest in the extension of BBM-type formulas beyond the isotropic setting in order to address possible applications to non-isotropic frameworks [Reference Davoli, Di Fratta and Pagliari12]. Besides, our
$s$. This is motivated by the recent interest in the extension of BBM-type formulas beyond the isotropic setting in order to address possible applications to non-isotropic frameworks [Reference Davoli, Di Fratta and Pagliari12]. Besides, our ![]() $\Gamma$-convergence result can be interpreted as a suitable extension to the weighted setting of the ones obtained in [Reference Brasco, Parini and Squassina5, Reference Crismale, De Luca, Kubin, Ninno and Ponsiglione9].
$\Gamma$-convergence result can be interpreted as a suitable extension to the weighted setting of the ones obtained in [Reference Brasco, Parini and Squassina5, Reference Crismale, De Luca, Kubin, Ninno and Ponsiglione9].
Our main result, Theorem 1.1 below, deals with the ![]() $\Gamma$-convergence of the energy (1.1) with respect to a uniformly converging family of weights
$\Gamma$-convergence of the energy (1.1) with respect to a uniformly converging family of weights ![]() $(f_n)_{n\in\mathbb{N}}$ in
$(f_n)_{n\in\mathbb{N}}$ in ![]() $L^\infty(\mathbb{R}^d;[0,\infty))$, whose limit
$L^\infty(\mathbb{R}^d;[0,\infty))$, whose limit ![]() $f$ is in
$f$ is in ![]() $\mathrm{Lip}_b(\mathbb{R}^d;(0,\infty))$. Precisely, we prove that the
$\mathrm{Lip}_b(\mathbb{R}^d;(0,\infty))$. Precisely, we prove that the ![]() $\Gamma$-limit is given by
$\Gamma$-limit is given by
 \begin{equation*}
u \mapsto
\begin{cases}
\displaystyle
K_{d,p}
\|\nabla u\|_{p,f^2}^p
=
K_{d,p}
\int_{\Omega} f^2\,\| \nabla u\|^p \,\mathrm{d} x,
&
\text{for}\ p \in (1,\infty),
\\[3ex]
\displaystyle
K_{d,1}
\|Du\|_{1,f^2}
=
K_{d,1}
\int_{\Omega} f^2\,\mathrm{d}|Du|,
&
\text{for}\ p=1,
\end{cases}
\end{equation*}
\begin{equation*}
u \mapsto
\begin{cases}
\displaystyle
K_{d,p}
\|\nabla u\|_{p,f^2}^p
=
K_{d,p}
\int_{\Omega} f^2\,\| \nabla u\|^p \,\mathrm{d} x,
&
\text{for}\ p \in (1,\infty),
\\[3ex]
\displaystyle
K_{d,1}
\|Du\|_{1,f^2}
=
K_{d,1}
\int_{\Omega} f^2\,\mathrm{d}|Du|,
&
\text{for}\ p=1,
\end{cases}
\end{equation*} where for every ![]() $p\in[1,\infty)$ (and here
$p\in[1,\infty)$ (and here ![]() $\Gamma$ being Euler’s Gamma function),
$\Gamma$ being Euler’s Gamma function),
 \begin{equation}
K_{d,p}
=
\frac{1}{p}\int_{\partial B_1} \vert x \cdot \mathrm{e}_d \vert^p\, \mathrm{d} \mathcal{H}^{d-1}(x)
=
\frac{2\pi^{\frac{d-1}2}}{p}
\frac{\Gamma\left(\frac{p+1}2\right)}{\Gamma\left(\frac{N+p}2\right)},
\end{equation}
\begin{equation}
K_{d,p}
=
\frac{1}{p}\int_{\partial B_1} \vert x \cdot \mathrm{e}_d \vert^p\, \mathrm{d} \mathcal{H}^{d-1}(x)
=
\frac{2\pi^{\frac{d-1}2}}{p}
\frac{\Gamma\left(\frac{p+1}2\right)}{\Gamma\left(\frac{N+p}2\right)},
\end{equation} see [Reference Bianchi, Stefani and Zagati3, Lem. 2.1]. Here and below, given a measurable function ![]() $u\colon\Omega\to\mathbb{R}$ on an open set
$u\colon\Omega\to\mathbb{R}$ on an open set ![]() $\Omega\subset\mathbb{R}^d$, we define
$\Omega\subset\mathbb{R}^d$, we define ![]() $\tilde u\colon\mathbb{R}^d\to\mathbb{R}$ be such that
$\tilde u\colon\mathbb{R}^d\to\mathbb{R}$ be such that ![]() $\tilde u=u$ on
$\tilde u=u$ on ![]() $\Omega$ and
$\Omega$ and ![]() $\tilde u=0$ on
$\tilde u=0$ on ![]() $\mathbb{R}^d\setminus\Omega$.
$\mathbb{R}^d\setminus\Omega$.
Theorem 1.1 ( $\Gamma$-convergence with weights)
$\Gamma$-convergence with weights)
Let ![]() $p\in[1,\infty)$,
$p\in[1,\infty)$, ![]() $(f_n)_{n\in\mathbb{N}}\subset L^\infty(\mathbb{R}^d;[0,\infty))$ and
$(f_n)_{n\in\mathbb{N}}\subset L^\infty(\mathbb{R}^d;[0,\infty))$ and ![]() $f\in\mathrm{Lip}_b(\mathbb{R}^d;(0,\infty))$ be such that
$f\in\mathrm{Lip}_b(\mathbb{R}^d;(0,\infty))$ be such that ![]() $f_n\to f$ in
$f_n\to f$ in ![]() $L^\infty(\mathbb{R}^d)$,
$L^\infty(\mathbb{R}^d)$, ![]() $\Omega\subset \mathbb{R}^d$ be a bounded open set with Lipschitz boundary and
$\Omega\subset \mathbb{R}^d$ be a bounded open set with Lipschitz boundary and ![]() $(s_n)_{n\in\mathbb{N}}\subset (0,1)$ be such that
$(s_n)_{n\in\mathbb{N}}\subset (0,1)$ be such that ![]() $s_n \to 1^-$.
$s_n \to 1^-$.
(i) (Compactness) If
 $(u^n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ is such that
(1.3)
$(u^n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ is such that
(1.3) \begin{equation}
\sup_{n \in \mathbb{N}}\left( (1-s_n)[\tilde u^n]^p_{s_n,p,f_n}+ \| u^n \|_{L^p(\Omega)}^p\right) \lt \infty,
\end{equation}
\begin{equation}
\sup_{n \in \mathbb{N}}\left( (1-s_n)[\tilde u^n]^p_{s_n,p,f_n}+ \| u^n \|_{L^p(\Omega)}^p\right) \lt \infty,
\end{equation}then, up to a subsequence,
 $u^n\to u$ in
$u^n\to u$ in  $L^p(\Omega)$ for some
$L^p(\Omega)$ for some  $u\in W^{1,p}_0(\Omega)$ if
$u\in W^{1,p}_0(\Omega)$ if  $p \gt 1$ or
$p \gt 1$ or  $u \in BV(\Omega)$ if
$u \in BV(\Omega)$ if  $p=1$.
$p=1$.(ii) (
 $\Gamma$-liminf inequality) If
$\Gamma$-liminf inequality) If  $(u^n)_{n\in\mathbb{N}}\subset L^p(\Omega)$ is such that
$(u^n)_{n\in\mathbb{N}}\subset L^p(\Omega)$ is such that  $u^n\to u$ in
$u^n\to u$ in  $L^p(\Omega)$ for some
$L^p(\Omega)$ for some  $u\in W^{1,p}_0(\Omega)$ if
$u\in W^{1,p}_0(\Omega)$ if  $p \gt 1$, or
$p \gt 1$, or  $u\in BV(\Omega)$ if
$u\in BV(\Omega)$ if  $p=1$, then
(1.4)
$p=1$, then
(1.4) \begin{equation}
\begin{aligned}
&K_{d,p} \| \nabla u \|^p_{p,f^2}
\le
\liminf_{n\to \infty}(1-s_n) [\tilde u^n]^p_{s_n,p,f_n} \quad \text{for}\ p \gt 1,\\
& K_{d,1} \| D u \|_{1,f^2}
\le
\liminf_{n\to \infty}(1-s_n) [\tilde u^n]_{s_n, 1, f_n} \quad \text{for}\ p=1.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
&K_{d,p} \| \nabla u \|^p_{p,f^2}
\le
\liminf_{n\to \infty}(1-s_n) [\tilde u^n]^p_{s_n,p,f_n} \quad \text{for}\ p \gt 1,\\
& K_{d,1} \| D u \|_{1,f^2}
\le
\liminf_{n\to \infty}(1-s_n) [\tilde u^n]_{s_n, 1, f_n} \quad \text{for}\ p=1.
\end{aligned}
\end{equation}(iii) (
 $\Gamma$-limsup inequality) If
$\Gamma$-limsup inequality) If  $u\in W^{1,p}_0(\Omega)$ if
$u\in W^{1,p}_0(\Omega)$ if  $p \gt 1$, or
$p \gt 1$, or  $u\in BV(\Omega)$ if
$u\in BV(\Omega)$ if  $p=1$, then there exists
$p=1$, then there exists  $(u^n)_{n\in\mathbb{N}}\subset L^p(\Omega)$ such that
$(u^n)_{n\in\mathbb{N}}\subset L^p(\Omega)$ such that  $u^n\to u$ in
$u^n\to u$ in  $L^p(\Omega)$ and
(1.5)
$L^p(\Omega)$ and
(1.5) \begin{equation}
\begin{aligned}
&K_{d,p} \| \nabla u \|^p_{p,f^2}
=
\lim_{n\to \infty} (1-s_n)[\tilde u^n]^p_{s_n,p,f_n} \quad \text{for}\ p \gt 1,\\
&K_{d,1} \| D u \|_{1,f^2}
=
\lim_{n\to \infty} (1-s_n)[\tilde u^n]_{s_n, 1, f_n} \quad \text{for}\ p =1.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
&K_{d,p} \| \nabla u \|^p_{p,f^2}
=
\lim_{n\to \infty} (1-s_n)[\tilde u^n]^p_{s_n,p,f_n} \quad \text{for}\ p \gt 1,\\
&K_{d,1} \| D u \|_{1,f^2}
=
\lim_{n\to \infty} (1-s_n)[\tilde u^n]_{s_n, 1, f_n} \quad \text{for}\ p =1.
\end{aligned}
\end{equation}
1.2. Convergence of flows
In the case ![]() $p=2$, the
$p=2$, the ![]() $\Gamma$-convergence result obtained in Theorem 1.1 can be complemented with a stability result for the corresponding parabolic flows associated to the energies, see Theorem 1.2 below. Here and below, given a weight
$\Gamma$-convergence result obtained in Theorem 1.1 can be complemented with a stability result for the corresponding parabolic flows associated to the energies, see Theorem 1.2 below. Here and below, given a weight ![]() $f\in L^\infty(\mathbb{R}^d;[0,\infty))$, we define the weighted Laplacian of
$f\in L^\infty(\mathbb{R}^d;[0,\infty))$, we define the weighted Laplacian of ![]() $u \in H^1_0(\Omega)$ as
$u \in H^1_0(\Omega)$ as
in the distributional sense in duality with ![]() $C^\infty_c(\Omega)$ functions. Moreover, given
$C^\infty_c(\Omega)$ functions. Moreover, given ![]() $u\in L^2(\Omega)$ such that
$u\in L^2(\Omega)$ such that ![]() $[u]_{s,2,f} \lt \infty$, we define the weighted fractional
$[u]_{s,2,f} \lt \infty$, we define the weighted fractional ![]() $s$-Laplacian of
$s$-Laplacian of ![]() $u$ as
$u$ as
 \begin{equation}
(-\mathfrak{D})^{s,f}u (x)
=
4f(x)\,\mathrm{p.v.}\int_{\mathbb{R}^d}\frac{\tilde u(x)-\tilde u(y)}{\|x-y\|^{d+2s}}\,f(y)\,\mathrm{d} y,
\end{equation}
\begin{equation}
(-\mathfrak{D})^{s,f}u (x)
=
4f(x)\,\mathrm{p.v.}\int_{\mathbb{R}^d}\frac{\tilde u(x)-\tilde u(y)}{\|x-y\|^{d+2s}}\,f(y)\,\mathrm{d} y,
\end{equation} again in the distributional sense in duality with ![]() $C^\infty_c(\Omega)$ functions. Note that, in the unweighted case
$C^\infty_c(\Omega)$ functions. Note that, in the unweighted case ![]() $f\equiv1$, up to a multiplicative constant, the operators (1.6) and (1.7) become the usual Laplacian and fractional
$f\equiv1$, up to a multiplicative constant, the operators (1.6) and (1.7) become the usual Laplacian and fractional ![]() $s$-Laplacian operators, respectively.
$s$-Laplacian operators, respectively.
Theorem 1.2 (Stability of parabolic flows)
Let ![]() $(f_n)_{n \in \mathbb{N}}$,
$(f_n)_{n \in \mathbb{N}}$, ![]() $f$,
$f$, ![]() $\Omega$, and
$\Omega$, and ![]() $(s_n)_{n\in\mathbb{N}}$ be as in Theorem 1.1. If
$(s_n)_{n\in\mathbb{N}}$ be as in Theorem 1.1. If ![]() $(u^n_0)_{n\in\mathbb{N}}\subset L^2(\Omega)$ is such that
$(u^n_0)_{n\in\mathbb{N}}\subset L^2(\Omega)$ is such that ![]() $u^n_0\to u^\infty_0$ in
$u^n_0\to u^\infty_0$ in ![]() $L^2(\Omega)$ for some function
$L^2(\Omega)$ for some function ![]() $u^\infty_0\in L^2(\Omega)$,
$u^\infty_0\in L^2(\Omega)$, ![]() $[\tilde{u}^n_{0}]_{s_n,2,f_n} \lt \infty$ for every
$[\tilde{u}^n_{0}]_{s_n,2,f_n} \lt \infty$ for every ![]() $n\in\mathbb{N}$, and
$n\in\mathbb{N}$, and
 \begin{equation*}
\sup_{n\in\mathbb{N}}
(1-s_n)[\tilde{u}^n_0]_{s_n,2,f_n}^2 \lt \infty,
\end{equation*}
\begin{equation*}
\sup_{n\in\mathbb{N}}
(1-s_n)[\tilde{u}^n_0]_{s_n,2,f_n}^2 \lt \infty,
\end{equation*}then the following hold:
(i)
 $u^\infty_0\in H^1_0(\Omega)$;
$u^\infty_0\in H^1_0(\Omega)$;(ii) for every
 $T \gt 0$ and for every
$T \gt 0$ and for every  $n\in\mathbb{N}$, the problem
$n\in\mathbb{N}$, the problem
 \begin{equation*}
\begin{cases}
\dot u(t) =(1-s_n)(-\mathfrak{D})^{s_n,f_n}u(t), \quad\textrm{for a.e. } t\in(0,T), \\[1ex]
u(0)=u^n_0,
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
\dot u(t) =(1-s_n)(-\mathfrak{D})^{s_n,f_n}u(t), \quad\textrm{for a.e. } t\in(0,T), \\[1ex]
u(0)=u^n_0,
\end{cases}
\end{equation*}admits a unique solution
 $u_n\in H^1([0,T]; L^2(\Omega))$ such that
$u_n\in H^1([0,T]; L^2(\Omega))$ such that
 \begin{equation*}
(-\mathfrak{D})^{s_n,f_n}u_n(t)\in L^2(\Omega)
\quad
\text{for a.e.} t\in(0,T);
\end{equation*}
\begin{equation*}
(-\mathfrak{D})^{s_n,f_n}u_n(t)\in L^2(\Omega)
\quad
\text{for a.e.} t\in(0,T);
\end{equation*}(iii) the problem
 \begin{equation*}
\begin{cases}
\dot u(t) =K_{d,2}(-\mathfrak{D})^{f} u(t), \quad\text{for a.e. } t\in[0,\infty),\\[1ex]
u(0)=u^\infty_0,
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
\dot u(t) =K_{d,2}(-\mathfrak{D})^{f} u(t), \quad\text{for a.e. } t\in[0,\infty),\\[1ex]
u(0)=u^\infty_0,
\end{cases}
\end{equation*}admits a unique solution
 $u_\infty\in H^1([0,T];H^1_0(\Omega))$;
$u_\infty\in H^1([0,T];H^1_0(\Omega))$;(iv)
 $(u_n)_{n\in\mathbb{N}}$ weakly converges to
$(u_n)_{n\in\mathbb{N}}$ weakly converges to  $u_\infty$ in
$u_\infty$ in  $H^1([0,T];L^2(\Omega))$.
$H^1([0,T];L^2(\Omega))$.
Moreover, if
 \begin{equation*}
\lim_{n\to \infty} (1-s_n)[\tilde{u}^n_0]^2_{s_n,2,f_n}
=
K_{d,2}\| \nabla u^\infty_0\|^2_{2,f^2},
\end{equation*}
\begin{equation*}
\lim_{n\to \infty} (1-s_n)[\tilde{u}^n_0]^2_{s_n,2,f_n}
=
K_{d,2}\| \nabla u^\infty_0\|^2_{2,f^2},
\end{equation*} then ![]() $(u_n)_{n\in\mathbb{N}}$ strongly converges to
$(u_n)_{n\in\mathbb{N}}$ strongly converges to ![]() $u_\infty$ in
$u_\infty$ in ![]() $H^1([0,T];L^2(\Omega))$ and also
$H^1([0,T];L^2(\Omega))$ and also
 \begin{align*}
& u_n(t) \xrightarrow{L^2} u_\infty(t)
\quad
\text{and}
\quad
(1-s_n)[\tilde{u}_n(t)]_{s_n,2,f_n}\to K_{d,2}\|\nabla u_\infty(t)\|_{2, f^2}
\end{align*}
\begin{align*}
& u_n(t) \xrightarrow{L^2} u_\infty(t)
\quad
\text{and}
\quad
(1-s_n)[\tilde{u}_n(t)]_{s_n,2,f_n}\to K_{d,2}\|\nabla u_\infty(t)\|_{2, f^2}
\end{align*} for every ![]() $t\in[0,T]$.
$t\in[0,T]$.
1.3. Organization of the paper
The paper is organized as follows. The notation and some useful preliminary results are detailed in Section 2. The proof of Theorem 1.1 is given in Section 3, while that of Theorem 1.2 can be found in Section 4.
2. Preliminaries
2.1. Notation
We briefly detail the main notation used throughout the paper.
The symbol ![]() $C(*,\cdots,*)$ indicates a generic positive constant that depends on
$C(*,\cdots,*)$ indicates a generic positive constant that depends on ![]() $*,\cdots,*$ only and may change from line to line.
$*,\cdots,*$ only and may change from line to line.
We let ![]() $d\in\mathbb{N}$ and work in the
$d\in\mathbb{N}$ and work in the ![]() $d$-dimensional Euclidean space
$d$-dimensional Euclidean space ![]() $\mathbb{R}^d$. We let
$\mathbb{R}^d$. We let ![]() $x\cdot y$ be the Euclidean inner product between
$x\cdot y$ be the Euclidean inner product between ![]() $x,y\in\mathbb{R}^d$ and
$x,y\in\mathbb{R}^d$ and ![]() $\|x\|$ be the Euclidean norm of
$\|x\|$ be the Euclidean norm of ![]() $x$.
$x$.
We let ![]() $B_r(x)$ be the open ball in
$B_r(x)$ be the open ball in ![]() $\mathbb{R}^d$ of center
$\mathbb{R}^d$ of center ![]() $x\in\mathbb{R}^d$ and radius
$x\in\mathbb{R}^d$ and radius ![]() $r \gt 0$, and we use the shorthand
$r \gt 0$, and we use the shorthand ![]() $B_r= B_r(0)$. Given an open set
$B_r= B_r(0)$. Given an open set ![]() $A\subset\mathbb{R}^d$, we let
$A\subset\mathbb{R}^d$, we let ![]() $A^c=\mathbb{R}^d\setminus A$ be the complement of
$A^c=\mathbb{R}^d\setminus A$ be the complement of ![]() $A$,
$A$, ![]() $\partial A$ be the topological boundary of
$\partial A$ be the topological boundary of ![]() $A$ and, for every
$A$ and, for every ![]() $t \gt 0$,
$t \gt 0$,
Throughout the paper, we let ![]() $\Omega\subset \mathbb{R}^d$ be a bounded open set with Lipschitz boundary.
$\Omega\subset \mathbb{R}^d$ be a bounded open set with Lipschitz boundary.
We let ![]() $\mathcal{L}^d$ be the
$\mathcal{L}^d$ be the ![]() $d$-dimensional Lebesgue measure and
$d$-dimensional Lebesgue measure and ![]() $\mathcal{H}^\alpha$ be the
$\mathcal{H}^\alpha$ be the ![]() $\alpha$-dimensional Hausdorff measure for every
$\alpha$-dimensional Hausdorff measure for every ![]() $\alpha\in[0,d]$. We set
$\alpha\in[0,d]$. We set ![]() $\omega_d=\mathcal{L}^d(B_1)$, so that
$\omega_d=\mathcal{L}^d(B_1)$, so that ![]() $\mathcal H^{d-1}(\partial B_1)=d\,\omega_d$. Throughout the paper, all functions and sets are tacitly assumed to be
$\mathcal H^{d-1}(\partial B_1)=d\,\omega_d$. Throughout the paper, all functions and sets are tacitly assumed to be ![]() $\mathcal L^d$-measurable.
$\mathcal L^d$-measurable.
Let ![]() $p\in[1,\infty)$ and
$p\in[1,\infty)$ and ![]() $f \in L^\infty(\mathbb{R}^d;[0,\infty))$. Given
$f \in L^\infty(\mathbb{R}^d;[0,\infty))$. Given ![]() $m\in\mathbb{N}$ and
$m\in\mathbb{N}$ and ![]() $v\colon\Omega \to \mathbb{R}^m$, we let
$v\colon\Omega \to \mathbb{R}^m$, we let
 \begin{equation}
\|v\|_{p,f}
=
\left( \int_{\Omega} \| v(x)\|^p \,f(x)\,\mathrm{d}x \right)^{\frac{1}{p}}\in[0,\infty],
\end{equation}
\begin{equation}
\|v\|_{p,f}
=
\left( \int_{\Omega} \| v(x)\|^p \,f(x)\,\mathrm{d}x \right)^{\frac{1}{p}}\in[0,\infty],
\end{equation} and we use the shorthand ![]() $\|v\|_p=\|v\|_{p,1}$. We thus let
$\|v\|_p=\|v\|_{p,1}$. We thus let
 \begin{equation*}
[L^p_f(\Omega)]^m = \left\{v\colon \Omega \to \mathbb{R}^m : \|v\|_{p,f} \lt \infty \right\}.
\end{equation*}
\begin{equation*}
[L^p_f(\Omega)]^m = \left\{v\colon \Omega \to \mathbb{R}^m : \|v\|_{p,f} \lt \infty \right\}.
\end{equation*} When ![]() $m=1$, we simply write
$m=1$, we simply write 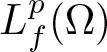 $L^p_f(\Omega)$. We point out that if additionally
$L^p_f(\Omega)$. We point out that if additionally ![]() $f$ takes values in
$f$ takes values in ![]() $(0,\infty)$, under our standing assumptions on
$(0,\infty)$, under our standing assumptions on ![]() $f$ and
$f$ and ![]() $\Omega$, the spaces
$\Omega$, the spaces ![]() $L^p(\Omega)$ and
$L^p(\Omega)$ and 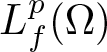 $L^p_f(\Omega)$ are equivalent, with
$L^p_f(\Omega)$ are equivalent, with
 \begin{equation}
(\operatorname{ess\,inf}_\Omega f)\,\|v\|_{p}^p
\le
\|v\|^p_{p,f}
\le
\|f\|_\infty \|v\|^p_{p}.
\end{equation}
\begin{equation}
(\operatorname{ess\,inf}_\Omega f)\,\|v\|_{p}^p
\le
\|v\|^p_{p,f}
\le
\|f\|_\infty \|v\|^p_{p}.
\end{equation} Given ![]() $u\colon\Omega\to\mathbb{R}$, we define
$u\colon\Omega\to\mathbb{R}$, we define ![]() $\tilde u\colon\mathbb{R}^d\to\mathbb{R}$ by letting
$\tilde u\colon\mathbb{R}^d\to\mathbb{R}$ by letting ![]() $\tilde u=u$ in
$\tilde u=u$ in ![]() $\Omega$ and
$\Omega$ and ![]() $\tilde u=0$ in
$\tilde u=0$ in ![]() $\mathbb{R}^d\setminus\Omega$. Thus, given
$\mathbb{R}^d\setminus\Omega$. Thus, given ![]() $s\in(0,1)$, we define
$s\in(0,1)$, we define
 \begin{equation}
[u]_{s,p,f}
=
\left( \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{|\tilde u(x)-\tilde u(y)|^p}{\|x-y\|^{d+sp}}\, f(x)\,f(y)\,\mathrm{d}x\,\mathrm{d}y \right)^{\frac{1}{p}},
\end{equation}
\begin{equation}
[u]_{s,p,f}
=
\left( \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{|\tilde u(x)-\tilde u(y)|^p}{\|x-y\|^{d+sp}}\, f(x)\,f(y)\,\mathrm{d}x\,\mathrm{d}y \right)^{\frac{1}{p}},
\end{equation} for every ![]() $u\colon\Omega\to\mathbb{R}$ and we use the shorthand
$u\colon\Omega\to\mathbb{R}$ and we use the shorthand ![]() $[u]_{s,p}=[u]_{s,p,1}$.
$[u]_{s,p}=[u]_{s,p,1}$.
Finally, we let  $W^{1,p}_0(\Omega)$ for
$W^{1,p}_0(\Omega)$ for ![]() $p \gt 1$, be the closure of
$p \gt 1$, be the closure of ![]() $C^\infty_c(\Omega)$ functions with respect to the Sobolev
$C^\infty_c(\Omega)$ functions with respect to the Sobolev ![]() $p$-norm
$p$-norm 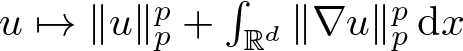 $u\mapsto\|u\|_p^p+\int_{\mathbb{R}^d}\|\nabla u\|_{p}^p\,\mathrm{d} x$, while
$u\mapsto\|u\|_p^p+\int_{\mathbb{R}^d}\|\nabla u\|_{p}^p\,\mathrm{d} x$, while ![]() $BV(\Omega)$ the weak
$BV(\Omega)$ the weak![]() $^*$ closure of
$^*$ closure of ![]() $C^\infty_c(\Omega)$ with respect to the Sobolev
$C^\infty_c(\Omega)$ with respect to the Sobolev ![]() $1$-norm. We also set
$1$-norm. We also set
 \begin{equation}
\|D u\|_{1,f}
=
\int_{\mathbb{R}^d} f\,\mathrm{d}|Du|,
\end{equation}
\begin{equation}
\|D u\|_{1,f}
=
\int_{\mathbb{R}^d} f\,\mathrm{d}|Du|,
\end{equation} whenever ![]() $u \in BV(\Omega)$ and
$u \in BV(\Omega)$ and ![]() $f\in L^\infty(\mathbb{R}^d;(0,\infty))$.
$f\in L^\infty(\mathbb{R}^d;(0,\infty))$.
2.2. Compactness and characterization
We recall the following well-known compactness result, see [Reference Brezis6, Thm. 4.26] for example. Here and below, we let ![]() $
\tau_h w (\,\cdot\,)= w(\,\cdot\,+h)$ for every
$
\tau_h w (\,\cdot\,)= w(\,\cdot\,+h)$ for every ![]() $h\in \mathbb{R}^d$ and
$h\in \mathbb{R}^d$ and ![]() $w\in L^p(\mathbb{R}^d)$.
$w\in L^p(\mathbb{R}^d)$.
Theorem 2.1 Let ![]() $p\in[1,\infty)$. If
$p\in[1,\infty)$. If ![]() $(v^n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ is such that
$(v^n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ is such that
 \begin{equation*}
\sup_{n\in\mathbb{N}}\|v^n\|_p \lt \infty
\quad
\text{and}
\quad
\lim_{h \to 0}
\sup_{n \in \mathbb{N}}
\| \tau_{h}\tilde v^n-\tilde v^n \|_{L^p(\mathbb{R}^d)}
=
0,
\end{equation*}
\begin{equation*}
\sup_{n\in\mathbb{N}}\|v^n\|_p \lt \infty
\quad
\text{and}
\quad
\lim_{h \to 0}
\sup_{n \in \mathbb{N}}
\| \tau_{h}\tilde v^n-\tilde v^n \|_{L^p(\mathbb{R}^d)}
=
0,
\end{equation*} then, up to a subsequence, ![]() $v^n\to v$ in
$v^n\to v$ in ![]() $L^p(\Omega)$ for some
$L^p(\Omega)$ for some ![]() $v\in L^p(\Omega)$.
$v\in L^p(\Omega)$.
We also recall the following well-known characterization of Sobolev and ![]() $BV$ functions, see [Reference Brezis6, Prop. 9.3 and Rem. 6] for example.
$BV$ functions, see [Reference Brezis6, Prop. 9.3 and Rem. 6] for example.
Theorem 2.2 Let ![]() $p\in[1,\infty)$ and
$p\in[1,\infty)$ and ![]() $v \in L^p(\mathbb{R}^d)$. The following are equivalent:
$v \in L^p(\mathbb{R}^d)$. The following are equivalent:
(i)
 $v \in W^{1,p}(\mathbb{R}^d)$ for
$v \in W^{1,p}(\mathbb{R}^d)$ for  $p \gt 1$ or
$p \gt 1$ or  $v \in BV(\mathbb{R}^d)$ for
$v \in BV(\mathbb{R}^d)$ for  $p=1$;
$p=1$;(ii)
 $\sup_{\|h\|\le1} \| \tau_{h}v-v \|_{p} \lt \infty$.
$\sup_{\|h\|\le1} \| \tau_{h}v-v \|_{p} \lt \infty$.
3. Proof of Theorem 1.1
Throughout this section, we let ![]() $p\in [1,\infty)$,
$p\in [1,\infty)$, ![]() $(s_n)_{n\in\mathbb{N}}\subset(0,1)$ be such that
$(s_n)_{n\in\mathbb{N}}\subset(0,1)$ be such that ![]() $s_n\to1^-$, and
$s_n\to1^-$, and ![]() $(f_n)_{n\in\mathbb{N}}\subset L^\infty(\mathbb{R}^d;[0,\infty))$ and
$(f_n)_{n\in\mathbb{N}}\subset L^\infty(\mathbb{R}^d;[0,\infty))$ and ![]() $ f\in\mathrm{Lip}_b(\mathbb{R}^d; (0,\infty))$ be such that
$ f\in\mathrm{Lip}_b(\mathbb{R}^d; (0,\infty))$ be such that ![]() $f_n\to f$ in
$f_n\to f$ in ![]() $L^\infty(\mathbb{R}^d)$.
$L^\infty(\mathbb{R}^d)$.
We preliminarily prove Theorem 1.1 in the case ![]() $f_n=f$ for every
$f_n=f$ for every ![]() $n\in\mathbb{N}$. We restate our result in this particular case for better clarity.
$n\in\mathbb{N}$. We restate our result in this particular case for better clarity.
Theorem 3.1 The following hold.
(i) (Compactness) If
 $(u^n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ is such that
(3.1)
$(u^n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ is such that
(3.1) \begin{equation}
\sup_{n \in \mathbb{N}}
\left(
(1-s_n)[\tilde u^n]^p_{s_n,p,f}+ \| u^n \|_{L^p(\Omega)}^p
\right) \lt \infty,
\end{equation}
\begin{equation}
\sup_{n \in \mathbb{N}}
\left(
(1-s_n)[\tilde u^n]^p_{s_n,p,f}+ \| u^n \|_{L^p(\Omega)}^p
\right) \lt \infty,
\end{equation}then, up to a subsequence,
 $u^n\to u$ in
$u^n\to u$ in  $L^p(\Omega)$ for some
$L^p(\Omega)$ for some  $u\in W^{1,p}_0(\Omega)$ if
$u\in W^{1,p}_0(\Omega)$ if  $p \in (1,\infty)$ or
$p \in (1,\infty)$ or  $ u \in BV(\Omega)$ if
$ u \in BV(\Omega)$ if  $p=1$.
$p=1$.(ii) (
 $\Gamma$-liminf inequality) If
$\Gamma$-liminf inequality) If  $(u_n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ is such that
$(u_n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ is such that  $u_n\to u$ in
$u_n\to u$ in  $L^p(\Omega)$ for some
$L^p(\Omega)$ for some  $u\in L^p(\Omega)$, then
(3.2)
$u\in L^p(\Omega)$, then
(3.2) \begin{equation}
\begin{aligned}
&K_{d,p} \| \nabla u \|^p_{p,f^2}
\le
\liminf_{n\to \infty}(1-s_n) [\tilde u^n]^p_{s_n,p,f} \quad \text{for}\ p \in (1,\infty),\\
& K_{d,1} \| D u \|_{1,f^2}
\le
\liminf_{n\to \infty}(1-s_n) [\tilde u^n]_{s_n, 1, f} \quad \text{for}\ p=1.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
&K_{d,p} \| \nabla u \|^p_{p,f^2}
\le
\liminf_{n\to \infty}(1-s_n) [\tilde u^n]^p_{s_n,p,f} \quad \text{for}\ p \in (1,\infty),\\
& K_{d,1} \| D u \|_{1,f^2}
\le
\liminf_{n\to \infty}(1-s_n) [\tilde u^n]_{s_n, 1, f} \quad \text{for}\ p=1.
\end{aligned}
\end{equation}(iii) (
 $\Gamma$-limsup inequality) If
$\Gamma$-limsup inequality) If  $u\in W^{1,p}_0(\Omega)$ if
$u\in W^{1,p}_0(\Omega)$ if  $p \gt 1$, or
$p \gt 1$, or  $u\in BV(\Omega)$ if
$u\in BV(\Omega)$ if  $p=1$, then there exists
$p=1$, then there exists  $(u^n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ such that
$(u^n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ such that  $u_n\to u$ in
$u_n\to u$ in  $L^p(\Omega)$ and
(3.3)
$L^p(\Omega)$ and
(3.3) \begin{equation}
\begin{aligned}
&K_{d,p} \| \nabla u \|^p_{p,f^2}
=
\lim_{n\to \infty} (1-s_n)[\tilde u^n]^p_{s_n,p,f} \quad \text{for}\ p \in (1,\infty),\\
&K_{d,1} \| D u \|_{1,f^2}
=
\lim_{n\to \infty} (1-s_n)[\tilde u^n]_{s_n,1, f} \quad \text{for}\ p =1.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
&K_{d,p} \| \nabla u \|^p_{p,f^2}
=
\lim_{n\to \infty} (1-s_n)[\tilde u^n]^p_{s_n,p,f} \quad \text{for}\ p \in (1,\infty),\\
&K_{d,1} \| D u \|_{1,f^2}
=
\lim_{n\to \infty} (1-s_n)[\tilde u^n]_{s_n,1, f} \quad \text{for}\ p =1.
\end{aligned}
\end{equation}
The proof of the three statements (i), (ii), and (iii) of Theorem 3.1 is split across Sections 3.1, 3.2, and 3.3. The proof of Theorem 1.1 is given in Section 3.4.
3.1. Proof of Theorem 3.1(i)
We adapt the strategy of [Reference Ambrosio, De Philippis and Martinazzi1] to our setting. To this aim, we need two preliminary results. The first one is the following, which generalizes [Reference Ambrosio, De Philippis and Martinazzi1, Prop. 5] to any ![]() $p\in[1,\infty)$ and weighted
$p\in[1,\infty)$ and weighted ![]() $L^p$ norms. We also refer to [Reference Crismale, De Luca, Kubin, Ninno and Ponsiglione9, Prop. 2.4] for the case
$L^p$ norms. We also refer to [Reference Crismale, De Luca, Kubin, Ninno and Ponsiglione9, Prop. 2.4] for the case ![]() $p=2$ without weights.
$p=2$ without weights.
Proposition 3.2. Let ![]() $f \in \mathrm{Lip}_b(\mathbb{R}^d; (0,\infty))$. There exists
$f \in \mathrm{Lip}_b(\mathbb{R}^d; (0,\infty))$. There exists ![]() $C=C(d,p) \gt 0$ such that
$C=C(d,p) \gt 0$ such that
 \begin{equation}
\| \tau_{h}v-v \|_{L^p_f(E)}^{p}
\leq
C\frac{\|h\|^{p}}{\varrho^{d+p}}\int_{B_\varrho}\|\tau_{y}v-v \|_{L^p_f(E_{\|h\|})}^p \,\mathrm{d} y
\end{equation}
\begin{equation}
\| \tau_{h}v-v \|_{L^p_f(E)}^{p}
\leq
C\frac{\|h\|^{p}}{\varrho^{d+p}}\int_{B_\varrho}\|\tau_{y}v-v \|_{L^p_f(E_{\|h\|})}^p \,\mathrm{d} y
\end{equation} for every ![]() $v \in L^p(\mathbb{R}^d)$,
$v \in L^p(\mathbb{R}^d)$, ![]() $h \in \mathbb{R}^d$,
$h \in \mathbb{R}^d$, ![]() $\varrho\in(0,\|h\|]$, and every bounded open set
$\varrho\in(0,\|h\|]$, and every bounded open set ![]() $E \subset\mathbb{R}^d$, where
$E \subset\mathbb{R}^d$, where ![]() $E_{\|h\|}$ is defined according to the notation in (2.1).
$E_{\|h\|}$ is defined according to the notation in (2.1).
Proof. The proof closely follows the one of [Reference Ambrosio, De Philippis and Martinazzi1, Prop. 5]. Let ![]() $\varphi \in C_{c}^1(B_1)$ be such that
$\varphi \in C_{c}^1(B_1)$ be such that
 \begin{equation}
\varphi\geq 0
\quad
\text{and}
\quad
\int_{B_1} \varphi(x)\,\mathrm{d} x=1.
\end{equation}
\begin{equation}
\varphi\geq 0
\quad
\text{and}
\quad
\int_{B_1} \varphi(x)\,\mathrm{d} x=1.
\end{equation} For every ![]() $\varrho \gt 0$, we let
$\varrho \gt 0$, we let ![]() $U_\varrho$ and
$U_\varrho$ and ![]() $V_\varrho$ be defined as
$V_\varrho$ be defined as
 \begin{align*}
U_\varrho(x)
&
=
\frac{1}{\varrho^d} \int_{B_\varrho} v(x+y) \varphi\left(\frac{y}{\varrho}\right)\,\mathrm{d} y,
\\
V_\varrho(x)
&
=\frac{1}{\varrho^d}\int_{B_\varrho}(v(x)-v(x+y))\varphi\left(\frac{y}{\varrho}\right)\,\mathrm{d} y,
\end{align*}
\begin{align*}
U_\varrho(x)
&
=
\frac{1}{\varrho^d} \int_{B_\varrho} v(x+y) \varphi\left(\frac{y}{\varrho}\right)\,\mathrm{d} y,
\\
V_\varrho(x)
&
=\frac{1}{\varrho^d}\int_{B_\varrho}(v(x)-v(x+y))\varphi\left(\frac{y}{\varrho}\right)\,\mathrm{d} y,
\end{align*} for every ![]() $x\in\mathbb{R}^d$.
Owing to (3.5), we have that
$x\in\mathbb{R}^d$.
Owing to (3.5), we have that ![]() $
v(x)
=
U_\varrho(x)+V_\varrho(x)$ for every
$
v(x)
=
U_\varrho(x)+V_\varrho(x)$ for every ![]() $\varrho \gt 0$ and
$\varrho \gt 0$ and ![]() $x\in\mathbb{R}^d$, so that
$x\in\mathbb{R}^d$, so that
We now estimate each term in the right-hand side of (3.6) separately. Concerning the second and third term, by Jensen’s inequality, we can estimate
 \begin{equation}
\vert V_\varrho(\xi) \vert^{p}
\leq
\frac{\omega_d}{\varrho^d}\,\|\varphi \|^p_{\infty} \int_{B_\varrho} \vert v(\xi)-\tau_{y}v(\xi) \vert^p\, \mathrm{d} y,
\end{equation}
\begin{equation}
\vert V_\varrho(\xi) \vert^{p}
\leq
\frac{\omega_d}{\varrho^d}\,\|\varphi \|^p_{\infty} \int_{B_\varrho} \vert v(\xi)-\tau_{y}v(\xi) \vert^p\, \mathrm{d} y,
\end{equation} for every ![]() $\xi\in\mathbb{R}^d$. Instead, concerning the first term, by the change of variables
$\xi\in\mathbb{R}^d$. Instead, concerning the first term, by the change of variables ![]() $z=x+y$, we can rewrite
$z=x+y$, we can rewrite
 \begin{equation*}
U_\varrho(x)
=
\frac{1}{\varrho^d}\int_{B_\varrho(x)}v(z)\,\varphi\left(\frac{z-x}{\varrho}\right) \,\mathrm{d} z.
\end{equation*}
\begin{equation*}
U_\varrho(x)
=
\frac{1}{\varrho^d}\int_{B_\varrho(x)}v(z)\,\varphi\left(\frac{z-x}{\varrho}\right) \,\mathrm{d} z.
\end{equation*} Thus, owing to the fact that ![]() $\varphi((z-\cdot)\varrho^{-1})\in C^1_c(B_{\varrho}(x))$, we can integrate by parts and get
$\varphi((z-\cdot)\varrho^{-1})\in C^1_c(B_{\varrho}(x))$, we can integrate by parts and get
 \begin{equation*}
\begin{aligned}
\nabla U_\varrho(x)
=
&
-\frac{1}{\varrho^{d+1}}\int_{B_\varrho(x)} v(z)\,\nabla\varphi\left(\frac{z-x}{\varrho}\right) \,\mathrm{d} z
\\
=
&
-\frac{1}{\varrho^{d+1}}\int_{B_\varrho(x)}(v(z)-v(x))\,\nabla\varphi\left(\frac{z-x}{\varrho}\right) \,\mathrm{d} z
\\
=
&
-\frac{1}{\varrho^{d+1}}\int_{B_\varrho}(v(x+y)-v(x))\,\nabla\varphi\left(\frac{y}{\varrho}\right) \,\mathrm{d} y.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
\nabla U_\varrho(x)
=
&
-\frac{1}{\varrho^{d+1}}\int_{B_\varrho(x)} v(z)\,\nabla\varphi\left(\frac{z-x}{\varrho}\right) \,\mathrm{d} z
\\
=
&
-\frac{1}{\varrho^{d+1}}\int_{B_\varrho(x)}(v(z)-v(x))\,\nabla\varphi\left(\frac{z-x}{\varrho}\right) \,\mathrm{d} z
\\
=
&
-\frac{1}{\varrho^{d+1}}\int_{B_\varrho}(v(x+y)-v(x))\,\nabla\varphi\left(\frac{y}{\varrho}\right) \,\mathrm{d} y.
\end{aligned}
\end{equation*}Therefore, by the Fundamental Theorem of Calculus and by Jensen’s inequality, we obtain
 \begin{align}
\vert U_\varrho(x&+h) - U_\varrho(x)\vert^{p}
\leq
\| h \|^{p} \int_{0}^{1} \vert \nabla U_\varrho(x+th) \vert^p \,\mathrm{d} t
\nonumber
\\
&
\leq \omega_d^{p-1}\frac{\|h\|^p}{\varrho^{d+p}}\| \nabla\varphi \|_{\infty}^p\int_{0}^{1} \int_{B_\varrho} \vert \tau_yv(x+th)-v(x+th)\vert^p \,\mathrm{d}y\,\mathrm{d}t.
\end{align}
\begin{align}
\vert U_\varrho(x&+h) - U_\varrho(x)\vert^{p}
\leq
\| h \|^{p} \int_{0}^{1} \vert \nabla U_\varrho(x+th) \vert^p \,\mathrm{d} t
\nonumber
\\
&
\leq \omega_d^{p-1}\frac{\|h\|^p}{\varrho^{d+p}}\| \nabla\varphi \|_{\infty}^p\int_{0}^{1} \int_{B_\varrho} \vert \tau_yv(x+th)-v(x+th)\vert^p \,\mathrm{d}y\,\mathrm{d}t.
\end{align} Now, using that ![]() $\varrho \lt \|h\|$ and combining (3.6), (3.7), and (3.8), we get that
$\varrho \lt \|h\|$ and combining (3.6), (3.7), and (3.8), we get that
 \begin{align}
\vert \tau_h v(x)-v(x)\vert^p
&
\leq
C \frac{\|h\|^p}{\varrho^{d+p}} \int_{0}^{1} \int_{B_\varrho} \vert \tau_y v(x+th)-v(x+th)\vert^p \,\mathrm{d}y\,\mathrm{d}t
\nonumber
\\
&\quad
+ C \frac{\|h\|^p}{\varrho^{d+p}} \int_{B_\varrho} \vert \tau_y v(x)-v(x)\vert^p \,\mathrm{d}y
\nonumber
\\
&\quad
+ C \frac{\|h\|^p}{\varrho^{d+p}}\int_{B_\varrho} \vert \tau_y v(x+h)-v(x+h)\vert^{p} \,\mathrm{d}y,
\end{align}
\begin{align}
\vert \tau_h v(x)-v(x)\vert^p
&
\leq
C \frac{\|h\|^p}{\varrho^{d+p}} \int_{0}^{1} \int_{B_\varrho} \vert \tau_y v(x+th)-v(x+th)\vert^p \,\mathrm{d}y\,\mathrm{d}t
\nonumber
\\
&\quad
+ C \frac{\|h\|^p}{\varrho^{d+p}} \int_{B_\varrho} \vert \tau_y v(x)-v(x)\vert^p \,\mathrm{d}y
\nonumber
\\
&\quad
+ C \frac{\|h\|^p}{\varrho^{d+p}}\int_{B_\varrho} \vert \tau_y v(x+h)-v(x+h)\vert^{p} \,\mathrm{d}y,
\end{align}where we have set
Multiplying inequality (3.9) by ![]() $f(x)$ and integrating with respect to
$f(x)$ and integrating with respect to ![]() $x\in E$, the claim immediately follows by Fubini’s Theorem. We omit the simple details.
$x\in E$, the claim immediately follows by Fubini’s Theorem. We omit the simple details.
We can now pass to the following result, which extends [Reference Ambrosio, De Philippis and Martinazzi1, Prop. 4] to any ![]() $p\in[1,\infty)$ also in the case of weighted
$p\in[1,\infty)$ also in the case of weighted ![]() $L^p$ norms.
$L^p$ norms.
Proposition 3.3. Let ![]() $f\in \mathrm{Lip}_b(\mathbb{R}^d; (0,\infty))$. There exists
$f\in \mathrm{Lip}_b(\mathbb{R}^d; (0,\infty))$. There exists ![]() $C=C(d,p) \gt 0$ such that
$C=C(d,p) \gt 0$ such that
 \begin{equation*}
\| \tau_{h}v-v \|_{L^p_f(E)}^{p}
\leq
C (1-s) \|h\|^{sp} \int_{B_{\|h\|}} \frac{\|\tau_{y}v-v \|_{L^{p}_f(E_{\| h \|})}^{p}}{\|y\|^{d+sp}} \,\mathrm{d}y
\end{equation*}
\begin{equation*}
\| \tau_{h}v-v \|_{L^p_f(E)}^{p}
\leq
C (1-s) \|h\|^{sp} \int_{B_{\|h\|}} \frac{\|\tau_{y}v-v \|_{L^{p}_f(E_{\| h \|})}^{p}}{\|y\|^{d+sp}} \,\mathrm{d}y
\end{equation*} for every ![]() $v \in L^p(\mathbb{R}^d)$,
$v \in L^p(\mathbb{R}^d)$, ![]() $h \in \mathbb{R}^d$, and every bounded open set
$h \in \mathbb{R}^d$, and every bounded open set ![]() $E \subset \mathbb{R}^d$, where
$E \subset \mathbb{R}^d$, where ![]() $E_{\|h\|}$ is defined according to the notation in (2.1).
$E_{\|h\|}$ is defined according to the notation in (2.1).
The proof of Proposition 3.3 requires the following Hardy-type inequality, which is taken from [Reference Ambrosio, De Philippis and Martinazzi1, Prop. 6].
Lemma 3.4. If ![]() $\varphi\colon\mathbb{R}\to [0,\infty)$ is a Borel function, then
$\varphi\colon\mathbb{R}\to [0,\infty)$ is a Borel function, then
 \begin{equation}
\int_{0}^{r} \frac{1}{\varrho^{d+l+1}} \int_{0}^{\varrho} \varphi(t)\,\mathrm{d}t\,\mathrm{d}\varrho
\leq
\frac{1}{d+l}\int_{0}^{r} \frac{\varphi(t)}{t^{d+l}}\,\mathrm{d}t,
\end{equation}
\begin{equation}
\int_{0}^{r} \frac{1}{\varrho^{d+l+1}} \int_{0}^{\varrho} \varphi(t)\,\mathrm{d}t\,\mathrm{d}\varrho
\leq
\frac{1}{d+l}\int_{0}^{r} \frac{\varphi(t)}{t^{d+l}}\,\mathrm{d}t,
\end{equation} for every ![]() $l,r\ge 0$.
$l,r\ge 0$.
Actually, in the proof of Proposition 3.3 we use the weaker estimate
 \begin{equation}
\int_{0}^{r} \frac{1}{\varrho^{d+l+1}} \int_{0}^{\varrho} \varphi(t)\,\mathrm{d}t\,\mathrm{d}\varrho
\leq
\frac{1}{d}\int_{0}^{r} \frac{\varphi(t)}{t^{d+l}}\,\mathrm{d}t,
\end{equation}
\begin{equation}
\int_{0}^{r} \frac{1}{\varrho^{d+l+1}} \int_{0}^{\varrho} \varphi(t)\,\mathrm{d}t\,\mathrm{d}\varrho
\leq
\frac{1}{d}\int_{0}^{r} \frac{\varphi(t)}{t^{d+l}}\,\mathrm{d}t,
\end{equation} that is, we can ignore the dependence on ![]() $l$ in the prefactor in the right-hand side of (3.10).
$l$ in the prefactor in the right-hand side of (3.10).
Proof of Proposition 3.3
We let ![]() $\varphi_v\colon[0,\|h\|]\to\mathbb{R}$ be defined as
$\varphi_v\colon[0,\|h\|]\to\mathbb{R}$ be defined as
 \begin{equation}
\varphi_v(t)
=
\int_{\partial B_t} \|\tau_{y} v - v \|_{L^{p}_f (E_{\|h\| })}^{p} \,\mathrm{d}\mathcal{H}^{d-1}(y),
\end{equation}
\begin{equation}
\varphi_v(t)
=
\int_{\partial B_t} \|\tau_{y} v - v \|_{L^{p}_f (E_{\|h\| })}^{p} \,\mathrm{d}\mathcal{H}^{d-1}(y),
\end{equation} for all ![]() $t \gt 0$. Owing to (3.4) and to the definition in (3.12), we can estimate
$t \gt 0$. Owing to (3.4) and to the definition in (3.12), we can estimate
 \begin{equation}
\| \tau_{h}v-v \|_{L_f^{p}(E)}^{p}
\leq
C\frac{\|h\|^{p}}{\varrho^{d+p}} \int_{0}^{\varrho} \varphi_v(t)\,\mathrm{d}t,
\end{equation}
\begin{equation}
\| \tau_{h}v-v \|_{L_f^{p}(E)}^{p}
\leq
C\frac{\|h\|^{p}}{\varrho^{d+p}} \int_{0}^{\varrho} \varphi_v(t)\,\mathrm{d}t,
\end{equation} for some ![]() $C=C(d,p) \gt 0$. We now multiply both sides of (3.13) by
$C=C(d,p) \gt 0$. We now multiply both sides of (3.13) by ![]() $\varrho^{-1+p-sp}$ and integrate in the interval
$\varrho^{-1+p-sp}$ and integrate in the interval ![]() $ [0,\|h\|]$ with respect to
$ [0,\|h\|]$ with respect to ![]() $\varrho$, getting
$\varrho$, getting
 \begin{equation*}
\| \tau_{h}v-v \|_{L_f^{p}(E)}^{p}
\leq
C p(1-s) \frac{\|h\|^{p}}{\|h\|^{p-sp}} \int_0^{\|h\|}\frac{1}{\varrho^{d+sp+1}} \int_{0}^{\varrho} \varphi_v(t)\,\mathrm{d}t \,\mathrm{d}\varrho.
\end{equation*}
\begin{equation*}
\| \tau_{h}v-v \|_{L_f^{p}(E)}^{p}
\leq
C p(1-s) \frac{\|h\|^{p}}{\|h\|^{p-sp}} \int_0^{\|h\|}\frac{1}{\varrho^{d+sp+1}} \int_{0}^{\varrho} \varphi_v(t)\,\mathrm{d}t \,\mathrm{d}\varrho.
\end{equation*} By exploiting (3.11) with ![]() $l=sp$ and
$l=sp$ and ![]() $\varphi=\varphi_v$, we thus obtain that
$\varphi=\varphi_v$, we thus obtain that
 \begin{equation*}
\| \tau_{h}v-v \|_{L^{p}_f(E)}^{p}
\leq
C(1-s) \|h\|^{sp} \int_{0}^{\|h\|}\frac{\varphi_v(t)}{t^{d+sp}}\,\mathrm{d}t,
\end{equation*}
\begin{equation*}
\| \tau_{h}v-v \|_{L^{p}_f(E)}^{p}
\leq
C(1-s) \|h\|^{sp} \int_{0}^{\|h\|}\frac{\varphi_v(t)}{t^{d+sp}}\,\mathrm{d}t,
\end{equation*} and the conclusion follows from the very definition of ![]() $\varphi_v$.
$\varphi_v$.
We are now ready to detail the proof of the compactness statement (i) in Theorem 3.1.
Proof of Theorem 3.1(i)
Given ![]() $h\in\mathbb{R}^d$ such that
$h\in\mathbb{R}^d$ such that ![]() $\|h\| \lt 1$, we have
$\|h\| \lt 1$, we have ![]() $\Omega_{\|h\|}\Subset \Omega_1 \Subset (\Omega_1)_{\|h\|}$ (recall the notation in (2.1)). We can hence set
$\Omega_{\|h\|}\Subset \Omega_1 \Subset (\Omega_1)_{\|h\|}$ (recall the notation in (2.1)). We can hence set
 \begin{equation*}
c = c(\Omega, f) =\inf_{(\Omega_1)_{\|h\|}} f \gt 0,
\end{equation*}
\begin{equation*}
c = c(\Omega, f) =\inf_{(\Omega_1)_{\|h\|}} f \gt 0,
\end{equation*}and observe that
 \begin{equation*}
c^2 \| \tau_{h}\tilde{u}^n-\tilde{u}^n \|^p_{L^{p}(\mathbb{R}^d)}
=
c^2 \| \tau_{h}\tilde{u}^n-\tilde{u}^n \|^p_{L^{p}(\Omega_{\|h\|})}
\le
c \| \tau_{h}\tilde{u}^n-\tilde{u}^n \|^p_{L^{p}_{f}(\Omega_1)}.
\end{equation*}
\begin{equation*}
c^2 \| \tau_{h}\tilde{u}^n-\tilde{u}^n \|^p_{L^{p}(\mathbb{R}^d)}
=
c^2 \| \tau_{h}\tilde{u}^n-\tilde{u}^n \|^p_{L^{p}(\Omega_{\|h\|})}
\le
c \| \tau_{h}\tilde{u}^n-\tilde{u}^n \|^p_{L^{p}_{f}(\Omega_1)}.
\end{equation*} By Proposition 3.3 applied on ![]() $\Omega_1$ and by the previous inequality, we have
$\Omega_1$ and by the previous inequality, we have
 \begin{equation*}
c^2 \| \tau_{h}\tilde{u}^n-\tilde{u}^n \|^p_{L^{p}(\mathbb{R}^d)}
\le
C(1-s_n)\|h\|^{s_n p} \int_{B_{\|h\|}} \frac{c \|\tau_{y}\tilde{u}^n-\tilde{u}^n \|_{L^{p}_f((\Omega_1)_{\| h \|})}^{p}}{\|y\|^{d+s_n p}} \,\mathrm{d}y,
\end{equation*}
\begin{equation*}
c^2 \| \tau_{h}\tilde{u}^n-\tilde{u}^n \|^p_{L^{p}(\mathbb{R}^d)}
\le
C(1-s_n)\|h\|^{s_n p} \int_{B_{\|h\|}} \frac{c \|\tau_{y}\tilde{u}^n-\tilde{u}^n \|_{L^{p}_f((\Omega_1)_{\| h \|})}^{p}}{\|y\|^{d+s_n p}} \,\mathrm{d}y,
\end{equation*} where ![]() $C=C(d,p) \gt 0$. Now, explicitly writing down the
$C=C(d,p) \gt 0$. Now, explicitly writing down the ![]() $L^p_f$ norm on the right-hand side, swapping order of integration, performing the change of variables
$L^p_f$ norm on the right-hand side, swapping order of integration, performing the change of variables ![]() $y=\xi-x$, and bounding
$y=\xi-x$, and bounding ![]() $c$ with
$c$ with ![]() $f(\xi)$, we obtain that
$f(\xi)$, we obtain that
 \begin{align*}
c^2 \| \tau_{h}\tilde{u}^n&-
\tilde{u}^n \|^p_{L^{p}(\mathbb{R}^d)}\\
&\le
C(1-s_n) \|h\|^{s_np} \int_{B_{\|h\|}} \int_{(\Omega_1)_{\|h\|}} \frac{|\tilde{u}^n(x+y)-\tilde{u}^n(x)|^p}{\|y\|^{d+s_n p}} c f(x) \,\mathrm{d}x \,\mathrm{d}y
\\
&
\leq
C(1-s_n) \|h\|^{s_np} \int_{(\Omega_1)_{\|h\|}} \int_{B_{\|h\|}(x)} \frac{|\tilde{u}^n(\xi)-\tilde{u}^n(x)|^p}{\|\xi-x\|^{d+s_n p}} f(\xi)f(x)\,\mathrm{d}\xi \,\mathrm{d}x
\\
&
\le
C(1-s_n) \|h\|^{s_np} [\tilde u^n]^p_{s_n, p,f}.
\end{align*}
\begin{align*}
c^2 \| \tau_{h}\tilde{u}^n&-
\tilde{u}^n \|^p_{L^{p}(\mathbb{R}^d)}\\
&\le
C(1-s_n) \|h\|^{s_np} \int_{B_{\|h\|}} \int_{(\Omega_1)_{\|h\|}} \frac{|\tilde{u}^n(x+y)-\tilde{u}^n(x)|^p}{\|y\|^{d+s_n p}} c f(x) \,\mathrm{d}x \,\mathrm{d}y
\\
&
\leq
C(1-s_n) \|h\|^{s_np} \int_{(\Omega_1)_{\|h\|}} \int_{B_{\|h\|}(x)} \frac{|\tilde{u}^n(\xi)-\tilde{u}^n(x)|^p}{\|\xi-x\|^{d+s_n p}} f(\xi)f(x)\,\mathrm{d}\xi \,\mathrm{d}x
\\
&
\le
C(1-s_n) \|h\|^{s_np} [\tilde u^n]^p_{s_n, p,f}.
\end{align*} Dividing by ![]() $c^2$ and owing to our equiboundedness assumption (3.1), we get that
$c^2$ and owing to our equiboundedness assumption (3.1), we get that
for all ![]() $h\in\mathbb{R}^d$ such that
$h\in\mathbb{R}^d$ such that ![]() $\|h\|\le 1$. Thus, owing to (3.1) and to (3.14), we can apply Theorem 2.1 and find
$\|h\|\le 1$. Thus, owing to (3.1) and to (3.14), we can apply Theorem 2.1 and find ![]() $u \in L^{p}(\mathbb{R}^d)$ such that, up to a subsequence,
$u \in L^{p}(\mathbb{R}^d)$ such that, up to a subsequence, ![]() $\tilde u^n \to u$ in
$\tilde u^n \to u$ in ![]() $L^p(\mathbb{R}^d)$. Furthermore, since
$L^p(\mathbb{R}^d)$. Furthermore, since ![]() $\tilde{u}^n = 0$ for all
$\tilde{u}^n = 0$ for all ![]() $n\in\mathbb{N}$ on
$n\in\mathbb{N}$ on ![]() $\mathbb{R}^d\setminus \Omega$, we also have that
$\mathbb{R}^d\setminus \Omega$, we also have that ![]() $u=0$ on
$u=0$ on ![]() $\mathbb{R}^d \setminus \Omega$. Finally, letting
$\mathbb{R}^d \setminus \Omega$. Finally, letting ![]() $n\to\infty$ in (3.14), we have
$n\to\infty$ in (3.14), we have
for all ![]() $h$ with
$h$ with ![]() $\|h\|\le 1$, so that
$\|h\|\le 1$, so that ![]() $u\in W^{1,p}(\mathbb{R}^d)$ for
$u\in W^{1,p}(\mathbb{R}^d)$ for ![]() $p \gt 1$ or
$p \gt 1$ or ![]() $u\in BV(\mathbb{R}^d)$ for
$u\in BV(\mathbb{R}^d)$ for ![]() $p=1$ by Theorem 2.2. Since
$p=1$ by Theorem 2.2. Since ![]() $u=0$ on
$u=0$ on ![]() $\mathbb{R}^d\setminus \Omega$ and
$\mathbb{R}^d\setminus \Omega$ and ![]() $\Omega$ has Lipschitz boundary, we get that
$\Omega$ has Lipschitz boundary, we get that 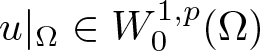 $u|_\Omega\in W^{1,p}_0(\Omega)$ for
$u|_\Omega\in W^{1,p}_0(\Omega)$ for ![]() $p \gt 1$, or
$p \gt 1$, or ![]() $u|_\Omega\in BV(\Omega)$ for
$u|_\Omega\in BV(\Omega)$ for ![]() $p=1$, concluding the proof.
$p=1$, concluding the proof.
3.2. Proof of Theorem 3.1(ii)
We adapt the strategy of the proof of [Reference Crismale, De Luca, Kubin, Ninno and Ponsiglione9, Thm. 2.1] to our setting. To this aim, we need some preliminaries.
Let us begin with some notation. We let ![]() $Q=(-1,1)^d$. Consequently, given
$Q=(-1,1)^d$. Consequently, given ![]() $\gamma \gt 0$, for every
$\gamma \gt 0$, for every ![]() $i \in \gamma \mathbb{Z}^d$ and
$i \in \gamma \mathbb{Z}^d$ and ![]() $a\ge0$, we let
$a\ge0$, we let ![]() $Q_i^a= i+ aQ$. Note that, if
$Q_i^a= i+ aQ$. Note that, if ![]() $a=\gamma$, then the family of cubes
$a=\gamma$, then the family of cubes ![]() $(Q^\gamma_i)_{i}$ is a tiling of
$(Q^\gamma_i)_{i}$ is a tiling of ![]() $\mathbb{R}^d$. Moreover, since
$\mathbb{R}^d$. Moreover, since ![]() $\Omega$ is bounded, the set
$\Omega$ is bounded, the set
 \begin{equation*}I_\gamma=\{i\in\gamma\mathbb{Z}^d:\mathcal L^d(Q_i^\gamma\cap\Omega) \gt 0\}\end{equation*}
\begin{equation*}I_\gamma=\{i\in\gamma\mathbb{Z}^d:\mathcal L^d(Q_i^\gamma\cap\Omega) \gt 0\}\end{equation*} is finite. In addition, given ![]() $f\colon\mathbb{R}^d\to\mathbb{R}$, we let
$f\colon\mathbb{R}^d\to\mathbb{R}$, we let ![]() $f_i^a= \inf_{Q_i^a}f$. Notice that, whenever
$f_i^a= \inf_{Q_i^a}f$. Notice that, whenever ![]() $f\in\mathrm{Lip}(\mathbb{R}^d;(0,\infty))$, then
$f\in\mathrm{Lip}(\mathbb{R}^d;(0,\infty))$, then ![]() $f_i^a \gt 0$. Finally, we let
$f_i^a \gt 0$. Finally, we let ![]() $\eta\in C_{c}^\infty(B_1)$ be such that
$\eta\in C_{c}^\infty(B_1)$ be such that ![]() $\eta\ge 0$ and
$\eta\ge 0$ and  $\int_{B_1}\eta\,\mathrm{d}x=1$ and, for every
$\int_{B_1}\eta\,\mathrm{d}x=1$ and, for every ![]() $\varepsilon \gt 0$, we set
$\varepsilon \gt 0$, we set ![]() $\eta_\varepsilon(\,\cdot\,)=\varepsilon^{-d}\eta(\,\cdot\,/\varepsilon)$. Accordingly, we let
$\eta_\varepsilon(\,\cdot\,)=\varepsilon^{-d}\eta(\,\cdot\,/\varepsilon)$. Accordingly, we let ![]() $u_\varepsilon= u \ast \eta_{\varepsilon}$ for every
$u_\varepsilon= u \ast \eta_{\varepsilon}$ for every ![]() $\varepsilon \gt 0$ and
$\varepsilon \gt 0$ and ![]() $u\in L^1_{\rm loc}(\mathbb{R}^d)$.
$u\in L^1_{\rm loc}(\mathbb{R}^d)$.
We can now prove the following preliminary estimate.
Lemma 3.5. Let ![]() $p\in [1, \infty)$,
$p\in [1, \infty)$, ![]() $f \in \mathrm{Lip}_b(\mathbb{R}^d;(0,\infty))$. There exist
$f \in \mathrm{Lip}_b(\mathbb{R}^d;(0,\infty))$. There exist ![]() $\varepsilon,\beta,\gamma \gt 0$ with
$\varepsilon,\beta,\gamma \gt 0$ with ![]() $\varepsilon \ll \beta \ll \gamma$ such that
$\varepsilon \ll \beta \ll \gamma$ such that
 \begin{equation}
\begin{aligned}
\int_{Q_i^{(1-\beta) \gamma}} \int_{Q_i^{(1-\beta) \gamma}}
&
\frac{|\tilde{u}_\varepsilon(x)- \tilde{u}_{\varepsilon}(y)|^p }{\|x-y\|^{d+sp}} (f_i^{\gamma})^2 \,\mathrm{d}x \,\mathrm{d}y
\\
&
\quad\qquad
\leq
\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} \frac{|\tilde u(x)- \tilde u(y)|^p}{\|x-y\|^{d+sp}}f(x)f(y) \,\mathrm{d}x \,\mathrm{d}y
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\int_{Q_i^{(1-\beta) \gamma}} \int_{Q_i^{(1-\beta) \gamma}}
&
\frac{|\tilde{u}_\varepsilon(x)- \tilde{u}_{\varepsilon}(y)|^p }{\|x-y\|^{d+sp}} (f_i^{\gamma})^2 \,\mathrm{d}x \,\mathrm{d}y
\\
&
\quad\qquad
\leq
\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} \frac{|\tilde u(x)- \tilde u(y)|^p}{\|x-y\|^{d+sp}}f(x)f(y) \,\mathrm{d}x \,\mathrm{d}y
\end{aligned}
\end{equation} holds for all ![]() $i\in \gamma\mathbb{Z}^d$ and
$i\in \gamma\mathbb{Z}^d$ and ![]() $ u \in L^p(\Omega)$.
$ u \in L^p(\Omega)$.
Proof. Clearly, we can choose ![]() $\varepsilon$,
$\varepsilon$, ![]() $\beta$, and
$\beta$, and ![]() $\gamma$ such that
$\gamma$ such that
 \begin{equation}
Q_i^{(1-\beta)\gamma}+z \subset Q_i^{\gamma}
\end{equation}
\begin{equation}
Q_i^{(1-\beta)\gamma}+z \subset Q_i^{\gamma}
\end{equation} for all ![]() $ z \in B_\varepsilon$ and all
$ z \in B_\varepsilon$ and all ![]() $i\in \gamma\mathbb{Z}^d$. Indeed,
$i\in \gamma\mathbb{Z}^d$. Indeed,
 \begin{equation*}Q_i^{(1-\beta)\gamma}+z \subset \{y \in \mathbb{R}^d : \operatorname{dist}(y,Q_i^{(1-\beta)\gamma} ) \lt \varepsilon \} \subset Q_{i}^{(1-\beta) \gamma+ \varepsilon}\end{equation*}
\begin{equation*}Q_i^{(1-\beta)\gamma}+z \subset \{y \in \mathbb{R}^d : \operatorname{dist}(y,Q_i^{(1-\beta)\gamma} ) \lt \varepsilon \} \subset Q_{i}^{(1-\beta) \gamma+ \varepsilon}\end{equation*} and therefore, to get (3.16), it is enough to choose ![]() $\varepsilon \lt \beta\gamma$ to ensure
$\varepsilon \lt \beta\gamma$ to ensure ![]() $(1-\beta)\gamma+\varepsilon \lt \gamma$. Using the definition of convolution, Jensen’s inequality, changing order of integration, performing the change of variables
$(1-\beta)\gamma+\varepsilon \lt \gamma$. Using the definition of convolution, Jensen’s inequality, changing order of integration, performing the change of variables ![]() $x-z=\xi$ and
$x-z=\xi$ and ![]() $y-z=\zeta$, owing to (3.16), changing once again order of integration, using the fact that
$y-z=\zeta$, owing to (3.16), changing once again order of integration, using the fact that ![]() $\eta_\varepsilon$ has unit
$\eta_\varepsilon$ has unit ![]() $L^1$ norm, and finally owing to the definition of
$L^1$ norm, and finally owing to the definition of  $f_i^{\gamma}=\inf_{Q_i^\gamma}f$, we obtain
$f_i^{\gamma}=\inf_{Q_i^\gamma}f$, we obtain
 \begin{align*}
\int_{Q_i^{(1-\beta) \gamma}} &
\int_{Q_i^{(1-\beta) \gamma}} \frac{|\tilde{u}_\varepsilon(x)- \tilde{u}_{\varepsilon}(y)|^p }{\|x-y\|^{d+sp}} (f_i^{\gamma})^2 \,\mathrm{d}x \,\mathrm{d}y
\\
&
\leq
\int_{Q_i^{(1-\beta) \gamma}} \int_{Q_i^{(1-\beta) \gamma}} \int_{B_\varepsilon} \frac{|\tilde{u}(x-z)- \tilde{u}(y-z)|^p }{\|x-z-(y-z)\|^{d+sp}} \eta_{\varepsilon}(z) (f_i^{\gamma})^2 \,\mathrm{d}z \,\mathrm{d}x \,\mathrm{d}y
\\
&
\leq
\int_{B_\varepsilon} \int_{Q_i^{(1-\beta) \gamma}+z} \int_{Q_i^{(1-\beta) \gamma}+z} \frac{|\tilde{u}(\xi)- \tilde{u}(\zeta)|^p }{\|\xi-\zeta\|^{d+sp}} \eta_{\varepsilon}(z) (f_i^{\gamma})^2 \,\mathrm{d}\xi \,\mathrm{d}\zeta \,\mathrm{d}z
\\
&
\leq
\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} \frac{|\tilde{u}(\xi)- \tilde{u}(\zeta)|^p }{\|\xi-\zeta\|^{d+sp}} \,f(\xi)\,f(\zeta) \,\mathrm{d}\xi \,\mathrm{d}\zeta,
\end{align*}
\begin{align*}
\int_{Q_i^{(1-\beta) \gamma}} &
\int_{Q_i^{(1-\beta) \gamma}} \frac{|\tilde{u}_\varepsilon(x)- \tilde{u}_{\varepsilon}(y)|^p }{\|x-y\|^{d+sp}} (f_i^{\gamma})^2 \,\mathrm{d}x \,\mathrm{d}y
\\
&
\leq
\int_{Q_i^{(1-\beta) \gamma}} \int_{Q_i^{(1-\beta) \gamma}} \int_{B_\varepsilon} \frac{|\tilde{u}(x-z)- \tilde{u}(y-z)|^p }{\|x-z-(y-z)\|^{d+sp}} \eta_{\varepsilon}(z) (f_i^{\gamma})^2 \,\mathrm{d}z \,\mathrm{d}x \,\mathrm{d}y
\\
&
\leq
\int_{B_\varepsilon} \int_{Q_i^{(1-\beta) \gamma}+z} \int_{Q_i^{(1-\beta) \gamma}+z} \frac{|\tilde{u}(\xi)- \tilde{u}(\zeta)|^p }{\|\xi-\zeta\|^{d+sp}} \eta_{\varepsilon}(z) (f_i^{\gamma})^2 \,\mathrm{d}\xi \,\mathrm{d}\zeta \,\mathrm{d}z
\\
&
\leq
\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} \frac{|\tilde{u}(\xi)- \tilde{u}(\zeta)|^p }{\|\xi-\zeta\|^{d+sp}} \,f(\xi)\,f(\zeta) \,\mathrm{d}\xi \,\mathrm{d}\zeta,
\end{align*}concluding the proof.
We are now ready to prove the ![]() $\liminf$ statement (ii) in Theorem 3.1.
$\liminf$ statement (ii) in Theorem 3.1.
Proof of Theorem 3.1(ii)
Let ![]() $(u^n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ be such that
$(u^n)_{n \in \mathbb{N}}\subset L^p(\Omega)$ be such that ![]() $u^n\to u$ in
$u^n\to u$ in ![]() $L^p(\Omega)$ for some
$L^p(\Omega)$ for some ![]() $u\in L^p(\Omega)$. As a consequence,
$u\in L^p(\Omega)$. As a consequence, ![]() $\sup_{n\in\mathbb{N}}\|u^n\|_{p} \lt \infty$. Furthermore, we can also assume that
$\sup_{n\in\mathbb{N}}\|u^n\|_{p} \lt \infty$. Furthermore, we can also assume that
 \begin{equation*}
\liminf_{n\to \infty}(1-s_n) [\tilde u^n]^p_{s_n,p,f} \lt \infty,
\end{equation*}
\begin{equation*}
\liminf_{n\to \infty}(1-s_n) [\tilde u^n]^p_{s_n,p,f} \lt \infty,
\end{equation*} otherwise inequality (3.2) is trivially true. Therefore, we can assume the validity of (3.1), which, in turn, implies that 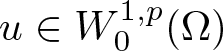 $u\in W^{1,p}_0(\Omega)$ for
$u\in W^{1,p}_0(\Omega)$ for ![]() $p \gt 1$, or
$p \gt 1$, or ![]() $u\in BV(\Omega)$ for
$u\in BV(\Omega)$ for ![]() $p=1$. By Lemma 3.5, there exist
$p=1$. By Lemma 3.5, there exist ![]() $\varepsilon,\beta,\gamma \gt 0$ with
$\varepsilon,\beta,\gamma \gt 0$ with ![]() $\varepsilon \ll \beta \ll \gamma$ such that
$\varepsilon \ll \beta \ll \gamma$ such that
 \begin{equation}
\begin{aligned}
\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}}
&
\frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+s_np}} f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&\quad
\geq
\int_{Q_i^{(1-\beta) \gamma}} \int_{Q_i^{(1-\beta) \gamma}}
\frac{|(\tilde{u}^n)_\varepsilon(x)- (\tilde{u}^n)_{\varepsilon}(y)|^p}{\|x-y\|^{d+s_np}} (f_i^{\gamma})^2 \,\mathrm{d}y \,\mathrm{d}x,
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}}
&
\frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+s_np}} f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&\quad
\geq
\int_{Q_i^{(1-\beta) \gamma}} \int_{Q_i^{(1-\beta) \gamma}}
\frac{|(\tilde{u}^n)_\varepsilon(x)- (\tilde{u}^n)_{\varepsilon}(y)|^p}{\|x-y\|^{d+s_np}} (f_i^{\gamma})^2 \,\mathrm{d}y \,\mathrm{d}x,
\end{aligned}
\end{equation} for every ![]() $ i \in \gamma\mathbb{Z}^d$ and
$ i \in \gamma\mathbb{Z}^d$ and ![]() $n \in \mathbb{N}$. We now perform a first-order Taylor expansion of
$n \in \mathbb{N}$. We now perform a first-order Taylor expansion of ![]() $(\tilde{u}^n)_\varepsilon$. Precisely, owing to the uniform bound on the
$(\tilde{u}^n)_\varepsilon$. Precisely, owing to the uniform bound on the ![]() $p$-norms granted by (3.1) and the boundedness of
$p$-norms granted by (3.1) and the boundedness of ![]() $\Omega$, we can estimate
$\Omega$, we can estimate
 \begin{align}
|\nabla (\tilde{u}^n)_\varepsilon(x)\cdot(x-y)|
&
\le
|(\tilde{u}^n)_\varepsilon(x)-(\tilde{u}^n)_\varepsilon(y)| + \frac 12 |\langle D^2(\tilde{u}^n)_\varepsilon (\xi) (x-y), (x-y) \rangle |
\nonumber
\\
&
\le
|(\tilde{u}^n)_\varepsilon(x)-(\tilde{u}^n)_\varepsilon(y)| +C(\Omega)\|u^n\|_{1}\,\|\eta_\varepsilon\|_{C^{2}(\mathbb{R}^d)}\,\|x-y\|^{2}
\nonumber
\\
&
\le
|(\tilde{u}^n)_\varepsilon(x)-(\tilde{u}^n)_\varepsilon(y)| +C(\varepsilon,M,\Omega)\|x-y\|^{2},
\end{align}
\begin{align}
|\nabla (\tilde{u}^n)_\varepsilon(x)\cdot(x-y)|
&
\le
|(\tilde{u}^n)_\varepsilon(x)-(\tilde{u}^n)_\varepsilon(y)| + \frac 12 |\langle D^2(\tilde{u}^n)_\varepsilon (\xi) (x-y), (x-y) \rangle |
\nonumber
\\
&
\le
|(\tilde{u}^n)_\varepsilon(x)-(\tilde{u}^n)_\varepsilon(y)| +C(\Omega)\|u^n\|_{1}\,\|\eta_\varepsilon\|_{C^{2}(\mathbb{R}^d)}\,\|x-y\|^{2}
\nonumber
\\
&
\le
|(\tilde{u}^n)_\varepsilon(x)-(\tilde{u}^n)_\varepsilon(y)| +C(\varepsilon,M,\Omega)\|x-y\|^{2},
\end{align} where ![]() $\xi$ belongs to the segment from
$\xi$ belongs to the segment from ![]() $x$ to
$x$ to ![]() $y$. Now, assuming
$y$. Now, assuming ![]() $\|x-y\|$ small enough (which is always possible by taking
$\|x-y\|$ small enough (which is always possible by taking ![]() $\gamma$ small enough), since
$\gamma$ small enough), since ![]() $\tilde{u}^n_\varepsilon$ is locally Lipschitz, we have
$\tilde{u}^n_\varepsilon$ is locally Lipschitz, we have
 \begin{align}
|(\tilde{u}^n)_\varepsilon(x)-(\tilde{u}^n)_\varepsilon(y)|
&+
C(\varepsilon,M,\Omega)\|x-y\|^{2}
\nonumber
\\
&
\le
\|\nabla(\tilde{u}^n)_\varepsilon\|_\infty \| x-y \| + C(\varepsilon,M,\Omega) \| x-y \|^2
\nonumber
\\
&
=
C(\Omega)\|u^n\|_1 \|\eta_\varepsilon\|_{C^1(\mathbb{R}^d)}\| x-y \| + C(\varepsilon,M,\Omega) \| x-y \|^2
\nonumber
\\
&
=
C(\varepsilon,M,\Omega) \| x-y \|.
\end{align}
\begin{align}
|(\tilde{u}^n)_\varepsilon(x)-(\tilde{u}^n)_\varepsilon(y)|
&+
C(\varepsilon,M,\Omega)\|x-y\|^{2}
\nonumber
\\
&
\le
\|\nabla(\tilde{u}^n)_\varepsilon\|_\infty \| x-y \| + C(\varepsilon,M,\Omega) \| x-y \|^2
\nonumber
\\
&
=
C(\Omega)\|u^n\|_1 \|\eta_\varepsilon\|_{C^1(\mathbb{R}^d)}\| x-y \| + C(\varepsilon,M,\Omega) \| x-y \|^2
\nonumber
\\
&
=
C(\varepsilon,M,\Omega) \| x-y \|.
\end{align} Taking ![]() $p$-th powers in (3.18), using that
$p$-th powers in (3.18), using that ![]() $(t_0+t)^p= t_0^p+p(t_0+\tau)^{p-1}t $ with
$(t_0+t)^p= t_0^p+p(t_0+\tau)^{p-1}t $ with ![]() $ \tau \in (0,t)$, and finally owing to (3.19), we get
$ \tau \in (0,t)$, and finally owing to (3.19), we get
Therefore, plugging the above inequality in the inner integral in the right-hand side of (3.17), we get that
 \begin{equation}
\int_{Q_i^{(1-\beta)\gamma}}
\frac{|(\tilde{u}^n)_\varepsilon(x)-(\tilde{u}^n)_\varepsilon(y)|^p}{\|x-y\|^{d+s_np}} (f_i^{\gamma})^2 \,\mathrm{d}y
\ge
I' + I'',
\end{equation}
\begin{equation}
\int_{Q_i^{(1-\beta)\gamma}}
\frac{|(\tilde{u}^n)_\varepsilon(x)-(\tilde{u}^n)_\varepsilon(y)|^p}{\|x-y\|^{d+s_np}} (f_i^{\gamma})^2 \,\mathrm{d}y
\ge
I' + I'',
\end{equation}having set
 \begin{equation}
\begin{aligned}
I'
&
=
\int_{Q_i^{(1-\beta)\gamma}}\frac{|\nabla (\tilde{u}^n)_\varepsilon(x)\cdot(x-y)|^p}{\|x-y\|^{d+s_np}}(f_i^{\gamma})^2 \,\mathrm{d}y,
\\
I''
&
=
- C \int_{Q_i^{(1-\beta)\gamma}}
\frac{\|x-y\|^{p+1}}{\|x-y\|^{d+s_np}} (f_i^{\gamma})^2 \,\mathrm{d}y.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
I'
&
=
\int_{Q_i^{(1-\beta)\gamma}}\frac{|\nabla (\tilde{u}^n)_\varepsilon(x)\cdot(x-y)|^p}{\|x-y\|^{d+s_np}}(f_i^{\gamma})^2 \,\mathrm{d}y,
\\
I''
&
=
- C \int_{Q_i^{(1-\beta)\gamma}}
\frac{\|x-y\|^{p+1}}{\|x-y\|^{d+s_np}} (f_i^{\gamma})^2 \,\mathrm{d}y.
\end{aligned}
\end{equation}We now estimate the two terms in (3.21) separately. On the one hand, we have
 \begin{align*}
I''
&
\ge
- C(p,\varepsilon, M, \Omega) \|f\|^2_\infty \int_{B_{\delta_1}} \frac{\mathrm{d}\xi}{\|\xi\|^{d+s_np-p-1}}
\\
&
=
-C(p,\varepsilon, M, \Omega, f) d\omega_d \int_0^{\delta_1} \frac{\mathrm{d}\varrho}{\varrho^{s_np-p}}
=
-\frac{C(d,p,\varepsilon, M, \Omega, f)}{1+p-s_np} \delta_1^{1+p-s_np}
\end{align*}
\begin{align*}
I''
&
\ge
- C(p,\varepsilon, M, \Omega) \|f\|^2_\infty \int_{B_{\delta_1}} \frac{\mathrm{d}\xi}{\|\xi\|^{d+s_np-p-1}}
\\
&
=
-C(p,\varepsilon, M, \Omega, f) d\omega_d \int_0^{\delta_1} \frac{\mathrm{d}\varrho}{\varrho^{s_np-p}}
=
-\frac{C(d,p,\varepsilon, M, \Omega, f)}{1+p-s_np} \delta_1^{1+p-s_np}
\end{align*} for 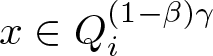 $x\in Q_i^{(1-\beta)\gamma}$, where we have set
$x\in Q_i^{(1-\beta)\gamma}$, where we have set ![]() $\delta_1 = 2\sqrt{d}(1-\beta)\gamma$. Integrating the above inequality over the cube
$\delta_1 = 2\sqrt{d}(1-\beta)\gamma$. Integrating the above inequality over the cube 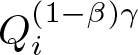 $Q_i^{(1-\beta)\gamma}$ with respect to
$Q_i^{(1-\beta)\gamma}$ with respect to ![]() $x$, we obtain
$x$, we obtain
 \begin{equation*}
\int_{Q_i^{(1-\beta)\gamma}} I'' \,\mathrm{d}x
\ge
- \frac{C(d,p,\varepsilon, M, \Omega, f)}{1+p-s_np} \big|Q_i^{(1-\beta)\gamma}\big| \delta_1^{1+p-s_np},
\end{equation*}
\begin{equation*}
\int_{Q_i^{(1-\beta)\gamma}} I'' \,\mathrm{d}x
\ge
- \frac{C(d,p,\varepsilon, M, \Omega, f)}{1+p-s_np} \big|Q_i^{(1-\beta)\gamma}\big| \delta_1^{1+p-s_np},
\end{equation*}so that
 \begin{equation}
\liminf_{n \to \infty} (1-s_n)\int_{Q_i^{(1-\beta)\gamma}} I'' \,\mathrm{d}x
\ge
0.
\end{equation}
\begin{equation}
\liminf_{n \to \infty} (1-s_n)\int_{Q_i^{(1-\beta)\gamma}} I'' \,\mathrm{d}x
\ge
0.
\end{equation} On the other hand, calling 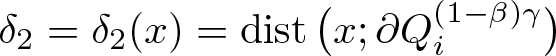 $\delta_2=\delta_2(x)=\operatorname{dist}\big(x; \partial Q_i^{(1-\beta)\gamma}\big)$, taking the normalization
$\delta_2=\delta_2(x)=\operatorname{dist}\big(x; \partial Q_i^{(1-\beta)\gamma}\big)$, taking the normalization ![]() $\nu(x)= \nabla (\tilde{u}^n)_\varepsilon(x)/\|\nabla (\tilde{u}^n)_\varepsilon(x)\|$, applying the change of variables
$\nu(x)= \nabla (\tilde{u}^n)_\varepsilon(x)/\|\nabla (\tilde{u}^n)_\varepsilon(x)\|$, applying the change of variables ![]() $z=x-y$, exploiting the invariance of the integral on
$z=x-y$, exploiting the invariance of the integral on ![]() $B_{\delta_2}$ with respect to rotations, applying the change of variable
$B_{\delta_2}$ with respect to rotations, applying the change of variable ![]() $z\mapsto z\delta_2^{-1}$, and observing that, for every
$z\mapsto z\delta_2^{-1}$, and observing that, for every ![]() $\nu\in\mathbb S^{d-1}$
$\nu\in\mathbb S^{d-1}$
 \begin{equation}(1-s_n)\int_{B_1}\frac{\vert z\cdot\nu\vert^p}{\Arrowvert z\Arrowvert^{d+s_np}}\,\mathrm dz=(1-s_n)\int_0^1\varrho^{p-s_np-1}\,\int_{\partial B_1}\vert\eta\cdot\nu\vert^p\,\mathrm d\eta\,\mathrm d\varrho=K_{d,p,}\end{equation}
\begin{equation}(1-s_n)\int_{B_1}\frac{\vert z\cdot\nu\vert^p}{\Arrowvert z\Arrowvert^{d+s_np}}\,\mathrm dz=(1-s_n)\int_0^1\varrho^{p-s_np-1}\,\int_{\partial B_1}\vert\eta\cdot\nu\vert^p\,\mathrm d\eta\,\mathrm d\varrho=K_{d,p,}\end{equation}we get that
 \begin{align*}
I'
&
=
|\nabla (\tilde{u}^n)_\varepsilon(x)|^p (f_i^{\gamma})^2 \int_{Q_i^{(1-\beta)\gamma}}\frac{|\nu(x)\cdot(x-y)|^p}{\|x-y\|^{d+s_np}} \,\mathrm{d}y
\\
&
\geq
|\nabla (\tilde{u}^n)_\varepsilon(x)|^p (f_i^{\gamma})^2 \int_{B_{\delta_2}} \frac{|\nu(x)\cdot z|^p}{\|z\|^{d+s_np}} \,\mathrm{d}z
=
\frac{K_{d,p} |\nabla (\tilde{u}^n)_\varepsilon(x)|^p \delta_2^{p(1-s_n)}(f_i^{\gamma})^2 }{1-s_n}.
\end{align*}
\begin{align*}
I'
&
=
|\nabla (\tilde{u}^n)_\varepsilon(x)|^p (f_i^{\gamma})^2 \int_{Q_i^{(1-\beta)\gamma}}\frac{|\nu(x)\cdot(x-y)|^p}{\|x-y\|^{d+s_np}} \,\mathrm{d}y
\\
&
\geq
|\nabla (\tilde{u}^n)_\varepsilon(x)|^p (f_i^{\gamma})^2 \int_{B_{\delta_2}} \frac{|\nu(x)\cdot z|^p}{\|z\|^{d+s_np}} \,\mathrm{d}z
=
\frac{K_{d,p} |\nabla (\tilde{u}^n)_\varepsilon(x)|^p \delta_2^{p(1-s_n)}(f_i^{\gamma})^2 }{1-s_n}.
\end{align*} Multiplying the above inequality by ![]() $(1-s_n)$, integrating over the cube
$(1-s_n)$, integrating over the cube 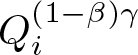 $Q_i^{(1-\beta)\gamma}$ with respect to
$Q_i^{(1-\beta)\gamma}$ with respect to ![]() $x$, taking the
$x$, taking the ![]() $\liminf$ as
$\liminf$ as ![]() $n\to\infty$, owing to Fatou’s lemma, we get that
$n\to\infty$, owing to Fatou’s lemma, we get that
 \begin{equation*}
\liminf_{n \to \infty}(1-s_n)
\int_{Q_i^{(1-\beta)\gamma}} I' \,\mathrm{d}x
\ge
K_{d,p} \int_{Q_i^{(1-\beta)\gamma}} \liminf_{n \to \infty}\big( |\nabla (\tilde u^n)_\varepsilon(x)|^p \delta_2^{p(1-s_n)} \big) (f_i^{\gamma})^2\,\mathrm{d}x.
\end{equation*}
\begin{equation*}
\liminf_{n \to \infty}(1-s_n)
\int_{Q_i^{(1-\beta)\gamma}} I' \,\mathrm{d}x
\ge
K_{d,p} \int_{Q_i^{(1-\beta)\gamma}} \liminf_{n \to \infty}\big( |\nabla (\tilde u^n)_\varepsilon(x)|^p \delta_2^{p(1-s_n)} \big) (f_i^{\gamma})^2\,\mathrm{d}x.
\end{equation*} Since ![]() $(u^n)_\varepsilon\to u_\varepsilon$ in any Sobolev norm as
$(u^n)_\varepsilon\to u_\varepsilon$ in any Sobolev norm as ![]() $n \to \infty$, up to passing to a suitable subsequence,
$n \to \infty$, up to passing to a suitable subsequence, ![]() $\nabla(\tilde u^n)_\varepsilon(x)\to\nabla\tilde u_\varepsilon(x)$ for a.e.
$\nabla(\tilde u^n)_\varepsilon(x)\to\nabla\tilde u_\varepsilon(x)$ for a.e. ![]() $x\in\mathbb{R}^d$. Therefore, we get that
$x\in\mathbb{R}^d$. Therefore, we get that
 \begin{equation}
\liminf_{n \to \infty}(1-s_n)
\int_{Q_i^{(1-\beta)\gamma}} I' \,\mathrm{d}x
\ge
K_{d,p} \int_{Q_i^{(1-\beta)\gamma}} |\nabla \tilde u_\varepsilon(x)|^p (f_i^{\gamma})^2\,\mathrm{d}x.
\end{equation}
\begin{equation}
\liminf_{n \to \infty}(1-s_n)
\int_{Q_i^{(1-\beta)\gamma}} I' \,\mathrm{d}x
\ge
K_{d,p} \int_{Q_i^{(1-\beta)\gamma}} |\nabla \tilde u_\varepsilon(x)|^p (f_i^{\gamma})^2\,\mathrm{d}x.
\end{equation} Thence, by taking the ![]() $\liminf$ as
$\liminf$ as ![]() $n\to\infty$ of
$n\to\infty$ of ![]() $(1-s_n)$ times (3.17) and owing to (3.20)–(3.24), we have
$(1-s_n)$ times (3.17) and owing to (3.20)–(3.24), we have
 \begin{equation*}
\begin{aligned}
\liminf_{n\to\infty} (1-s_n)\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+sp}}
&
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
\ge
K_{d,p} \int_{Q_i^{(1-\beta)\gamma}} |\nabla \tilde u_\varepsilon(x)|^p (f_i^{\gamma})^2\,\mathrm{d}x
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
\liminf_{n\to\infty} (1-s_n)\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+sp}}
&
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
\ge
K_{d,p} \int_{Q_i^{(1-\beta)\gamma}} |\nabla \tilde u_\varepsilon(x)|^p (f_i^{\gamma})^2\,\mathrm{d}x
\end{aligned}
\end{equation*} whenever ![]() $\varepsilon\ll\beta\ll\gamma\ll1$. Now first letting
$\varepsilon\ll\beta\ll\gamma\ll1$. Now first letting ![]() $\varepsilon \to 0^+$, and then
$\varepsilon \to 0^+$, and then ![]() $\beta\to 0^+$, we get
$\beta\to 0^+$, we get
 \begin{equation}
\begin{aligned}
\liminf_{n\to\infty} (1-s_n)\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} & \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+sp}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
\ge
K_{d,p} \int_{Q_i^\gamma} |\nabla \tilde u(x)|^p (f_i^{\gamma})^2\,\mathrm{d}x, \quad \text{if}\ p \in (1,\infty),\\
\liminf_{n\to \infty} (1-s_n)\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} & \frac{|\tilde u^n(x)- \tilde u^n(y)|}{\|x-y\|^{d+s}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
\ge
K_{d,1} \int_{Q_i^\gamma} (f_i^{\gamma})^2\,\mathrm{d} \vert D u \vert(x), \quad \text{if}\ p =1.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\liminf_{n\to\infty} (1-s_n)\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} & \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+sp}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
\ge
K_{d,p} \int_{Q_i^\gamma} |\nabla \tilde u(x)|^p (f_i^{\gamma})^2\,\mathrm{d}x, \quad \text{if}\ p \in (1,\infty),\\
\liminf_{n\to \infty} (1-s_n)\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} & \frac{|\tilde u^n(x)- \tilde u^n(y)|}{\|x-y\|^{d+s}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
\ge
K_{d,1} \int_{Q_i^\gamma} (f_i^{\gamma})^2\,\mathrm{d} \vert D u \vert(x), \quad \text{if}\ p =1.
\end{aligned}
\end{equation}We notice now that, by the Lebesgue’s Dominated Convergence Theorem
 \begin{equation*}
\begin{aligned}
\lim_{\gamma \to 0^+} \sum_{i \in I_\gamma} K_{d,p} \int_{Q_i^\gamma} |\nabla\tilde{u}(x)|^p (f_i^{\gamma})^2 \,\mathrm{d}x
=
K_{d,p} \| \nabla u \|^p_{p,f^2} \\
\text{and} \lim_{\gamma \to 0^+} \sum_{i \in I_\gamma} K_{d,1} \int_{Q_i^\gamma} (f_i^{\gamma})^2 \,\mathrm{d} \vert D u \vert
=
K_{d,1} \| D u \|_{1,f^2}.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
\lim_{\gamma \to 0^+} \sum_{i \in I_\gamma} K_{d,p} \int_{Q_i^\gamma} |\nabla\tilde{u}(x)|^p (f_i^{\gamma})^2 \,\mathrm{d}x
=
K_{d,p} \| \nabla u \|^p_{p,f^2} \\
\text{and} \lim_{\gamma \to 0^+} \sum_{i \in I_\gamma} K_{d,1} \int_{Q_i^\gamma} (f_i^{\gamma})^2 \,\mathrm{d} \vert D u \vert
=
K_{d,1} \| D u \|_{1,f^2}.
\end{aligned}
\end{equation*} Pairing this with (3.25) allows to conclude. Indeed, if ![]() $p \in (1,\infty)$ (the case
$p \in (1,\infty)$ (the case ![]() $p =1$ being analogous and thus omitted), then we have
$p =1$ being analogous and thus omitted), then we have
 \begin{align*}
K_{d,p}
&
\int_{\Omega} \vert \nabla u(x) \vert^p f^2(x)\,\mathrm{d}x
\\
&
\le
\lim_{\gamma \to0^+}
\sum_{i \in I_\gamma}
\liminf_{n \to \infty} (1-s_n)\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+s_np}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
=
\lim_{\gamma \to 0^+}\liminf_{n \to \infty} \sum_{i \in I_\gamma}(1-s_n)\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+s_np}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
\le
\lim_{\gamma \to 0^+}\liminf_{n \to \infty} (1-s_n)\int_{\Omega} \int_{\Omega} \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+s_np}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
=
\liminf_{n \to \infty}(1-s_n) \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+s_np}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x,
\end{align*}
\begin{align*}
K_{d,p}
&
\int_{\Omega} \vert \nabla u(x) \vert^p f^2(x)\,\mathrm{d}x
\\
&
\le
\lim_{\gamma \to0^+}
\sum_{i \in I_\gamma}
\liminf_{n \to \infty} (1-s_n)\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+s_np}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
=
\lim_{\gamma \to 0^+}\liminf_{n \to \infty} \sum_{i \in I_\gamma}(1-s_n)\int_{Q_i^{\gamma}} \int_{Q_i^{\gamma}} \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+s_np}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
\le
\lim_{\gamma \to 0^+}\liminf_{n \to \infty} (1-s_n)\int_{\Omega} \int_{\Omega} \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+s_np}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
=
\liminf_{n \to \infty}(1-s_n) \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{|\tilde u^n(x)- \tilde u^n(y)|^p}{\|x-y\|^{d+s_np}}
f(x)f(y) \,\mathrm{d}y \,\mathrm{d}x,
\end{align*}which is exactly the claimed inequality.
3.3. Proof of Theorem 3.1(iii)
We begin with the following preliminary result, establishing the ![]() $\limsup$ inequality (iii) in Theorem 3.1 for smooth functions supported in
$\limsup$ inequality (iii) in Theorem 3.1 for smooth functions supported in ![]() $\Omega$.
$\Omega$.
Theorem 3.6 If ![]() $v \in C_c^{\infty}(\mathbb{R}^d)$, then
$v \in C_c^{\infty}(\mathbb{R}^d)$, then
 \begin{equation}
\begin{aligned}
\lim_{s \to 1^-} (1-s) \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp}}
&
f(x)f(y)\,\mathrm{d}x\,\mathrm{d}y
\\
&
=
K_{d,p}\int_{\mathbb{R}^d}\|\nabla v(z)\|^p f^2(z) \,\mathrm{d}z.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\lim_{s \to 1^-} (1-s) \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp}}
&
f(x)f(y)\,\mathrm{d}x\,\mathrm{d}y
\\
&
=
K_{d,p}\int_{\mathbb{R}^d}\|\nabla v(z)\|^p f^2(z) \,\mathrm{d}z.
\end{aligned}
\end{equation}Proof. Let us write
 \begin{equation}
\int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp}} f(x) f(y) \,\mathrm{d}x \,\mathrm{d}y
=
I_1+I_2+I_3,
\end{equation}
\begin{equation}
\int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp}} f(x) f(y) \,\mathrm{d}x \,\mathrm{d}y
=
I_1+I_2+I_3,
\end{equation}where
 \begin{equation}
\begin{aligned}
I_1
&
=
\int_{\mathbb{R}^d} \int_{\{\|x-y\| \lt 1 \}} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp}} f^2(y) \,\mathrm{d}x \,\mathrm{d}y,
\\
I_2
&
=
\int_{\mathbb{R}^d} \int_{\{\|x-y\| \lt 1 \}} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp}} f(y)(f(x)-f(y)) \,\mathrm{d}x \,\mathrm{d}y,
\\
I_3
&
=
\int_{\mathbb{R}^d} \int_{\{\|x-y\| \geq 1 \}} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp}} f(x) f(y) \,\mathrm{d}x \,\mathrm{d}y.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
I_1
&
=
\int_{\mathbb{R}^d} \int_{\{\|x-y\| \lt 1 \}} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp}} f^2(y) \,\mathrm{d}x \,\mathrm{d}y,
\\
I_2
&
=
\int_{\mathbb{R}^d} \int_{\{\|x-y\| \lt 1 \}} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp}} f(y)(f(x)-f(y)) \,\mathrm{d}x \,\mathrm{d}y,
\\
I_3
&
=
\int_{\mathbb{R}^d} \int_{\{\|x-y\| \geq 1 \}} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp}} f(x) f(y) \,\mathrm{d}x \,\mathrm{d}y.
\end{aligned}
\end{equation} We estimate the three terms separately. Concerning ![]() $I_3$, we have that
$I_3$, we have that
 \begin{align}
I_3
&
\le
2^p\|f\|^2_\infty \int_{\mathbb{R}^d} \int_{\{\|x-y\| \geq 1\}} \frac{|v(x)|^p+|v(y)|^p}{\|x-y\|^{d+sp}} \,\mathrm{d}x \,\mathrm{d}y
\nonumber
\\
&
\leq
2^{p+1}\| f \|^2_{\infty}\int_{\mathbb{R}^d} \int_{B_1(y)^c} \frac{|v(y)|^p}{\|x-y\|^{d+sp}} \,\mathrm{d}x \,\mathrm{d}y
\nonumber
\\
&
=
2^{p+1}\| f \|^2_{\infty} \| v \|^p_{p} \int_{1}^{\infty} \frac{d \omega_d}{\varrho^{1+sp}} \,\mathrm{d} \varrho
=
\frac{2^{p+1}}{sp} \| f \|^2_{\infty} \|v\|^p_{p}.
\end{align}
\begin{align}
I_3
&
\le
2^p\|f\|^2_\infty \int_{\mathbb{R}^d} \int_{\{\|x-y\| \geq 1\}} \frac{|v(x)|^p+|v(y)|^p}{\|x-y\|^{d+sp}} \,\mathrm{d}x \,\mathrm{d}y
\nonumber
\\
&
\leq
2^{p+1}\| f \|^2_{\infty}\int_{\mathbb{R}^d} \int_{B_1(y)^c} \frac{|v(y)|^p}{\|x-y\|^{d+sp}} \,\mathrm{d}x \,\mathrm{d}y
\nonumber
\\
&
=
2^{p+1}\| f \|^2_{\infty} \| v \|^p_{p} \int_{1}^{\infty} \frac{d \omega_d}{\varrho^{1+sp}} \,\mathrm{d} \varrho
=
\frac{2^{p+1}}{sp} \| f \|^2_{\infty} \|v\|^p_{p}.
\end{align} For ![]() $I_2$ instead, we can write, recalling the notation in (2.1),
$I_2$ instead, we can write, recalling the notation in (2.1),
 \begin{align}
I_2
&
\leq
\| f \|_{\infty} \| \nabla f \|_{\infty}\int_{\mathbb{R}^d} \int_{B_1(y)} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp-1}} \,\mathrm{d}x \,\mathrm{d}y
\nonumber
\\
&
\leq
C(f) \| \nabla v \|_{\infty}^p \int_{(\operatorname{spt}{v})_1} \int_{B_1(y)} \frac{1}{\|x-y\|^{d-1-p+sp}} \,\mathrm{d}x \,\mathrm{d}y
\nonumber
\\
&
\leq
C(f,v) d\omega_d |(\operatorname{spt}{v})_1| \int_{0}^{1} \frac{1}{\varrho^{-p+sp}} \,\mathrm{d}\varrho
\nonumber
\\
&
\leq
\frac{C(d,f,v)}{p-sp+1}
\le
C(d,p,f,v).
\end{align}
\begin{align}
I_2
&
\leq
\| f \|_{\infty} \| \nabla f \|_{\infty}\int_{\mathbb{R}^d} \int_{B_1(y)} \frac{|v(x)-v(y)|^p}{\|x-y\|^{d+sp-1}} \,\mathrm{d}x \,\mathrm{d}y
\nonumber
\\
&
\leq
C(f) \| \nabla v \|_{\infty}^p \int_{(\operatorname{spt}{v})_1} \int_{B_1(y)} \frac{1}{\|x-y\|^{d-1-p+sp}} \,\mathrm{d}x \,\mathrm{d}y
\nonumber
\\
&
\leq
C(f,v) d\omega_d |(\operatorname{spt}{v})_1| \int_{0}^{1} \frac{1}{\varrho^{-p+sp}} \,\mathrm{d}\varrho
\nonumber
\\
&
\leq
\frac{C(d,f,v)}{p-sp+1}
\le
C(d,p,f,v).
\end{align} We are thus left with estimating ![]() $I_1$. To this aim, let us observe that
$I_1$. To this aim, let us observe that
Thus ![]() $I_1\le I'_1+I''_1$, where, owing to the fact that
$I_1\le I'_1+I''_1$, where, owing to the fact that ![]() $v$ has compact support and recalling the notation in (2.1),
$v$ has compact support and recalling the notation in (2.1),
 \begin{equation*}
\begin{aligned}
I'_1
&
=
\int_{\mathbb{R}^d} \int_{B_1(y)} \frac{\vert \nabla v(y) \cdot (x-y)\vert^p}{\|x-y\|^{d+sp}} f^2(y) \,\mathrm{d}x \,\mathrm{d}y,
\\
I''_1
&
=
\int_{(\operatorname{spt}{v})_1} \int_{B_1(y)} \frac{\| D^2 v \|_{\infty}^{2p}}{\|x-y\|^{d+sp-2p}} f^2(y) \,\mathrm{d}x \,\mathrm{d}y.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
I'_1
&
=
\int_{\mathbb{R}^d} \int_{B_1(y)} \frac{\vert \nabla v(y) \cdot (x-y)\vert^p}{\|x-y\|^{d+sp}} f^2(y) \,\mathrm{d}x \,\mathrm{d}y,
\\
I''_1
&
=
\int_{(\operatorname{spt}{v})_1} \int_{B_1(y)} \frac{\| D^2 v \|_{\infty}^{2p}}{\|x-y\|^{d+sp-2p}} f^2(y) \,\mathrm{d}x \,\mathrm{d}y.
\end{aligned}
\end{equation*}Now, on the one hand, we have that
 \begin{align}
I''_1
&
\leq
\|f\|_{\infty}^2 \|D^2 v\|_{\infty}^{2p} \int_{(\operatorname{spt}{v})_1}\int_{B_1(y)} \frac{1}{\|x-y\|^{d+sp-2p}}\,\mathrm{d}x \,\mathrm{d}y
\nonumber
\\
&
\leq
C(f,v) d\omega_d |(\operatorname{spt}{v})_1| \int_{0}^{1}\varrho^{p-1+p(1-s)} \,\mathrm{d}\varrho
\nonumber\\
&
=
\frac{C(d,f,v)}{2p-sp} \le C(d,p,f,v).
\end{align}
\begin{align}
I''_1
&
\leq
\|f\|_{\infty}^2 \|D^2 v\|_{\infty}^{2p} \int_{(\operatorname{spt}{v})_1}\int_{B_1(y)} \frac{1}{\|x-y\|^{d+sp-2p}}\,\mathrm{d}x \,\mathrm{d}y
\nonumber
\\
&
\leq
C(f,v) d\omega_d |(\operatorname{spt}{v})_1| \int_{0}^{1}\varrho^{p-1+p(1-s)} \,\mathrm{d}\varrho
\nonumber\\
&
=
\frac{C(d,f,v)}{2p-sp} \le C(d,p,f,v).
\end{align} By the non-negativity of ![]() $I''_1,I_2,I_3$, and by (3.29)–(3.31), we thus get that
$I''_1,I_2,I_3$, and by (3.29)–(3.31), we thus get that
 \begin{equation}
\lim_{s\to 1^-}(1-s)(I''_1+I_2+I_3) = 0.
\end{equation}
\begin{equation}
\lim_{s\to 1^-}(1-s)(I''_1+I_2+I_3) = 0.
\end{equation} Therefore, in order to conclude, we are left with showing that ![]() $\lim_{s\to1^-} (1-s)I'_1$ equals the right hand side of (3.26). Indeed, by the change of variables
$\lim_{s\to1^-} (1-s)I'_1$ equals the right hand side of (3.26). Indeed, by the change of variables ![]() $z=x-y$, by setting
$z=x-y$, by setting ![]() $\nu(y)=\nabla v(y)/\|\nabla v(y)\|$, and using (3.23), we have
$\nu(y)=\nabla v(y)/\|\nabla v(y)\|$, and using (3.23), we have
 \begin{align}
{I'}_1
&
=
\int_{\mathbb{R}^d} \int_{B_1} \frac{|\nabla v(y) \cdot z|^p}{\|z\|^{d+sp}} f^2(y) \,\mathrm{d}z \,\mathrm{d}y
\nonumber
\\
&
=
\int_{\mathbb{R}^d} \|\nabla v(y)\|^p f^2(y)\int_{B_1} \frac{|\nu(y)\cdot z|^p}{\|z\|^{d+sp}} \,\mathrm{d}z \,\mathrm{d}y
\nonumber
\\
&
=
\frac{K_{d,p}}{(1-s)}
\int_{\mathbb{R}^d}\|\nabla v(x)\|^p f^2(y)\, \mathrm{d}y.
\end{align}
\begin{align}
{I'}_1
&
=
\int_{\mathbb{R}^d} \int_{B_1} \frac{|\nabla v(y) \cdot z|^p}{\|z\|^{d+sp}} f^2(y) \,\mathrm{d}z \,\mathrm{d}y
\nonumber
\\
&
=
\int_{\mathbb{R}^d} \|\nabla v(y)\|^p f^2(y)\int_{B_1} \frac{|\nu(y)\cdot z|^p}{\|z\|^{d+sp}} \,\mathrm{d}z \,\mathrm{d}y
\nonumber
\\
&
=
\frac{K_{d,p}}{(1-s)}
\int_{\mathbb{R}^d}\|\nabla v(x)\|^p f^2(y)\, \mathrm{d}y.
\end{align}The conclusion hence follows by combining (3.32) and (3.33).
Remark 3.7. We underline that, in the chain of inequalities leading to (3.30), the Lipschitz regularity of the weight ![]() $f$ is crucial in order to ensure the finiteness of the integral in
$f$ is crucial in order to ensure the finiteness of the integral in ![]() $\varrho$. If
$\varrho$. If ![]() $f$ were only
$f$ were only ![]() $\alpha$-Hölder, for some
$\alpha$-Hölder, for some ![]() $\alpha\in(0,1)$, one would end up with
$\alpha\in(0,1)$, one would end up with ![]() $\varrho$ to the power
$\varrho$ to the power ![]() $-(\alpha-1-p+sp)$, which is not integrable in a neighborhood of the origin.
$-(\alpha-1-p+sp)$, which is not integrable in a neighborhood of the origin.
We are now ready to prove the ![]() $\limsup$ statement (iii) in Theorem 3.1.
$\limsup$ statement (iii) in Theorem 3.1.
Proof of Theorem 3.1(iii)
Let 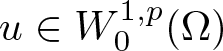 $u\in W^{1,p}_0(\Omega)$ for
$u\in W^{1,p}_0(\Omega)$ for ![]() $p \gt 1$, or
$p \gt 1$, or ![]() $ u \in BV(\Omega)$ for
$ u \in BV(\Omega)$ for ![]() $p=1$. By the density of
$p=1$. By the density of ![]() $C_c^{\infty}(\Omega)$ in
$C_c^{\infty}(\Omega)$ in 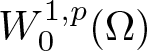 $W^{1,p}_0(\Omega)$ for
$W^{1,p}_0(\Omega)$ for ![]() $p \gt 1$, or in
$p \gt 1$, or in ![]() $BV(\Omega)$ for
$BV(\Omega)$ for ![]() $p=1$, we can find
$p=1$, we can find ![]() $(v^k)_{k\in\mathbb{N}} \subset C_c^{\infty}(\Omega)$ such that
$(v^k)_{k\in\mathbb{N}} \subset C_c^{\infty}(\Omega)$ such that ![]() $ v^{k} \to u$ in
$ v^{k} \to u$ in  $W^{1,p}_0(\Omega)$ for
$W^{1,p}_0(\Omega)$ for ![]() $p \gt 1$, or in energy in
$p \gt 1$, or in energy in ![]() $BV(\Omega)$ for
$BV(\Omega)$ for ![]() $p=1$. In view of Theorem 3.6, we thus get that
$p=1$. In view of Theorem 3.6, we thus get that
 \begin{equation*}
\begin{aligned}
\lim_{n \to \infty} (1-s_n) [\tilde v^k]^p_{s_n,p,f}
&
=
\lim_{n\to\infty} (1-s_n) \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{|\tilde v^k(x)-\tilde v^k(y)|^p}{\|x-y\|^{d+s_np}}f(x) f(y)\,\mathrm{d}x \,\mathrm{d}y
\\
&
=
K_{d,p} \int_{\mathbb{R}^d} \|\nabla \tilde v^k(x)\|^2 f^2(x)\,\mathrm{d}x
\\
&
=
K_{d,p} \int_{\Omega} \|\nabla v^k(x)\|^p f^2(x) \,\mathrm{d}x
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
\lim_{n \to \infty} (1-s_n) [\tilde v^k]^p_{s_n,p,f}
&
=
\lim_{n\to\infty} (1-s_n) \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{|\tilde v^k(x)-\tilde v^k(y)|^p}{\|x-y\|^{d+s_np}}f(x) f(y)\,\mathrm{d}x \,\mathrm{d}y
\\
&
=
K_{d,p} \int_{\mathbb{R}^d} \|\nabla \tilde v^k(x)\|^2 f^2(x)\,\mathrm{d}x
\\
&
=
K_{d,p} \int_{\Omega} \|\nabla v^k(x)\|^p f^2(x) \,\mathrm{d}x
\end{aligned}
\end{equation*} for every ![]() $k\in\mathbb{N}$. The conclusion hence follows by a standard diagonal argument.
$k\in\mathbb{N}$. The conclusion hence follows by a standard diagonal argument.
3.4. Proof of Theorem 1.1
We can now prove Theorem 1.1 in full generality. Indeed, the result easily follows by combining Theorem 3.1 with Lemmas 3.8 and 3.9 below (under the same standing assumptions as stated at the very beginning of Section 3).
Lemma 3.8. If ![]() $(u^n)_{n\in\mathbb{N}}\subset L^p(\Omega)$ is such that
$(u^n)_{n\in\mathbb{N}}\subset L^p(\Omega)$ is such that
 \begin{equation}
\sup_{n \in \mathbb{N}}\left( (1-s_n)[\tilde u^n]^p_{s_n,p}+ \| u^n \|_{L^p(\Omega)}^p\right) \lt \infty,
\end{equation}
\begin{equation}
\sup_{n \in \mathbb{N}}\left( (1-s_n)[\tilde u^n]^p_{s_n,p}+ \| u^n \|_{L^p(\Omega)}^p\right) \lt \infty,
\end{equation}then
 \begin{equation}
\lim_{n\to\infty}
(1-s_n)\big| [\tilde u^n]^p_{s_n,p,f_n}-[\tilde u^n]^p_{s_n,p,f} \big|=0.
\end{equation}
\begin{equation}
\lim_{n\to\infty}
(1-s_n)\big| [\tilde u^n]^p_{s_n,p,f_n}-[\tilde u^n]^p_{s_n,p,f} \big|=0.
\end{equation}Proof. Since we can estimate
 \begin{align*}
\big| [\tilde u^n]^p_{s_n,p,f_n}-[\tilde u^n]^p_{s_n,p,f} \big|
&
\leq
[\tilde u^n]^p_{s_n, p} \sup_{(x,y) \in \mathbb{R}^{2d}} \vert f_n(x)f_n(y)-f(x)f(y)\vert
\\
&
\leq
2 [\tilde u^n]^p_{s_n, p} \sup\{\| f_n \|_{\infty} : n \in \mathbb{N}\}\| f_n -f \|_{\infty},
\end{align*}
\begin{align*}
\big| [\tilde u^n]^p_{s_n,p,f_n}-[\tilde u^n]^p_{s_n,p,f} \big|
&
\leq
[\tilde u^n]^p_{s_n, p} \sup_{(x,y) \in \mathbb{R}^{2d}} \vert f_n(x)f_n(y)-f(x)f(y)\vert
\\
&
\leq
2 [\tilde u^n]^p_{s_n, p} \sup\{\| f_n \|_{\infty} : n \in \mathbb{N}\}\| f_n -f \|_{\infty},
\end{align*}the conclusion immediately follows from (3.34).
Lemma 3.9. If ![]() $(u^n)_{n\in\mathbb{N}}\subset L^p(\Omega)$ is such that
$(u^n)_{n\in\mathbb{N}}\subset L^p(\Omega)$ is such that
 \begin{equation}
\sup_{n \in \mathbb{N}}\left( (1-s_n)[\tilde u^n]^p_{s_n,p,f_n}+ \|u^n \|_{L^p(\Omega)}^p\right) \lt \infty,
\end{equation}
\begin{equation}
\sup_{n \in \mathbb{N}}\left( (1-s_n)[\tilde u^n]^p_{s_n,p,f_n}+ \|u^n \|_{L^p(\Omega)}^p\right) \lt \infty,
\end{equation}then
 \begin{equation*}
\sup_{n \in \mathbb{N}} (1-s_n)[\tilde u^n]^p_{s_n,p}+ \| u^n \|_{L^p(\Omega)}^p \lt \infty.
\end{equation*}
\begin{equation*}
\sup_{n \in \mathbb{N}} (1-s_n)[\tilde u^n]^p_{s_n,p}+ \| u^n \|_{L^p(\Omega)}^p \lt \infty.
\end{equation*}Proof. On the one hand, by the inequality ![]() $(a+b)^p\le 2^p(a^p+b^p)$ for
$(a+b)^p\le 2^p(a^p+b^p)$ for ![]() $a,b\ge0$, exploiting symmetry, and passing to the
$a,b\ge0$, exploiting symmetry, and passing to the ![]() $d$-dimensional spherical coordinates, we can estimate
$d$-dimensional spherical coordinates, we can estimate
 \begin{equation}
\begin{aligned}
\int_{\mathbb{R}^d} \int_{B_1(y)^c}
&
\frac{|\tilde{u}^n(x)-\tilde{u}^n(y)|^p}{\|x-y\|^{d+s_n p}} \,\mathrm{d}x \,\mathrm{d}y
\le
2^p \int_{\mathbb{R}^d} \int_{B_1(y)^c} \frac{|\tilde u^n (x)|^p+|\tilde{u}^n(y)|^p}{\|x-y\|^{d+s_n p}} \,\mathrm{d}x \,\mathrm{d}y
\\
&
\leq
2^{p+1}\int_{\mathbb{R}^d} |\tilde u^n(y)|^p \int_{B_1(y)^c} \frac{\mathrm{d}x}{\|x-y\|^{d+s_n p}} \,\mathrm{d}y
\\
&
=
2^{p+1} \| u^n \|^p_{p} \int_{1}^{\infty} \frac{d\omega_d}{\varrho^{1+s_n p}} \,\mathrm{d} \varrho
=
\frac{C(d, p) \|u^n\|^p_p}{s_n}
\le
C(d, p) \|u^n\|^p_p
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\int_{\mathbb{R}^d} \int_{B_1(y)^c}
&
\frac{|\tilde{u}^n(x)-\tilde{u}^n(y)|^p}{\|x-y\|^{d+s_n p}} \,\mathrm{d}x \,\mathrm{d}y
\le
2^p \int_{\mathbb{R}^d} \int_{B_1(y)^c} \frac{|\tilde u^n (x)|^p+|\tilde{u}^n(y)|^p}{\|x-y\|^{d+s_n p}} \,\mathrm{d}x \,\mathrm{d}y
\\
&
\leq
2^{p+1}\int_{\mathbb{R}^d} |\tilde u^n(y)|^p \int_{B_1(y)^c} \frac{\mathrm{d}x}{\|x-y\|^{d+s_n p}} \,\mathrm{d}y
\\
&
=
2^{p+1} \| u^n \|^p_{p} \int_{1}^{\infty} \frac{d\omega_d}{\varrho^{1+s_n p}} \,\mathrm{d} \varrho
=
\frac{C(d, p) \|u^n\|^p_p}{s_n}
\le
C(d, p) \|u^n\|^p_p
\end{aligned}
\end{equation} for all ![]() $n\in\mathbb{N}$, since
$n\in\mathbb{N}$, since ![]() $s_n\to 1^-$, thus we can assume
$s_n\to 1^-$, thus we can assume  $s_n \gt \frac{1}{2}$. On the other hand, recalling the notation in (2.1), since
$s_n \gt \frac{1}{2}$. On the other hand, recalling the notation in (2.1), since ![]() $\tilde u^n(y)$ is supported on
$\tilde u^n(y)$ is supported on ![]() $\Omega$, then
$\Omega$, then ![]() $\tilde{u}^n(x)$ for
$\tilde{u}^n(x)$ for ![]() $x\in B_1(y)$ is supported on
$x\in B_1(y)$ is supported on ![]() $\Omega_1$, and since
$\Omega_1$, and since ![]() $f_n\to f$ uniformly and
$f_n\to f$ uniformly and ![]() $f \gt 0$, we have
$f \gt 0$, we have
 \begin{equation}
\begin{aligned}
\int_{\mathbb{R}^d} \int_{B_1(y)}
&\frac{|\tilde{u}^n(x)-\tilde{u}^n(y)|^p}{\|x-y\|^{d+s_n p}} \,\mathrm{d}x \,\mathrm{d}y
=
\int_{\Omega_1} \int_{\Omega_1} \frac{|\tilde{u}^n(x)-\tilde{u}^n(y)|^p}{\|x-y\|^{d+s_n p}} \,\mathrm{d}x \,\mathrm{d}y
\\
&
\leq
\int_{\Omega_1} \int_{\Omega_1} \frac{|\tilde{u}^n(x)-\tilde{u}^n(y)|^p}{\|x-y\|^{d+s_n p}} \frac{f_n(x)f_n(y)}{\inf_{(x,n) \in \Omega_1 \times \mathbb{N} } f_n^2(x)} \,\mathrm{d}x \,\mathrm{d}y
\\
&
=
\frac{[\tilde u^n]^p_{s_n,p,f_n}}{\inf_{(x,n) \in \Omega_1 \times \mathbb{N} } f_n^2(x)}
=
C(\Omega_1, f_n) [\tilde u^n]^p_{s_n,p,f_n}.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\int_{\mathbb{R}^d} \int_{B_1(y)}
&\frac{|\tilde{u}^n(x)-\tilde{u}^n(y)|^p}{\|x-y\|^{d+s_n p}} \,\mathrm{d}x \,\mathrm{d}y
=
\int_{\Omega_1} \int_{\Omega_1} \frac{|\tilde{u}^n(x)-\tilde{u}^n(y)|^p}{\|x-y\|^{d+s_n p}} \,\mathrm{d}x \,\mathrm{d}y
\\
&
\leq
\int_{\Omega_1} \int_{\Omega_1} \frac{|\tilde{u}^n(x)-\tilde{u}^n(y)|^p}{\|x-y\|^{d+s_n p}} \frac{f_n(x)f_n(y)}{\inf_{(x,n) \in \Omega_1 \times \mathbb{N} } f_n^2(x)} \,\mathrm{d}x \,\mathrm{d}y
\\
&
=
\frac{[\tilde u^n]^p_{s_n,p,f_n}}{\inf_{(x,n) \in \Omega_1 \times \mathbb{N} } f_n^2(x)}
=
C(\Omega_1, f_n) [\tilde u^n]^p_{s_n,p,f_n}.
\end{aligned}
\end{equation} Since ![]() $f_n\to f$ uniformly and
$f_n\to f$ uniformly and ![]() $f \gt 0$, the constant
$f \gt 0$, the constant ![]() $C$ can be made independent of
$C$ can be made independent of ![]() $n$, and only dependent on the uniform limit
$n$, and only dependent on the uniform limit ![]() $f$. The conclusion hence follows by combining (3.37) and (3.38), multiplying by
$f$. The conclusion hence follows by combining (3.37) and (3.38), multiplying by ![]() $(1-s_n)$, and owing to the assumption (3.36). We omit the plain details.
$(1-s_n)$, and owing to the assumption (3.36). We omit the plain details.
4. Proof of Theorem 1.2
4.1. Stability of Hilbertian gradient flows
We briefly recall some abstract machinery from [Reference Crismale, De Luca, Kubin, Ninno and Ponsiglione9] concerning Hilbertian gradient flows.
Let ![]() $\mathscr{H}$ be a Hilbert space endowed with scalar product
$\mathscr{H}$ be a Hilbert space endowed with scalar product ![]() $\langle\cdot,\cdot\rangle_\mathscr{H}$ and norm
$\langle\cdot,\cdot\rangle_\mathscr{H}$ and norm ![]() $\|\cdot\|_\mathscr{H}$. Given
$\|\cdot\|_\mathscr{H}$. Given ![]() $\mathscr{F} \colon \mathscr{H} \to (-\infty,+\infty]$, we let
$\mathscr{F} \colon \mathscr{H} \to (-\infty,+\infty]$, we let ![]() $\mathscr{D}(\mathscr{F}) = \{\, x\in\mathscr{H} \colon \mathscr{F}(x) \lt + \infty\, \}$ and
$\mathscr{D}(\mathscr{F}) = \{\, x\in\mathscr{H} \colon \mathscr{F}(x) \lt + \infty\, \}$ and
 \begin{equation*}
\partial\mathscr{F}(x)
=
\left\{\,v\in\mathscr{H} \colon \liminf_{y\to x} \frac{\mathscr{F}(y)-\mathscr{F}(x)-\langle v,y-x\rangle_\mathscr{H}}{\|y-x\|_\mathscr{H} }\ge0 \,\right\}
\end{equation*}
\begin{equation*}
\partial\mathscr{F}(x)
=
\left\{\,v\in\mathscr{H} \colon \liminf_{y\to x} \frac{\mathscr{F}(y)-\mathscr{F}(x)-\langle v,y-x\rangle_\mathscr{H}}{\|y-x\|_\mathscr{H} }\ge0 \,\right\}
\end{equation*} be the subdifferential of ![]() $\mathscr{F}$ at
$\mathscr{F}$ at ![]() $x\in\mathscr{D}(\mathscr{F})$.
$x\in\mathscr{D}(\mathscr{F})$.
We recall the following result, which is a particular case of [Reference Crismale, De Luca, Kubin, Ninno and Ponsiglione9, Prop. 3.7]. Here and below, given any vector space ![]() $\mathscr{V}$, we let
$\mathscr{V}$, we let ![]() $\mathscr{V}^*$ be the algebraic dual space of
$\mathscr{V}^*$ be the algebraic dual space of ![]() $\mathscr{V}$ and
$\mathscr{V}$ and ![]() $\mathscr{V}'$ the topological dual space of
$\mathscr{V}'$ the topological dual space of ![]() $\mathscr{V}$.
$\mathscr{V}$.
Proposition 4.1. Let ![]() $\mathscr{K}$ be a dense subspace of
$\mathscr{K}$ be a dense subspace of ![]() $\mathscr{H}$. Let
$\mathscr{H}$. Let ![]() $\mathscr{F}\colon\mathscr{H}\to(-\infty,+\infty]$ be a proper, convex, and strongly lower semicontinuous functional and let
$\mathscr{F}\colon\mathscr{H}\to(-\infty,+\infty]$ be a proper, convex, and strongly lower semicontinuous functional and let ![]() $x\in\mathscr{D}(\mathscr{F})$. If there exists
$x\in\mathscr{D}(\mathscr{F})$. If there exists ![]() $T\in\mathscr{K}^*$ such that
$T\in\mathscr{K}^*$ such that
 \begin{equation*}
\lim_{t\to 0}\frac{\mathscr{F}(x+ty)-\mathscr{F}(x)}{t}=T(y),\quad\textrm{for every }y\in\mathscr{K}\,,
\end{equation*}
\begin{equation*}
\lim_{t\to 0}\frac{\mathscr{F}(x+ty)-\mathscr{F}(x)}{t}=T(y),\quad\textrm{for every }y\in\mathscr{K}\,,
\end{equation*} then either ![]() $\partial\mathscr{F}(x)=\emptyset$ or
$\partial\mathscr{F}(x)=\emptyset$ or ![]() $\partial\mathscr{F}(x)=\{v\}$, where
$\partial\mathscr{F}(x)=\{v\}$, where ![]() $v$ is the (unique) element in
$v$ is the (unique) element in ![]() $\mathscr{H}$ satisfying
$\mathscr{H}$ satisfying ![]() $T(y)=\langle v,y\rangle_\mathscr{H}$ for every
$T(y)=\langle v,y\rangle_\mathscr{H}$ for every ![]() $y\in\mathscr{K}$. In particular,
$y\in\mathscr{K}$. In particular, ![]() $T\in \mathscr{K}'$ and
$T\in \mathscr{K}'$ and ![]() $v$ is its unique continuous extension to
$v$ is its unique continuous extension to ![]() $\mathscr{H}'$.
$\mathscr{H}'$.
We also recall the following stability result, which is contained in [Reference Crismale, De Luca, Kubin, Ninno and Ponsiglione9, Thm. 3.8].
Theorem 4.2 Let ![]() $\mathscr{F}_n\colon\mathscr{H}\to(-\infty,+\infty]$ be a proper, strongly lower semicontinuous, convex, and positive functional for every
$\mathscr{F}_n\colon\mathscr{H}\to(-\infty,+\infty]$ be a proper, strongly lower semicontinuous, convex, and positive functional for every ![]() $n\in\mathbb{N}$. Assume the following:
$n\in\mathbb{N}$. Assume the following:
(a)
 $(\mathscr{F}_n)_{n\in\mathbb{N}}$
$(\mathscr{F}_n)_{n\in\mathbb{N}}$  $\Gamma$-converges to some proper functional
$\Gamma$-converges to some proper functional  $\mathscr{F}_\infty\colon\mathscr{H}\to(-\infty,+\infty]$ with respect to the strong
$\mathscr{F}_\infty\colon\mathscr{H}\to(-\infty,+\infty]$ with respect to the strong  $\mathscr{H}$-convergence;
$\mathscr{H}$-convergence;(b) any bounded sequence
 $(x_n)_{n\in\mathbb{N}}\subset\mathscr{H}$ such that
$(x_n)_{n\in\mathbb{N}}\subset\mathscr{H}$ such that  $\displaystyle\sup_{n\in\mathbb{N}}\mathscr{F}_n(x_n) \lt \infty$ admits a strongly
$\displaystyle\sup_{n\in\mathbb{N}}\mathscr{F}_n(x_n) \lt \infty$ admits a strongly  $\mathscr{H}$-convergent subsequence.
$\mathscr{H}$-convergent subsequence.
If ![]() $(x^n_{0})_{n\in\mathbb{N}}\subset\mathscr{H}$ is such that
$(x^n_{0})_{n\in\mathbb{N}}\subset\mathscr{H}$ is such that ![]() $x^n_{0}\in \mathscr{D}(\mathscr{F}_n)$ for every
$x^n_{0}\in \mathscr{D}(\mathscr{F}_n)$ for every ![]() $n\in\mathbb{N}$,
$n\in\mathbb{N}$, 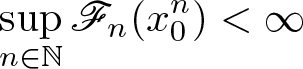 $\displaystyle\sup_{n\in\mathbb{N}}\mathscr{F}_n(x^n_{0}) \lt \infty$ and
$\displaystyle\sup_{n\in\mathbb{N}}\mathscr{F}_n(x^n_{0}) \lt \infty$ and ![]() $x^n_{0}\to x^\infty_{0}$ strongly in
$x^n_{0}\to x^\infty_{0}$ strongly in ![]() $\mathscr{H}$ for some
$\mathscr{H}$ for some ![]() $x^\infty_{0}\in\mathscr{H}$, then the following hold:
$x^\infty_{0}\in\mathscr{H}$, then the following hold:
(i)
 $x^\infty_{0}\in\mathscr{D}(\mathscr{F}_\infty)$;
$x^\infty_{0}\in\mathscr{D}(\mathscr{F}_\infty)$;(ii) for every
 $T \gt 0$, the problem
$T \gt 0$, the problem
 \begin{equation*}
\begin{cases}
\dot{x}(t)\in -\partial \mathscr{F}_n(x(t)), \quad \text{for a.e. }t \in (0,T)\,, \\[1ex]
x(0)=x^n_{0},
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
\dot{x}(t)\in -\partial \mathscr{F}_n(x(t)), \quad \text{for a.e. }t \in (0,T)\,, \\[1ex]
x(0)=x^n_{0},
\end{cases}
\end{equation*}admits a unique solution
 $x_n\in H^1([0,T];\mathscr{H})$ for every
$x_n\in H^1([0,T];\mathscr{H})$ for every  $n\in\mathbb{N} \cup \{\infty\}$;
$n\in\mathbb{N} \cup \{\infty\}$;(iii)
 $(x_n)_{n\in\mathbb{N}}$ weakly converges to
$(x_n)_{n\in\mathbb{N}}$ weakly converges to  $x_\infty$ in
$x_\infty$ in  $H^1([0,T];\mathscr{H})$.
$H^1([0,T];\mathscr{H})$.
Moreover, if 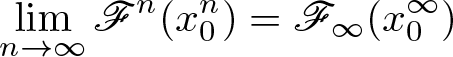 $\displaystyle\lim_{n\to\infty} \mathscr{F}^n(x^n_{0})=\mathscr{F}_\infty(x^\infty_{0})$, then actually
$\displaystyle\lim_{n\to\infty} \mathscr{F}^n(x^n_{0})=\mathscr{F}_\infty(x^\infty_{0})$, then actually ![]() $(x_n)_{n\in\mathbb{N}}$ strongly converges to
$(x_n)_{n\in\mathbb{N}}$ strongly converges to ![]() $x_\infty$ in
$x_\infty$ in ![]() $H^1([0,T];\mathscr{H})$ and also
$H^1([0,T];\mathscr{H})$ and also
 \begin{equation*}
x_n(t)\xrightarrow{\mathscr{H}}x_{\infty}(t)
\quad
\text{and}
\quad
\mathscr{F}_n(x_n(t))\to\mathscr{F}_{\infty}(x_{\infty}(t))
\quad\text{for every}\ t\in[0,T].
\end{equation*}
\begin{equation*}
x_n(t)\xrightarrow{\mathscr{H}}x_{\infty}(t)
\quad
\text{and}
\quad
\mathscr{F}_n(x_n(t))\to\mathscr{F}_{\infty}(x_{\infty}(t))
\quad\text{for every}\ t\in[0,T].
\end{equation*}4.2. Proof of Theorem 1.2
The validity of Theorem 1.2 follows by combining the abstract results above with the following proposition. Here and below, ![]() $\langle\cdot,\cdot\rangle$ denotes the standard scalar product in
$\langle\cdot,\cdot\rangle$ denotes the standard scalar product in ![]() $L^2(\mathbb{R}^d)$.
$L^2(\mathbb{R}^d)$.
Proposition 4.3. Let ![]() $\varphi\in C_c^\infty(\Omega)$ and
$\varphi\in C_c^\infty(\Omega)$ and ![]() $u\in L^2(\Omega)$. The following hold:
$u\in L^2(\Omega)$. The following hold:
(i) if
 $u\in H^1_0(\Omega)$, then
(4.1)
$u\in H^1_0(\Omega)$, then
(4.1) \begin{equation}
\lim_{t\to 0}\frac{\|\nabla(u+t\varphi)\|^2_{2,f^2}-\|\nabla u\|_{2,f^2}^2}{t}=\langle(-\mathfrak{D})^{f} u,\varphi \rangle;
\end{equation}
\begin{equation}
\lim_{t\to 0}\frac{\|\nabla(u+t\varphi)\|^2_{2,f^2}-\|\nabla u\|_{2,f^2}^2}{t}=\langle(-\mathfrak{D})^{f} u,\varphi \rangle;
\end{equation}(ii) if
 $ [\tilde{u}]_{s,2,f} \lt \infty$ for some
$ [\tilde{u}]_{s,2,f} \lt \infty$ for some  $s\in (0,1)$, then
(4.2)
$s\in (0,1)$, then
(4.2) \begin{equation}
\lim_{t\to 0}\frac{[u+t\varphi]_{s,2,f}^2-[u]_{s,2,f}^2}{t}=\langle(-\mathfrak{D})^{s,f} u,\varphi \rangle.
\end{equation}
\begin{equation}
\lim_{t\to 0}\frac{[u+t\varphi]_{s,2,f}^2-[u]_{s,2,f}^2}{t}=\langle(-\mathfrak{D})^{s,f} u,\varphi \rangle.
\end{equation}
Proof. We only prove (4.2), the proof of (4.1) being straightforward. We note that
 \begin{align*}
[u+t\varphi]_{s,2,f}^2
&
=
[u]_{s,2,f}^2
+
t^2 [\varphi]_{s,2,f}^2
\\
&
\quad
+2 t \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{(u(x)-u(y))(\varphi(x)-\varphi(y))}{\|x-y\|^{d+2s}}f(x)f(y) \,\mathrm{d}x\,\mathrm{d}y
\end{align*}
\begin{align*}
[u+t\varphi]_{s,2,f}^2
&
=
[u]_{s,2,f}^2
+
t^2 [\varphi]_{s,2,f}^2
\\
&
\quad
+2 t \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{(u(x)-u(y))(\varphi(x)-\varphi(y))}{\|x-y\|^{d+2s}}f(x)f(y) \,\mathrm{d}x\,\mathrm{d}y
\end{align*} for every ![]() $t\in\mathbb{R}$, and thus we easily get that
$t\in\mathbb{R}$, and thus we easily get that
 \begin{align*}
\lim_{t\to 0} \frac{[u+t\varphi]_{s,2,f}^2-[u]_{s,2,f}^2}{t}
&
=
2 \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{(u(x)-u(y))(\varphi(x)-\varphi(y))}{\|x-y\|^{d+2s}}f(x)f(y) \,\mathrm{d}x \,\mathrm{d}y
\\
&
=
4 \int_{\mathbb{R}^d} u(x)f(x) \lim_{r \to 0^+} \int_{\mathbb{R}^d \setminus B_r} \frac{\varphi(x)-\varphi(y)}{\|x-y\|^{d+2s}} f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
=
\langle u,(- \mathfrak{D})^{s,f} \varphi \rangle= \langle (- \mathfrak{D})^{s,f} u,\varphi \rangle
\end{align*}
\begin{align*}
\lim_{t\to 0} \frac{[u+t\varphi]_{s,2,f}^2-[u]_{s,2,f}^2}{t}
&
=
2 \int_{\mathbb{R}^d} \int_{\mathbb{R}^d} \frac{(u(x)-u(y))(\varphi(x)-\varphi(y))}{\|x-y\|^{d+2s}}f(x)f(y) \,\mathrm{d}x \,\mathrm{d}y
\\
&
=
4 \int_{\mathbb{R}^d} u(x)f(x) \lim_{r \to 0^+} \int_{\mathbb{R}^d \setminus B_r} \frac{\varphi(x)-\varphi(y)}{\|x-y\|^{d+2s}} f(y) \,\mathrm{d}y \,\mathrm{d}x
\\
&
=
\langle u,(- \mathfrak{D})^{s,f} \varphi \rangle= \langle (- \mathfrak{D})^{s,f} u,\varphi \rangle
\end{align*}in virtue of the distributional definition in (1.7), concluding the proof.
We are now ready to prove Theorem 1.2.
Proof of Theorem 1.2
Since ![]() $f_n\to f$ uniformly and
$f_n\to f$ uniformly and ![]() $f \gt 0$, the functionals given by
$f \gt 0$, the functionals given by 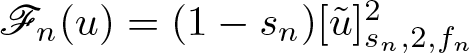 $\mathscr{F}_n(u)=(1-s_n)[\tilde{u}]_{s_n,2,f_n}^2$ are positive for
$\mathscr{F}_n(u)=(1-s_n)[\tilde{u}]_{s_n,2,f_n}^2$ are positive for ![]() $n\gg1$. Further, they are easily shown to be convex. By Theorem 1.1(ii)–(iii),
$n\gg1$. Further, they are easily shown to be convex. By Theorem 1.1(ii)–(iii), ![]() $(\mathscr{F}_n)_{n\in\mathbb{N}}$
$(\mathscr{F}_n)_{n\in\mathbb{N}}$ ![]() $\Gamma$-converges to the functional
$\Gamma$-converges to the functional 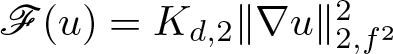 $\mathscr{F}(u)= K_{d,2}\| \nabla u \|^2_{2,f^2}$ in the strong topology of
$\mathscr{F}(u)= K_{d,2}\| \nabla u \|^2_{2,f^2}$ in the strong topology of ![]() $L^2(\Omega)$, whereas by Theorem 1.1(i) every sequence
$L^2(\Omega)$, whereas by Theorem 1.1(i) every sequence ![]() $(u_n)_{n\in\mathbb{N}}\subset L^2(\Omega)$ such that
$(u_n)_{n\in\mathbb{N}}\subset L^2(\Omega)$ such that ![]() $\sup_{n\in\mathbb{N}}\mathscr{F}_n(u_n) \lt \infty$ admits a strong
$\sup_{n\in\mathbb{N}}\mathscr{F}_n(u_n) \lt \infty$ admits a strong ![]() $L^2$-limit
$L^2$-limit ![]() $u\in L^2(\Omega)$. The conclusion hence follows by Theorem 4.2 and Proposition 4.1 combined with Proposition 4.3.
$u\in L^2(\Omega)$. The conclusion hence follows by Theorem 4.2 and Proposition 4.1 combined with Proposition 4.3.
Acknowledgements
The second-named and third-named authors are members of the Istituto Nazionale di Alta Matematica (INdAM), Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA). The first-named author is supported by the Academy of Finland (grant agreement No. 314227). The second-named author has received funding from INdAM under the INdAM–GNAMPA Project 2025 Disuguaglianze funzionali di tipo geometrico e spettrale (grant agreement No. CUP_E5324001950001). The third-named author has received funding from INdAM under the INdAM–GNAMPA Project 2025 Metodi variazionali per problemi dipendenti da operatori frazionari isotropi e anisotropi (grant agreement No. CUP_E5324001950001) and from the European Union—NextGenerationEU and the University of Padua under the 2023 STARS@UNIPD Starting Grant Project New Directions in Fractional Calculus—NewFrac (grant agreement No. CUP_C95F21009990001).