Article contents
Surfaces of prescribed linear Weingarten curvature in $\mathbb {R}^{3}$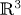
Published online by Cambridge University Press: 22 July 2022
Abstract
Given $a,\,b\in \mathbb {R}$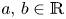 and $\Phi \in C^{1}(\mathbb {S}^{2})$
and $\Phi \in C^{1}(\mathbb {S}^{2})$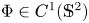 , we study immersed oriented surfaces $\Sigma$
, we study immersed oriented surfaces $\Sigma$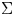 in the Euclidean 3-space $\mathbb {R}^{3}$
in the Euclidean 3-space $\mathbb {R}^{3}$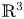 whose mean curvature $H$
whose mean curvature $H$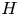 and Gauss curvature $K$
and Gauss curvature $K$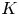 satisfy $2aH+bK=\Phi (N)$
satisfy $2aH+bK=\Phi (N)$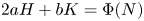 , where $N:\Sigma \rightarrow \mathbb {S}^{2}$
, where $N:\Sigma \rightarrow \mathbb {S}^{2}$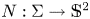 is the Gauss map. This theory widely generalizes some of paramount importance such as the ones constant mean and Gauss curvature surfaces, linear Weingarten surfaces and self-translating solitons of the mean curvature flow. Under mild assumptions on the prescribed function $\Phi$
is the Gauss map. This theory widely generalizes some of paramount importance such as the ones constant mean and Gauss curvature surfaces, linear Weingarten surfaces and self-translating solitons of the mean curvature flow. Under mild assumptions on the prescribed function $\Phi$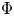 , we exhibit a classification result for rotational surfaces in the case that the underlying fully nonlinear PDE that governs these surfaces is elliptic or hyperbolic.
, we exhibit a classification result for rotational surfaces in the case that the underlying fully nonlinear PDE that governs these surfaces is elliptic or hyperbolic.
Keywords
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 4 , August 2023 , pp. 1347 - 1370
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
Footnotes
This paper is dedicated to the first author's mother, whose daily fight, strength and spirit of overcoming adversity prove that there are way more difficult and important issues in life than a mathematical problem
References
- 2
- Cited by


