Contents
Research Article
A comparison of mean concentrations in a diffusion problem
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 153-170
-
- Article
-
- You have access
- Export citation
Note on a paper by Singh and Dhaliwal
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 81
-
- Article
-
- You have access
- Export citation
Nonimmersions of complex Grassmann manifolds
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-3
-
- Article
-
- You have access
- Export citation
Primary decomposition in enveloping algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 83-85
-
- Article
-
- You have access
- Export citation
A characterisation of semisimple classes
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 5-7
-
- Article
-
- You have access
- Export citation
Factorisable right adequate semigroups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 171-178
-
- Article
-
- You have access
- Export citation
On the attached prime ideals of certain Artinian local cohomology modules
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 9-14
-
- Article
-
- You have access
- Export citation
On semigroup algebras and semisimple semilattice sums of rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 87-90
-
- Article
-
- You have access
- Export citation
On a generalisation of a result of Ramanujan connected with the exponential series
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 179-195
-
- Article
-
- You have access
- Export citation
On complex projective hypersurfaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 91-97
-
- Article
-
- You have access
- Export citation
The normal subgroup structure of the infinite general linear group
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 197-202
-
- Article
-
- You have access
- Export citation
On certain cycles in graphs
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 15-17
-
- Article
-
- You have access
- Export citation
Non-unital Banach Jordan algebras and C*-triple systems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 19-29
-
- Article
-
- You have access
- Export citation
Matrices with prescribed characteristic polynomial and principal blocks
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 203-208
-
- Article
-
- You have access
- Export citation
Counting balanced signed graphs using marked graphs
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 99-104
-
- Article
-
- You have access
- Export citation
Radicals of rings and their subrings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 209-215
-
- Article
-
- You have access
- Export citation
Higher point derivations on commutative Banach algebras, III
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 31-40
-
- Article
-
- You have access
- Export citation
Limit circle criteria for fourth order differential operators with an oscillatory coefficient
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 105-117
-
- Article
-
- You have access
- Export citation
Lie algebras all of whose maximal subalgebras have codimension one
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 217-219
-
- Article
-
- You have access
- Export citation
Spectral measures on spaces not containing l∞
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 41-45
-
- Article
-
- You have access
- Export citation
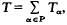
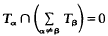 for each α∈
for each α∈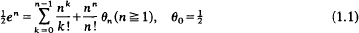
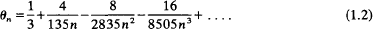
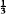 and that θ
and that θ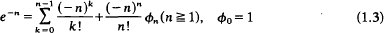
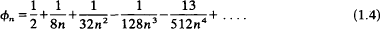
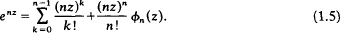
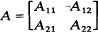

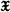 denote the class of finite-dimensional Lie algebras
denote the class of finite-dimensional Lie algebras