Contents
Research Article
Countable-codimensional subspaces of locally convex spaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 167-172
-
- Article
-
- You have access
- Export citation
Group algebras of some generalised soluble groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-5
-
- Article
-
- You have access
- Export citation
On the algebra generated by a Hermitian operator
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 89-91
-
- Article
-
- You have access
- Export citation
A problem on cyclic subgroups of finite groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 247-249
-
- Article
-
- You have access
- Export citation
Scalar and matrix complex nonoscillation criteria
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 173-189
-
- Article
-
- You have access
- Export citation
Characterizations of linear differential systems with a regular singular point
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 93-98
-
- Article
-
- You have access
- Export citation
Primary and coprimary decompositions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 251-264
-
- Article
-
- You have access
- Export citation
The weak-star closure of the unit ball in a hyperplane
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 7-11
-
- Article
-
- You have access
- Export citation
Generating varieties of topological groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 191-197
-
- Article
-
- You have access
- Export citation
On (J, pn)-summability of Fourier series
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 13-17
-
- Article
-
- You have access
- Export citation
Generalisations of nilpotency of rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 265-272
-
- Article
-
- You have access
- Export citation
Convergence criteria for bounded sequences
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 99-103
-
- Article
-
- You have access
- Export citation
A characterisation of a certain class of convolution algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 198
-
- Article
-
- You have access
- Export citation
Sequences in genetic algebras for overlapping generations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 19-29
-
- Article
-
- You have access
- Export citation
A configuration of lines in three dimensions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 105-123
-
- Article
-
- You have access
- Export citation
Contributions to genetic algebras II
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 273-279
-
- Article
-
- You have access
- Export citation
On the existence of positive solutions of Au = λBu
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 281-285
-
- Article
-
- You have access
- Export citation
A generalization of an early multivariate integral
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 125-128
-
- Article
-
- You have access
- Export citation
Some inequalities for a hypergeometric integral
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 31-34
-
- Article
-
- You have access
- Export citation
A question of C. R. Hobby on regular p-groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 207-208
-
- Article
-
- You have access
- Export citation
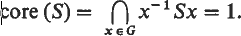


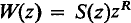
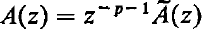






 be its closure and let
be its closure and let  .
.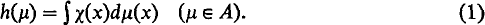
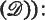
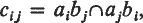 , where
, where