Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-25T08:00:20.256Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Ricci flow on aligned homogeneous spaces

Part of: Global differential geometry Stability theory

Published online by Cambridge University Press:  26 November 2024

Valeria Gutiérrez Open the ORCID record for Valeria Gutiérrez [Opens in a new window]
Valeria Gutiérrez*
Affiliation:
FAMAF, Universidad Nacional de Córdoba and CIEM, CONICET, Córdoba, Argentina
*
Email: valeria.gutierrez@unc.edu.ar
Get access Rights & Permissions [Opens in a new window]

Abstract

The fixed points of the generalized Ricci flow are the Bismut Ricci flat (BRF) metrics, i.e., a generalized metric (g, H) on a manifold M, where g is a Riemannian metric and H a closed 3-form, such that H is g-harmonic and 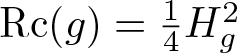$\operatorname{Rc}(g)=\tfrac{1}{4} H_g^2$. Given two standard Einstein homogeneous spaces 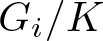$G_i/K$, where each Gi is a compact simple Lie group and K is a closed subgroup of them holding some extra assumption, we consider $M=G_1\times G_2/\Delta K$. Recently, Lauret and Will proved the existence of a BRF metric on any of these spaces. We proved that this metric is always asymptotically stable for the generalized Ricci flow on M among a subset of G-invariant metrics and, if $G_1=G_2$, then it is globally stable.

Keywords

homogeneous spacesBismut Ricci flat metricsgeneralized Ricci flowstability

MSC classification

Primary: 53C25: Special Riemannian manifolds (Einstein, Sasakian, etc.) 34D35: Stability of manifolds of solutions
Secondary: 57S25: Groups acting on specific manifolds 34D23: Global stability
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 68 , Issue 1 , February 2025 , pp. 226 - 246
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Besse, A., Einstein manifolds, Ergebnisse der Mathematik und ihrer Grenzgebiete, Volume 10 (Springer-Verlag, Berlin-Heidelberg, 1987).CrossRefGoogle Scholar
Bredon, G., Topology and geometry, GTM Graduate Texts in Mathematics, Volume 139 (New York, NY: Springer, 1993).CrossRefGoogle Scholar
Cortes, V. and Krusche, D., Classification of generalized Einstein metrics on 3-dimensional Lie groups, Canad. J. Math. 75(6) (2023), 2038–2095.CrossRefGoogle Scholar
Garcia-Fernandez, M., Ricci flow, Killing spinors, and T-duality in generalized geometry, Adv. Math. 350 (2019), 1059–1108.CrossRefGoogle Scholar
Garcia-Fernandez, M., and Streets, J., Generalized Ricci flow, Volume 76 (University Lecture Series, AMS, 2021).CrossRefGoogle Scholar
Lauret, E. A. and Lauret, J., The stability of standard homogeneous Einstein manifolds, Math. Z. 303 (2023), .CrossRefGoogle Scholar
Lauret, J. and Will, C. E., Bismut Ricci flat generalized metrics on compact homogeneous spaces, Trans. Amer. Math. Soc. 376 (2023), 7495–7519.Google Scholar
Lauret, J., and Will, C. E., Harmonic 3-forms on compact homogeneous spaces, J. Geom. Anal. 33 (2023), 175.CrossRefGoogle Scholar
Lauret, J., and Will, C.E., Einstein metrics on homogeneous spaces $H \times H/ \Delta K$ Communications in Contemporary Mathematics in press.Google Scholar
Lauret, J. and Will, C.E., Bismut Ricci flat generalized metrics on compact homogeneous spaces (including a Corrigendum), preprint 2023 (arXiv).CrossRefGoogle Scholar
Lee, K.-H., The stability of generalized Ricci solitons, J. Geom. Anal. 33(9) (2023), .CrossRefGoogle Scholar
Perko, L. , Differential equations and dynamical systems, Text in Applied Mathematics, Volume 7 (New York, NY: Springer, 2001).Google Scholar
Podestà, F., and Raffero, A., Bismut Ricci flat manifolds with symmetries, Proc. Roy. Soc. Edinburgh Sect. A 153(4) (2023), 1371–1390.CrossRefGoogle Scholar
Podestà, F. and Raffero, A., Infinite families of homogeneous Bismut Ricci flat manifolds, Comm. Contemp. Math. 26(2) (2024), .CrossRefGoogle Scholar
Rubio, R., and Tipler, C., The Lie group of automorphisms of a courant algebroid and the moduli space of generalized metrics, Rev. Mat. Iberoam. 36(2) (2019), 485–536.CrossRefGoogle Scholar
Streets, J., Regularity and expanding entropy for connection Ricci flow, J. Geom. Phys. 58(7) (2008), 900–912.CrossRefGoogle Scholar
Streets, J., Generalized geometry, T-duality, and renormalization group flow, J. Geom. Phys. 114 (2017), 506–522.CrossRefGoogle Scholar