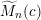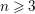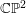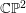1 Introduction
Let
![]() $M$
be a
$M$
be a
![]() $(2n-1)$
-dimensional manifold and
$(2n-1)$
-dimensional manifold and
![]() $TM$
be its tangent bundle. A CR-structure on
$TM$
be its tangent bundle. A CR-structure on
![]() $M$
is a complex rank
$M$
is a complex rank
![]() $(n-1)$
subbundle
$(n-1)$
subbundle
![]() ${\mathcal{H}}\subset \mathbb{C}TM=TM\otimes \mathbb{C}$
satisfying
${\mathcal{H}}\subset \mathbb{C}TM=TM\otimes \mathbb{C}$
satisfying
where
![]() $\bar{{\mathcal{H}}}$
denotes the complex conjugation of
$\bar{{\mathcal{H}}}$
denotes the complex conjugation of
![]() ${\mathcal{H}}.$
${\mathcal{H}}.$
Then there exists a unique subbundle
![]() $D=Re\{{\mathcal{H}}\oplus \bar{{\mathcal{H}}}\}$
, called the Levi subbundle (maximally holomorphic subbundle) of
$D=Re\{{\mathcal{H}}\oplus \bar{{\mathcal{H}}}\}$
, called the Levi subbundle (maximally holomorphic subbundle) of
![]() $(M,{\mathcal{H}})$
, and a unique bundle map
$(M,{\mathcal{H}})$
, and a unique bundle map
![]() $J$
such that
$J$
such that
![]() $J^{2}=-I$
and
$J^{2}=-I$
and
![]() ${\mathcal{H}}=\{X-iJX|X\in D\}$
. We call
${\mathcal{H}}=\{X-iJX|X\in D\}$
. We call
![]() $(D,J)$
the real representation of
$(D,J)$
the real representation of
![]() ${\mathcal{H}}$
. Let
${\mathcal{H}}$
. Let
![]() $E\subset T^{\ast }M$
be the conormal bundle of
$E\subset T^{\ast }M$
be the conormal bundle of
![]() $D$
. If
$D$
. If
![]() $M$
is an oriented CR-manifold then
$M$
is an oriented CR-manifold then
![]() $E$
is a trivial bundle, hence admits globally defined a nowhere zero section
$E$
is a trivial bundle, hence admits globally defined a nowhere zero section
![]() $\unicode[STIX]{x1D702}$
, that is, a real one-form on
$\unicode[STIX]{x1D702}$
, that is, a real one-form on
![]() $M$
such that Ker
$M$
such that Ker
![]() $(\unicode[STIX]{x1D702})=D$
. For
$(\unicode[STIX]{x1D702})=D$
. For
![]() $(D,J)$
we define the Levi form by
$(D,J)$
we define the Levi form by
where
![]() ${\mathcal{F}}(M)$
denotes the algebra of differential functions on
${\mathcal{F}}(M)$
denotes the algebra of differential functions on
![]() $M$
. If the Levi form is nondegenerate (positive or negative definite, resp.), then the CR-structure is called a nondegenerate (strongly pseudo-convex, resp.) pseudo-Hermitian CR-structure.
$M$
. If the Levi form is nondegenerate (positive or negative definite, resp.), then the CR-structure is called a nondegenerate (strongly pseudo-convex, resp.) pseudo-Hermitian CR-structure.
Now, let
![]() $\widetilde{M}^{n}$
be an
$\widetilde{M}^{n}$
be an
![]() $n$
-dimensional Kähler manifold and let
$n$
-dimensional Kähler manifold and let
![]() $M^{2n-1}$
be a real hypersurface in
$M^{2n-1}$
be a real hypersurface in
![]() $\widetilde{M}$
. Then
$\widetilde{M}$
. Then
![]() $M$
is called Levi-flat if the Levi form vanishes. In the present paper, we introduce the so-called Levi-umbilicity. If the Levi form
$M$
is called Levi-flat if the Levi form vanishes. In the present paper, we introduce the so-called Levi-umbilicity. If the Levi form
![]() $L$
is proportional to the induced metric
$L$
is proportional to the induced metric
![]() $g$
by a nonzero constant
$g$
by a nonzero constant
![]() $k$
, then
$k$
, then
![]() $M$
is said to be Levi-umbilical.
$M$
is said to be Levi-umbilical.
A complex
![]() $n$
-dimensional complete and simply connected Kähler manifold of constant holomorphic sectional curvature
$n$
-dimensional complete and simply connected Kähler manifold of constant holomorphic sectional curvature
![]() $c$
is called a complex space form, which is denoted by
$c$
is called a complex space form, which is denoted by
![]() $\widetilde{M}_{n}(c)$
. A complex space form consists of a complex projective space
$\widetilde{M}_{n}(c)$
. A complex space form consists of a complex projective space
![]() $\mathbb{C}\mathbb{P}^{n}$
, a complex Euclidean space
$\mathbb{C}\mathbb{P}^{n}$
, a complex Euclidean space
![]() $\mathbb{CE}^{n}$
or a complex hyperbolic space
$\mathbb{CE}^{n}$
or a complex hyperbolic space
![]() $\mathbb{CH}^{n}$
, according as
$\mathbb{CH}^{n}$
, according as
![]() $c>0$
,
$c>0$
,
![]() $c=0$
or
$c=0$
or
![]() $c<0$
. Recently, Siu [Reference Siu14] proved the nonexistence of compact smooth Levi-flat hypersurfaces in
$c<0$
. Recently, Siu [Reference Siu14] proved the nonexistence of compact smooth Levi-flat hypersurfaces in
![]() $\mathbb{C}\mathbb{P}^{n}$
of dimensions
$\mathbb{C}\mathbb{P}^{n}$
of dimensions
![]() ${\geqslant}3$
. When
${\geqslant}3$
. When
![]() $n=2$
, Ohsawa [Reference Ohsawa13] proved the nonexistence of compact real analytic Levi-flat hypersurfaces in
$n=2$
, Ohsawa [Reference Ohsawa13] proved the nonexistence of compact real analytic Levi-flat hypersurfaces in
![]() $\mathbb{C}\mathbb{P}^{2}$
. Here, it is remarkable that the assumption of compactness has a crucial role. Indeed, there are noncomplete examples which are realized as ruled hypersurfaces and Levi-flat in
$\mathbb{C}\mathbb{P}^{2}$
. Here, it is remarkable that the assumption of compactness has a crucial role. Indeed, there are noncomplete examples which are realized as ruled hypersurfaces and Levi-flat in
![]() $\mathbb{C}\mathbb{P}^{n}$
(see Section 3). We also find that there does not exist a Levi-flat Hopf hypersurface in
$\mathbb{C}\mathbb{P}^{n}$
(see Section 3). We also find that there does not exist a Levi-flat Hopf hypersurface in
![]() $\mathbb{C}\mathbb{P}^{n}$
or
$\mathbb{C}\mathbb{P}^{n}$
or
![]() $\mathbb{CH}^{n}$
(cf. [Reference Cho6]). In the present paper, we give noncompact examples of Levi-flat real hypersurfaces which are not ruled hypersurfaces in
$\mathbb{CH}^{n}$
(cf. [Reference Cho6]). In the present paper, we give noncompact examples of Levi-flat real hypersurfaces which are not ruled hypersurfaces in
![]() $\mathbb{C}\mathbb{P}^{2}$
(see Section 5).
$\mathbb{C}\mathbb{P}^{2}$
(see Section 5).
On the other hand, Takagi [Reference Takagi16], [Reference Takagi17] classified the homogeneous real hypersurfaces in
![]() $\mathbb{C}\mathbb{P}^{n}$
into six types. Cecil and Ryan [Reference Cecil and Ryan4] extensively studied a real hypersurface whose structure vector
$\mathbb{C}\mathbb{P}^{n}$
into six types. Cecil and Ryan [Reference Cecil and Ryan4] extensively studied a real hypersurface whose structure vector
![]() $\unicode[STIX]{x1D709}$
is a principal curvature vector, which is realized as tubes over certain submanifolds in
$\unicode[STIX]{x1D709}$
is a principal curvature vector, which is realized as tubes over certain submanifolds in
![]() $\mathbb{C}\mathbb{P}^{n}$
, by using its focal map. A real hypersurface of a complex space form is said to be a Hopf hypersurface if its structure vector is a principal curvature vector. By making use of those results and the mentioned work of Takagi, Makoto Kimura [Reference Kimura8] proved the classification theorem for Hopf hypersurfaces of
$\mathbb{C}\mathbb{P}^{n}$
, by using its focal map. A real hypersurface of a complex space form is said to be a Hopf hypersurface if its structure vector is a principal curvature vector. By making use of those results and the mentioned work of Takagi, Makoto Kimura [Reference Kimura8] proved the classification theorem for Hopf hypersurfaces of
![]() $\mathbb{C}\mathbb{P}^{n}$
whose all principal curvatures are constant. For the case
$\mathbb{C}\mathbb{P}^{n}$
whose all principal curvatures are constant. For the case
![]() $\mathbb{CH}^{n}$
, Berndt [Reference Berndt2] proved the classification theorem for Hopf hypersurfaces whose all principal curvatures are constant.
$\mathbb{CH}^{n}$
, Berndt [Reference Berndt2] proved the classification theorem for Hopf hypersurfaces whose all principal curvatures are constant.
The main purpose of the present paper is to give a classification of Levi-umbilical real hypersurfaces in a complex space form.
Theorem 1. If a real hypersurface
![]() $M$
of a complex space form
$M$
of a complex space form
![]() $\widetilde{M}_{n}(c)$
is Levi-umbilical, then
$\widetilde{M}_{n}(c)$
is Levi-umbilical, then
![]() $n=2$
or
$n=2$
or
![]() $M$
is a Hopf hypersurface. Moreover, in case that
$M$
is a Hopf hypersurface. Moreover, in case that
![]() $M$
is connected, complete and
$M$
is connected, complete and
![]() $n\geqslant 3$
, we have the following.
$n\geqslant 3$
, we have the following.
-
(I) If
 $\widetilde{M}_{n}(c)=\mathbb{C}\mathbb{P}^{n}$
, then
$\widetilde{M}_{n}(c)=\mathbb{C}\mathbb{P}^{n}$
, then
 $M$
is congruent to one of the following:
$M$
is congruent to one of the following:-
(1) a geodesic hypersphere, that is, a tube of radius
 $r$
over
$r$
over
 $\mathbb{C}\mathbb{P}^{n-1}$
, where
$\mathbb{C}\mathbb{P}^{n-1}$
, where
 $0<r<\frac{\unicode[STIX]{x1D70B}}{2}$
,
$0<r<\frac{\unicode[STIX]{x1D70B}}{2}$
, -
(2) a tube of radius
 $r$
over a complex quadric
$r$
over a complex quadric
 $\mathbb{CQ}^{n-1}$
, where
$\mathbb{CQ}^{n-1}$
, where
 $0<r<\frac{\unicode[STIX]{x1D70B}}{4}$
.
$0<r<\frac{\unicode[STIX]{x1D70B}}{4}$
.
-
-
(II) If
 $\widetilde{M}_{n}(c)=\mathbb{CH}^{n}$
, then
$\widetilde{M}_{n}(c)=\mathbb{CH}^{n}$
, then
 $M$
is congruent to one of the following:
$M$
is congruent to one of the following:-
(1) a horosphere in
 $\mathbb{CH}^{n}$
,
$\mathbb{CH}^{n}$
, -
(2) a geodesic hypersphere or a tube of radius
 $r\in \mathbb{R}_{+}$
over a totally geodesic
$r\in \mathbb{R}_{+}$
over a totally geodesic
 $\mathbb{CH}^{n-1}$
,
$\mathbb{CH}^{n-1}$
, -
(3) a tube of radius
 $r\in \mathbb{R}_{+}$
over a totally real hyperbolic space
$r\in \mathbb{R}_{+}$
over a totally real hyperbolic space
 $\mathbb{RH}^{n}$
.
$\mathbb{RH}^{n}$
.
-
-
(III) If
 $\widetilde{M}_{n}(c)=\mathbb{CE}^{n}$
, then
$\widetilde{M}_{n}(c)=\mathbb{CE}^{n}$
, then
 $M$
is locally congruent to one of the following:
$M$
is locally congruent to one of the following:-
(1) a sphere
 $S^{2n-1}(r)$
of radius
$S^{2n-1}(r)$
of radius
 $r\in \mathbb{R}_{+}$
,
$r\in \mathbb{R}_{+}$
, -
(2) a generalized cylinder
 $S^{n-1}(r)\times \mathbb{E}^{n}$
of radius
$S^{n-1}(r)\times \mathbb{E}^{n}$
of radius
 $r\in \mathbb{R}_{+}$
.
$r\in \mathbb{R}_{+}$
.
-
In Section 5, we give a construction of Levi-umbilical non-Hopf hypersurfaces in
![]() $\mathbb{C}\mathbb{P}^{2}$
.
$\mathbb{C}\mathbb{P}^{2}$
.
2 Almost contact metric structures and the associated CR-structures
In this paper, all manifolds are assumed to be connected and of class
![]() $C^{\infty }$
. First, we give a brief review of several fundamental concepts and formulas which we need later on. An odd-dimensional differentiable manifold
$C^{\infty }$
. First, we give a brief review of several fundamental concepts and formulas which we need later on. An odd-dimensional differentiable manifold
![]() $M$
has an almost contact structure if it admits a (1,1)-tensor field
$M$
has an almost contact structure if it admits a (1,1)-tensor field
![]() $\unicode[STIX]{x1D719}$
, a vector field
$\unicode[STIX]{x1D719}$
, a vector field
![]() $\unicode[STIX]{x1D709}$
and a 1-form
$\unicode[STIX]{x1D709}$
and a 1-form
![]() $\unicode[STIX]{x1D702}$
satisfying
$\unicode[STIX]{x1D702}$
satisfying
Then we can find always a compatible Riemannian metric, namely which satisfies
for all vector fields on
![]() $M$
. We call
$M$
. We call
![]() $(\unicode[STIX]{x1D702},\unicode[STIX]{x1D719},\unicode[STIX]{x1D709},g)$
an almost contact metric structure of
$(\unicode[STIX]{x1D702},\unicode[STIX]{x1D719},\unicode[STIX]{x1D709},g)$
an almost contact metric structure of
![]() $M$
and
$M$
and
![]() $M=(M;\unicode[STIX]{x1D702},\unicode[STIX]{x1D719},\unicode[STIX]{x1D709},g)$
an almost contact metric manifold. The fundamental 2-form
$M=(M;\unicode[STIX]{x1D702},\unicode[STIX]{x1D719},\unicode[STIX]{x1D709},g)$
an almost contact metric manifold. The fundamental 2-form
![]() $\unicode[STIX]{x1D6F7}$
is defined by
$\unicode[STIX]{x1D6F7}$
is defined by
![]() $\unicode[STIX]{x1D6F7}(X,Y)=g(\unicode[STIX]{x1D719}X,Y)$
. If
$\unicode[STIX]{x1D6F7}(X,Y)=g(\unicode[STIX]{x1D719}X,Y)$
. If
![]() $M$
satisfies in addition
$M$
satisfies in addition
![]() $d\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6F7}$
, then
$d\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6F7}$
, then
![]() $M$
is called a contact metric manifold, where
$M$
is called a contact metric manifold, where
![]() $d$
is the exterior differential operator. From (1) and (2) we easily get
$d$
is the exterior differential operator. From (1) and (2) we easily get
The tangent space
![]() $T_{p}M$
of
$T_{p}M$
of
![]() $M$
at each point
$M$
at each point
![]() $p\in M$
is decomposed as
$p\in M$
is decomposed as
![]() $T_{p}M=D_{p}\oplus \{\unicode[STIX]{x1D709}\}_{p}$
(direct sum), where we denote
$T_{p}M=D_{p}\oplus \{\unicode[STIX]{x1D709}\}_{p}$
(direct sum), where we denote
![]() $D_{p}=\{v\in T_{p}M|\unicode[STIX]{x1D702}(v)=0\}$
. Then
$D_{p}=\{v\in T_{p}M|\unicode[STIX]{x1D702}(v)=0\}$
. Then
![]() $D:p\rightarrow D_{p}$
defines a distribution orthogonal to
$D:p\rightarrow D_{p}$
defines a distribution orthogonal to
![]() $\unicode[STIX]{x1D709}$
. For an almost contact metric manifold
$\unicode[STIX]{x1D709}$
. For an almost contact metric manifold
![]() $M$
, one may define naturally an almost complex structure on the product manifold
$M$
, one may define naturally an almost complex structure on the product manifold
![]() $M\times \mathbb{R}$
, where
$M\times \mathbb{R}$
, where
![]() $\mathbb{R}$
denotes the real line. If the almost complex structure is integrable,
$\mathbb{R}$
denotes the real line. If the almost complex structure is integrable,
![]() $M$
is said to be normal. The integrability condition for the almost complex structure is the vanishing of the tensor
$M$
is said to be normal. The integrability condition for the almost complex structure is the vanishing of the tensor
![]() $[\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}]+2d\unicode[STIX]{x1D702}\otimes \unicode[STIX]{x1D709}$
, where
$[\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}]+2d\unicode[STIX]{x1D702}\otimes \unicode[STIX]{x1D709}$
, where
![]() $[\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}]$
denotes the Nijenhuis torsion of
$[\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}]$
denotes the Nijenhuis torsion of
![]() $\unicode[STIX]{x1D719}$
. For more details about the general theory of almost contact metric manifolds, we refer to [Reference Blair3].
$\unicode[STIX]{x1D719}$
. For more details about the general theory of almost contact metric manifolds, we refer to [Reference Blair3].
On the other hand, for an almost contact metric manifold
![]() $M$
, the restriction
$M$
, the restriction
![]() $J=\unicode[STIX]{x1D719}|D$
of
$J=\unicode[STIX]{x1D719}|D$
of
![]() $\unicode[STIX]{x1D719}$
to
$\unicode[STIX]{x1D719}$
to
![]() $D$
defines an almost complex structure in
$D$
defines an almost complex structure in
![]() $D$
. As soon as
$D$
. As soon as
![]() $M$
satisfies
$M$
satisfies
and
for all
![]() $X,Y\in D$
, where
$X,Y\in D$
, where
![]() $[J,J]$
is the Nijenhuis torsion of
$[J,J]$
is the Nijenhuis torsion of
![]() $J$
, then the pair
$J$
, then the pair
![]() $(\unicode[STIX]{x1D702},J)$
is called an (integrable) CR-structure associated with the almost contact metric structure
$(\unicode[STIX]{x1D702},J)$
is called an (integrable) CR-structure associated with the almost contact metric structure
![]() $(\unicode[STIX]{x1D702},\unicode[STIX]{x1D719},\unicode[STIX]{x1D709},g)$
. For example, a normal almost contact metric manifold has an integrable CR-structure [Reference Ianus7]. In addition, the associated Levi form
$(\unicode[STIX]{x1D702},\unicode[STIX]{x1D719},\unicode[STIX]{x1D709},g)$
. For example, a normal almost contact metric manifold has an integrable CR-structure [Reference Ianus7]. In addition, the associated Levi form
![]() $L$
defined by
$L$
defined by
![]() $L(X,Y)=d\unicode[STIX]{x1D702}(X,JY)$
,
$L(X,Y)=d\unicode[STIX]{x1D702}(X,JY)$
,
![]() $X,Y\in D$
, is nondegenerate (positive or negative definite, resp.), then
$X,Y\in D$
, is nondegenerate (positive or negative definite, resp.), then
![]() $(\unicode[STIX]{x1D702},J)$
is called a nondegenerate (strongly pseudo-convex, resp.) pseudo-Hermitian CR-structure. We may refer to [Reference Cho5], [Reference Ianus7], [Reference Tanno18] about CR-structures associated with (almost) contact metric structures.
$(\unicode[STIX]{x1D702},J)$
is called a nondegenerate (strongly pseudo-convex, resp.) pseudo-Hermitian CR-structure. We may refer to [Reference Cho5], [Reference Ianus7], [Reference Tanno18] about CR-structures associated with (almost) contact metric structures.
3 Real hypersurfaces in a complex space form
Let
![]() $M$
be an immersed real hypersurface of a Kähler manifold
$M$
be an immersed real hypersurface of a Kähler manifold
![]() $\widetilde{M}=(\widetilde{M};\tilde{J},\tilde{g})$
and
$\widetilde{M}=(\widetilde{M};\tilde{J},\tilde{g})$
and
![]() $N$
a local unit normal vector in a neighborhood of each point. By
$N$
a local unit normal vector in a neighborhood of each point. By
![]() $\tilde{\unicode[STIX]{x1D6FB}}$
,
$\tilde{\unicode[STIX]{x1D6FB}}$
,
![]() $\unicode[STIX]{x1D70E}$
we denote the Levi-Civita connection in
$\unicode[STIX]{x1D70E}$
we denote the Levi-Civita connection in
![]() $\widetilde{M}$
and the second fundamental form associated with the shape operator
$\widetilde{M}$
and the second fundamental form associated with the shape operator
![]() $A$
with respect to
$A$
with respect to
![]() $N$
, respectively. Then the Gauss and Weingarten formulas are given respectively by
$N$
, respectively. Then the Gauss and Weingarten formulas are given respectively by
for any vector fields
![]() $X$
and
$X$
and
![]() $Y$
tangent to
$Y$
tangent to
![]() $M$
. Here, we note that
$M$
. Here, we note that
![]() $\unicode[STIX]{x1D70E}(X,Y)=g(AX,Y)$
, where
$\unicode[STIX]{x1D70E}(X,Y)=g(AX,Y)$
, where
![]() $g$
denotes the Riemannian metric of
$g$
denotes the Riemannian metric of
![]() $M$
induced from
$M$
induced from
![]() $\tilde{g}$
. An eigenvector (resp. eigenvalue) of the shape operator
$\tilde{g}$
. An eigenvector (resp. eigenvalue) of the shape operator
![]() $A$
is called a principal curvature vector (resp. principal curvature). For any vector field
$A$
is called a principal curvature vector (resp. principal curvature). For any vector field
![]() $X$
tangent to
$X$
tangent to
![]() $M$
, we put
$M$
, we put
We easily see that the structure
![]() $(\unicode[STIX]{x1D702},\unicode[STIX]{x1D719},\unicode[STIX]{x1D709},g)$
is an almost contact metric structure on
$(\unicode[STIX]{x1D702},\unicode[STIX]{x1D719},\unicode[STIX]{x1D709},g)$
is an almost contact metric structure on
![]() $M$
, that is, satisfies (1) and (2). From the condition
$M$
, that is, satisfies (1) and (2). From the condition
![]() $\tilde{\unicode[STIX]{x1D6FB}}\tilde{J}=0$
, the relations (6) and by making use of the Gauss and Weingarten formulas, we have
$\tilde{\unicode[STIX]{x1D6FB}}\tilde{J}=0$
, the relations (6) and by making use of the Gauss and Weingarten formulas, we have
From now, let
![]() $\widetilde{M}_{n}(c)$
be a complex space form of constant holomorphic sectional curvature
$\widetilde{M}_{n}(c)$
be a complex space form of constant holomorphic sectional curvature
![]() $c$
. Then, from the Codazzi equation, we have
$c$
. Then, from the Codazzi equation, we have
By using (7) and (8), we see that a real hypersurface in a Kähler manifold always satisfies (4) and (5), the integrability condition of the associated CR-structure. From (8) we find that
![]() $M$
is Levi-flat if and only if
$M$
is Levi-flat if and only if
and
![]() $M$
is Levi-umbilical if and only if there exists nonzero constant
$M$
is Levi-umbilical if and only if there exists nonzero constant
![]() $k\in \mathbb{R}$
such that
$k\in \mathbb{R}$
such that
Here we recall ruled real hypersurfaces in
![]() $\mathbb{C}\mathbb{P}^{n}$
or
$\mathbb{C}\mathbb{P}^{n}$
or
![]() $\mathbb{CH}^{n}$
. Such a space is a foliated real hypersurface whose leaves are complex hyperplanes
$\mathbb{CH}^{n}$
. Such a space is a foliated real hypersurface whose leaves are complex hyperplanes
![]() $\mathbb{C}\mathbb{P}^{n-1}$
or
$\mathbb{C}\mathbb{P}^{n-1}$
or
![]() $\mathbb{CH}^{n-1}$
, respectively in
$\mathbb{CH}^{n-1}$
, respectively in
![]() $\mathbb{C}\mathbb{P}^{n}$
or
$\mathbb{C}\mathbb{P}^{n}$
or
![]() $\mathbb{CH}^{n}$
. That is, let
$\mathbb{CH}^{n}$
. That is, let
![]() $\unicode[STIX]{x1D6FE}:I\rightarrow \widetilde{M}_{n}(c)$
be a regular curve in
$\unicode[STIX]{x1D6FE}:I\rightarrow \widetilde{M}_{n}(c)$
be a regular curve in
![]() $\widetilde{M}_{n}(c)$
$\widetilde{M}_{n}(c)$
![]() $(\mathbb{C}\mathbb{P}^{n}or\mathbb{CH}^{n})$
. Then for each
$(\mathbb{C}\mathbb{P}^{n}or\mathbb{CH}^{n})$
. Then for each
![]() $t\in I$
, let
$t\in I$
, let
![]() $M_{n-1}^{(t)}(c)$
be a totally geodesic complex hypersurface which is orthogonal to holomorphic plane Span
$M_{n-1}^{(t)}(c)$
be a totally geodesic complex hypersurface which is orthogonal to holomorphic plane Span
![]() $\{\dot{\unicode[STIX]{x1D6FE}},J\dot{\unicode[STIX]{x1D6FE}}\}$
. We have a ruled real hypersurface
$\{\dot{\unicode[STIX]{x1D6FE}},J\dot{\unicode[STIX]{x1D6FE}}\}$
. We have a ruled real hypersurface
![]() $M=\bigcup _{t\in I}M_{n-1}^{(t)}(c)$
. A ruled real hypersurface is non-Hopf and particularly it is noncomplete real hypersurface in
$M=\bigcup _{t\in I}M_{n-1}^{(t)}(c)$
. A ruled real hypersurface is non-Hopf and particularly it is noncomplete real hypersurface in
![]() $\mathbb{C}\mathbb{P}^{n}$
(see, [Reference Kimura and Maeda10] for the case
$\mathbb{C}\mathbb{P}^{n}$
(see, [Reference Kimura and Maeda10] for the case
![]() $\mathbb{C}\mathbb{P}^{n}$
and see [Reference Ahn, Lee and Suh1] for the case
$\mathbb{C}\mathbb{P}^{n}$
and see [Reference Ahn, Lee and Suh1] for the case
![]() $\mathbb{CH}^{n}$
, respectively). The shape operator
$\mathbb{CH}^{n}$
, respectively). The shape operator
![]() $A$
is written by the following form:
$A$
is written by the following form:
 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}A\unicode[STIX]{x1D709}\ & =\ & \unicode[STIX]{x1D707}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D708}V~(\unicode[STIX]{x1D708}\neq 0),\\ AV\ & =\ & \unicode[STIX]{x1D708}\unicode[STIX]{x1D709},\\ AX\ & =\ & 0\quad \text{for any}~X\bot \unicode[STIX]{x1D709},V,\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}A\unicode[STIX]{x1D709}\ & =\ & \unicode[STIX]{x1D707}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D708}V~(\unicode[STIX]{x1D708}\neq 0),\\ AV\ & =\ & \unicode[STIX]{x1D708}\unicode[STIX]{x1D709},\\ AX\ & =\ & 0\quad \text{for any}~X\bot \unicode[STIX]{x1D709},V,\end{array}\end{eqnarray}$$
where
![]() $V$
is a unit vector orthogonal to
$V$
is a unit vector orthogonal to
![]() $\unicode[STIX]{x1D709}$
, and
$\unicode[STIX]{x1D709}$
, and
![]() $\unicode[STIX]{x1D707}$
,
$\unicode[STIX]{x1D707}$
,
![]() $\unicode[STIX]{x1D708}$
are differentiable functions on
$\unicode[STIX]{x1D708}$
are differentiable functions on
![]() $M$
. Then, we easily see that ruled real hypersurfaces in
$M$
. Then, we easily see that ruled real hypersurfaces in
![]() $\mathbb{C}\mathbb{P}^{n}$
or in
$\mathbb{C}\mathbb{P}^{n}$
or in
![]() $\mathbb{CH}^{n}$
are Levi-flat.
$\mathbb{CH}^{n}$
are Levi-flat.
4 Proof of Theorem 1
In this section, we prove Theorem 1. Let
![]() $M$
be a Levi-umbilical real hypersurface in a complex space form
$M$
be a Levi-umbilical real hypersurface in a complex space form
![]() $\widetilde{M}_{n}(c)$
. If we differentiate (11) covariantly, then we have
$\widetilde{M}_{n}(c)$
. If we differentiate (11) covariantly, then we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle g(\,(\unicode[STIX]{x1D6FB}_{X}A)\unicode[STIX]{x1D719}Y+A(\unicode[STIX]{x1D6FB}_{X}\unicode[STIX]{x1D719})Y+A\unicode[STIX]{x1D719}\unicode[STIX]{x1D6FB}_{X}Y+(\unicode[STIX]{x1D6FB}_{X}\unicode[STIX]{x1D719})AY\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{X}A)Y+\unicode[STIX]{x1D719}A\unicode[STIX]{x1D6FB}_{X}Y,Z)\!\,+\,g((A\unicode[STIX]{x1D719}+\unicode[STIX]{x1D719}A)Y,\unicode[STIX]{x1D6FB}_{X}Z)\nonumber\\ \displaystyle & & \displaystyle \quad =k(g((\unicode[STIX]{x1D6FB}_{X}\unicode[STIX]{x1D719})Y,Z)+g(\unicode[STIX]{x1D719}\unicode[STIX]{x1D6FB}_{X}Y,Z)+g(\unicode[STIX]{x1D719}Y,\unicode[STIX]{x1D6FB}_{X}Z)),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle g(\,(\unicode[STIX]{x1D6FB}_{X}A)\unicode[STIX]{x1D719}Y+A(\unicode[STIX]{x1D6FB}_{X}\unicode[STIX]{x1D719})Y+A\unicode[STIX]{x1D719}\unicode[STIX]{x1D6FB}_{X}Y+(\unicode[STIX]{x1D6FB}_{X}\unicode[STIX]{x1D719})AY\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{X}A)Y+\unicode[STIX]{x1D719}A\unicode[STIX]{x1D6FB}_{X}Y,Z)\!\,+\,g((A\unicode[STIX]{x1D719}+\unicode[STIX]{x1D719}A)Y,\unicode[STIX]{x1D6FB}_{X}Z)\nonumber\\ \displaystyle & & \displaystyle \quad =k(g((\unicode[STIX]{x1D6FB}_{X}\unicode[STIX]{x1D719})Y,Z)+g(\unicode[STIX]{x1D719}\unicode[STIX]{x1D6FB}_{X}Y,Z)+g(\unicode[STIX]{x1D719}Y,\unicode[STIX]{x1D6FB}_{X}Z)),\end{eqnarray}$$
for any vector fields
![]() $X,Y,Z\bot \unicode[STIX]{x1D709}$
. Use (7) to get
$X,Y,Z\bot \unicode[STIX]{x1D709}$
. Use (7) to get
 $$\begin{eqnarray}\displaystyle & & \displaystyle g((\unicode[STIX]{x1D6FB}_{X}A)\unicode[STIX]{x1D719}Y+\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{X}A)Y,Z)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,g(\unicode[STIX]{x1D702}(Y)A^{2}X-g(AX,Y)A\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702}(AY)AX-g(AX,AY)\unicode[STIX]{x1D709},Z)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,g((A\unicode[STIX]{x1D719}+\unicode[STIX]{x1D719}A)\unicode[STIX]{x1D6FB}_{X}Y,Z)-g((A\unicode[STIX]{x1D719}+\unicode[STIX]{x1D719}A)\unicode[STIX]{x1D6FB}_{X}Z,Y)\nonumber\\ \displaystyle & & \displaystyle \quad =k(g(\unicode[STIX]{x1D719}\unicode[STIX]{x1D6FB}_{X}Y,Z)-g(\unicode[STIX]{x1D719}\unicode[STIX]{x1D6FB}_{X}Z,Y)).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle g((\unicode[STIX]{x1D6FB}_{X}A)\unicode[STIX]{x1D719}Y+\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{X}A)Y,Z)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,g(\unicode[STIX]{x1D702}(Y)A^{2}X-g(AX,Y)A\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702}(AY)AX-g(AX,AY)\unicode[STIX]{x1D709},Z)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,g((A\unicode[STIX]{x1D719}+\unicode[STIX]{x1D719}A)\unicode[STIX]{x1D6FB}_{X}Y,Z)-g((A\unicode[STIX]{x1D719}+\unicode[STIX]{x1D719}A)\unicode[STIX]{x1D6FB}_{X}Z,Y)\nonumber\\ \displaystyle & & \displaystyle \quad =k(g(\unicode[STIX]{x1D719}\unicode[STIX]{x1D6FB}_{X}Y,Z)-g(\unicode[STIX]{x1D719}\unicode[STIX]{x1D6FB}_{X}Z,Y)).\end{eqnarray}$$
We decompose
![]() $\unicode[STIX]{x1D6FB}_{X}Y=\unicode[STIX]{x1D6FB}_{X}Y^{\bot }+\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FB}_{X}Y)\unicode[STIX]{x1D709}$
, where
$\unicode[STIX]{x1D6FB}_{X}Y=\unicode[STIX]{x1D6FB}_{X}Y^{\bot }+\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FB}_{X}Y)\unicode[STIX]{x1D709}$
, where
![]() $\unicode[STIX]{x1D6FB}_{X}Y^{\bot }$
denotes the part of
$\unicode[STIX]{x1D6FB}_{X}Y^{\bot }$
denotes the part of
![]() $\unicode[STIX]{x1D6FB}_{X}Y$
orthogonal to
$\unicode[STIX]{x1D6FB}_{X}Y$
orthogonal to
![]() $\unicode[STIX]{x1D709}$
. Using (8) and (11), (14) becomes
$\unicode[STIX]{x1D709}$
. Using (8) and (11), (14) becomes
 $$\begin{eqnarray}\displaystyle & & \displaystyle g((\unicode[STIX]{x1D6FB}_{X}A)\unicode[STIX]{x1D719}Y+\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{X}A)Y,Z)\nonumber\\ \displaystyle & & \displaystyle \quad +\,g(\unicode[STIX]{x1D702}(Y)A^{2}X-g(AX,Y)A\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702}(AY)AX-g(AX,AY)\unicode[STIX]{x1D709},Z)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FB}_{X}Y)g(U,Z)-\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FB}_{X}Z)g(U,Y)=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle g((\unicode[STIX]{x1D6FB}_{X}A)\unicode[STIX]{x1D719}Y+\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{X}A)Y,Z)\nonumber\\ \displaystyle & & \displaystyle \quad +\,g(\unicode[STIX]{x1D702}(Y)A^{2}X-g(AX,Y)A\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702}(AY)AX-g(AX,AY)\unicode[STIX]{x1D709},Z)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FB}_{X}Y)g(U,Z)-\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FB}_{X}Z)g(U,Y)=0,\end{eqnarray}$$
where we have put
![]() $U=\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D709}$
. Use (8) to obtain
$U=\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D709}$
. Use (8) to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle g((\unicode[STIX]{x1D6FB}_{X}A)Z,\unicode[STIX]{x1D719}Y)-g((\unicode[STIX]{x1D6FB}_{X}A)Y,\unicode[STIX]{x1D719}Z)\nonumber\\ \displaystyle & & \displaystyle \quad =g(\unicode[STIX]{x1D719}AX,Y)g(U,Z)-g(\unicode[STIX]{x1D719}AX,Z)g(U,Y)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D702}(Z)g(A^{2}X,Y)-\unicode[STIX]{x1D702}(Y)g(A^{2}X,Z)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D702}(AZ)g(AX,Y)-\unicode[STIX]{x1D702}(AY)g(AX,Z).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle g((\unicode[STIX]{x1D6FB}_{X}A)Z,\unicode[STIX]{x1D719}Y)-g((\unicode[STIX]{x1D6FB}_{X}A)Y,\unicode[STIX]{x1D719}Z)\nonumber\\ \displaystyle & & \displaystyle \quad =g(\unicode[STIX]{x1D719}AX,Y)g(U,Z)-g(\unicode[STIX]{x1D719}AX,Z)g(U,Y)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D702}(Z)g(A^{2}X,Y)-\unicode[STIX]{x1D702}(Y)g(A^{2}X,Z)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D702}(AZ)g(AX,Y)-\unicode[STIX]{x1D702}(AY)g(AX,Z).\end{eqnarray}$$
Taking the cyclic sum of (16) for
![]() $X,Y,Z$
, using (9) we have
$X,Y,Z$
, using (9) we have
Using (11) in (17) again, we have
If we put
![]() $Z=U$
in (18), then we have
$Z=U$
in (18), then we have
Replace
![]() $Y$
by
$Y$
by
![]() $\unicode[STIX]{x1D719}X$
in (19), then it turns to
$\unicode[STIX]{x1D719}X$
in (19), then it turns to
For an adapted orthonormal basis
![]() $\{e_{i},\unicode[STIX]{x1D709}\}$
,
$\{e_{i},\unicode[STIX]{x1D709}\}$
,
![]() $i=1,\cdots \,,2n-2$
, we put
$i=1,\cdots \,,2n-2$
, we put
![]() $X=e_{i}$
and taking the sum for
$X=e_{i}$
and taking the sum for
![]() $i=1,\cdots \,,2n-2$
, then since
$i=1,\cdots \,,2n-2$
, then since
![]() $k\neq 0$
we have
$k\neq 0$
we have
From this, we find that
![]() $n=2$
or
$n=2$
or
![]() $M$
is a Hopf hypersurface, that is,
$M$
is a Hopf hypersurface, that is,
![]() $A\unicode[STIX]{x1D709}=\unicode[STIX]{x1D707}\unicode[STIX]{x1D709}$
, where we have used (8). Now, we assume that
$A\unicode[STIX]{x1D709}=\unicode[STIX]{x1D707}\unicode[STIX]{x1D709}$
, where we have used (8). Now, we assume that
![]() $n\geqslant 3$
. Then Levi-umbilicity condition (11) yields that
$n\geqslant 3$
. Then Levi-umbilicity condition (11) yields that
![]() $\unicode[STIX]{x1D719}A+A\unicode[STIX]{x1D719}=k\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}A+A\unicode[STIX]{x1D719}=k\unicode[STIX]{x1D719}$
,
![]() $k\neq 0$
. Due to results of [Reference Kon11] (in case of
$k\neq 0$
. Due to results of [Reference Kon11] (in case of
![]() $\mathbb{C}\mathbb{P}^{n}$
), [Reference Vernon19], [Reference Suh15] (in case of
$\mathbb{C}\mathbb{P}^{n}$
), [Reference Vernon19], [Reference Suh15] (in case of
![]() $\mathbb{CH}^{n}$
), and [Reference Okumura12] (in case of
$\mathbb{CH}^{n}$
), and [Reference Okumura12] (in case of
![]() $\mathbb{CE}^{n}$
) we find the following.
$\mathbb{CE}^{n}$
) we find the following.
-
(I) If
 $\widetilde{M}_{n}(c)=\mathbb{C}\mathbb{P}^{n}$
, then
$\widetilde{M}_{n}(c)=\mathbb{C}\mathbb{P}^{n}$
, then
 $M$
is locally congruent to one of the following:
$M$
is locally congruent to one of the following:-
(1) a geodesic hypersphere, that is, a tube of radius
 $r$
over
$r$
over
 $P_{n-1}\mathbb{C}$
, where
$P_{n-1}\mathbb{C}$
, where
 $0<r<\frac{\unicode[STIX]{x1D70B}}{2}$
,
$0<r<\frac{\unicode[STIX]{x1D70B}}{2}$
, -
(2) a tube of radius
 $r$
over a complex quadric
$r$
over a complex quadric
 $\mathbb{CQ}^{n-1}$
, where
$\mathbb{CQ}^{n-1}$
, where
 $0<r<\frac{\unicode[STIX]{x1D70B}}{4}$
.
$0<r<\frac{\unicode[STIX]{x1D70B}}{4}$
.
-
-
(II) If
 $\widetilde{M}_{n}(c)=\mathbb{CH}^{n}$
, then
$\widetilde{M}_{n}(c)=\mathbb{CH}^{n}$
, then
 $M$
is locally congruent to one of the following:
$M$
is locally congruent to one of the following:-
(1) a horosphere in
 $\mathbb{CH}^{n}$
,
$\mathbb{CH}^{n}$
, -
(2) a geodesic hypersphere or a tube of radius
 $r\in \mathbb{R}_{+}$
over a totally geodesic
$r\in \mathbb{R}_{+}$
over a totally geodesic
 $\mathbb{CH}^{n-1}$
,
$\mathbb{CH}^{n-1}$
, -
(3) a tube of radius
 $r\in \mathbb{R}_{+}$
over a totally real hyperbolic space
$r\in \mathbb{R}_{+}$
over a totally real hyperbolic space
 $\mathbb{RH}^{n}$
.
$\mathbb{RH}^{n}$
.
-
-
(III) If
 $\widetilde{M}_{n}(c)=\mathbb{CE}^{n}$
, then
$\widetilde{M}_{n}(c)=\mathbb{CE}^{n}$
, then
 $M$
is locally congruent to one of the following:
$M$
is locally congruent to one of the following:-
(1) a sphere
 $S^{2n-1}(r)$
of radius
$S^{2n-1}(r)$
of radius
 $r\in \mathbb{R}_{+}$
,
$r\in \mathbb{R}_{+}$
, -
(2) a generalized cylinder
 $S^{n-1}(r)\times \mathbb{E}^{n}$
of radius
$S^{n-1}(r)\times \mathbb{E}^{n}$
of radius
 $r\in \mathbb{R}_{+}$
.
$r\in \mathbb{R}_{+}$
.
-
Then, we have Theorem 1. ◻
5 Three-dimensional Levi-umbilical hypersurfaces in
 $\mathbb{C}\mathbb{P}^{2}$
$\mathbb{C}\mathbb{P}^{2}$
In this section, we give a construction of
![]() $3$
-dimensional Levi-flat or Levi-umbilical real hypersurfaces in
$3$
-dimensional Levi-flat or Levi-umbilical real hypersurfaces in
![]() $\mathbb{C}\mathbb{P}^{2}$
. First, we prepare
$\mathbb{C}\mathbb{P}^{2}$
. First, we prepare
Lemma 2. Let
![]() $M^{2n-1}$
$M^{2n-1}$
![]() $(n\geqslant 2)$
be a Levi-flat hypersurface in a Kähler manifold
$(n\geqslant 2)$
be a Levi-flat hypersurface in a Kähler manifold
![]() $\widetilde{M}^{n}$
. Then
$\widetilde{M}^{n}$
. Then
![]() $\operatorname{trace}A=\unicode[STIX]{x1D702}(A\unicode[STIX]{x1D709})$
on
$\operatorname{trace}A=\unicode[STIX]{x1D702}(A\unicode[STIX]{x1D709})$
on
![]() $M$
. The converse holds when
$M$
. The converse holds when
![]() $n=2$
.
$n=2$
.
Lemma 3. Let
![]() $M^{2n-1}$
$M^{2n-1}$
![]() $(n\geqslant 2)$
be a Levi-umbilical hypersurface in a Kähler manifold
$(n\geqslant 2)$
be a Levi-umbilical hypersurface in a Kähler manifold
![]() $\widetilde{M}^{n}$
. Then
$\widetilde{M}^{n}$
. Then
![]() $\operatorname{trace}A-\unicode[STIX]{x1D702}(A\unicode[STIX]{x1D709})$
is a nonzero constant on
$\operatorname{trace}A-\unicode[STIX]{x1D702}(A\unicode[STIX]{x1D709})$
is a nonzero constant on
![]() $M$
. The converse holds when
$M$
. The converse holds when
![]() $n=2$
.
$n=2$
.
Now, according to [Reference Kimura9], we construct Levi-flat or Levi-umbilical hypersurfaces respectively in
![]() $\mathbb{C}\mathbb{P}^{2}$
. We denote
$\mathbb{C}\mathbb{P}^{2}$
. We denote
![]() $S^{n}$
as the unit sphere of which the center is the origin in
$S^{n}$
as the unit sphere of which the center is the origin in
![]() $\mathbb{R}^{n+1}$
. We consider the following submanifolds of
$\mathbb{R}^{n+1}$
. We consider the following submanifolds of
![]() $\mathbb{C}^{3}$
:
$\mathbb{C}^{3}$
:
 $$\begin{eqnarray}\displaystyle \mathbb{C}^{3} & \supset & \displaystyle S^{5}\nonumber\\ \displaystyle & \supset & \displaystyle \sin rS^{3}\times \cos rS^{1}\nonumber\\ \displaystyle & \supset & \displaystyle \sin r(\sin \unicode[STIX]{x1D703}S^{1}\times \cos \unicode[STIX]{x1D703}S^{1})\times \cos rS^{1},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{C}^{3} & \supset & \displaystyle S^{5}\nonumber\\ \displaystyle & \supset & \displaystyle \sin rS^{3}\times \cos rS^{1}\nonumber\\ \displaystyle & \supset & \displaystyle \sin r(\sin \unicode[STIX]{x1D703}S^{1}\times \cos \unicode[STIX]{x1D703}S^{1})\times \cos rS^{1},\nonumber\end{eqnarray}$$
where
![]() $0<r,\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}/2$
. Let
$0<r,\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}/2$
. Let
![]() $\unicode[STIX]{x1D6FE}:I\rightarrow (0,\unicode[STIX]{x1D70B}/2)\times (0,\unicode[STIX]{x1D70B}/2)$
,
$\unicode[STIX]{x1D6FE}:I\rightarrow (0,\unicode[STIX]{x1D70B}/2)\times (0,\unicode[STIX]{x1D70B}/2)$
,
![]() $\unicode[STIX]{x1D6FE}(s)=(r(s),\unicode[STIX]{x1D703}(s))$
be a (nonconstant) curve defined on an interval
$\unicode[STIX]{x1D6FE}(s)=(r(s),\unicode[STIX]{x1D703}(s))$
be a (nonconstant) curve defined on an interval
![]() $I$
. We put
$I$
. We put
where
![]() $\unicode[STIX]{x1D70B}:S^{5}\rightarrow \mathbb{C}\mathbb{P}^{2}$
is the Hopf fibration. Then
$\unicode[STIX]{x1D70B}:S^{5}\rightarrow \mathbb{C}\mathbb{P}^{2}$
is the Hopf fibration. Then
![]() $\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
is a hypersurface of
$\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
is a hypersurface of
![]() $S^{5}$
, and since
$S^{5}$
, and since
![]() $\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
is invariant under the
$\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
is invariant under the
![]() $S^{1}$
-action,
$S^{1}$
-action,
![]() $M_{\unicode[STIX]{x1D6FE}}$
is a real hypersurface of
$M_{\unicode[STIX]{x1D6FE}}$
is a real hypersurface of
![]() $\mathbb{C}\mathbb{P}^{2}$
. Note that
$\mathbb{C}\mathbb{P}^{2}$
. Note that
![]() $M_{\unicode[STIX]{x1D6FE}}$
is foliated by flat Lagrangian torus
$M_{\unicode[STIX]{x1D6FE}}$
is foliated by flat Lagrangian torus
![]() $T^{2}$
in
$T^{2}$
in
![]() $\mathbb{C}\mathbb{P}^{2}$
.
$\mathbb{C}\mathbb{P}^{2}$
.
Let
![]() $x,y,z\in S^{1}\subset \mathbb{C}$
and denote
$x,y,z\in S^{1}\subset \mathbb{C}$
and denote
where
![]() $0<r,\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}/2$
. Then the position vector
$0<r,\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}/2$
. Then the position vector
![]() $\unicode[STIX]{x1D6F9}$
of
$\unicode[STIX]{x1D6F9}$
of
![]() $\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
is given by
$\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
is given by
and unit normal vectors
![]() $N_{1}$
and
$N_{1}$
and
![]() $N_{2}$
of
$N_{2}$
of
![]() $3$
-dimensional submanifold
$3$
-dimensional submanifold
in
![]() $S^{5}$
at
$S^{5}$
at
![]() $\unicode[STIX]{x1D6F9}$
are given as
$\unicode[STIX]{x1D6F9}$
are given as
and
Put
![]() $\dot{\unicode[STIX]{x1D6F9}}=\frac{d}{ds}\unicode[STIX]{x1D6F9}(r(s),\unicode[STIX]{x1D703}(s))$
. Then we have
$\dot{\unicode[STIX]{x1D6F9}}=\frac{d}{ds}\unicode[STIX]{x1D6F9}(r(s),\unicode[STIX]{x1D703}(s))$
. Then we have
By taking an arc-length parameterization, we may put
![]() $({\dot{r}})^{2}+(\dot{\unicode[STIX]{x1D703}})^{2}\sin ^{2}r=1$
and
$({\dot{r}})^{2}+(\dot{\unicode[STIX]{x1D703}})^{2}\sin ^{2}r=1$
and
Hence
![]() $\dot{\unicode[STIX]{x1D6F9}}=\cos \unicode[STIX]{x1D6FC}N_{1}+\sin \unicode[STIX]{x1D6FC}N_{2}$
. Let
$\dot{\unicode[STIX]{x1D6F9}}=\cos \unicode[STIX]{x1D6FC}N_{1}+\sin \unicode[STIX]{x1D6FC}N_{2}$
. Let
Then
![]() $\widetilde{N}$
is a unit normal vector field of
$\widetilde{N}$
is a unit normal vector field of
![]() $\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
in
$\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
in
![]() $S^{5}$
. Since
$S^{5}$
. Since
![]() $\widetilde{N}$
is
$\widetilde{N}$
is
![]() $S^{1}$
-invariant,
$S^{1}$
-invariant,
![]() $N:=\unicode[STIX]{x1D70B}_{\ast }(\widetilde{N})$
is a unit normal vector field of
$N:=\unicode[STIX]{x1D70B}_{\ast }(\widetilde{N})$
is a unit normal vector field of
![]() $M_{\unicode[STIX]{x1D6FE}}$
in
$M_{\unicode[STIX]{x1D6FE}}$
in
![]() $\mathbb{C}\mathbb{P}^{2}$
. We have
$\mathbb{C}\mathbb{P}^{2}$
. We have
 $$\begin{eqnarray}\displaystyle \dot{\unicode[STIX]{x1D6F9}} & = & \displaystyle \left(\left(\cos \unicode[STIX]{x1D6FC}\cot r+\sin \unicode[STIX]{x1D6FC}\frac{\cot \unicode[STIX]{x1D703}}{\sin r}\right)\tilde{x},\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left(\cos \unicode[STIX]{x1D6FC}\cot r-\sin \unicode[STIX]{x1D6FC}\frac{\tan \unicode[STIX]{x1D703}}{\sin r}\right){\tilde{y}},-\cos \unicode[STIX]{x1D6FC}\tan r\tilde{z}\right)\nonumber\\ \displaystyle & = & \displaystyle \left(\left(\cos \unicode[STIX]{x1D6FC}\cos r\sin \unicode[STIX]{x1D703}+\sin \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D703}\right)x,\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left(\cos \unicode[STIX]{x1D6FC}\cos r\cos \unicode[STIX]{x1D703}-\sin \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D703}\right)y,-\cos \unicode[STIX]{x1D6FC}\sin rz\right),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dot{\unicode[STIX]{x1D6F9}} & = & \displaystyle \left(\left(\cos \unicode[STIX]{x1D6FC}\cot r+\sin \unicode[STIX]{x1D6FC}\frac{\cot \unicode[STIX]{x1D703}}{\sin r}\right)\tilde{x},\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left(\cos \unicode[STIX]{x1D6FC}\cot r-\sin \unicode[STIX]{x1D6FC}\frac{\tan \unicode[STIX]{x1D703}}{\sin r}\right){\tilde{y}},-\cos \unicode[STIX]{x1D6FC}\tan r\tilde{z}\right)\nonumber\\ \displaystyle & = & \displaystyle \left(\left(\cos \unicode[STIX]{x1D6FC}\cos r\sin \unicode[STIX]{x1D703}+\sin \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D703}\right)x,\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left(\cos \unicode[STIX]{x1D6FC}\cos r\cos \unicode[STIX]{x1D703}-\sin \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D703}\right)y,-\cos \unicode[STIX]{x1D6FC}\sin rz\right),\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle \widetilde{N} & = & \displaystyle \left(\left(-\!\sin \unicode[STIX]{x1D6FC}\cot r+\cos \unicode[STIX]{x1D6FC}\frac{\cot \unicode[STIX]{x1D703}}{\sin r}\right)\tilde{x},\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left(-\!\sin \unicode[STIX]{x1D6FC}\cot r-\cos \unicode[STIX]{x1D6FC}\frac{\tan \unicode[STIX]{x1D703}}{\sin r}\right){\tilde{y}},\sin \unicode[STIX]{x1D6FC}\tan r\tilde{z}\right)\nonumber\\ \displaystyle & = & \displaystyle \left(\left(-\!\sin \unicode[STIX]{x1D6FC}\cos r\sin \unicode[STIX]{x1D703}+\cos \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D703}\right)x,\right.\nonumber\\ \displaystyle & & \displaystyle \left.(-\!\sin \unicode[STIX]{x1D6FC}\cos r\cos \unicode[STIX]{x1D703}-\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D703})y,\sin \unicode[STIX]{x1D6FC}\sin rz\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{N} & = & \displaystyle \left(\left(-\!\sin \unicode[STIX]{x1D6FC}\cot r+\cos \unicode[STIX]{x1D6FC}\frac{\cot \unicode[STIX]{x1D703}}{\sin r}\right)\tilde{x},\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left(-\!\sin \unicode[STIX]{x1D6FC}\cot r-\cos \unicode[STIX]{x1D6FC}\frac{\tan \unicode[STIX]{x1D703}}{\sin r}\right){\tilde{y}},\sin \unicode[STIX]{x1D6FC}\tan r\tilde{z}\right)\nonumber\\ \displaystyle & = & \displaystyle \left(\left(-\!\sin \unicode[STIX]{x1D6FC}\cos r\sin \unicode[STIX]{x1D703}+\cos \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D703}\right)x,\right.\nonumber\\ \displaystyle & & \displaystyle \left.(-\!\sin \unicode[STIX]{x1D6FC}\cos r\cos \unicode[STIX]{x1D703}-\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D703})y,\sin \unicode[STIX]{x1D6FC}\sin rz\right).\nonumber\end{eqnarray}$$
The tangent space of
![]() $\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
at
$\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
at
![]() $\unicode[STIX]{x1D6F9}$
is spanned by the following orthonormal vectors:
$\unicode[STIX]{x1D6F9}$
is spanned by the following orthonormal vectors:
Here
![]() $i\unicode[STIX]{x1D6F9}$
is a unit vertical vector of the Hopf fibration
$i\unicode[STIX]{x1D6F9}$
is a unit vertical vector of the Hopf fibration
![]() $\unicode[STIX]{x1D70B}:S^{5}\rightarrow \mathbb{C}\mathbb{P}^{2}$
and the others are horizontal.
$\unicode[STIX]{x1D70B}:S^{5}\rightarrow \mathbb{C}\mathbb{P}^{2}$
and the others are horizontal.
Let
![]() $D$
and
$D$
and
![]() $\widetilde{A}$
be the flat connection of
$\widetilde{A}$
be the flat connection of
![]() $\mathbb{C}^{3}$
and the shape operator of the hypersurface
$\mathbb{C}^{3}$
and the shape operator of the hypersurface
![]() $\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
in
$\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
in
![]() $S^{5}$
, respectively. Then by the Weingarten formula, we have
$S^{5}$
, respectively. Then by the Weingarten formula, we have
Covariant differentiation of
![]() $\widetilde{N}$
for
$\widetilde{N}$
for
![]() $\dot{\unicode[STIX]{x1D6F9}}$
is given by
$\dot{\unicode[STIX]{x1D6F9}}$
is given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle D_{\dot{\unicode[STIX]{x1D6F9}}}\widetilde{N}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\widetilde{N}=-\dot{\unicode[STIX]{x1D6FC}}\dot{\unicode[STIX]{x1D6F9}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\Big((-\!\sin \unicode[STIX]{x1D6FC}(-{\dot{r}}\sin r\sin \unicode[STIX]{x1D703}+\dot{\unicode[STIX]{x1D703}}\cos r\cos \unicode[STIX]{x1D703})-\dot{\unicode[STIX]{x1D703}}\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D703})x,\nonumber\\ \displaystyle & & \displaystyle \quad (-\!\sin \unicode[STIX]{x1D6FC}(-{\dot{r}}\sin r\cos \unicode[STIX]{x1D703}-\dot{\unicode[STIX]{x1D703}}\cos r\sin \unicode[STIX]{x1D703})-\dot{\unicode[STIX]{x1D703}}\cos \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D703})y,{\dot{r}}\sin \unicode[STIX]{x1D6FC}\cos rz\Big)\nonumber\\ \displaystyle & & \displaystyle ~=-\dot{\unicode[STIX]{x1D6FC}}\dot{\unicode[STIX]{x1D6F9}}+\!\left((\sin \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D6FC}\sin r\sin \unicode[STIX]{x1D703}-\frac{\sin \unicode[STIX]{x1D6FC}}{\sin r}(\sin \unicode[STIX]{x1D6FC}\cos r\cos \unicode[STIX]{x1D703}\,+\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D703}))x,\right.\nonumber\\ \displaystyle & & \displaystyle \quad (\sin \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D6FC}\sin r\cos \unicode[STIX]{x1D703}+\frac{\sin \unicode[STIX]{x1D6FC}}{\sin r}(\sin \unicode[STIX]{x1D6FC}\cos r\sin \unicode[STIX]{x1D703}-\cos \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D703}))y,\nonumber\\ \displaystyle & & \displaystyle \qquad \cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}\cos rz\Big)\nonumber\\ \displaystyle & & \displaystyle ~=-(\dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\cot r)\dot{\unicode[STIX]{x1D6F9}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle D_{\dot{\unicode[STIX]{x1D6F9}}}\widetilde{N}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\widetilde{N}=-\dot{\unicode[STIX]{x1D6FC}}\dot{\unicode[STIX]{x1D6F9}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\Big((-\!\sin \unicode[STIX]{x1D6FC}(-{\dot{r}}\sin r\sin \unicode[STIX]{x1D703}+\dot{\unicode[STIX]{x1D703}}\cos r\cos \unicode[STIX]{x1D703})-\dot{\unicode[STIX]{x1D703}}\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D703})x,\nonumber\\ \displaystyle & & \displaystyle \quad (-\!\sin \unicode[STIX]{x1D6FC}(-{\dot{r}}\sin r\cos \unicode[STIX]{x1D703}-\dot{\unicode[STIX]{x1D703}}\cos r\sin \unicode[STIX]{x1D703})-\dot{\unicode[STIX]{x1D703}}\cos \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D703})y,{\dot{r}}\sin \unicode[STIX]{x1D6FC}\cos rz\Big)\nonumber\\ \displaystyle & & \displaystyle ~=-\dot{\unicode[STIX]{x1D6FC}}\dot{\unicode[STIX]{x1D6F9}}+\!\left((\sin \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D6FC}\sin r\sin \unicode[STIX]{x1D703}-\frac{\sin \unicode[STIX]{x1D6FC}}{\sin r}(\sin \unicode[STIX]{x1D6FC}\cos r\cos \unicode[STIX]{x1D703}\,+\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D703}))x,\right.\nonumber\\ \displaystyle & & \displaystyle \quad (\sin \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D6FC}\sin r\cos \unicode[STIX]{x1D703}+\frac{\sin \unicode[STIX]{x1D6FC}}{\sin r}(\sin \unicode[STIX]{x1D6FC}\cos r\sin \unicode[STIX]{x1D703}-\cos \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D703}))y,\nonumber\\ \displaystyle & & \displaystyle \qquad \cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}\cos rz\Big)\nonumber\\ \displaystyle & & \displaystyle ~=-(\dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\cot r)\dot{\unicode[STIX]{x1D6F9}}.\nonumber\end{eqnarray}$$
Hence we obtain
Also we have
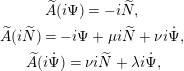 $$\begin{eqnarray}\displaystyle & \widetilde{A}(i\unicode[STIX]{x1D6F9})=-i\widetilde{N}, & \displaystyle \nonumber\\ \displaystyle & \widetilde{A}(i\widetilde{N})=-i\unicode[STIX]{x1D6F9}+\unicode[STIX]{x1D707}i\widetilde{N}+\unicode[STIX]{x1D708}i\dot{\unicode[STIX]{x1D6F9}}, & \displaystyle \nonumber\\ \displaystyle & \widetilde{A}(i\dot{\unicode[STIX]{x1D6F9}})=\unicode[STIX]{x1D708}i\widetilde{N}+\unicode[STIX]{x1D706}i\dot{\unicode[STIX]{x1D6F9}}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \widetilde{A}(i\unicode[STIX]{x1D6F9})=-i\widetilde{N}, & \displaystyle \nonumber\\ \displaystyle & \widetilde{A}(i\widetilde{N})=-i\unicode[STIX]{x1D6F9}+\unicode[STIX]{x1D707}i\widetilde{N}+\unicode[STIX]{x1D708}i\dot{\unicode[STIX]{x1D6F9}}, & \displaystyle \nonumber\\ \displaystyle & \widetilde{A}(i\dot{\unicode[STIX]{x1D6F9}})=\unicode[STIX]{x1D708}i\widetilde{N}+\unicode[STIX]{x1D706}i\dot{\unicode[STIX]{x1D6F9}}, & \displaystyle \nonumber\end{eqnarray}$$
where
Computations (2.8) of [Reference Kimura9] yield:
Let
![]() $U=-\unicode[STIX]{x1D70B}_{\ast }(i\dot{\unicode[STIX]{x1D6F9}})$
. Then
$U=-\unicode[STIX]{x1D70B}_{\ast }(i\dot{\unicode[STIX]{x1D6F9}})$
. Then
![]() $\unicode[STIX]{x1D719}U=\unicode[STIX]{x1D70B}_{\ast }(\dot{\unicode[STIX]{x1D6F9}})$
. Also we have
$\unicode[STIX]{x1D719}U=\unicode[STIX]{x1D70B}_{\ast }(\dot{\unicode[STIX]{x1D6F9}})$
. Also we have
![]() $\unicode[STIX]{x1D709}=-JN=-\unicode[STIX]{x1D70B}_{\ast }(i\widetilde{N})$
. Then the shape operator
$\unicode[STIX]{x1D709}=-JN=-\unicode[STIX]{x1D70B}_{\ast }(i\widetilde{N})$
. Then the shape operator
![]() $A$
of
$A$
of
![]() $M_{\unicode[STIX]{x1D6FE}}$
in
$M_{\unicode[STIX]{x1D6FE}}$
in
![]() $\mathbb{C}\mathbb{P}^{2}$
with respect to
$\mathbb{C}\mathbb{P}^{2}$
with respect to
![]() $N$
is given by
$N$
is given by
Hence with respect to
![]() $M_{\unicode[STIX]{x1D6FE}}$
in
$M_{\unicode[STIX]{x1D6FE}}$
in
![]() $\mathbb{C}\mathbb{P}^{2}$
, we have
$\mathbb{C}\mathbb{P}^{2}$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{trace}A-\unicode[STIX]{x1D702}(A\unicode[STIX]{x1D709})=\dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\cot r+\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & & \displaystyle \quad =\dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\bigg((1+\sin ^{2}\unicode[STIX]{x1D6FC})\cot r-\frac{\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}}{\sin r}(\cot \unicode[STIX]{x1D703}-\tan \unicode[STIX]{x1D703})\nonumber\\ \displaystyle & & \displaystyle \qquad -\cos ^{2}\unicode[STIX]{x1D6FC}(\cot r+\tan r)\bigg).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{trace}A-\unicode[STIX]{x1D702}(A\unicode[STIX]{x1D709})=\dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\cot r+\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & & \displaystyle \quad =\dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\bigg((1+\sin ^{2}\unicode[STIX]{x1D6FC})\cot r-\frac{\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}}{\sin r}(\cot \unicode[STIX]{x1D703}-\tan \unicode[STIX]{x1D703})\nonumber\\ \displaystyle & & \displaystyle \qquad -\cos ^{2}\unicode[STIX]{x1D6FC}(\cot r+\tan r)\bigg).\end{eqnarray}$$
Proposition 4. Let
![]() $(r(s),\unicode[STIX]{x1D703}(s),\unicode[STIX]{x1D6FC}(s))$
be a solution of the system of nonlinear ODE,
$(r(s),\unicode[STIX]{x1D703}(s),\unicode[STIX]{x1D6FC}(s))$
be a solution of the system of nonlinear ODE,
 $$\begin{eqnarray}\displaystyle {\dot{r}} & = & \displaystyle \cos \unicode[STIX]{x1D6FC},\qquad \dot{\unicode[STIX]{x1D703}}=\frac{\sin \unicode[STIX]{x1D6FC}}{\sin r},\nonumber\\ \displaystyle & & \displaystyle \dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\bigg((1+\sin ^{2}\unicode[STIX]{x1D6FC})\cot r-\frac{\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}}{\sin r}(\cot \unicode[STIX]{x1D703}-\tan \unicode[STIX]{x1D703})\nonumber\\ \displaystyle & & \displaystyle -\cos ^{2}\unicode[STIX]{x1D6FC}(\cot r+\tan r)\bigg)=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{r}} & = & \displaystyle \cos \unicode[STIX]{x1D6FC},\qquad \dot{\unicode[STIX]{x1D703}}=\frac{\sin \unicode[STIX]{x1D6FC}}{\sin r},\nonumber\\ \displaystyle & & \displaystyle \dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\bigg((1+\sin ^{2}\unicode[STIX]{x1D6FC})\cot r-\frac{\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}}{\sin r}(\cot \unicode[STIX]{x1D703}-\tan \unicode[STIX]{x1D703})\nonumber\\ \displaystyle & & \displaystyle -\cos ^{2}\unicode[STIX]{x1D6FC}(\cot r+\tan r)\bigg)=0,\end{eqnarray}$$
such that the initial condition satisfying
![]() $0<r(0),\unicode[STIX]{x1D703}(0)<\unicode[STIX]{x1D70B}/2$
. Then the real hypersurface
$0<r(0),\unicode[STIX]{x1D703}(0)<\unicode[STIX]{x1D70B}/2$
. Then the real hypersurface
![]() $M_{\unicode[STIX]{x1D6FE}}$
in
$M_{\unicode[STIX]{x1D6FE}}$
in
![]() $\mathbb{C}\mathbb{P}^{2}$
, defined by (21) is Levi-flat.
$\mathbb{C}\mathbb{P}^{2}$
, defined by (21) is Levi-flat.
A special solution of (29) is given by
In this case, we have
![]() $\dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\cot r=\unicode[STIX]{x1D706}=0$
and
$\dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\cot r=\unicode[STIX]{x1D706}=0$
and
![]() $M_{\unicode[STIX]{x1D6FE}}$
is a ruled real hypersurface.
$M_{\unicode[STIX]{x1D6FE}}$
is a ruled real hypersurface.
Proposition 5. Let
![]() $k$
be a nonzero constant and let
$k$
be a nonzero constant and let
![]() $(r(s),\unicode[STIX]{x1D703}(s),\unicode[STIX]{x1D6FC}(s))$
be a solution of the system of nonlinear ODE,
$(r(s),\unicode[STIX]{x1D703}(s),\unicode[STIX]{x1D6FC}(s))$
be a solution of the system of nonlinear ODE,
 $$\begin{eqnarray}\displaystyle {\dot{r}} & = & \displaystyle \cos \unicode[STIX]{x1D6FC},\qquad \dot{\unicode[STIX]{x1D703}}=\frac{\sin \unicode[STIX]{x1D6FC}}{\sin r},\nonumber\\ \displaystyle & & \displaystyle \dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\bigg((1+\sin ^{2}\unicode[STIX]{x1D6FC})\cot r-\frac{\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}}{\sin r}(\cot \unicode[STIX]{x1D703}-\tan \unicode[STIX]{x1D703})\nonumber\\ \displaystyle & & \displaystyle -\,\cos ^{2}\unicode[STIX]{x1D6FC}(\cot r+\tan r)\bigg)=k,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{r}} & = & \displaystyle \cos \unicode[STIX]{x1D6FC},\qquad \dot{\unicode[STIX]{x1D703}}=\frac{\sin \unicode[STIX]{x1D6FC}}{\sin r},\nonumber\\ \displaystyle & & \displaystyle \dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\bigg((1+\sin ^{2}\unicode[STIX]{x1D6FC})\cot r-\frac{\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}}{\sin r}(\cot \unicode[STIX]{x1D703}-\tan \unicode[STIX]{x1D703})\nonumber\\ \displaystyle & & \displaystyle -\,\cos ^{2}\unicode[STIX]{x1D6FC}(\cot r+\tan r)\bigg)=k,\end{eqnarray}$$
such that the initial condition satisfying
![]() $0<r(0),\unicode[STIX]{x1D703}(0)<\unicode[STIX]{x1D70B}/2$
. Then the real hypersurface
$0<r(0),\unicode[STIX]{x1D703}(0)<\unicode[STIX]{x1D70B}/2$
. Then the real hypersurface
![]() $M_{\unicode[STIX]{x1D6FE}}$
in
$M_{\unicode[STIX]{x1D6FE}}$
in
![]() $\mathbb{C}\mathbb{P}^{2}$
, defined by (21) is Levi-umbilical.
$\mathbb{C}\mathbb{P}^{2}$
, defined by (21) is Levi-umbilical.
A special solution of (30) is given by
In the case
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70B}/2$
, we have
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70B}/2$
, we have
![]() $\unicode[STIX]{x1D707}=2\cot 2r$
,
$\unicode[STIX]{x1D707}=2\cot 2r$
,
![]() $\unicode[STIX]{x1D708}=0$
and
$\unicode[STIX]{x1D708}=0$
and
![]() $\dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\cot r=\unicode[STIX]{x1D706}=\cot r$
. Hence
$\dot{\unicode[STIX]{x1D6FC}}+\sin \unicode[STIX]{x1D6FC}\cot r=\unicode[STIX]{x1D706}=\cot r$
. Hence
![]() $M_{\unicode[STIX]{x1D6FE}}$
is a geodesic sphere of radius
$M_{\unicode[STIX]{x1D6FE}}$
is a geodesic sphere of radius
![]() $r$
$r$
![]() $(0<r<\unicode[STIX]{x1D70B}/2)$
with
$(0<r<\unicode[STIX]{x1D70B}/2)$
with
![]() $k=2\cot r$
.
$k=2\cot r$
.