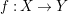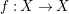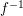1 Introduction
Blow-analytic maps were introduced in the early 1980s by Kuo in order to classify real singularities [Reference Kuo26–Reference Kuo28]. A map
![]() $f:X\rightarrow Y$
between real algebraic sets is called blow-analytic if there exists
$f:X\rightarrow Y$
between real algebraic sets is called blow-analytic if there exists
![]() ${\it\sigma}:M\rightarrow X$
a finite sequence of blowings-up with nonsingular centers such that
${\it\sigma}:M\rightarrow X$
a finite sequence of blowings-up with nonsingular centers such that
![]() $f\circ {\it\sigma}$
is analytic. In the same vein a semialgebraic map between real algebraic sets is called blow-Nash if the composition with some finite sequence of blowings-up with nonsingular centers is Nash (i.e., semialgebraic and analytic). Arc-analytic maps were introduced by Kurdyka [Reference Kurdyka29]. A map
$f\circ {\it\sigma}$
is analytic. In the same vein a semialgebraic map between real algebraic sets is called blow-Nash if the composition with some finite sequence of blowings-up with nonsingular centers is Nash (i.e., semialgebraic and analytic). Arc-analytic maps were introduced by Kurdyka [Reference Kurdyka29]. A map
![]() $f:X\rightarrow Y$
between two real algebraic sets is called arc-analytic if every real analytic arc on
$f:X\rightarrow Y$
between two real algebraic sets is called arc-analytic if every real analytic arc on
![]() $X$
is mapped by
$X$
is mapped by
![]() $f$
to a real analytic arc on
$f$
to a real analytic arc on
![]() $Y$
. By a result of Bierstone and Milman [Reference Bierstone and Milman5] in response to a question of Kurdyka, if
$Y$
. By a result of Bierstone and Milman [Reference Bierstone and Milman5] in response to a question of Kurdyka, if
![]() $f:X\rightarrow Y$
is semialgebraic (i.e., its graph is semialgebraic) and if
$f:X\rightarrow Y$
is semialgebraic (i.e., its graph is semialgebraic) and if
![]() $X$
is nonsingular then
$X$
is nonsingular then
![]() $f$
is arc-analytic if and only if it is blow-Nash. When
$f$
is arc-analytic if and only if it is blow-Nash. When
![]() $X$
is nonsingular, the set of points where such a map is analytic is dense [Reference Kurdyka29, 5.2] and thus the Jacobian determinant of
$X$
is nonsingular, the set of points where such a map is analytic is dense [Reference Kurdyka29, 5.2] and thus the Jacobian determinant of
![]() $f$
is defined everywhere except on a nowhere dense subset of
$f$
is defined everywhere except on a nowhere dense subset of
![]() $X$
.
$X$
.
The following Inverse Function theorem is known for
![]() $X$
nonsingular [Reference Fukui, Kurdyka and Parusiński13]: if the Jacobian determinant of a blow-Nash self-homeomorphism
$X$
nonsingular [Reference Fukui, Kurdyka and Parusiński13]: if the Jacobian determinant of a blow-Nash self-homeomorphism
![]() $h:X\rightarrow X$
is locally bounded from below by a nonzero constant, on the set it is defined, then
$h:X\rightarrow X$
is locally bounded from below by a nonzero constant, on the set it is defined, then
![]() $h^{-1}$
is blow-Nash and its Jacobian determinant is also locally bounded from below by a nonzero constant on the set it is defined.
$h^{-1}$
is blow-Nash and its Jacobian determinant is also locally bounded from below by a nonzero constant on the set it is defined.
In this paper, we generalize this theorem to singular algebraic sets.
We first introduce, in Section 2.3, the notion of generically arc-analytic maps which are maps
![]() $f:X\rightarrow Y$
between real algebraic sets such that there exists a nowhere dense subset
$f:X\rightarrow Y$
between real algebraic sets such that there exists a nowhere dense subset
![]() $S$
of
$S$
of
![]() $X$
with the property that every arc on
$X$
with the property that every arc on
![]() $X$
not entirely included in
$X$
not entirely included in
![]() $S$
is mapped by
$S$
is mapped by
![]() $f$
to a real analytic arc on
$f$
to a real analytic arc on
![]() $Y$
. When
$Y$
. When
![]() $\operatorname{dim}\operatorname{Sing}(X)\geqslant 1$
, we see that this condition is strictly weaker than being arc-analytic, otherwise a continuous generically arc-analytic map is an arc-analytic map. Then we show that the semialgebraic generically arc-analytic maps are exactly the blow-Nash ones.
$\operatorname{dim}\operatorname{Sing}(X)\geqslant 1$
, we see that this condition is strictly weaker than being arc-analytic, otherwise a continuous generically arc-analytic map is an arc-analytic map. Then we show that the semialgebraic generically arc-analytic maps are exactly the blow-Nash ones.
Given
![]() $f:X\rightarrow X$
a blow-Nash self-map on a real algebraic set
$f:X\rightarrow X$
a blow-Nash self-map on a real algebraic set
![]() $X$
, we have the following diagram
$X$
, we have the following diagram
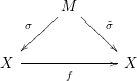
with
![]() ${\it\sigma}$
given by a sequence of blowings-up with nonsingular centers and
${\it\sigma}$
given by a sequence of blowings-up with nonsingular centers and
![]() $\tilde{{\it\sigma}}$
a Nash map.
$\tilde{{\it\sigma}}$
a Nash map.
We may now give an analogue of the lower bound of the Jacobian determinant condition: we say that
![]() $f$
satisfies the Jacobian hypothesis if the Jacobian ideal of
$f$
satisfies the Jacobian hypothesis if the Jacobian ideal of
![]() ${\it\sigma}$
is included in the Jacobian ideal of
${\it\sigma}$
is included in the Jacobian ideal of
![]() $\tilde{{\it\sigma}}$
. This condition does not depend on the choice of
$\tilde{{\it\sigma}}$
. This condition does not depend on the choice of
![]() ${\it\sigma}$
.
${\it\sigma}$
.
We are now able to state the main theorem of this paper: let
![]() $f:X\rightarrow X$
be a semialgebraic self-homeomorphism with
$f:X\rightarrow X$
be a semialgebraic self-homeomorphism with
![]() $X$
an algebraic subset then
$X$
an algebraic subset then
![]() $f$
is blow-Nash and satisfies the Jacobian hypothesis if and only if
$f$
is blow-Nash and satisfies the Jacobian hypothesis if and only if
![]() $f^{-1}$
satisfies the same conditions.
$f^{-1}$
satisfies the same conditions.
Heuristically, the main idea of the proof consists in comparing the “motivic volume” of the set of arcs on
![]() $X$
and the “motivic volume” of the set of arcs on
$X$
and the “motivic volume” of the set of arcs on
![]() $X$
coming from arcs on
$X$
coming from arcs on
![]() $M$
by
$M$
by
![]() $\tilde{{\it\sigma}}$
. This allows us to prove that we can uniquely lift by
$\tilde{{\it\sigma}}$
. This allows us to prove that we can uniquely lift by
![]() $\tilde{{\it\sigma}}$
an arc not entirely included in some nowhere dense subset of
$\tilde{{\it\sigma}}$
an arc not entirely included in some nowhere dense subset of
![]() $X$
. Thereby, such an arc is mapped to an analytic arc by
$X$
. Thereby, such an arc is mapped to an analytic arc by
![]() $f^{-1}$
. Thus
$f^{-1}$
. Thus
![]() $f^{-1}$
is generically arc-analytic and so blow-Nash.
$f^{-1}$
is generically arc-analytic and so blow-Nash.
Therefore, we first define the arc space on an algebraic subset
![]() $X$
of
$X$
of
![]() $\mathbb{R}^{N}$
as the set of germs of analytic arcs on
$\mathbb{R}^{N}$
as the set of germs of analytic arcs on
![]() $\mathbb{R}^{N}$
which lie in
$\mathbb{R}^{N}$
which lie in
![]() $X$
, that is,
$X$
, that is,
![]() ${\it\gamma}:(\mathbb{R},0)\rightarrow X$
such that
${\it\gamma}:(\mathbb{R},0)\rightarrow X$
such that
![]() $\text{for all }f\in I(X),f({\it\gamma})=0$
. For
$\text{for all }f\in I(X),f({\it\gamma})=0$
. For
![]() $n\in \mathbb{N}$
, we define the space of
$n\in \mathbb{N}$
, we define the space of
![]() $n$
-jets on
$n$
-jets on
![]() $X$
as the set of
$X$
as the set of
![]() $n$
-jets
$n$
-jets
![]() ${\it\gamma}$
on
${\it\gamma}$
on
![]() $\mathbb{R}^{N}$
such that
$\mathbb{R}^{N}$
such that
![]() $\text{for all }f\in I(X),f({\it\gamma}(t))\equiv 0\operatorname{mod}t^{n+1}$
. The Section 2.4 contains some general properties of these objects and some useful results for the proof of the main theorem.
$\text{for all }f\in I(X),f({\it\gamma}(t))\equiv 0\operatorname{mod}t^{n+1}$
. The Section 2.4 contains some general properties of these objects and some useful results for the proof of the main theorem.
The additive invariant used in order to apply motivic integration arguments is the virtual Poincaré polynomial which associates to a set of a certain class, denoted
![]() ${\mathcal{A}}{\mathcal{S}}$
, a polynomial with integer coefficients. We recall the main properties of the collection
${\mathcal{A}}{\mathcal{S}}$
, a polynomial with integer coefficients. We recall the main properties of the collection
![]() ${\mathcal{A}}{\mathcal{S}}$
in Section 2.1. The virtual Poincaré polynomial was constructed by McCrory and Parusiński [Reference McCrory and Parusiński36] and Fichou [Reference Fichou11]. The Section 2.2 contains the main properties of this invariant and motivates its use.
${\mathcal{A}}{\mathcal{S}}$
in Section 2.1. The virtual Poincaré polynomial was constructed by McCrory and Parusiński [Reference McCrory and Parusiński36] and Fichou [Reference Fichou11]. The Section 2.2 contains the main properties of this invariant and motivates its use.
In order to compute the above-cited “motivic volumes”, we first prove a version of Denef–Loeser key lemma for the motivic change of variables formula which fulfills our requirements and with a weaker hypothesis: we do not assume the map to be birational but only generically one-to-one.
Based on these results, we may finally prove there exists a subset on
![]() $X$
such that every analytic arc on
$X$
such that every analytic arc on
![]() $X$
not entirely included in this subset may be uniquely lifted by
$X$
not entirely included in this subset may be uniquely lifted by
![]() $\tilde{{\it\sigma}}$
. This part relies on real analysis arguments and on the fact that an arc not entirely included in the center of a blowing-up may be lifted by this blowing-up.
$\tilde{{\it\sigma}}$
. This part relies on real analysis arguments and on the fact that an arc not entirely included in the center of a blowing-up may be lifted by this blowing-up.
2 Preliminaries
2.1 Constructible sets and maps
Arc-symmetric sets have been first defined and studied by Kurdyka in [Reference Kurdyka29]. A subset of an analytic manifold
![]() $M$
is arc-symmetric if all analytic arcs on
$M$
is arc-symmetric if all analytic arcs on
![]() $M$
meet it at isolated points or are entirely included in it. Semialgebraic arc-symmetric sets are exactly the closed sets of a Noetherian topology
$M$
meet it at isolated points or are entirely included in it. Semialgebraic arc-symmetric sets are exactly the closed sets of a Noetherian topology
![]() ${\mathcal{A}}$
on
${\mathcal{A}}$
on
![]() $\mathbb{R}^{N}$
. We work with a slightly different framework defined by Parusiński in [Reference Parusiński41] and consider the collection of sets
$\mathbb{R}^{N}$
. We work with a slightly different framework defined by Parusiński in [Reference Parusiński41] and consider the collection of sets
![]() ${\mathcal{A}}{\mathcal{S}}$
defined as the Boolean algebra generated by semialgebraic arc-symmetric subsets of
${\mathcal{A}}{\mathcal{S}}$
defined as the Boolean algebra generated by semialgebraic arc-symmetric subsets of
![]() $\mathbb{P}_{\mathbb{R}}^{n}$
. The advantages of
$\mathbb{P}_{\mathbb{R}}^{n}$
. The advantages of
![]() ${\mathcal{A}}{\mathcal{S}}$
over
${\mathcal{A}}{\mathcal{S}}$
over
![]() ${\mathcal{A}}$
are that we get a constructible category in the sense of [Reference Parusiński41] as explained below and a better control of the behavior at infinity. We refer the reader to [Reference Kurdyka and Parusiński31] for a survey.
${\mathcal{A}}$
are that we get a constructible category in the sense of [Reference Parusiński41] as explained below and a better control of the behavior at infinity. We refer the reader to [Reference Kurdyka and Parusiński31] for a survey.
Definition 2.1. [Reference Parusiński41, 2.4]
Let
![]() ${\mathcal{C}}$
be a collection of semialgebraic sets. A map between two
${\mathcal{C}}$
be a collection of semialgebraic sets. A map between two
![]() ${\mathcal{C}}$
-sets is a
${\mathcal{C}}$
-sets is a
![]() ${\mathcal{C}}$
-map if its graph is a
${\mathcal{C}}$
-map if its graph is a
![]() ${\mathcal{C}}$
-set. We say that
${\mathcal{C}}$
-set. We say that
![]() ${\mathcal{C}}$
is a constructible category if it satisfies the following axioms:
${\mathcal{C}}$
is a constructible category if it satisfies the following axioms:
- (A1)
-
 ${\mathcal{C}}$
contains the algebraic sets.
${\mathcal{C}}$
contains the algebraic sets. - (A2)
-
 ${\mathcal{C}}$
is stable by Boolean operations
${\mathcal{C}}$
is stable by Boolean operations
 $\cap$
,
$\cap$
,
 $\cup$
and
$\cup$
and
 $\setminus$
.
$\setminus$
. - (A3)
-
-
(a) The inverse image of a
 ${\mathcal{C}}$
-set by a
${\mathcal{C}}$
-set by a
 ${\mathcal{C}}$
-map is a
${\mathcal{C}}$
-map is a
 ${\mathcal{C}}$
-set.
${\mathcal{C}}$
-set. -
(b) The image of a
 ${\mathcal{C}}$
-set by an injective
${\mathcal{C}}$
-set by an injective
 ${\mathcal{C}}$
-map is a
${\mathcal{C}}$
-map is a
 ${\mathcal{C}}$
-set.
${\mathcal{C}}$
-set.
-
- (A4)
-
Each locally compact
 $X\in {\mathcal{C}}$
is Euler in codimension 1, that is, there is a semialgebraic subset
$X\in {\mathcal{C}}$
is Euler in codimension 1, that is, there is a semialgebraic subset
 $Y\subset X$
with
$Y\subset X$
with
 $\operatorname{dim}Y\leqslant \operatorname{dim}X-2$
such that
$\operatorname{dim}Y\leqslant \operatorname{dim}X-2$
such that
 $X\setminus Y$
is EulerFootnote
1
.
$X\setminus Y$
is EulerFootnote
1
.
Remark 2.2. A locally compact semialgebraic set
![]() $X$
is Euler in codimension
$X$
is Euler in codimension
![]() $1$
if and only if it admits a fundamental class for the homology with coefficient in
$1$
if and only if it admits a fundamental class for the homology with coefficient in
![]() $\mathbb{Z}_{2}$
. For instance, this property is crucial in the construction of the virtual Poincaré polynomial in order to use the Poincaré duality.
$\mathbb{Z}_{2}$
. For instance, this property is crucial in the construction of the virtual Poincaré polynomial in order to use the Poincaré duality.
Given a constructible category
![]() ${\mathcal{C}}$
, we have a notion of
${\mathcal{C}}$
, we have a notion of
![]() ${\mathcal{C}}$
-closure.
${\mathcal{C}}$
-closure.
Theorem 2.3. [Reference Parusiński41, 2.5]
Let
![]() ${\mathcal{C}}$
be a constructible category and let
${\mathcal{C}}$
be a constructible category and let
![]() $X\in {\mathcal{C}}$
be a locally closed set. Then for any subset
$X\in {\mathcal{C}}$
be a locally closed set. Then for any subset
![]() $A\subset X$
there is a smallest closed subset of
$A\subset X$
there is a smallest closed subset of
![]() $X$
which belongs to
$X$
which belongs to
![]() ${\mathcal{C}}$
and contains
${\mathcal{C}}$
and contains
![]() $A$
. It is denoted by
$A$
. It is denoted by
![]() $\overline{A}^{\,{\mathcal{C}}}$
. Any other closed subset of
$\overline{A}^{\,{\mathcal{C}}}$
. Any other closed subset of
![]() $X$
that is in
$X$
that is in
![]() ${\mathcal{C}}$
and contains
${\mathcal{C}}$
and contains
![]() $A$
must contain
$A$
must contain
![]() $\overline{A}^{\,{\mathcal{C}}}$
.
$\overline{A}^{\,{\mathcal{C}}}$
.
Remark 2.4. [Reference Parusiński41, 2.7]
If
![]() $A$
is semialgebraic then
$A$
is semialgebraic then
![]() $\operatorname{dim}\overline{A}^{\,{\mathcal{C}}}=\operatorname{dim}A$
. In particular, if
$\operatorname{dim}\overline{A}^{\,{\mathcal{C}}}=\operatorname{dim}A$
. In particular, if
![]() $A\in {\mathcal{C}}$
then
$A\in {\mathcal{C}}$
then
![]() $\overline{A}^{\,{\mathcal{C}}}=A\cup \overline{\overline{A}\setminus A}^{\,{\mathcal{C}}}$
and hence
$\overline{A}^{\,{\mathcal{C}}}=A\cup \overline{\overline{A}\setminus A}^{\,{\mathcal{C}}}$
and hence
![]() $\operatorname{dim}\big(\overline{A}^{\,{\mathcal{C}}}\setminus A\big)<\operatorname{dim}A$
.
$\operatorname{dim}\big(\overline{A}^{\,{\mathcal{C}}}\setminus A\big)<\operatorname{dim}A$
.
Definition 2.5. [Reference Parusiński41, Section 4.2]
A semialgebraic subset
![]() $A\subset \mathbb{P}_{\mathbb{R}}^{n}$
is an
$A\subset \mathbb{P}_{\mathbb{R}}^{n}$
is an
![]() ${\mathcal{A}}{\mathcal{S}}$
-set if for every real analytic arc
${\mathcal{A}}{\mathcal{S}}$
-set if for every real analytic arc
![]() ${\it\gamma}:(-1,1)\rightarrow \mathbb{P}_{\mathbb{R}}^{n}$
such that
${\it\gamma}:(-1,1)\rightarrow \mathbb{P}_{\mathbb{R}}^{n}$
such that
![]() ${\it\gamma}((-1,0))\subset A$
there exists
${\it\gamma}((-1,0))\subset A$
there exists
![]() ${\it\varepsilon}>0$
such that
${\it\varepsilon}>0$
such that
![]() ${\it\gamma}((0,{\it\varepsilon}))\subset A$
.
${\it\gamma}((0,{\it\varepsilon}))\subset A$
.
Using the proof of [Reference Parusiński41, Theorem 2.5], we get the following proposition.
Proposition 2.6. There exists a unique Noetherian topology on
![]() $\mathbb{P}_{\mathbb{R}}^{n}$
whose closed sets are exactly the closed
$\mathbb{P}_{\mathbb{R}}^{n}$
whose closed sets are exactly the closed
![]() ${\mathcal{A}}{\mathcal{S}}$
-subsets.
${\mathcal{A}}{\mathcal{S}}$
-subsets.
Theorem 2.7. [Reference Parusiński41]
-
∙ The algebraically constructible sets form a constructible category denoted by
 ${\mathcal{A}}{\mathcal{C}}$
.
${\mathcal{A}}{\mathcal{C}}$
. -
∙
 ${\mathcal{A}}{\mathcal{S}}$
is a constructible category.
${\mathcal{A}}{\mathcal{S}}$
is a constructible category. -
∙ Every constructible category contains
 ${\mathcal{A}}{\mathcal{C}}$
and is contained in
${\mathcal{A}}{\mathcal{C}}$
and is contained in
 ${\mathcal{A}}{\mathcal{S}}$
. This implies that each locally compact set in a constructible category is Euler.
${\mathcal{A}}{\mathcal{S}}$
. This implies that each locally compact set in a constructible category is Euler. -
∙
 ${\mathcal{A}}{\mathcal{S}}$
is the only constructible category which contains the connected components of compact real algebraic sets.
${\mathcal{A}}{\mathcal{S}}$
is the only constructible category which contains the connected components of compact real algebraic sets.
In what follows, constructible subset stands for
![]() ${\mathcal{A}}{\mathcal{S}}$
-subset, constructible map stands for map with constructible graph and constructible isomorphism stands for
${\mathcal{A}}{\mathcal{S}}$
-subset, constructible map stands for map with constructible graph and constructible isomorphism stands for
![]() ${\mathcal{A}}{\mathcal{S}}$
-homeomorphism.
${\mathcal{A}}{\mathcal{S}}$
-homeomorphism.
In our proof of Lemma 4.5 we need the following result which is, in some sense, a replacement of Chevalley’s theorem for Zariski-constructible sets over an algebraically closed field.
Theorem 2.8. [Reference Parusiński41, 4.3]
Let
![]() $A$
be a semialgebraic subset of a real algebraic subset
$A$
be a semialgebraic subset of a real algebraic subset
![]() $X$
of
$X$
of
![]() $\mathbb{P}_{\mathbb{R}}^{n}$
. Then
$\mathbb{P}_{\mathbb{R}}^{n}$
. Then
![]() $A\in {\mathcal{A}}{\mathcal{S}}$
if and only if there exist a regular morphism of real algebraic varieties
$A\in {\mathcal{A}}{\mathcal{S}}$
if and only if there exist a regular morphism of real algebraic varieties
![]() $f:Z\rightarrow X$
and
$f:Z\rightarrow X$
and
![]() $Z^{\prime }$
the union of some connected components of
$Z^{\prime }$
the union of some connected components of
![]() $Z$
such that
$Z$
such that
where
![]() ${\it\chi}$
is the Euler characteristic with compact support.
${\it\chi}$
is the Euler characteristic with compact support.
In particular the image of an
![]() ${\mathcal{A}}{\mathcal{S}}$
-subset by a regular map whose Euler characteristics with compact support of all the fibers are odd is an
${\mathcal{A}}{\mathcal{S}}$
-subset by a regular map whose Euler characteristics with compact support of all the fibers are odd is an
![]() ${\mathcal{A}}{\mathcal{S}}$
-subset.
${\mathcal{A}}{\mathcal{S}}$
-subset.
In this paper, we need to work with
![]() ${\mathcal{A}}{\mathcal{S}}$
-sets in order to use the virtual Poincaré polynomial discussed below.
${\mathcal{A}}{\mathcal{S}}$
-sets in order to use the virtual Poincaré polynomial discussed below.
In our settings, the Noetherianity of the
![]() ${\mathcal{A}}{\mathcal{S}}$
topology will also allow us to prove a version of Denef and Loeser key lemma for the motivic change of variables formula with a weaker hypothesis. Indeed, we will not assume that the map is birational but only Nash, proper and generically one-to-one.
${\mathcal{A}}{\mathcal{S}}$
topology will also allow us to prove a version of Denef and Loeser key lemma for the motivic change of variables formula with a weaker hypothesis. Indeed, we will not assume that the map is birational but only Nash, proper and generically one-to-one.
2.2 The virtual Poincaré polynomial
McCrory and Parusiński proved in [Reference McCrory and Parusiński36] there exists a unique additive invariant of real algebraic varieties which coincides with the Poincaré polynomial for (co)homology with
![]() $\mathbb{Z}_{2}$
coefficients for compact and nonsingular real algebraic varieties. Moreover, this invariant behaves well since its degree is exactly the dimension and the leading coefficient is positive. This virtual Poincaré polynomial has been generalized to
$\mathbb{Z}_{2}$
coefficients for compact and nonsingular real algebraic varieties. Moreover, this invariant behaves well since its degree is exactly the dimension and the leading coefficient is positive. This virtual Poincaré polynomial has been generalized to
![]() ${\mathcal{A}}{\mathcal{S}}$
-subsets by Fichou in [Reference Fichou11]. Furthermore Nash-equivalent
${\mathcal{A}}{\mathcal{S}}$
-subsets by Fichou in [Reference Fichou11]. Furthermore Nash-equivalent
![]() ${\mathcal{A}}{\mathcal{S}}$
-subsets have the same virtual Poincaré polynomial. These proofs use the weak factorization theorem [Reference Abramovich, Karu, Matsuki and Włodarczyk1, Reference Włodarczyk49] in a way similar of what has been done by Bittner in [Reference Bittner7] to give a new description of the Grothendieck ring in terms of blowings-up.
${\mathcal{A}}{\mathcal{S}}$
-subsets have the same virtual Poincaré polynomial. These proofs use the weak factorization theorem [Reference Abramovich, Karu, Matsuki and Włodarczyk1, Reference Włodarczyk49] in a way similar of what has been done by Bittner in [Reference Bittner7] to give a new description of the Grothendieck ring in terms of blowings-up.
Theorem 2.9. [Reference Fichou11]
There is an additive invariant
![]() ${\it\beta}:{\mathcal{A}}{\mathcal{S}}\rightarrow \mathbb{Z}[u]$
, called the virtual Poincaré polynomial, which associates to an
${\it\beta}:{\mathcal{A}}{\mathcal{S}}\rightarrow \mathbb{Z}[u]$
, called the virtual Poincaré polynomial, which associates to an
![]() ${\mathcal{A}}{\mathcal{S}}$
-subset a polynomial with integer coefficients
${\mathcal{A}}{\mathcal{S}}$
-subset a polynomial with integer coefficients
![]() ${\it\beta}(X)=\sum {\it\beta}_{i}(X)u^{i}\in \mathbb{Z}[u]$
and satisfies the following properties:
${\it\beta}(X)=\sum {\it\beta}_{i}(X)u^{i}\in \mathbb{Z}[u]$
and satisfies the following properties:
-
∙
 ${\it\beta}\left(\sqcup _{i=1}^{k}X_{i}\right)=\sum _{i=1}^{k}{\it\beta}(X_{i})$
.
${\it\beta}\left(\sqcup _{i=1}^{k}X_{i}\right)=\sum _{i=1}^{k}{\it\beta}(X_{i})$
. -
∙
 ${\it\beta}(X\times Y)={\it\beta}(X){\it\beta}(Y)$
.
${\it\beta}(X\times Y)={\it\beta}(X){\it\beta}(Y)$
. -
∙ For
 $X\neq \varnothing$
,
$X\neq \varnothing$
,
 $\operatorname{deg}{\it\beta}(X)=\operatorname{dim}X$
and the leading coefficient of
$\operatorname{deg}{\it\beta}(X)=\operatorname{dim}X$
and the leading coefficient of
 ${\it\beta}(X)$
is positiveFootnote
2
.
${\it\beta}(X)$
is positiveFootnote
2
. -
∙ If
 $X$
is nonsingular and compact then
$X$
is nonsingular and compact then
 ${\it\beta}_{i}(X)=\operatorname{dim}H_{i}(X,\mathbb{Z}_{2})$
.
${\it\beta}_{i}(X)=\operatorname{dim}H_{i}(X,\mathbb{Z}_{2})$
. -
∙ If
 $X$
and
$X$
and
 $Y$
are Nash-equivalent then
$Y$
are Nash-equivalent then
 ${\it\beta}(X)={\it\beta}(Y)$
.
${\it\beta}(X)={\it\beta}(Y)$
.
The virtual Poincaré polynomial is a more interesting additive invariant than the Euler characteristic with compact support since it stores more information, like the dimension. Notice that it is well known that if we forget the arc-symmetric hypothesis and work with all semialgebraic sets, the Euler characteristic with compact support is the only additive invariant [Reference Quarez45].
2.3 Geometric settings
For the sake of convenience, we recall some basics of Nash geometry and arc-analytic maps before introducing generically arc-analytic maps.
A Nash function on an open semialgebraic subset of
![]() $\mathbb{R}^{N}$
is an analytic function which satisfies a nontrivial polynomial equation. This notion coincides with
$\mathbb{R}^{N}$
is an analytic function which satisfies a nontrivial polynomial equation. This notion coincides with
![]() $C^{\infty }$
semialgebraic functions. We can therefore define the notion of Nash submanifold in an obvious way. This notion is powerful since we can use tools from both algebraic and analytic geometries, for example, we have a Nash implicit function theorem. For more details on Nash geometry, we refer the reader to [Reference Bochnak, Coste and Roy8] and [Reference Shiota47].
$C^{\infty }$
semialgebraic functions. We can therefore define the notion of Nash submanifold in an obvious way. This notion is powerful since we can use tools from both algebraic and analytic geometries, for example, we have a Nash implicit function theorem. For more details on Nash geometry, we refer the reader to [Reference Bochnak, Coste and Roy8] and [Reference Shiota47].
Arc-analytic maps were first introduced by Kurdyka in relation with arc-symmetric sets in [Reference Kurdyka29]. These are maps that send analytic arcs to analytic arcs by composition and hence it is suitable to work with arc-analytic maps between arc-symmetric sets. A semialgebraic map
![]() $f:M\rightarrow N$
is blow-Nash if there is a finite sequence of blowings-up with nonsingular centers
$f:M\rightarrow N$
is blow-Nash if there is a finite sequence of blowings-up with nonsingular centers
![]() ${\it\sigma}:\tilde{M}\rightarrow M$
such that
${\it\sigma}:\tilde{M}\rightarrow M$
such that
![]() $f\circ {\it\sigma}:\tilde{M}\rightarrow N$
is Nash. Let
$f\circ {\it\sigma}:\tilde{M}\rightarrow N$
is Nash. Let
![]() $M$
be an analytic manifold and
$M$
be an analytic manifold and
![]() $f:M\rightarrow \mathbb{R}$
a blow-analytic map, since we can lift an analytic arc by a blowing-up with nonsingular center of a nonsingular variety,
$f:M\rightarrow \mathbb{R}$
a blow-analytic map, since we can lift an analytic arc by a blowing-up with nonsingular center of a nonsingular variety,
![]() $f$
is clearly arc-analytic. Kurdyka conjectured the converse with an additional semialgebraicityFootnote
3
hypothesis and Bierstone and Milman brought us the proof in [Reference Bierstone and Milman5]. Parusiński gave another proof in [Reference Parusiński40]. We refer the reader to [Reference Kurdyka and Parusiński31] for a survey on arc-symmetric sets and arc-analytic maps.
$f$
is clearly arc-analytic. Kurdyka conjectured the converse with an additional semialgebraicityFootnote
3
hypothesis and Bierstone and Milman brought us the proof in [Reference Bierstone and Milman5]. Parusiński gave another proof in [Reference Parusiński40]. We refer the reader to [Reference Kurdyka and Parusiński31] for a survey on arc-symmetric sets and arc-analytic maps.
Definition 2.10. Let
![]() $U$
be a semialgebraic open subset of
$U$
be a semialgebraic open subset of
![]() $\mathbb{R}^{N}$
. Then an analytic function
$\mathbb{R}^{N}$
. Then an analytic function
![]() $f:U\rightarrow \mathbb{R}$
is said to be Nash if there are polynomials
$f:U\rightarrow \mathbb{R}$
is said to be Nash if there are polynomials
![]() $a_{0},\ldots ,a_{d}$
with
$a_{0},\ldots ,a_{d}$
with
![]() $a_{d}\neq 0$
such that
$a_{d}\neq 0$
such that
Theorem 2.11. [Reference Bochnak, Coste and Roy8, Proposition 8.1.8]
Let
![]() $U$
be a semialgebraic open subset of
$U$
be a semialgebraic open subset of
![]() $\mathbb{R}^{N}$
. Then
$\mathbb{R}^{N}$
. Then
![]() $f:U\rightarrow \mathbb{R}$
is a Nash function if and only if
$f:U\rightarrow \mathbb{R}$
is a Nash function if and only if
![]() $f$
is semialgebraic and of class
$f$
is semialgebraic and of class
![]() $C^{\infty }$
.
$C^{\infty }$
.
Definition 2.12. A Nash submanifold of dimension
![]() $d$
is a semialgebraic subset
$d$
is a semialgebraic subset
![]() $M$
of
$M$
of
![]() $\mathbb{R}^{p}$
such that every
$\mathbb{R}^{p}$
such that every
![]() $x\in M$
admits a Nash chart
$x\in M$
admits a Nash chart
![]() $(V,{\it\varphi})$
, that is, there are
$(V,{\it\varphi})$
, that is, there are
![]() $U$
an open semialgebraic neighborhood of
$U$
an open semialgebraic neighborhood of
![]() $0\in \mathbb{R}^{p}$
,
$0\in \mathbb{R}^{p}$
,
![]() $V$
an open semialgebraic neighborhood of
$V$
an open semialgebraic neighborhood of
![]() $x$
in
$x$
in
![]() $\mathbb{R}^{p}$
and
$\mathbb{R}^{p}$
and
![]() ${\it\varphi}:U\rightarrow V$
a Nash-diffeomorphism satisfying
${\it\varphi}:U\rightarrow V$
a Nash-diffeomorphism satisfying
![]() ${\it\varphi}(0)=x$
and
${\it\varphi}(0)=x$
and
![]() ${\it\varphi}((\mathbb{R}^{d}\times \{0\})\cap U)=M\cap V$
.
${\it\varphi}((\mathbb{R}^{d}\times \{0\})\cap U)=M\cap V$
.
Remark 2.13. A nonsingular algebraic subset
![]() $M$
of
$M$
of
![]() $\mathbb{R}^{p}$
has a natural structure of Nash submanifold given by the Jacobian criterion and the Nash implicit function theorem.
$\mathbb{R}^{p}$
has a natural structure of Nash submanifold given by the Jacobian criterion and the Nash implicit function theorem.
Definition 2.14. [Reference Kurdyka29]
Let
![]() $X$
and
$X$
and
![]() $Y$
be arc-symmetric subsets of two analytic manifolds. Then
$Y$
be arc-symmetric subsets of two analytic manifolds. Then
![]() $f:X\rightarrow Y$
is arc-analytic if for all analytic arcs
$f:X\rightarrow Y$
is arc-analytic if for all analytic arcs
![]() ${\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow X$
the composition
${\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow X$
the composition
![]() $f\circ {\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow Y$
is again an analytic arc.
$f\circ {\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow Y$
is again an analytic arc.
Theorem 2.15. [Reference Bierstone and Milman5]
Let
![]() $f$
be a semialgebraic map defined on a nonsingular algebraic subset. Then
$f$
be a semialgebraic map defined on a nonsingular algebraic subset. Then
![]() $f$
is arc-analytic if and only if
$f$
is arc-analytic if and only if
![]() $f$
is blow-Nash.
$f$
is blow-Nash.
Remark 2.16. Let
![]() $f:X\rightarrow Y$
be a semialgebraic arc-analytic map between algebraic sets. Then
$f:X\rightarrow Y$
be a semialgebraic arc-analytic map between algebraic sets. Then
![]() $f$
is blow-Nash even if
$f$
is blow-Nash even if
![]() $X$
is singular. Indeed we may first use a resolution of singularities
$X$
is singular. Indeed we may first use a resolution of singularities
![]() ${\it\rho}:U\rightarrow X$
given by a sequence of blowings-up with nonsingular centers [Reference Hironaka19] and apply Theorem 2.15 to
${\it\rho}:U\rightarrow X$
given by a sequence of blowings-up with nonsingular centers [Reference Hironaka19] and apply Theorem 2.15 to
![]() $f\circ {\it\rho}:U\rightarrow Y$
.
$f\circ {\it\rho}:U\rightarrow Y$
.
Remark 2.17. If
![]() $M$
is a nonsingular algebraic set and
$M$
is a nonsingular algebraic set and
![]() ${\it\rho}:\tilde{M}\rightarrow M$
the blowing-up of
${\it\rho}:\tilde{M}\rightarrow M$
the blowing-up of
![]() $M$
with a nonsingular center, it is well known that we can lift an arc on
$M$
with a nonsingular center, it is well known that we can lift an arc on
![]() $M$
by
$M$
by
![]() ${\it\rho}$
to an arc on
${\it\rho}$
to an arc on
![]() $\tilde{M}$
. This result is obviously false for a singular algebraic set as shown in the following examples. However, if
$\tilde{M}$
. This result is obviously false for a singular algebraic set as shown in the following examples. However, if
![]() $X$
is a singular algebraic set and
$X$
is a singular algebraic set and
![]() ${\it\rho}:\tilde{X}\rightarrow X$
the blowing-up of
${\it\rho}:\tilde{X}\rightarrow X$
the blowing-up of
![]() $X$
with a nonsingular center we can lift an arc on
$X$
with a nonsingular center we can lift an arc on
![]() $X$
not entirely included in the centerFootnote
4
and this lifting is unique.
$X$
not entirely included in the centerFootnote
4
and this lifting is unique.
Example 2.18. Consider the Whitney umbrella
![]() $X=V(x^{2}-zy^{2})$
and
$X=V(x^{2}-zy^{2})$
and
![]() ${\it\rho}:\tilde{X}\rightarrow X$
the blowing-up along the singular locus
${\it\rho}:\tilde{X}\rightarrow X$
the blowing-up along the singular locus
![]() $I(X_{\text{sing}})=(x,y)$
. Then we cannot lift by
$I(X_{\text{sing}})=(x,y)$
. Then we cannot lift by
![]() ${\it\rho}$
an arc included in the handle
${\it\rho}$
an arc included in the handle
![]() $\{x=0,y=0,z<0\}$
(
$\{x=0,y=0,z<0\}$
(
![]() ${\it\rho}$
is not even surjective).
${\it\rho}$
is not even surjective).
Example 2.19. This phenomenon still remains in the pure dimensional case. Let
![]() $X=V(x^{3}-zy^{3})$
. Then
$X=V(x^{3}-zy^{3})$
. Then
![]() $X$
is of pure dimension
$X$
is of pure dimension
![]() $2$
and the blowing-up
$2$
and the blowing-up
![]() ${\it\rho}:\tilde{X}\rightarrow X$
along the singular locus
${\it\rho}:\tilde{X}\rightarrow X$
along the singular locus
![]() $I(X_{\text{sing}})=(x,y)$
is surjective. However we cannot lift the (germ of) analytic arc
$I(X_{\text{sing}})=(x,y)$
is surjective. However we cannot lift the (germ of) analytic arc
![]() ${\it\gamma}(t)=(0,0,t)$
to an analytic arc. In the
${\it\gamma}(t)=(0,0,t)$
to an analytic arc. In the
![]() $y$
-chart,
$y$
-chart,
![]() $\tilde{X}=\{(X,Y,Z)\in \mathbb{R}^{3},X^{3}=Z\}$
and
$\tilde{X}=\{(X,Y,Z)\in \mathbb{R}^{3},X^{3}=Z\}$
and
![]() ${\it\rho}(X,Y,Z)=(XY,Y,Z)$
. Then the lifting of
${\it\rho}(X,Y,Z)=(XY,Y,Z)$
. Then the lifting of
![]() ${\it\gamma}$
should have the form
${\it\gamma}$
should have the form
![]() $\tilde{{\it\gamma}}(t)=(t^{\frac{1}{3}},0,t)$
.
$\tilde{{\it\gamma}}(t)=(t^{\frac{1}{3}},0,t)$
.
Remark 2.20. A continuous subanalytic map
![]() $f:U\rightarrow V$
is locally Hölder, that is, for each compact subset
$f:U\rightarrow V$
is locally Hölder, that is, for each compact subset
![]() $K\subset U$
, there exist
$K\subset U$
, there exist
![]() ${\it\alpha}>0$
and
${\it\alpha}>0$
and
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $x,y\in K$
,
$x,y\in K$
,
![]() $\Vert f(x)-f(y)\Vert \leqslant C\Vert x-y\Vert ^{{\it\alpha}}$
. See for instance [Reference Hardt17], it is a consequence of [Reference Hironaka20, Section 9, Inequality III]. See also [Reference Bierstone and Milman4, Corollary 6.7]. Or we can directly use Łojasiewicz inequality [Reference Bierstone and Milman4, Theorem 6.4] with
$\Vert f(x)-f(y)\Vert \leqslant C\Vert x-y\Vert ^{{\it\alpha}}$
. See for instance [Reference Hardt17], it is a consequence of [Reference Hironaka20, Section 9, Inequality III]. See also [Reference Bierstone and Milman4, Corollary 6.7]. Or we can directly use Łojasiewicz inequality [Reference Bierstone and Milman4, Theorem 6.4] with
![]() $(x,y)\mapsto |f(x)-f(y)|$
and
$(x,y)\mapsto |f(x)-f(y)|$
and
![]() $(x,y)\mapsto |x-y|$
.
$(x,y)\mapsto |x-y|$
.
The following result will be useful.
Proposition 2.21. Let
![]() $f:X\rightarrow Y$
be a surjective proper subanalytic map (resp. proper semialgebraic map) and
$f:X\rightarrow Y$
be a surjective proper subanalytic map (resp. proper semialgebraic map) and
![]() ${\it\gamma}:[0,{\it\varepsilon})\rightarrow Y$
a real analytic (resp. Nash) arc. Then there exist
${\it\gamma}:[0,{\it\varepsilon})\rightarrow Y$
a real analytic (resp. Nash) arc. Then there exist
![]() $m\in \mathbb{N}_{{>}0}$
and
$m\in \mathbb{N}_{{>}0}$
and
![]() $\tilde{{\it\gamma}}:[0,{\it\delta})\rightarrow X$
analytic (resp. Nash) with
$\tilde{{\it\gamma}}:[0,{\it\delta})\rightarrow X$
analytic (resp. Nash) with
![]() ${\it\delta}^{m}\leqslant {\it\varepsilon}$
such that
${\it\delta}^{m}\leqslant {\it\varepsilon}$
such that
![]() $f\circ \tilde{{\it\gamma}}(t)={\it\gamma}(t^{m})$
.
$f\circ \tilde{{\it\gamma}}(t)={\it\gamma}(t^{m})$
.
Proof. The proof is divided into two parts. First we use the properness of
![]() $f$
to lift
$f$
to lift
![]() ${\it\gamma}$
to an arc on
${\it\gamma}$
to an arc on
![]() $X$
and then we conclude thanks to Puiseux theorem.
$X$
and then we conclude thanks to Puiseux theorem.
Consider the following diagram
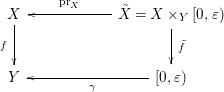
Let
![]() $X_{1}=\tilde{f}^{-1}((0,{\it\varepsilon}))$
. Since
$X_{1}=\tilde{f}^{-1}((0,{\it\varepsilon}))$
. Since
![]() $f$
is proper,
$f$
is proper,
![]() $\overline{X}_{1}\setminus X_{1}\subset \tilde{X}$
. Let
$\overline{X}_{1}\setminus X_{1}\subset \tilde{X}$
. Let
![]() $x_{0}\in \overline{X}_{1}\setminus X_{1}$
, then by the curve selection lemma ([Reference Bochnak, Coste and Roy8, Proposition 8.1.13] for the semialgebraic case) there exists
$x_{0}\in \overline{X}_{1}\setminus X_{1}$
, then by the curve selection lemma ([Reference Bochnak, Coste and Roy8, Proposition 8.1.13] for the semialgebraic case) there exists
![]() ${\it\gamma}_{1}:[0,{\it\eta})\rightarrow \tilde{X}$
analytic (resp. Nash) such that
${\it\gamma}_{1}:[0,{\it\eta})\rightarrow \tilde{X}$
analytic (resp. Nash) such that
![]() ${\it\gamma}_{1}(0)=x_{0}$
and
${\it\gamma}_{1}(0)=x_{0}$
and
![]() ${\it\gamma}_{1}((0,{\it\eta}))\subset X_{1}$
. We have the following diagram
${\it\gamma}_{1}((0,{\it\eta}))\subset X_{1}$
. We have the following diagram
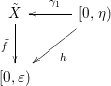
Then,
![]() $h(0)=0$
and
$h(0)=0$
and
![]() $h((0,{\it\eta}))\subset (0,{\it\varepsilon})$
. Hence there exists
$h((0,{\it\eta}))\subset (0,{\it\varepsilon})$
. Hence there exists
![]() ${\it\alpha}\in (0,{\it\eta})$
such that
${\it\alpha}\in (0,{\it\eta})$
such that
![]() $h:[0,{\it\alpha})\rightarrow [0,{\it\beta})$
is a subanalytic (resp. semialgebraic) homeomorphism.
$h:[0,{\it\alpha})\rightarrow [0,{\it\beta})$
is a subanalytic (resp. semialgebraic) homeomorphism.
By Puiseux theorem ([Reference Bochnak, Coste and Roy8, Proposition 8.1.12] for the semialgebraic case; see also [Reference Pawłucki42]), there exist
![]() $m\in \mathbb{N}_{{>}0}$
and
$m\in \mathbb{N}_{{>}0}$
and
![]() ${\it\delta}\leqslant {\it\beta}^{\frac{1}{m}}$
such that
${\it\delta}\leqslant {\it\beta}^{\frac{1}{m}}$
such that
![]() $h^{-1}(t^{m})$
is analytic (resp. Nash) for
$h^{-1}(t^{m})$
is analytic (resp. Nash) for
![]() $t\in [0,{\it\delta})$
.
$t\in [0,{\it\delta})$
.
Finally,
![]() $\tilde{{\it\gamma}}:[0,{\it\delta})\rightarrow X$
defined by
$\tilde{{\it\gamma}}:[0,{\it\delta})\rightarrow X$
defined by
![]() $\tilde{{\it\gamma}}(t)=\text{pr}_{X}{\it\gamma}_{1}h^{-1}(t^{m})$
satisfies
$\tilde{{\it\gamma}}(t)=\text{pr}_{X}{\it\gamma}_{1}h^{-1}(t^{m})$
satisfies
![]() $f\circ \tilde{{\it\gamma}}(t)={\it\gamma}(t^{m})$
.◻
$f\circ \tilde{{\it\gamma}}(t)={\it\gamma}(t^{m})$
.◻
In the singular case we will work with a slightly different framework.
Definition 2.22. Let
![]() $X$
and
$X$
and
![]() $Y$
be two algebraic sets. A map
$Y$
be two algebraic sets. A map
![]() $f:X\rightarrow Y$
is said to be generically arc-analytic in dimension
$f:X\rightarrow Y$
is said to be generically arc-analytic in dimension
![]() $d=\operatorname{dim}X$
if there exists an algebraic subset
$d=\operatorname{dim}X$
if there exists an algebraic subset
![]() $S$
of
$S$
of
![]() $X$
with
$X$
with
![]() $\operatorname{dim}S<\operatorname{dim}X$
such that for all analytic arc
$\operatorname{dim}S<\operatorname{dim}X$
such that for all analytic arc
![]() ${\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow X$
not entirely includedFootnote
5
in
${\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow X$
not entirely includedFootnote
5
in
![]() $S$
,
$S$
,
![]() $f\circ {\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow Y$
is analytic.
$f\circ {\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow Y$
is analytic.
If
![]() $X$
is nonsingular, these maps are exactly the arc-analytic ones.
$X$
is nonsingular, these maps are exactly the arc-analytic ones.
Lemma 2.23. Let
![]() $X$
be a nonsingular algebraic set of dimensionFootnote
6
$X$
be a nonsingular algebraic set of dimensionFootnote
6
![]() $d$
and
$d$
and
![]() $Y$
an algebraic set. Let
$Y$
an algebraic set. Let
![]() $f:X\rightarrow Y$
be a continuous semialgebraic map. If
$f:X\rightarrow Y$
be a continuous semialgebraic map. If
![]() $f$
is generically arc-analytic in dimension
$f$
is generically arc-analytic in dimension
![]() $d$
then
$d$
then
![]() $f$
is arc-analytic.
$f$
is arc-analytic.
Proof. Let
![]() $S$
be as in Definition 2.22. By the Jacobian criterion and the Nash implicit function theorem we may assume that
$S$
be as in Definition 2.22. By the Jacobian criterion and the Nash implicit function theorem we may assume that
![]() $S$
is locally a Nash subset of
$S$
is locally a Nash subset of
![]() $\mathbb{R}^{d}$
. Taking the Zariski closure we may moreover assume that
$\mathbb{R}^{d}$
. Taking the Zariski closure we may moreover assume that
![]() $S$
is an algebraic subset of
$S$
is an algebraic subset of
![]() $\mathbb{R}^{d}$
since it does not change the dimension. Let
$\mathbb{R}^{d}$
since it does not change the dimension. Let
![]() ${\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow \mathbb{R}^{d}$
be an analytic arc entirely included in
${\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow \mathbb{R}^{d}$
be an analytic arc entirely included in
![]() $S$
.
$S$
.
As in [Reference Kurdyka30, Corollaire 2.7], by Puiseux theorem, we may assume that
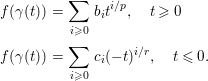 $$\begin{eqnarray}\displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i\geqslant 0}b_{i}t^{i/p},\quad t\geqslant 0\nonumber\\ \displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i\geqslant 0}c_{i}(-t)^{i/r},\quad t\leqslant 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i\geqslant 0}b_{i}t^{i/p},\quad t\geqslant 0\nonumber\\ \displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i\geqslant 0}c_{i}(-t)^{i/r},\quad t\leqslant 0.\nonumber\end{eqnarray}$$
By [Reference Kurdyka30, Corollaire 2.8 and Corollaire 2.9], two phenomena may prevent
![]() $f({\it\gamma}(t))$
from being analytic: either one of these expansions has a noninteger exponent or these expansions do not coincide.
$f({\it\gamma}(t))$
from being analytic: either one of these expansions has a noninteger exponent or these expansions do not coincide.
To handle the first case, we assume that one of these expansions, for instance for
![]() $t\geqslant 0$
, has a noninteger exponent, that is,
$t\geqslant 0$
, has a noninteger exponent, that is,
It follows from Remark 2.20 there exists
![]() $N\in \mathbb{N}$
such that for every analytic arc
$N\in \mathbb{N}$
such that for every analytic arc
![]() ${\it\delta}$
we have
${\it\delta}$
we have
![]() $f({\it\gamma}(t)+t^{N}{\it\delta}(t))\equiv f({\it\gamma}(t))\operatorname{mod}t^{m+1}$
. We are going to prove that for
$f({\it\gamma}(t)+t^{N}{\it\delta}(t))\equiv f({\it\gamma}(t))\operatorname{mod}t^{m+1}$
. We are going to prove that for
![]() ${\it\eta}\in \mathbb{R}^{d}$
generic, the arc
${\it\eta}\in \mathbb{R}^{d}$
generic, the arc
![]() $\tilde{{\it\gamma}}(t)={\it\gamma}(t)+t^{N}{\it\eta}$
is not entirely included in
$\tilde{{\it\gamma}}(t)={\it\gamma}(t)+t^{N}{\it\eta}$
is not entirely included in
![]() $S$
in order to get a contradiction since
$S$
in order to get a contradiction since
![]() $f(\tilde{{\it\gamma}}(t))\equiv f({\it\gamma}(t))\operatorname{mod}t^{m+1}$
.
$f(\tilde{{\it\gamma}}(t))\equiv f({\it\gamma}(t))\operatorname{mod}t^{m+1}$
.
Let
![]() $t_{0}\in (-{\it\varepsilon},{\it\varepsilon})\setminus \{0\}$
. Since
$t_{0}\in (-{\it\varepsilon},{\it\varepsilon})\setminus \{0\}$
. Since
![]() $\operatorname{dim}S<d$
, there is
$\operatorname{dim}S<d$
, there is
![]() $\tilde{{\it\eta}}\in \mathbb{R}^{d}\setminus C_{{\it\gamma}(t_{0})}S$
where
$\tilde{{\it\eta}}\in \mathbb{R}^{d}\setminus C_{{\it\gamma}(t_{0})}S$
where
![]() $C_{{\it\gamma}(t_{0})}S$
is the tangent cone of
$C_{{\it\gamma}(t_{0})}S$
is the tangent cone of
![]() $S$
at
$S$
at
![]() ${\it\gamma}(t_{0})$
. Thus there exists
${\it\gamma}(t_{0})$
. Thus there exists
![]() $F\in I(S)$
with
$F\in I(S)$
with
![]() $F({\it\gamma}(t_{0})+x)=F_{{\it\mu}}(x)+\cdots +F_{{\it\mu}+r}(x)$
where
$F({\it\gamma}(t_{0})+x)=F_{{\it\mu}}(x)+\cdots +F_{{\it\mu}+r}(x)$
where
![]() $\operatorname{deg}F_{i}=i$
and such that
$\operatorname{deg}F_{i}=i$
and such that
![]() $F_{{\it\mu}}(\tilde{{\it\eta}})\neq 0$
. Then
$F_{{\it\mu}}(\tilde{{\it\eta}})\neq 0$
. Then
![]() $F\left({\it\gamma}(t_{0})+st_{0}^{N}\tilde{{\it\eta}}\right)=\left(st_{0}^{N}\right)^{{\it\mu}}F_{{\it\mu}}(\tilde{{\it\eta}})+\left(st_{0}^{N}\right)^{{\it\mu}+1}G(s,t)$
and hence for
$F\left({\it\gamma}(t_{0})+st_{0}^{N}\tilde{{\it\eta}}\right)=\left(st_{0}^{N}\right)^{{\it\mu}}F_{{\it\mu}}(\tilde{{\it\eta}})+\left(st_{0}^{N}\right)^{{\it\mu}+1}G(s,t)$
and hence for
![]() $s$
small enough the arc
$s$
small enough the arc
![]() ${\it\gamma}(t)+t^{N}s\tilde{{\it\eta}}$
is not entirely included in
${\it\gamma}(t)+t^{N}s\tilde{{\it\eta}}$
is not entirely included in
![]() $S$
.
$S$
.
Then we prove that the expansions coincide in a similar way. Assume that the expansions are different, that is,
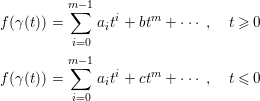 $$\begin{eqnarray}\displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i=0}^{m-1}a_{i}t^{i}+bt^{m}+\cdots \,,\quad t\geqslant 0\nonumber\\ \displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i=0}^{m-1}a_{i}t^{i}+ct^{m}+\cdots \,,\quad t\leqslant 0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i=0}^{m-1}a_{i}t^{i}+bt^{m}+\cdots \,,\quad t\geqslant 0\nonumber\\ \displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i=0}^{m-1}a_{i}t^{i}+ct^{m}+\cdots \,,\quad t\leqslant 0\nonumber\end{eqnarray}$$
with
![]() $b\neq c$
. As in the previous case, we may construct an arc
$b\neq c$
. As in the previous case, we may construct an arc
![]() $\tilde{{\it\gamma}}$
not entirely included in
$\tilde{{\it\gamma}}$
not entirely included in
![]() $S$
such that
$S$
such that
![]() $f{\it\gamma}(t)$
and
$f{\it\gamma}(t)$
and
![]() $f\tilde{{\it\gamma}}(t)$
coincide up to order
$f\tilde{{\it\gamma}}(t)$
coincide up to order
![]() $m+1$
. That leads to a contradiction.◻
$m+1$
. That leads to a contradiction.◻
Remark 2.24. If
![]() $\operatorname{dim}\operatorname{Sing}(X)=0$
then a generically arc-analytic map
$\operatorname{dim}\operatorname{Sing}(X)=0$
then a generically arc-analytic map
![]() $X\rightarrow Y$
is also arc-analytic since the analytic arcs contained in the singular locus are constant.
$X\rightarrow Y$
is also arc-analytic since the analytic arcs contained in the singular locus are constant.
Remark 2.25. The previous proof fails when
![]() $X$
is not assumed to be nonsingular. Let
$X$
is not assumed to be nonsingular. Let
![]() $X=V(x^{3}-zy^{3})$
and
$X=V(x^{3}-zy^{3})$
and
![]() $S=X_{\text{sing}}=O_{z}$
. Consider (germ of) analytic arc
$S=X_{\text{sing}}=O_{z}$
. Consider (germ of) analytic arc
![]() ${\it\gamma}(t)=(0,0,t)$
entirely included in
${\it\gamma}(t)=(0,0,t)$
entirely included in
![]() $S$
. Given any
$S$
. Given any
![]() $N\in \mathbb{N}$
we cannot find
$N\in \mathbb{N}$
we cannot find
![]() ${\it\eta}(t)$
such that
${\it\eta}(t)$
such that
![]() $\tilde{{\it\gamma}}(t)={\it\gamma}(t)+t^{N}{\it\eta}(t)$
is not entirely included in
$\tilde{{\it\gamma}}(t)={\it\gamma}(t)+t^{N}{\it\eta}(t)$
is not entirely included in
![]() $S$
. Indeed, if we inject the coordinates of
$S$
. Indeed, if we inject the coordinates of
![]() $\tilde{{\it\gamma}}$
in the equation
$\tilde{{\it\gamma}}$
in the equation
![]() $x^{3}=zy^{3}$
we get a contradiction considering the orders of vanishing.
$x^{3}=zy^{3}$
we get a contradiction considering the orders of vanishing.
Remark 2.26. A continuous semialgebraic generically arc-analytic in dimension
![]() $d=\operatorname{dim}X$
map
$d=\operatorname{dim}X$
map
![]() $f:X\rightarrow Y$
may not be arc-analytic if
$f:X\rightarrow Y$
may not be arc-analytic if
![]() $\operatorname{dim}\operatorname{Sing}(X)\geqslant 1$
. Indeed, let
$\operatorname{dim}\operatorname{Sing}(X)\geqslant 1$
. Indeed, let
![]() $X=V(x^{3}-zy^{3})$
and
$X=V(x^{3}-zy^{3})$
and
![]() $f:X\rightarrow \mathbb{R}$
be defined by
$f:X\rightarrow \mathbb{R}$
be defined by
![]() $f(x,y,z)=\frac{x}{y}$
. Then
$f(x,y,z)=\frac{x}{y}$
. Then
![]() $f(0,0,t)=t^{\frac{1}{3}}$
is not analytic.
$f(0,0,t)=t^{\frac{1}{3}}$
is not analytic.
In the nonsingular case, by Theorem 2.15, the blow-Nash maps are exactly the semialgebraic arc-analytic ones. With the following proposition, we notice that more generally the blow-Nash maps are exactly the semialgebraic generically arc-analytic ones.
Proposition 2.27. Let
![]() $X$
be an algebraic set of dimension
$X$
be an algebraic set of dimension
![]() $d$
. Let
$d$
. Let
![]() $f:X\rightarrow Y$
be a semialgebraic map which is continuous on
$f:X\rightarrow Y$
be a semialgebraic map which is continuous on
![]() $\overline{\operatorname{Reg}_{d}X}$
. Then
$\overline{\operatorname{Reg}_{d}X}$
. Then
![]() $f$
is generically arc-analytic in dimension
$f$
is generically arc-analytic in dimension
![]() $d$
if and only if it is blow-Nash.
$d$
if and only if it is blow-Nash.
Proof. Assume that
![]() $f$
is generically arc-analytic. Let
$f$
is generically arc-analytic. Let
![]() ${\it\rho}:U\rightarrow X$
be a resolution of singularities given by a sequence of blowings-up with nonsingular centers, then
${\it\rho}:U\rightarrow X$
be a resolution of singularities given by a sequence of blowings-up with nonsingular centers, then
![]() $f\circ {\it\rho}:U\rightarrow Y$
is semialgebraic and generically arc-analytic with
$f\circ {\it\rho}:U\rightarrow Y$
is semialgebraic and generically arc-analytic with
![]() $U$
nonsingular. Thus
$U$
nonsingular. Thus
![]() $f\circ {\it\rho}$
is arc-analytic by Lemma 2.23. By Theorem 2.15, there exists a sequence of blowings-up with nonsingular centers
$f\circ {\it\rho}$
is arc-analytic by Lemma 2.23. By Theorem 2.15, there exists a sequence of blowings-up with nonsingular centers
![]() ${\it\eta}:M\rightarrow U$
such that
${\it\eta}:M\rightarrow U$
such that
![]() $f\circ {\it\rho}\circ {\it\eta}$
is Nash. Finally
$f\circ {\it\rho}\circ {\it\eta}$
is Nash. Finally
![]() $f\circ {\it\sigma}$
is Nash where
$f\circ {\it\sigma}$
is Nash where
![]() ${\it\sigma}={\it\rho}\circ {\it\eta}:M\rightarrow X$
is a sequence of blowings-up with nonsingular centers.
${\it\sigma}={\it\rho}\circ {\it\eta}:M\rightarrow X$
is a sequence of blowings-up with nonsingular centers.
Assume that
![]() $f$
is blow-Nash. Then there is
$f$
is blow-Nash. Then there is
![]() ${\it\sigma}:M\rightarrow X$
a sequence of blowings-up with nonsingular centers such that
${\it\sigma}:M\rightarrow X$
a sequence of blowings-up with nonsingular centers such that
![]() $f\circ {\it\sigma}:M\rightarrow Y$
is Nash. Let
$f\circ {\it\sigma}:M\rightarrow Y$
is Nash. Let
![]() ${\it\gamma}$
be an arc on
${\it\gamma}$
be an arc on
![]() $X$
not entirely included in the singular locus of
$X$
not entirely included in the singular locus of
![]() $X$
and the center of
$X$
and the center of
![]() ${\it\sigma}$
, then there is
${\it\sigma}$
, then there is
![]() $\tilde{{\it\gamma}}$
an arc on
$\tilde{{\it\gamma}}$
an arc on
![]() $M$
such that
$M$
such that
![]() ${\it\gamma}={\it\sigma}(\tilde{{\it\gamma}})$
. Thus
${\it\gamma}={\it\sigma}(\tilde{{\it\gamma}})$
. Thus
![]() $f({\it\gamma}(t))=f\circ {\it\sigma}(\tilde{{\it\gamma}}(t))$
is analytic.◻
$f({\it\gamma}(t))=f\circ {\it\sigma}(\tilde{{\it\gamma}}(t))$
is analytic.◻
2.4 Arcs and jets
Arc spaces and truncations of arcs were first introduced by Nash in 1964 [Reference Nash38] and their study has gained new momentum with the works of Kontsevich [Reference Kontsevich24], Denef and Loeser [Reference Denef and Loeser9] on motivic integration. We can notice that Kurdyka [Reference Kurdyka29], Nobile [Reference Nobile39], Lejeune-Jalabert [Reference Lejeune-Jalabert34], [Reference Gonzalez-Sprinberg and Lejeune-Jalabert15], Hickel [Reference Hickel18] and others studied arc spaces and jet spaces before the advent of motivic integration. Most of these works concern the relationship between the singularities of a variety and its jet spaces.
In this section, we define the arc space and the jet spaces of a real algebraic set. We first work with the whole ambient Euclidean space and then use the equations of the algebraic set to define arcs and jets on it. Finally we will give and prove a collection of results concerning these objects.
The arc space on
![]() $\mathbb{R}^{N}$
is defined by
$\mathbb{R}^{N}$
is defined by
and, for
![]() $n\in \mathbb{N}$
, the set of
$n\in \mathbb{N}$
, the set of
![]() $n$
-jets on
$n$
-jets on
![]() $\mathbb{R}^{N}$
is defined by
$\mathbb{R}^{N}$
is defined by
where
![]() ${\it\gamma}_{1}{\sim}_{n}{\it\gamma}_{2}$
if and only if
${\it\gamma}_{1}{\sim}_{n}{\it\gamma}_{2}$
if and only if
![]() ${\it\gamma}_{1}\equiv {\it\gamma}_{2}\operatorname{mod}t^{n+1}$
. Obviously,
${\it\gamma}_{1}\equiv {\it\gamma}_{2}\operatorname{mod}t^{n+1}$
. Obviously,
![]() $L_{n}(\mathbb{R}^{N})\simeq (\mathbb{R}\{t\}/t^{n+1})^{N}$
. We also consider the truncation maps
$L_{n}(\mathbb{R}^{N})\simeq (\mathbb{R}\{t\}/t^{n+1})^{N}$
. We also consider the truncation maps
![]() ${\it\pi}_{n}:{\mathcal{L}}(\mathbb{R}^{N})\rightarrow {\mathcal{L}}_{n}(\mathbb{R}^{N})$
and
${\it\pi}_{n}:{\mathcal{L}}(\mathbb{R}^{N})\rightarrow {\mathcal{L}}_{n}(\mathbb{R}^{N})$
and
![]() ${\it\pi}_{n}^{m}:{\mathcal{L}}_{m}(\mathbb{R}^{N})\rightarrow {\mathcal{L}}_{n}(\mathbb{R}^{N})$
, where
${\it\pi}_{n}^{m}:{\mathcal{L}}_{m}(\mathbb{R}^{N})\rightarrow {\mathcal{L}}_{n}(\mathbb{R}^{N})$
, where
![]() $m>n$
. These maps are clearly surjective.
$m>n$
. These maps are clearly surjective.
Next, assume that
![]() $X\subset \mathbb{R}^{N}$
is an algebraic subset. The set of analytic arcs on
$X\subset \mathbb{R}^{N}$
is an algebraic subset. The set of analytic arcs on
![]() $X$
is
$X$
is
and, for
![]() $n\in \mathbb{N}$
, the set of
$n\in \mathbb{N}$
, the set of
![]() $n$
-jets on
$n$
-jets on
![]() $X$
is
$X$
is
When
![]() $X$
is singular, we will see that the truncation maps may not be surjective.
$X$
is singular, we will see that the truncation maps may not be surjective.
Example 2.28. Let
![]() $X\subset \mathbb{R}^{N}$
be an algebraic subset, then
$X\subset \mathbb{R}^{N}$
be an algebraic subset, then
![]() ${\mathcal{L}}_{0}(X)\simeq X$
and
${\mathcal{L}}_{0}(X)\simeq X$
and
![]() ${\mathcal{L}}_{1}(X)\simeq T^{\text{Zar}}X=\sqcup T_{x}^{\text{Zar}}X$
. Indeed, we just apply Taylor expansion to
${\mathcal{L}}_{1}(X)\simeq T^{\text{Zar}}X=\sqcup T_{x}^{\text{Zar}}X$
. Indeed, we just apply Taylor expansion to
![]() $f(a+bt)$
where
$f(a+bt)$
where
![]() $f\in I(X)$
(or we may directly use that the Zariski tangent space at a point is given by the linear parts of the polynomials
$f\in I(X)$
(or we may directly use that the Zariski tangent space at a point is given by the linear parts of the polynomials
![]() $f\in I(X)$
after a translation).
$f\in I(X)$
after a translation).
The following lemma is useful to find examples which are hypersurfaces since the constructions of arc space and jet spaces on an algebraic set are algebraic. See [Reference Bochnak, Coste and Roy8, Theorem 4.5.1] for a more general result with another proof. We may find similar results for nonprincipal ideals in [Reference Bochnak, Coste and Roy8, Proposition 3.3.16, Theorem 4.1.4]. See also [Reference Lam33, Section 6].
Lemma 2.29. Let
![]() $f\in \mathbb{R}[x_{1},\ldots ,x_{N}]$
be an irreducible polynomial which changes sign, then
$f\in \mathbb{R}[x_{1},\ldots ,x_{N}]$
be an irreducible polynomial which changes sign, then
![]() $I(V(f))=(f)$
.
$I(V(f))=(f)$
.
Proof. The following proof comes from [Reference Lam33, Lemma 6.14]. After an affine change of coordinates, we may assume that
![]() $f(a,b_{1})<0<f(a,b_{2})$
with
$f(a,b_{1})<0<f(a,b_{2})$
with
![]() $a=(a_{1},\ldots ,a_{N-1})$
. Let
$a=(a_{1},\ldots ,a_{N-1})$
. Let
![]() $g\in I(V(f))$
and assume that
$g\in I(V(f))$
and assume that
![]() $f\nmid g$
in
$f\nmid g$
in
![]() $\mathbb{R}[x_{1},\ldots ,x_{N}]$
. In the PID (and hence UFD)
$\mathbb{R}[x_{1},\ldots ,x_{N}]$
. In the PID (and hence UFD)
![]() $\mathbb{R}(x_{1},\ldots ,x_{N-1})[x_{N}]$
,
$\mathbb{R}(x_{1},\ldots ,x_{N-1})[x_{N}]$
,
![]() $f$
is also irreducible and
$f$
is also irreducible and
![]() $f\nmid g$
too. In this PID, we may find
$f\nmid g$
too. In this PID, we may find
![]() ${\it\varphi}$
and
${\it\varphi}$
and
![]() ${\it\gamma}$
such that
${\it\gamma}$
such that
![]() ${\it\varphi}f+{\it\gamma}g=1$
. Let
${\it\varphi}f+{\it\gamma}g=1$
. Let
![]() ${\it\varphi}={\it\varphi}_{0}/h$
and
${\it\varphi}={\it\varphi}_{0}/h$
and
![]() ${\it\gamma}={\it\gamma}_{0}/h$
with
${\it\gamma}={\it\gamma}_{0}/h$
with
![]() $0\neq h\in \mathbb{R}[x_{1},\ldots ,x_{N-1}]$
and
$0\neq h\in \mathbb{R}[x_{1},\ldots ,x_{N-1}]$
and
![]() ${\it\varphi}_{0},{\it\gamma}_{0}\in \mathbb{R}[x_{1},\ldots ,x_{N-1}][x_{N}]$
. Then
${\it\varphi}_{0},{\it\gamma}_{0}\in \mathbb{R}[x_{1},\ldots ,x_{N-1}][x_{N}]$
. Then
![]() ${\it\varphi}_{0}f+{\it\gamma}_{0}g=h$
. Let
${\it\varphi}_{0}f+{\it\gamma}_{0}g=h$
. Let
![]() $V$
be a neighborhood of
$V$
be a neighborhood of
![]() $a$
in
$a$
in
![]() $\mathbb{R}^{N-1}$
such that
$\mathbb{R}^{N-1}$
such that
![]() $\text{for all }v\in V,f(v,b_{1})<0<f(v,b_{2})$
. By the IVT, for all
$\text{for all }v\in V,f(v,b_{1})<0<f(v,b_{2})$
. By the IVT, for all
![]() $v\in V$
, there is
$v\in V$
, there is
![]() $b_{1}\leqslant b_{v}\leqslant b_{2}$
such that
$b_{1}\leqslant b_{v}\leqslant b_{2}$
such that
![]() $f(v,b_{v})=0$
, and so
$f(v,b_{v})=0$
, and so
![]() $g(v,b_{v})=0$
. Then
$g(v,b_{v})=0$
. Then
![]() $\text{for all }v\in V,h(v)=0$
and hence
$\text{for all }v\in V,h(v)=0$
and hence
![]() $h\equiv 0$
which is a contradiction.◻
$h\equiv 0$
which is a contradiction.◻
Example 2.30. Let
![]() $X=V\left(y^{2}-x^{3}\right)$
. Since
$X=V\left(y^{2}-x^{3}\right)$
. Since
![]() $y^{2}-x^{3}$
is irreducible and changes sign, we have
$y^{2}-x^{3}$
is irreducible and changes sign, we have
![]() $I(X)=\left(y^{2}-x^{3}\right)$
by Lemma 2.29. Hence we get,
$I(X)=\left(y^{2}-x^{3}\right)$
by Lemma 2.29. Hence we get,
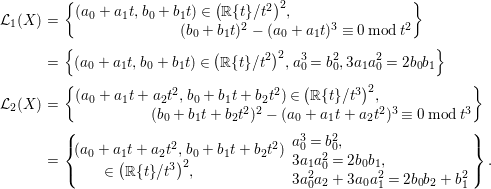 $$\begin{eqnarray}\displaystyle {\mathcal{L}}_{1}(X) & = & \displaystyle \left\{\begin{array}{@{}l@{}}(a_{0}+a_{1}t,b_{0}+b_{1}t)\in \left(\mathbb{R}\{t\}/t^{2}\right)^{2}\!,\\ \hspace{75.60004pt}(b_{0}+b_{1}t)^{2}-(a_{0}+a_{1}t)^{3}\equiv 0\operatorname{mod}t^{2}\end{array}\right\}\nonumber\\ \displaystyle & = & \displaystyle \left\{(a_{0}+a_{1}t,b_{0}+b_{1}t)\in \left(\mathbb{R}\{t\}/t^{2}\right)^{2}\!,a_{0}^{3}=b_{0}^{2},3a_{1}a_{0}^{2}=2b_{0}b_{1}\right\}\nonumber\\ \displaystyle {\mathcal{L}}_{2}(X) & = & \displaystyle \left\{\begin{array}{@{}l@{}}(a_{0}+a_{1}t+a_{2}t^{2},b_{0}+b_{1}t+b_{2}t^{2})\in \left(\mathbb{R}\{t\}/t^{3}\right)^{2}\!,\\ \quad \quad \quad \quad \quad (b_{0}+b_{1}t+b_{2}t^{2})^{2}-(a_{0}+a_{1}t+a_{2}t^{2})^{3}\equiv 0\operatorname{mod}t^{3}\end{array}\right\}\nonumber\\ \displaystyle & = & \displaystyle \left\{\!\begin{array}{@{}l@{}}(a_{0}+a_{1}t+a_{2}t^{2},b_{0}+b_{1}t+b_{2}t^{2})\\ \qquad \in \left(\mathbb{R}\{t\}/t^{3}\right)^{2}\!,\end{array}\begin{array}{@{}l@{}}a_{0}^{3}=b_{0}^{2},\\ 3a_{1}a_{0}^{2}=2b_{0}b_{1},\\ 3a_{0}^{2}a_{2}+3a_{0}a_{1}^{2}=2b_{0}b_{2}+b_{1}^{2}\end{array}\!\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{L}}_{1}(X) & = & \displaystyle \left\{\begin{array}{@{}l@{}}(a_{0}+a_{1}t,b_{0}+b_{1}t)\in \left(\mathbb{R}\{t\}/t^{2}\right)^{2}\!,\\ \hspace{75.60004pt}(b_{0}+b_{1}t)^{2}-(a_{0}+a_{1}t)^{3}\equiv 0\operatorname{mod}t^{2}\end{array}\right\}\nonumber\\ \displaystyle & = & \displaystyle \left\{(a_{0}+a_{1}t,b_{0}+b_{1}t)\in \left(\mathbb{R}\{t\}/t^{2}\right)^{2}\!,a_{0}^{3}=b_{0}^{2},3a_{1}a_{0}^{2}=2b_{0}b_{1}\right\}\nonumber\\ \displaystyle {\mathcal{L}}_{2}(X) & = & \displaystyle \left\{\begin{array}{@{}l@{}}(a_{0}+a_{1}t+a_{2}t^{2},b_{0}+b_{1}t+b_{2}t^{2})\in \left(\mathbb{R}\{t\}/t^{3}\right)^{2}\!,\\ \quad \quad \quad \quad \quad (b_{0}+b_{1}t+b_{2}t^{2})^{2}-(a_{0}+a_{1}t+a_{2}t^{2})^{3}\equiv 0\operatorname{mod}t^{3}\end{array}\right\}\nonumber\\ \displaystyle & = & \displaystyle \left\{\!\begin{array}{@{}l@{}}(a_{0}+a_{1}t+a_{2}t^{2},b_{0}+b_{1}t+b_{2}t^{2})\\ \qquad \in \left(\mathbb{R}\{t\}/t^{3}\right)^{2}\!,\end{array}\begin{array}{@{}l@{}}a_{0}^{3}=b_{0}^{2},\\ 3a_{1}a_{0}^{2}=2b_{0}b_{1},\\ 3a_{0}^{2}a_{2}+3a_{0}a_{1}^{2}=2b_{0}b_{2}+b_{1}^{2}\end{array}\!\right\}.\nonumber\end{eqnarray}$$
Then the preimage of
![]() $(0,t)\in {\mathcal{L}}_{1}(X)$
by
$(0,t)\in {\mathcal{L}}_{1}(X)$
by
![]() ${\it\pi}_{1}^{2}$
is obviously empty.
${\it\pi}_{1}^{2}$
is obviously empty.
We therefore take care not to confuse the set
![]() ${\mathcal{L}}_{n}(X)$
of
${\mathcal{L}}_{n}(X)$
of
![]() $n$
-jets on
$n$
-jets on
![]() $X$
and the set
$X$
and the set
![]() ${\it\pi}_{n}\left({\mathcal{L}}(X)\right)$
of
${\it\pi}_{n}\left({\mathcal{L}}(X)\right)$
of
![]() $n$
-jets on
$n$
-jets on
![]() $X$
which can be lifted to analytic arcs. Thanks to Hensel’s lemma and Artin approximation theorem [Reference Artin2], this phenomenon disappears in the nonsingular case.
$X$
which can be lifted to analytic arcs. Thanks to Hensel’s lemma and Artin approximation theorem [Reference Artin2], this phenomenon disappears in the nonsingular case.
Proposition 2.31. Let
![]() $X$
be an algebraic subset of
$X$
be an algebraic subset of
![]() $\mathbb{R}^{N}$
. The following are equivalent:
$\mathbb{R}^{N}$
. The following are equivalent:
-
(i) For all
 $n$
,
$n$
,
 ${\it\pi}_{n}^{n+1}:L_{n+1}(X)\rightarrow {\mathcal{L}}_{n}(X)$
is surjective.
${\it\pi}_{n}^{n+1}:L_{n+1}(X)\rightarrow {\mathcal{L}}_{n}(X)$
is surjective. -
(ii) For all
 $n$
,
$n$
,
 ${\it\pi}_{n}:{\mathcal{L}}(X)\rightarrow {\mathcal{L}}_{n}(X)$
is surjective.
${\it\pi}_{n}:{\mathcal{L}}(X)\rightarrow {\mathcal{L}}_{n}(X)$
is surjective. -
(iii)
 $X$
is nonsingular.
$X$
is nonsingular.
Proof.
(iii)
![]() $\Rightarrow$
(ii) is obvious using Hensel’s lemma and Artin approximation theorem [Reference Artin2].
$\Rightarrow$
(ii) is obvious using Hensel’s lemma and Artin approximation theorem [Reference Artin2].
(ii)
![]() $\Rightarrow$
(i) is obvious since
$\Rightarrow$
(i) is obvious since
![]() ${\it\pi}_{n}={\it\pi}_{n}^{n+1}\circ {\it\pi}_{n+1}$
.
${\it\pi}_{n}={\it\pi}_{n}^{n+1}\circ {\it\pi}_{n+1}$
.
(i)
![]() $\Rightarrow$
(iii): Assume that
$\Rightarrow$
(iii): Assume that
![]() $0$
is a singular point of
$0$
is a singular point of
![]() $X$
. We can find
$X$
. We can find
![]() ${\it\gamma}={\it\alpha}t\in {\mathcal{L}}_{1}(X)$
which does not lie in the tangent cone of
${\it\gamma}={\it\alpha}t\in {\mathcal{L}}_{1}(X)$
which does not lie in the tangent cone of
![]() $X$
at
$X$
at
![]() $0$
, that is, such that
$0$
, that is, such that
![]() $f({\it\alpha}t)\not \equiv 0\operatorname{mod}t^{m+1}$
for some
$f({\it\alpha}t)\not \equiv 0\operatorname{mod}t^{m+1}$
for some
![]() $f\in I(X)$
of order
$f\in I(X)$
of order
![]() $m$
. Such a
$m$
. Such a
![]() $1$
-jet cannot be lifted to
$1$
-jet cannot be lifted to
![]() ${\mathcal{L}}_{m}(X)$
.◻
${\mathcal{L}}_{m}(X)$
.◻
The set
![]() ${\mathcal{L}}_{n}(X)$
of
${\mathcal{L}}_{n}(X)$
of
![]() $n$
-jets on
$n$
-jets on
![]() $X\subset \mathbb{R}^{N}$
can be seen as a algebraic subset of
$X\subset \mathbb{R}^{N}$
can be seen as a algebraic subset of
![]() $\mathbb{R}^{(n+1)N}$
. By a theorem of Greenberg [Reference Greenberg16], given an algebraic subset
$\mathbb{R}^{(n+1)N}$
. By a theorem of Greenberg [Reference Greenberg16], given an algebraic subset
![]() $X\subset \mathbb{R}^{N}$
, there exists
$X\subset \mathbb{R}^{N}$
, there exists
![]() $c\in \mathbb{N}_{{>}0}$
such that for all
$c\in \mathbb{N}_{{>}0}$
such that for all
![]() $n\in \mathbb{N}$
,
$n\in \mathbb{N}$
,
![]() ${\it\pi}_{n}({\mathcal{L}}(X))={\it\pi}_{n}^{cn}({\mathcal{L}}_{cn}(X))$
. Then if we work over
${\it\pi}_{n}({\mathcal{L}}(X))={\it\pi}_{n}^{cn}({\mathcal{L}}_{cn}(X))$
. Then if we work over
![]() $\mathbb{C}$
the sets
$\mathbb{C}$
the sets
![]() ${\it\pi}_{n}({\mathcal{L}}(X))$
are Zariski-constructible by Chevalley theorem. See for instance [Reference Lejeune-Jalabert34]Footnote
7
, [Reference Gonzalez-Sprinberg and Lejeune-Jalabert15] or [Reference Denef and Loeser9].
${\it\pi}_{n}({\mathcal{L}}(X))$
are Zariski-constructible by Chevalley theorem. See for instance [Reference Lejeune-Jalabert34]Footnote
7
, [Reference Gonzalez-Sprinberg and Lejeune-Jalabert15] or [Reference Denef and Loeser9].
In our framework, the following example shows that the
![]() ${\it\pi}_{n}({\mathcal{L}}(X))$
may not even be
${\it\pi}_{n}({\mathcal{L}}(X))$
may not even be
![]() ${\mathcal{A}}{\mathcal{S}}$
.
${\mathcal{A}}{\mathcal{S}}$
.
Example 2.32. Let
![]() $X=V(x^{2}-zy^{2})$
. Then for every
$X=V(x^{2}-zy^{2})$
. Then for every
![]() $a\in \mathbb{R}$
,
$a\in \mathbb{R}$
,
![]() ${\it\gamma}_{a}(t)=(0,t^{2},at^{2})\in {\mathcal{L}}_{2}(X)$
. Let
${\it\gamma}_{a}(t)=(0,t^{2},at^{2})\in {\mathcal{L}}_{2}(X)$
. Let
![]() ${\it\eta}(t)=(bt^{3}+t^{4}{\it\eta}_{1}(t),t^{2}+t^{3}{\it\eta}_{2}(t),at^{2}+t^{3}{\it\eta}_{3}(t))\in {\mathcal{L}}(\mathbb{R}^{3})$
. Let
${\it\eta}(t)=(bt^{3}+t^{4}{\it\eta}_{1}(t),t^{2}+t^{3}{\it\eta}_{2}(t),at^{2}+t^{3}{\it\eta}_{3}(t))\in {\mathcal{L}}(\mathbb{R}^{3})$
. Let
![]() $f(x,y,z)=x^{2}-zy^{2}$
, then
$f(x,y,z)=x^{2}-zy^{2}$
, then
![]() $f({\it\eta}(t))=(b^{2}-a)t^{6}+t^{7}\tilde{{\it\eta}}(t)$
. So if
$f({\it\eta}(t))=(b^{2}-a)t^{6}+t^{7}\tilde{{\it\eta}}(t)$
. So if
![]() $a<0$
,
$a<0$
,
![]() ${\it\gamma}_{a}(t)\notin {\it\pi}_{2}({\mathcal{L}}(X))$
. However if
${\it\gamma}_{a}(t)\notin {\it\pi}_{2}({\mathcal{L}}(X))$
. However if
![]() $a\geqslant 0$
,
$a\geqslant 0$
,
![]() ${\it\gamma}_{a}(t)={\it\pi}_{2}(\sqrt{at}^{3},t^{2},at^{2})\in {\it\pi}_{2}({\mathcal{L}}(X))$
.
${\it\gamma}_{a}(t)={\it\pi}_{2}(\sqrt{at}^{3},t^{2},at^{2})\in {\it\pi}_{2}({\mathcal{L}}(X))$
.
Proposition 2.33. Let
![]() $X\subset \mathbb{R}^{N}$
be an algebraic subset of dimension
$X\subset \mathbb{R}^{N}$
be an algebraic subset of dimension
![]() $d$
. Then:
$d$
. Then:
-
(i)
 $\operatorname{dim}({\it\pi}_{n}({\mathcal{L}}(X)))=(n+1)d$
.
$\operatorname{dim}({\it\pi}_{n}({\mathcal{L}}(X)))=(n+1)d$
. -
(ii)
 $\operatorname{dim}({\mathcal{L}}_{n}(X))\geqslant (n+1)d$
.
$\operatorname{dim}({\mathcal{L}}_{n}(X))\geqslant (n+1)d$
. -
(iii) The fibers of
 $\tilde{{\it\pi}}_{n}^{m}={{\it\pi}_{n}^{m}}_{|{\it\pi}_{m}({\mathcal{L}}(X))}:{\it\pi}_{m}({\mathcal{L}}(X))\rightarrow {\it\pi}_{n}({\mathcal{L}}(X))$
are of dimension smaller than or equal to
$\tilde{{\it\pi}}_{n}^{m}={{\it\pi}_{n}^{m}}_{|{\it\pi}_{m}({\mathcal{L}}(X))}:{\it\pi}_{m}({\mathcal{L}}(X))\rightarrow {\it\pi}_{n}({\mathcal{L}}(X))$
are of dimension smaller than or equal to
 $(m-n)d$
where
$(m-n)d$
where
 $m\geqslant n$
.
$m\geqslant n$
. -
(iv) A fiber
 $({\it\pi}_{n}^{n+1})^{-1}({\it\gamma})$
of
$({\it\pi}_{n}^{n+1})^{-1}({\it\gamma})$
of
 ${\it\pi}_{n}^{n+1}:{\mathcal{L}}_{n+1}(X)\rightarrow {\mathcal{L}}_{n}(X)$
is either empty or isomorphic to
${\it\pi}_{n}^{n+1}:{\mathcal{L}}_{n+1}(X)\rightarrow {\mathcal{L}}_{n}(X)$
is either empty or isomorphic to
 $T_{{\it\gamma}(0)}^{\text{Zar}}X$
.
$T_{{\it\gamma}(0)}^{\text{Zar}}X$
.
If moreover we assume that
![]() $X$
is nonsingular, we get the following statement since
$X$
is nonsingular, we get the following statement since
![]() ${\mathcal{L}}_{n}(X)={\it\pi}_{n}({\mathcal{L}}(X))$
;
${\mathcal{L}}_{n}(X)={\it\pi}_{n}({\mathcal{L}}(X))$
;
-
(v)
 $\operatorname{dim}({\mathcal{L}}_{n}(X))=(n+1)d$
.
$\operatorname{dim}({\mathcal{L}}_{n}(X))=(n+1)d$
.
Proof. We first notice that (i) is a direct consequence of (iii).
(ii)
![]() $({\it\pi}_{0}^{n})^{-1}(X\setminus X_{\text{sing}})$
is of dimension
$({\it\pi}_{0}^{n})^{-1}(X\setminus X_{\text{sing}})$
is of dimension
![]() $(n+1)d$
since the fiber of
$(n+1)d$
since the fiber of
![]() ${\it\pi}_{0}^{n}$
over a nonsingular point is of dimension
${\it\pi}_{0}^{n}$
over a nonsingular point is of dimension
![]() $nd$
.
$nd$
.
(iii) We may assume that
![]() $m=n+1$
. Let
$m=n+1$
. Let
![]() ${\it\gamma}\in {\it\pi}_{n}({\mathcal{L}}(X))$
. We may assume that
${\it\gamma}\in {\it\pi}_{n}({\mathcal{L}}(X))$
. We may assume that
![]() ${\it\gamma}\in (\mathbb{R}_{n}[t])^{N}$
. We consider the following diagram
${\it\gamma}\in (\mathbb{R}_{n}[t])^{N}$
. We consider the following diagram
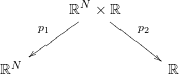
with
![]() $p_{1}(x,t)={\it\gamma}(t)+t^{n+1}x$
and
$p_{1}(x,t)={\it\gamma}(t)+t^{n+1}x$
and
![]() $p_{2}(x,t)=t$
. Let
$p_{2}(x,t)=t$
. Let
![]() $\mathfrak{X}=\overline{p_{1}^{-1}(X)\cap \{t\neq 0\}}^{\,Zar}$
. For
$\mathfrak{X}=\overline{p_{1}^{-1}(X)\cap \{t\neq 0\}}^{\,Zar}$
. For
![]() $c\neq 0$
,
$c\neq 0$
,
![]() $\mathfrak{X}\cap p_{2}^{-1}(c)\simeq X$
and
$\mathfrak{X}\cap p_{2}^{-1}(c)\simeq X$
and
![]() $\operatorname{dim}\mathfrak{X}\cap p_{2}^{-1}(c)=\operatorname{dim}\mathfrak{X}-1$
. Hence
$\operatorname{dim}\mathfrak{X}\cap p_{2}^{-1}(c)=\operatorname{dim}\mathfrak{X}-1$
. Hence
![]() $\operatorname{dim}\mathfrak{X}\cap p_{2}^{-1}(0)\leqslant \operatorname{dim}\mathfrak{X}-1=\operatorname{dim}X$
.
$\operatorname{dim}\mathfrak{X}\cap p_{2}^{-1}(0)\leqslant \operatorname{dim}\mathfrak{X}-1=\operatorname{dim}X$
.
We are looking for objects of the form
![]() ${\it\pi}_{n+1}({\it\gamma}(t)+t^{n+1}{\it\alpha}(t))$
with
${\it\pi}_{n+1}({\it\gamma}(t)+t^{n+1}{\it\alpha}(t))$
with
![]() ${\it\gamma}(t)+t^{n+1}{\it\alpha}(t)\in {\mathcal{L}}(X)$
. Such an
${\it\gamma}(t)+t^{n+1}{\it\alpha}(t)\in {\mathcal{L}}(X)$
. Such an
![]() ${\it\alpha}$
is equivalent to a section of
${\it\alpha}$
is equivalent to a section of
![]() ${p_{2}}_{|\mathfrak{X}}$
, that is,
${p_{2}}_{|\mathfrak{X}}$
, that is,
![]() $\begin{array}{@{}rcl@{}}\mathbb{R}\ & \rightarrow \ & \mathfrak{X}\\ ~\\ ~\\ t\ & \mapsto \ & ({\it\alpha}(t),t)\end{array}\!\!$
. Since we want an arc modulo
$\begin{array}{@{}rcl@{}}\mathbb{R}\ & \rightarrow \ & \mathfrak{X}\\ ~\\ ~\\ t\ & \mapsto \ & ({\it\alpha}(t),t)\end{array}\!\!$
. Since we want an arc modulo
![]() $t^{n+2}$
, we are looking for the constant term of
$t^{n+2}$
, we are looking for the constant term of
![]() ${\it\alpha}$
, therefore
${\it\alpha}$
, therefore
![]() $(\tilde{{\it\pi}}_{n}^{n+1})^{-1}({\it\gamma})\subset \mathfrak{X}\cap p_{2}^{-1}(0)$
.
$(\tilde{{\it\pi}}_{n}^{n+1})^{-1}({\it\gamma})\subset \mathfrak{X}\cap p_{2}^{-1}(0)$
.
(iv) Let
![]() ${\it\gamma}\in {\mathcal{L}}_{n}(X)$
. Let
${\it\gamma}\in {\mathcal{L}}_{n}(X)$
. Let
![]() ${\it\eta}\in \mathbb{R}^{N}$
. Assume that
${\it\eta}\in \mathbb{R}^{N}$
. Assume that
![]() $I(X)=(f_{1},\ldots ,f_{r})$
. By Taylor expansion we get
$I(X)=(f_{1},\ldots ,f_{r})$
. By Taylor expansion we get
Assume that
![]() $f_{i}({\it\gamma}(t))\equiv t^{n+1}{\it\alpha}_{i}\operatorname{mod}t^{n+2}$
. Since
$f_{i}({\it\gamma}(t))\equiv t^{n+1}{\it\alpha}_{i}\operatorname{mod}t^{n+2}$
. Since
we have
Hence,
![]() ${\it\gamma}(t)+t^{n+1}{\it\eta}$
is in the fiber
${\it\gamma}(t)+t^{n+1}{\it\eta}$
is in the fiber
![]() $({\it\pi}_{n}^{n+1})^{-1}({\it\gamma})$
if and only if
$({\it\pi}_{n}^{n+1})^{-1}({\it\gamma})$
if and only if
![]() ${\it\alpha}_{i}+({\rm\nabla}_{{\it\gamma}(0)}f_{i})({\it\eta})=0,i=1,\ldots ,r$
.◻
${\it\alpha}_{i}+({\rm\nabla}_{{\it\gamma}(0)}f_{i})({\it\eta})=0,i=1,\ldots ,r$
.◻
An arc-analytic map
![]() $f:X\rightarrow Y$
induces a map
$f:X\rightarrow Y$
induces a map
![]() $f_{\ast }:{\mathcal{L}}(X)\rightarrow {\mathcal{L}}(Y)$
. Moreover, if
$f_{\ast }:{\mathcal{L}}(X)\rightarrow {\mathcal{L}}(Y)$
. Moreover, if
![]() $f:X\rightarrow Y$
is analytic, then we also have maps at the level of
$f:X\rightarrow Y$
is analytic, then we also have maps at the level of
![]() $n$
-jets
$n$
-jets
![]() $f_{\ast n}:{\mathcal{L}}_{n}(X)\rightarrow {\mathcal{L}}_{n}(Y)$
such that the following diagram commutes
$f_{\ast n}:{\mathcal{L}}_{n}(X)\rightarrow {\mathcal{L}}_{n}(Y)$
such that the following diagram commutes
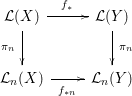
In particular, if
![]() $X$
is nonsingular,
$X$
is nonsingular,
![]() $\operatorname{Im}f_{\ast n}\subset {\it\pi}_{n}\left({\mathcal{L}}(Y)\right)$
since
$\operatorname{Im}f_{\ast n}\subset {\it\pi}_{n}\left({\mathcal{L}}(Y)\right)$
since
![]() ${\it\pi}_{n}:{\mathcal{L}}(X)\rightarrow {\mathcal{L}}_{n}(X)$
is surjective.
${\it\pi}_{n}:{\mathcal{L}}(X)\rightarrow {\mathcal{L}}_{n}(X)$
is surjective.
For
![]() $M$
a nonsingular algebraic set and
$M$
a nonsingular algebraic set and
![]() ${\it\sigma}:M\rightarrow X\subset \mathbb{R}^{N}$
analytic, we define
${\it\sigma}:M\rightarrow X\subset \mathbb{R}^{N}$
analytic, we define
![]() $\operatorname{Jac}_{{\it\sigma}}(x)$
the Jacobian matrix of
$\operatorname{Jac}_{{\it\sigma}}(x)$
the Jacobian matrix of
![]() ${\it\sigma}$
at
${\it\sigma}$
at
![]() $x$
with respect to a coordinate system at
$x$
with respect to a coordinate system at
![]() $x$
in
$x$
in
![]() $M$
. For
$M$
. For
![]() ${\it\gamma}$
an arc on
${\it\gamma}$
an arc on
![]() $M$
with origin
$M$
with origin
![]() ${\it\gamma}(0)=x$
, we define the order of vanishing of
${\it\gamma}(0)=x$
, we define the order of vanishing of
![]() ${\it\gamma}$
along
${\it\gamma}$
along
![]() $\operatorname{Jac}_{{\it\sigma}}$
by
$\operatorname{Jac}_{{\it\sigma}}$
by
![]() $\operatorname{ord}_{t}\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))=\min \{\operatorname{ord}_{t}{\it\delta}({\it\gamma}(t)),\text{for all }{\it\delta}\text{ being a }m\text{-minor of }\operatorname{Jac}_{{\it\sigma}}\}$
where
$\operatorname{ord}_{t}\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))=\min \{\operatorname{ord}_{t}{\it\delta}({\it\gamma}(t)),\text{for all }{\it\delta}\text{ being a }m\text{-minor of }\operatorname{Jac}_{{\it\sigma}}\}$
where
![]() $m=\min (d,N)$
and
$m=\min (d,N)$
and
![]() ${\it\gamma}$
is expressed in the local coordinate system. This order of vanishing is independent of the choice of the coordinate system.
${\it\gamma}$
is expressed in the local coordinate system. This order of vanishing is independent of the choice of the coordinate system.
The critical locus of
![]() ${\it\sigma}$
is
${\it\sigma}$
is
![]() $C_{{\it\sigma}}=\{x\in M,{\it\delta}(x)=0,\text{for all }{\it\delta}\text{ being a }m-\text{minor of }\operatorname{Jac}_{{\it\sigma}}\}$
. If
$C_{{\it\sigma}}=\{x\in M,{\it\delta}(x)=0,\text{for all }{\it\delta}\text{ being a }m-\text{minor of }\operatorname{Jac}_{{\it\sigma}}\}$
. If
![]() $E\subset M$
is locally described by an equation
$E\subset M$
is locally described by an equation
![]() $f=0$
around
$f=0$
around
![]() $x$
and if
$x$
and if
![]() ${\it\gamma}$
is an arc with origin
${\it\gamma}$
is an arc with origin
![]() ${\it\gamma}(0)=x$
then
${\it\gamma}(0)=x$
then
![]() $\operatorname{ord}_{{\it\gamma}}E=\operatorname{ord}_{t}f({\it\gamma}(t))$
.
$\operatorname{ord}_{{\it\gamma}}E=\operatorname{ord}_{t}f({\it\gamma}(t))$
.
3 The main theorem
Lemma 3.1. Let
![]() $X$
be an algebraic subset of
$X$
be an algebraic subset of
![]() $\mathbb{R}^{N}$
and
$\mathbb{R}^{N}$
and
![]() $f:X\rightarrow X$
a blow-Nash map. Let
$f:X\rightarrow X$
a blow-Nash map. Let
![]() ${\it\sigma}:M\rightarrow X$
be a sequence of blowings-up with nonsingular centers such that
${\it\sigma}:M\rightarrow X$
be a sequence of blowings-up with nonsingular centers such that
![]() $\tilde{{\it\sigma}}=f\circ {\it\sigma}:M\rightarrow X$
is Nash.
$\tilde{{\it\sigma}}=f\circ {\it\sigma}:M\rightarrow X$
is Nash.
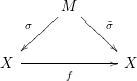
After adding more blowings-up, we may assume that the critical loci of
![]() ${\it\sigma}$
and
${\it\sigma}$
and
![]() $\tilde{{\it\sigma}}$
are simultaneously normal crossing and denote them by
$\tilde{{\it\sigma}}$
are simultaneously normal crossing and denote them by
![]() $\sum _{i\in I}{\it\nu}_{i}E_{i}$
and
$\sum _{i\in I}{\it\nu}_{i}E_{i}$
and
![]() $\sum _{i\in I}\tilde{{\it\nu}}_{i}E_{i}$
.
$\sum _{i\in I}\tilde{{\it\nu}}_{i}E_{i}$
.
Then the property
does not depend on the choice of
![]() ${\it\sigma}$
.
${\it\sigma}$
.
Proof. Given
![]() ${\it\sigma}_{1}$
and
${\it\sigma}_{1}$
and
![]() ${\it\sigma}_{2}$
as in the statement and using Hironaka flattening theorem [Reference Hironaka21] (which works as it is in the real algebraic case), there exist
${\it\sigma}_{2}$
as in the statement and using Hironaka flattening theorem [Reference Hironaka21] (which works as it is in the real algebraic case), there exist
![]() ${\it\pi}_{1}$
and
${\it\pi}_{1}$
and
![]() ${\it\pi}_{2}$
regular such that the following diagram commutes:
${\it\pi}_{2}$
regular such that the following diagram commutes:
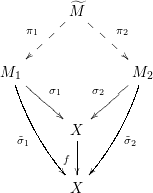
The relation 1 means exactly that the Jacobian ideal of
![]() ${\it\sigma}_{i}$
is included in the Jacobian ideal of
${\it\sigma}_{i}$
is included in the Jacobian ideal of
![]() $\tilde{{\it\sigma}}_{i}$
. By the chain rule, the relations at the level
$\tilde{{\it\sigma}}_{i}$
. By the chain rule, the relations at the level
![]() $M_{i}$
are preserved in
$M_{i}$
are preserved in
![]() $\widetilde{M}$
. Again by the chain rule and since the previous diagram commutes, the relations in
$\widetilde{M}$
. Again by the chain rule and since the previous diagram commutes, the relations in
![]() $M_{1}$
and
$M_{1}$
and
![]() $M_{2}$
must coincide.◻
$M_{2}$
must coincide.◻
Definition 3.2. We say that a map
![]() $f:X\rightarrow X$
as in Lemma 3.1 verifying the relation (1) satisfies the Jacobian hypothesis.
$f:X\rightarrow X$
as in Lemma 3.1 verifying the relation (1) satisfies the Jacobian hypothesis.
Question 3.3. May we find a geometric interpretation of this hypothesis?
The following example is a direct consequence of the chain rule.
Example 3.4. Let
![]() $X$
be a nonsingular algebraic set and
$X$
be a nonsingular algebraic set and
![]() $f:X\rightarrow X$
a regular map satisfying
$f:X\rightarrow X$
a regular map satisfying
![]() $|\operatorname{det}\text{d}f|>c$
for a constant
$|\operatorname{det}\text{d}f|>c$
for a constant
![]() $c>0$
, then
$c>0$
, then
![]() $f$
satisfies the Jacobian hypothesis.
$f$
satisfies the Jacobian hypothesis.
Theorem 3.5. (Main theorem)
Let
![]() $X$
be an algebraic subset of
$X$
be an algebraic subset of
![]() $\mathbb{R}^{N}$
and
$\mathbb{R}^{N}$
and
![]() $f:X\rightarrow X$
a semialgebraic homeomorphism (for the Euclidean topology). If
$f:X\rightarrow X$
a semialgebraic homeomorphism (for the Euclidean topology). If
![]() $f$
is blow-Nash and satisfies the Jacobian hypothesis then
$f$
is blow-Nash and satisfies the Jacobian hypothesis then
![]() $f^{-1}$
is blow-Nash and satisfies the Jacobian hypothesis too.
$f^{-1}$
is blow-Nash and satisfies the Jacobian hypothesis too.
By Lemma 2.23 and Proposition 2.27, if
![]() $X$
is a nonsingular algebraic subset we get the following corollary.
$X$
is a nonsingular algebraic subset we get the following corollary.
Corollary 3.6. [Reference Fukui, Kurdyka and Parusiński13]
Let
![]() $X$
be a nonsingular algebraic subset and
$X$
be a nonsingular algebraic subset and
![]() $f:X\rightarrow X$
a semialgebraic homeomorphism (for the Euclidean topology). If
$f:X\rightarrow X$
a semialgebraic homeomorphism (for the Euclidean topology). If
![]() $f$
is arc-analytic and if there exists
$f$
is arc-analytic and if there exists
![]() $c>0$
satisfying
$c>0$
satisfying
![]() $|\operatorname{det}\text{d}f|>c$
then
$|\operatorname{det}\text{d}f|>c$
then
![]() $f^{-1}$
is arc-analytic and there exists
$f^{-1}$
is arc-analytic and there exists
![]() $\tilde{c}>0$
satisfying
$\tilde{c}>0$
satisfying
![]() $|\operatorname{det}\text{d}f^{-1}|>\tilde{c}$
.
$|\operatorname{det}\text{d}f^{-1}|>\tilde{c}$
.
Remark 3.7. We recover [Reference Fukui, Kurdyka and Parusiński13, Theorem 1.1] using the last corollary and [Reference Fukui, Kurdyka and Parusiński13, Corollaries 2.2 and 2.3].
4 Proof of the main theorem
4.1 Change of variables
An algebraic version of the following lemma was already known in [Reference Elkik10], [Reference Popescu43] or [Reference Popescu44, Section 2] with a proof in [Reference Swan48, 4.1]. The statement given below is more geometric and the proof is quite elementary.
Lemma 4.1. Let
![]() $X$
be a
$X$
be a
![]() $d$
-dimensional algebraic subset of
$d$
-dimensional algebraic subset of
![]() $\mathbb{R}^{N}$
. We consider the following ideal of
$\mathbb{R}^{N}$
. We consider the following ideal of
![]() $\mathbb{R}[x_{1},\ldots ,x_{N}]$
$\mathbb{R}[x_{1},\ldots ,x_{N}]$
where
![]() ${\rm\Delta}(f_{1},\ldots ,f_{N-d})$
is the ideal generated by the
${\rm\Delta}(f_{1},\ldots ,f_{N-d})$
is the ideal generated by the
![]() $(N-d)$
-minors of the matrix
$(N-d)$
-minors of the matrix
![]() $\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
. Then
$\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
. Then
![]() $V(H)$
is the singular locusFootnote
8
$V(H)$
is the singular locusFootnote
8
![]() $X_{\text{sing}}$
of
$X_{\text{sing}}$
of
![]() $X$
.
$X$
.
Proof. Let
![]() $x\notin V(H)$
then there exist
$x\notin V(H)$
then there exist
![]() $f_{1},\ldots ,f_{N-d}\in I(X)$
,
$f_{1},\ldots ,f_{N-d}\in I(X)$
,
![]() ${\it\delta}$
a
${\it\delta}$
a
![]() $(N-d)$
-minor of
$(N-d)$
-minor of
![]() $\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
and
$\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
and
![]() $h\in \mathbb{R}[x_{1},\ldots ,x_{N}]$
with
$h\in \mathbb{R}[x_{1},\ldots ,x_{N}]$
with
![]() $hI(X)\subset (f_{1},\ldots ,f_{N-d})$
and
$hI(X)\subset (f_{1},\ldots ,f_{N-d})$
and
![]() $h{\it\delta}(x)\neq 0$
. Since
$h{\it\delta}(x)\neq 0$
. Since
![]() ${\it\delta}(x)\neq 0$
,
${\it\delta}(x)\neq 0$
,
![]() $x$
is a nonsingular point of
$x$
is a nonsingular point of
![]() $V(f_{1},\ldots ,f_{N-d})$
. Furthermore we have
$V(f_{1},\ldots ,f_{N-d})$
. Furthermore we have
![]() $X=V(I(X))\subset V(f_{1},\ldots ,f_{N-d})\subset V(hI(X))$
and, since
$X=V(I(X))\subset V(f_{1},\ldots ,f_{N-d})\subset V(hI(X))$
and, since
![]() $h(x)\neq 0$
, in an open neighborhood
$h(x)\neq 0$
, in an open neighborhood
![]() $U$
of
$U$
of
![]() $x$
in
$x$
in
![]() $\mathbb{R}^{N}$
we have
$\mathbb{R}^{N}$
we have
![]() $V(hI(X))\cap U=X\cap U$
. Hence
$V(hI(X))\cap U=X\cap U$
. Hence
![]() $V(f_{1},\ldots ,f_{N-d})\cap U=X\cap U$
. So
$V(f_{1},\ldots ,f_{N-d})\cap U=X\cap U$
. So
![]() $x$
is a nonsingular point of
$x$
is a nonsingular point of
![]() $X$
by [Reference Bochnak, Coste and Roy8, Proposition 3.3.10]. We proved that
$X$
by [Reference Bochnak, Coste and Roy8, Proposition 3.3.10]. We proved that
![]() $X_{\text{sing}}\subset V(H)$
.
$X_{\text{sing}}\subset V(H)$
.
Now, assume that
![]() $x\in X\setminus X_{\text{sing}}$
. With the notation of [Reference Bochnak, Coste and Roy8, Section 3], the local ring
$x\in X\setminus X_{\text{sing}}$
. With the notation of [Reference Bochnak, Coste and Roy8, Section 3], the local ring
![]() ${\mathcal{R}}_{X,x}={\mathcal{R}}_{\mathbb{R}^{N},x}/I(X){\mathcal{R}}_{\mathbb{R}^{N},x}$
is regular, so we may find a regular system of parameters
${\mathcal{R}}_{X,x}={\mathcal{R}}_{\mathbb{R}^{N},x}/I(X){\mathcal{R}}_{\mathbb{R}^{N},x}$
is regular, so we may find a regular system of parameters
![]() $(f_{1},\ldots ,f_{N})$
of
$(f_{1},\ldots ,f_{N})$
of
![]() ${\mathcal{R}}_{X,x}$
such that
${\mathcal{R}}_{X,x}$
such that
![]() $I(X){\mathcal{R}}_{\mathbb{R}^{N},x}=(f_{1},\ldots ,f_{N-d}){\mathcal{R}}_{\mathbb{R}^{N},x}$
by [Reference Kunz25, VI.1.8 and VI.1.10]Footnote
9
(see also [Reference Bochnak, Coste and Roy8, Proposition 3.3.7]). Moreover, we may assume that the
$I(X){\mathcal{R}}_{\mathbb{R}^{N},x}=(f_{1},\ldots ,f_{N-d}){\mathcal{R}}_{\mathbb{R}^{N},x}$
by [Reference Kunz25, VI.1.8 and VI.1.10]Footnote
9
(see also [Reference Bochnak, Coste and Roy8, Proposition 3.3.7]). Moreover, we may assume that the
![]() $f_{1},\ldots ,f_{N-d}$
are polynomials. We may use the following classical argument.
$f_{1},\ldots ,f_{N-d}$
are polynomials. We may use the following classical argument.
![]() ${\it\theta}:\mathbb{R}[x_{1},\ldots ,x_{N}]\rightarrow \mathbb{R}^{N}$
defined by
${\it\theta}:\mathbb{R}[x_{1},\ldots ,x_{N}]\rightarrow \mathbb{R}^{N}$
defined by
![]() $f\mapsto f(x)$
induces an isomorphism
$f\mapsto f(x)$
induces an isomorphism
![]() ${\it\theta}^{\prime }:\mathfrak{m}_{x}/\mathfrak{m}_{x}^{2}\rightarrow \mathbb{R}^{N}$
. Then
${\it\theta}^{\prime }:\mathfrak{m}_{x}/\mathfrak{m}_{x}^{2}\rightarrow \mathbb{R}^{N}$
. Then
![]() $\operatorname{rk}\left(\frac{\partial f_{i}}{\partial x_{j}}(x)\right)=\operatorname{dim}{\it\theta}((f_{1},\ldots ,f_{N-d}))$
which is, by
$\operatorname{rk}\left(\frac{\partial f_{i}}{\partial x_{j}}(x)\right)=\operatorname{dim}{\it\theta}((f_{1},\ldots ,f_{N-d}))$
which is, by
![]() ${\it\theta}^{\prime }$
, the dimension of
${\it\theta}^{\prime }$
, the dimension of
![]() $((f_{1},\ldots ,f_{N-d})+\mathfrak{m}_{x}^{2})/\mathfrak{m}_{x}^{2}$
as a subspace of
$((f_{1},\ldots ,f_{N-d})+\mathfrak{m}_{x}^{2})/\mathfrak{m}_{x}^{2}$
as a subspace of
![]() $\mathfrak{m}_{x}/\mathfrak{m}_{x}^{2}$
. If we denote by
$\mathfrak{m}_{x}/\mathfrak{m}_{x}^{2}$
. If we denote by
![]() $\mathfrak{m}$
the maximal ideal of
$\mathfrak{m}$
the maximal ideal of
![]() ${\mathcal{R}}_{X,x}=\left(\mathbb{R}[x_{1},\ldots ,x_{N}]/(f_{1},\ldots ,f_{N-d})\right)_{\mathfrak{m}_{x}}$
, we have
${\mathcal{R}}_{X,x}=\left(\mathbb{R}[x_{1},\ldots ,x_{N}]/(f_{1},\ldots ,f_{N-d})\right)_{\mathfrak{m}_{x}}$
, we have
![]() $\mathfrak{m}/\mathfrak{m}^{2}\simeq \mathfrak{m}_{x}/((f_{1},\ldots ,f_{N-d})+\mathfrak{m}_{x}^{2})$
. So we have
$\mathfrak{m}/\mathfrak{m}^{2}\simeq \mathfrak{m}_{x}/((f_{1},\ldots ,f_{N-d})+\mathfrak{m}_{x}^{2})$
. So we have
![]() $\operatorname{dim}\left(\mathfrak{m}/\mathfrak{m}^{2}\right)+\operatorname{rk}\left(\frac{\partial f_{i}}{\partial x_{j}}(x)\right)=N$
.
$\operatorname{dim}\left(\mathfrak{m}/\mathfrak{m}^{2}\right)+\operatorname{rk}\left(\frac{\partial f_{i}}{\partial x_{j}}(x)\right)=N$
.
Furthermore, since
![]() ${\mathcal{R}}_{X,x}$
is a
${\mathcal{R}}_{X,x}$
is a
![]() $d$
-dimensional regular local ring,
$d$
-dimensional regular local ring,
![]() $\operatorname{dim}\left(\mathfrak{m}/\mathfrak{m}^{2}\right)=d$
. Hence
$\operatorname{dim}\left(\mathfrak{m}/\mathfrak{m}^{2}\right)=d$
. Hence
![]() $\left(\frac{\partial f_{i}}{\partial x_{j}}(x)\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
is of rank
$\left(\frac{\partial f_{i}}{\partial x_{j}}(x)\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
is of rank
![]() $N-d$
and so there exists
$N-d$
and so there exists
![]() ${\it\delta}$
a
${\it\delta}$
a
![]() $(N-d)$
-minor of
$(N-d)$
-minor of
![]() $\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
such that
$\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
such that
![]() ${\it\delta}(x)\neq 0$
. Assume that
${\it\delta}(x)\neq 0$
. Assume that
![]() $I(X)=(g_{1},\ldots ,g_{r})$
in
$I(X)=(g_{1},\ldots ,g_{r})$
in
![]() $\mathbb{R}[x_{1},\ldots ,x_{N}]$
. Then
$\mathbb{R}[x_{1},\ldots ,x_{N}]$
. Then
![]() $g_{i}=\sum \frac{f_{j}}{q_{j}}$
with
$g_{i}=\sum \frac{f_{j}}{q_{j}}$
with
![]() $q_{j}(x)\neq 0$
, so
$q_{j}(x)\neq 0$
, so
![]() $g_{i}h_{i}\subset (f_{1},\ldots ,f_{N-d})$
with
$g_{i}h_{i}\subset (f_{1},\ldots ,f_{N-d})$
with
![]() $h_{i}=\prod q_{j}$
. Then
$h_{i}=\prod q_{j}$
. Then
![]() $h=\prod h_{i}$
satisfies
$h=\prod h_{i}$
satisfies
![]() $h(x)\neq 0$
and
$h(x)\neq 0$
and
![]() $hI(X)\subset (f_{1},\ldots ,f_{N-d})$
. So
$hI(X)\subset (f_{1},\ldots ,f_{N-d})$
. So
![]() $x\notin V(H)$
. Hence
$x\notin V(H)$
. Hence
![]() $V(H)\subset X_{\text{sing}}\cup (\mathbb{R}^{N}\setminus X)$
.
$V(H)\subset X_{\text{sing}}\cup (\mathbb{R}^{N}\setminus X)$
.
To complete the proof, it remains to prove that
![]() $V(H)\subset X$
. Let
$V(H)\subset X$
. Let
![]() $x\notin X$
. There exist
$x\notin X$
. There exist
![]() $f_{1},\ldots ,f_{N-d}\in I(X)$
such that
$f_{1},\ldots ,f_{N-d}\in I(X)$
such that
![]() $f_{i}(x)\neq 0$
. We construct by induction
$f_{i}(x)\neq 0$
. We construct by induction
![]() $N-d$
polynomials of the form
$N-d$
polynomials of the form
![]() $g_{i}=a_{i}f_{i}$
with
$g_{i}=a_{i}f_{i}$
with
![]() $g_{i}(x)\neq 0$
and
$g_{i}(x)\neq 0$
and
![]() $(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{N-d})_{x}\neq 0$
. Suppose that
$(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{N-d})_{x}\neq 0$
. Suppose that
![]() $g_{1},\ldots ,g_{j-1}$
are constructed, if
$g_{1},\ldots ,g_{j-1}$
are constructed, if
![]() $(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}f_{j})_{x}\neq 0$
, we can take
$(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}f_{j})_{x}\neq 0$
, we can take
![]() $a_{j}=1$
, so we may assume that
$a_{j}=1$
, so we may assume that
![]() $(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}f_{j})_{x}=0$
. Then we just have to take some
$(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}f_{j})_{x}=0$
. Then we just have to take some
![]() $a_{j}$
satisfying
$a_{j}$
satisfying
![]() $(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}a_{j})_{x}\neq 0$
and
$(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}a_{j})_{x}\neq 0$
and
![]() $a_{j}(x)\neq 0$
since
$a_{j}(x)\neq 0$
since
![]() $(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}(a_{j}f_{j}))_{x}=f_{j}(x)(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}a_{j})_{x}$
. Then we have
$(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}(a_{j}f_{j}))_{x}=f_{j}(x)(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}a_{j})_{x}$
. Then we have
![]() $g_{1},\ldots ,g_{N-d}\in I(X)$
whose a
$g_{1},\ldots ,g_{N-d}\in I(X)$
whose a
![]() $(N-d)$
-minor
$(N-d)$
-minor
![]() ${\it\delta}$
satisfies
${\it\delta}$
satisfies
![]() ${\it\delta}(x)\neq 0$
. Moreover we have
${\it\delta}(x)\neq 0$
. Moreover we have
![]() $g_{i}(x)\neq 0$
and
$g_{i}(x)\neq 0$
and
![]() $g_{i}I\subset (g_{1},\ldots ,g_{N-d})$
. So
$g_{i}I\subset (g_{1},\ldots ,g_{N-d})$
. So
![]() $x\notin V(H)$
.◻
$x\notin V(H)$
.◻
Definition 4.2. Let
![]() $X$
be an algebraic subset of
$X$
be an algebraic subset of
![]() $\mathbb{R}^{N}$
. For
$\mathbb{R}^{N}$
. For
![]() $e\in \mathbb{N}$
, we set
$e\in \mathbb{N}$
, we set
where
![]() $H$
is defined in Lemma 4.1.
$H$
is defined in Lemma 4.1.
Remark 4.3.
![]() ${\mathcal{L}}(X)=\left(\bigcup _{e\in \mathbb{N}}{\mathcal{L}}^{(e)}(X)\right)\sqcup {\mathcal{L}}(X_{\text{sing}})$
${\mathcal{L}}(X)=\left(\bigcup _{e\in \mathbb{N}}{\mathcal{L}}^{(e)}(X)\right)\sqcup {\mathcal{L}}(X_{\text{sing}})$
Remark 4.4. In [Reference Denef and Loeser9], Denef–Loeser set
![]() ${\mathcal{L}}^{(e)}(X)={\mathcal{L}}(X)\setminus {\it\pi}_{e}^{-1}({\mathcal{L}}_{e}(X_{\text{sing}}))$
and used the Nullstellensatz to get that
${\mathcal{L}}^{(e)}(X)={\mathcal{L}}(X)\setminus {\it\pi}_{e}^{-1}({\mathcal{L}}_{e}(X_{\text{sing}}))$
and used the Nullstellensatz to get that
![]() $I(X_{\text{sing}})^{c}\subset H$
for some
$I(X_{\text{sing}})^{c}\subset H$
for some
![]() $c$
since
$c$
since
![]() $X_{\text{sing}}=V(H)$
. Since we cannot do that in our case, we defined differently
$X_{\text{sing}}=V(H)$
. Since we cannot do that in our case, we defined differently
![]() ${\mathcal{L}}^{(e)}(X)$
.
${\mathcal{L}}^{(e)}(X)$
.
The following lemma is an adaptation of Denef–Loeser key lemma [Reference Denef and Loeser9, Lemma 3.4] to fulfill our settings. The aim of the above-mentioned lemma is to prove a generalization of Kontsevich’s birational transformation rule (change of variables) of [Reference Kontsevich24] to handle singularities. We can find a first adaption to our settings in the nonsingular case in [Reference Koike and Parusiński23, Lemma 4.2].
Lemma 4.5. Let
![]() ${\it\sigma}:M\rightarrow X$
be a proper genericallyFootnote
10
one-to-one Nash map where
${\it\sigma}:M\rightarrow X$
be a proper genericallyFootnote
10
one-to-one Nash map where
![]() $M$
is a nonsingular algebraic subset of
$M$
is a nonsingular algebraic subset of
![]() $\mathbb{R}^{p}$
of dimension
$\mathbb{R}^{p}$
of dimension
![]() $d$
and
$d$
and
![]() $X$
an algebraic subset of
$X$
an algebraic subset of
![]() $\mathbb{R}^{N}$
of dimension
$\mathbb{R}^{N}$
of dimension
![]() $d$
. For
$d$
. For
![]() $e,e^{\prime }\in \mathbb{N}$
, we set
$e,e^{\prime }\in \mathbb{N}$
, we set
For
![]() $n\in \mathbb{N}$
, let
$n\in \mathbb{N}$
, let
![]() ${\rm\Delta}_{e,e^{\prime },n}$
be the image of
${\rm\Delta}_{e,e^{\prime },n}$
be the image of
![]() ${\rm\Delta}_{e,e^{\prime }}$
by
${\rm\Delta}_{e,e^{\prime }}$
by
![]() ${\it\pi}_{n}$
. Let
${\it\pi}_{n}$
. Let
![]() $e,e^{\prime },n\in \mathbb{N}$
with
$e,e^{\prime },n\in \mathbb{N}$
with
![]() $n\geqslant \operatorname{max}(2e,e^{\prime })$
, then:
$n\geqslant \operatorname{max}(2e,e^{\prime })$
, then:
-
(i) Given
 ${\it\gamma}\in {\rm\Delta}_{e,e^{\prime }}$
and
${\it\gamma}\in {\rm\Delta}_{e,e^{\prime }}$
and
 ${\it\delta}\in {\mathcal{L}}(X)$
with
${\it\delta}\in {\mathcal{L}}(X)$
with
 ${\it\sigma}_{\ast }({\it\gamma})\equiv {\it\delta}\operatorname{mod}t^{n+1}$
there exists a unique
${\it\sigma}_{\ast }({\it\gamma})\equiv {\it\delta}\operatorname{mod}t^{n+1}$
there exists a unique
 ${\it\eta}\in {\mathcal{L}}(M)$
such that
${\it\eta}\in {\mathcal{L}}(M)$
such that
 ${\it\sigma}_{\ast }({\it\eta})={\it\delta}$
and
${\it\sigma}_{\ast }({\it\eta})={\it\delta}$
and
 ${\it\eta}\equiv {\it\gamma}\operatorname{mod}t^{n-e+1}$
.
${\it\eta}\equiv {\it\gamma}\operatorname{mod}t^{n-e+1}$
. -
(ii) Let
 ${\it\gamma},{\it\eta}\in {\mathcal{L}}(M)$
. If
${\it\gamma},{\it\eta}\in {\mathcal{L}}(M)$
. If
 ${\it\gamma}\in {\rm\Delta}_{e,e^{\prime }}$
and
${\it\gamma}\in {\rm\Delta}_{e,e^{\prime }}$
and
 ${\it\sigma}({\it\gamma})\equiv {\it\sigma}({\it\eta})\operatorname{mod}t^{n+1}$
then
${\it\sigma}({\it\gamma})\equiv {\it\sigma}({\it\eta})\operatorname{mod}t^{n+1}$
then
 ${\it\gamma}\equiv {\it\eta}\operatorname{mod}t^{n-e+1}$
and
${\it\gamma}\equiv {\it\eta}\operatorname{mod}t^{n-e+1}$
and
 ${\it\eta}\in {\rm\Delta}_{e,e^{\prime }}$
.
${\it\eta}\in {\rm\Delta}_{e,e^{\prime }}$
. -
(iii) The set
 ${\rm\Delta}_{e,e^{\prime },n}$
is a union of fibers of
${\rm\Delta}_{e,e^{\prime },n}$
is a union of fibers of
 ${\it\sigma}_{\ast n}$
.
${\it\sigma}_{\ast n}$
. -
(iv)
 ${\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$
is constructible and
${\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$
is constructible and
 ${\it\sigma}_{\ast n|{\rm\Delta}_{e,e^{\prime },n}}:{\rm\Delta}_{e,e^{\prime },n}\rightarrow {\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$
is a piecewise trivial fibrationFootnote
11
with fiber
${\it\sigma}_{\ast n|{\rm\Delta}_{e,e^{\prime },n}}:{\rm\Delta}_{e,e^{\prime },n}\rightarrow {\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$
is a piecewise trivial fibrationFootnote
11
with fiber
 $\mathbb{R}^{e}$
.
$\mathbb{R}^{e}$
.
Remark 4.6. It is natural to use Taylor expansion to prove some approximation theorems concerning power series as we are going to do for 4.5
(i). For instance, we may find similar argument in [Reference Greenberg16], [Reference Artin3], or [Reference Elkik10]. For 4.5
(i), we will follow the proof of [Reference Denef and Loeser9, Lemma 3.4] with some differences to match our framework. Concerning 4.5
(iv), we cannot use anymore the section argument of [Reference Denef and Loeser9] since
![]() ${\it\sigma}$
is not assumed to be birational.
${\it\sigma}$
is not assumed to be birational.
Lemma 4.7. (Reduction to complete intersection)
Let
![]() $X$
be an algebraic subset of
$X$
be an algebraic subset of
![]() $\mathbb{R}^{N}$
of dimension
$\mathbb{R}^{N}$
of dimension
![]() $d$
. For each
$d$
. For each
![]() $e\in \mathbb{N}$
,
$e\in \mathbb{N}$
,
![]() ${\mathcal{L}}^{(e)}(X)$
is covered by a finite number of sets of the form
${\mathcal{L}}^{(e)}(X)$
is covered by a finite number of sets of the form
with
![]() ${\it\delta}$
a
${\it\delta}$
a
![]() $(N-d)$
-minor of the matrix
$(N-d)$
-minor of the matrix
![]() $\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
and
$\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
and
for some
![]() $f_{1},\ldots ,f_{N-d}\in I(X)$
.
$f_{1},\ldots ,f_{N-d}\in I(X)$
.
Moreover,
Remark 4.8. We may have different polynomials
![]() $f_{1},\ldots ,f_{N-d}$
for two different
$f_{1},\ldots ,f_{N-d}$
for two different
![]() $A_{h,{\it\delta}}$
.
$A_{h,{\it\delta}}$
.
Proof. By Noetherianity, we may assume that
![]() $H=(h_{1}{\it\delta}_{1},\ldots ,h_{r}{\it\delta}_{r})$
with
$H=(h_{1}{\it\delta}_{1},\ldots ,h_{r}{\it\delta}_{r})$
with
![]() $h_{i},{\it\delta}_{i}$
as desired. Therefore,
$h_{i},{\it\delta}_{i}$
as desired. Therefore,
![]() ${\mathcal{L}}^{(e)}(X)\subset \cup A_{h_{i},{\it\delta}_{i}}$
.
${\mathcal{L}}^{(e)}(X)\subset \cup A_{h_{i},{\it\delta}_{i}}$
.
Finally,
Indeed, for the second equality, if
![]() $f\in I(X)$
then
$f\in I(X)$
then
![]() $hf\in (f_{1},\ldots ,f_{N-d})$
, hence if
$hf\in (f_{1},\ldots ,f_{N-d})$
, hence if
![]() ${\it\gamma}$
vanishes the
${\it\gamma}$
vanishes the
![]() $f_{i}$
, then
$f_{i}$
, then
![]() $hf({\it\gamma})=0$
, and so
$hf({\it\gamma})=0$
, and so
![]() $f({\it\gamma})=0$
since
$f({\it\gamma})=0$
since
![]() $h({\it\gamma})\neq 0$
.◻
$h({\it\gamma})\neq 0$
.◻
Proof of Lemma 4.5.
We first notice that 4.5
(iii) is a consequence of 4.5
(ii):
![]() $\text{for all }{\it\pi}_{n}({\it\gamma})\in {\rm\Delta}_{e,e^{\prime },n}$
we have
$\text{for all }{\it\pi}_{n}({\it\gamma})\in {\rm\Delta}_{e,e^{\prime },n}$
we have
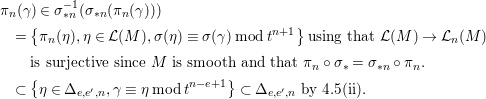 $$\begin{eqnarray}\displaystyle & & \displaystyle {\it\pi}_{n}({\it\gamma})\in {\it\sigma}_{\ast n}^{-1}({\it\sigma}_{\ast n}({\it\pi}_{n}({\it\gamma})))\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\pi}_{n}({\it\eta}),{\it\eta}\in {\mathcal{L}}(M),{\it\sigma}({\it\eta})\equiv {\it\sigma}({\it\gamma})\operatorname{mod}t^{n+1}\right\}\!\,\text{using that }{\mathcal{L}}(M)\rightarrow {\mathcal{L}}_{n}(M)\nonumber\\ \displaystyle & & \displaystyle \qquad \text{is surjective since }M\text{ is smooth and that }{\it\pi}_{n}\circ {\it\sigma}_{\ast }={\it\sigma}_{\ast n}\circ {\it\pi}_{n}.\nonumber\\ \displaystyle & & \displaystyle \quad \subset \left\{{\it\eta}\in {\rm\Delta}_{e,e^{\prime },n},{\it\gamma}\equiv {\it\eta}\operatorname{mod}t^{n-e+1}\right\}\subset {\rm\Delta}_{e,e^{\prime },n}\text{ by 4.5(ii)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\pi}_{n}({\it\gamma})\in {\it\sigma}_{\ast n}^{-1}({\it\sigma}_{\ast n}({\it\pi}_{n}({\it\gamma})))\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\pi}_{n}({\it\eta}),{\it\eta}\in {\mathcal{L}}(M),{\it\sigma}({\it\eta})\equiv {\it\sigma}({\it\gamma})\operatorname{mod}t^{n+1}\right\}\!\,\text{using that }{\mathcal{L}}(M)\rightarrow {\mathcal{L}}_{n}(M)\nonumber\\ \displaystyle & & \displaystyle \qquad \text{is surjective since }M\text{ is smooth and that }{\it\pi}_{n}\circ {\it\sigma}_{\ast }={\it\sigma}_{\ast n}\circ {\it\pi}_{n}.\nonumber\\ \displaystyle & & \displaystyle \quad \subset \left\{{\it\eta}\in {\rm\Delta}_{e,e^{\prime },n},{\it\gamma}\equiv {\it\eta}\operatorname{mod}t^{n-e+1}\right\}\subset {\rm\Delta}_{e,e^{\prime },n}\text{ by 4.5(ii)}.\nonumber\end{eqnarray}$$
Next 4.5
(ii) is a direct consequence of 4.5
(i). We apply 4.5
(i) to
![]() ${\it\gamma}$
with
${\it\gamma}$
with
![]() ${\it\delta}={\it\sigma}_{\ast }({\it\eta})$
, hence there exists a unique
${\it\delta}={\it\sigma}_{\ast }({\it\eta})$
, hence there exists a unique
![]() $\tilde{{\it\eta}}$
such that
$\tilde{{\it\eta}}$
such that
![]() $\tilde{{\it\eta}}\equiv {\it\gamma}\operatorname{mod}t^{n-e+1}$
and
$\tilde{{\it\eta}}\equiv {\it\gamma}\operatorname{mod}t^{n-e+1}$
and
![]() ${\it\sigma}_{\ast }(\tilde{{\it\eta}})={\it\sigma}_{\ast }({\it\eta})$
. By the assumptions on
${\it\sigma}_{\ast }(\tilde{{\it\eta}})={\it\sigma}_{\ast }({\it\eta})$
. By the assumptions on
![]() ${\it\sigma}$
and the definition of
${\it\sigma}$
and the definition of
![]() ${\rm\Delta}_{e,e^{\prime }}$
, for
${\rm\Delta}_{e,e^{\prime }}$
, for
![]() ${\it\varphi}_{1}\in {\mathcal{L}}(M)$
and
${\it\varphi}_{1}\in {\mathcal{L}}(M)$
and
![]() ${\it\varphi}_{2}\in {\rm\Delta}_{e,e^{\prime }}$
with
${\it\varphi}_{2}\in {\rm\Delta}_{e,e^{\prime }}$
with
![]() ${\it\varphi}_{1}\neq {\it\varphi}_{2}$
we have
${\it\varphi}_{1}\neq {\it\varphi}_{2}$
we have
![]() ${\it\sigma}({\it\varphi}_{1})\neq {\it\sigma}({\it\varphi}_{2})$
. Hence
${\it\sigma}({\it\varphi}_{1})\neq {\it\sigma}({\it\varphi}_{2})$
. Hence
![]() ${\it\eta}=\tilde{{\it\eta}}$
and
${\it\eta}=\tilde{{\it\eta}}$
and
![]() ${\it\eta}\equiv {\it\gamma}\operatorname{mod}t^{n-e+1}$
. Since
${\it\eta}\equiv {\it\gamma}\operatorname{mod}t^{n-e+1}$
. Since
![]() ${\it\sigma}({\it\gamma})\equiv {\it\sigma}({\it\eta})\operatorname{mod}t^{n+1}$
and
${\it\sigma}({\it\gamma})\equiv {\it\sigma}({\it\eta})\operatorname{mod}t^{n+1}$
and
![]() $n\geqslant e^{\prime }$
,
$n\geqslant e^{\prime }$
,
![]() ${\it\sigma}({\it\eta})\in {\mathcal{L}}^{(e^{\prime })}(X)$
. We may write
${\it\sigma}({\it\eta})\in {\mathcal{L}}^{(e^{\prime })}(X)$
. We may write
![]() ${\it\eta}(t)={\it\gamma}(t)+t^{n+1-e}u(t)$
and applying Taylor expansion to
${\it\eta}(t)={\it\gamma}(t)+t^{n+1-e}u(t)$
and applying Taylor expansion to
![]() $\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t)+t^{n+1-e}u(t))$
we get that
$\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t)+t^{n+1-e}u(t))$
we get that
![]() $\operatorname{Jac}_{{\it\sigma}}({\it\eta}(t))\equiv \operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))\operatorname{mod}t^{e+1}$
since
$\operatorname{Jac}_{{\it\sigma}}({\it\eta}(t))\equiv \operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))\operatorname{mod}t^{e+1}$
since
![]() $n+1-e\geqslant e+1$
. So
$n+1-e\geqslant e+1$
. So
![]() ${\it\eta}\in {\rm\Delta}_{e,e^{\prime }}$
.
${\it\eta}\in {\rm\Delta}_{e,e^{\prime }}$
.
So we just have to prove 4.5 (i) and 4.5 (iv).
We begin to refine the cover of Lemma 4.7: for
![]() $e^{\prime \prime }\leqslant e^{\prime }$
, we set
$e^{\prime \prime }\leqslant e^{\prime }$
, we set
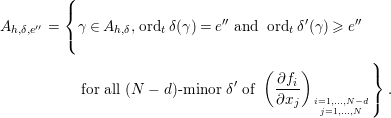 $$\begin{eqnarray}\displaystyle A_{h,{\it\delta},e^{\prime \prime }} & = & \displaystyle \left\{{\it\gamma}\in A_{h,{\it\delta}},\operatorname{ord}_{t}{\it\delta}({\it\gamma})=e^{\prime \prime }\text{and }\operatorname{ord}_{t}{\it\delta}^{\prime }({\it\gamma})\geqslant e^{\prime \prime }\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\text{for all }(N-d)\text{-minor }{\it\delta}^{\prime }\text{of }\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{h,{\it\delta},e^{\prime \prime }} & = & \displaystyle \left\{{\it\gamma}\in A_{h,{\it\delta}},\operatorname{ord}_{t}{\it\delta}({\it\gamma})=e^{\prime \prime }\text{and }\operatorname{ord}_{t}{\it\delta}^{\prime }({\it\gamma})\geqslant e^{\prime \prime }\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\text{for all }(N-d)\text{-minor }{\it\delta}^{\prime }\text{of }\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}\right\}.\nonumber\end{eqnarray}$$
Fix some
![]() $A=A_{h,{\it\delta},e^{\prime \prime }}$
, then it suffices to prove the lemma for
$A=A_{h,{\it\delta},e^{\prime \prime }}$
, then it suffices to prove the lemma for
![]() ${\rm\Delta}_{e,e^{\prime }}\cap {\it\sigma}^{-1}(A)$
.
${\rm\Delta}_{e,e^{\prime }}\cap {\it\sigma}^{-1}(A)$
.
Up to renumbering the coordinates, we may also assume that
![]() ${\it\delta}$
is the determinant of the first
${\it\delta}$
is the determinant of the first
![]() $N-d$
columns of
$N-d$
columns of
![]() ${\rm\Delta}=\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
.
${\rm\Delta}=\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$
.
We choose a local coordinate system of
![]() $M$
at
$M$
at
![]() ${\it\gamma}(0)$
in order to define
${\it\gamma}(0)$
in order to define
![]() $\operatorname{Jac}_{{\it\sigma}}$
and express arcs of
$\operatorname{Jac}_{{\it\sigma}}$
and express arcs of
![]() $M$
as elements of
$M$
as elements of
![]() $\mathbb{R}\{t\}^{d}$
.
$\mathbb{R}\{t\}^{d}$
.
Now, a crucial observation is that the first
![]() $N-d$
rows of
$N-d$
rows of
![]() $\operatorname{Jac}_{{\it\sigma}}({\it\gamma})$
are
$\operatorname{Jac}_{{\it\sigma}}({\it\gamma})$
are
![]() $\mathbb{R}\{t\}$
-linear combinations of the last
$\mathbb{R}\{t\}$
-linear combinations of the last
![]() $d$
rows: the application
$d$
rows: the application
is identically zero, so its Jacobian matrix is identically zero too and thus
![]() ${\rm\Delta}({\it\sigma}({\it\gamma}))\operatorname{Jac}_{{\it\sigma}}({\it\gamma})=0$
. Let
${\rm\Delta}({\it\sigma}({\it\gamma}))\operatorname{Jac}_{{\it\sigma}}({\it\gamma})=0$
. Let
![]() $P$
be the transpose of the comatrix of the submatrix of
$P$
be the transpose of the comatrix of the submatrix of
![]() ${\rm\Delta}$
given by the first
${\rm\Delta}$
given by the first
![]() $N-d$
columns of
$N-d$
columns of
![]() ${\rm\Delta}$
, then
${\rm\Delta}$
, then
![]() $P{\rm\Delta}=({\it\delta}I_{N-d},W)$
. Moreover, we have
$P{\rm\Delta}=({\it\delta}I_{N-d},W)$
. Moreover, we have
![]() $W({\it\sigma}({\it\gamma}))\equiv 0\operatorname{mod}t^{e^{\prime \prime }}$
. Indeed, if we denote
$W({\it\sigma}({\it\gamma}))\equiv 0\operatorname{mod}t^{e^{\prime \prime }}$
. Indeed, if we denote
![]() ${\rm\Delta}_{1},\ldots ,{\rm\Delta}_{N-d}$
the
${\rm\Delta}_{1},\ldots ,{\rm\Delta}_{N-d}$
the
![]() $N-d$
first columns of
$N-d$
first columns of
![]() ${\rm\Delta}$
and
${\rm\Delta}$
and
![]() $W_{1},\ldots ,W_{d}$
the columns of
$W_{1},\ldots ,W_{d}$
the columns of
![]() $W$
, then
$W$
, then
![]() $W_{j}({\it\sigma}({\it\gamma}))$
is solution of
$W_{j}({\it\sigma}({\it\gamma}))$
is solution of
![]() $({\rm\Delta}_{1}({\it\sigma}({\it\gamma})),\ldots ,{\rm\Delta}_{N-d}({\it\sigma}({\it\gamma})))X={\it\delta}({\it\sigma}({\it\gamma})){\rm\Delta}_{N-d+j}({\it\sigma}({\it\gamma}))$
since
$({\rm\Delta}_{1}({\it\sigma}({\it\gamma})),\ldots ,{\rm\Delta}_{N-d}({\it\sigma}({\it\gamma})))X={\it\delta}({\it\sigma}({\it\gamma})){\rm\Delta}_{N-d+j}({\it\sigma}({\it\gamma}))$
since
So, by Cramer’s rule,
Finally, the congruence arises because the minor formed by the
![]() $N-d$
first columns is of minimal order by definition of
$N-d$
first columns is of minimal order by definition of
![]() $A$
.
$A$
.
Now the columns of
![]() $\operatorname{Jac}_{{\it\sigma}}({\it\gamma})$
are solutions of
$\operatorname{Jac}_{{\it\sigma}}({\it\gamma})$
are solutions of
but since
![]() $t^{-e^{\prime \prime }}\cdot P({\it\sigma}({\it\gamma}))\cdot {\rm\Delta}({\it\sigma}({\it\gamma}))=(t^{-e^{\prime \prime }}{\it\delta}({\it\sigma}({\it\gamma}))I_{N-d},t^{-e^{\prime \prime }}W({\it\sigma}({\it\gamma})))$
we may express the first
$t^{-e^{\prime \prime }}\cdot P({\it\sigma}({\it\gamma}))\cdot {\rm\Delta}({\it\sigma}({\it\gamma}))=(t^{-e^{\prime \prime }}{\it\delta}({\it\sigma}({\it\gamma}))I_{N-d},t^{-e^{\prime \prime }}W({\it\sigma}({\it\gamma})))$
we may express the first
![]() $N-d$
coordinates of each solution in terms of the last
$N-d$
coordinates of each solution in terms of the last
![]() $d$
coordinates. This completes the proof of the observation.
$d$
coordinates. This completes the proof of the observation.
For 4.5
(i), it suffices to prove that for all
![]() $v\in \mathbb{R}\{t\}^{N}$
satisfying
$v\in \mathbb{R}\{t\}^{N}$
satisfying
![]() ${\it\sigma}({\it\gamma})+t^{n+1}v\in {\mathcal{L}}(X)$
there exists a unique
${\it\sigma}({\it\gamma})+t^{n+1}v\in {\mathcal{L}}(X)$
there exists a unique
![]() $u\in \mathbb{R}\{t\}^{d}$
such that
$u\in \mathbb{R}\{t\}^{d}$
such that
By Taylor expansion, we have
with
![]() $R({\it\gamma}(t),u)$
analytic in
$R({\it\gamma}(t),u)$
analytic in
![]() $t$
and
$t$
and
![]() $u$
. By (4), (3) is equivalent to
$u$
. By (4), (3) is equivalent to
with
![]() $n+1-2e\geqslant 1$
by hypothesis.
$n+1-2e\geqslant 1$
by hypothesis.
Since
![]() ${\it\sigma}({\it\gamma}(t))+t^{n+1}v\in {\mathcal{L}}(X)$
and using Taylor expansion, we get
${\it\sigma}({\it\gamma}(t))+t^{n+1}v\in {\mathcal{L}}(X)$
and using Taylor expansion, we get
with
![]() $S({\it\gamma}(t),v)$
analytic in
$S({\it\gamma}(t),v)$
analytic in
![]() $t$
and
$t$
and
![]() $v$
. So
$v$
. So
![]() $v$
is a solution of (2) and hence the first
$v$
is a solution of (2) and hence the first
![]() $N-d$
coefficients of
$N-d$
coefficients of
![]() $v$
are
$v$
are
![]() $\mathbb{R}\{t\}$
-linear combinations of the last
$\mathbb{R}\{t\}$
-linear combinations of the last
![]() $d$
coefficients with the same relations that for
$d$
coefficients with the same relations that for
![]() $\operatorname{Jac}_{{\it\sigma}}({\it\gamma})$
. This allows us to reduce (5) to
$\operatorname{Jac}_{{\it\sigma}}({\it\gamma})$
. This allows us to reduce (5) to
where
![]() $p:\mathbb{R}^{N}\rightarrow \mathbb{R}^{d}$
is the projection on the last
$p:\mathbb{R}^{N}\rightarrow \mathbb{R}^{d}$
is the projection on the last
![]() $d$
coordinates. The observation ensures that
$d$
coordinates. The observation ensures that
![]() $\operatorname{ord}_{t}\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))=\operatorname{ord}_{t}\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))=e$
and thus (6) is equivalent to
$\operatorname{ord}_{t}\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))=\operatorname{ord}_{t}\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))=e$
and thus (6) is equivalent to
Applying the implicit function theorem to
![]() $u(t,v)$
ensures that given an analytic arc
$u(t,v)$
ensures that given an analytic arc
![]() $v(t)$
there exists a solution
$v(t)$
there exists a solution
![]() $u_{v}(t)=u(t,v(t))$
. Using the same argument as in the proof of 4.5
(ii), the solution
$u_{v}(t)=u(t,v(t))$
. Using the same argument as in the proof of 4.5
(ii), the solution
![]() $u_{v}(t)$
is unique. This proves 4.5
(i).
$u_{v}(t)$
is unique. This proves 4.5
(i).
Let us prove 4.5
(iv). Let
![]() ${\it\gamma}\in {\rm\Delta}_{e,e^{\prime }}\cap {\it\sigma}^{-1}(A)$
then
${\it\gamma}\in {\rm\Delta}_{e,e^{\prime }}\cap {\it\sigma}^{-1}(A)$
then
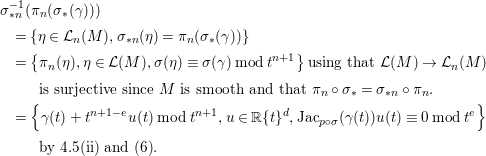 $$\begin{eqnarray}\displaystyle & & \displaystyle {\it\sigma}_{\ast n}^{-1}({\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma})))\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\eta}\in {\mathcal{L}}_{n}(M),{\it\sigma}_{\ast n}({\it\eta})={\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma}))\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\pi}_{n}({\it\eta}),{\it\eta}\in {\mathcal{L}}(M),{\it\sigma}({\it\eta})\equiv {\it\sigma}({\it\gamma})\operatorname{mod}t^{n+1}\right\}\,\!\text{using that }{\mathcal{L}}(M)\rightarrow {\mathcal{L}}_{n}(M)\nonumber\\ \displaystyle & & \displaystyle \qquad \;\text{is surjective since }M\text{ is smooth and that }{\it\pi}_{n}\circ {\it\sigma}_{\ast }={\it\sigma}_{\ast n}\circ {\it\pi}_{n}.\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\gamma}(t)+t^{n+1-e}u(t)\operatorname{mod}t^{n+1},u\in \mathbb{R}\{t\}^{d},\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))u(t)\equiv 0\operatorname{mod}t^{e}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \;\text{by 4.5(ii) and (6)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\sigma}_{\ast n}^{-1}({\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma})))\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\eta}\in {\mathcal{L}}_{n}(M),{\it\sigma}_{\ast n}({\it\eta})={\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma}))\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\pi}_{n}({\it\eta}),{\it\eta}\in {\mathcal{L}}(M),{\it\sigma}({\it\eta})\equiv {\it\sigma}({\it\gamma})\operatorname{mod}t^{n+1}\right\}\,\!\text{using that }{\mathcal{L}}(M)\rightarrow {\mathcal{L}}_{n}(M)\nonumber\\ \displaystyle & & \displaystyle \qquad \;\text{is surjective since }M\text{ is smooth and that }{\it\pi}_{n}\circ {\it\sigma}_{\ast }={\it\sigma}_{\ast n}\circ {\it\pi}_{n}.\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\gamma}(t)+t^{n+1-e}u(t)\operatorname{mod}t^{n+1},u\in \mathbb{R}\{t\}^{d},\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))u(t)\equiv 0\operatorname{mod}t^{e}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \;\text{by 4.5(ii) and (6)}.\nonumber\end{eqnarray}$$
Thus, the fiber is an affine subspace of
![]() $\mathbb{R}^{de}$
. There are invertible matrices
$\mathbb{R}^{de}$
. There are invertible matrices
![]() $A$
and
$A$
and
![]() $B$
with coordinates in
$B$
with coordinates in
![]() $\mathbb{R}\{t\}$
such that
$\mathbb{R}\{t\}$
such that
![]() $A\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))B$
is diagonal with entries
$A\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))B$
is diagonal with entries
![]() $t^{e_{1}},\ldots ,t^{e_{d}}$
such that
$t^{e_{1}},\ldots ,t^{e_{d}}$
such that
![]() $e=e_{1}+\cdots +e_{d}$
. Therefore the fiber is of dimension
$e=e_{1}+\cdots +e_{d}$
. Therefore the fiber is of dimension
![]() $e$
.
$e$
.
Since
![]() ${\it\sigma}$
is not assumed to be birational, we cannot use the section argument of [Reference Denef and Loeser9, 3.4] or [Reference Koike and Parusiński23, 4.2], instead we use a topological Noetherianity argument to prove that
${\it\sigma}$
is not assumed to be birational, we cannot use the section argument of [Reference Denef and Loeser9, 3.4] or [Reference Koike and Parusiński23, 4.2], instead we use a topological Noetherianity argument to prove that
![]() ${\it\sigma}_{\ast n|{\rm\Delta}_{e,e^{\prime },n}}$
is a piecewise trivial fibration.
${\it\sigma}_{\ast n|{\rm\Delta}_{e,e^{\prime },n}}$
is a piecewise trivial fibration.
We may assume that
![]() $M$
is semialgebraically connected, then by Artin-Mazur theorem [Reference Bochnak, Coste and Roy8, 8.4.4], there exist
$M$
is semialgebraically connected, then by Artin-Mazur theorem [Reference Bochnak, Coste and Roy8, 8.4.4], there exist
![]() $Y\subset \mathbb{R}^{p+q}$
a nonsingular irreducible algebraic set of dimension
$Y\subset \mathbb{R}^{p+q}$
a nonsingular irreducible algebraic set of dimension
![]() $\operatorname{dim}M$
,
$\operatorname{dim}M$
,
![]() $M^{\prime }\subset Y$
an open semialgebraic subset of
$M^{\prime }\subset Y$
an open semialgebraic subset of
![]() $Y$
,
$Y$
,
![]() $s:M\rightarrow M^{\prime }$
a Nash-diffeomorphism and
$s:M\rightarrow M^{\prime }$
a Nash-diffeomorphism and
![]() $g:Y\rightarrow \mathbb{R}^{N}$
a polynomial map such that the following diagram commutes
$g:Y\rightarrow \mathbb{R}^{N}$
a polynomial map such that the following diagram commutes
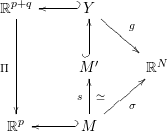
Thus, we have
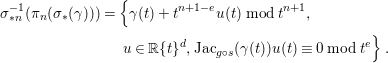 $$\begin{eqnarray}\displaystyle & & \displaystyle {\it\sigma}_{\ast n}^{-1}({\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma})))=\left\{\vphantom{u\in \mathbb{R}\{t\}^{d},\operatorname{Jac}_{g\circ s}({\it\gamma}(t))u(t)\equiv 0\operatorname{mod}t^{e}}{\it\gamma}(t)+t^{n+1-e}u(t)\operatorname{mod}t^{n+1},\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \qquad \qquad \left.u\in \mathbb{R}\{t\}^{d},\operatorname{Jac}_{g\circ s}({\it\gamma}(t))u(t)\equiv 0\operatorname{mod}t^{e}\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\sigma}_{\ast n}^{-1}({\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma})))=\left\{\vphantom{u\in \mathbb{R}\{t\}^{d},\operatorname{Jac}_{g\circ s}({\it\gamma}(t))u(t)\equiv 0\operatorname{mod}t^{e}}{\it\gamma}(t)+t^{n+1-e}u(t)\operatorname{mod}t^{n+1},\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \qquad \qquad \left.u\in \mathbb{R}\{t\}^{d},\operatorname{Jac}_{g\circ s}({\it\gamma}(t))u(t)\equiv 0\operatorname{mod}t^{e}\right\}.\nonumber\end{eqnarray}$$
So
![]() ${\rm\Delta}_{e,e^{\prime },n}$
is constructible and we may assume that
${\rm\Delta}_{e,e^{\prime },n}$
is constructible and we may assume that
![]() ${\it\sigma}_{\ast n}:{\rm\Delta}_{e,e^{\prime },n}\rightarrow {\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$
is polynomial up to working with arcs over
${\it\sigma}_{\ast n}:{\rm\Delta}_{e,e^{\prime },n}\rightarrow {\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$
is polynomial up to working with arcs over
![]() $M^{\prime }$
via
$M^{\prime }$
via
![]() $s$
. The fibers (i.e.,
$s$
. The fibers (i.e.,
![]() $\mathbb{R}^{e}$
) have odd Euler characteristic with compact support, so by Theorem 2.8 the image
$\mathbb{R}^{e}$
) have odd Euler characteristic with compact support, so by Theorem 2.8 the image
![]() ${\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$
is constructible.
${\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$
is constructible.
Let
![]() $V=\{u_{0}+u_{1}t+\cdots +u_{n}t^{n},u_{i}\in \mathbb{R}^{d}\}$
and fix
$V=\{u_{0}+u_{1}t+\cdots +u_{n}t^{n},u_{i}\in \mathbb{R}^{d}\}$
and fix
![]() ${\rm\Lambda}_{0}:V\rightarrow V_{0}$
a linear projection on a subspace of dimension
${\rm\Lambda}_{0}:V\rightarrow V_{0}$
a linear projection on a subspace of dimension
![]() $e$
. The set
$e$
. The set
![]() ${\rm\Omega}_{0}=\{{\it\pi}_{n}({\it\gamma}(t))\in {\rm\Delta}_{e,e^{\prime },n},\operatorname{dim}{\rm\Lambda}_{0}({\it\sigma}_{\ast n}^{-1}({\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma}))))<e\}$
is closed, constructible and union of fibers of
${\rm\Omega}_{0}=\{{\it\pi}_{n}({\it\gamma}(t))\in {\rm\Delta}_{e,e^{\prime },n},\operatorname{dim}{\rm\Lambda}_{0}({\it\sigma}_{\ast n}^{-1}({\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma}))))<e\}$
is closed, constructible and union of fibers of
![]() ${\it\sigma}_{\ast n}$
. Therefore
${\it\sigma}_{\ast n}$
. Therefore
![]() $({\it\sigma}_{\ast n},{\rm\Lambda}_{0}):{\rm\Delta}_{e,e^{\prime },n}\setminus {\rm\Omega}_{0}\rightarrow {\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n}\setminus {\rm\Omega}_{0})\times V_{0}$
is a constructible isomorphism. We now repeat the argument to the closed constructible subset
$({\it\sigma}_{\ast n},{\rm\Lambda}_{0}):{\rm\Delta}_{e,e^{\prime },n}\setminus {\rm\Omega}_{0}\rightarrow {\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n}\setminus {\rm\Omega}_{0})\times V_{0}$
is a constructible isomorphism. We now repeat the argument to the closed constructible subset
![]() ${\it\sigma}_{\ast n}({\rm\Omega}_{0})$
and so on. Indeed, assume that
${\it\sigma}_{\ast n}({\rm\Omega}_{0})$
and so on. Indeed, assume that
![]() ${\rm\Delta}_{e,e^{\prime },n}\supsetneq {\rm\Omega}_{0}\supsetneq {\rm\Omega}_{1}\supsetneq \cdots \supsetneq {\rm\Omega}_{i-1}$
are constructed as previously and that
${\rm\Delta}_{e,e^{\prime },n}\supsetneq {\rm\Omega}_{0}\supsetneq {\rm\Omega}_{1}\supsetneq \cdots \supsetneq {\rm\Omega}_{i-1}$
are constructed as previously and that
![]() ${\rm\Omega}_{i-1}\neq \varnothing$
, then we may choose
${\rm\Omega}_{i-1}\neq \varnothing$
, then we may choose
![]() ${\rm\Lambda}_{i}$
such that
${\rm\Lambda}_{i}$
such that
![]() ${\rm\Omega}_{i}\subsetneq {\rm\Omega}_{i-1}$
. So on the one hand the process continues until one
${\rm\Omega}_{i}\subsetneq {\rm\Omega}_{i-1}$
. So on the one hand the process continues until one
![]() ${\rm\Omega}_{i}$
is empty, on the other hand it must stop because of the Noetherianity of the
${\rm\Omega}_{i}$
is empty, on the other hand it must stop because of the Noetherianity of the
![]() ${\mathcal{A}}{\mathcal{S}}$
-topology. Therefore after a finite number of steps, one
${\mathcal{A}}{\mathcal{S}}$
-topology. Therefore after a finite number of steps, one
![]() ${\rm\Omega}_{i}$
is necessarily empty.◻
${\rm\Omega}_{i}$
is necessarily empty.◻
4.2 Essence of the proof
By our hypothesis, there exists a sequence of blowings-up
![]() ${\it\sigma}:M\rightarrow X$
with nonsingular centers such that
${\it\sigma}:M\rightarrow X$
with nonsingular centers such that
![]() $\tilde{{\it\sigma}}=f\circ {\it\sigma}:M\rightarrow X$
is Nash.
$\tilde{{\it\sigma}}=f\circ {\it\sigma}:M\rightarrow X$
is Nash.
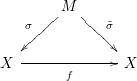
After adding more blowings-up, we may assume that the critical loci of
![]() ${\it\sigma}$
and
${\it\sigma}$
and
![]() $\tilde{{\it\sigma}}$
are simultaneously normal crossing and denote them by
$\tilde{{\it\sigma}}$
are simultaneously normal crossing and denote them by
![]() $\sum {\it\nu}_{i}E_{i}$
and
$\sum {\it\nu}_{i}E_{i}$
and
![]() $\sum \tilde{{\it\nu}}_{i}E_{i}$
. Our hypothesis ensures that
$\sum \tilde{{\it\nu}}_{i}E_{i}$
. Our hypothesis ensures that
![]() ${\it\nu}_{i}\geqslant \tilde{{\it\nu}}_{i}$
.
${\it\nu}_{i}\geqslant \tilde{{\it\nu}}_{i}$
.
In the same way, we may ensure that the inverse images of
![]() $H$
(defined in Lemma 4.1) by
$H$
(defined in Lemma 4.1) by
![]() ${\it\sigma}$
and
${\it\sigma}$
and
![]() $\tilde{{\it\sigma}}$
are also simultaneously normal crossing and denote them
$\tilde{{\it\sigma}}$
are also simultaneously normal crossing and denote them
![]() ${\it\sigma}^{-1}(H)=\sum _{i\in I}{\it\lambda}_{i}E_{i}$
(resp.
${\it\sigma}^{-1}(H)=\sum _{i\in I}{\it\lambda}_{i}E_{i}$
(resp.
![]() $\tilde{{\it\sigma}}^{-1}(H)=\sum _{i\in I}\tilde{{\it\lambda}}_{i}E_{i}$
).
$\tilde{{\it\sigma}}^{-1}(H)=\sum _{i\in I}\tilde{{\it\lambda}}_{i}E_{i}$
).
We recall the usual notationFootnote
12
. For
![]() $\mathbf{j}=(j_{i})_{i\in I}\in \mathbb{N}^{I}$
, we set
$\mathbf{j}=(j_{i})_{i\in I}\in \mathbb{N}^{I}$
, we set
![]() $J=J(\mathbf{j})=\{i,j_{i}\neq 0\}\subset I$
,
$J=J(\mathbf{j})=\{i,j_{i}\neq 0\}\subset I$
,
![]() $E_{J}=\cap _{i\in J}E_{i}$
and
$E_{J}=\cap _{i\in J}E_{i}$
and
![]() $E_{J}^{\bullet }=E_{J}\setminus \cup _{i\in I\setminus J}E_{i}$
.
$E_{J}^{\bullet }=E_{J}\setminus \cup _{i\in I\setminus J}E_{i}$
.
We also define:
![]() ${\mathcal{B}}_{\mathbf{j}}=\{{\it\gamma}\in {\mathcal{L}}(M),\text{for all }i\in J,\operatorname{ord}_{{\it\gamma}}E_{i}=j_{i},{\it\gamma}(0)\in E_{J}^{\bullet }\}$
and for all
${\mathcal{B}}_{\mathbf{j}}=\{{\it\gamma}\in {\mathcal{L}}(M),\text{for all }i\in J,\operatorname{ord}_{{\it\gamma}}E_{i}=j_{i},{\it\gamma}(0)\in E_{J}^{\bullet }\}$
and for all
![]() $n\in \mathbb{N}$
,
$n\in \mathbb{N}$
,
![]() ${\mathcal{B}}_{\mathbf{j},n}={\it\pi}_{n}({\mathcal{B}}_{\mathbf{j}})$
and
${\mathcal{B}}_{\mathbf{j},n}={\it\pi}_{n}({\mathcal{B}}_{\mathbf{j}})$
and
![]() $X_{\mathbf{j},n}({\it\sigma})={\it\pi}_{n}({\it\sigma}_{\ast }{\mathcal{B}}_{\mathbf{j}})={\it\sigma}_{\ast n}({\mathcal{B}}_{\mathbf{j},n})$
.
$X_{\mathbf{j},n}({\it\sigma})={\it\pi}_{n}({\it\sigma}_{\ast }{\mathcal{B}}_{\mathbf{j}})={\it\sigma}_{\ast n}({\mathcal{B}}_{\mathbf{j},n})$
.
Lemma 4.9. We have
![]() ${\mathcal{B}}_{\mathbf{j}}\subset {\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j})}({\it\sigma})$
where
${\mathcal{B}}_{\mathbf{j}}\subset {\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j})}({\it\sigma})$
where
![]() $e(\mathbf{j})=\sum _{i\in I}{\it\nu}_{i}j_{i}$
and
$e(\mathbf{j})=\sum _{i\in I}{\it\nu}_{i}j_{i}$
and
![]() $e^{\prime }(\mathbf{j})=\sum _{i\in I}{\it\lambda}_{i}j_{i}$
.
$e^{\prime }(\mathbf{j})=\sum _{i\in I}{\it\lambda}_{i}j_{i}$
.
Proof. Let
![]() ${\it\gamma}\in {\mathcal{B}}_{\mathbf{j}}$
and choose a local coordinate system of
${\it\gamma}\in {\mathcal{B}}_{\mathbf{j}}$
and choose a local coordinate system of
![]() $M$
at
$M$
at
![]() ${\it\gamma}(0)$
such that the critical locus of
${\it\gamma}(0)$
such that the critical locus of
![]() ${\it\sigma}$
is locally described by the equation
${\it\sigma}$
is locally described by the equation
![]() $\prod _{i\in J}x_{i}^{{\it\nu}_{i}}=0$
and
$\prod _{i\in J}x_{i}^{{\it\nu}_{i}}=0$
and
![]() $E_{i}$
by the equation
$E_{i}$
by the equation
![]() $x_{i}=0$
. Since
$x_{i}=0$
. Since
![]() $\operatorname{ord}_{{\it\gamma}}E_{i}=j_{i}$
, we have
$\operatorname{ord}_{{\it\gamma}}E_{i}=j_{i}$
, we have
![]() ${\it\gamma}_{i}(t)=c_{j_{i}}t^{j_{i}}+\cdots \,$
and
${\it\gamma}_{i}(t)=c_{j_{i}}t^{j_{i}}+\cdots \,$
and
![]() $c_{j_{i}}\neq 0$
. Then
$c_{j_{i}}\neq 0$
. Then
![]() $\prod _{i\in J}{\it\gamma}_{i}^{{\it\nu}_{i}}=ct^{e(\mathbf{j})}+\cdots \,$
with
$\prod _{i\in J}{\it\gamma}_{i}^{{\it\nu}_{i}}=ct^{e(\mathbf{j})}+\cdots \,$
with
![]() $c\neq 0$
.
$c\neq 0$
.
So we have
![]() $\operatorname{ord}_{t}\left(\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))\right)=e(\mathbf{j})$
.
$\operatorname{ord}_{t}\left(\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))\right)=e(\mathbf{j})$
.
In the same way,
![]() $\operatorname{ord}_{{\it\gamma}}{\it\sigma}^{-1}(H)=e^{\prime }(\mathbf{j})$
thus
$\operatorname{ord}_{{\it\gamma}}{\it\sigma}^{-1}(H)=e^{\prime }(\mathbf{j})$
thus
![]() $\operatorname{ord}_{{\it\sigma}({\it\gamma})}(H)=e^{\prime }(\mathbf{j})$
.◻
$\operatorname{ord}_{{\it\sigma}({\it\gamma})}(H)=e^{\prime }(\mathbf{j})$
.◻
Therefore we set
![]() $A_{n}({\it\sigma})=\left\{\mathbf{j},\sum _{i\in I}{\it\nu}_{i}j_{i}\leqslant \frac{n}{2},\sum _{i\in I}{\it\lambda}_{i}j_{i}\leqslant n\right\}$
. Indeed, for each
$A_{n}({\it\sigma})=\left\{\mathbf{j},\sum _{i\in I}{\it\nu}_{i}j_{i}\leqslant \frac{n}{2},\sum _{i\in I}{\it\lambda}_{i}j_{i}\leqslant n\right\}$
. Indeed, for each
![]() $\mathbf{j}\in A_{n}({\it\sigma})$
,
$\mathbf{j}\in A_{n}({\it\sigma})$
,
![]() ${\mathcal{B}}_{\mathbf{j}}\subset {\rm\Delta}_{e(j),e^{\prime }(j)}({\it\sigma})$
and we may apply Lemma 4.5 at the level of
${\mathcal{B}}_{\mathbf{j}}\subset {\rm\Delta}_{e(j),e^{\prime }(j)}({\it\sigma})$
and we may apply Lemma 4.5 at the level of
![]() $n$
-jets.
$n$
-jets.
The argument of the following lemma is essentially the same as [Reference Fukui, Kurdyka and Parusiński13, Section 4.2].
Lemma 4.10. (A decomposition of jet spaces)
For all
![]() $\mathbf{j}\in A_{n}({\it\sigma})$
, the sets
$\mathbf{j}\in A_{n}({\it\sigma})$
, the sets
![]() $X_{\mathbf{j},n}({\it\sigma})$
are constructible subsets of
$X_{\mathbf{j},n}({\it\sigma})$
are constructible subsets of
![]() ${\mathcal{L}}_{n}(X)$
and
${\mathcal{L}}_{n}(X)$
and
![]() $\operatorname{dim}X_{\mathbf{j},n}({\it\sigma})=d(n+1)-s_{\mathbf{j}}-\sum _{i\in I}{\it\nu}_{i}j_{i}$
where
$\operatorname{dim}X_{\mathbf{j},n}({\it\sigma})=d(n+1)-s_{\mathbf{j}}-\sum _{i\in I}{\it\nu}_{i}j_{i}$
where
![]() $s_{\mathbf{j}}=\sum _{i\in I}j_{i}$
. Moreover
$s_{\mathbf{j}}=\sum _{i\in I}j_{i}$
. Moreover
![]() $\operatorname{Im}({\it\sigma}_{\ast n})=Z_{n}({\it\sigma})\sqcup \sqcup _{\mathbf{j}\in A_{n}({\it\sigma})}X_{\mathbf{j},n}({\it\sigma})$
and the set
$\operatorname{Im}({\it\sigma}_{\ast n})=Z_{n}({\it\sigma})\sqcup \sqcup _{\mathbf{j}\in A_{n}({\it\sigma})}X_{\mathbf{j},n}({\it\sigma})$
and the set
![]() $Z_{n}({\it\sigma})$
satisfies
$Z_{n}({\it\sigma})$
satisfies
![]() $\operatorname{dim}Z_{n}({\it\sigma})<d(n+1)-\frac{n}{c}$
where
$\operatorname{dim}Z_{n}({\it\sigma})<d(n+1)-\frac{n}{c}$
where
![]() $c=\operatorname{max}(2{\it\nu}_{\operatorname{max}},{\it\lambda}_{\operatorname{max}})$
.
$c=\operatorname{max}(2{\it\nu}_{\operatorname{max}},{\it\lambda}_{\operatorname{max}})$
.
Proof. Consider
![]() $\mathbf{j}$
such that
$\mathbf{j}$
such that
![]() $E_{J}^{\bullet }\neq \varnothing$
and
$E_{J}^{\bullet }\neq \varnothing$
and
![]() $\text{for all }i\in I,0\leqslant j_{i}\leqslant n$
. The fiber of
$\text{for all }i\in I,0\leqslant j_{i}\leqslant n$
. The fiber of
![]() ${\mathcal{B}}_{\mathbf{j},n}\rightarrow E_{J}^{\bullet }$
is
${\mathcal{B}}_{\mathbf{j},n}\rightarrow E_{J}^{\bullet }$
is
since truncating the coordinates of
![]() ${\it\gamma}\in {\mathcal{B}}_{\mathbf{j}}$
to degree
${\it\gamma}\in {\mathcal{B}}_{\mathbf{j}}$
to degree
![]() $n$
produces
$n$
produces
![]() $d-|J|$
polynomials of degree
$d-|J|$
polynomials of degree
![]() $n$
with fixed constant terms and for
$n$
with fixed constant terms and for
![]() $i\in J$
a polynomial of the form
$i\in J$
a polynomial of the form
![]() $c_{j_{i}}t^{j_{i}}+c_{j_{i}+1}t^{j_{i}+1}+\cdots +c_{n}t^{n}$
with
$c_{j_{i}}t^{j_{i}}+c_{j_{i}+1}t^{j_{i}+1}+\cdots +c_{n}t^{n}$
with
![]() $c_{j_{i}}\in \mathbb{R}^{\ast }$
and other
$c_{j_{i}}\in \mathbb{R}^{\ast }$
and other
![]() $c_{k}\in \mathbb{R}$
. We conclude that
$c_{k}\in \mathbb{R}$
. We conclude that
![]() $\operatorname{dim}{\mathcal{B}}_{\mathbf{j},n}=d(n+1)-s_{\mathbf{j}}$
.
$\operatorname{dim}{\mathcal{B}}_{\mathbf{j},n}=d(n+1)-s_{\mathbf{j}}$
.
We first assume that
![]() $\mathbf{j}\in A_{n}({\it\sigma})$
. By Lemma 4.9,
$\mathbf{j}\in A_{n}({\it\sigma})$
. By Lemma 4.9,
![]() ${\mathcal{B}}_{\mathbf{j}}\subset {\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j})}({\it\sigma})$
. Hence by 4.5
(iv),
${\mathcal{B}}_{\mathbf{j}}\subset {\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j})}({\it\sigma})$
. Hence by 4.5
(iv),
![]() $X_{\mathbf{j},n}({\it\sigma})$
is constructible since it is the image of the constructible set
$X_{\mathbf{j},n}({\it\sigma})$
is constructible since it is the image of the constructible set
![]() ${\mathcal{B}}_{\mathbf{j},n}$
by the map
${\mathcal{B}}_{\mathbf{j},n}$
by the map
![]() ${\it\sigma}_{\ast n|{\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j}),n}}$
with fibers of odd Euler characteristic with compact support. Let
${\it\sigma}_{\ast n|{\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j}),n}}$
with fibers of odd Euler characteristic with compact support. Let
![]() ${\it\gamma}_{1}\in {\mathcal{B}}_{\mathbf{j},n}$
and
${\it\gamma}_{1}\in {\mathcal{B}}_{\mathbf{j},n}$
and
![]() ${\it\gamma}_{2}\in {\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j}),n}$
with
${\it\gamma}_{2}\in {\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j}),n}$
with
![]() ${\it\sigma}_{\ast n}({\it\gamma}_{1})={\it\sigma}_{\ast n}({\it\gamma}_{2})$
, then, by 4.5
(ii),
${\it\sigma}_{\ast n}({\it\gamma}_{1})={\it\sigma}_{\ast n}({\it\gamma}_{2})$
, then, by 4.5
(ii),
![]() ${\it\gamma}_{1}\equiv {\it\gamma}_{2}\operatorname{mod}t^{n-e(\mathbf{j})+1}$
with
${\it\gamma}_{1}\equiv {\it\gamma}_{2}\operatorname{mod}t^{n-e(\mathbf{j})+1}$
with
![]() $n-e(\mathbf{j})\geqslant e(\mathbf{j})$
and hence
$n-e(\mathbf{j})\geqslant e(\mathbf{j})$
and hence
![]() ${\it\gamma}_{2}\in {\mathcal{B}}_{\mathbf{j},n}$
. Thus by 4.5
(iv) the map
${\it\gamma}_{2}\in {\mathcal{B}}_{\mathbf{j},n}$
. Thus by 4.5
(iv) the map
![]() ${\mathcal{B}}_{\mathbf{j},n}\rightarrow X_{\mathbf{j},n}({\it\sigma})$
is a piecewise trivial fibration with fiber
${\mathcal{B}}_{\mathbf{j},n}\rightarrow X_{\mathbf{j},n}({\it\sigma})$
is a piecewise trivial fibration with fiber
![]() $\mathbb{R}^{e(\mathbf{j})}$
. So we have
$\mathbb{R}^{e(\mathbf{j})}$
. So we have
![]() $\operatorname{dim}X_{\mathbf{j},n}({\it\sigma})=d(n+1)-s_{\mathbf{j}}-e(\mathbf{j})$
as claimed.
$\operatorname{dim}X_{\mathbf{j},n}({\it\sigma})=d(n+1)-s_{\mathbf{j}}-e(\mathbf{j})$
as claimed.
Otherwise
![]() $\mathbf{j}\notin A_{n}({\it\sigma})$
and then
$\mathbf{j}\notin A_{n}({\it\sigma})$
and then
![]() $\operatorname{dim}X_{\mathbf{j},n}\leqslant \operatorname{dim}{\mathcal{B}}_{\mathbf{j},n}=d(n+1)-s_{\mathbf{j}}<d(n+1)-\frac{n}{c}$
(since
$\operatorname{dim}X_{\mathbf{j},n}\leqslant \operatorname{dim}{\mathcal{B}}_{\mathbf{j},n}=d(n+1)-s_{\mathbf{j}}<d(n+1)-\frac{n}{c}$
(since
![]() $\frac{n}{2}<e(\mathbf{j})\leqslant {\it\nu}_{\operatorname{max}}s_{\mathbf{j}}$
or
$\frac{n}{2}<e(\mathbf{j})\leqslant {\it\nu}_{\operatorname{max}}s_{\mathbf{j}}$
or
![]() $n<e^{\prime }(\mathbf{j})\leqslant {\it\lambda}_{\operatorname{max}}s_{\mathbf{j}}$
).◻
$n<e^{\prime }(\mathbf{j})\leqslant {\it\lambda}_{\operatorname{max}}s_{\mathbf{j}}$
).◻
Remark 4.11. The two previous lemmas work as they are if we replace
![]() ${\it\sigma}$
by
${\it\sigma}$
by
![]() $\tilde{{\it\sigma}}$
,
$\tilde{{\it\sigma}}$
,
![]() ${\it\nu}_{i}$
by
${\it\nu}_{i}$
by
![]() $\tilde{{\it\nu}}_{i}$
,
$\tilde{{\it\nu}}_{i}$
,
![]() ${\it\lambda}_{i}$
by
${\it\lambda}_{i}$
by
![]() $\tilde{{\it\lambda}}_{i}$
and
$\tilde{{\it\lambda}}_{i}$
and
![]() $c$
by
$c$
by
![]() $\tilde{c}$
.
$\tilde{c}$
.
Remark 4.12. Remember that
![]() $\operatorname{Im}{\it\sigma}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X))$
(resp.
$\operatorname{Im}{\it\sigma}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X))$
(resp.
![]() $\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X))$
). Moreover, since we may lift by
$\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X))$
). Moreover, since we may lift by
![]() ${\it\sigma}$
an arc not entirely included in the singular locus,
${\it\sigma}$
an arc not entirely included in the singular locus,
![]() ${\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X_{\text{sing}}))$
. The second part only works for
${\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X_{\text{sing}}))$
. The second part only works for
![]() ${\it\sigma}$
and does not stand for
${\it\sigma}$
and does not stand for
![]() $\tilde{{\it\sigma}}$
.
$\tilde{{\it\sigma}}$
.
In order to apply the virtual Poincaré polynomial, we are going to modify the objects of the partitions of Lemma 4.10.
Notation 4.13. We set
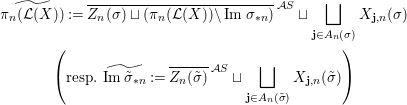 $$\begin{eqnarray}\displaystyle & \displaystyle \widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}:=\overline{Z_{n}({\it\sigma})\sqcup ({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n})}^{\,{\mathcal{A}}S}\sqcup \mathop{\sqcup }_{\mathbf{j}\in A_{n}({\it\sigma})}X_{\mathbf{j},n}({\it\sigma}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(\text{resp. }\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}:=\overline{Z_{n}(\tilde{{\it\sigma}})}^{\,{\mathcal{A}}S}\sqcup \mathop{\sqcup }_{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})}X_{\mathbf{j},n}(\tilde{{\it\sigma}})\right) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}:=\overline{Z_{n}({\it\sigma})\sqcup ({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n})}^{\,{\mathcal{A}}S}\sqcup \mathop{\sqcup }_{\mathbf{j}\in A_{n}({\it\sigma})}X_{\mathbf{j},n}({\it\sigma}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(\text{resp. }\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}:=\overline{Z_{n}(\tilde{{\it\sigma}})}^{\,{\mathcal{A}}S}\sqcup \mathop{\sqcup }_{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})}X_{\mathbf{j},n}(\tilde{{\it\sigma}})\right) & \displaystyle \nonumber\end{eqnarray}$$
where the closure is taken in the complement of
![]() $\sqcup _{\mathbf{j}\in A_{n}({\it\sigma})}X_{\mathbf{j},n}({\it\sigma})(\text{resp. in }\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\setminus \sqcup _{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})}X_{\mathbf{j},n}(\tilde{{\it\sigma}}))$
. Hence we still have the inclusion
$\sqcup _{\mathbf{j}\in A_{n}({\it\sigma})}X_{\mathbf{j},n}({\it\sigma})(\text{resp. in }\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\setminus \sqcup _{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})}X_{\mathbf{j},n}(\tilde{{\it\sigma}}))$
. Hence we still have the inclusion
![]() $\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\subset \widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}$
, the unions are still disjoint and the dimensions remain the same.
$\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\subset \widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}$
, the unions are still disjoint and the dimensions remain the same.
Lemma 4.14. For
![]() $\mathbf{j}\in A_{n}({\it\sigma})$
we have
$\mathbf{j}\in A_{n}({\it\sigma})$
we have
(resp. for
![]() $\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})$
we have
$\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})$
we have
![]() ${\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))={\it\beta}(E_{J}^{\bullet })(u-1)^{|J|}u^{nd-\sum (\tilde{{\it\nu}}_{i}+1)j_{i}}$
).
${\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))={\it\beta}(E_{J}^{\bullet })(u-1)^{|J|}u^{nd-\sum (\tilde{{\it\nu}}_{i}+1)j_{i}}$
).
Proof. We have
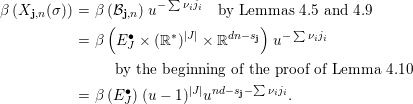 $$\begin{eqnarray}\displaystyle {\it\beta}\left(X_{\mathbf{j},n}({\it\sigma})\right) & = & \displaystyle {\it\beta}\left({\mathcal{B}}_{\mathbf{j},n}\right)u^{-\sum {\it\nu}_{i}j_{i}}~~\text{ by Lemmas 4.5 and 4.9}\nonumber\\ \displaystyle & = & \displaystyle {\it\beta}\left(E_{J}^{\bullet }\times (\mathbb{R}^{\ast })^{|J|}\times \mathbb{R}^{dn-s_{\mathbf{j}}}\right)u^{-\sum {\it\nu}_{i}j_{i}}\nonumber\\ \displaystyle & & \displaystyle \quad \text{by the beginning of the proof of Lemma 4.10}\nonumber\\ \displaystyle & = & \displaystyle {\it\beta}\left(E_{J}^{\bullet }\right)(u-1)^{|J|}u^{nd-s_{\mathbf{j}}-\sum {\it\nu}_{i}j_{i}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\beta}\left(X_{\mathbf{j},n}({\it\sigma})\right) & = & \displaystyle {\it\beta}\left({\mathcal{B}}_{\mathbf{j},n}\right)u^{-\sum {\it\nu}_{i}j_{i}}~~\text{ by Lemmas 4.5 and 4.9}\nonumber\\ \displaystyle & = & \displaystyle {\it\beta}\left(E_{J}^{\bullet }\times (\mathbb{R}^{\ast })^{|J|}\times \mathbb{R}^{dn-s_{\mathbf{j}}}\right)u^{-\sum {\it\nu}_{i}j_{i}}\nonumber\\ \displaystyle & & \displaystyle \quad \text{by the beginning of the proof of Lemma 4.10}\nonumber\\ \displaystyle & = & \displaystyle {\it\beta}\left(E_{J}^{\bullet }\right)(u-1)^{|J|}u^{nd-s_{\mathbf{j}}-\sum {\it\nu}_{i}j_{i}}.\nonumber\end{eqnarray}$$
The same argument works for
![]() $\tilde{{\it\sigma}}$
too.◻
$\tilde{{\it\sigma}}$
too.◻
Lemma 4.15.
![]() $\text{For all }i\in I,{\it\nu}_{i}=\tilde{{\it\nu}}_{i}$
.
$\text{For all }i\in I,{\it\nu}_{i}=\tilde{{\it\nu}}_{i}$
.
Proof. Applying the virtual Poincaré polynomial to the partitions of Notation 4.13, we get
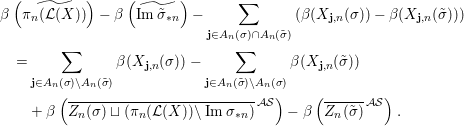 $$\begin{eqnarray}\displaystyle & & \displaystyle {\it\beta}\left(\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\right)-{\it\beta}\left(\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\right)-\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\cap A_{n}(\tilde{{\it\sigma}})}\left({\it\beta}(X_{\mathbf{j},n}({\it\sigma}))-{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\setminus A_{n}(\tilde{{\it\sigma}})}{\it\beta}(X_{\mathbf{j},n}({\it\sigma}))-\mathop{\sum }_{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})\setminus A_{n}({\it\sigma})}{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,{\it\beta}\left(\overline{Z_{n}({\it\sigma})\sqcup ({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n})}^{\,{\mathcal{A}}{\mathcal{S}}}\right)-{\it\beta}\left(\overline{Z_{n}(\tilde{{\it\sigma}})}^{\,{\mathcal{A}}{\mathcal{S}}}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\beta}\left(\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\right)-{\it\beta}\left(\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\right)-\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\cap A_{n}(\tilde{{\it\sigma}})}\left({\it\beta}(X_{\mathbf{j},n}({\it\sigma}))-{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\setminus A_{n}(\tilde{{\it\sigma}})}{\it\beta}(X_{\mathbf{j},n}({\it\sigma}))-\mathop{\sum }_{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})\setminus A_{n}({\it\sigma})}{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,{\it\beta}\left(\overline{Z_{n}({\it\sigma})\sqcup ({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n})}^{\,{\mathcal{A}}{\mathcal{S}}}\right)-{\it\beta}\left(\overline{Z_{n}(\tilde{{\it\sigma}})}^{\,{\mathcal{A}}{\mathcal{S}}}\right).\nonumber\end{eqnarray}$$
We set
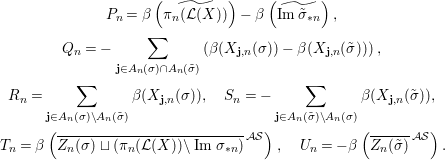 $$\begin{eqnarray}\displaystyle & \displaystyle P_{n}={\it\beta}\left(\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\right)-{\it\beta}\left(\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle Q_{n}=-\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\cap A_{n}(\tilde{{\it\sigma}})}\left({\it\beta}(X_{\mathbf{j},n}({\it\sigma}))-{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle R_{n}=\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\setminus A_{n}(\tilde{{\it\sigma}})}{\it\beta}(X_{\mathbf{j},n}({\it\sigma})),\quad \displaystyle S_{n}=-\mathop{\sum }_{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})\setminus A_{n}({\it\sigma})}{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}})), & \displaystyle \nonumber\\ \displaystyle & \displaystyle T_{n}={\it\beta}\left(\overline{Z_{n}({\it\sigma})\sqcup ({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n})}^{\,{\mathcal{A}}{\mathcal{S}}}\right),\quad \displaystyle U_{n}=-{\it\beta}\left(\overline{Z_{n}(\tilde{{\it\sigma}})}^{\,{\mathcal{A}}{\mathcal{S}}}\right). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle P_{n}={\it\beta}\left(\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\right)-{\it\beta}\left(\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle Q_{n}=-\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\cap A_{n}(\tilde{{\it\sigma}})}\left({\it\beta}(X_{\mathbf{j},n}({\it\sigma}))-{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle R_{n}=\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\setminus A_{n}(\tilde{{\it\sigma}})}{\it\beta}(X_{\mathbf{j},n}({\it\sigma})),\quad \displaystyle S_{n}=-\mathop{\sum }_{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})\setminus A_{n}({\it\sigma})}{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}})), & \displaystyle \nonumber\\ \displaystyle & \displaystyle T_{n}={\it\beta}\left(\overline{Z_{n}({\it\sigma})\sqcup ({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n})}^{\,{\mathcal{A}}{\mathcal{S}}}\right),\quad \displaystyle U_{n}=-{\it\beta}\left(\overline{Z_{n}(\tilde{{\it\sigma}})}^{\,{\mathcal{A}}{\mathcal{S}}}\right). & \displaystyle \nonumber\end{eqnarray}$$
Assume there exists
![]() $i_{0}\in I$
such that
$i_{0}\in I$
such that
![]() ${\it\nu}_{i_{0}}>\tilde{{\it\nu}}_{i_{0}}$
.
${\it\nu}_{i_{0}}>\tilde{{\it\nu}}_{i_{0}}$
.
Then for
![]() $n$
big enough,
$n$
big enough,
is not empty. The minimum
![]() $k_{n}=\min K_{n}$
stabilizes for
$k_{n}=\min K_{n}$
stabilizes for
![]() $n$
greater than some rank
$n$
greater than some rank
![]() $n_{0}$
. Let
$n_{0}$
. Let
![]() $k=k_{n_{0}}$
. Then, for
$k=k_{n_{0}}$
. Then, for
![]() $n\geqslant n_{0}$
, the degree of
$n\geqslant n_{0}$
, the degree of
![]() $Q_{n}$
is
$Q_{n}$
is
![]() $\operatorname{max}\left\{d(n+1)-s_{\mathbf{j}}-\sum _{i\in I}\tilde{{\it\nu}}_{i}j_{i}\right\}=d(n+1)-k$
using the computation at the beginning of the proof of Lemma 4.10.
$\operatorname{max}\left\{d(n+1)-s_{\mathbf{j}}-\sum _{i\in I}\tilde{{\it\nu}}_{i}j_{i}\right\}=d(n+1)-k$
using the computation at the beginning of the proof of Lemma 4.10.
The leading coefficients of
![]() $P_{n}$
is positive since
$P_{n}$
is positive since
![]() $P_{n}={\it\beta}\left(\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\setminus \widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\right)$
. The leading coefficient of
$P_{n}={\it\beta}\left(\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\setminus \widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\right)$
. The leading coefficient of
![]() $Q_{n}$
is also positive. Hence the degree of the LHS is at least
$Q_{n}$
is also positive. Hence the degree of the LHS is at least
![]() $d(n+1)-k$
.
$d(n+1)-k$
.
Moreover, we have
![]() $\operatorname{deg}R_{n}<d(n+1)-\frac{n}{\tilde{c}}$
,
$\operatorname{deg}R_{n}<d(n+1)-\frac{n}{\tilde{c}}$
,
![]() $\operatorname{deg}S_{n}<d(n+1)-\frac{n}{c}$
,
$\operatorname{deg}S_{n}<d(n+1)-\frac{n}{c}$
,
![]() $\operatorname{deg}T_{n}<d(n+1)-\frac{n}{\operatorname{max}(c,1)}$
and
$\operatorname{deg}T_{n}<d(n+1)-\frac{n}{\operatorname{max}(c,1)}$
and
![]() $\operatorname{deg}U_{n}<d(n+1)-\frac{n}{\tilde{c}}$
. Indeed, for
$\operatorname{deg}U_{n}<d(n+1)-\frac{n}{\tilde{c}}$
. Indeed, for
![]() $T_{n}$
,
$T_{n}$
,
![]() ${\it\pi}_{n}({\mathcal{L}}(X))\setminus \!\operatorname{Im}{\it\sigma}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X_{\text{sing}}))$
and
${\it\pi}_{n}({\mathcal{L}}(X))\setminus \!\operatorname{Im}{\it\sigma}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X_{\text{sing}}))$
and
![]() $\operatorname{dim}\left({\it\pi}_{n}({\mathcal{L}}(X_{\text{sing}}))\right)\leqslant (n+1)(d-1)<d(n+1)-n$
by 2.33
(i). So the degree of the RHS is less than
$\operatorname{dim}\left({\it\pi}_{n}({\mathcal{L}}(X_{\text{sing}}))\right)\leqslant (n+1)(d-1)<d(n+1)-n$
by 2.33
(i). So the degree of the RHS is less than
![]() $d(n+1)-\frac{n}{\operatorname{max}(c,\tilde{c},1)}$
.
$d(n+1)-\frac{n}{\operatorname{max}(c,\tilde{c},1)}$
.
We get a contradiction for
![]() $n$
big enough.◻
$n$
big enough.◻
Corollary 4.16.
![]() $Q_{n}=0$
.
$Q_{n}=0$
.
Since
![]() $\tilde{{\it\sigma}}:M\rightarrow X$
is a proper Nash map generically one-to-one, there exists a closed semialgebraic subsets
$\tilde{{\it\sigma}}:M\rightarrow X$
is a proper Nash map generically one-to-one, there exists a closed semialgebraic subsets
![]() $S\subset X$
with
$S\subset X$
with
![]() $\operatorname{dim}S<d$
such that for every
$\operatorname{dim}S<d$
such that for every
![]() $p\in X\setminus S$
,
$p\in X\setminus S$
,
![]() $\tilde{{\it\sigma}}^{-1}(p)$
is a singleton.
$\tilde{{\it\sigma}}^{-1}(p)$
is a singleton.
Lemma 4.17. Every arc on
![]() $X$
not entirely included in
$X$
not entirely included in
![]() $S\cup X_{\text{sing}}$
may be uniquely lifted by
$S\cup X_{\text{sing}}$
may be uniquely lifted by
![]() $\tilde{{\it\sigma}}$
.
$\tilde{{\it\sigma}}$
.
Proof. Let
![]() ${\it\gamma}$
be an analytic arc on
${\it\gamma}$
be an analytic arc on
![]() $X$
not entirely in
$X$
not entirely in
![]() $S$
and not entirely in the singular locus of
$S$
and not entirely in the singular locus of
![]() $X$
.
$X$
.
Assume that
![]() ${\it\gamma}\notin \operatorname{Im}\tilde{{\it\sigma}}_{\ast }$
. Then, by Proposition 2.21, we have
${\it\gamma}\notin \operatorname{Im}\tilde{{\it\sigma}}_{\ast }$
. Then, by Proposition 2.21, we have
Since
![]() $\tilde{{\it\sigma}}^{-1}$
is locally Hölder by Remark 2.20, there is
$\tilde{{\it\sigma}}^{-1}$
is locally Hölder by Remark 2.20, there is
![]() $N\in \mathbb{N}$
such that for every analytic arc
$N\in \mathbb{N}$
such that for every analytic arc
![]() ${\it\eta}$
on
${\it\eta}$
on
![]() $X$
with
$X$
with
![]() ${\it\gamma}\equiv {\it\eta}\operatorname{mod}t^{N}$
we have
${\it\gamma}\equiv {\it\eta}\operatorname{mod}t^{N}$
we have
![]() $\tilde{{\it\sigma}}^{-1}({\it\eta}(t))\equiv \tilde{{\it\sigma}}^{-1}({\it\gamma}(t))\operatorname{mod}t^{m+1}$
. Hence such an analytic arc
$\tilde{{\it\sigma}}^{-1}({\it\eta}(t))\equiv \tilde{{\it\sigma}}^{-1}({\it\gamma}(t))\operatorname{mod}t^{m+1}$
. Hence such an analytic arc
![]() ${\it\eta}$
is not in the image of
${\it\eta}$
is not in the image of
![]() $\tilde{{\it\sigma}}_{\ast }$
and for
$\tilde{{\it\sigma}}_{\ast }$
and for
![]() $n\geqslant N$
,
$n\geqslant N$
,
![]() ${\it\pi}_{n}({\it\eta})$
is not in the image of
${\it\pi}_{n}({\it\eta})$
is not in the image of
![]() $\tilde{{\it\sigma}}_{\ast n}:{\mathcal{L}}_{n}(M)\rightarrow {\it\pi}_{n}({\mathcal{L}}(X))$
. Hence
$\tilde{{\it\sigma}}_{\ast n}:{\mathcal{L}}_{n}(M)\rightarrow {\it\pi}_{n}({\mathcal{L}}(X))$
. Hence
![]() $({{\it\pi}_{N}^{n}}_{|{\it\pi}_{n}({\mathcal{L}}(X))})^{-1}({\it\pi}_{N}({\it\gamma}))\subset {\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}(\tilde{{\it\sigma}}_{\ast n})$
.
$({{\it\pi}_{N}^{n}}_{|{\it\pi}_{n}({\mathcal{L}}(X))})^{-1}({\it\pi}_{N}({\it\gamma}))\subset {\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}(\tilde{{\it\sigma}}_{\ast n})$
.
The first step consists in computing the dimension of the fiber
![]() $({{\it\pi}_{N}^{n}}_{|{\it\pi}_{n}({\mathcal{L}}(X))})^{-1}({\it\pi}_{N}({\it\gamma}))$
where
$({{\it\pi}_{N}^{n}}_{|{\it\pi}_{n}({\mathcal{L}}(X))})^{-1}({\it\pi}_{N}({\it\gamma}))$
where
![]() $n\geqslant N$
. For that, we will work with a resolution
$n\geqslant N$
. For that, we will work with a resolution
![]() ${\it\rho}:\tilde{X}\rightarrow X$
(for instance
${\it\rho}:\tilde{X}\rightarrow X$
(for instance
![]() ${\it\sigma}$
) instead of
${\it\sigma}$
) instead of
![]() $\tilde{{\it\sigma}}$
since every analytic arc on
$\tilde{{\it\sigma}}$
since every analytic arc on
![]() $X$
not entirely included in
$X$
not entirely included in
![]() $X_{\text{sing}}$
may be lifted to
$X_{\text{sing}}$
may be lifted to
![]() $\tilde{X}$
by
$\tilde{X}$
by
![]() ${\it\rho}$
. Let
${\it\rho}$
. Let
![]() ${\it\theta}$
be the unique analytic arc on
${\it\theta}$
be the unique analytic arc on
![]() $\tilde{X}$
such that
$\tilde{X}$
such that
![]() ${\it\rho}({\it\theta})={\it\gamma}$
. Let
${\it\rho}({\it\theta})={\it\gamma}$
. Let
![]() $e=\operatorname{ord}_{t}(\operatorname{Jac}_{{\it\rho}}({\it\theta}(t)))$
and
$e=\operatorname{ord}_{t}(\operatorname{Jac}_{{\it\rho}}({\it\theta}(t)))$
and
![]() $e^{\prime }$
be such that
$e^{\prime }$
be such that
![]() ${\it\gamma}\in {\mathcal{L}}^{(e^{\prime })}(X)$
. We may assume that
${\it\gamma}\in {\mathcal{L}}^{(e^{\prime })}(X)$
. We may assume that
![]() $N\geqslant \operatorname{max}(2e,e^{\prime })$
in order to apply Lemma 4.5 to
$N\geqslant \operatorname{max}(2e,e^{\prime })$
in order to apply Lemma 4.5 to
![]() ${\it\rho}$
for
${\it\rho}$
for
![]() ${\it\gamma}$
.
${\it\gamma}$
.
We consider the following diagram
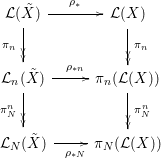
Since the fibers of
![]() ${{\it\rho}_{\ast n}}_{|{\rm\Delta}_{e,e^{\prime },n}}$
and
${{\it\rho}_{\ast n}}_{|{\rm\Delta}_{e,e^{\prime },n}}$
and
![]() ${{\it\rho}_{\ast N}}_{|{\rm\Delta}_{e,e^{\prime },N}}$
are of dimension
${{\it\rho}_{\ast N}}_{|{\rm\Delta}_{e,e^{\prime },N}}$
are of dimension
![]() $e$
, and since the fibers of
$e$
, and since the fibers of
![]() ${\it\pi}_{N}^{n}:{\mathcal{L}}_{n}(\tilde{X})\rightarrow {\mathcal{L}}_{N}(\tilde{X})$
are of dimension
${\it\pi}_{N}^{n}:{\mathcal{L}}_{n}(\tilde{X})\rightarrow {\mathcal{L}}_{N}(\tilde{X})$
are of dimension
![]() $(n-N)d$
, we have
$(n-N)d$
, we have
![]() $\operatorname{dim}\big(\big({{\it\pi}_{N}^{n}}_{|{\it\pi}_{n}({\mathcal{L}}(X))}\big)^{-1}({\it\pi}_{N}({\it\gamma}))\big)=(n-N)d$
.
$\operatorname{dim}\big(\big({{\it\pi}_{N}^{n}}_{|{\it\pi}_{n}({\mathcal{L}}(X))}\big)^{-1}({\it\pi}_{N}({\it\gamma}))\big)=(n-N)d$
.
Hence
![]() $\operatorname{dim}\left({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}(\tilde{{\it\sigma}}_{\ast n})\right)\geqslant (n-N)d$
. And so, with the notation of Lemma 4.15, we have
$\operatorname{dim}\left({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}(\tilde{{\it\sigma}}_{\ast n})\right)\geqslant (n-N)d$
. And so, with the notation of Lemma 4.15, we have
with
![]() $\operatorname{deg}P_{n}\geqslant (n-N)d=(n+1)d-(N+1)d$
and
$\operatorname{deg}P_{n}\geqslant (n-N)d=(n+1)d-(N+1)d$
and
![]() $\operatorname{deg}(R_{n}+S_{n}+T_{n}+U_{n})<(n+1)d-\frac{n}{\operatorname{max}(c,\tilde{c},1)}$
.
$\operatorname{deg}(R_{n}+S_{n}+T_{n}+U_{n})<(n+1)d-\frac{n}{\operatorname{max}(c,\tilde{c},1)}$
.
We get a contradiction for
![]() $n$
big enough.◻
$n$
big enough.◻
End of the proof of Theorem 3.5.
Let
![]() ${\it\gamma}$
be an analytic arc on
${\it\gamma}$
be an analytic arc on
![]() $X$
not entirely included in
$X$
not entirely included in
![]() $S\cup X_{\text{sing}}$
. By Lemma 4.17 and since
$S\cup X_{\text{sing}}$
. By Lemma 4.17 and since
![]() ${\it\gamma}$
is not entirely included in
${\it\gamma}$
is not entirely included in
![]() $S\cup X_{\text{sing}}$
,
$S\cup X_{\text{sing}}$
,
![]() $\tilde{{\it\sigma}}^{-1}({\it\gamma}(t))$
is well defined and analytic. Hence
$\tilde{{\it\sigma}}^{-1}({\it\gamma}(t))$
is well defined and analytic. Hence
![]() $f^{-1}({\it\gamma}(t))={\it\sigma}(\tilde{{\it\sigma}}^{-1}({\it\gamma}(t)))$
is real analytic. Finally
$f^{-1}({\it\gamma}(t))={\it\sigma}(\tilde{{\it\sigma}}^{-1}({\it\gamma}(t)))$
is real analytic. Finally
![]() $f^{-1}$
is generically arc-analytic in dimension
$f^{-1}$
is generically arc-analytic in dimension
![]() $d=\operatorname{dim}X$
.
$d=\operatorname{dim}X$
.
So
![]() $f^{-1}$
is blow-Nash by Proposition 2.27 and
$f^{-1}$
is blow-Nash by Proposition 2.27 and
![]() $\text{for all }i\in I,{\it\nu}_{i}=\tilde{{\it\nu}}_{i}$
by Lemma 4.15. Then, arguing as in Lemma 3.1,
$\text{for all }i\in I,{\it\nu}_{i}=\tilde{{\it\nu}}_{i}$
by Lemma 4.15. Then, arguing as in Lemma 3.1,
![]() $f^{-1}$
satisfies the Jacobian hypothesis too.◻
$f^{-1}$
satisfies the Jacobian hypothesis too.◻
Acknowledgment
The author is very grateful to his thesis advisor Adam Parusiński for his help and support during the preparation of this work.