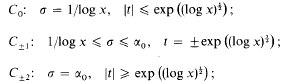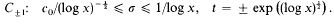Contents
Research Article
The distribution of integral and prime-integral values of systems of full-norm polynomials and affine-decomposable polynomials
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 80-87
-
- Article
- Export citation
The measure of the s-skeleton of a convex body
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 290-301
-
- Article
- Export citation
An approach to the zero-divisor question for group rings
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-93
-
- Article
- Export citation
A decomposition theorem in tensor products of Archimedean vector lattices
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 302-305
-
- Article
- Export citation
A distal property of groups and the growth of connected locally compact groups
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-98
-
- Article
- Export citation
Corrigendum
On a problem of Barban and Vehov, Corrigendum
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 306
-
- Article
-
- You have access
- Export citation
Index
Index to volume 26
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 307
-
- Article
- Export citation
Research Article
An embedding for groups with length functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-102
-
- Article
- Export citation
Outer automorphisms and non-trivial Picard groups
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-105
-
- Article
- Export citation
Front matter
MTK volume 26 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Inner contact measures
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 106-112
-
- Article
- Export citation
The ambiguous class group and the genius group of certain non-normal extensions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-124
-
- Article
- Export citation
Borel isomorphisms at the first level—I
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-156
-
- Article
- Export citation
Front matter
MTK volume 26 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
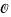 denote the ring of integers of
denote the ring of integers of 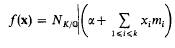
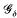 -set [see 6] and it is therefore measurable with respect to the
-set [see 6] and it is therefore measurable with respect to the