Contents
Research Article
On the reverse Lp–busemann–petty centroid inequality
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-11
-
- Article
- Export citation
Uniqueness theorems for convex bodies in non-Euclidean spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 13-31
-
- Article
- Export citation
Absolute curvature measures for unions of sets with positive reach
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 33-44
-
- Article
- Export citation
The longest segment in the complement of a packing
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-49
-
- Article
- Export citation
Quick asymptotic upper bounds for lattice kissing numbers
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-57
-
- Article
- Export citation
Characterizations of a two dimensional Euclidean ring among near-rings
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 59-64
-
- Article
- Export citation
Irreducible and end type group actions on Λ-trees
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 65-70
-
- Article
- Export citation
Hilbert function and fractional powers
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-75
-
- Article
- Export citation
Rational homology of spaces of complex monic polynomials with multiple roots
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-91
-
- Article
- Export citation
On minimal pairs and residually transcendental extensions of valuations
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-106
-
- Article
- Export citation
On extensions generated by roots of lifting polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-118
-
- Article
- Export citation
Multiplicities of eigenvalues of a vector-valued Sturm-Liouville problem
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-127
-
- Article
- Export citation
Non-linear boundary value problems on the semi-infinite interval: an upper and lower solution approach
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 129-140
-
- Article
- Export citation
Local inversion for differentiable functions and the Darboux property
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-158
-
- Article
- Export citation
Lipschitz quotient mappings with good ratio of constants
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-165
-
- Article
- Export citation
An analogue of Van der Corput's A5-process for exponential sums
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 167-183
-
- Article
- Export citation
Small positive values of indefinite ternary forms
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-196
-
- Article
- Export citation
The universal quaternary quadratic form with the maximal discriminant
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 197-199
-
- Article
- Export citation
The Hooley–Huxley contour method, for problems in number fields II: factorization and divisibility
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 201-225
-
- Article
- Export citation
On shifted products which are powers
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 227-230
-
- Article
- Export citation
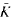 of
of 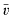 its unique prolongation to a fixed algebraic closure
its unique prolongation to a fixed algebraic closure 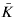 of
of 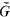 . For any subfield
. For any subfield 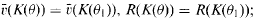 in case (
in case (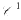 functions extends in finite dimension to everywhere differentiable functions. As usual, a theorem of implicit functions can be deduced from this “Local Inversion Theorem”. The deepest part of the local inversion theorem consists of showing that a differentiable function with non-vanishing Jacobian determinant is locally one-to-one. In turn, this fact allows one to extend the Darboux property of derivative functions on ℝ (the range of the derivative is an interval) to the Jacobian function
functions extends in finite dimension to everywhere differentiable functions. As usual, a theorem of implicit functions can be deduced from this “Local Inversion Theorem”. The deepest part of the local inversion theorem consists of showing that a differentiable function with non-vanishing Jacobian determinant is locally one-to-one. In turn, this fact allows one to extend the Darboux property of derivative functions on ℝ (the range of the derivative is an interval) to the Jacobian function 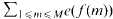 . The saving has now to be taken to the exponent 1/20 instead of 1/32. Our main application is a “ninth derivative test” for exponential sums which is essential for giving new exponent pairs in [3].
. The saving has now to be taken to the exponent 1/20 instead of 1/32. Our main application is a “ninth derivative test” for exponential sums which is essential for giving new exponent pairs in [3].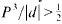 .
.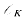 , the ring of integers of
, the ring of integers of 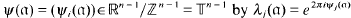 . Then the small region of
. Then the small region of 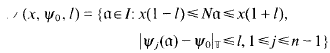
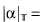 β. where β is the unique real satisyfing
β. where β is the unique real satisyfing 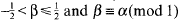 .
.