Article contents
COMPLEX MOMENTS AND THE DISTRIBUTION OF VALUES OF 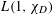 $L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
$L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
Published online by Cambridge University Press: 05 December 2018
Abstract
In this paper we investigate the moments and the distribution of 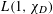 $L(1,\unicode[STIX]{x1D712}_{D})$, where
$L(1,\unicode[STIX]{x1D712}_{D})$, where 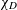 $\unicode[STIX]{x1D712}_{D}$ varies over quadratic characters associated to square-free polynomials
$\unicode[STIX]{x1D712}_{D}$ varies over quadratic characters associated to square-free polynomials 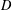 $D$ of degree
$D$ of degree  $n$ over
$n$ over 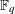 $\mathbb{F}_{q}$, as
$\mathbb{F}_{q}$, as 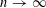 $n\rightarrow \infty$. Our first result gives asymptotic formulas for the complex moments of
$n\rightarrow \infty$. Our first result gives asymptotic formulas for the complex moments of 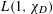 $L(1,\unicode[STIX]{x1D712}_{D})$ in a large uniform range. Previously, only the first moment has been computed due to the work of Andrade and Jung. Using our asymptotic formulas together with the saddle-point method, we show that the distribution function of
$L(1,\unicode[STIX]{x1D712}_{D})$ in a large uniform range. Previously, only the first moment has been computed due to the work of Andrade and Jung. Using our asymptotic formulas together with the saddle-point method, we show that the distribution function of 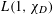 $L(1,\unicode[STIX]{x1D712}_{D})$ is very close to that of a corresponding probabilistic model. In particular, we uncover an interesting feature in the distribution of large (and small) values of
$L(1,\unicode[STIX]{x1D712}_{D})$ is very close to that of a corresponding probabilistic model. In particular, we uncover an interesting feature in the distribution of large (and small) values of 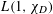 $L(1,\unicode[STIX]{x1D712}_{D})$, which is not present in the number field setting. We also obtain
$L(1,\unicode[STIX]{x1D712}_{D})$, which is not present in the number field setting. We also obtain 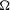 $\unicode[STIX]{x1D6FA}$-results for the extreme values of
$\unicode[STIX]{x1D6FA}$-results for the extreme values of 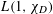 $L(1,\unicode[STIX]{x1D712}_{D})$, which we conjecture to be the best possible. Specializing
$L(1,\unicode[STIX]{x1D712}_{D})$, which we conjecture to be the best possible. Specializing 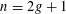 $n=2g+1$ and making use of one case of Artin’s class number formula, we obtain similar results for the class number
$n=2g+1$ and making use of one case of Artin’s class number formula, we obtain similar results for the class number 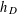 $h_{D}$ associated to
$h_{D}$ associated to 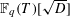 $\mathbb{F}_{q}(T)[\sqrt{D}]$. Similarly, specializing to
$\mathbb{F}_{q}(T)[\sqrt{D}]$. Similarly, specializing to 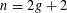 $n=2g+2$ we can appeal to the second case of Artin’s class number formula and deduce analogous results for
$n=2g+2$ we can appeal to the second case of Artin’s class number formula and deduce analogous results for 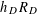 $h_{D}R_{D}$, where
$h_{D}R_{D}$, where 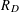 $R_{D}$ is the regulator of
$R_{D}$ is the regulator of 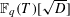 $\mathbb{F}_{q}(T)[\sqrt{D}]$.
$\mathbb{F}_{q}(T)[\sqrt{D}]$.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2018
References
- 10
- Cited by

