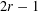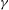Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Labbé, Jean-Philippe
and
Nevo, Eran
2017.
Bounds for Entries of $\gamma$-Vectors of Flag Homology Spheres.
SIAM Journal on Discrete Mathematics,
Vol. 31,
Issue. 3,
p.
2064.
Zheng, Hailun
2017.
The flag upper bound theorem for 3- and 5-manifolds.
Israel Journal of Mathematics,
Vol. 222,
Issue. 1,
p.
401.
Chudnovsky, Maria
and
Nevo, Eran
2020.
Induced equators in flag spheres.
Journal of Combinatorial Theory, Series A,
Vol. 176,
Issue. ,
p.
105283.
Zheng, Hailun
2020.
The upper bound theorem for flag homology 5-manifolds.
Journal of Combinatorial Theory, Series A,
Vol. 175,
Issue. ,
p.
105259.
Rowlands, Rowan
2023.
Relating CAT(0) cubical complexes and flag simplicial complexes.
Advances in Applied Mathematics,
Vol. 147,
Issue. ,
p.
102502.