No CrossRef data available.
Article contents
SHUTOUT GAMES ON GRAPHS
Published online by Cambridge University Press: 03 February 2015
Abstract
Two players take it in turn to claim edges from a graph 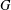 $G$. The first player (“Maker”) wins if at any point he has claimed
$G$. The first player (“Maker”) wins if at any point he has claimed  $s$ edges at a vertex without the second player (“Breaker”) having claimed a single edge at that vertex. If, by the end of play, this does not occur we say that Breaker wins. Our main aim is to show that for every
$s$ edges at a vertex without the second player (“Breaker”) having claimed a single edge at that vertex. If, by the end of play, this does not occur we say that Breaker wins. Our main aim is to show that for every  $s$ there is a graph
$s$ there is a graph 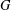 $G$ in which Maker has a winning strategy.
$G$ in which Maker has a winning strategy.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2015
References
Beck, J., Combinatorial Games: Tic-Tac-Toe Theory (Encyclopedia of Mathematics and Its Applications 114), Cambridge University Press (Cambridge, 2008).CrossRefGoogle Scholar
Leader, I., Hypergraph Games. Notes available online at http://tartarus.org/gareth/maths/notes/.Google Scholar

