Here we study (in a more general setting) the following problem. Let C be a smooth projective curve, E and F vector bundles on C and V ⊆ H0 (C, E) (resp. W ⊆ H0 (C, F)) vector spaces generically spanning E (resp. F); find lower bounds for the dimension of the image of the multiplication map V ⊗ W → H0 (C, E ⊗ F) generalizing the case rank(E) = rank(F) = 1.

By using a Fourier-Mukai transform for sheaves on K3 surfaces we show that for a wide class of K3 surfaces X the Hilbert schemes Hilbn(X) can be identified for all n ≥ 1 with moduli spaces of Gieseker stable vector bundles on X. We also introduce a new Fourier-Mukai type transform for such surfaces.

We compute the subring of H*(CP∞ × CP∞; ) annihilated by the Steenrod algebra, , p being an odd prime. By calculating the subring's structure as a GL(2, )-space we may obtain information about the modular representations of that group.

Throughout this paper, k denotes a commutative ring. We will develop a theory of homological finiteness conditions for modules over certain graded k-algebras which generalizes known theory for group algebras. The simplest of our results, Theorem A below, generalizes certain results of Aljadeff and Yi on crossed products of polycyclic-by-finite groups (cf. [1, 11]), but also applies to many other crossed products in cases where little was previously known. Before stating the results, we recall definitions of graded and strongly graded rings. Let G be a monoid. Naively, a G-graded k-algebra is a k-algebra R which admits a k-module decomposition,

in such a way that Rg Rh ⊆ for all g, h ∈ G. If R is a G-graded k-algebra and X is any subset of G, then we write Rx for the k-submodule of R supported on X; that is

Note that if H is a submonoid of G then RH is a subalgebra of R.

We shall work with rational Mn(K)-modules, where K is an infinite field of prime characteristic p > 0, and Mn(K) is the full matrix semigroup of n × n matrices over K. Recall that equivalence classes of simple rational Mn(K)-modules are parametrized by the set of all partitions λ = (λ1, λ2, …, λl) of length l = l(λ) ≤ n, and that the socle L(λ) of the Schur module (or dual Weyl module) H0(λ) is a simple Mn(K)-module whose highest weight corresponds to the partition λ.

A. M. Sinclair has proved that if is a semisimple Banach algebra then every continuous Jordan derivation from into is a derivation ([12, theorem 3·3]; ‘Jordan derivation’ is denned in Section 6 below). If is a Banach -bimodule one can consider Jordan derivations from into and ask whether Sinclair's theorem is still true. More recent work in this area appears in [1]. Simple examples show that it cannot hold for all modules and all semisimple algebras. However, for more restricted classes of algebras, including C*-algebras one does get a positive result and we develop two approaches. The first depends on symmetric amenability, a development of the theory of amenable Banach algebras which we present here for the first time in Sections 2, 3 and 4. A Banach algebra is symmetrically amenable if it has an approximate diagonal consisting of symmetric tensors. Most, but not all, amenable Banach algebras are symmetrically amenable and one can prove results for symmetric amenability similar to those in [8] for amenability. However, unlike amenability, symmetric amenability does not seem to have a concise homological characterisation. One of our results [Theorem 6·2] is that if is symmetrically amenable then every continuous Jordan derivation into an -bimodule is a derivation. Special techniques enable this result to be extended to other algebras, for example all C*-algebras. This approach to Jordan derivations appears in Section 6.

1·1. Groups of the first kind. In [11], Patterson proved a hyperbolic space analogue of Khintchine's theorem on simultaneous Diophantine approximation. In order to state Patterson's theorem, some notation and terminology are needed. Let ‖x‖ denote the usual Euclidean norm of a vector x in k+1, k + 1-dimensional Euclidean space, and letbe the unit ball model of k + 1-dimensional hyperbolic space with Poincaré metric ρ. A non-elementary geometrically finite group G acting on Bk + 1 is a discrete subgroup of Möb (Bk+l), the group of orientation preserving Mobius transformations preserving Bk + 1, for which there exists some convex fundamental polyhedron with finitely many faces. Since G is non-elementary, the limit set L(G) of G – the set of limit points in the unit sphere Sk of any orbit of G in Bk+1 – is uncountable. The group G is said to be of the first kind if L(G) = Sk and of the second kind otherwise.

The aim of this paper is to contribute to the foundations of homotopy theory for simplicial sheaves, as we believe this is the natural context for the development of non-abelian, as well as extraordinary, sheaf cohomology.

In [11] we began constructing a theory of classifying spaces for sheaves of simplicial groupoids, and that study is continued here. Such a theory is essential for the development of basic tools such as Postnikov systems, Atiyah-Hirzebruch spectral sequences, characteristic classes, and cohomology operations in extraordinary cohomology of sheaves. Thus, in some sense, we are continuing the program initiated by Illusie[7], Brown[2], and Brown and Gersten[3], though our basic homotopy theory of simplicial sheaves is different from theirs. In fact, the homotopy theory we use is the global one of [10]. As a result, there is some similarity between our theory and the theory of Jardine[8], which is also partially based on [10]

It is well known that the cotangent bundle of any manifold has a canonical symplectic structure. If we specialize to the case when the manifold is a compact Lie group G, then this structure is preserved by the actions of G on T*G induced by left and right translation on G. We refer to these as the left and right actions of G on T*G.

In [3], B. Y. Chen proved that, for any Lagrangian submanifold M in a complex space-form Mn(4c) (c = ± 1), the squared mean curvature and the scalar curvature of M satisfy the following inequality:

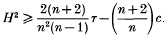
He then introduced three families of Riemannian n-manifolds 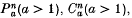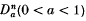and two exceptional n-spaces Fn, Ln and proved the existence of a Lagrangian isometric immersion pa from 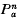into ℂPn(4) and the existence of Lagrangian isometric immersions f, l, ca, da from Fn, Ln, 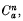, 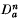into ℂHn(− 4), respectively, which satisfy the equality case of the inequality. He also proved that, beside the totally geodesie ones, these are the only Lagrangian submanifolds in ℂPn(4) and in ℂHn(− 4) which satisfy this basic equality. In this article, we obtain the explicit expressions of these Lagrangian immersions. As an application, we obtain new Lagrangian immersions of the topological n-sphere into ℂPn(4) and ℂHn(−4).

Let G be a locally compact group and F a left introverted subalgebra of C(G). For each of the algebras L1(G), M(G), F* and L∞(G)* we determine the finite-dimensional minimal left ideals of the algebra (if any); in some cases we also determine the finite-dimensional minimal two-sided ideals, and in certain cases show that all minimal ideals of the algebra are finite-dimensional.

Let Γ be a discrete group. Γ is said to have finite virtual cohomological dimension (vcd) if there exists a finite index torsion-free subgroup Γ' of Γ such that Γ' has finite cohomological dimension over . Examples of such groups include the fundamental group of a finite graph of finite groups, arithmetic groups, mapping class groups and outer automorphism groups of free groups. One of the fundamental problems in topology is to understand the cohomology of these finite vcd-groups.

An open continuous function from an open Riemann surface with finite genus and finite number of boundary components into a closed Riemann surface is termed a (p, q)-map, 0 < q < p, if it has a finite number of branch points and assumes every point in the image surface either p or q times, counting multiplicity, with possibly a finite number of exceptions.

The object of this paper is to prove that the geometry of any (p, q)-map resembles that of a (p, q)-map whose q-set (the set of image points of f that are taken on exactly q times, counting multiplicity), constitutes a finite set of Jordan arcs or curves (loops). This leads to interesting geometrie results regarding (p, q)-maps without exceptional points. Further, it yields that every (p, q)-map is homotopic to a simplicial (p, q)-map having the same covering properties.

The present work has its motivation in the papers [2] and [6] on distinguished Fréchet function spaces. Recall that a Fréchet space E is distinguished if it is the projective limit of a sequence of Banach spaces En such that the strong dual E′β is the inductive limit of the sequence of the duals E′n. Clearly, the property of being distinguished is inherited by complemented subspaces and in [6] Taskinen proved that the Fréchet function space C(R) ∩ L1(R) (intersection topology) is not distinguished, by showing that it contains a complemented subspace of Moscatelli type (see Section 1) that is not distinguished. Because of the criterion in [1], it is easy to decide when a Frechet space of Moscatelli type is distinguished. Using this, in [2], Bonet and Taskinen obtained that the spaces open in RN) are distinguished, by proving that they are isomorphic to complemented subspaces of distinguished Fréchet spaces of Moscatelli type.

While trying to place the grade-theoretic analogue of the Cousin complex (for a commutative Noetherian ring A) of K. R. Hughes [7], and the complexes of modules of generalized fractions studied by the first author and H. Zakeri[18], and by L. O'Carroll [10, p. 420], on a similar footing, Sharp and M. Yassi[15] introduced the concept of generalized Hughes complex. Such complexes are described as follows.

Given a knot K in a 3-manifold M, we use N(K) to denote a regular neighbourhood of K. Suppose γ is a slope (i.e. an isotopy class of essential simple closed curves) on ∂N(K). The surgered manifold along γ is denoted by (H, K; γ), which by definition is the manifold obtained by gluing a solid torus to H – Int N(K) so that γ bounds a meridional disc. We say that M is ∂-reducible if ∂M is compressible in M, and we call γ a ∂-reducing slope of K if (H, K; γ) is ∂-reducible. Since incompressible surfaces play an important rôle in 3-manifold theory, it is important to know what slopes of a given knot are ∂-reducing. In the generic case there are at most three ∂-reducing slopes for a given knot [12], but there is no known algorithm to find these slopes. An exceptional case is when M is a solid torus, which has been well studied by Berge, Gabai and Scharlemann [1, 4, 5, 10]. It is now known that a knot in a solid torus has ∂-reducing slopes only if it is a 1-bridge braid. Moreover, all such knots and their corresponding ∂-reducing slopes are classified in [1]. For 1-bridge braids with small bridge width, a geometric method of detecting ∂-reducing slopes has also been given in [5]. It was conjectured that a similar result holds for handlebodies, i.e. if K is a knot in a handlebody with H – K ∂-irreducible, then K has ∂-reducing slopes only if K is a 1-bridge knot (see below for definitions). One is referred to [13] for some discussion of this conjecture and related problems.

Improving earlier result of Hardy and Littlewood[1] and McGehee, Pigno and Smith[2] we show for analytic functions on the unit disc that

The properties p-convexity and q-concavity are fundamental in the study of Banach sequence spaces (see [L-TzII]), and in recent years have been shown to be of great significance in the theory of the corresponding Schatten ideals ([G-TJ], [LP-P] and many other papers). In particular, the notions 2-convex and 2-concave are meaningful in Schatten ideals. It seems to have been noted only recently [LP-P] that a Schatten ideal has either of these properties if the underlying sequence space has. One way of establishing this is to use the fact that if (E, ‖ ‖E) is 2-convex, then there is another Banach sequence space (F, ‖ ‖F) such that ‖x;‖ = ‖x2‖F for all x ε E. The 2-concave case can then be deduced using duality, though this raises some difficulties, for example when E is inseparable.

The Hopkins–Levitzki Theorem, discovered independently in 1939 by C. Hopkins and J. Levitzki states that a right Artinian ring with identity is right Noetherian. In the 1970s and 1980s it has been generalized to modules over non-unital rings by Shock[10], to modules satisfying the descending chain condition relative to a heriditary torsion theory by Miller-Teply[7], to Grothendieck categories by Năstăsescu [8], and to upper continuous modular lattices by Albu [1]. The importance of the relative Hopkins-Levitzki Theorem in investigating the structure of some relevant classes of modules, including injectives as well as projectives is revealed in [3] and [6], where the main body of both these monographs deals with this topic. A discussion on the various forms of the Hopkins–Levitzki Theorem for modules and Grothendieck categories and the connection between them may be found in [3].

Given a vector field X on the real plane, we study the influence of the curvature of the orbits of ẋ = X┴(x) in the stability of those of the system x˙ = X(x). We pay special attention to the case in which this curvature is negative in the whole plane. Under this assumption, we classify the possible critical points and give a criterion for a point to be globally asymptotically stable. In the general case, we also provide expressions for the first three derivatives of the Poincaré map associated to a periodic orbit in terms of geometrical quantities.