The following two-player game which we have named Euclid was devised as a source of examples to illustrate the use of a winning strategy algorithm based on the proof of a similar existence theorem[1].

Among the complicated rectilinear patterns employed in Saracenic art there is a group which may be described as “geometrical arabesques,” drawn by a curious method which may be of interest to mathematicians.

In recent years there has been a great development in the design and use of machines for carrying out calculations of various kinds, and this is a technical advance of some importance, not only because of the saving of time and labour in calculations which would be carried out in any case, but still more because it makes it possible to carry out extensive calculations which would be too laborious and time-consuming to undertake without such mechanical or electrical aids.

In the autumn of 1693 the Writing Master of Christ’s Hospital, one John Smith, asked Samuel Pepys the diarist, who was a Governor of Christ’s Hospital and eventually became its Vice-President, for the answer to the following question:

Let Gn be a complete directed graph of order n. That is, Gn has n nodes and every pair of nodes is connected by exactly one directed edge. We say, Gn has the property Sk (after Schütte who posed the problem) if for every set of k nodes there is at least one node in Gn from which the edges go out to the given k nodes.

The classical river crossing problem of the jealous husbands involves three couples who have to cross a river using a boat that holds just two people. The jealousy of the husbands requires that no wife can be in the presence of another man without her husband being present. This can be accomplished in 11 crossings (i.e. one-way trips). Tartaglia gave a sketchy solution for four couples but Bachet pointed out that this was erroneous and that four couples could not get across the river. In 1879, De Fontenay pointed out that four or more couples could cross the river if there was an island in the river and gave a solution for n couples in 8n – 8 crossings. Dudeney improved the solution for n = 4 and Ball noted that this gives 6n – 7 crossings for n couples.

The ideal aimed at in Saracenic designs is that each “ pattern space ” should have either radial or bilateral symmetry. It is surprising that this ideal is so nearly achieved in a pattern in which the very awkward constituent of seven-rayed stars is combined with octagons and regular square-shaped outlines.

1. In this note we consider polynomials of a real variable x and of degree at most n,

The coefficients ak , may be complex. We are given a “mass distribution”, that is, a set of n + 1 real numbers xi , 0 ≤ i ≤ n, such that

Several writers have studied algebras in which multiplication is non-associative, that is, x yz≠xy z. It is necessary in a non-associative algebra to distinguish the possible interpretations of a power xn In a non-commutative non-associative algebra x 2 is unique, x 3 can mean xx 2 or x 2 x; x 4 can mean x xx 2, x x 2 x, x 2 x 2, xx 2x or x 2 x x, x 5 has 14 interpretations; x 6 has 42; and so on. In a commutative non-associative algebra, the possible interpretations are fewer x 3 is unique, x 4 can mean xx 3 or x 2 x 2, x 5 can mean x xx 3, x x 2 x 2 or x 2 x 3, x 6 has 6 interpretations, and so on. The problem considered here is how many meanings are there for xn (A) in a general non-commutative non-associative algebra ? (B) in a general commutative non-associative algebra ? The answer to (A) is 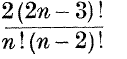I am not able to find any such simple formula for (B).

For numbers a ≥ b ≥ l we shall denote by (a, b) the set of numbers b, b + 1, …, a. We shall say that a set S of numbers is perfect if there exists a sequence containing just one pair of each of the numbers in S, satisfying the condition: for every number r in the set, the two r’s are separated by exactly r places, and having no gaps (a perfect sequence).

If we draw a lot of circles centred on the x-axis and all having radius 1, as in the diagram, then the eye picks out the horizontal lines y = ± 1 running along the tops and bottoms of the circles.

The design shown in Fig. 1 is unusual in the amount of pattern that

goes to one repeat, only one complete repeat being included in the illustration. It is also unusual in that it includes fifteen-rayed stars.

It is well known that any line through the “mid-point” of a parallelogram bisects the area. What can be discovered about lines which bisect the area of a triangle?

Obviously any median bisects the area. It is also bisected by eachline which is parallel to one side and divides the others in the ratio