Article contents
A sieve algorithm based on overlattices
Published online by Cambridge University Press: 01 August 2014
Abstract
In this paper, we present a heuristic algorithm for solving exact, as well as approximate, shortest vector and closest vector problems on lattices. The algorithm can be seen as a modified sieving algorithm for which the vectors of the intermediate sets lie in overlattices or translated cosets of overlattices. The key idea is hence no longer to work with a single lattice but to move the problems around in a tower of related lattices. We initiate the algorithm by sampling very short vectors in an overlattice of the original lattice that admits a quasi-orthonormal basis and hence an efficient enumeration of vectors of bounded norm. Taking sums of vectors in the sample, we construct short vectors in the next lattice. Finally, we obtain solution vector(s) in the initial lattice as a sum of vectors of an overlattice. The complexity analysis relies on the Gaussian heuristic. This heuristic is backed by experiments in low and high dimensions that closely reflect these estimates when solving hard lattice problems in the average case.
This new approach allows us to solve not only shortest vector problems, but also closest vector problems, in lattices of dimension  $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}n$ in time
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}n$ in time 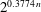 $2^{0.3774\, n}$ using memory
$2^{0.3774\, n}$ using memory 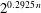 $2^{0.2925\, n}$. Moreover, the algorithm is straightforward to parallelize on most computer architectures.
$2^{0.2925\, n}$. Moreover, the algorithm is straightforward to parallelize on most computer architectures.
Information
- Type
- Research Article
- Information
- LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 49 - 70
- Copyright
- © The Author(s) 2014
References
- 27
- Cited by

