Article contents
Genus-2 curves and Jacobians with a given number of points
Published online by Cambridge University Press: 01 February 2015
Abstract
We study the problem of efficiently constructing a curve 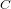 $C$ of genus
$C$ of genus  $2$ over a finite field
$2$ over a finite field  $\mathbb{F}$ for which either the curve
$\mathbb{F}$ for which either the curve 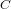 $C$ itself or its Jacobian has a prescribed number
$C$ itself or its Jacobian has a prescribed number 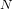 $N$ of
$N$ of  $\mathbb{F}$ -rational points.
$\mathbb{F}$ -rational points.
In the case of the Jacobian, we show that any ‘CM-construction’ to produce the required genus-  $2$ curves necessarily takes time exponential in the size of its input.
$2$ curves necessarily takes time exponential in the size of its input.
On the other hand, we provide an algorithm for producing a genus-  $2$ curve with a given number of points that, heuristically, takes polynomial time for most input values. We illustrate the practical applicability of this algorithm by constructing a genus-
$2$ curve with a given number of points that, heuristically, takes polynomial time for most input values. We illustrate the practical applicability of this algorithm by constructing a genus-  $2$ curve having exactly
$2$ curve having exactly 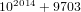 $10^{2014}+9703$ (prime) points, and two genus-
$10^{2014}+9703$ (prime) points, and two genus-  $2$ curves each having exactly
$2$ curves each having exactly 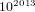 $10^{2013}$ points.
$10^{2013}$ points.
In an appendix we provide a complete parametrization, over an arbitrary base field  $k$ of characteristic neither two nor three, of the family of genus-
$k$ of characteristic neither two nor three, of the family of genus-  $2$ curves over
$2$ curves over  $k$ that have
$k$ that have  $k$ -rational degree-
$k$ -rational degree-  $3$ maps to elliptic curves, including formulas for the genus-
$3$ maps to elliptic curves, including formulas for the genus-  $2$ curves, the associated elliptic curves, and the degree-
$2$ curves, the associated elliptic curves, and the degree-  $3$ maps.
$3$ maps.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2015
References
- 10
- Cited by

