Article contents
Examples of CM curves of genus two defined over the reflex field
Published online by Cambridge University Press: 01 August 2015
Abstract
Van Wamelen [Math. Comp. 68 (1999) no. 225, 307–320] lists 19 curves of genus two over  $\mathbf{Q}$ with complex multiplication (CM). However, for each curve, the CM-field turns out to be cyclic Galois over
$\mathbf{Q}$ with complex multiplication (CM). However, for each curve, the CM-field turns out to be cyclic Galois over 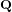 $\mathbf{Q}$ , and the generic case of a non-Galois quartic CM-field did not feature in this list. The reason is that the field of definition in that case always contains the real quadratic subfield of the reflex field.
$\mathbf{Q}$ , and the generic case of a non-Galois quartic CM-field did not feature in this list. The reason is that the field of definition in that case always contains the real quadratic subfield of the reflex field.
We extend Van Wamelen’s list to include curves of genus two defined over this real quadratic field. Our list therefore contains the smallest ‘generic’ examples of CM curves of genus two.
We explain our methods for obtaining this list, including a new height-reduction algorithm for arbitrary hyperelliptic curves over totally real number fields. Unlike Van Wamelen, we also give a proof of our list, which is made possible by our implementation of denominator bounds of Lauter and Viray for Igusa class polynomials.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2015
References
- 11
- Cited by

