Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Klug, Michael
Musty, Michael
Schiavone, Sam
and
Voight, John
2014.
Numerical calculation of three-point branched covers of the projective line.
LMS Journal of Computation and Mathematics,
Vol. 17,
Issue. 1,
p.
379.
Sutherland, Nicole
2015.
Computing Galois groups of polynomials (especially over function fields of prime characteristic).
Journal of Symbolic Computation,
Vol. 71,
Issue. ,
p.
73.
Awtrey, Chad
Mistry, Nakhila
and
Soltz, Nicole
2015.
Centralizers of Transitive Permutation Groups and Applications to Galois Theory.
Missouri Journal of Mathematical Sciences,
Vol. 27,
Issue. 1,
Elsenhans, Andreas-Stephan
2016.
Mathematical and Computational Approaches in Advancing Modern Science and Engineering.
p.
621.
WHITE, GARETH ANDREW
2016.
ALGORITHMS FOR GALOIS GROUP COMPUTATIONS OVER MULTIVARIATE FUNCTION FIELDS.
Bulletin of the Australian Mathematical Society,
Vol. 94,
Issue. 1,
p.
169.
Elsenhans, Andreas-Stephan
2017.
Improved methods for the construction of relative invariants for permutation groups.
Journal of Symbolic Computation,
Vol. 79,
Issue. ,
p.
211.
Krumm, David
2018.
Galois groups in a family of dynatomic polynomials.
Journal of Number Theory,
Vol. 187,
Issue. ,
p.
469.
Elsenhans, Andreas-Stephan
and
Klüners, Jürgen
2019.
Computing subfields of number fields and applications to Galois group computations.
Journal of Symbolic Computation,
Vol. 93,
Issue. ,
p.
1.
Krumm, David
2019.
A finiteness theorem for specializations of dynatomic polynomials.
Algebra & Number Theory,
Vol. 13,
Issue. 4,
p.
963.
Doris, Christopher
2020.
Computing the Galois group of a polynomial over a p-adic field.
International Journal of Number Theory,
Vol. 16,
Issue. 08,
p.
1767.
Krumm, David
and
Sutherland, Nicole
2021.
Galois groups over rational function fields and Explicit Hilbert Irreducibility.
Journal of Symbolic Computation,
Vol. 103,
Issue. ,
p.
108.
Fieker, Claus
and
Sutherland, Nicole
2023.
Computing splitting fields using Galois theory and other Galois constructions.
Journal of Symbolic Computation,
Vol. 116,
Issue. ,
p.
243.
Kodrnja, Iva
and
Muić, Goran
2023.
Hilbert's irreducibility, modular forms, and computation of certain Galois groups.
Journal of Number Theory,
Vol. 253,
Issue. ,
p.
114.
Krumm, David
and
Lacy, Allan
2024.
Dynatomic Galois groups for a family of quadratic rational maps.
International Journal of Number Theory,
Vol. 20,
Issue. 07,
p.
1701.
Korhonen, Mikko
2024.
Maximal Solvable Subgroups of Finite Classical Groups.
Vol. 2346,
Issue. ,
p.
1.
Pritee, Pritee
and
Jakhar, Manjeet singh
2025.
Arithmetic Progression and Binary Recurrence.
International Journal of Applied and Behavioral Sciences,
Vol. 02,
Issue. 01,
p.
109.
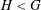 $H<G$ , a
$H<G$ , a 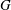 $G$ -relative
$G$ -relative 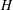 $H$ -invariant, that is a multivariate polynomial
$H$ -invariant, that is a multivariate polynomial 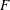 $F$ that is
$F$ that is 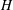 $H$ -invariant, but not
$H$ -invariant, but not 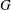 $G$ -invariant. While generic, theoretical methods are known to find such
$G$ -invariant. While generic, theoretical methods are known to find such 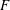 $F$ , in general they yield impractical answers. We give a general method for computing invariants of large degree which improves on previous known methods, as well as various special invariants that are derived from the structure of the groups. We then apply our new invariants to the task of computing the Galois groups of polynomials over the rational numbers, resulting in the first practical degree independent algorithm.
$F$ , in general they yield impractical answers. We give a general method for computing invariants of large degree which improves on previous known methods, as well as various special invariants that are derived from the structure of the groups. We then apply our new invariants to the task of computing the Galois groups of polynomials over the rational numbers, resulting in the first practical degree independent algorithm.
