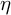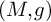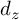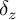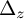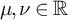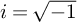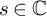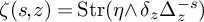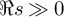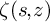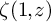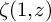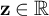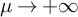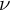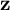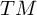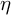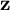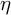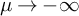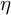1. Introduction
1.1. Witten’s perturbed operators
Let M be a closed n-manifold. For any smooth function h on M, Witten [Reference Witten74] introduced a perturbed de Rham differential operator
![]() $d_\mu =d+\mu \,{dh\wedge }$
, depending on a parameter
$d_\mu =d+\mu \,{dh\wedge }$
, depending on a parameter
![]() $\mu \in \mathbb {R}$
. Endowing M with a Riemannian metric g, we have a corresponding perturbed codifferential operator
$\mu \in \mathbb {R}$
. Endowing M with a Riemannian metric g, we have a corresponding perturbed codifferential operator
![]() $\delta _\mu =\delta -\mu \,{dh\lrcorner }$
, and a perturbed Laplacian
$\delta _\mu =\delta -\mu \,{dh\lrcorner }$
, and a perturbed Laplacian
![]() $\Delta _\mu =d_\mu \delta _\mu +\delta _\mu d_\mu $
. Since
$\Delta _\mu =d_\mu \delta _\mu +\delta _\mu d_\mu $
. Since
![]() $d_\mu =e^{-\mu h}\,d\,e^{\mu h}$
, it defines the same Betti numbers as d. However,
$d_\mu =e^{-\mu h}\,d\,e^{\mu h}$
, it defines the same Betti numbers as d. However,
![]() $\Delta _\mu $
and the usual Laplacian
$\Delta _\mu $
and the usual Laplacian
![]() $\Delta $
have different spectrum in general. In fact, if h is a Morse function and g is Euclidean with respect to Morse coordinates around the critical points, then the spectrum of
$\Delta $
have different spectrum in general. In fact, if h is a Morse function and g is Euclidean with respect to Morse coordinates around the critical points, then the spectrum of
![]() $\Delta _\mu $
develops a long gap as
$\Delta _\mu $
develops a long gap as
![]() $\mu \to +\infty $
, giving rise to the small and large spectrum. The eigenforms of the small/large eigenvalues generate the small/large subcomplex,
$\mu \to +\infty $
, giving rise to the small and large spectrum. The eigenforms of the small/large eigenvalues generate the small/large subcomplex,
![]() $(E_{\mu ,\mathrm {sm/la}},d_\mu )$
. When h is a Morse function, Witten gave a beautiful analytic proof of the Morse inequalities by analyzing the small spectrum. This was refined by subsequent work of Helffer and Sjöstrand [Reference Helffer and Sjöstrand35] and Bismut and Zhang [Reference Bismut, Zhang and Laudenbach10, Reference Bismut and Zhang11], showing that, if moreover
$(E_{\mu ,\mathrm {sm/la}},d_\mu )$
. When h is a Morse function, Witten gave a beautiful analytic proof of the Morse inequalities by analyzing the small spectrum. This was refined by subsequent work of Helffer and Sjöstrand [Reference Helffer and Sjöstrand35] and Bismut and Zhang [Reference Bismut, Zhang and Laudenbach10, Reference Bismut and Zhang11], showing that, if moreover
![]() $X:=-\operatorname {grad} h$
is a Smale vector field, then the Morse complex
$X:=-\operatorname {grad} h$
is a Smale vector field, then the Morse complex
![]() $(\mathbf {C}^{\bullet },\mathbf {d})$
of X can be considered as the limit of
$(\mathbf {C}^{\bullet },\mathbf {d})$
of X can be considered as the limit of
![]() $(E_{\mu ,\mathrm {sm}},d_\mu )$
. More precisely, for certain perturbed Morse complex
$(E_{\mu ,\mathrm {sm}},d_\mu )$
. More precisely, for certain perturbed Morse complex
![]() $(\mathbf {C}^{\bullet },\mathbf {d}_\mu )$
, isomorphic to
$(\mathbf {C}^{\bullet },\mathbf {d}_\mu )$
, isomorphic to
![]() $(\mathbf {C}^{\bullet },\mathbf {d})$
, there is a quasi-isomorphism
$(\mathbf {C}^{\bullet },\mathbf {d})$
, there is a quasi-isomorphism
![]() $\Phi _\mu :(E_{z,\mathrm {sm}},d_\mu )\to (\mathbf {C}^{\bullet },\mathbf {d}_\mu )$
, defined by integration on the unstable cells of the zero points of X, which becomes an isomorphism for
$\Phi _\mu :(E_{z,\mathrm {sm}},d_\mu )\to (\mathbf {C}^{\bullet },\mathbf {d}_\mu )$
, defined by integration on the unstable cells of the zero points of X, which becomes an isomorphism for
![]() $\mu \gg 0$
and almost isometric as
$\mu \gg 0$
and almost isometric as
![]() $\mu \to +\infty $
(after rescaling at every degree).
$\mu \to +\infty $
(after rescaling at every degree).
We can replace
![]() $dh$
with any closed real 1-form
$dh$
with any closed real 1-form
![]() $\eta $
, obtaining a generalization of the Witten’s perturbations,
$\eta $
, obtaining a generalization of the Witten’s perturbations,
![]() $d_\mu $
,
$d_\mu $
,
![]() $\delta _\mu $
and
$\delta _\mu $
and
![]() $\Delta _\mu $
. Now,
$\Delta _\mu $
. Now,
![]() $d_\mu $
need not be gauge equivalent to d, obtaining new twisted Betti numbers
$d_\mu $
need not be gauge equivalent to d, obtaining new twisted Betti numbers
![]() $\beta ^k_\mu $
. However, the numbers
$\beta ^k_\mu $
. However, the numbers
![]() $\beta ^k_\mu $
have well-defined ground values
$\beta ^k_\mu $
have well-defined ground values
![]() $\beta _{\mathrm {No}}^k$
, called the Novikov numbers, which depend upon the de Rham cohomology class
$\beta _{\mathrm {No}}^k$
, called the Novikov numbers, which depend upon the de Rham cohomology class
![]() $[\eta ]\in H^1(M,\mathbb {R})$
. Assume that:
$[\eta ]\in H^1(M,\mathbb {R})$
. Assume that:
-
(a)
 $\eta $
is a Morse form (it has Morse-type zeros), and g is Euclidean with respect to Morse coordinates around the zero points of
$\eta $
is a Morse form (it has Morse-type zeros), and g is Euclidean with respect to Morse coordinates around the zero points of
 $\eta $
.
$\eta $
.
(Some concepts used in this section are recalled in Sections 4.1 and 6.1.) Then
![]() $\Delta _\mu $
also develops a long gap separating a small spectrum and a large spectrum, and the analysis of the small spectrum gives Morse inequalities for the Novikov numbers. Take any auxiliary vector field X such that:
$\Delta _\mu $
also develops a long gap separating a small spectrum and a large spectrum, and the analysis of the small spectrum gives Morse inequalities for the Novikov numbers. Take any auxiliary vector field X such that:
-
(b) X has Morse-type zeros and is gradient-like and Smale; and
-
(c)
 $\eta $
is Lyapunov for X, and
$\eta $
is Lyapunov for X, and
 $\eta $
and g are in standard form with respect to X.
$\eta $
and g are in standard form with respect to X.
Then the small complex approaches a perturbed Morse complex of X. We refer to work by Novikov [Reference Novikov55, Reference Novikov56], Pajitnov [Reference Pajitnov58], Braverman and Farber [Reference Braverman and Farber14], Burghelea and Haller [Reference Burghelea and Haller17, Reference Burghelea and Haller18, Reference Burghelea and Haller20] and Harvey and Minervini [Reference Harvey and Minervini34, Reference Minervini52].
We can similarly define the perturbation
![]() $d_z=d+z\,{\eta \wedge }$
with parameter
$d_z=d+z\,{\eta \wedge }$
with parameter
![]() $z=\mu +i\nu \in \mathbb {C}$
(
$z=\mu +i\nu \in \mathbb {C}$
(
![]() $\mu ,\nu \in \mathbb {R}$
and
$\mu ,\nu \in \mathbb {R}$
and
![]() $i=\sqrt {-1}$
). Its adjoint is
$i=\sqrt {-1}$
). Its adjoint is
![]() $\delta _z=\delta -\bar z\,{\eta \lrcorner }$
, and we have a corresponding perturbed Laplacian
$\delta _z=\delta -\bar z\,{\eta \lrcorner }$
, and we have a corresponding perturbed Laplacian
![]() $\Delta _z=d_z\delta _z+\delta _z d_z$
. As a first step in our study, we prove extensions of the above results to this case, taking limits as
$\Delta _z=d_z\delta _z+\delta _z d_z$
. As a first step in our study, we prove extensions of the above results to this case, taking limits as
![]() $|\mu |\to +\infty $
, uniformly on
$|\mu |\to +\infty $
, uniformly on
![]() $\nu $
. First, assuming (a), we get the long gap in the spectrum of
$\nu $
. First, assuming (a), we get the long gap in the spectrum of
![]() $\Delta _z$
separating the small and large spectrum, which depends only on
$\Delta _z$
separating the small and large spectrum, which depends only on
![]() $\mu $
(Theorem 4.10). Second, assuming (a)–(c), we show that the quasi-isomorphism
$\mu $
(Theorem 4.10). Second, assuming (a)–(c), we show that the quasi-isomorphism
![]() $\Phi _z:(E_{z,\mathrm {sm}},d_z)\to (\mathbf {C}^{\bullet },\mathbf {d}_z)$
becomes an isomorphism for
$\Phi _z:(E_{z,\mathrm {sm}},d_z)\to (\mathbf {C}^{\bullet },\mathbf {d}_z)$
becomes an isomorphism for
![]() $|\mu |\gg 0$
and almost isometric as
$|\mu |\gg 0$
and almost isometric as
![]() $|\mu |\to +\infty $
(Theorem 6.3). To get that the convergence is uniform on
$|\mu |\to +\infty $
(Theorem 6.3). To get that the convergence is uniform on
![]() $\nu $
, the key ingredient is a version of a Sobolev inequality for integers
$\nu $
, the key ingredient is a version of a Sobolev inequality for integers
![]() $m>n/2$
: on smooth complex differential forms,
$m>n/2$
: on smooth complex differential forms,
where
![]() $C_m>0$
is independent of
$C_m>0$
is independent of
![]() $\nu $
and
$\nu $
and
![]() $\|\alpha \|_{m,i\nu }=\sum _{k=0}^m\langle \Delta _{i\nu }^k\alpha ,\alpha \rangle ^{1/2}$
(Proposition 2.2). (The analogous property for
$\|\alpha \|_{m,i\nu }=\sum _{k=0}^m\langle \Delta _{i\nu }^k\alpha ,\alpha \rangle ^{1/2}$
(Proposition 2.2). (The analogous property for
![]() $\Delta _\mu $
is wrong.) Then we adapt the arguments of Bismut and Zhang [Reference Bismut, Zhang and Laudenbach10, Reference Bismut and Zhang11] (see also [Reference Zhang75]).
$\Delta _\mu $
is wrong.) Then we adapt the arguments of Bismut and Zhang [Reference Bismut, Zhang and Laudenbach10, Reference Bismut and Zhang11] (see also [Reference Zhang75]).
The indicated properties of
![]() $\Delta _z$
, holding uniformly on
$\Delta _z$
, holding uniformly on
![]() $\mu $
, depend on remarkable differences between
$\mu $
, depend on remarkable differences between
![]() $\Delta _{i\nu }$
and
$\Delta _{i\nu }$
and
![]() $\Delta _\mu $
. For instance, if
$\Delta _\mu $
. For instance, if
![]() $\eta $
is exact, all operators
$\eta $
is exact, all operators
![]() $\Delta _{i\nu }$
are gauge equivalent, whereas this is not true for the operators
$\Delta _{i\nu }$
are gauge equivalent, whereas this is not true for the operators
![]() $\Delta _\mu $
when
$\Delta _\mu $
when
![]() $\eta \ne 0$
. If
$\eta \ne 0$
. If
![]() $\eta $
is not exact, the operators
$\eta $
is not exact, the operators
![]() $\Delta _{i\nu }$
are not gauge equivalent either. Moreover,
$\Delta _{i\nu }$
are not gauge equivalent either. Moreover,
![]() $\Delta _{i\nu }-\Delta $
is of order one when
$\Delta _{i\nu }-\Delta $
is of order one when
![]() $\nu \ne 0$
, whereas
$\nu \ne 0$
, whereas
![]() $\Delta _{\mu }-\Delta $
is of order zero.
$\Delta _{\mu }-\Delta $
is of order zero.
1.2. Zeta invariants of Morse forms
To begin with,
![]() $\eta $
is only assumed to be an arbitrary closed real 1-form. Let
$\eta $
is only assumed to be an arbitrary closed real 1-form. Let
![]() $\Pi _z^\perp $
and
$\Pi _z^\perp $
and
![]() $\Pi _z^1$
be the orthogonal projections to the images of
$\Pi _z^1$
be the orthogonal projections to the images of
![]() $\Delta _z$
and
$\Delta _z$
and
![]() $d_z$
. We consider a zeta function
$d_z$
. We consider a zeta function
![]() $\zeta (s,z)$
associated with
$\zeta (s,z)$
associated with
![]() $\eta $
and the parameter
$\eta $
and the parameter
![]() $z\in \mathbb {C}$
. As a function of
$z\in \mathbb {C}$
. As a function of
![]() $s\in \mathbb {C}$
, it is the meromorphic extension of the holomorphic function
$s\in \mathbb {C}$
, it is the meromorphic extension of the holomorphic function
defined for
![]() $\Re s\gg 0$
, where
$\Re s\gg 0$
, where
![]() $\operatorname {Str}$
stands for the supertrace. We are interested in the zeta invariant
$\operatorname {Str}$
stands for the supertrace. We are interested in the zeta invariant
![]() $\zeta (1,z)$
that can be interpreted as a renormalization of the supertrace of
$\zeta (1,z)$
that can be interpreted as a renormalization of the supertrace of
![]() ${\eta \wedge }\,d_z^{-1}\Pi ^1_z$
, which is not of trace class by the Weyl’s law. According to the general theory of zeta functions of elliptic operators,
${\eta \wedge }\,d_z^{-1}\Pi ^1_z$
, which is not of trace class by the Weyl’s law. According to the general theory of zeta functions of elliptic operators,
![]() $\zeta (s,z)$
might have a simple pole at
$\zeta (s,z)$
might have a simple pole at
![]() $s=1$
. However, our first main theorem states that
$s=1$
. However, our first main theorem states that
![]() $\zeta (s,z)$
is smooth at
$\zeta (s,z)$
is smooth at
![]() $s=1$
and gives a formula for
$s=1$
and gives a formula for
![]() $\zeta (1,z)$
in terms of the associated heat semigroup.
$\zeta (1,z)$
in terms of the associated heat semigroup.
Theorem 1.1. Let
![]() $M\equiv (M,g)$
be a closed Riemannian n-manifold, and let
$M\equiv (M,g)$
be a closed Riemannian n-manifold, and let
![]() $\eta $
be a closed real
$\eta $
be a closed real
![]() $1$
-form on M. If n is even (resp., odd), then, for any
$1$
-form on M. If n is even (resp., odd), then, for any
![]() $z\in \mathbb {C}$
,
$z\in \mathbb {C}$
,
![]() $s\mapsto \zeta (s,z)$
is smooth on the half-plane
$s\mapsto \zeta (s,z)$
is smooth on the half-plane
![]() $\Re s>0$
(resp.,
$\Re s>0$
(resp.,
![]() $\Re s>1/2$
). Furthermore,
$\Re s>1/2$
). Furthermore,
The existence of the limit of Theorem 1.1 is surprising because
![]() ${\eta \wedge }\,d_z^{-1}e^{-t\Delta _z}\Pi _z^1$
is weakly convergent to
${\eta \wedge }\,d_z^{-1}e^{-t\Delta _z}\Pi _z^1$
is weakly convergent to
![]() ${\eta \wedge }\,d_z^{-1}\Pi _z^1$
. An expression similar to
${\eta \wedge }\,d_z^{-1}\Pi _z^1$
. An expression similar to
![]() $\operatorname {Str}({\eta \wedge }\,d_z^{-1}e^{-t\Delta _z}\Pi _z^1)$
was used by Mrowka, Ruberman and Saveliev to define a cyclic eta invariant [Reference Mrowka, Ruberman and Saveliev53].
$\operatorname {Str}({\eta \wedge }\,d_z^{-1}e^{-t\Delta _z}\Pi _z^1)$
was used by Mrowka, Ruberman and Saveliev to define a cyclic eta invariant [Reference Mrowka, Ruberman and Saveliev53].
Next, we additionally assume that
![]() $\eta $
is a Morse form and use the results described in the previous section. The zeta-function decomposes as the sum of terms defined by the contributions from the small/large spectrum,
$\eta $
is a Morse form and use the results described in the previous section. The zeta-function decomposes as the sum of terms defined by the contributions from the small/large spectrum,
![]() $\zeta _{\mathrm {sm/la}}(s,z)=\zeta _{\mathrm {sm/la}}(s,z,\eta )$
, where
$\zeta _{\mathrm {sm/la}}(s,z)=\zeta _{\mathrm {sm/la}}(s,z,\eta )$
, where
![]() $\zeta _{\mathrm {sm}}(s,z)$
is an entire function of s. Our second main theorem describes the asymptotic behavior of
$\zeta _{\mathrm {sm}}(s,z)$
is an entire function of s. Our second main theorem describes the asymptotic behavior of
![]() $\zeta (1,z)$
as
$\zeta (1,z)$
as
![]() $\mu \to \pm \infty $
, uniformly on
$\mu \to \pm \infty $
, uniformly on
![]() $\nu $
. In fact, since
$\nu $
. In fact, since
it is enough to consider the case where
![]() $\mu \gg 0$
and take the limit as
$\mu \gg 0$
and take the limit as
![]() $\mu \to +\infty $
.
$\mu \to +\infty $
.
We use the current
![]() $\psi (M,\nabla ^M)$
of degree
$\psi (M,\nabla ^M)$
of degree
![]() $n-1$
on
$n-1$
on
![]() $TM$
constructed by Mathai and Quillen in [Reference Mathai and Quillen44], depending on the Levi–Civita connection
$TM$
constructed by Mathai and Quillen in [Reference Mathai and Quillen44], depending on the Levi–Civita connection
![]() $\nabla ^M$
. This current is smooth on the complement of the zero section, where it is given by the solid angle. It is also locally integrable, and its wave front set is contained in the conormal bundle in
$\nabla ^M$
. This current is smooth on the complement of the zero section, where it is given by the solid angle. It is also locally integrable, and its wave front set is contained in the conormal bundle in
![]() $T^* TM$
of the zero section of
$T^* TM$
of the zero section of
![]() $T M$
. Since this set does not meet the conormal bundle of the map
$T M$
. Since this set does not meet the conormal bundle of the map
![]() $X: M \rightarrow T M$
(assuming (b)),
$X: M \rightarrow T M$
(assuming (b)),
![]() $(-X)^*\psi (M,\nabla ^M)$
is well defined as a current on M. Assuming also (a)–(c), consider the real number
$(-X)^*\psi (M,\nabla ^M)$
is well defined as a current on M. Assuming also (a)–(c), consider the real number
which is known to be independent of X [Reference Bismut, Zhang and Laudenbach10, Proposition 6.1].
Now, suppose also that:
-
(d) for every zero point p of X with Morse index k, the maximum value of the integrals of
 $\eta $
along the instantons of X with
$\eta $
along the instantons of X with
 $\alpha $
-limit p only depends on k.
$\alpha $
-limit p only depends on k.
This maximum value is denoted by
![]() $-a_k$
for some
$-a_k$
for some
![]() $a_k>0$
. Let
$a_k>0$
. Let
![]() $m^1_k=\dim d_z(E_{z,\mathrm {sm}}^{k-1})$
for
$m^1_k=\dim d_z(E_{z,\mathrm {sm}}^{k-1})$
for
![]() $\mu \gg 0$
, which is independent of z. Consider also the real number
$\mu \gg 0$
, which is independent of z. Consider also the real number
 $$\begin{align*}\mathbf{z}_{\mathrm{sm}}=\mathbf{z}_{\mathrm{sm}}(M,g,\eta,X)=\sum_{k=1}^n(-1)^k\big(1-e^{a_k}\big)m^1_k\;, \end{align*}$$
$$\begin{align*}\mathbf{z}_{\mathrm{sm}}=\mathbf{z}_{\mathrm{sm}}(M,g,\eta,X)=\sum_{k=1}^n(-1)^k\big(1-e^{a_k}\big)m^1_k\;, \end{align*}$$
and let
![]() $\mathbf {z}=\mathbf {z}(M,g,\eta ,X)=\mathbf {z}_{\mathrm {sm}}+\mathbf {z}_{\mathrm {la}}$
.
$\mathbf {z}=\mathbf {z}(M,g,\eta ,X)=\mathbf {z}_{\mathrm {sm}}+\mathbf {z}_{\mathrm {la}}$
.
Recall that we write
![]() $z= \mu + i \nu $
.
$z= \mu + i \nu $
.
Theorem 1.2. Let
![]() $M\equiv (M,g)$
be a closed Riemannian n-manifold, let
$M\equiv (M,g)$
be a closed Riemannian n-manifold, let
![]() $\eta $
be a closed real
$\eta $
be a closed real
![]() $1$
-form on M satisfying (a) and let X be a vector field on M satisfying (b)–(c).
$1$
-form on M satisfying (a) and let X be a vector field on M satisfying (b)–(c).
-
(i) We have
as $$\begin{align*}\zeta_{\mathrm{la}}(1,z)=\mathbf{z}_{\mathrm{la}}+O(\mu^{-1}) \end{align*}$$
$$\begin{align*}\zeta_{\mathrm{la}}(1,z)=\mathbf{z}_{\mathrm{la}}+O(\mu^{-1}) \end{align*}$$
 $\mu \to +\infty $
, uniformly on
$\mu \to +\infty $
, uniformly on
 $\nu $
.
$\nu $
.
-
(ii) If moreover (d) holds, then
as $$\begin{align*}\zeta_{\mathrm{sm}}(1,z)=\mathbf{z}_{\mathrm{sm}}+O(\mu^{-1}) \end{align*}$$
$$\begin{align*}\zeta_{\mathrm{sm}}(1,z)=\mathbf{z}_{\mathrm{sm}}+O(\mu^{-1}) \end{align*}$$
 $\mu \to +\infty $
, uniformly on
$\mu \to +\infty $
, uniformly on
 $\nu $
.
$\nu $
.
Theorem 1.2 (ii) shows that
![]() $\mathbf {z}_{\mathrm {sm}}$
and
$\mathbf {z}_{\mathrm {sm}}$
and
![]() $\mathbf {z}$
are also independent of X. Thus, X will be omitted in their notation. In the notation of
$\mathbf {z}$
are also independent of X. Thus, X will be omitted in their notation. In the notation of
![]() $\mathbf {z}_{\mathrm {sm/la}}$
and
$\mathbf {z}_{\mathrm {sm/la}}$
and
![]() $\mathbf {z}$
, we may also omit M or g if they are fixed.
$\mathbf {z}$
, we may also omit M or g if they are fixed.
By Equation (1.2), if we take
![]() $\mu \to -\infty $
in Theorem 1.2, we have to replace
$\mu \to -\infty $
in Theorem 1.2, we have to replace
![]() $\mathbf {z}_{\mathrm {sm/la}}(\eta )$
with
$\mathbf {z}_{\mathrm {sm/la}}(\eta )$
with
![]() $-\mathbf {z}_{\mathrm {sm/la}}(-\eta )$
. Descriptions of
$-\mathbf {z}_{\mathrm {sm/la}}(-\eta )$
. Descriptions of
![]() $-\mathbf {z}_{\mathrm {sm/la}}(-\eta )$
are given in Equations (7.9) and (8.1).
$-\mathbf {z}_{\mathrm {sm/la}}(-\eta )$
are given in Equations (7.9) and (8.1).
Our third main theorem is about the prescription of
![]() $\mathbf {z}=\mathbf {z}(M,g,\eta )$
without changing the cohomology class of
$\mathbf {z}=\mathbf {z}(M,g,\eta )$
without changing the cohomology class of
![]() $\eta $
.
$\eta $
.
Theorem 1.3. Let M be a smooth closed n-manifold. If n is even (resp., odd), for all
![]() $\xi \in H^1(M,\mathbb {R})$
and
$\xi \in H^1(M,\mathbb {R})$
and
![]() $\tau \in \mathbb {R}$
(resp.,
$\tau \in \mathbb {R}$
(resp.,
![]() $\tau \gg 0$
), there is some
$\tau \gg 0$
), there is some
![]() $\eta \in \xi $
, a Riemannian metric g and a vector field X satisfying (a)–(d) such that
$\eta \in \xi $
, a Riemannian metric g and a vector field X satisfying (a)–(d) such that
![]() $\pm \mathbf {z}(M,g,\pm \eta )=\tau $
(resp.,
$\pm \mathbf {z}(M,g,\pm \eta )=\tau $
(resp.,
![]() $\mathbf {z}(M,g,\eta )=\tau $
).
$\mathbf {z}(M,g,\eta )=\tau $
).
1.3. A distribution associated to some Morse forms
A trace formula for simple foliated flows on closed foliated manifolds was conjectured by C. Deninger (see, e.g., [Reference Deninger24]). He was motivated by analogies with Weil’s explicit formulas in arithmetics and previous work of Guillemin and Sternberg [Reference Guillemin32]. This trace formula is an expression for a Lefschetz distribution in terms of infinitesimal data of the flow at the fixed points and closed orbits. This Lefschetz distribution should be an analogue of the Lefschetz number for the action induced by the flow on some leafwise cohomology, whose value is a distribution on
![]() $\mathbb {R}$
—the precise definition of these notions is part of the problem. In [Reference Álvarez López and Kordyukov4, Reference López and Kordyukov5], the first two authors proved such a trace formula when the flow has no preserved leaves; see also the contributions [Reference Leichtnam42, Reference Leichtnam43] by the third author. The general case is considerably more involved. In [Reference Álvarez López, Kordyukov and Leichtnam6], we propose a solution to this problem using a few additional ingredients. One of them is the b-trace introduced by Melrose [Reference Melrose46]. Since the b-trace is not really a trace, it produces an extra term, denoted by Z, in the same way as the eta invariant shows up in Index Theory on manifolds with boundary. In our trace formula, the term Z is a contribution from the compact leaves preserved by the flow, which depends on the choice of a form defining the foliation and a metric on the ambient manifold. But Z may not be well defined in general; it will be proved that appropriate choices of the form and the metric guarantee its existence.
$\mathbb {R}$
—the precise definition of these notions is part of the problem. In [Reference Álvarez López and Kordyukov4, Reference López and Kordyukov5], the first two authors proved such a trace formula when the flow has no preserved leaves; see also the contributions [Reference Leichtnam42, Reference Leichtnam43] by the third author. The general case is considerably more involved. In [Reference Álvarez López, Kordyukov and Leichtnam6], we propose a solution to this problem using a few additional ingredients. One of them is the b-trace introduced by Melrose [Reference Melrose46]. Since the b-trace is not really a trace, it produces an extra term, denoted by Z, in the same way as the eta invariant shows up in Index Theory on manifolds with boundary. In our trace formula, the term Z is a contribution from the compact leaves preserved by the flow, which depends on the choice of a form defining the foliation and a metric on the ambient manifold. But Z may not be well defined in general; it will be proved that appropriate choices of the form and the metric guarantee its existence.
Precisely, we would like to define
in the space of tempered distributions on
![]() $\mathbb {R}$
, where
$\mathbb {R}$
, where
![]() $Z_\mu =Z_\mu (M,g,\eta )$
(
$Z_\mu =Z_\mu (M,g,\eta )$
(
![]() $\mu \gg 0$
) should be a tempered distribution defined by
$\mu \gg 0$
) should be a tempered distribution defined by
 $$ \begin{align} \langle Z_\mu,f\rangle=-\frac{1}{2\pi}\int_0^\infty\int_{-\infty}^\infty\operatorname{Str}\left({\eta\wedge}\,\delta_ze^{-u\Delta_z}\right) \,\hat f(\nu)\,d\nu\,du\;, \end{align} $$
$$ \begin{align} \langle Z_\mu,f\rangle=-\frac{1}{2\pi}\int_0^\infty\int_{-\infty}^\infty\operatorname{Str}\left({\eta\wedge}\,\delta_ze^{-u\Delta_z}\right) \,\hat f(\nu)\,d\nu\,du\;, \end{align} $$
for any Schwartz function f, where
![]() $\hat f$
stands for the Fourier transform of f.
$\hat f$
stands for the Fourier transform of f.
Let
![]() $\delta _0$
denote the Dirac distribution at
$\delta _0$
denote the Dirac distribution at
![]() $0$
on
$0$
on
![]() $\mathbb {R}$
. The problem about the definition of Z is solved in our fourth main theorem for the same class of Morse forms as before.
$\mathbb {R}$
. The problem about the definition of Z is solved in our fourth main theorem for the same class of Morse forms as before.
Theorem 1.4. Let
![]() $M\equiv (M,g)$
be a closed Riemannian n-manifold. Let
$M\equiv (M,g)$
be a closed Riemannian n-manifold. Let
![]() $\eta $
be a closed
$\eta $
be a closed
![]() $1$
-form on M satisfying (a), (c) and (d) with some vector field satisfying (b). Then Equations (1.3) and (1.4) define the tempered distribution
$1$
-form on M satisfying (a), (c) and (d) with some vector field satisfying (b). Then Equations (1.3) and (1.4) define the tempered distribution
![]() $Z=\mathbf {z}\delta _0$
.
$Z=\mathbf {z}\delta _0$
.
According to Theorems 1.3 and 1.4, we can choose
![]() $\eta $
and g in the trace formula for foliated flows so that
$\eta $
and g in the trace formula for foliated flows so that
![]() $Z(M,g,\pm \eta )=0$
if n is even, achieving the original expression of Deninger’s conjecture.
$Z(M,g,\pm \eta )=0$
if n is even, achieving the original expression of Deninger’s conjecture.
It looks clear that extensions of Theorems 1.1 to 1.4 with coefficients in flat vector bundles could be similarly proved. We only consider complex coefficients for the sake of simplicity since this is enough for our application.
1.4. Some ideas of the proofs of Theorems 1.1 to 1.4
As mentioned before, the inequality (1.1) is essential to obtain the uniformity on
![]() $\nu $
of our estimates. To prove it, we can take
$\nu $
of our estimates. To prove it, we can take
![]() $\nu =1$
by considering an arbitrary closed real 1-form
$\nu =1$
by considering an arbitrary closed real 1-form
![]() $\eta $
(Proposition 2.2). Let
$\eta $
(Proposition 2.2). Let
![]() $\|\ \|_{m,i\eta }$
be the mth Sobolev norm defined with the perturbed Laplacian
$\|\ \|_{m,i\eta }$
be the mth Sobolev norm defined with the perturbed Laplacian
![]() $\Delta _{i\eta }$
induced by
$\Delta _{i\eta }$
induced by
![]() $i\eta $
as above. By ellipticity,
$i\eta $
as above. By ellipticity,
![]() $\|\ \|_{L^\infty }\le C_{m,i\eta }\|\ \|_{m,i\eta }$
for some
$\|\ \|_{L^\infty }\le C_{m,i\eta }\|\ \|_{m,i\eta }$
for some
![]() $C_{m,i\eta }>0$
depending on
$C_{m,i\eta }>0$
depending on
![]() $\eta $
, which can be chosen to be optimal. For two such forms,
$\eta $
, which can be chosen to be optimal. For two such forms,
![]() $\eta $
and
$\eta $
and
![]() $\eta '$
, the cohomology class
$\eta '$
, the cohomology class
![]() $[\eta -\eta ']$
is in the lattice
$[\eta -\eta ']$
is in the lattice
![]() $2\pi H^1(M,\mathbb {Z})$
of
$2\pi H^1(M,\mathbb {Z})$
of
![]() $H^1(M,\mathbb {R})$
just when
$H^1(M,\mathbb {R})$
just when
![]() $\eta -\eta '=h^*d\theta $
for some smooth map
$\eta -\eta '=h^*d\theta $
for some smooth map
![]() $h:M\to \mathbb {S}^1$
, where
$h:M\to \mathbb {S}^1$
, where
![]() $\theta $
is the multivalued angle function on the circle
$\theta $
is the multivalued angle function on the circle
![]() $\mathbb {S}^1$
. This gives the gauge equivalence
$\mathbb {S}^1$
. This gives the gauge equivalence
![]() $\Delta _{i\eta '}=e^{-ih^*\theta }\,\Delta _{i\eta }\,e^{ih^*\theta }$
, where
$\Delta _{i\eta '}=e^{-ih^*\theta }\,\Delta _{i\eta }\,e^{ih^*\theta }$
, where
![]() $e^{\pm ih^*\theta }$
is well defined on M. It follows that
$e^{\pm ih^*\theta }$
is well defined on M. It follows that
![]() $\eta \mapsto C_{m,i\eta }$
induces a function on the torus
$\eta \mapsto C_{m,i\eta }$
induces a function on the torus
![]() $H^1(M,\mathbb {R})/2\pi H^1(M,\mathbb {Z})$
. On the other hand, every
$H^1(M,\mathbb {R})/2\pi H^1(M,\mathbb {Z})$
. On the other hand, every
![]() $C_{m,i\eta }$
can be estimated in terms of the
$C_{m,i\eta }$
can be estimated in terms of the
![]() $C^m$
norm of
$C^m$
norm of
![]() $\eta $
(Proposition 2.1). Hence, by compactness of
$\eta $
(Proposition 2.1). Hence, by compactness of
![]() $H^1(M,\mathbb {R})/2\pi H^1(M,\mathbb {Z})$
, the values
$H^1(M,\mathbb {R})/2\pi H^1(M,\mathbb {Z})$
, the values
![]() $C_{m,i\eta }$
have an upper bound
$C_{m,i\eta }$
have an upper bound
![]() $C_m$
, which satisfies the desired inequality
$C_m$
, which satisfies the desired inequality
![]() $\|\ \|_{L^\infty }\le C_m\|\ \|_{m,i\eta }$
.
$\|\ \|_{L^\infty }\le C_m\|\ \|_{m,i\eta }$
.
For an arbitrary closed real 1-form
![]() $\eta $
and for all
$\eta $
and for all
![]() $t>0$
and
$t>0$
and
![]() $z\in \mathbb {C}$
, a supersymmetric argument shows that (Proposition 3.7)
$z\in \mathbb {C}$
, a supersymmetric argument shows that (Proposition 3.7)
where
![]() ${\mathsf {N}}$
is the number operator on
${\mathsf {N}}$
is the number operator on
![]() $\Omega (M)$
(Section 2.1.1). Then we apply that the coefficients of the asymptotic expansion of
$\Omega (M)$
(Section 2.1.1). Then we apply that the coefficients of the asymptotic expansion of
![]() $\operatorname {Str}({\mathsf {N}} e^{-t\Delta _z})$
as
$\operatorname {Str}({\mathsf {N}} e^{-t\Delta _z})$
as
![]() $t\downarrow 0$
(the derived heat trace invariants) are independent of z up to order n [Reference Bismut, Zhang and Laudenbach10, Theorem 7.10] (see also [Reference Álvarez López and Gilkey3]). Thus, by Equation (1.5), the coefficients of the asymptotic expansion of
$t\downarrow 0$
(the derived heat trace invariants) are independent of z up to order n [Reference Bismut, Zhang and Laudenbach10, Theorem 7.10] (see also [Reference Álvarez López and Gilkey3]). Thus, by Equation (1.5), the coefficients of the asymptotic expansion of
![]() $\operatorname {Str}({\eta \wedge }\,D_ze^{-t\Delta _z})$
as
$\operatorname {Str}({\eta \wedge }\,D_ze^{-t\Delta _z})$
as
![]() $t\downarrow 0$
vanish up to order n. Now, Theorem 1.1 follows by the general theory of zeta functions of operators (Section 3.6).
$t\downarrow 0$
vanish up to order n. Now, Theorem 1.1 follows by the general theory of zeta functions of operators (Section 3.6).
The theta function
![]() $\theta (s,z)$
is defined like
$\theta (s,z)$
is defined like
![]() $\zeta (s,z)$
by using
$\zeta (s,z)$
by using
![]() $-\operatorname {Str}({\mathsf {N}}\Delta _z^{-s}\Pi _z^\perp )$
instead of
$-\operatorname {Str}({\mathsf {N}}\Delta _z^{-s}\Pi _z^\perp )$
instead of
![]() $\operatorname {Str}({\eta \wedge }\,\delta _z\Delta _z^{-s}\Pi _z^\perp )$
. Assuming the hypotheses of Theorem 1.2, write
$\operatorname {Str}({\eta \wedge }\,\delta _z\Delta _z^{-s}\Pi _z^\perp )$
. Assuming the hypotheses of Theorem 1.2, write
![]() $\theta (s,z)$
as the sum of contributions from the small/large spectrum,
$\theta (s,z)$
as the sum of contributions from the small/large spectrum,
![]() $\theta _{\mathrm {sm/la}}(s,z)$
, as before. Thus,
$\theta _{\mathrm {sm/la}}(s,z)$
, as before. Thus,
![]() $e^{\theta '(0,z)/2}$
is the factor used to define the Ray–Singer metric on
$e^{\theta '(0,z)/2}$
is the factor used to define the Ray–Singer metric on
![]() $\det H_z^{\bullet }(M)$
[Reference Bismut, Zhang and Laudenbach10], where the prime denotes
$\det H_z^{\bullet }(M)$
[Reference Bismut, Zhang and Laudenbach10], where the prime denotes
![]() $\partial _s$
. We obtain (Corollary 5.10)
$\partial _s$
. We obtain (Corollary 5.10)
This equality allows us to use the deep relation between the Ray–Singer metric and the Milnor metric on
![]() $\det H_z^{\bullet }(M)$
, proved by Bismut and Zhang [Reference Bismut, Zhang and Laudenbach10, Reference Bismut and Zhang11]. To apply this result, we have to make involved computations concerning derivatives with respect to z of the orthogonal projection to
$\det H_z^{\bullet }(M)$
, proved by Bismut and Zhang [Reference Bismut, Zhang and Laudenbach10, Reference Bismut and Zhang11]. To apply this result, we have to make involved computations concerning derivatives with respect to z of the orthogonal projection to
![]() $E_{z,\mathrm {sm}}$
and of other operators related with the isomorphism
$E_{z,\mathrm {sm}}$
and of other operators related with the isomorphism
![]() $\Phi _z:E_{z,\mathrm { sm}}\to \mathbf {C}^{\bullet }$
, as well as estimates of the asymptotic behavior as
$\Phi _z:E_{z,\mathrm { sm}}\to \mathbf {C}^{\bullet }$
, as well as estimates of the asymptotic behavior as
![]() $\mu \to +\infty $
of these operators and their derivatives (Sections 4.4, 4.5, 6.3, 6.4 and 7.2). In this way, we obtain that
$\mu \to +\infty $
of these operators and their derivatives (Sections 4.4, 4.5, 6.3, 6.4 and 7.2). In this way, we obtain that
![]() $\zeta _{\mathrm {la}}(1,z)$
is asymptotic to
$\zeta _{\mathrm {la}}(1,z)$
is asymptotic to
![]() $\mathbf {z}_{\mathrm {la}}$
as
$\mathbf {z}_{\mathrm {la}}$
as
![]() $\mu \to +\infty $
(Section 7.2). This proves Theorem 1.2 (i).
$\mu \to +\infty $
(Section 7.2). This proves Theorem 1.2 (i).
When
![]() $\eta $
is exact, we show this asymptotic expression of
$\eta $
is exact, we show this asymptotic expression of
![]() $\zeta _{\mathrm {la}}(1,z)$
assuming only (a) (Section 5.5), without using Equation (1.6) and the indicated strong result of Bismut and Zhang. Instead, we apply that the index density of
$\zeta _{\mathrm {la}}(1,z)$
assuming only (a) (Section 5.5), without using Equation (1.6) and the indicated strong result of Bismut and Zhang. Instead, we apply that the index density of
![]() $\Delta _z$
is independent of z, also proved by Bismut and Zhang [Reference Bismut, Zhang and Laudenbach10, Theorem 13.4]; see also [Reference Álvarez López and Gilkey1, Theorem 1.5] and [Reference Álvarez López, Kordyukov and Leichtnam6].
$\Delta _z$
is independent of z, also proved by Bismut and Zhang [Reference Bismut, Zhang and Laudenbach10, Theorem 13.4]; see also [Reference Álvarez López and Gilkey1, Theorem 1.5] and [Reference Álvarez López, Kordyukov and Leichtnam6].
On the other hand, given any
![]() $\xi \in H^1(M,\mathbb {R})$
and a vector field X satisfying (b), we prove that there is some
$\xi \in H^1(M,\mathbb {R})$
and a vector field X satisfying (b), we prove that there is some
![]() $\eta \in \xi $
and a metric g satisfying (a), (c) and (d) (Theorem 8.1). This can be considered as an extension of a theorem of Smale stating the existence of nice Morse functions [Reference Smale69, Theorem B] (the case where
$\eta \in \xi $
and a metric g satisfying (a), (c) and (d) (Theorem 8.1). This can be considered as an extension of a theorem of Smale stating the existence of nice Morse functions [Reference Smale69, Theorem B] (the case where
![]() $\xi =0$
). Its proof is relegated to Appendix A because of its different nature.
$\xi =0$
). Its proof is relegated to Appendix A because of its different nature.
The properties (a)–(d) are used to give an asymptotic description of
![]() $\mathbf {d}_z$
as
$\mathbf {d}_z$
as
![]() $\mu \to +\infty $
(Section 8.2). From this asymptotic description and using that
$\mu \to +\infty $
(Section 8.2). From this asymptotic description and using that
![]() $\Phi _z:E_{z,\mathrm { sm}}\to \mathbf {C}^{\bullet }$
is an isomorphism for
$\Phi _z:E_{z,\mathrm { sm}}\to \mathbf {C}^{\bullet }$
is an isomorphism for
![]() $\mu \gg 0$
, we get upper and lower bounds of the nonzero small spectrum of
$\mu \gg 0$
, we get upper and lower bounds of the nonzero small spectrum of
![]() $\Delta _z$
(Theorem 8.4), which are independent of
$\Delta _z$
(Theorem 8.4), which are independent of
![]() $\nu $
. This is a partial extension of accurate descriptions of the nonzero small eigenvalues achieved in the case where
$\nu $
. This is a partial extension of accurate descriptions of the nonzero small eigenvalues achieved in the case where
![]() $\eta $
is exact and the parameter is real [Reference Le Peutrec, Nier and Viterbo41, Reference Michel48]. With the same procedure and using the bounds of the nonzero small spectrum, it also follows that
$\eta $
is exact and the parameter is real [Reference Le Peutrec, Nier and Viterbo41, Reference Michel48]. With the same procedure and using the bounds of the nonzero small spectrum, it also follows that
![]() $\zeta _{\mathrm {sm}}(1,z)=\mathbf {z}_{\mathrm {sm}}+O(\mu ^{-1})$
as
$\zeta _{\mathrm {sm}}(1,z)=\mathbf {z}_{\mathrm {sm}}+O(\mu ^{-1})$
as
![]() $\mu \to +\infty $
(Section 8.4), showing Theorem 1.2 (ii).
$\mu \to +\infty $
(Section 8.4), showing Theorem 1.2 (ii).
Next, by modifying
![]() $\eta $
and X around its zero points of index
$\eta $
and X around its zero points of index
![]() $0$
and n, without changing the cohomology class of
$0$
and n, without changing the cohomology class of
![]() $\eta $
, we can achieve any real number as
$\eta $
, we can achieve any real number as
![]() $\pm \mathbf {z}(\pm \eta )$
if n is even, or any large enough real number as
$\pm \mathbf {z}(\pm \eta )$
if n is even, or any large enough real number as
![]() $\mathbf {z}(\eta )$
if n is odd (Section 9). This shows Theorem 1.3.
$\mathbf {z}(\eta )$
if n is odd (Section 9). This shows Theorem 1.3.
If it is possible to switch the order of integration in Equation (1.4),
 $$ \begin{align} \langle Z_\mu,f\rangle &=-\frac{1}{2\pi}\int_{-\infty}^\infty\int_0^\infty\operatorname{Str}\left({\eta\wedge}\,\delta_ze^{-u\Delta_z}\right)\,\hat f(\nu)\,du\,d\nu\nonumber\\ &=\frac{1}{2\pi}\int_{-\infty}^\infty\lim_{t\downarrow0} \operatorname{Str}\left({\eta\wedge}\,d_z^{-1}e^{-t\Delta_z}\Pi_z^1\right)\,\hat f(\nu)\,d\nu\;, \end{align} $$
$$ \begin{align} \langle Z_\mu,f\rangle &=-\frac{1}{2\pi}\int_{-\infty}^\infty\int_0^\infty\operatorname{Str}\left({\eta\wedge}\,\delta_ze^{-u\Delta_z}\right)\,\hat f(\nu)\,du\,d\nu\nonumber\\ &=\frac{1}{2\pi}\int_{-\infty}^\infty\lim_{t\downarrow0} \operatorname{Str}\left({\eta\wedge}\,d_z^{-1}e^{-t\Delta_z}\Pi_z^1\right)\,\hat f(\nu)\,d\nu\;, \end{align} $$
then Theorem 1.4 is an easy consequence of Theorem 1.1. Thus, it only remains to prove that both Equations (1.4) and (1.7) define the same tempered distribution
![]() $Z_\mu $
. This follows from the Lebesgue’s dominated convergence theorem and Fubini’s theorem (Section 10). The verification of the hypothesis of the Fubini’s theorem requires the above lower estimate of the nonzero spectrum.
$Z_\mu $
. This follows from the Lebesgue’s dominated convergence theorem and Fubini’s theorem (Section 10). The verification of the hypothesis of the Fubini’s theorem requires the above lower estimate of the nonzero spectrum.
For the readers convenience, we recall the needed preliminaries about the many topics involved: Witten’s perturbations, Morse forms, asymptotic expansions of heat kernels, zeta functions of operators, Morse and Smale vector fields, the Morse complex and Quillen metrics (Reidemeister, Milnor and Ray–Singer metrics).
2. Witten’s perturbations
2.1. Preliminaries on the Witten’s perturbations
2.1.1. Basic notation
Let
![]() $M\equiv (M,g)$
be a closed Riemannian n-manifold. For any smooth Euclidean/Hermitian vector bundle E over M, let
$M\equiv (M,g)$
be a closed Riemannian n-manifold. For any smooth Euclidean/Hermitian vector bundle E over M, let
![]() $C^m(M;E)$
,
$C^m(M;E)$
,
![]() $C^\infty (M;E)$
,
$C^\infty (M;E)$
,
![]() $L^2(M;E)$
,
$L^2(M;E)$
,
![]() $L^\infty (M;E)$
and
$L^\infty (M;E)$
and
![]() $H^m(M;E)$
denote the spaces of distributional sections that are
$H^m(M;E)$
denote the spaces of distributional sections that are
![]() $C^m$
,
$C^m$
,
![]() $C^\infty $
,
$C^\infty $
,
![]() $L^2$
,
$L^2$
,
![]() $L^\infty $
and of Sobolev order m, respectively; as usual, E is removed from this notation if it is the trivial line bundle. Consider the induced scalar product
$L^\infty $
and of Sobolev order m, respectively; as usual, E is removed from this notation if it is the trivial line bundle. Consider the induced scalar product
![]() $\langle \ ,\ \rangle $
and norm
$\langle \ ,\ \rangle $
and norm
![]() $\|\ \|$
on
$\|\ \|$
on
![]() $L^2(M;E)$
, and the induced norm
$L^2(M;E)$
, and the induced norm
![]() $\|\ \|_{L^\infty }$
on
$\|\ \|_{L^\infty }$
on
![]() $L^\infty (M;E)$
. Fix also norms,
$L^\infty (M;E)$
. Fix also norms,
![]() $\|\ \|_m$
on every
$\|\ \|_m$
on every
![]() $H^m(M;E)$
and
$H^m(M;E)$
and
![]() $\|\ \|_{C^m}$
on
$\|\ \|_{C^m}$
on
![]() $C^m(M;E)$
. If P is the orthogonal projection of
$C^m(M;E)$
. If P is the orthogonal projection of
![]() $L^2(M;E)$
to some closed subspace V, then
$L^2(M;E)$
to some closed subspace V, then
![]() $P^\perp $
denotes the orthogonal projection to
$P^\perp $
denotes the orthogonal projection to
![]() $V^\perp $
. Let
$V^\perp $
. Let
![]() $o(E)$
denote the flat real orientation line bundle of E. It is said that E is orientable when
$o(E)$
denote the flat real orientation line bundle of E. It is said that E is orientable when
![]() $o(E)$
is trivial. In this case, an orientation of E is described by a (necessarily smooth) nonvanishing flat section
$o(E)$
is trivial. In this case, an orientation of E is described by a (necessarily smooth) nonvanishing flat section
![]() $\mathcal {O}_E$
of
$\mathcal {O}_E$
of
![]() $o(E)$
; for simplicity, it will be said that
$o(E)$
; for simplicity, it will be said that
![]() $\mathcal {O}_E$
itself is an orientation. In particular, an orientation of M is described using
$\mathcal {O}_E$
itself is an orientation. In particular, an orientation of M is described using
![]() $o(M):=o(TM)$
. The flat line bundle
$o(M):=o(TM)$
. The flat line bundle
![]() $o(E)\otimes o(E)$
is always trivial.
$o(E)\otimes o(E)$
is always trivial.
Let
![]() $T_{\mathbb {C}} M=TM\otimes \mathbb {C}$
and
$T_{\mathbb {C}} M=TM\otimes \mathbb {C}$
and
![]() $T_{\mathbb {C}}^*M=T^*M\otimes \mathbb {C}$
. The exterior bundle with coefficients in
$T_{\mathbb {C}}^*M=T^*M\otimes \mathbb {C}$
. The exterior bundle with coefficients in
![]() $\mathbb {K}=\mathbb {R},\mathbb {C}$
is denoted by
$\mathbb {K}=\mathbb {R},\mathbb {C}$
is denoted by
![]() $\Lambda _{\mathbb {K}}=\Lambda _{\mathbb {K}} M$
, and let
$\Lambda _{\mathbb {K}}=\Lambda _{\mathbb {K}} M$
, and let
![]() $\Omega (M,\mathbb {K})=C^\infty (M;\Lambda _{\mathbb {K}})$
; in particular,
$\Omega (M,\mathbb {K})=C^\infty (M;\Lambda _{\mathbb {K}})$
; in particular,
![]() $C^\infty (M,\mathbb {K})=\Omega ^0(M,\mathbb {K})$
. The Levi–Civita connection is denoted by
$C^\infty (M,\mathbb {K})=\Omega ^0(M,\mathbb {K})$
. The Levi–Civita connection is denoted by
![]() $\nabla =\nabla ^M$
. As usual, d and
$\nabla =\nabla ^M$
. As usual, d and
![]() $\delta $
denote the de Rham derivative and coderivative, and let
$\delta $
denote the de Rham derivative and coderivative, and let
![]() $D=d+\delta $
and
$D=d+\delta $
and
![]() $\Delta =D^2=d\delta +\delta d$
(the Laplacian). Let
$\Delta =D^2=d\delta +\delta d$
(the Laplacian). Let
![]() $Z(M,\mathbb {K})$
and
$Z(M,\mathbb {K})$
and
![]() $B(M,\mathbb {K})$
denote the kernel and image of d in
$B(M,\mathbb {K})$
denote the kernel and image of d in
![]() $\Omega (M,\mathbb {K})$
. Thus,
$\Omega (M,\mathbb {K})$
. Thus,
![]() $H^{\bullet }(M,\mathbb {K})=Z(M,\mathbb {K})/B(M,\mathbb {K})$
is the de Rham cohomology with coefficients in
$H^{\bullet }(M,\mathbb {K})=Z(M,\mathbb {K})/B(M,\mathbb {K})$
is the de Rham cohomology with coefficients in
![]() $\mathbb {K}$
. We typically consider complex coefficients, so we will omit
$\mathbb {K}$
. We typically consider complex coefficients, so we will omit
![]() $\mathbb {K}$
from all of the above notation just when
$\mathbb {K}$
from all of the above notation just when
![]() $\mathbb {K}=\mathbb {C}$
. Take
$\mathbb {K}=\mathbb {C}$
. Take
![]() $\|\ \|_m$
and
$\|\ \|_m$
and
![]() $\|\ \|_{C^m}$
given on
$\|\ \|_{C^m}$
given on
![]() $\Omega (M)$
by
$\Omega (M)$
by
 $$\begin{align*}\|\alpha\|_m=\sum_{k=0}^m\|D^k\alpha\|\;,\quad\|\alpha\|_{C^m}=\sum_{k=0}^m\|\nabla^k\alpha\|_{L^\infty}. \end{align*}$$
$$\begin{align*}\|\alpha\|_m=\sum_{k=0}^m\|D^k\alpha\|\;,\quad\|\alpha\|_{C^m}=\sum_{k=0}^m\|\nabla^k\alpha\|_{L^\infty}. \end{align*}$$
In particular, we take
![]() $\|\ \|=\|\ \|_0$
and
$\|\ \|=\|\ \|_0$
and
![]() $\|\ \|_{C^0}=\|\ \|_{L^\infty }|_{C^0(M;E)}$
.
$\|\ \|_{C^0}=\|\ \|_{L^\infty }|_{C^0(M;E)}$
.
On any graded vector space
![]() $V^{\bullet }$
, let
$V^{\bullet }$
, let
![]() $\mathsf {w}$
and
$\mathsf {w}$
and
![]() ${\mathsf {N}}$
be the degree involution and number operator; that is,
${\mathsf {N}}$
be the degree involution and number operator; that is,
![]() $\mathsf {w}=(-1)^k$
and
$\mathsf {w}=(-1)^k$
and
![]() ${\mathsf {N}}=k$
on
${\mathsf {N}}=k$
on
![]() $V^k$
. For any homogeneous linear operator between graded vector spaces,
$V^k$
. For any homogeneous linear operator between graded vector spaces,
![]() $T:V^{\bullet }\to W^{\bullet }$
, the notation
$T:V^{\bullet }\to W^{\bullet }$
, the notation
![]() $T_k$
means its precomposition with the canonical projection of
$T_k$
means its precomposition with the canonical projection of
![]() $V^{\bullet }$
to
$V^{\bullet }$
to
![]() $V^k$
. If T is of degree l (
$V^k$
. If T is of degree l (
![]() $T(V^k)\subset W^{k+l}$
for all k), then
$T(V^k)\subset W^{k+l}$
for all k), then
For any
![]() $\eta \in \Omega ^1(M,\mathbb {R})$
with
$\eta \in \Omega ^1(M,\mathbb {R})$
with
![]() $\eta ^\sharp =X\in \mathfrak {X}(M):=C^\infty (M;TM)$
(
$\eta ^\sharp =X\in \mathfrak {X}(M):=C^\infty (M;TM)$
(
![]() $\eta =g(X,{\cdot })$
), let
$\eta =g(X,{\cdot })$
), let
![]() $\mathcal {L}_X$
and
$\mathcal {L}_X$
and
![]() $\iota _X$
denote the Lie derivative and interior product with respect to X, and let
$\iota _X$
denote the Lie derivative and interior product with respect to X, and let
![]() ${\eta \lrcorner }=-(\eta \wedge )^*=-\iota _X$
. Using the identity
${\eta \lrcorner }=-(\eta \wedge )^*=-\iota _X$
. Using the identity
![]() $\operatorname {Cl}(T^*M)\equiv \Lambda _{\mathbb {R}} M$
defined by the symbol of filtered algebras, the left Clifford multiplication by
$\operatorname {Cl}(T^*M)\equiv \Lambda _{\mathbb {R}} M$
defined by the symbol of filtered algebras, the left Clifford multiplication by
![]() $\eta $
is
$\eta $
is
![]() $c(\eta )={\eta \wedge }+{\eta \lrcorner }$
, and the composition of
$c(\eta )={\eta \wedge }+{\eta \lrcorner }$
, and the composition of
![]() $\mathsf {w}$
with the right Clifford multiplication by
$\mathsf {w}$
with the right Clifford multiplication by
![]() $\eta $
is
$\eta $
is
![]() $\hat c(\eta )={\eta \wedge }-{\eta \lrcorner }$
; in particular,
$\hat c(\eta )={\eta \wedge }-{\eta \lrcorner }$
; in particular,
![]() $c(\eta )^*=-c(\eta )$
and
$c(\eta )^*=-c(\eta )$
and
![]() $\hat c(\eta )^*=\hat c(\eta )$
. Recall that, for any
$\hat c(\eta )^*=\hat c(\eta )$
. Recall that, for any
![]() $h\in C^\infty (M,\mathbb {R})$
,
$h\in C^\infty (M,\mathbb {R})$
,
In the whole paper, unless otherwise indicated, we will use the following notation without further comment. We use constants
![]() $C,c>0$
without even mentioning their existence, and their precise values may change from line to line. We may add subindices or primes to these constants if needed. We also use a complex parameter
$C,c>0$
without even mentioning their existence, and their precise values may change from line to line. We may add subindices or primes to these constants if needed. We also use a complex parameter
![]() $z=\mu +i\nu \in \mathbb {C}$
(
$z=\mu +i\nu \in \mathbb {C}$
(
![]() $\mu ,\nu \in \mathbb {R}$
and
$\mu ,\nu \in \mathbb {R}$
and
![]() $i=\sqrt {-1}$
). Recall that
$i=\sqrt {-1}$
). Recall that
![]() $\partial _z=(\partial _\mu -i\partial _\nu )/2$
and
$\partial _z=(\partial _\mu -i\partial _\nu )/2$
and
![]() $\partial _{\bar z}=(\partial _\mu +i\partial _\nu )/2$
.
$\partial _{\bar z}=(\partial _\mu +i\partial _\nu )/2$
.
2.1.2. Perturbations defined by a closed real 1-form
For any
![]() $\omega \in Z^1(M)$
, we have the Witten’s type perturbations
$\omega \in Z^1(M)$
, we have the Witten’s type perturbations
![]() $d_\omega $
,
$d_\omega $
,
![]() $\delta _\omega $
,
$\delta _\omega $
,
![]() $D_\omega $
and
$D_\omega $
and
![]() $\Delta _\omega $
of d,
$\Delta _\omega $
of d,
![]() $\delta $
, D and
$\delta $
, D and
![]() $\Delta $
. Given
$\Delta $
. Given
![]() $\eta \in Z^1(M,\mathbb {R})$
and
$\eta \in Z^1(M,\mathbb {R})$
and
![]() $z\in \mathbb {C}$
, we write
$z\in \mathbb {C}$
, we write
![]() $d_z=d_{z\eta }$
,
$d_z=d_{z\eta }$
,
![]() $\delta _z=\delta _{z\eta} $
,
$\delta _z=\delta _{z\eta} $
,
![]() $D_z=D_{z\eta }$
and
$D_z=D_{z\eta }$
and
![]() $\Delta _z=\Delta _{z\eta }$
. These operators have the following expressions:
$\Delta _z=\Delta _{z\eta }$
. These operators have the following expressions:
 $$ \begin{align} \left. \begin{aligned} d_z&=d+z\,\eta\wedge\;,\quad \delta_z=d_z^*=\delta-\bar z\,{\eta\lrcorner}\;,\\ D_z&=d_z+\delta_z=D+\mu\hat c(\eta)+i\nu c(\eta) =D_{i\nu}+\mu\hat c(\eta)\;,\\ \Delta_z&=D_z^2=d_z\delta_z+\delta_zd_z =\Delta+\mu\mathsf{H}_\eta+i\nu\mathsf{J}_\eta+|z|^2|\eta|^2\\ &=\Delta_{i\nu}+\mu\mathsf{H}_\eta+\mu^2|\eta|^2\;, \end{aligned} \right\} \end{align} $$
$$ \begin{align} \left. \begin{aligned} d_z&=d+z\,\eta\wedge\;,\quad \delta_z=d_z^*=\delta-\bar z\,{\eta\lrcorner}\;,\\ D_z&=d_z+\delta_z=D+\mu\hat c(\eta)+i\nu c(\eta) =D_{i\nu}+\mu\hat c(\eta)\;,\\ \Delta_z&=D_z^2=d_z\delta_z+\delta_zd_z =\Delta+\mu\mathsf{H}_\eta+i\nu\mathsf{J}_\eta+|z|^2|\eta|^2\\ &=\Delta_{i\nu}+\mu\mathsf{H}_\eta+\mu^2|\eta|^2\;, \end{aligned} \right\} \end{align} $$
where, for
![]() $X=\eta ^\sharp $
,
$X=\eta ^\sharp $
,
Note that
![]() $\mathsf {H}_\eta $
is of order zero and
$\mathsf {H}_\eta $
is of order zero and
![]() $\mathsf {J}_\eta $
of order one.
$\mathsf {J}_\eta $
of order one.
As families of operators,
![]() $d_z$
and
$d_z$
and
![]() $\delta _z$
are holomorphic and antiholomorphic functions of z, respectively. More precisely, it follows from Equation (2.3) that
$\delta _z$
are holomorphic and antiholomorphic functions of z, respectively. More precisely, it follows from Equation (2.3) that
 $$ \begin{align} \left. \begin{alignedat}{3} \partial_zd_z&={\eta\wedge}\;,&\quad\partial_z\delta_z&=0\;,&\quad\partial_z\Delta_z&={\eta\wedge}\,\delta_z+\delta_z\,{\eta\wedge}\;,\\ \partial_{\bar z}d_z&=0\;,&\quad\partial_{\bar z}\delta_z&=-{\eta\lrcorner}\;,&\quad\partial_{\bar z}\Delta_z&=-{\eta\lrcorner}\,d_z-d_z\,{\eta\lrcorner}. \end{alignedat} \right\} \end{align} $$
$$ \begin{align} \left. \begin{alignedat}{3} \partial_zd_z&={\eta\wedge}\;,&\quad\partial_z\delta_z&=0\;,&\quad\partial_z\Delta_z&={\eta\wedge}\,\delta_z+\delta_z\,{\eta\wedge}\;,\\ \partial_{\bar z}d_z&=0\;,&\quad\partial_{\bar z}\delta_z&=-{\eta\lrcorner}\;,&\quad\partial_{\bar z}\Delta_z&=-{\eta\lrcorner}\,d_z-d_z\,{\eta\lrcorner}. \end{alignedat} \right\} \end{align} $$
The operator
![]() $d_z$
defines an elliptic complex on
$d_z$
defines an elliptic complex on
![]() $\Omega (M)$
, whose cohomology is denoted by
$\Omega (M)$
, whose cohomology is denoted by
![]() $H_z^{\bullet }(M)$
. Since
$H_z^{\bullet }(M)$
. Since
![]() $d_z$
has the same principal symbol as d, it is a generalized Dirac complex and
$d_z$
has the same principal symbol as d, it is a generalized Dirac complex and
![]() $\Delta _z$
a self-adjoint generalized Laplacian [Reference Berline, Getzler and Vergne7, Definition 2.2]. If
$\Delta _z$
a self-adjoint generalized Laplacian [Reference Berline, Getzler and Vergne7, Definition 2.2]. If
![]() $\theta =\eta +dh$
for some
$\theta =\eta +dh$
for some
![]() $h\in C^\infty (M,\mathbb {R})$
, then the multiplication operator
$h\in C^\infty (M,\mathbb {R})$
, then the multiplication operator
is an isomorphism of differential complexes, and therefore it induces an isomorphism
![]() $H_{z\theta }^{\bullet }(M)\cong H_{z\eta }^{\bullet }(M)$
. Thus, the isomorphism class of
$H_{z\theta }^{\bullet }(M)\cong H_{z\eta }^{\bullet }(M)$
. Thus, the isomorphism class of
![]() $H_z^{\bullet }(M)$
only depends on
$H_z^{\bullet }(M)$
only depends on
![]() $\xi :=[\eta ]\in H^1(M,\mathbb {R})$
and
$\xi :=[\eta ]\in H^1(M,\mathbb {R})$
and
![]() $z\in \mathbb {C}$
. By ellipticity,
$z\in \mathbb {C}$
. By ellipticity,
![]() $D_z$
and
$D_z$
and
![]() $\Delta _z$
have a discrete spectrum, and there is a decomposition, equalities and isomorphism of Hodge type,
$\Delta _z$
have a discrete spectrum, and there is a decomposition, equalities and isomorphism of Hodge type,
 $$ \begin{align} \left. \begin{gathered} \Omega(M)=\ker\Delta_z\oplus\operatorname{im} d_z\oplus\operatorname{im}\delta_z\;,\\ \ker\Delta_z=\ker D_z=\ker d_z\cap\ker\delta_z\;,\quad \operatorname{im}\Delta_z=\operatorname{im} D_z=\operatorname{im} d_z\oplus\operatorname{im}\delta_z\;,\\ H_z^{\bullet}(M)\cong\ker\Delta_z\;, \end{gathered} \right\} \end{align} $$
$$ \begin{align} \left. \begin{gathered} \Omega(M)=\ker\Delta_z\oplus\operatorname{im} d_z\oplus\operatorname{im}\delta_z\;,\\ \ker\Delta_z=\ker D_z=\ker d_z\cap\ker\delta_z\;,\quad \operatorname{im}\Delta_z=\operatorname{im} D_z=\operatorname{im} d_z\oplus\operatorname{im}\delta_z\;,\\ H_z^{\bullet}(M)\cong\ker\Delta_z\;, \end{gathered} \right\} \end{align} $$
as topological vector spaces. The orthogonal projections of
![]() $\Omega (M)$
to
$\Omega (M)$
to
![]() $\ker \Delta _z$
,
$\ker \Delta _z$
,
![]() $\operatorname {im} d_z$
and
$\operatorname {im} d_z$
and
![]() $\operatorname {im}\delta _z$
are denoted by
$\operatorname {im}\delta _z$
are denoted by
![]() $\Pi _z=\Pi ^0_z$
,
$\Pi _z=\Pi ^0_z$
,
![]() $\Pi ^1_z$
and
$\Pi ^1_z$
and
![]() $\Pi ^2_z$
, respectively; thus,
$\Pi ^2_z$
, respectively; thus,
![]() $\Pi _z^\perp =\Pi ^1_z+\Pi ^2_z$
. The restrictions
$\Pi _z^\perp =\Pi ^1_z+\Pi ^2_z$
. The restrictions
![]() $d_z:\operatorname {im}\delta _z\to \operatorname {im} d_z$
,
$d_z:\operatorname {im}\delta _z\to \operatorname {im} d_z$
,
![]() $\delta _z:\operatorname {im} d_z\to \operatorname {im}\delta _z$
and
$\delta _z:\operatorname {im} d_z\to \operatorname {im}\delta _z$
and
![]() $D_z:\operatorname {im} D_z\to \operatorname {im} D_z$
are topological isomorphisms, and therefore the compositions
$D_z:\operatorname {im} D_z\to \operatorname {im} D_z$
are topological isomorphisms, and therefore the compositions
![]() $d_z^{-1}\Pi _z^1$
,
$d_z^{-1}\Pi _z^1$
,
![]() $\delta _z^{-1}\Pi _z^2$
and
$\delta _z^{-1}\Pi _z^2$
and
![]() $D_z^{-1}\Pi _z^\perp $
are defined and continuous on
$D_z^{-1}\Pi _z^\perp $
are defined and continuous on
![]() $\Omega (M)$
. For every degree k, the diagram
$\Omega (M)$
. For every degree k, the diagram

is commutative. The twisted Betti numbers
![]() $\beta _z^k=\beta _z^k(M,\xi )=\dim H_z^k(M)$
give rise to the usual Euler characteristic [Reference Farber28, Proposition 1.40],
$\beta _z^k=\beta _z^k(M,\xi )=\dim H_z^k(M)$
give rise to the usual Euler characteristic [Reference Farber28, Proposition 1.40],
(This is also a consequence of the index theorem.) For every degree k,
![]() $\beta _z^k$
is independent of z outside a discrete subset of
$\beta _z^k$
is independent of z outside a discrete subset of
![]() $\mathbb {C}$
, where
$\mathbb {C}$
, where
![]() $\beta _z^k$
jumps (Mityagin and Novikov [Reference Novikov57, Theorem 1]). This ground value of
$\beta _z^k$
jumps (Mityagin and Novikov [Reference Novikov57, Theorem 1]). This ground value of
![]() $\beta _z^k$
is called the k-th Novikov Betti number, denoted by
$\beta _z^k$
is called the k-th Novikov Betti number, denoted by
![]() $\beta _{\mathrm {No}}^k=\beta _{\mathrm {No}}^k(M,\xi )$
. It will be shown in Section 6.2.4 that
$\beta _{\mathrm {No}}^k=\beta _{\mathrm {No}}^k(M,\xi )$
. It will be shown in Section 6.2.4 that
(When z is real, this is proved in [Reference Farber27, Theorem 2.8], [Reference Braverman and Farber14, Lemma 1.3], [Reference Burghelea and Haller18, Proposition 4].) Thus, the discrete set of parameters
![]() $z\in \mathbb {C}$
with
$z\in \mathbb {C}$
with
![]() $\beta _z^k(M,\xi )>\beta _{\mathrm {No}}^k(M,\xi )$
for some degree k is contained in a strip
$\beta _z^k(M,\xi )>\beta _{\mathrm {No}}^k(M,\xi )$
for some degree k is contained in a strip
![]() $|\mu |\le C$
.
$|\mu |\le C$
.
By Equation (2.3) and since
![]() $\eta $
is real, for all
$\eta $
is real, for all
![]() $\alpha \in \Omega (M)$
,
$\alpha \in \Omega (M)$
,
So conjugation induces
![]() $\mathbb {C}$
-antilinear isomorphisms
$\mathbb {C}$
-antilinear isomorphisms
yielding
![]() $\beta _z^k=\beta _{\bar z}^k$
.
$\beta _z^k=\beta _{\bar z}^k$
.
2.1.3. Case of an exact form
When
![]() $\eta =dh$
for some
$\eta =dh$
for some
![]() $h\in C^\infty (M,\mathbb {R})$
, we have the original Witten’s perturbations, which satisfy
$h\in C^\infty (M,\mathbb {R})$
, we have the original Witten’s perturbations, which satisfy
 $$ \begin{align} \left. \begin{gathered} d_z=e^{-zh}\,d\,e^{zh}=e^{-i\nu h}\,d_\mu\,e^{i\nu h}\;,\quad \delta_z=e^{\bar zh}\,\delta\,e^{-\bar zh}=e^{-i\nu h}\,\delta_\mu\,e^{i\nu h}\;,\\ D_z=e^{-i\nu h}\,D_\mu\,e^{i\nu h}\;,\quad \Delta_z=e^{-i\nu h}\,\Delta_\mu\,e^{i\nu h}. \end{gathered} \right\} \end{align} $$
$$ \begin{align} \left. \begin{gathered} d_z=e^{-zh}\,d\,e^{zh}=e^{-i\nu h}\,d_\mu\,e^{i\nu h}\;,\quad \delta_z=e^{\bar zh}\,\delta\,e^{-\bar zh}=e^{-i\nu h}\,\delta_\mu\,e^{i\nu h}\;,\\ D_z=e^{-i\nu h}\,D_\mu\,e^{i\nu h}\;,\quad \Delta_z=e^{-i\nu h}\,\Delta_\mu\,e^{i\nu h}. \end{gathered} \right\} \end{align} $$
Thus, the multiplication operator
is an isomorphism of differential complexes. Therefore,
![]() $H_z^{\bullet }(M)\cong H^{\bullet }(M)$
, yielding
$H_z^{\bullet }(M)\cong H^{\bullet }(M)$
, yielding
![]() $\beta _z^k=\beta ^k=\beta ^k(M)$
(the kth Betti number) in this case. Moreover multiplication by
$\beta _z^k=\beta ^k=\beta ^k(M)$
(the kth Betti number) in this case. Moreover multiplication by
![]() $e^{i\nu h}$
defines a unitary isomorphism
$e^{i\nu h}$
defines a unitary isomorphism
![]() $\ker \Delta _z\cong \ker \Delta _\mu $
.
$\ker \Delta _z\cong \ker \Delta _\mu $
.
2.1.4. Interpretation of the closed form as a flat connection
There is a unique flat connection
![]() $\nabla ^{M\times \mathbb {C}}$
on the trivial complex line bundle
$\nabla ^{M\times \mathbb {C}}$
on the trivial complex line bundle
![]() $M\times \mathbb {C}$
so that
$M\times \mathbb {C}$
so that
![]() $\nabla ^{M\times \mathbb {C}}1=\eta $
. The corresponding flat complex line bundle is denoted by
$\nabla ^{M\times \mathbb {C}}1=\eta $
. The corresponding flat complex line bundle is denoted by
![]() $\mathcal {L}=\mathcal {L}_\eta $
. Note that
$\mathcal {L}=\mathcal {L}_\eta $
. Note that
![]() $\mathcal {L}_{z\eta }=\mathcal {L}^z$
. Let
$\mathcal {L}_{z\eta }=\mathcal {L}^z$
. Let
![]() $(\Omega (M,\mathcal {L}^z)=(\Omega (M),d^{\mathcal {L}^z})$
be the de Rham complex with coefficients in
$(\Omega (M,\mathcal {L}^z)=(\Omega (M),d^{\mathcal {L}^z})$
be the de Rham complex with coefficients in
![]() $\mathcal {L}^z$
. It is well known that
$\mathcal {L}^z$
. It is well known that
![]() $d_z=d^{\mathcal {L}^z}$
on
$d_z=d^{\mathcal {L}^z}$
on
![]() $\Omega (M)=\Omega (M,\mathcal {L}^z)$
, and therefore
$\Omega (M)=\Omega (M,\mathcal {L}^z)$
, and therefore
![]() $H^{\bullet }(M,\mathcal {L}^z)=H_z^{\bullet }(M)$
. Since every
$H^{\bullet }(M,\mathcal {L}^z)=H_z^{\bullet }(M)$
. Since every
![]() $\mathcal {L}^z$
is canonically trivial as a line bundle, it has a canonical Hermitian structure
$\mathcal {L}^z$
is canonically trivial as a line bundle, it has a canonical Hermitian structure
![]() $g^{\mathcal {L}^z}$
. An easy local computation shows that (see the example given in [Reference Bismut, Zhang and Laudenbach10, pp. 11–12])
$g^{\mathcal {L}^z}$
. An easy local computation shows that (see the example given in [Reference Bismut, Zhang and Laudenbach10, pp. 11–12])
2.1.5. Perturbed operators on oriented manifolds
The mappings
![]() $(\alpha ,\beta )\mapsto \alpha \wedge \beta $
and
$(\alpha ,\beta )\mapsto \alpha \wedge \beta $
and
![]() $(\alpha ,\beta )\mapsto \alpha \wedge \bar \beta $
induce respective bilinear and sesquilinear maps,
$(\alpha ,\beta )\mapsto \alpha \wedge \bar \beta $
induce respective bilinear and sesquilinear maps,
as follows from the interpretation of
![]() $d_z$
given in Section 2.1.4, or by a direct check.
$d_z$
given in Section 2.1.4, or by a direct check.
Now, assume M is oriented. Then the above maps and integration on M define respective nondegenerate bilinear and sesquilinear pairings
Thus
Let
![]() $\star $
and
$\star $
and
![]() $\bar \star $
denote the
$\bar \star $
denote the
![]() $\mathbb {C}$
-linear and
$\mathbb {C}$
-linear and
![]() $\mathbb {C}$
-antilinear extensions to
$\mathbb {C}$
-antilinear extensions to
![]() $\Lambda M$
of the Hodge operator
$\Lambda M$
of the Hodge operator
![]() $\star $
on
$\star $
on
![]() $\Lambda _{\mathbb {R}} M$
, respectively. These operators are determined by the conditions
$\Lambda _{\mathbb {R}} M$
, respectively. These operators are determined by the conditions
for
![]() $\alpha ,\beta \in \Omega (M)$
, where
$\alpha ,\beta \in \Omega (M)$
, where
![]() $\operatorname {dvol}=\star 1$
is the volume form. The following equalities on
$\operatorname {dvol}=\star 1$
is the volume form. The following equalities on
![]() $\Omega ^k(M)$
follow from Equation (2.3) and the usual equalities relating
$\Omega ^k(M)$
follow from Equation (2.3) and the usual equalities relating
![]() $\star $
, d,
$\star $
, d,
![]() $\delta $
,
$\delta $
,
![]() ${\eta \wedge }$
and
${\eta \wedge }$
and
![]() ${\eta \lrcorner }$
(see, e.g., [Reference Roe63, Chapters 1 and 3], [Reference Gilkey31, Section 1.5.2], [Reference Berline, Getzler and Vergne7, Section 3.6]):
${\eta \lrcorner }$
(see, e.g., [Reference Roe63, Chapters 1 and 3], [Reference Gilkey31, Section 1.5.2], [Reference Berline, Getzler and Vergne7, Section 3.6]):
 $$ \begin{align} \left. \begin{alignedat}{3} d_z\,\star&=(-1)^k\star\,\delta_{-\bar z}\;,&\quad\delta_z\,\star&=(-1)^{k+1}\star\,d_{-\bar z}\;,&\quad \Delta_z\,\star&=\star\,\Delta_{-\bar z}\;,\\ d_z\,\bar\star&=(-1)^k\;\bar\star\;\delta_{-z}\;,&\quad\delta_z\;\bar\star&=(-1)^{k+1}\,\bar\star\;d_{-z}\;,&\quad \Delta_z\;\bar\star&=\bar\star\;\Delta_{-z}. \end{alignedat} \right\} \end{align} $$
$$ \begin{align} \left. \begin{alignedat}{3} d_z\,\star&=(-1)^k\star\,\delta_{-\bar z}\;,&\quad\delta_z\,\star&=(-1)^{k+1}\star\,d_{-\bar z}\;,&\quad \Delta_z\,\star&=\star\,\Delta_{-\bar z}\;,\\ d_z\,\bar\star&=(-1)^k\;\bar\star\;\delta_{-z}\;,&\quad\delta_z\;\bar\star&=(-1)^{k+1}\,\bar\star\;d_{-z}\;,&\quad \Delta_z\;\bar\star&=\bar\star\;\Delta_{-z}. \end{alignedat} \right\} \end{align} $$
Then we get a linear isomorphism
![]() $\star :\ker \Delta _z\to \ker \Delta _{-\bar z}$
and an antilinear isomorphism
$\star :\ker \Delta _z\to \ker \Delta _{-\bar z}$
and an antilinear isomorphism
![]() $\bar \star :\ker \Delta _z\to \ker \Delta _{-z}$
, inducing a linear isomorphism
$\bar \star :\ker \Delta _z\to \ker \Delta _{-z}$
, inducing a linear isomorphism
![]() $H_z^k(M)\cong H_{-\bar z}^{n-k}(M)$
and an antilinear isomorphism
$H_z^k(M)\cong H_{-\bar z}^{n-k}(M)$
and an antilinear isomorphism
![]() $H_z^k(M)\cong H_{-z}^{n-k}(M)$
by Equation (2.6).
$H_z^k(M)\cong H_{-z}^{n-k}(M)$
by Equation (2.6).
2.2. Perturbation of the Sobolev norms
For
![]() $m\in \mathbb {N}_0$
and
$m\in \mathbb {N}_0$
and
![]() $\omega \in Z^1(M)$
, define the norm
$\omega \in Z^1(M)$
, define the norm
![]() $\|\ \|_{m,\omega }$
on
$\|\ \|_{m,\omega }$
on
![]() $H^m(M;\Lambda )$
by
$H^m(M;\Lambda )$
by
 $$\begin{align*}\|\alpha\|_{m,\omega}=\sum_{k=0}^m\big\|D_\omega^k\alpha\big\|. \end{align*}$$
$$\begin{align*}\|\alpha\|_{m,\omega}=\sum_{k=0}^m\big\|D_\omega^k\alpha\big\|. \end{align*}$$
Proposition 2.1. For all
![]() $\omega \in Z^1(M)$
and
$\omega \in Z^1(M)$
and
![]() $\alpha \in H^m(M;\Lambda )$
,
$\alpha \in H^m(M;\Lambda )$
,
 $$ \begin{gather*} \|\alpha\|_{m,\omega}\le C_m\sum_{k=0}^m\|\omega\|_{C^k}^{m-k}\|\alpha\|_k\;,\quad \|\alpha\|_m\le C_m\sum_{k=0}^m\|\omega\|_{C^k}^{m-k}\|\alpha\|_{k,\omega}. \end{gather*} $$
$$ \begin{gather*} \|\alpha\|_{m,\omega}\le C_m\sum_{k=0}^m\|\omega\|_{C^k}^{m-k}\|\alpha\|_k\;,\quad \|\alpha\|_m\le C_m\sum_{k=0}^m\|\omega\|_{C^k}^{m-k}\|\alpha\|_{k,\omega}. \end{gather*} $$
Proof. We proceed by induction on m. We have
![]() $\|\ \|_{0,\omega }=\|\ \|$
. Now, take
$\|\ \|_{0,\omega }=\|\ \|$
. Now, take
![]() $m>0$
and assume these inequalities hold for
$m>0$
and assume these inequalities hold for
![]() $m-1$
. For
$m-1$
. For
![]() $\eta \in Z^1(M,\mathbb {R})$
and
$\eta \in Z^1(M,\mathbb {R})$
and
![]() $\alpha \in \Omega (M)$
, we have
$\alpha \in \Omega (M)$
, we have
Applying these inequalities to the real and imaginary parts of
![]() $\omega $
and using the induction hypothesis and Equation (2.3), we get
$\omega $
and using the induction hypothesis and Equation (2.3), we get
 $$ \begin{align*} \|\alpha\|_{m,\omega}&=\|\alpha\|+\|D_{\omega}\alpha\|_{m-1,\omega} \le\|\alpha\|+C_{m-1}\sum_{k=0}^{m-1}\|\omega\|_{C^k}^{m-1-k}\|D_{\omega}\alpha\|_k\\ &\le\|\alpha\|+C_{m-1}\sum_{k=0}^{m-1}\|\omega\|_{C^k}^{m-1-k}\big(\|D\alpha\|_k+C^{\prime}_k\|\omega\|_{C^k}\|\alpha\|_k\big)\\ &\le\|\alpha\|+C_{m-1}\sum_{k=0}^{m-1}\|\omega\|_{C^k}^{m-1-k}\big(\|\alpha\|_{k+1}+C^{\prime}_k\|\omega\|_{C^k}\|\alpha\|_k\big)\\ &\le C_m\sum_{l=0}^m\|\omega\|_{C^l}^{m-l}\|\alpha\|_l\;, \end{align*} $$
$$ \begin{align*} \|\alpha\|_{m,\omega}&=\|\alpha\|+\|D_{\omega}\alpha\|_{m-1,\omega} \le\|\alpha\|+C_{m-1}\sum_{k=0}^{m-1}\|\omega\|_{C^k}^{m-1-k}\|D_{\omega}\alpha\|_k\\ &\le\|\alpha\|+C_{m-1}\sum_{k=0}^{m-1}\|\omega\|_{C^k}^{m-1-k}\big(\|D\alpha\|_k+C^{\prime}_k\|\omega\|_{C^k}\|\alpha\|_k\big)\\ &\le\|\alpha\|+C_{m-1}\sum_{k=0}^{m-1}\|\omega\|_{C^k}^{m-1-k}\big(\|\alpha\|_{k+1}+C^{\prime}_k\|\omega\|_{C^k}\|\alpha\|_k\big)\\ &\le C_m\sum_{l=0}^m\|\omega\|_{C^l}^{m-l}\|\alpha\|_l\;, \end{align*} $$
 $$ \begin{align*} \|\alpha\|_m&=\|\alpha\|+\|D\alpha\|_{m-1} \le\|\alpha\|+\|D_{\omega}\alpha\|_{m-1}+C^{\prime}_{m-1}\|\omega\|_{C^{m-1}}\|\alpha\|_{m-1}\\ &\le\|\alpha\|+C_{m-1}\sum_{k=0}^{m-1}\big(\|\omega\|_{C^k}^{m-1-k}\|D_{\omega}\alpha\|_{k,\omega} +C^{\prime}_{m-1}\|\omega\|_{C^k}^{m-k}\|\alpha\|_{k,\omega}\big)\\ &\le\|\alpha\|+C_{m-1}\sum_{k=0}^{m-1}\big(\|\omega\|_{C^k}^{m-1-k}\|\alpha\|_{k+1,\omega} +C^{\prime}_{m-1}\|\omega\|_{C^k}^{m-k}\|\alpha\|_{k,\omega}\big)\\ &\le C_m\sum_{l=0}^m\|\omega\|_{C^l}^{m-l}\|\alpha\|_{l,\omega}. \; \end{align*} $$
$$ \begin{align*} \|\alpha\|_m&=\|\alpha\|+\|D\alpha\|_{m-1} \le\|\alpha\|+\|D_{\omega}\alpha\|_{m-1}+C^{\prime}_{m-1}\|\omega\|_{C^{m-1}}\|\alpha\|_{m-1}\\ &\le\|\alpha\|+C_{m-1}\sum_{k=0}^{m-1}\big(\|\omega\|_{C^k}^{m-1-k}\|D_{\omega}\alpha\|_{k,\omega} +C^{\prime}_{m-1}\|\omega\|_{C^k}^{m-k}\|\alpha\|_{k,\omega}\big)\\ &\le\|\alpha\|+C_{m-1}\sum_{k=0}^{m-1}\big(\|\omega\|_{C^k}^{m-1-k}\|\alpha\|_{k+1,\omega} +C^{\prime}_{m-1}\|\omega\|_{C^k}^{m-k}\|\alpha\|_{k,\omega}\big)\\ &\le C_m\sum_{l=0}^m\|\omega\|_{C^l}^{m-l}\|\alpha\|_{l,\omega}. \; \end{align*} $$
Let
![]() $Z(M,\mathbb {Z})\subset Z(M,\mathbb {R})$
denote the graded additive subgroup of forms that represent cohomology classes in the image of the canonical homomorphism
$Z(M,\mathbb {Z})\subset Z(M,\mathbb {R})$
denote the graded additive subgroup of forms that represent cohomology classes in the image of the canonical homomorphism
![]() $H^{\bullet }(M,\mathbb {Z})\to H^{\bullet }(M,\mathbb {R})$
. Recall that we can consider
$H^{\bullet }(M,\mathbb {Z})\to H^{\bullet }(M,\mathbb {R})$
. Recall that we can consider
![]() $H^1(M,\mathbb {Z})$
as a lattice in
$H^1(M,\mathbb {Z})$
as a lattice in
![]() $H^1(M,\mathbb {R})$
by the universal coefficient theorem for cohomology. Let
$H^1(M,\mathbb {R})$
by the universal coefficient theorem for cohomology. Let
![]() $\theta $
be the multivalued angle function on
$\theta $
be the multivalued angle function on
![]() $\mathbb {S}^1$
. Then
$\mathbb {S}^1$
. Then
![]() $d\theta $
is the angular form on
$d\theta $
is the angular form on
![]() $\mathbb {S}^1$
with
$\mathbb {S}^1$
with
![]() $\int _{\mathbb {S}^1}d\theta =2\pi $
. For
$\int _{\mathbb {S}^1}d\theta =2\pi $
. For
![]() $\eta \in Z^1(M,\mathbb {R})$
, we have
$\eta \in Z^1(M,\mathbb {R})$
, we have
![]() $\eta \in 2\pi Z^1(M,\mathbb {Z})$
if and only if there is some smooth map
$\eta \in 2\pi Z^1(M,\mathbb {Z})$
if and only if there is some smooth map
![]() $h:M\to \mathbb {S}^1$
such that
$h:M\to \mathbb {S}^1$
such that
![]() $\eta =h^*d\theta $
(see, e.g., [Reference Farber28, Lemma 2.1]).
$\eta =h^*d\theta $
(see, e.g., [Reference Farber28, Lemma 2.1]).
In Proposition 2.1, the dependence of the constants on
![]() $\omega $
cannot be avoided. For instance, for
$\omega $
cannot be avoided. For instance, for
![]() $M=\mathbb {S}^1$
with the standard metric
$M=\mathbb {S}^1$
with the standard metric
![]() $g=(d\theta )^2$
, we have
$g=(d\theta )^2$
, we have
![]() $\|1\|_m=\sqrt {2\pi }$
, whereas
$\|1\|_m=\sqrt {2\pi }$
, whereas
![]() $\|1\|_{m,i\eta }=\sqrt {2\pi }\sum _{k=0}^m|\nu |^k$
for
$\|1\|_{m,i\eta }=\sqrt {2\pi }\sum _{k=0}^m|\nu |^k$
for
![]() $\eta =\nu \,d\theta $
(
$\eta =\nu \,d\theta $
(
![]() $\nu \in \mathbb {R}$
). However, the following version of a Sobolev inequality for
$\nu \in \mathbb {R}$
). However, the following version of a Sobolev inequality for
![]() $\|\ \|_{m,i\eta }$
involves a constant independent of
$\|\ \|_{m,i\eta }$
involves a constant independent of
![]() $\eta $
.
$\eta $
.
Proposition 2.2. If
![]() $m>n/2$
, for all
$m>n/2$
, for all
![]() $\eta \in Z^1(M,\mathbb {R})$
and
$\eta \in Z^1(M,\mathbb {R})$
and
![]() $\alpha \in H^m(M;\Lambda )$
,
$\alpha \in H^m(M;\Lambda )$
,
Proof. By the Sobolev embedding theorem, we have
 $$\begin{align*}C_{m,i\eta}:=\sup_{0\ne\alpha\in\Omega(M)}\frac{\|\alpha\|_{L^\infty}}{\|\alpha\|_{m,i\eta}}>0. \end{align*}$$
$$\begin{align*}C_{m,i\eta}:=\sup_{0\ne\alpha\in\Omega(M)}\frac{\|\alpha\|_{L^\infty}}{\|\alpha\|_{m,i\eta}}>0. \end{align*}$$
Take any
![]() $\eta \in Z^1(M,\mathbb {R})$
and
$\eta \in Z^1(M,\mathbb {R})$
and
![]() $\omega \in 2\pi Z^1(M,\mathbb {Z})$
, and let
$\omega \in 2\pi Z^1(M,\mathbb {Z})$
, and let
![]() $\eta '=\eta +\omega $
. Then
$\eta '=\eta +\omega $
. Then
![]() $\omega =h^*d\theta $
for some smooth function
$\omega =h^*d\theta $
for some smooth function
![]() $h:M\to \mathbb {S}^1$
. Since the difference between the multiple values of
$h:M\to \mathbb {S}^1$
. Since the difference between the multiple values of
![]() $\theta $
at every point of
$\theta $
at every point of
![]() $\mathbb {S}^1$
are in
$\mathbb {S}^1$
are in
![]() $2\pi \mathbb {Z}$
, the functions
$2\pi \mathbb {Z}$
, the functions
![]() $e^{\pm ih^*\theta }$
are well defined and smooth on M. Moreover, applying Equation (2.11) locally, we get
$e^{\pm ih^*\theta }$
are well defined and smooth on M. Moreover, applying Equation (2.11) locally, we get
![]() $D_{i\eta '}=e^{-ih^*\theta }\,D_{i\eta }\,e^{ih^*\theta }$
. So, for
$D_{i\eta '}=e^{-ih^*\theta }\,D_{i\eta }\,e^{ih^*\theta }$
. So, for
![]() $0\ne \alpha \in \Omega (M)$
,
$0\ne \alpha \in \Omega (M)$
,
 $$ \begin{align*} \|\alpha\|_{L^\infty}&=\|e^{i\,h^*\theta}\alpha\|_{L^\infty}\le C_{m,i\eta}\|e^{ih^*\theta}\alpha\|_{m,i\eta}\\ &=C_{m,i\eta}\sum_{k=0}^m\|D_{i\eta}^k\,e^{ih^*\theta}\alpha\| =C_{m,i\eta}\sum_{k=0}^m\|e^{-ih^*\theta}\,D_{i\eta}^k\,e^{ih^*\theta}\alpha\|\\ &=C_{m,i\eta}\sum_{k=0}^m\|D_{i\eta'}^k\alpha\| =C_{m,i\eta}\|\alpha\|_{m,i\eta'}. \end{align*} $$
$$ \begin{align*} \|\alpha\|_{L^\infty}&=\|e^{i\,h^*\theta}\alpha\|_{L^\infty}\le C_{m,i\eta}\|e^{ih^*\theta}\alpha\|_{m,i\eta}\\ &=C_{m,i\eta}\sum_{k=0}^m\|D_{i\eta}^k\,e^{ih^*\theta}\alpha\| =C_{m,i\eta}\sum_{k=0}^m\|e^{-ih^*\theta}\,D_{i\eta}^k\,e^{ih^*\theta}\alpha\|\\ &=C_{m,i\eta}\sum_{k=0}^m\|D_{i\eta'}^k\alpha\| =C_{m,i\eta}\|\alpha\|_{m,i\eta'}. \end{align*} $$
This shows that
Since
![]() $2\pi H^1(M,\mathbb {Z})$
is a lattice in
$2\pi H^1(M,\mathbb {Z})$
is a lattice in
![]() $H^1(M,\mathbb {R})$
, there is a compact subset
$H^1(M,\mathbb {R})$
, there is a compact subset
![]() $K\subset H^1(M,\mathbb {R})$
such that
$K\subset H^1(M,\mathbb {R})$
such that
Take a linear subspace
![]() $V\subset Z^1(M,\mathbb {R})$
such that the canonical projection
$V\subset Z^1(M,\mathbb {R})$
such that the canonical projection
![]() $V\to H^1(M,\mathbb {R})$
is an isomorphism, and let
$V\to H^1(M,\mathbb {R})$
is an isomorphism, and let
![]() $L\subset V$
be the compact subset that corresponds to K. By Equation (2.18),
$L\subset V$
be the compact subset that corresponds to K. By Equation (2.18),
Moreover, L is bounded with respect to
![]() $\|\ \|_{C^m}$
. Therefore, by Proposition 2.1, for all
$\|\ \|_{C^m}$
. Therefore, by Proposition 2.1, for all
![]() $\eta \in L$
and
$\eta \in L$
and
![]() $\alpha \in \Omega (M)$
,
$\alpha \in \Omega (M)$
,
yielding
The result follows from Equations (2.17), (2.19) and (2.20).
Given
![]() $\eta \in Z^1(M,\mathbb {R})$
, we write
$\eta \in Z^1(M,\mathbb {R})$
, we write
![]() $\|\ \|_{m,z}=\|\ \|_{m,z\eta }$
. Proposition 2.1 has the following direct consequence.
$\|\ \|_{m,z}=\|\ \|_{m,z\eta }$
. Proposition 2.1 has the following direct consequence.
Corollary 2.3. For all
![]() $\alpha \in H^m(M;\Lambda )$
and
$\alpha \in H^m(M;\Lambda )$
and
![]() $z\in \mathbb {C}$
,
$z\in \mathbb {C}$
,
 $$\begin{align*}\|\alpha\|_{m,z}\le C_m\sum_{k=0}^m|z|^{m-k}\|\alpha\|_k\;,\quad \|\alpha\|_m\le C_m\sum_{k=0}^m|z|^{m-k}\|\alpha\|_{k,z}. \end{align*}$$
$$\begin{align*}\|\alpha\|_{m,z}\le C_m\sum_{k=0}^m|z|^{m-k}\|\alpha\|_k\;,\quad \|\alpha\|_m\le C_m\sum_{k=0}^m|z|^{m-k}\|\alpha\|_{k,z}. \end{align*}$$
Proposition 2.4. For all
![]() $\alpha \in H^1(M;\Lambda )$
and
$\alpha \in H^1(M;\Lambda )$
and
![]() $z\in \mathbb {C}$
,
$z\in \mathbb {C}$
,
Proof. By Equations (2.3) and (2.16),
 $$ \begin{align*} \|\alpha\|_{1,z}&=\|\alpha\|+\|D_z\alpha\| \le\|\alpha\|+\|D_{i\nu}\alpha\|+C'|\mu|\|\alpha\| \le C\big(\|\alpha\|_{1,i\nu}+|\mu|\|\alpha\|\big)\;,\\ \|\alpha\|_{1,i\nu}&=\|\alpha\|+\|D_{i\nu}\alpha\| \le\|\alpha\|+\|D_z\alpha\|+C'|\mu|\|\alpha\| \le C\big(\|\alpha\|_{1,z}+|\mu|\|\alpha\|\big). \; \end{align*} $$
$$ \begin{align*} \|\alpha\|_{1,z}&=\|\alpha\|+\|D_z\alpha\| \le\|\alpha\|+\|D_{i\nu}\alpha\|+C'|\mu|\|\alpha\| \le C\big(\|\alpha\|_{1,i\nu}+|\mu|\|\alpha\|\big)\;,\\ \|\alpha\|_{1,i\nu}&=\|\alpha\|+\|D_{i\nu}\alpha\| \le\|\alpha\|+\|D_z\alpha\|+C'|\mu|\|\alpha\| \le C\big(\|\alpha\|_{1,z}+|\mu|\|\alpha\|\big). \; \end{align*} $$
3. Zeta invariants of closed real 1-forms
3.1. Preliminaries on asymptotic expansions of heat kernels
Let A be a positive semidefinite symmetric elliptic differential operator of order a, and B a differential operator of order b; both of them are defined in
![]() $C^\infty (M;E)$
for some Hermitian vector bundle E over M. Then
$C^\infty (M;E)$
for some Hermitian vector bundle E over M. Then
![]() $Be^{-tA}$
is a smoothing operator with Schwartz kernel
$Be^{-tA}$
is a smoothing operator with Schwartz kernel
![]() $K_t(x,y)$
in
$K_t(x,y)$
in
![]() $C^\infty (M^2;E\boxtimes E^*)$
(omitting the Riemannian density
$C^\infty (M^2;E\boxtimes E^*)$
(omitting the Riemannian density
![]() $\operatorname {dvol}(y)$
of the second factor). On the diagonal, there is an asymptotic expansion (as
$\operatorname {dvol}(y)$
of the second factor). On the diagonal, there is an asymptotic expansion (as
![]() $t\downarrow 0$
) with respect to the seminorms
$t\downarrow 0$
) with respect to the seminorms
![]() $\|\ \|_{C^m}$
(
$\|\ \|_{C^m}$
(
![]() $m\in \mathbb {N}_0$
) on
$m\in \mathbb {N}_0$
) on
![]() $C^\infty (M;E\otimes E^*)$
[Reference Gilkey31, Lemma 1.9.1], [Reference Berline, Getzler and Vergne7, Theorem 2.30, Proposition 2.46 and the paragraph that follows],
$C^\infty (M;E\otimes E^*)$
[Reference Gilkey31, Lemma 1.9.1], [Reference Berline, Getzler and Vergne7, Theorem 2.30, Proposition 2.46 and the paragraph that follows],
 $$ \begin{align} K_t(x,x)\sim\sum_{l=0}^\infty e_l(x)t^{(l-n-b)/a}\;, \end{align} $$
$$ \begin{align} K_t(x,x)\sim\sum_{l=0}^\infty e_l(x)t^{(l-n-b)/a}\;, \end{align} $$
with
![]() $e_l\in C^\infty (M;E\otimes E^*)$
. Moreover, using a local system of coordinates, a local trivialization of E and standard multi-index notation, if
$e_l\in C^\infty (M;E\otimes E^*)$
. Moreover, using a local system of coordinates, a local trivialization of E and standard multi-index notation, if
![]() $B=\sum _\alpha b_\alpha (x)D^\alpha _x$
, then
$B=\sum _\alpha b_\alpha (x)D^\alpha _x$
, then
![]() $e_l(x)=\sum _\alpha b_\alpha (x)e_{l,\alpha }(x)$
, where the
$e_l(x)=\sum _\alpha b_\alpha (x)e_{l,\alpha }(x)$
, where the
![]() $e_{l,\alpha }(x)$
are smooth local invariants of the symbol of A which are homogeneous of degree
$e_{l,\alpha }(x)$
are smooth local invariants of the symbol of A which are homogeneous of degree
![]() $l+|\alpha |-b$
. They vanish if
$l+|\alpha |-b$
. They vanish if
![]() $l+b$
is odd or if
$l+b$
is odd or if
![]() $l+|\alpha |-b<0$
. Hence, the function
$l+|\alpha |-b<0$
. Hence, the function
has an asymptotic expansion
 $$ \begin{align} h(t)\sim\sum_{l=0}^\infty a_lt^{(l-n-b)/a}\;, \end{align} $$
$$ \begin{align} h(t)\sim\sum_{l=0}^\infty a_lt^{(l-n-b)/a}\;, \end{align} $$
where
which vanishes if
![]() $l+b$
is odd.
$l+b$
is odd.
The case of truncated heat kernels, in the following sense, is also needed. Given any
![]() $\lambda \ge 0$
, let
$\lambda \ge 0$
, let
![]() $P_{A,\lambda }$
be the spectral projection of A corresponding to
$P_{A,\lambda }$
be the spectral projection of A corresponding to
![]() $[0,\lambda ]$
; thus,
$[0,\lambda ]$
; thus,
![]() $P_{A,\lambda }^\perp $
is the spectral projection corresponding to
$P_{A,\lambda }^\perp $
is the spectral projection corresponding to
![]() $(\lambda ,\infty )$
. By ellipticity,
$(\lambda ,\infty )$
. By ellipticity,
![]() $P_{A,\lambda }$
is of finite rank, and
$P_{A,\lambda }$
is of finite rank, and
![]() $Be^{-tA}P_{A,\lambda }$
is a smoothing operator defined for all
$Be^{-tA}P_{A,\lambda }$
is a smoothing operator defined for all
![]() $t\in \mathbb {R}$
. Take any orthonormal frame
$t\in \mathbb {R}$
. Take any orthonormal frame
![]() $\phi _1,\dots ,\phi _\kappa $
of
$\phi _1,\dots ,\phi _\kappa $
of
![]() $\operatorname {im} P_{A,\lambda }$
, consisting of eigensections with corresponding eigenvalues
$\operatorname {im} P_{A,\lambda }$
, consisting of eigensections with corresponding eigenvalues
![]() $0\le \lambda _1\le \dots \le \lambda _\kappa \le \lambda $
. Then the Schwartz kernel
$0\le \lambda _1\le \dots \le \lambda _\kappa \le \lambda $
. Then the Schwartz kernel
![]() $H_t(x,y)$
of
$H_t(x,y)$
of
![]() $Be^{-tA}P_{A,\lambda }$
(
$Be^{-tA}P_{A,\lambda }$
(
![]() $t\ge 0$
) is given by
$t\ge 0$
) is given by
 $$\begin{align*}H_t(x,y)=\sum_{j=1}^\kappa e^{-t\lambda_j}(B\phi_j)(x)\otimes\phi_j(y)\;, \end{align*}$$
$$\begin{align*}H_t(x,y)=\sum_{j=1}^\kappa e^{-t\lambda_j}(B\phi_j)(x)\otimes\phi_j(y)\;, \end{align*}$$
using the isomorphism
![]() $E\cong E^*$
given by the Hermitian structure. Thus,
$E\cong E^*$
given by the Hermitian structure. Thus,
![]() $H_t(x,y)$
is defined for all
$H_t(x,y)$
is defined for all
![]() $t\in \mathbb {R}$
and smooth. So
$t\in \mathbb {R}$
and smooth. So
In particular, for
![]() $t=0$
, we have
$t=0$
, we have
 $$ \begin{align} \; \; H_0(x,x)&=\sum_{j=1}^\kappa(B\phi_j)(x)\otimes\phi_j(x)\;, \end{align} $$
$$ \begin{align} \; \; H_0(x,x)&=\sum_{j=1}^\kappa(B\phi_j)(x)\otimes\phi_j(x)\;, \end{align} $$
The Schwartz kernel of
![]() $Be^{-tA}P_{A,\lambda }^\perp $
is
$Be^{-tA}P_{A,\lambda }^\perp $
is
![]() $\widetilde K_t(x,y)=K_t(x,y)-H_t(x,y)$
(
$\widetilde K_t(x,y)=K_t(x,y)-H_t(x,y)$
(
![]() $t>0$
), which has an asymptotic expansion
$t>0$
), which has an asymptotic expansion
 $$ \begin{align} \widetilde K_t(x,x)\sim\sum_{l=0}^\infty\tilde e_l(x)t^{(l-n-b)/a}\;, \end{align} $$
$$ \begin{align} \widetilde K_t(x,x)\sim\sum_{l=0}^\infty\tilde e_l(x)t^{(l-n-b)/a}\;, \end{align} $$
where the first
![]() $n+b$
sections
$n+b$
sections
![]() $\tilde e_l$
are given by
$\tilde e_l$
are given by
 $$\begin{align*}\tilde e_l(x)= \begin{cases} e_l(x) & \text{if}\ l<n+b\\ e_l(x)-H_0(x,x) & \text{if}\ l=n+b. \end{cases} \end{align*}$$
$$\begin{align*}\tilde e_l(x)= \begin{cases} e_l(x) & \text{if}\ l<n+b\\ e_l(x)-H_0(x,x) & \text{if}\ l=n+b. \end{cases} \end{align*}$$
Then the function
has an asymptotic expansion
 $$ \begin{align} \tilde h_\lambda(t)=\int_M\widetilde K_t(x,x)\,\operatorname{dvol}(x)\sim\sum_{l=0}^\infty\tilde a_lt^{(l-n-b)/a}\;, \end{align} $$
$$ \begin{align} \tilde h_\lambda(t)=\int_M\widetilde K_t(x,x)\,\operatorname{dvol}(x)\sim\sum_{l=0}^\infty\tilde a_lt^{(l-n-b)/a}\;, \end{align} $$
where the first
![]() $n+b$
coefficients
$n+b$
coefficients
![]() $\tilde a_l$
are given by
$\tilde a_l$
are given by
 $$ \begin{align} \tilde a_l= \begin{cases} a_l & \text{if}\ l<n+b\\ a_l-\operatorname{Tr}(BP_{A,\lambda}) & \text{if}\ l=n+b. \end{cases} \end{align} $$
$$ \begin{align} \tilde a_l= \begin{cases} a_l & \text{if}\ l<n+b\\ a_l-\operatorname{Tr}(BP_{A,\lambda}) & \text{if}\ l=n+b. \end{cases} \end{align} $$
Consider also smooth families of such operators,
![]() $\{A_\epsilon \}$
and
$\{A_\epsilon \}$
and
![]() $\{B_\epsilon \}$
, for
$\{B_\epsilon \}$
, for
![]() $\epsilon $
in some parameter space. Then
$\epsilon $
in some parameter space. Then
![]() $\operatorname {Tr}(B_\epsilon e^{-tA_\epsilon })$
is smooth in
$\operatorname {Tr}(B_\epsilon e^{-tA_\epsilon })$
is smooth in
![]() $(t,\epsilon )$
, and we add
$(t,\epsilon )$
, and we add
![]() $\epsilon $
to the above notation, writing for instance
$\epsilon $
to the above notation, writing for instance
![]() $K_t(x,y,\epsilon )$
,
$K_t(x,y,\epsilon )$
,
![]() $e_l(x,\epsilon )$
,
$e_l(x,\epsilon )$
,
![]() $h(t,\epsilon )$
,
$h(t,\epsilon )$
,
![]() $a_l(\epsilon )$
,
$a_l(\epsilon )$
,
![]() $\widetilde K_t(x,y,\epsilon )$
,
$\widetilde K_t(x,y,\epsilon )$
,
![]() $\tilde e_l(x,\epsilon )$
,
$\tilde e_l(x,\epsilon )$
,
![]() $\tilde h(t,\epsilon )$
and
$\tilde h(t,\epsilon )$
and
![]() $\tilde a_l(\epsilon )$
in Equations (3.1), (3.2), (3.6) and (3.8). The operator
$\tilde a_l(\epsilon )$
in Equations (3.1), (3.2), (3.6) and (3.8). The operator
![]() $B_\epsilon P_{A_\epsilon ,\lambda }$
may not be smooth in
$B_\epsilon P_{A_\epsilon ,\lambda }$
may not be smooth in
![]() $\epsilon $
when some nonconstant spectral branch of
$\epsilon $
when some nonconstant spectral branch of
![]() $\{A_\epsilon \}$
reaches the value
$\{A_\epsilon \}$
reaches the value
![]() $\lambda $
. If the values of all nonconstant spectral branches of
$\lambda $
. If the values of all nonconstant spectral branches of
![]() $\{A_\epsilon \}$
stay away from some neighborhood of
$\{A_\epsilon \}$
stay away from some neighborhood of
![]() $\lambda $
, then
$\lambda $
, then
![]() $\tilde h_\lambda (t,\epsilon )$
is smooth in
$\tilde h_\lambda (t,\epsilon )$
is smooth in
![]() $(t,\epsilon )$
.
$(t,\epsilon )$
.
3.2. Preliminaries on zeta functions of operators
Proposition 3.1 (See [Reference Gilkey31, Theorems 1.12.2 and 1.12.5], [Reference Berline, Getzler and Vergne7, Propositions 9.35–9.37])
The following holds:
-
(i) For every
 $\lambda \in \mathbb {R}$
, there is a meromorphic function
$\lambda \in \mathbb {R}$
, there is a meromorphic function
 $\zeta (s,A,B,\lambda )$
on
$\zeta (s,A,B,\lambda )$
on
 $\mathbb {C}$
such that, for
$\mathbb {C}$
such that, for
 $\Re s\gg 0$
, (3.10)
$\Re s\gg 0$
, (3.10) $$ \begin{align} \zeta(s,A,B,\lambda)=\operatorname{Tr}\big(BA^{-s}P_{A,\lambda}^\perp\big) =\frac{1}{\Gamma(s)}\int_0^\infty t^{s-1}\tilde h_\lambda(t)\,dt. \end{align} $$
$$ \begin{align} \zeta(s,A,B,\lambda)=\operatorname{Tr}\big(BA^{-s}P_{A,\lambda}^\perp\big) =\frac{1}{\Gamma(s)}\int_0^\infty t^{s-1}\tilde h_\lambda(t)\,dt. \end{align} $$
-
(ii) The meromorphic function
 $\Gamma (s)\zeta (s,A,B,\lambda )$
has simple poles at the points
$\Gamma (s)\zeta (s,A,B,\lambda )$
has simple poles at the points
 $s=(n+b-l)/a$
, for
$s=(n+b-l)/a$
, for
 $l\in \mathbb {N}_0$
with
$l\in \mathbb {N}_0$
with
 $\tilde a_l\ne 0$
. The corresponding residues are
$\tilde a_l\ne 0$
. The corresponding residues are
 $\tilde a_l$
, and
$\tilde a_l$
, and
 $\zeta (s,A,B,\lambda )$
is smooth away from these exceptional values of s.
$\zeta (s,A,B,\lambda )$
is smooth away from these exceptional values of s. -
(iii) For
 $\mu>\lambda \ge 0$
, let
$\mu>\lambda \ge 0$
, let
 $\lambda _1\le \dots \le \lambda _k$
denote the eigenvalues of A in
$\lambda _1\le \dots \le \lambda _k$
denote the eigenvalues of A in
 $(\lambda ,\mu ]$
, taking multiplicities into account, and let
$(\lambda ,\mu ]$
, taking multiplicities into account, and let
 $\psi _1,\dots ,\psi _k$
be corresponding orthonormal eigensections. Then, for all s,
$\psi _1,\dots ,\psi _k$
be corresponding orthonormal eigensections. Then, for all s,  $$\begin{align*}\zeta(s,A,B,\mu)-\zeta(s,A,B,\lambda)=\sum_{j=1}^k\lambda_k^{-s}\langle B\psi_j,\psi_j\rangle. \end{align*}$$
$$\begin{align*}\zeta(s,A,B,\mu)-\zeta(s,A,B,\lambda)=\sum_{j=1}^k\lambda_k^{-s}\langle B\psi_j,\psi_j\rangle. \end{align*}$$
-
(iv) For smooth families
 $\{A_\epsilon \}$
and
$\{A_\epsilon \}$
and
 $\{B_\epsilon \}$
of such operators, if the values of all nonconstant branches of eigenvalues of
$\{B_\epsilon \}$
of such operators, if the values of all nonconstant branches of eigenvalues of
 $\{A_\epsilon \}$
stay away from some neighborhood of
$\{A_\epsilon \}$
stay away from some neighborhood of
 $\lambda $
, then
$\lambda $
, then
 $\zeta (s,A_\epsilon ,B_\epsilon ,\lambda )$
is smooth in
$\zeta (s,A_\epsilon ,B_\epsilon ,\lambda )$
is smooth in
 $(s,\epsilon )$
away from the exceptional values of s given in (ii).
$(s,\epsilon )$
away from the exceptional values of s given in (ii). -
(v) Consider the conditions of (iv) for
 $\epsilon $
in some open neighborhood of
$\epsilon $
in some open neighborhood of
 $0$
in
$0$
in
 $\mathbb {R}$
. If
$\mathbb {R}$
. If
 $A_0$
and
$A_0$
and
 $B_0$
commute, then where the dot denotes
$B_0$
commute, then where the dot denotes $$\begin{align*}\partial_\epsilon\zeta(s,A_\epsilon,B_\epsilon,\lambda)\big|_{\epsilon=0} =\zeta(s,A_0,\dot B_0,\lambda)-s\zeta(s+1,A_0,\dot A_0B_0,\lambda)\;, \end{align*}$$
$$\begin{align*}\partial_\epsilon\zeta(s,A_\epsilon,B_\epsilon,\lambda)\big|_{\epsilon=0} =\zeta(s,A_0,\dot B_0,\lambda)-s\zeta(s+1,A_0,\dot A_0B_0,\lambda)\;, \end{align*}$$
 $\partial _\epsilon $
.
$\partial _\epsilon $
.
The last expression of Equation (3.10) is the Mellin transform of the function
![]() $\tilde h_\lambda (t)$
divided by
$\tilde h_\lambda (t)$
divided by
![]() $\Gamma (s)$
. This function
$\Gamma (s)$
. This function
![]() $\zeta (s,A,B,\lambda )$
is called the zeta function of
$\zeta (s,A,B,\lambda )$
is called the zeta function of
![]() $(A,B,\lambda )$
. If
$(A,B,\lambda )$
. If
![]() $B=1$
or
$B=1$
or
![]() $\lambda =0$
, they may be omitted from the notation.
$\lambda =0$
, they may be omitted from the notation.
We will also use
![]() $\zeta (s,A,B,\lambda )$
when B is not a differential operator, with the same definition. Then the asymptotic expansion (3.8) and the properties stated in Proposition 3.1 need to be checked. With this generality, we can write
$\zeta (s,A,B,\lambda )$
when B is not a differential operator, with the same definition. Then the asymptotic expansion (3.8) and the properties stated in Proposition 3.1 need to be checked. With this generality, we can write
 $$ \begin{align*} \zeta(s,A,B,\lambda) &=\zeta(s,A,BP_{A,\lambda}^\perp)=\zeta(s,A,P_{A,\lambda}^\perp B)\;,\\ \zeta(s,A,B) &=\zeta(s,A,BP_{A,\lambda})+\zeta(s,A,B,\lambda). \end{align*} $$
$$ \begin{align*} \zeta(s,A,B,\lambda) &=\zeta(s,A,BP_{A,\lambda}^\perp)=\zeta(s,A,P_{A,\lambda}^\perp B)\;,\\ \zeta(s,A,B) &=\zeta(s,A,BP_{A,\lambda})+\zeta(s,A,B,\lambda). \end{align*} $$
Since
![]() $P_{A,\lambda }$
is of finite rank,
$P_{A,\lambda }$
is of finite rank,
![]() $\zeta (s,A,BP_{A,\lambda })$
is always defined and holomorphic on
$\zeta (s,A,BP_{A,\lambda })$
is always defined and holomorphic on
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
3.3. Zeta invariants of closed real 1-forms
According to Proposition 3.1 (i), let
which is a meromorphic function of
![]() $s\in \mathbb {C}$
. For
$s\in \mathbb {C}$
. For
![]() $\Re s\gg 0$
,
$\Re s\gg 0$
,
 $$ \begin{align*} \zeta(s,z)&=\operatorname{Str}\big({\eta\wedge}\,D_z\Delta_z^{-s}\Pi_z^\perp\big) =\operatorname{Str}\big({\eta\wedge}\,\delta_z\Delta_z^{-s}\Pi_z^1\big)\\ &=\operatorname{Str}\big({\eta\wedge}\,D_z^{-1}\Delta_z^{-s+1}\Pi_z^\perp\big)=\operatorname{Str}\big({\eta\wedge}\,d_z^{-1}\Delta_z^{-s+1}\Pi^1_z\big)\;, \end{align*} $$
$$ \begin{align*} \zeta(s,z)&=\operatorname{Str}\big({\eta\wedge}\,D_z\Delta_z^{-s}\Pi_z^\perp\big) =\operatorname{Str}\big({\eta\wedge}\,\delta_z\Delta_z^{-s}\Pi_z^1\big)\\ &=\operatorname{Str}\big({\eta\wedge}\,D_z^{-1}\Delta_z^{-s+1}\Pi_z^\perp\big)=\operatorname{Str}\big({\eta\wedge}\,d_z^{-1}\Delta_z^{-s+1}\Pi^1_z\big)\;, \end{align*} $$
using that
![]() ${\eta \wedge }\,d_z$
and
${\eta \wedge }\,d_z$
and
![]() ${\eta \wedge }\,\delta _z^{-1}$
change the degree of homogeneous forms. So, when
${\eta \wedge }\,\delta _z^{-1}$
change the degree of homogeneous forms. So, when
![]() $\zeta (s,z)$
is regular at
$\zeta (s,z)$
is regular at
![]() $s=1$
, the value
$s=1$
, the value
![]() $\zeta (1,z)$
is a renormalized version of the super-trace of
$\zeta (1,z)$
is a renormalized version of the super-trace of
![]() ${\eta \wedge }\,d_z^{-1}\Pi ^1_z$
, which is called the zeta invariant of
${\eta \wedge }\,d_z^{-1}\Pi ^1_z$
, which is called the zeta invariant of
![]() $(M,g,\eta ,z)$
for the scope of this paper. According to Proposition 3.1 (ii) and since
$(M,g,\eta ,z)$
for the scope of this paper. According to Proposition 3.1 (ii) and since
![]() $\Gamma (s)$
is regular at
$\Gamma (s)$
is regular at
![]() $s=1$
,
$s=1$
,
![]() $\zeta (s,z)$
might have a simple pole at
$\zeta (s,z)$
might have a simple pole at
![]() $s=1$
. But it will be shown that
$s=1$
. But it will be shown that
![]() $\zeta (s,z)$
is regular at
$\zeta (s,z)$
is regular at
![]() $s=1$
for all
$s=1$
for all
![]() $\eta \in Z^1(M,\mathbb {R})$
and
$\eta \in Z^1(M,\mathbb {R})$
and
![]() $z\in \mathbb {C}$
(Corollary 3.9).
$z\in \mathbb {C}$
(Corollary 3.9).
3.4. Heat invariants of perturbed operators
Consider the notation of Section 2.1.2. For
![]() $k=0,\dots ,n$
, let
$k=0,\dots ,n$
, let
![]() $K_{z,k,t}(x,y)$
denote the Schwartz kernel of
$K_{z,k,t}(x,y)$
denote the Schwartz kernel of
![]() $e^{-t\Delta _{z,k}}$
. By Equation (3.1), its restriction to the diagonal has an asymptotic expansion (as
$e^{-t\Delta _{z,k}}$
. By Equation (3.1), its restriction to the diagonal has an asymptotic expansion (as
![]() $t\downarrow 0$
),
$t\downarrow 0$
),
 $$\begin{align*}K_{z,k,t}(x,x)\sim\sum_{l=0}^\infty e_{k,l}(x,z)t^{(l-n)/2}\;, \end{align*}$$
$$\begin{align*}K_{z,k,t}(x,x)\sim\sum_{l=0}^\infty e_{k,l}(x,z)t^{(l-n)/2}\;, \end{align*}$$
where every
![]() $e_{k,l}(x,z)$
is a smooth local invariant of z and the jets of the local coefficients of g and
$e_{k,l}(x,z)$
is a smooth local invariant of z and the jets of the local coefficients of g and
![]() $\eta $
, which is homogeneous of degree l, and vanishes if l is odd. According to Equations (3.2) and (3.3),
$\eta $
, which is homogeneous of degree l, and vanishes if l is odd. According to Equations (3.2) and (3.3),
 $$\begin{align*}h_k(t,z):=\operatorname{Tr}\big(e^{-t\Delta_{z,k}}\big)\sim\sum_{l=0}^\infty a_{k,l}(z)t^{(l-n)/2}\;, \end{align*}$$
$$\begin{align*}h_k(t,z):=\operatorname{Tr}\big(e^{-t\Delta_{z,k}}\big)\sim\sum_{l=0}^\infty a_{k,l}(z)t^{(l-n)/2}\;, \end{align*}$$
where
The Schwartz kernel of
![]() $e^{-t\Delta _z}\mathsf {w}$
is
$e^{-t\Delta _z}\mathsf {w}$
is
 $$\begin{align*}K_{z,t}(x,y)=\sum_{k=0}^n(-1)^kK_{z,k,t}(x,y). \end{align*}$$
$$\begin{align*}K_{z,t}(x,y)=\sum_{k=0}^n(-1)^kK_{z,k,t}(x,y). \end{align*}$$
We have induced asymptotic expansions,
 $$ \begin{gather*} K_{z,t}(x,x)\sim\sum_{l=0}^\infty e_l(x,z)t^{(l-n)/2}\;,\\ h(t,z):=\operatorname{Str}\big(e^{-t\Delta_z}\big)\sim\sum_{l=0}^\infty a_l(z)t^{(l-n)/2}\;, \end{gather*} $$
$$ \begin{gather*} K_{z,t}(x,x)\sim\sum_{l=0}^\infty e_l(x,z)t^{(l-n)/2}\;,\\ h(t,z):=\operatorname{Str}\big(e^{-t\Delta_z}\big)\sim\sum_{l=0}^\infty a_l(z)t^{(l-n)/2}\;, \end{gather*} $$
where
 $$\begin{align*}e_l(x,z)=\sum_{k=0}^n(-1)^ke_{k,l}(x,z)\;,\quad a_l(z)=\sum_{k=0}^n(-1)^ka_{k,l}(z). \end{align*}$$
$$\begin{align*}e_l(x,z)=\sum_{k=0}^n(-1)^ke_{k,l}(x,z)\;,\quad a_l(z)=\sum_{k=0}^n(-1)^ka_{k,l}(z). \end{align*}$$
Theorem 3.2 ([Reference Bismut, Zhang and Laudenbach10, Theorem 13.4]; see also [Reference Álvarez López and Gilkey1, Theorem 1.5] and [Reference Álvarez López, Kordyukov and Leichtnam6])
We have:
-
(i)
 $e_l(x,z)=0$
for
$e_l(x,z)=0$
for
 $l<n$
; and,
$l<n$
; and, -
(ii) if n is even, then
 $e_n(x,z)=e(M,\nabla ^M)(x)$
.
$e_n(x,z)=e(M,\nabla ^M)(x)$
.
Remark 3.3. The analog of Theorem 3.2 fails for Witten’s type perturbations of the Dolbeault complex on Kähler manifolds [Reference Álvarez López and Gilkey2].
3.5. Derived heat invariants of perturbed operators
The following are sometimes called the derived heat density and derived heat invariant of order l of
![]() $d_z$
or
$d_z$
or
![]() $\Delta _z$
[Reference Günther and Schimming33], [Reference Ray and Singer61], [Reference Gilkey31, page 181], [Reference Álvarez López and Gilkey3]:
$\Delta _z$
[Reference Günther and Schimming33], [Reference Ray and Singer61], [Reference Gilkey31, page 181], [Reference Álvarez López and Gilkey3]:
 $$ \begin{gather*} \mathfrak{e}_l(x,z)=\sum_{k=0}^n(-1)^kke_{k,l}(x,z)\;,\\ \mathfrak{a}_l(z)=\sum_{k=0}^n(-1)^kka_{k,l}(z)=\int_M\operatorname{str}\mathfrak{e}_l(x,z)\,\operatorname{dvol}(x). \end{gather*} $$
$$ \begin{gather*} \mathfrak{e}_l(x,z)=\sum_{k=0}^n(-1)^kke_{k,l}(x,z)\;,\\ \mathfrak{a}_l(z)=\sum_{k=0}^n(-1)^kka_{k,l}(z)=\int_M\operatorname{str}\mathfrak{e}_l(x,z)\,\operatorname{dvol}(x). \end{gather*} $$
We have
 $$ \begin{align} \operatorname{Str}\big({\mathsf{N}} e^{-t\Delta_z}\big)\sim\sum_{l=0}^\infty\mathfrak{a}_l(z)t^{(l-n)/2}. \end{align} $$
$$ \begin{align} \operatorname{Str}\big({\mathsf{N}} e^{-t\Delta_z}\big)\sim\sum_{l=0}^\infty\mathfrak{a}_l(z)t^{(l-n)/2}. \end{align} $$
Theorem 3.4 [Reference Bismut, Zhang and Laudenbach10, Theorem 7.10]
For
![]() $l\le n$
,
$l\le n$
,
![]() $\mathfrak {a}_l(z)$
is independent of z.
$\mathfrak {a}_l(z)$
is independent of z.
Remark 3.5. [Reference Bismut, Zhang and Laudenbach10, Theorem 7.10] gives Theorem 3.4 for real z. But, since the functions
![]() $\mathfrak {e}_l(x,z)$
have local expressions, we can assume
$\mathfrak {e}_l(x,z)$
have local expressions, we can assume
![]() $\eta $
is exact. Then the result can be extended to nonreal z using Equation (2.11). The exactness of
$\eta $
is exact. Then the result can be extended to nonreal z using Equation (2.11). The exactness of
![]() $\eta $
in [Reference Bismut, Zhang and Laudenbach10, Theorem 7.10] is irrelevant because a general flat vector bundle is considered. Moreover, [Reference Bismut, Zhang and Laudenbach10, Theorem 7.10] gives an explicit expression of
$\eta $
in [Reference Bismut, Zhang and Laudenbach10, Theorem 7.10] is irrelevant because a general flat vector bundle is considered. Moreover, [Reference Bismut, Zhang and Laudenbach10, Theorem 7.10] gives an explicit expression of
![]() $\mathfrak {a}_l(z)$
for
$\mathfrak {a}_l(z)$
for
![]() $l\le n$
.
$l\le n$
.
Remark 3.6. A refinement of Theorem 3.4 is given in [Reference Álvarez López and Gilkey3, Theorem 1.3 (1b)], where
![]() $\mathfrak {e}_l(x,z)$
is described for
$\mathfrak {e}_l(x,z)$
is described for
![]() $l\le n$
, showing its independence of z.
$l\le n$
, showing its independence of z.
3.6. Regularity
By Equations (3.2) and (3.3), we have an asymptotic expansion of the form
 $$ \begin{align} \operatorname{Str}\big({\eta\wedge}\,D_ze^{-t\Delta_z}\big)\sim\sum_{l=0}^\infty b_l(z)t^{(l-n-1)/2}\;, \end{align} $$
$$ \begin{align} \operatorname{Str}\big({\eta\wedge}\,D_ze^{-t\Delta_z}\big)\sim\sum_{l=0}^\infty b_l(z)t^{(l-n-1)/2}\;, \end{align} $$
where
![]() $b_l(z)=0$
if l is even.
$b_l(z)=0$
if l is even.
Proposition 3.7. For all
![]() $t>0$
and
$t>0$
and
![]() $z\in \mathbb {C}$
, the equality (1.5) is true.
$z\in \mathbb {C}$
, the equality (1.5) is true.
Proof. For all k, we have [Reference Berline, Getzler and Vergne7, Corollary 2.50]
So, by Equations (2.1) and (2.4),
 $$ \begin{align*} \partial_z\operatorname{Str}\big({\mathsf{N}} e^{-t\Delta_z}\big)&=-t\operatorname{Str}\big({\mathsf{N}}(\partial_z\Delta_z)e^{-t\Delta_z}\big)\\ &=-t\operatorname{Str}\big({\mathsf{N}}\,{\eta\wedge}\,\delta_ze^{-t\Delta_z}\big)-t\operatorname{Str}\big({\mathsf{N}}\delta_z\,{\eta\wedge}\,e^{-t\Delta_z}\big)\\ &=-t\operatorname{Str}\big({\mathsf{N}}\,{\eta\wedge}\,\delta_ze^{-t\Delta_z}\big)-t\operatorname{Str}\big(\delta_z({\mathsf{N}}-1)\,{\eta\wedge}\,e^{-t\Delta_z}\big)\\ &=-t\operatorname{Str}\big({\mathsf{N}}\,{\eta\wedge}\,\delta_ze^{-t\Delta_z}\big)+t\operatorname{Str}\big(({\mathsf{N}}-1)\,{\eta\wedge}\,\delta_ze^{-t\Delta_z}\big)\\ &=-t\operatorname{Str}\big({\eta\wedge}\,D_ze^{-t\Delta_z}\big). \; \end{align*} $$
$$ \begin{align*} \partial_z\operatorname{Str}\big({\mathsf{N}} e^{-t\Delta_z}\big)&=-t\operatorname{Str}\big({\mathsf{N}}(\partial_z\Delta_z)e^{-t\Delta_z}\big)\\ &=-t\operatorname{Str}\big({\mathsf{N}}\,{\eta\wedge}\,\delta_ze^{-t\Delta_z}\big)-t\operatorname{Str}\big({\mathsf{N}}\delta_z\,{\eta\wedge}\,e^{-t\Delta_z}\big)\\ &=-t\operatorname{Str}\big({\mathsf{N}}\,{\eta\wedge}\,\delta_ze^{-t\Delta_z}\big)-t\operatorname{Str}\big(\delta_z({\mathsf{N}}-1)\,{\eta\wedge}\,e^{-t\Delta_z}\big)\\ &=-t\operatorname{Str}\big({\mathsf{N}}\,{\eta\wedge}\,\delta_ze^{-t\Delta_z}\big)+t\operatorname{Str}\big(({\mathsf{N}}-1)\,{\eta\wedge}\,\delta_ze^{-t\Delta_z}\big)\\ &=-t\operatorname{Str}\big({\eta\wedge}\,D_ze^{-t\Delta_z}\big). \; \end{align*} $$
Corollary 3.8. For
![]() $l\le n-1$
,
$l\le n-1$
,
![]() $b_l(z)=0$
.
$b_l(z)=0$
.
Proof. By Equations (3.11) and (3.12); Theorem 3.4; and Proposition 3.7, for
![]() $l\le n-1$
,
$l\le n-1$
,
Corollary 3.9. If n is even and
![]() $\Re s>0$
, or n is odd and
$\Re s>0$
, or n is odd and
![]() $\Re s>1/2$
, then
$\Re s>1/2$
, then
 $$\begin{align*}\zeta(s,z)=\frac{1}{\Gamma(s)}\int_0^\infty t^{s-1}\operatorname{Str}\big({\eta\wedge}\,D_ze^{-t\Delta_z}\big)\,dt\;, \end{align*}$$
$$\begin{align*}\zeta(s,z)=\frac{1}{\Gamma(s)}\int_0^\infty t^{s-1}\operatorname{Str}\big({\eta\wedge}\,D_ze^{-t\Delta_z}\big)\,dt\;, \end{align*}$$
where the integral is absolutely convergent, and therefore
![]() $\zeta (s,z)$
is smooth in this half-plane.
$\zeta (s,z)$
is smooth in this half-plane.
Proof. By Equation (3.12) and Corollary 3.8,
 $$ \begin{align} \operatorname{Str}\big({\eta\wedge}\,D_ze^{-t\Delta_z}\big)= \begin{cases} O(1) & \text{if}\ n\ \text{is even}\\ O\big(t^{-1/2}\big) & \text{if}\ n\ \text{is odd} \end{cases} \quad(t\downarrow0). \end{align} $$
$$ \begin{align} \operatorname{Str}\big({\eta\wedge}\,D_ze^{-t\Delta_z}\big)= \begin{cases} O(1) & \text{if}\ n\ \text{is even}\\ O\big(t^{-1/2}\big) & \text{if}\ n\ \text{is odd} \end{cases} \quad(t\downarrow0). \end{align} $$
On the other hand, there is some
![]() $c>0$
such that
$c>0$
such that
So the stated integral is absolutely convergent for
![]() $\Re s>0$
if n is even, or for
$\Re s>0$
if n is even, or for
![]() $\Re s>1/2$
if n is odd, defining a holomorphic function of s on this half-plane. Then the stated equality is true because it holds for
$\Re s>1/2$
if n is odd, defining a holomorphic function of s on this half-plane. Then the stated equality is true because it holds for
![]() $\Re s\gg 0$
.
$\Re s\gg 0$
.
Remark 3.10. From Proposition 3.1 (ii) and Corollary 3.8, it also follows that, if n is even (resp., odd), then
![]() $\zeta (s,z)$
is smooth on
$\zeta (s,z)$
is smooth on
![]() $\mathbb {C}$
(resp., on
$\mathbb {C}$
(resp., on
![]() $\mathbb {C}\setminus ((1-\mathbb {N}_0)/2)$
). But this additional regularity is not needed in this work.
$\mathbb {C}\setminus ((1-\mathbb {N}_0)/2)$
). But this additional regularity is not needed in this work.
Corollary 3.11. For all
![]() $z\in \mathbb {C}$
,
$z\in \mathbb {C}$
,
Proof. By Corollary 3.9, Equation (3.13) and Equation (3.14), and since
we get
 $$ \begin{align*} \zeta(1,z)&=\int_0^\infty\operatorname{Str}\big({\eta\wedge}\,D_ze^{-u\Delta_z}\Pi_z^\perp\big)\,du =\lim_{t\downarrow0}\int_t^\infty\operatorname{Str}\big({\eta\wedge}\,D_ze^{-u\Delta_z}\Pi_z^\perp\big)\,du\\ &=\lim_{t\downarrow0}\operatorname{Str}\big({\eta\wedge}\,D_z^{-1}e^{-t\Delta_z}\Pi_z^\perp\big). \; \end{align*} $$
$$ \begin{align*} \zeta(1,z)&=\int_0^\infty\operatorname{Str}\big({\eta\wedge}\,D_ze^{-u\Delta_z}\Pi_z^\perp\big)\,du =\lim_{t\downarrow0}\int_t^\infty\operatorname{Str}\big({\eta\wedge}\,D_ze^{-u\Delta_z}\Pi_z^\perp\big)\,du\\ &=\lim_{t\downarrow0}\operatorname{Str}\big({\eta\wedge}\,D_z^{-1}e^{-t\Delta_z}\Pi_z^\perp\big). \; \end{align*} $$
3.7. The case of the differential of a function
Let us consider the special case where
![]() $\eta =dh$
for a smooth real-valued function h.
$\eta =dh$
for a smooth real-valued function h.
Lemma 3.12. We have
Proof. Since
![]() ${\eta \wedge }=[d,h]$
,
${\eta \wedge }=[d,h]$
,
 $$ \begin{align*} \operatorname{Str}\big({\eta\wedge}\,d_z^{-1}e^{-t\Delta_z}\Pi^1_z\big) &=\operatorname{Str}\big([d_z,h]\,d_z^{-1}e^{-t\Delta_z}\Pi^1_z\big)\\ &=\operatorname{Str}\big(d_z\,h\,d_z^{-1}e^{-t\Delta_z}\Pi^1_z\big)-\operatorname{Str}\big(h\,d_zd_z^{-1}e^{-t\Delta_z}\Pi^1_z\big)\\ &=-\operatorname{Str}\big(h\,d_z^{-1}e^{-t\Delta_z}\Pi^1_zd_z\big)-\operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi^1_z\big)\\ &=-\operatorname{Str}\big(h\,d_z^{-1}d_ze^{-t\Delta_z}\Pi^2_z\big)-\operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi^1_z\big)\\ &=-\operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi^2_z\big)-\operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi^1_z\big)\\ &=-\operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi_z^\perp\big). \; \end{align*} $$
$$ \begin{align*} \operatorname{Str}\big({\eta\wedge}\,d_z^{-1}e^{-t\Delta_z}\Pi^1_z\big) &=\operatorname{Str}\big([d_z,h]\,d_z^{-1}e^{-t\Delta_z}\Pi^1_z\big)\\ &=\operatorname{Str}\big(d_z\,h\,d_z^{-1}e^{-t\Delta_z}\Pi^1_z\big)-\operatorname{Str}\big(h\,d_zd_z^{-1}e^{-t\Delta_z}\Pi^1_z\big)\\ &=-\operatorname{Str}\big(h\,d_z^{-1}e^{-t\Delta_z}\Pi^1_zd_z\big)-\operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi^1_z\big)\\ &=-\operatorname{Str}\big(h\,d_z^{-1}d_ze^{-t\Delta_z}\Pi^2_z\big)-\operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi^1_z\big)\\ &=-\operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi^2_z\big)-\operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi^1_z\big)\\ &=-\operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi_z^\perp\big). \; \end{align*} $$
Corollary 3.13. We have
Corollary 3.14. We have
![]() $\zeta (1,z)\in \mathbb {R}$
.
$\zeta (1,z)\in \mathbb {R}$
.
Proof. By Corollary 3.13, it is enough to prove that
![]() $\operatorname {Str}(h\,e^{-t\Delta _z}\Pi _z^\perp )\in \mathbb {R}$
. But, taking adjoints,
$\operatorname {Str}(h\,e^{-t\Delta _z}\Pi _z^\perp )\in \mathbb {R}$
. But, taking adjoints,
Corollary 3.15. If M is oriented, then
Proof. By Equation (2.15),
 $$ \begin{align*} \operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi_z^\perp\big)&=\operatorname{Str}\big(\star\star^{-1}h\,e^{-t\Delta_z}\Pi_z^\perp\big) =\operatorname{Str}\big(\star^{-1}h\,e^{-t\Delta_z}\Pi_z^\perp\star\big)\\ &=\operatorname{Str}\big(\star^{-1}\star h\,e^{-t\Delta_{-\bar z}}\Pi_{-\bar z}^\perp\big) =\operatorname{Str}\big(h\,e^{-t\Delta_{-\bar z}}\Pi_{-\bar z}^\perp\big). \end{align*} $$
$$ \begin{align*} \operatorname{Str}\big(h\,e^{-t\Delta_z}\Pi_z^\perp\big)&=\operatorname{Str}\big(\star\star^{-1}h\,e^{-t\Delta_z}\Pi_z^\perp\big) =\operatorname{Str}\big(\star^{-1}h\,e^{-t\Delta_z}\Pi_z^\perp\star\big)\\ &=\operatorname{Str}\big(\star^{-1}\star h\,e^{-t\Delta_{-\bar z}}\Pi_{-\bar z}^\perp\big) =\operatorname{Str}\big(h\,e^{-t\Delta_{-\bar z}}\Pi_{-\bar z}^\perp\big). \end{align*} $$
Thus, the first equality of the statement holds by Corollary 3.13. The second equality follows with a similar argument, using
![]() $\bar \star $
instead of
$\bar \star $
instead of
![]() $\star $
. The third equality is equivalent to the first one.
$\star $
. The third equality is equivalent to the first one.
4. Small and large complexes of Morse forms
4.1. Preliminaries on Morse forms
Recall that a critical point p of any
![]() $h\in C^\infty (M,\mathbb {R})$
is called nondegenerate if the symmetric bilinear form
$h\in C^\infty (M,\mathbb {R})$
is called nondegenerate if the symmetric bilinear form
![]() $\operatorname {Hess}_ph$
on
$\operatorname {Hess}_ph$
on
![]() $T_pM$
is nondegenerate; then the index of
$T_pM$
is nondegenerate; then the index of
![]() $\operatorname {Hess}_ph$
is denoted by
$\operatorname {Hess}_ph$
is denoted by
![]() $\operatorname {ind}(p)$
. By the Morse lemma [Reference Milnor, Spivak and Wells49, Lemma 2.2], this means that
$\operatorname {ind}(p)$
. By the Morse lemma [Reference Milnor, Spivak and Wells49, Lemma 2.2], this means that
 $$ \begin{align} h-h(p)=\frac{1}{2}\sum_{j=1}^n\epsilon_{p,j}(x_p^j)^2=\frac{1}{2}\big(|x_p^+|^2-|x_p^-|^2\big)\;, \end{align} $$
$$ \begin{align} h-h(p)=\frac{1}{2}\sum_{j=1}^n\epsilon_{p,j}(x_p^j)^2=\frac{1}{2}\big(|x_p^+|^2-|x_p^-|^2\big)\;, \end{align} $$
where
 $$ \begin{align} \epsilon_{p,j}= \begin{cases} -1 & \text{if}\ j\le\operatorname{ind}(p)\\ 1 & \text{if}\ j>\operatorname{ind}(p)\;, \end{cases} \end{align} $$
$$ \begin{align} \epsilon_{p,j}= \begin{cases} -1 & \text{if}\ j\le\operatorname{ind}(p)\\ 1 & \text{if}\ j>\operatorname{ind}(p)\;, \end{cases} \end{align} $$
on some chart
![]() $(U_p,x_p=(x_p^1,\dots ,x_p^n))$
(centered) at p (Morse coordinates), where
$(U_p,x_p=(x_p^1,\dots ,x_p^n))$
(centered) at p (Morse coordinates), where
![]() $x_p^-=(x_p^1,\dots ,x_p^{\operatorname {ind}(p)})$
and
$x_p^-=(x_p^1,\dots ,x_p^{\operatorname {ind}(p)})$
and
![]() $x_p^+=(x_p^{\operatorname {ind}(p)+1},\dots ,x_p^n)$
.
$x_p^+=(x_p^{\operatorname {ind}(p)+1},\dots ,x_p^n)$
.
Recall that h is called a Morse function when all of its critical points are nondegenerate. Then its critical points form a finite set denoted by
![]() $\operatorname {Crit}(h)$
. The Morse functions form an open and dense subset of
$\operatorname {Crit}(h)$
. The Morse functions form an open and dense subset of
![]() $C^\infty (M,\mathbb {R})$
[Reference Hirsch36, Theorem 6.1.2]. On every
$C^\infty (M,\mathbb {R})$
[Reference Hirsch36, Theorem 6.1.2]. On every
![]() $U_p$
, we can assume the metric is Euclidean with respect to Morse coordinates:
$U_p$
, we can assume the metric is Euclidean with respect to Morse coordinates:
 $$ \begin{align} g=\sum_{j=1}^n(dx_p^j)^2. \end{align} $$
$$ \begin{align} g=\sum_{j=1}^n(dx_p^j)^2. \end{align} $$
Now, take any
![]() $\eta \in Z^1(M,\mathbb {R})$
. We can show that if p is a zero of
$\eta \in Z^1(M,\mathbb {R})$
. We can show that if p is a zero of
![]() $\eta $
, then
$\eta $
, then
![]() $(\nabla \eta )_p$
is independent of the choice of the connection
$(\nabla \eta )_p$
is independent of the choice of the connection
![]() $\nabla $
, and is symmetric. The zero p is called nondegenerate of index k if
$\nabla $
, and is symmetric. The zero p is called nondegenerate of index k if
![]() $(\nabla \eta )_p$
is nondegenerate of index k. In this case, any local primitive
$(\nabla \eta )_p$
is nondegenerate of index k. In this case, any local primitive
![]() $h_{\eta ,p}$
of
$h_{\eta ,p}$
of
![]() $\eta $
near p is a Morse function, and we can choose it so that
$\eta $
near p is a Morse function, and we can choose it so that
![]() $h_{\eta ,p}(p)=0$
. On a domain
$h_{\eta ,p}(p)=0$
. On a domain
![]() $U_p$
of Morse coordinates
$U_p$
of Morse coordinates
![]() $x_p=(x_p^1,\dots ,x_p^n)$
for
$x_p=(x_p^1,\dots ,x_p^n)$
for
![]() $h_{\eta ,p}$
at p, also called Morse coordinates for
$h_{\eta ,p}$
at p, also called Morse coordinates for
![]() $\eta $
at p,
$\eta $
at p,
![]() $h_{\eta ,p}$
is given by the center and right-hand side of Equation (4.1), and
$h_{\eta ,p}$
is given by the center and right-hand side of Equation (4.1), and
 $$ \begin{align} \eta=\sum_{j=1}^n\epsilon_{p,j}x_p^j\,dx_p^j. \end{align} $$
$$ \begin{align} \eta=\sum_{j=1}^n\epsilon_{p,j}x_p^j\,dx_p^j. \end{align} $$
If all zeros are nondegenerate, then
![]() $\eta $
is called a Morse form. In this case, its zeros form a finite set,
$\eta $
is called a Morse form. In this case, its zeros form a finite set,
![]() $\mathcal {X}=\operatorname {Zero}(\eta )$
; subsets of
$\mathcal {X}=\operatorname {Zero}(\eta )$
; subsets of
![]() $\mathcal {X}$
defined by conditions on the index are denoted by writing the conditions as subscripts; for instance,
$\mathcal {X}$
defined by conditions on the index are denoted by writing the conditions as subscripts; for instance,
![]() $\mathcal {X}_k$
,
$\mathcal {X}_k$
,
![]() $\mathcal {X}_+$
and
$\mathcal {X}_+$
and
![]() $\mathcal {X}_{<k}$
are the subsets of zeros of index k, of positive index and of index
$\mathcal {X}_{<k}$
are the subsets of zeros of index k, of positive index and of index
![]() ${}<k$
, respectively. For any
${}<k$
, respectively. For any
![]() $\xi \in H^1(M,\mathbb {R})$
, the Morse representatives of
$\xi \in H^1(M,\mathbb {R})$
, the Morse representatives of
![]() $\xi $
form a dense open subset of
$\xi $
form a dense open subset of
![]() $\xi $
, considering
$\xi $
, considering
![]() $\xi \subset \Omega ^1(M,\mathbb {R})$
with the
$\xi \subset \Omega ^1(M,\mathbb {R})$
with the
![]() $C^\infty $
topology (see, e.g., [Reference Pajitnov59, Theorem 2.1.25]). If
$C^\infty $
topology (see, e.g., [Reference Pajitnov59, Theorem 2.1.25]). If
![]() $\xi =0$
, this is just the classical property of Morse functions mentioned before.
$\xi =0$
, this is just the classical property of Morse functions mentioned before.
From now on, unless otherwise stated, we will use some
![]() $\eta \in Z^1(M,\mathbb {R})$
and a Riemannian metric g on M satisfying (a) (Section 1.1).
$\eta \in Z^1(M,\mathbb {R})$
and a Riemannian metric g on M satisfying (a) (Section 1.1).
The Hopf index of
![]() $\eta ^\sharp $
at any
$\eta ^\sharp $
at any
![]() $p\in \mathcal {X}_k$
is
$p\in \mathcal {X}_k$
is
![]() $(-1)^k$
(Section 6.1.1). Thus, by the Hopf index theorem,
$(-1)^k$
(Section 6.1.1). Thus, by the Hopf index theorem,
 $$ \begin{align} \sum_{k=0}^n(-1)^k|\mathcal{X}_k|=\chi(M). \end{align} $$
$$ \begin{align} \sum_{k=0}^n(-1)^k|\mathcal{X}_k|=\chi(M). \end{align} $$
4.2. The small and large spectrum
Consider the perturbed operators (2.3) defined by
![]() $\eta $
and g. We can suppose the closures
$\eta $
and g. We can suppose the closures
![]() $\overline {U_p}$
(
$\overline {U_p}$
(
![]() $p\in \mathcal {X}$
) are disjoint from each other, and
$p\in \mathcal {X}$
) are disjoint from each other, and
![]() $x_p(U_p)=(-4r,4r)^n$
for some
$x_p(U_p)=(-4r,4r)^n$
for some
![]() $r>0$
independent of p with
$r>0$
independent of p with
![]() $4r<1$
. Let
$4r<1$
. Let
![]() $U=\bigcup _{p\in \mathcal {X}}U_p$
.
$U=\bigcup _{p\in \mathcal {X}}U_p$
.
Denoting also the coordinates of
![]() $\mathbb {R}^n$
by
$\mathbb {R}^n$
by
![]() $(x_p^1,\dots ,x_p^n)$
, consider the function
$(x_p^1,\dots ,x_p^n)$
, consider the function
![]() $h_p\in C^\infty (\mathbb {R}^n)$
defined by the center and right-hand side of Equation (4.1). Let
$h_p\in C^\infty (\mathbb {R}^n)$
defined by the center and right-hand side of Equation (4.1). Let
![]() $d^{\prime }_{p,z}$
,
$d^{\prime }_{p,z}$
,
![]() $\delta ^{\prime }_{p,z}$
,
$\delta ^{\prime }_{p,z}$
,
![]() $D^{\prime }_{p,z}$
and
$D^{\prime }_{p,z}$
and
![]() $\Delta ^{\prime }_{p,z}$
(
$\Delta ^{\prime }_{p,z}$
(
![]() $z\in \mathbb {C}$
) denote the corresponding Witten’s operators on
$z\in \mathbb {C}$
) denote the corresponding Witten’s operators on
![]() $\mathbb {R}^n$
, whose restrictions to
$\mathbb {R}^n$
, whose restrictions to
![]() $(-4r,4r)^n$
agree via
$(-4r,4r)^n$
agree via
![]() $x_p$
with
$x_p$
with
![]() $d_z$
,
$d_z$
,
![]() $\delta _z$
,
$\delta _z$
,
![]() $D_z$
and
$D_z$
and
![]() $\Delta _z$
on
$\Delta _z$
on
![]() $U_p$
.
$U_p$
.
Proposition 4.1 (See, e.g., [Reference Roe63, Chapters 9 and 14], [Reference Zhang75, Sections 4.5 and 4.7])
The following holds for
![]() $\mu \in \mathbb {R}$
:
$\mu \in \mathbb {R}$
:
-
(i) We have
(4.6)Here, $$ \begin{align} \Delta^{\prime}_{p,\mu}=\sum_{j=1}^n\Big(-\Big(\frac{\partial}{\partial x_p^j}\Big)^2+\mu^2(x_p^j)^2+\mu\epsilon_{p,j}[{dx_p^j\lrcorner},{dx_p^j\wedge}]\Big). \end{align} $$
$$ \begin{align} \Delta^{\prime}_{p,\mu}=\sum_{j=1}^n\Big(-\Big(\frac{\partial}{\partial x_p^j}\Big)^2+\mu^2(x_p^j)^2+\mu\epsilon_{p,j}[{dx_p^j\lrcorner},{dx_p^j\wedge}]\Big). \end{align} $$
 $[{\cdot },{\cdot }]$
stands for the commutator of operators. Using multi-index notation, we can write
$[{\cdot },{\cdot }]$
stands for the commutator of operators. Using multi-index notation, we can write  $$\begin{align*}[{dx_p^j\lrcorner},{dx_p^j\wedge}]dx_p^J= \begin{cases} dx_p^J & \text{if}\ j\in J\\ -dx_p^J & \text{if}\ j\notin J. \end{cases} \end{align*}$$
$$\begin{align*}[{dx_p^j\lrcorner},{dx_p^j\wedge}]dx_p^J= \begin{cases} dx_p^J & \text{if}\ j\in J\\ -dx_p^J & \text{if}\ j\notin J. \end{cases} \end{align*}$$
-
(ii)
 $\Delta ^{\prime }_{p,\mu }$
is a nonnegative selfadjoint operator in
$\Delta ^{\prime }_{p,\mu }$
is a nonnegative selfadjoint operator in
 $L^2(\mathbb {R}^n;\Lambda )$
with a discrete spectrum, which consists of the eigenvalues (4.7)where
$L^2(\mathbb {R}^n;\Lambda )$
with a discrete spectrum, which consists of the eigenvalues (4.7)where $$ \begin{align} \mu\sum_{j=1}^n(1+2u_j+\epsilon_{p,j}v_j)\;, \end{align} $$
$$ \begin{align} \mu\sum_{j=1}^n(1+2u_j+\epsilon_{p,j}v_j)\;, \end{align} $$
 $u_j\in \mathbb {N}_0$
and
$u_j\in \mathbb {N}_0$
and
 $v_j=\pm 1$
. For the restriction of
$v_j=\pm 1$
. For the restriction of
 $\Delta ^{\prime }_{p,\mu }$
to k-forms, the spectrum has the additional requirement that exactly k of the numbers
$\Delta ^{\prime }_{p,\mu }$
to k-forms, the spectrum has the additional requirement that exactly k of the numbers
 $v_j$
are equal to
$v_j$
are equal to
 $1$
. In particular,
$1$
. In particular,
 $0$
is an eigenvalue of
$0$
is an eigenvalue of
 $\Delta ^{\prime }_{p,\mu }$
with multiplicity
$\Delta ^{\prime }_{p,\mu }$
with multiplicity
 $1$
(choosing
$1$
(choosing
 $u_j=0$
and
$u_j=0$
and
 $v_j=-\epsilon _{p,j}$
for all j), and the nonzero eigenvalues are of order
$v_j=-\epsilon _{p,j}$
for all j), and the nonzero eigenvalues are of order
 $\mu $
as
$\mu $
as
 $\mu \to +\infty $
.
$\mu \to +\infty $
.
 $D^{\prime }_{p,\mu }$
is also a self-adjoint operator in
$D^{\prime }_{p,\mu }$
is also a self-adjoint operator in
 $L^2(\mathbb {R}^n;\Lambda )$
with a discrete spectrum, which consists of the positive and negative square roots of Equation (4.7).
$L^2(\mathbb {R}^n;\Lambda )$
with a discrete spectrum, which consists of the positive and negative square roots of Equation (4.7).
-
(iii) The kernel of
 $D^{\prime }_{p,\mu }$
and
$D^{\prime }_{p,\mu }$
and
 $\Delta ^{\prime }_{p,\mu }$
is generated by the normalized form
$\Delta ^{\prime }_{p,\mu }$
is generated by the normalized form  $$\begin{align*}e^{\prime}_{p,\mu}=\Big(\frac\mu\pi\Big)^{n/4}e^{-\mu|x_p|^2/2}\,dx_p^1\wedge\dots\wedge dx_p^{\operatorname{ind}(p)}. \end{align*}$$
$$\begin{align*}e^{\prime}_{p,\mu}=\Big(\frac\mu\pi\Big)^{n/4}e^{-\mu|x_p|^2/2}\,dx_p^1\wedge\dots\wedge dx_p^{\operatorname{ind}(p)}. \end{align*}$$
For any
![]() $z\in \mathbb {C}$
with
$z\in \mathbb {C}$
with
![]() $\mu>0$
, let
$\mu>0$
, let
![]() $\Delta ^{\prime }_{p,z}=e^{-i\nu h_p}\Delta ^{\prime }_{p,\mu }e^{i\nu h_p}$
. Since the operator of multiplication by
$\Delta ^{\prime }_{p,z}=e^{-i\nu h_p}\Delta ^{\prime }_{p,\mu }e^{i\nu h_p}$
. Since the operator of multiplication by
![]() $e^{-i\nu h_p}$
is unitary,
$e^{-i\nu h_p}$
is unitary,
![]() $\Delta ^{\prime }_{p,z}$
is also selfadjoint and nonnegative in
$\Delta ^{\prime }_{p,z}$
is also selfadjoint and nonnegative in
![]() $L^2(\mathbb {R}^n;\Lambda )$
, it has a discrete spectrum with the same eigenvalues and multiplicities as
$L^2(\mathbb {R}^n;\Lambda )$
, it has a discrete spectrum with the same eigenvalues and multiplicities as
![]() $\Delta ^{\prime }_{p,\mu }$
, and its kernel is generated by the normalized form
$\Delta ^{\prime }_{p,\mu }$
, and its kernel is generated by the normalized form
![]() $e^{\prime }_{p,z}:=e^{-i\nu h_p}e^{\prime }_{p,\mu }$
. We will also use the notation
$e^{\prime }_{p,z}:=e^{-i\nu h_p}e^{\prime }_{p,\mu }$
. We will also use the notation
The function
![]() $x_p^*h_p\in C^\infty (U_p)$
agrees with
$x_p^*h_p\in C^\infty (U_p)$
agrees with
![]() $h_{\eta ,p}$
, which is also denoted by
$h_{\eta ,p}$
, which is also denoted by
![]() $h_p$
in this section.
$h_p$
in this section.
Fix an even
![]() $C^\infty $
function
$C^\infty $
function
![]() $\rho :\mathbb {R}\to [0,1]$
such that
$\rho :\mathbb {R}\to [0,1]$
such that
![]() $\rho =1$
on
$\rho =1$
on
![]() $[-r,r]$
and
$[-r,r]$
and
![]() $\operatorname {supp}\rho \subset [-2r,2r]$
. For every
$\operatorname {supp}\rho \subset [-2r,2r]$
. For every
![]() $p\in \mathcal {X}$
, let
$p\in \mathcal {X}$
, let
where
 $$ \begin{align} a_\mu=\bigg(\int_{-2r}^{2r}\rho(x)^2e^{-\mu x^2}\,dx\bigg)^{\frac n2}=\Big(\frac\pi\mu\Big)^{\frac n4}+O(e^{-c\mu})\;, \end{align} $$
$$ \begin{align} a_\mu=\bigg(\int_{-2r}^{2r}\rho(x)^2e^{-\mu x^2}\,dx\bigg)^{\frac n2}=\Big(\frac\pi\mu\Big)^{\frac n4}+O(e^{-c\mu})\;, \end{align} $$
as
![]() $\mu \to +\infty $
. The extensions by zero of the forms
$\mu \to +\infty $
. The extensions by zero of the forms
![]() $e_{p,z}$
to M are also denoted by
$e_{p,z}$
to M are also denoted by
![]() $e_{p,z}$
. They form an orthonormal basis of a graded subspace
$e_{p,z}$
. They form an orthonormal basis of a graded subspace
![]() $E_z\subset \Omega (M)$
with
$E_z\subset \Omega (M)$
with
![]() $\dim E_z=|\mathcal {X}|$
. Observe that
$\dim E_z=|\mathcal {X}|$
. Observe that
![]() $d_z$
does not preserve
$d_z$
does not preserve
![]() $E_z$
so that
$E_z$
so that
![]() $E_z$
is not a subcomplex of
$E_z$
is not a subcomplex of
![]() $(\Omega (M), d_z)$
. Let
$(\Omega (M), d_z)$
. Let
![]() $P_z$
be the orthogonal projection of
$P_z$
be the orthogonal projection of
![]() $L^2(M;\Lambda )$
to
$L^2(M;\Lambda )$
to
![]() $E_z$
.
$E_z$
.
Remark 4.2. For the sake of simplicity, most of our results are stated for
![]() $\mu \gg 0$
or as
$\mu \gg 0$
or as
![]() $\mu \to +\infty $
, but they have obvious versions for
$\mu \to +\infty $
, but they have obvious versions for
![]() $\mu \ll 0$
or as
$\mu \ll 0$
or as
![]() $\mu \to -\infty $
, as follows by considering
$\mu \to -\infty $
, as follows by considering
![]() $-\eta $
and using that
$-\eta $
and using that
![]() $\mathcal {X}_k(-\eta )=\mathcal {X}_{n-k}(\eta )$
.
$\mathcal {X}_k(-\eta )=\mathcal {X}_{n-k}(\eta )$
.
Proposition 4.3. If
![]() $\mu \gg 0$
and
$\mu \gg 0$
and
![]() $\beta \in H^1(M;\Lambda )$
with
$\beta \in H^1(M;\Lambda )$
with
![]() $\operatorname {supp}\beta \subset M\setminus U$
, then
$\operatorname {supp}\beta \subset M\setminus U$
, then
Proof. This follows like [Reference Zhang75, Proposition 4.7], using that
![]() $\mathsf {H}_\eta $
is of order zero in Equation (2.3). Actually, according to the statement of [Reference Zhang75, Proposition 4.7], this inequality would hold with
$\mathsf {H}_\eta $
is of order zero in Equation (2.3). Actually, according to the statement of [Reference Zhang75, Proposition 4.7], this inequality would hold with
![]() $\sqrt {\mu }$
instead of
$\sqrt {\mu }$
instead of
![]() $\mu $
, but its proof clearly shows that using
$\mu $
, but its proof clearly shows that using
![]() $\mu $
is fine.
$\mu $
is fine.
Proposition 4.4. The following properties hold:
-
(i)
 $P_zD_zP_z=0$
.
$P_zD_zP_z=0$
. -
(ii) If
 $\mu \gg 0$
,
$\mu \gg 0$
,
 $\alpha \in E_z$
and
$\alpha \in E_z$
and
 $\beta \in E_z^\perp \cap H^1(M;\Lambda )$
, then
$\beta \in E_z^\perp \cap H^1(M;\Lambda )$
, then  $$\begin{align*}\|P_z^\perp D_z\alpha\|\le e^{-c\mu}\|\alpha\|\;,\quad\|P_zD_z\beta\|\le e^{-c\mu}\|\beta\|. \end{align*}$$
$$\begin{align*}\|P_z^\perp D_z\alpha\|\le e^{-c\mu}\|\alpha\|\;,\quad\|P_zD_z\beta\|\le e^{-c\mu}\|\beta\|. \end{align*}$$
-
(iii) If
 $\mu \gg 0$
and
$\mu \gg 0$
and
 $\beta \in E_z^\perp \cap H^1(M;\Lambda )$
, then
$\beta \in E_z^\perp \cap H^1(M;\Lambda )$
, then  $$\begin{align*}\|P_z^\perp D_z\beta\|\ge C\sqrt{\mu}\,\|\beta\|. \end{align*}$$
$$\begin{align*}\|P_z^\perp D_z\beta\|\ge C\sqrt{\mu}\,\|\beta\|. \end{align*}$$
Proof. This follows like [Reference Zhang75, Propositions 4.11, 4.12 and 5.6]. Property (i) is true because every
![]() $D_z e_{p,z}$
is supported in
$D_z e_{p,z}$
is supported in
![]() $U_p$
and has homogeneous components of degree different from
$U_p$
and has homogeneous components of degree different from
![]() $\operatorname {ind}(p)$
; therefore, it is orthogonal to
$\operatorname {ind}(p)$
; therefore, it is orthogonal to
![]() $\ker \Delta _z$
. The other properties are consequences of Propositions 4.1 and 4.3 and Equations (4.8)–(4.11). According to [Reference Zhang75, Proposition 4.11], the inequalities of (ii) hold with
$\ker \Delta _z$
. The other properties are consequences of Propositions 4.1 and 4.3 and Equations (4.8)–(4.11). According to [Reference Zhang75, Proposition 4.11], the inequalities of (ii) hold with
![]() $1/\mu $
instead of
$1/\mu $
instead of
![]() $e^{-c\mu }$
, but its proof shows that indeed
$e^{-c\mu }$
, but its proof shows that indeed
![]() $e^{-c\mu }$
can be achieved.
$e^{-c\mu }$
can be achieved.
Proposition 4.5. For all
![]() $m\in \mathbb {N}_0$
, if
$m\in \mathbb {N}_0$
, if
![]() $\mu \gg 0$
, then
$\mu \gg 0$
, then
Proof. From Proposition 4.1 (iii) and Equations (2.2), (4.9) and (4.10), we get
 $$ \begin{align} D_ze_{p,z}=D_z\Big(\frac{\rho_p}{a_\mu}e^{\prime}_{p,z}\Big) =e^{-i\nu h_p}\frac1{a_\mu}\Big(\frac{\pi}4\Big)^{n/4}\hat c(d\rho_p)e^{\prime}_{p,\mu}. \end{align} $$
$$ \begin{align} D_ze_{p,z}=D_z\Big(\frac{\rho_p}{a_\mu}e^{\prime}_{p,z}\Big) =e^{-i\nu h_p}\frac1{a_\mu}\Big(\frac{\pi}4\Big)^{n/4}\hat c(d\rho_p)e^{\prime}_{p,\mu}. \end{align} $$
Thus, the stated estimate of
![]() $\|D_ze_{p,z}\|_m$
is true by Equations (4.9) and (4.11), since
$\|D_ze_{p,z}\|_m$
is true by Equations (4.9) and (4.11), since
![]() $d\rho _p=0$
around p, and using the definition of
$d\rho _p=0$
around p, and using the definition of
![]() $h_p$
and the condition
$h_p$
and the condition
![]() $4r<1$
. (When
$4r<1$
. (When
![]() $\nu =0$
, this is indicated in [Reference Zhang75, Eq. (6.17)].)
$\nu =0$
, this is indicated in [Reference Zhang75, Eq. (6.17)].)
By Equation (2.11), for all
![]() $k\in \mathbb {N}_0$
and
$k\in \mathbb {N}_0$
and
![]() $p\in \mathcal {X}$
, the form
$p\in \mathcal {X}$
, the form
![]() $D_{i\nu }^kD_ze_{p,z}$
is the extension by zero of the form
$D_{i\nu }^kD_ze_{p,z}$
is the extension by zero of the form
![]() $e^{-i\nu h_p}D^kD_\mu e_{p,\mu }$
on
$e^{-i\nu h_p}D^kD_\mu e_{p,\mu }$
on
![]() $U_p$
. Then the stated estimate of
$U_p$
. Then the stated estimate of
![]() $\|D_ze_{p,z}\|_{m,i\nu }$
follows from the case
$\|D_ze_{p,z}\|_{m,i\nu }$
follows from the case
![]() $\nu =0$
.
$\nu =0$
.
Proposition 4.6. If
![]() $\mu \gg 0$
, then
$\mu \gg 0$
, then
Consider the partition of
![]() $\operatorname {spec}\Delta _z$
into its intersections with
$\operatorname {spec}\Delta _z$
into its intersections with
![]() $[0,1]$
and
$[0,1]$
and
![]() $(1,\infty )$
, called the small and large spectrum; the term small/large eigenvalues may be also used. Let
$(1,\infty )$
, called the small and large spectrum; the term small/large eigenvalues may be also used. Let
![]() $E_{z,\mathrm {sm}}\subset \Omega (M)$
denote the graded finite-dimensional subspace generated by the eigenforms of the small eigenvalues, let
$E_{z,\mathrm {sm}}\subset \Omega (M)$
denote the graded finite-dimensional subspace generated by the eigenforms of the small eigenvalues, let
![]() $E_{z,\mathrm {la}}=E_{z,\mathrm {sm}}^\perp $
in
$E_{z,\mathrm {la}}=E_{z,\mathrm {sm}}^\perp $
in
![]() $L^2(M;\Lambda )$
, and let
$L^2(M;\Lambda )$
, and let
![]() $P_{z,\mathrm {sm/la}}$
be the orthogonal projection to
$P_{z,\mathrm {sm/la}}$
be the orthogonal projection to
![]() $E_{z,\mathrm {sm/la}}$
, called small/large projection. Moreover,
$E_{z,\mathrm {sm/la}}$
, called small/large projection. Moreover,
![]() $(\Omega (M),d_z)$
splits into a topological direct sum of the subcomplexes
$(\Omega (M),d_z)$
splits into a topological direct sum of the subcomplexes
![]() $E_{z,\mathrm {sm}}$
and
$E_{z,\mathrm {sm}}$
and
![]() $E_{z,\mathrm {la}}\cap \Omega (M)$
, called the small and large complexes, and Equation (2.6) gives
$E_{z,\mathrm {la}}\cap \Omega (M)$
, called the small and large complexes, and Equation (2.6) gives
For any operator B defined on
![]() $\Omega (M)$
or
$\Omega (M)$
or
![]() $L^2(M;\Lambda )$
, let
$L^2(M;\Lambda )$
, let
![]() $B_{z,\mathrm {sm/la}}=BP_{z,\mathrm {sm/la}}$
.
$B_{z,\mathrm {sm/la}}=BP_{z,\mathrm {sm/la}}$
.
Proposition 4.7. For all
![]() $m\in \mathbb {N}_0$
,
$m\in \mathbb {N}_0$
,
![]() $\mu \gg 0$
and
$\mu \gg 0$
and
![]() $\alpha \in E_z$
,
$\alpha \in E_z$
,
Proof. This follows like [Reference Zhang75, Lemma 5.8 and Theorem 6.7], using
![]() $\|\ \|_{m,i\nu }$
instead of
$\|\ \|_{m,i\nu }$
instead of
![]() $\|\ \|_m$
. The following are the main steps of the proof.
$\|\ \|_m$
. The following are the main steps of the proof.
Let
![]() $\mathbb {S}^1=\{\,\omega \in \mathbb {C}\mid |\omega |=1\,\}$
. With the argument of the proof of [Reference Zhang75, Eq. (5.27)], using Proposition 4.4, we get that, for all
$\mathbb {S}^1=\{\,\omega \in \mathbb {C}\mid |\omega |=1\,\}$
. With the argument of the proof of [Reference Zhang75, Eq. (5.27)], using Proposition 4.4, we get that, for all
![]() $\alpha \in H^1(M;\Lambda )$
,
$\alpha \in H^1(M;\Lambda )$
,
![]() $w\in \mathbb {S}^1$
and
$w\in \mathbb {S}^1$
and
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
Thus,
![]() $w-D_z:H^1(M;\Lambda )\to L^2(M;\Lambda )$
is bijective, and, for all
$w-D_z:H^1(M;\Lambda )\to L^2(M;\Lambda )$
is bijective, and, for all
![]() $\beta \in L^2(M;\Lambda )$
,
$\beta \in L^2(M;\Lambda )$
,
![]() $w\in \mathbb {S}^1$
and
$w\in \mathbb {S}^1$
and
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
On the other hand, arguing like in the proof of [Reference Zhang75, Eq. (6.18)], it follows that, for all
![]() $\gamma \in H^m(M;\Lambda )$
,
$\gamma \in H^m(M;\Lambda )$
,
![]() $w\in \mathbb {S}^1$
and
$w\in \mathbb {S}^1$
and
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
Continuing by induction on
![]() $m\in \mathbb {N}_0$
, we obtain
$m\in \mathbb {N}_0$
, we obtain
 $$\begin{align*}\|\gamma\|_{m,i\nu}\le C_m\Big(\mu^m\|\gamma\|+\sum_{k=1}^m\mu^{k-1}\|(w-D_z)\gamma\big\|_{m-k,i\nu}\Big). \end{align*}$$
$$\begin{align*}\|\gamma\|_{m,i\nu}\le C_m\Big(\mu^m\|\gamma\|+\sum_{k=1}^m\mu^{k-1}\|(w-D_z)\gamma\big\|_{m-k,i\nu}\Big). \end{align*}$$
In other words, for all
![]() $\beta \in H^{m-1}(M;\Lambda )$
,
$\beta \in H^{m-1}(M;\Lambda )$
,
 $$\begin{align*}\big\|(w-D_z)^{-1}\beta\big\|_{m,i\nu}\le C_m\Big(\mu^m\big\|(w-D_z)^{-1}\beta\big\|+\sum_{k=1}^m\mu^{k-1}\|\beta\|_{m-k,i\nu}\Big). \end{align*}$$
$$\begin{align*}\big\|(w-D_z)^{-1}\beta\big\|_{m,i\nu}\le C_m\Big(\mu^m\big\|(w-D_z)^{-1}\beta\big\|+\sum_{k=1}^m\mu^{k-1}\|\beta\|_{m-k,i\nu}\Big). \end{align*}$$
Applying Equation (4.14) to this inequality, we get, for
![]() $m\ge 1$
,
$m\ge 1$
,
From Equations (4.14) and (4.15) and Proposition 4.5, it follows that, for
![]() $m\in \mathbb {N}_0$
,
$m\in \mathbb {N}_0$
,
as
![]() $\mu \to +\infty $
, uniformly on
$\mu \to +\infty $
, uniformly on
![]() $w\in \mathbb {S}^1$
. But, endowing
$w\in \mathbb {S}^1$
. But, endowing
![]() $\mathbb {S}^1$
with the counterclockwise orientation, basic spectral theory gives (see, e.g., [Reference Dunford and Schwartz25, Section VII.3])
$\mathbb {S}^1$
with the counterclockwise orientation, basic spectral theory gives (see, e.g., [Reference Dunford and Schwartz25, Section VII.3])
 $$ \begin{align} P_{z,\mathrm{sm}} e_{p,z}- e_{p,z}&=\frac{1}{2\pi i}\int_{\mathbb{S}^1}\big((w-D_z)^{-1}-w^{-1}\big) e_{p,z}\,dw \nonumber \\ &=\frac{1}{2\pi i}\int_{\mathbb{S}^1}w^{-1}(w-D_z)^{-1}D_z e_{p,z}\,dw. \end{align} $$
$$ \begin{align} P_{z,\mathrm{sm}} e_{p,z}- e_{p,z}&=\frac{1}{2\pi i}\int_{\mathbb{S}^1}\big((w-D_z)^{-1}-w^{-1}\big) e_{p,z}\,dw \nonumber \\ &=\frac{1}{2\pi i}\int_{\mathbb{S}^1}w^{-1}(w-D_z)^{-1}D_z e_{p,z}\,dw. \end{align} $$
The result follows using Equation (4.16) in Equation (4.17).
Corollary 4.8. For
![]() $\mu \gg 0$
and
$\mu \gg 0$
and
![]() $\alpha \in E_z$
,
$\alpha \in E_z$
,
Proof. Apply Propositions 2.2 and 4.7.
Alternatively, the proof of Proposition 4.7 can be modified as follows to get this result (some step of this alternative argument will be used later). Iterating Equation (4.15), we get
for all
![]() $\beta \in L^2(M;\Lambda )$
. Then, by Proposition 2.2,
$\beta \in L^2(M;\Lambda )$
. Then, by Proposition 2.2,
Thus, by Proposition 4.5,
as
![]() $\mu \to +\infty $
. Finally, apply this expression in Equation (4.17).
$\mu \to +\infty $
. Finally, apply this expression in Equation (4.17).
Corollary 4.9. If
![]() $\mu \gg 0$
, then
$\mu \gg 0$
, then
![]() $P_{z,\mathrm {sm}}:E_z\to E_{z,\mathrm {sm}}$
is an isomorphism; in particular,
$P_{z,\mathrm {sm}}:E_z\to E_{z,\mathrm {sm}}$
is an isomorphism; in particular,
![]() $\dim E_{z,\mathrm {sm}}=|\mathcal {X}|$
and
$\dim E_{z,\mathrm {sm}}=|\mathcal {X}|$
and
![]() $\dim E_{z,\mathrm {sm}}^k=|\mathcal {X}_k|$
.
$\dim E_{z,\mathrm {sm}}^k=|\mathcal {X}_k|$
.
Proof. This follows from Propositions 4.4 and 4.7 for
![]() $m=0$
like [Reference Zhang75, Proposition 5.5].
$m=0$
like [Reference Zhang75, Proposition 5.5].
When
![]() $\mu \gg 0$
, Equation (4.5) also follows from Corollary 4.9 and Equations (2.8) and (4.13).
$\mu \gg 0$
, Equation (4.5) also follows from Corollary 4.9 and Equations (2.8) and (4.13).
Theorem 4.10 (Cf. [Reference Burghelea and Haller17, Theorem 3])
We have
Proof. First, we establish the theorem for
![]() $|\mu |\gg 0$
, and then the constants will be changed to cover all
$|\mu |\gg 0$
, and then the constants will be changed to cover all
![]() $\mu $
.
$\mu $
.
We can assume
![]() $\mu \ge 0$
according to Remark 4.2. By Propositions 4.4, 4.7 and 2.4, for all
$\mu \ge 0$
according to Remark 4.2. By Propositions 4.4, 4.7 and 2.4, for all
![]() $\alpha \in E_z$
,
$\alpha \in E_z$
,
 $$ \begin{align*} \|D_z P_{z,\mathrm{sm}}\alpha\| &\le\|D_z\alpha\|+\|D_z(\alpha- P_{z,\mathrm{sm}}\alpha)\|\le\|D_z\alpha\|+\|\alpha- P_{z,\mathrm{sm}}\alpha\|_{1,z}\\ &\le\| P_z^\perp D_z\alpha\|+C(\mu\|\alpha- P_{z,\mathrm{sm}}\alpha\|+\|\alpha- P_{z,\mathrm{sm}}\alpha\|_{1,i\nu})\\ &\le\big(e^{-c\mu}+C\big(\mu e^{-c_0\mu}+e^{-c_1\mu}\big)\big)\|\alpha\|. \end{align*} $$
$$ \begin{align*} \|D_z P_{z,\mathrm{sm}}\alpha\| &\le\|D_z\alpha\|+\|D_z(\alpha- P_{z,\mathrm{sm}}\alpha)\|\le\|D_z\alpha\|+\|\alpha- P_{z,\mathrm{sm}}\alpha\|_{1,z}\\ &\le\| P_z^\perp D_z\alpha\|+C(\mu\|\alpha- P_{z,\mathrm{sm}}\alpha\|+\|\alpha- P_{z,\mathrm{sm}}\alpha\|_{1,i\nu})\\ &\le\big(e^{-c\mu}+C\big(\mu e^{-c_0\mu}+e^{-c_1\mu}\big)\big)\|\alpha\|. \end{align*} $$
Hence, by Corollary 4.9, for all
![]() $\beta \in E_{z,\mathrm {sm}}$
,
$\beta \in E_{z,\mathrm {sm}}$
,
This shows that
Now, let
![]() $\phi \in E_{z,\mathrm {la}}\cap H^1(M;\Lambda )$
, and write
$\phi \in E_{z,\mathrm {la}}\cap H^1(M;\Lambda )$
, and write
![]() $\alpha = P_z\phi \in E_z$
and
$\alpha = P_z\phi \in E_z$
and
![]() $\beta = P_z^\perp \phi \in E_z^\perp \cap H^1(M;\Lambda )$
. By Proposition 4.7,
$\beta = P_z^\perp \phi \in E_z^\perp \cap H^1(M;\Lambda )$
. By Proposition 4.7,
yielding
So
Then, by Proposition 4.4,
 $$ \begin{align*} \|D_z\phi\|&\ge\|D_z\beta\|-\|D_z\alpha\| \ge\| P_z^\perp D_z\beta\|-e^{-c\mu}\|\alpha\|\\ &\ge C\sqrt{\mu}\,\|\beta\|-e^{-c\mu}\|\phi\| \ge\big(C\sqrt{\mu}\big(1-e^{-c_0\mu}\big)-e^{-c\mu}\big)\|\phi\|. \end{align*} $$
$$ \begin{align*} \|D_z\phi\|&\ge\|D_z\beta\|-\|D_z\alpha\| \ge\| P_z^\perp D_z\beta\|-e^{-c\mu}\|\alpha\|\\ &\ge C\sqrt{\mu}\,\|\beta\|-e^{-c\mu}\|\phi\| \ge\big(C\sqrt{\mu}\big(1-e^{-c_0\mu}\big)-e^{-c\mu}\big)\|\phi\|. \end{align*} $$
Therefore, for all
![]() $\phi \in E_{z,\mathrm {la}}\cap H^1(M;\Lambda )$
,
$\phi \in E_{z,\mathrm {la}}\cap H^1(M;\Lambda )$
,
This proves that
The inclusions (4.19) and (4.20) give the result for
![]() $\mu \gg 0$
. But, in those inclusions, we can take c and C so small that, if one of them is not true for some
$\mu \gg 0$
. But, in those inclusions, we can take c and C so small that, if one of them is not true for some
![]() $\mu \ge 0$
, then
$\mu \ge 0$
, then
![]() $C\mu \le e^{-c\mu }$
.
$C\mu \le e^{-c\mu }$
.
4.3. Ranks of some projections in the small complex
Recall that
![]() $(\Pi _z^\perp )_{\mathrm {sm},k}$
,
$(\Pi _z^\perp )_{\mathrm {sm},k}$
,
![]() $\Pi ^1_{z,\mathrm {sm},k}$
and
$\Pi ^1_{z,\mathrm {sm},k}$
and
![]() $\Pi ^2_{z,\mathrm {sm},k}$
denote the orthogonal projections to the images of
$\Pi ^2_{z,\mathrm {sm},k}$
denote the orthogonal projections to the images of
![]() $\Delta _{z,\mathrm {sm},k}$
,
$\Delta _{z,\mathrm {sm},k}$
,
![]() $d_{z,\mathrm {sm},k-1}$
and
$d_{z,\mathrm {sm},k-1}$
and
![]() $\delta _{z,\mathrm {sm},k+1}$
, respectively. Let
$\delta _{z,\mathrm {sm},k+1}$
, respectively. Let
![]() $m_{z,k}$
,
$m_{z,k}$
,
![]() $m_{z,k}^1$
and
$m_{z,k}^1$
and
![]() $m_{z,k}^2$
be the corresponding ranks (or traces) of these projections. They satisfy
$m_{z,k}^2$
be the corresponding ranks (or traces) of these projections. They satisfy
where the last equality is true because
![]() $d_z:\operatorname {im}\delta _z\to \operatorname {im} d_z$
is an isomorphism. For
$d_z:\operatorname {im}\delta _z\to \operatorname {im} d_z$
is an isomorphism. For
![]() $\mu \gg 0$
, we have
$\mu \gg 0$
, we have
![]() $m_{z,k},m_{z,k}^j\le |\mathcal {X}_k|$
by Corollary 4.9 and Equation (4.21).
$m_{z,k},m_{z,k}^j\le |\mathcal {X}_k|$
by Corollary 4.9 and Equation (4.21).
Lemma 4.11. The numbers
![]() $m_{z,k}^j$
are determined by the numbers
$m_{z,k}^j$
are determined by the numbers
![]() $m_{z,k}$
:
$m_{z,k}$
:
 $$\begin{align*}m_{z,k+1}^1=m_{z,k}^2=\sum_{p=0}^k(-1)^{k-p}m_{z,p} =\sum_{q=k+1}^n(-1)^{q-k-1}m_{z,q}. \end{align*}$$
$$\begin{align*}m_{z,k+1}^1=m_{z,k}^2=\sum_{p=0}^k(-1)^{k-p}m_{z,p} =\sum_{q=k+1}^n(-1)^{q-k-1}m_{z,q}. \end{align*}$$
Proof. This follows from Equation (4.21) with an easy induction argument on k.
Lemma 4.12. For
![]() $\mu \gg 0$
, we have
$\mu \gg 0$
, we have
![]() $m_{z,k}=|\mathcal {X}_k|-\beta _z^k$
.
$m_{z,k}=|\mathcal {X}_k|-\beta _z^k$
.
Corollary 4.13.
![]() $\operatorname {Str}((\Pi _z^\perp )_{\mathrm {sm}})=0$
.
$\operatorname {Str}((\Pi _z^\perp )_{\mathrm {sm}})=0$
.
Proof. By Equations (2.8) and (4.5) and Lemma 4.12,
Lemma 4.14. If M is oriented, then, for
![]() $k=0,\dots ,n$
,
$k=0,\dots ,n$
,
Proof. This is true because, by Equation (2.15),
 $$\begin{align*} (\Pi_z^\perp)_{\mathrm{sm},k}\,\star&=\star\,(\Pi_{-\bar z}^\perp)_{\mathrm{sm},n-k}\;,\quad \Pi^1_{z,\mathrm{sm},k}\,\star=\star\,\Pi^2_{-\bar z,\mathrm{sm},n-k}\;,\\ (\Pi_z^\perp)_{\mathrm{sm},k}\,\bar\star&=\bar\star\,(\Pi_{-z}^\perp)_{\mathrm{sm},n-k}\;,\quad \Pi^1_{z,\mathrm{sm},k}\,\bar\star=\bar\star\,\Pi^2_{-z,\mathrm{sm},n-k}. \; \end{align*}$$
$$\begin{align*} (\Pi_z^\perp)_{\mathrm{sm},k}\,\star&=\star\,(\Pi_{-\bar z}^\perp)_{\mathrm{sm},n-k}\;,\quad \Pi^1_{z,\mathrm{sm},k}\,\star=\star\,\Pi^2_{-\bar z,\mathrm{sm},n-k}\;,\\ (\Pi_z^\perp)_{\mathrm{sm},k}\,\bar\star&=\bar\star\,(\Pi_{-z}^\perp)_{\mathrm{sm},n-k}\;,\quad \Pi^1_{z,\mathrm{sm},k}\,\bar\star=\bar\star\,\Pi^2_{-z,\mathrm{sm},n-k}. \; \end{align*}$$
Corollary 4.15. For
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
![]() $m_{z,k}$
and
$m_{z,k}$
and
![]() $m^j_{z,k}$
only depend on
$m^j_{z,k}$
only depend on
![]() $|\mathcal {X}_k|$
and the class
$|\mathcal {X}_k|$
and the class
![]() $\xi =[\eta ]\in H^1(M,\mathbb {R})$
.
$\xi =[\eta ]\in H^1(M,\mathbb {R})$
.
By Corollary 4.15, we write
![]() $m_k=m_k(\eta )=m_{z,k}$
and
$m_k=m_k(\eta )=m_{z,k}$
and
![]() $m_k^j=m_k^j(\eta )=m_{z,k}^j$
for
$m_k^j=m_k^j(\eta )=m_{z,k}^j$
for
![]() $\mu \gg 0$
.
$\mu \gg 0$
.
Corollary 4.16. If M is oriented, then, for
![]() $k=0,\dots ,n$
,
$k=0,\dots ,n$
,
Proof. Apply Equation (4.21), Lemma 4.14 and Corollary 4.15. Alternatively, we can apply Equations (2.9), (2.14) and (4.21); Remark 4.2; and Lemma 4.12.
Corollary 4.17. For
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
 $$\begin{align*}\operatorname{Str}(\Pi_{z,\mathrm{sm}}^1)=-\operatorname{Str}(\Pi_{z,\mathrm{sm}}^2)=\sum_{k=0}^n(-1)^kkm_k. \end{align*}$$
$$\begin{align*}\operatorname{Str}(\Pi_{z,\mathrm{sm}}^1)=-\operatorname{Str}(\Pi_{z,\mathrm{sm}}^2)=\sum_{k=0}^n(-1)^kkm_k. \end{align*}$$
If moreover M is oriented and n is even, then
 $$\begin{align*}\sum_{k=0}^n(-1)^kkm_k=\sum_{k=0}^n(-1)^kk|\mathcal{X}_k|-\frac n2\chi(M). \end{align*}$$
$$\begin{align*}\sum_{k=0}^n(-1)^kkm_k=\sum_{k=0}^n(-1)^kk|\mathcal{X}_k|-\frac n2\chi(M). \end{align*}$$
Proof. Corollary 4.13 gives the first equality. By Lemma 4.11 and Corollary 4.13,
 $$ \begin{align*} \operatorname{Str}(\Pi_{z,\mathrm{sm}}^1)=\sum_{k=0}^n(-1)^k\sum_{q=k}^n(-1)^{q-k}m_q =\sum_{q=0}^n(-1)^q(q+1)m_q=\sum_{q=0}^n(-1)^qqm_q. \end{align*} $$
$$ \begin{align*} \operatorname{Str}(\Pi_{z,\mathrm{sm}}^1)=\sum_{k=0}^n(-1)^k\sum_{q=k}^n(-1)^{q-k}m_q =\sum_{q=0}^n(-1)^q(q+1)m_q=\sum_{q=0}^n(-1)^qqm_q. \end{align*} $$
Now, assume M is oriented and n is even. Then, by Equations (2.8), (2.9) and (2.14),
 $$ \begin{align*} \sum_{k=0}^n(-1)^kk\beta_{\mathrm{No}}^k&=\sum_{l=0}^n(-1)^{n-l}(n-l)\beta_{\mathrm{No}}^{n-l} =\sum_{l=0}^n(-1)^l(n-l)\beta_{\mathrm{No}}^l\\ &=n\chi(M)-\sum_{l=0}^n(-1)^ll\beta_{\mathrm{No}}^l. \end{align*} $$
$$ \begin{align*} \sum_{k=0}^n(-1)^kk\beta_{\mathrm{No}}^k&=\sum_{l=0}^n(-1)^{n-l}(n-l)\beta_{\mathrm{No}}^{n-l} =\sum_{l=0}^n(-1)^l(n-l)\beta_{\mathrm{No}}^l\\ &=n\chi(M)-\sum_{l=0}^n(-1)^ll\beta_{\mathrm{No}}^l. \end{align*} $$
Hence, the last equality of the statement follows from Lemma 4.12.
4.4. Asymptotic properties of the small projection
Notation 4.18. Consider a function
![]() $f(x)>0$
(
$f(x)>0$
(
![]() $x>0$
). When referring to vectors in Banach spaces, the order notation
$x>0$
). When referring to vectors in Banach spaces, the order notation
![]() $O(f(|\mu |))$
(
$O(f(|\mu |))$
(
![]() $\mu \to \pm \infty $
) will be used for a family of vectors
$\mu \to \pm \infty $
) will be used for a family of vectors
![]() $v=v(z)$
(
$v=v(z)$
(
![]() $z\in \mathbb {C}$
) with
$z\in \mathbb {C}$
) with
![]() $\|v(z)\|=O(f(|\mu |))$
. This notation applies, for example, to bounded operators between Banach spaces. We may also consider this notation when the Banach spaces depend on z.
$\|v(z)\|=O(f(|\mu |))$
. This notation applies, for example, to bounded operators between Banach spaces. We may also consider this notation when the Banach spaces depend on z.
Proposition 4.19. For every
![]() $\tau \in \mathbb {R}$
, on
$\tau \in \mathbb {R}$
, on
![]() $L^2(M;\Lambda )$
, as
$L^2(M;\Lambda )$
, as
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Proof. By Corollary 4.9, for
![]() $\mu \gg 0$
, the elements
$\mu \gg 0$
, the elements
![]() $P_{z,\mathrm {sm}} e_{p,z}$
(
$P_{z,\mathrm {sm}} e_{p,z}$
(
![]() $p\in \mathcal {X}$
) form a base of
$p\in \mathcal {X}$
) form a base of
![]() $E_{z,\mathrm {sm}}$
. Applying the Gram–Schmidt process to this base, we get an orthonormal base
$E_{z,\mathrm {sm}}$
. Applying the Gram–Schmidt process to this base, we get an orthonormal base
![]() $\tilde e_{p,z}$
. By Proposition 4.7,
$\tilde e_{p,z}$
. By Proposition 4.7,
This gives the first equality of the statement: for any
![]() $\alpha \in L^2(M;\Lambda )$
,
$\alpha \in L^2(M;\Lambda )$
,
Since the sets
![]() $U_p$
(
$U_p$
(
![]() $p\in \mathcal {X}$
) are disjoint one another, for
$p\in \mathcal {X}$
) are disjoint one another, for
![]() $p\ne q$
in
$p\ne q$
in
![]() $\mathcal {X}$
,
$\mathcal {X}$
,
On the other hand, by Equations (4.8)–(4.11), we can also assume
 $$ \begin{align} \langle e_{p,z}, e_{p,z+\tau}\rangle&=\langle e^{-i\nu h_p}e_{p,\mu},e^{-i\nu h_p} e_{p,\mu+\tau}\rangle =\langle e_{p,\mu}, e_{p,\mu+\tau}\rangle\nonumber\\ &=\frac{(\mu(\mu+\tau))^{n/4}}{\pi^{n/2}}\big\langle\rho_pe^{-\mu|x_p|^2/2},\rho_pe^{-(\mu+\tau)|x_p|^2/2}\big\rangle +O\big(e^{-c\mu}\big)\nonumber\\ &=\frac{(\mu(\mu+\tau))^{n/4}}{\pi^{n/2}}\int_{\mathbb{R}^n}e^{-(\mu+\tau/2)|x_p|^2}\,dx_p+O\big(e^{-c\mu}\big)\nonumber\\ &=\frac{(\mu(\mu+\tau))^{n/4}}{(\mu+\tau/2)^{n/2}}+O\big(e^{-c\mu}\big)=1+O\big(\mu^{-2}\big)\;, \end{align} $$
$$ \begin{align} \langle e_{p,z}, e_{p,z+\tau}\rangle&=\langle e^{-i\nu h_p}e_{p,\mu},e^{-i\nu h_p} e_{p,\mu+\tau}\rangle =\langle e_{p,\mu}, e_{p,\mu+\tau}\rangle\nonumber\\ &=\frac{(\mu(\mu+\tau))^{n/4}}{\pi^{n/2}}\big\langle\rho_pe^{-\mu|x_p|^2/2},\rho_pe^{-(\mu+\tau)|x_p|^2/2}\big\rangle +O\big(e^{-c\mu}\big)\nonumber\\ &=\frac{(\mu(\mu+\tau))^{n/4}}{\pi^{n/2}}\int_{\mathbb{R}^n}e^{-(\mu+\tau/2)|x_p|^2}\,dx_p+O\big(e^{-c\mu}\big)\nonumber\\ &=\frac{(\mu(\mu+\tau))^{n/4}}{(\mu+\tau/2)^{n/2}}+O\big(e^{-c\mu}\big)=1+O\big(\mu^{-2}\big)\;, \end{align} $$
where
![]() $dx_p=dx_p^1\dots dx_p^n=\operatorname {dvol}(x_p)$
. Combining Equation (4.22) for z and
$dx_p=dx_p^1\dots dx_p^n=\operatorname {dvol}(x_p)$
. Combining Equation (4.22) for z and
![]() $z+\tau $
with Equations (4.23) and (4.24), we obtain
$z+\tau $
with Equations (4.23) and (4.24), we obtain
 $$ \begin{align} P_{z+\tau,\mathrm{sm}}\tilde e_{p,z}&=\sum_{q\in\mathcal{X}}\langle \tilde e_{p,z},\tilde e_{q,z+\tau}\rangle\tilde e_{q,z+\tau} =\sum_{q\in\mathcal{X}}\langle e_{p,z}, e_{q,z+\tau}\rangle e_{q,z+\tau}+O\big(e^{-c\mu}\big)\nonumber\\ &= e_{p,z+\tau}+O\big(\mu^{-2}\big)=\tilde e_{p,z+\tau}+O\big(\mu^{-2}\big). \end{align} $$
$$ \begin{align} P_{z+\tau,\mathrm{sm}}\tilde e_{p,z}&=\sum_{q\in\mathcal{X}}\langle \tilde e_{p,z},\tilde e_{q,z+\tau}\rangle\tilde e_{q,z+\tau} =\sum_{q\in\mathcal{X}}\langle e_{p,z}, e_{q,z+\tau}\rangle e_{q,z+\tau}+O\big(e^{-c\mu}\big)\nonumber\\ &= e_{p,z+\tau}+O\big(\mu^{-2}\big)=\tilde e_{p,z+\tau}+O\big(\mu^{-2}\big). \end{align} $$
Repeating Equation (4.25) interchanging the roles of z and
![]() $z+\tau $
, we get
$z+\tau $
, we get
This gives the second equality of the statement: For any
![]() $\alpha \in L^2(M;\Lambda )$
,
$\alpha \in L^2(M;\Lambda )$
,
 $$ \begin{align*} P_{z,\mathrm{sm}}\alpha&=\sum_{p\in\mathcal{X}}\langle\alpha,\tilde e_{p,z}\rangle\tilde e_{p,z} =P_{z,\mathrm{sm}}P_{z+\tau,\mathrm{sm}}\sum_{p\in\mathcal{X}}\langle\alpha,\tilde e_{p,z}\rangle\tilde e_{p,z} +O\big(\mu^{-2}\big)\|\alpha\|\\&=P_{z,\mathrm{sm}}P_{z+\tau,\mathrm{sm}}P_{z,\mathrm{sm}}\alpha+O\big(\mu^{-2}\big)\|\alpha\|. \end{align*} $$
$$ \begin{align*} P_{z,\mathrm{sm}}\alpha&=\sum_{p\in\mathcal{X}}\langle\alpha,\tilde e_{p,z}\rangle\tilde e_{p,z} =P_{z,\mathrm{sm}}P_{z+\tau,\mathrm{sm}}\sum_{p\in\mathcal{X}}\langle\alpha,\tilde e_{p,z}\rangle\tilde e_{p,z} +O\big(\mu^{-2}\big)\|\alpha\|\\&=P_{z,\mathrm{sm}}P_{z+\tau,\mathrm{sm}}P_{z,\mathrm{sm}}\alpha+O\big(\mu^{-2}\big)\|\alpha\|. \end{align*} $$
By Equation (4.25),
 $$ \begin{align*} \|\tilde e_{p,z}-\tilde e_{p,z+\tau}\big\|^2 &=\|\tilde e_{p,z}\|^2-2\Re\langle\tilde e_{p,z},\tilde e_{p,z+\tau}\rangle+\|\tilde e_{p,z+\tau}\|^2=2-2\Re\langle P_{z+\tau,\mathrm{sm}}\tilde e_{p,z},\tilde e_{p,z+\tau}\rangle\\ & =2-2\Re\langle\tilde e_{p,z+\tau},\tilde e_{p,z+\tau}\rangle+O\big(\mu^{-2}\big)=O\big(\mu^{-2}\big)\;, \end{align*} $$
$$ \begin{align*} \|\tilde e_{p,z}-\tilde e_{p,z+\tau}\big\|^2 &=\|\tilde e_{p,z}\|^2-2\Re\langle\tilde e_{p,z},\tilde e_{p,z+\tau}\rangle+\|\tilde e_{p,z+\tau}\|^2=2-2\Re\langle P_{z+\tau,\mathrm{sm}}\tilde e_{p,z},\tilde e_{p,z+\tau}\rangle\\ & =2-2\Re\langle\tilde e_{p,z+\tau},\tilde e_{p,z+\tau}\rangle+O\big(\mu^{-2}\big)=O\big(\mu^{-2}\big)\;, \end{align*} $$
which means
The last stated equality follows from Equations (4.25) and (4.26): For any
![]() $\alpha \in L^2(M;\Lambda )$
,
$\alpha \in L^2(M;\Lambda )$
,
 $$ \begin{align*} P_{z,\mathrm{sm}}\alpha &=\sum_{p\in\mathcal{X}}\langle\alpha,\tilde e_{p,z}\rangle\tilde e_{p,z} =\sum_{p\in\mathcal{X}}\langle\alpha,\tilde e_{p,z+\tau}\rangle\tilde e_{p,z+\tau}+O\big(\mu^{-1}\big)\alpha\\ &=P_{z+\tau,\mathrm{sm}}\alpha+O\big(\mu^{-1}\big)\alpha. \; \end{align*} $$
$$ \begin{align*} P_{z,\mathrm{sm}}\alpha &=\sum_{p\in\mathcal{X}}\langle\alpha,\tilde e_{p,z}\rangle\tilde e_{p,z} =\sum_{p\in\mathcal{X}}\langle\alpha,\tilde e_{p,z+\tau}\rangle\tilde e_{p,z+\tau}+O\big(\mu^{-1}\big)\alpha\\ &=P_{z+\tau,\mathrm{sm}}\alpha+O\big(\mu^{-1}\big)\alpha. \; \end{align*} $$
Corollary 4.20. For every
![]() $\tau \in \mathbb {R}$
, on
$\tau \in \mathbb {R}$
, on
![]() $L^2(M;\Lambda )$
,
$L^2(M;\Lambda )$
,
Proof. Since
![]() $d_{z+\tau }=d_z+\tau \,{\eta \wedge }$
, it follows from Theorem 4.10 that
$d_{z+\tau }=d_z+\tau \,{\eta \wedge }$
, it follows from Theorem 4.10 that
![]() $d_{z+\tau }$
is bounded on
$d_{z+\tau }$
is bounded on
![]() $E_{z,\mathrm {sm}}+E_{z+\tau ,\mathrm {sm}}$
, uniformly on
$E_{z,\mathrm {sm}}+E_{z+\tau ,\mathrm {sm}}$
, uniformly on
![]() $\mu \gg 0$
. Hence, by Proposition 4.19,
$\mu \gg 0$
. Hence, by Proposition 4.19,
Proposition 4.21. On
![]() $L^2(M;\Lambda )$
,
$L^2(M;\Lambda )$
,
Proof. By Theorem 4.10, for all
![]() $\alpha \in \Omega (M)$
,
$\alpha \in \Omega (M)$
,
yielding
![]() $d_zP_{z,\mathrm {sm}}=O\big (e^{-c\mu }\big )$
. This is also true with the parameter
$d_zP_{z,\mathrm {sm}}=O\big (e^{-c\mu }\big )$
. This is also true with the parameter
![]() $z+1$
. So, by Corollary 4.20,
$z+1$
. So, by Corollary 4.20,
4.5. Derivatives of the small projection
Remark 4.22. For reasons of brevity, most of the results about derivatives are stated for
![]() $\partial _z$
, which may be simply denoted with a dot. But there are obvious versions of those results for
$\partial _z$
, which may be simply denoted with a dot. But there are obvious versions of those results for
![]() $\partial _{\bar z}$
with analogous proofs.
$\partial _{\bar z}$
with analogous proofs.
Proposition 4.23. We have
Proof. By Equation (2.4) and Theorem 4.10, for
![]() $\mu \gg 0$
and every
$\mu \gg 0$
and every
![]() $\omega \in \mathbb {S}^1$
, a standard computation gives
$\omega \in \mathbb {S}^1$
, a standard computation gives
Then, by Equation (4.14),
![]() $\partial _z\big ((w-D_z)^{-1}\big )$
defines an operator on
$\partial _z\big ((w-D_z)^{-1}\big )$
defines an operator on
![]() $L^2(M;\Lambda )$
, bounded uniformly on
$L^2(M;\Lambda )$
, bounded uniformly on
![]() $w\in \mathbb {S}^1$
and
$w\in \mathbb {S}^1$
and
![]() $z\in \mathbb {C}$
. By Equation (4.14) and Proposition 4.21, we also get
$z\in \mathbb {C}$
. By Equation (4.14) and Proposition 4.21, we also get
 $$ \begin{align*} & P_{z,\mathrm{la/sm}}\partial_z\big((w-D_z)^{-1}\big)\,P_{z,\mathrm{sm/la}}\\ &\quad =(w-D_z)^{-1}P_{z,\mathrm{la/sm}}\,{\eta\wedge}\,P_{z,\mathrm{sm/la}}(w-D_z)^{-1} =O\big(\mu^{-1}\big)\;, \end{align*} $$
$$ \begin{align*} & P_{z,\mathrm{la/sm}}\partial_z\big((w-D_z)^{-1}\big)\,P_{z,\mathrm{sm/la}}\\ &\quad =(w-D_z)^{-1}P_{z,\mathrm{la/sm}}\,{\eta\wedge}\,P_{z,\mathrm{sm/la}}(w-D_z)^{-1} =O\big(\mu^{-1}\big)\;, \end{align*} $$
uniformly on
![]() $w\in \mathbb {S}^1$
.
$w\in \mathbb {S}^1$
.
On the other hand, applying again basic spectral theory, we obtain
for
![]() $\mu \gg 0$
, yielding
$\mu \gg 0$
, yielding
which defines an operator on
![]() $L^2(M;\Lambda )$
, bounded uniformly on z.
$L^2(M;\Lambda )$
, bounded uniformly on z.
Using that
![]() $P_{z,\mathrm {sm}}$
is an orthogonal projection, the argument of the proof of [Reference Berline, Getzler and Vergne7, Proposition 9.37] shows that
$P_{z,\mathrm {sm}}$
is an orthogonal projection, the argument of the proof of [Reference Berline, Getzler and Vergne7, Proposition 9.37] shows that
So
![]() $\operatorname {rank}\dot P_{z,\mathrm {sm}}\le 2\operatorname {rank} P_{z,\mathrm {sm}}\le 2|\mathcal {X}|$
by Corollary 4.9, and
$\operatorname {rank}\dot P_{z,\mathrm {sm}}\le 2\operatorname {rank} P_{z,\mathrm {sm}}\le 2|\mathcal {X}|$
by Corollary 4.9, and
 $$ \begin{align*} \dot P_{z,\mathrm{sm}}&=\frac{1}{2\pi i}\int_{\mathbb{S}^1}P_{z,\mathrm{la}}\partial_z\big((w-D_z)^{-1}\big)\,P_{z,\mathrm{sm}}\,dw\\ &\phantom{=\text{}}\text{}+\frac{1}{2\pi i}\int_{\mathbb{S}^1}P_{z,\mathrm{sm}}\partial_z\big((w-D_z)^{-1}\big)\,P_{z,\mathrm{la}}\,dw =O\big(\mu^{-1}\big). \; \end{align*} $$
$$ \begin{align*} \dot P_{z,\mathrm{sm}}&=\frac{1}{2\pi i}\int_{\mathbb{S}^1}P_{z,\mathrm{la}}\partial_z\big((w-D_z)^{-1}\big)\,P_{z,\mathrm{sm}}\,dw\\ &\phantom{=\text{}}\text{}+\frac{1}{2\pi i}\int_{\mathbb{S}^1}P_{z,\mathrm{sm}}\partial_z\big((w-D_z)^{-1}\big)\,P_{z,\mathrm{la}}\,dw =O\big(\mu^{-1}\big). \; \end{align*} $$
Lemma 4.24. For all
![]() $p\in \mathcal {X}$
,
$p\in \mathcal {X}$
,
 $$\begin{align*}\partial_ze_{p,z}=\bigg(\frac n{8\mu}-\frac{|x^+_p|^2}{2}+O(e^{-c\mu})\bigg)e_{p,z}\quad(\mu\to+\infty). \end{align*}$$
$$\begin{align*}\partial_ze_{p,z}=\bigg(\frac n{8\mu}-\frac{|x^+_p|^2}{2}+O(e^{-c\mu})\bigg)e_{p,z}\quad(\mu\to+\infty). \end{align*}$$
Proof. Using integration by parts, and since
![]() $\rho $
is an even function and
$\rho $
is an even function and
![]() $\rho '$
vanishes on
$\rho '$
vanishes on
![]() $[-r,r]$
, we obtain
$[-r,r]$
, we obtain
 $$ \begin{align} \int_{-2r}^{2r}\rho(x)^2x^2e^{-\mu x^2}\,dx &=\frac1{2\mu}\int_{-2r}^{2r}(2\rho(x)\rho'(x)x+\rho(x)^2)e^{-\mu x^2}\,dx \nonumber\\ &=\frac1{2\mu}\Big(\frac\pi\mu\Big)^{\frac12}+O(e^{-c\mu}). \end{align} $$
$$ \begin{align} \int_{-2r}^{2r}\rho(x)^2x^2e^{-\mu x^2}\,dx &=\frac1{2\mu}\int_{-2r}^{2r}(2\rho(x)\rho'(x)x+\rho(x)^2)e^{-\mu x^2}\,dx \nonumber\\ &=\frac1{2\mu}\Big(\frac\pi\mu\Big)^{\frac12}+O(e^{-c\mu}). \end{align} $$
So
 $$ \begin{align*} \partial_\mu a_\mu&=\partial_\mu\bigg(\bigg(\int_{-2r}^{2r}\rho(x)^2e^{-\mu x^2}\,dx\bigg)^{\frac n2}\bigg)\\ &=-\frac n2\bigg(\int_{-2r}^{2r}\rho(x)^2e^{-\mu x^2}\,dx\bigg)^{\frac n2-1} \int_{-2r}^{2r}\rho(x)^2x^2e^{-\mu x^2}\,dx\\ &=-\frac n2\Big(\frac\pi\mu\Big)^{\frac n4-\frac12}\frac1{2\mu}\Big(\frac\pi\mu\Big)^{\frac12}+O(e^{-c\mu}) =-\frac n{4\mu}\Big(\frac\pi\mu\Big)^{\frac n4}+O(e^{-c\mu}). \end{align*} $$
$$ \begin{align*} \partial_\mu a_\mu&=\partial_\mu\bigg(\bigg(\int_{-2r}^{2r}\rho(x)^2e^{-\mu x^2}\,dx\bigg)^{\frac n2}\bigg)\\ &=-\frac n2\bigg(\int_{-2r}^{2r}\rho(x)^2e^{-\mu x^2}\,dx\bigg)^{\frac n2-1} \int_{-2r}^{2r}\rho(x)^2x^2e^{-\mu x^2}\,dx\\ &=-\frac n2\Big(\frac\pi\mu\Big)^{\frac n4-\frac12}\frac1{2\mu}\Big(\frac\pi\mu\Big)^{\frac12}+O(e^{-c\mu}) =-\frac n{4\mu}\Big(\frac\pi\mu\Big)^{\frac n4}+O(e^{-c\mu}). \end{align*} $$
Hence, by Equation (4.11),
 $$ \begin{align} \partial_\mu\Big(\frac1{a_\mu}\Big) =-\frac{\partial_\mu a_\mu}{a_\mu^2} =\frac n{4\mu}\Big(\frac\pi\mu\Big)^{\frac n4} \Big(\frac\mu\pi\Big)^{\frac n2}+O(e^{-c\mu}) =\frac n{4\mu}\Big(\frac\mu\pi\Big)^{\frac n4}+O(e^{-c\mu}). \end{align} $$
$$ \begin{align} \partial_\mu\Big(\frac1{a_\mu}\Big) =-\frac{\partial_\mu a_\mu}{a_\mu^2} =\frac n{4\mu}\Big(\frac\pi\mu\Big)^{\frac n4} \Big(\frac\mu\pi\Big)^{\frac n2}+O(e^{-c\mu}) =\frac n{4\mu}\Big(\frac\mu\pi\Big)^{\frac n4}+O(e^{-c\mu}). \end{align} $$
It also follows from Proposition 4.1 (iii) and Equations (4.9), (4.11) and (4.31) that
 $$ \begin{align} \partial_\mu e_{p,\mu} &=\partial_\mu\Big(\frac{\rho_p}{a_\mu}e^{-\mu|x_p|^2/2}\,dx_p^1\wedge\dots\wedge dx_p^{\operatorname{ind}(p)}\Big) \nonumber\\ &=\bigg(\partial_\mu\Big(\frac1{a_\mu}\Big)a_\mu-\frac{|x_p|^2}2\bigg)e_{p,\mu} =\bigg(\frac n{4\mu}-\frac{|x_p|^2}2+O(e^{-c\mu})\bigg)e_{p,\mu}. \end{align} $$
$$ \begin{align} \partial_\mu e_{p,\mu} &=\partial_\mu\Big(\frac{\rho_p}{a_\mu}e^{-\mu|x_p|^2/2}\,dx_p^1\wedge\dots\wedge dx_p^{\operatorname{ind}(p)}\Big) \nonumber\\ &=\bigg(\partial_\mu\Big(\frac1{a_\mu}\Big)a_\mu-\frac{|x_p|^2}2\bigg)e_{p,\mu} =\bigg(\frac n{4\mu}-\frac{|x_p|^2}2+O(e^{-c\mu})\bigg)e_{p,\mu}. \end{align} $$
So, by Equation (4.10),
 $$ \begin{align} \partial_\mu e_{p,z}=\bigg(\frac n{4\mu}-\frac{|x_p|^2}2+O(e^{-c\mu})\bigg)e_{p,z}\;,\quad \partial_\nu e_{p,z}=-ih_pe_{p,z}. \end{align} $$
$$ \begin{align} \partial_\mu e_{p,z}=\bigg(\frac n{4\mu}-\frac{|x_p|^2}2+O(e^{-c\mu})\bigg)e_{p,z}\;,\quad \partial_\nu e_{p,z}=-ih_pe_{p,z}. \end{align} $$
Then the result follows using the right-hand side of Equation (4.1).
Proposition 4.25. For all
![]() $p\in \mathcal {X}$
,
$p\in \mathcal {X}$
,
Proof. From Equation (4.12), we get
 $$ \begin{align} \partial_z(D_ze_{p,z}) &=\frac12\bigg(e^{-i\nu h_p} \partial_\mu\Big(\frac1{a_\mu}\Big(\frac\pi\mu\Big)^{\frac n4}\Big)\hat c(d\rho_p)e_{p,\mu} \nonumber\\ &\quad {}+e^{-i\nu h_p}\frac1{a_\mu}\Big(\frac\pi\mu\Big)^{\frac n4}\hat c(d\rho_p)\partial_\mu e_{p,\mu}-h_pe^{-i\nu h_p}\frac1{a_\mu}\Big(\frac\pi\mu\Big)^{\frac n4}\hat c(d\rho_p)e_{p,\mu}\bigg). \end{align} $$
$$ \begin{align} \partial_z(D_ze_{p,z}) &=\frac12\bigg(e^{-i\nu h_p} \partial_\mu\Big(\frac1{a_\mu}\Big(\frac\pi\mu\Big)^{\frac n4}\Big)\hat c(d\rho_p)e_{p,\mu} \nonumber\\ &\quad {}+e^{-i\nu h_p}\frac1{a_\mu}\Big(\frac\pi\mu\Big)^{\frac n4}\hat c(d\rho_p)\partial_\mu e_{p,\mu}-h_pe^{-i\nu h_p}\frac1{a_\mu}\Big(\frac\pi\mu\Big)^{\frac n4}\hat c(d\rho_p)e_{p,\mu}\bigg). \end{align} $$
By Equations (4.11) and (4.31),
 $$ \begin{align} \partial_\mu\Big(\frac1{a_\mu}\Big(\frac\pi\mu\Big)^{\frac n4}\Big) &=\partial_\mu\Big(\frac1{a_\mu}\Big)\Big(\frac\pi\mu\Big)^{\frac n4} -\frac{n\pi}{4a_\mu\mu^2}\Big(\frac\pi\mu\Big)^{\frac n4-1}\nonumber\\ &=\frac n{4\mu}\Big(\frac\mu\pi\Big)^{\frac n4}\Big(\frac\pi\mu\Big)^{\frac n4} -\frac{n\pi}{4\mu^2}\Big(\frac\pi\mu\Big)^{\frac n4-1}\Big(\frac\mu\pi\Big)^{\frac n4}+O(e^{-c\mu}) =O(e^{-c\mu}). \end{align} $$
$$ \begin{align} \partial_\mu\Big(\frac1{a_\mu}\Big(\frac\pi\mu\Big)^{\frac n4}\Big) &=\partial_\mu\Big(\frac1{a_\mu}\Big)\Big(\frac\pi\mu\Big)^{\frac n4} -\frac{n\pi}{4a_\mu\mu^2}\Big(\frac\pi\mu\Big)^{\frac n4-1}\nonumber\\ &=\frac n{4\mu}\Big(\frac\mu\pi\Big)^{\frac n4}\Big(\frac\pi\mu\Big)^{\frac n4} -\frac{n\pi}{4\mu^2}\Big(\frac\pi\mu\Big)^{\frac n4-1}\Big(\frac\mu\pi\Big)^{\frac n4}+O(e^{-c\mu}) =O(e^{-c\mu}). \end{align} $$
The result follows applying Proposition 4.1 (iii) and Equations (4.9), (4.11), (4.32) and (4.35) to Equation (4.34), and using that
![]() $d\rho _p=0$
around p.
$d\rho _p=0$
around p.
Proposition 4.26. For every
![]() $p\in \mathcal {X}$
,
$p\in \mathcal {X}$
,
Proof. By Equation (4.17),
 $$ \begin{align*} \partial_z(P_{z,\mathrm{sm}}e_{p,z}-e_{p,z}) &=\frac1{2\pi i}\int_{\mathbb{S}^1}w^{-1}\partial_z\big((w-D_z)^{-1}\big)D_ze_{p,z}\,dw\\ &\quad {}+\frac1{2\pi i}\int_{\mathbb{S}^1}w^{-1}(w-D_z)^{-1}\partial_z(D_ze_{p,z})\,dw. \end{align*} $$
$$ \begin{align*} \partial_z(P_{z,\mathrm{sm}}e_{p,z}-e_{p,z}) &=\frac1{2\pi i}\int_{\mathbb{S}^1}w^{-1}\partial_z\big((w-D_z)^{-1}\big)D_ze_{p,z}\,dw\\ &\quad {}+\frac1{2\pi i}\int_{\mathbb{S}^1}w^{-1}(w-D_z)^{-1}\partial_z(D_ze_{p,z})\,dw. \end{align*} $$
Now, apply Equations (4.18) and (4.27) and Propositions 4.6 and 4.25.
5. Small and large zeta invariants of Morse forms
5.1. Small and large zeta invariants
According to Sections 3.2 and 4.2, if B is an operator in
![]() $L^2(M;\Lambda )$
so that
$L^2(M;\Lambda )$
so that
![]() $\zeta (s,\Delta _z,B)$
is defined, we have
$\zeta (s,\Delta _z,B)$
is defined, we have
where
These are the contributions from the small/large spectrum to
![]() $\zeta (s,\Delta _z,B)$
, which are called the small/large zeta functions of
$\zeta (s,\Delta _z,B)$
, which are called the small/large zeta functions of
![]() $(\Delta _z,B)$
. In particular, we can write
$(\Delta _z,B)$
. In particular, we can write
where
![]() $\zeta _{\mathrm {sm/la}}(s,z)=\zeta _{\mathrm {sm/la}}(s,z,\eta )$
is the small/large zeta function of
$\zeta _{\mathrm {sm/la}}(s,z)=\zeta _{\mathrm {sm/la}}(s,z,\eta )$
is the small/large zeta function of
![]() $(\Delta _z,{\eta \wedge }\,D_z\mathsf {w})$
. Since
$(\Delta _z,{\eta \wedge }\,D_z\mathsf {w})$
. Since
![]() $\zeta _{\mathrm {sm}}(s,z)$
is an entire function,
$\zeta _{\mathrm {sm}}(s,z)$
is an entire function,
![]() $\zeta _{\mathrm {la}}(s,z)$
has the same poles as
$\zeta _{\mathrm {la}}(s,z)$
has the same poles as
![]() $\zeta (s,z)$
(Remark 3.10), with the same residues. The value
$\zeta (s,z)$
(Remark 3.10), with the same residues. The value
![]() $\zeta _{\mathrm {sm/la}}(1,z)$
will be called the small/large zeta invariant of
$\zeta _{\mathrm {sm/la}}(1,z)$
will be called the small/large zeta invariant of
![]() $(M,g,\eta ,z)$
. The following results follow like Corollaries 3.9 and 3.11.
$(M,g,\eta ,z)$
. The following results follow like Corollaries 3.9 and 3.11.
Corollary 5.1. If
![]() $\Re s>1/2$
, then
$\Re s>1/2$
, then
 $$\begin{align*}\zeta_{\mathrm{la}}(s,z)=\frac{1}{\Gamma(s)}\int_0^\infty t^{s-1}\operatorname{Str}\big({\eta\wedge}\,D_ze^{-t\Delta_z}P_{z,\mathrm{la}}\big)\,dt\;, \end{align*}$$
$$\begin{align*}\zeta_{\mathrm{la}}(s,z)=\frac{1}{\Gamma(s)}\int_0^\infty t^{s-1}\operatorname{Str}\big({\eta\wedge}\,D_ze^{-t\Delta_z}P_{z,\mathrm{la}}\big)\,dt\;, \end{align*}$$
where the integral is absolutely convergent.
Corollary 5.2. We have
 $$ \begin{align*} \zeta_{\mathrm{sm}}(1,z)&=\operatorname{Str}({\eta\wedge}\,D_z^{-1}(\Pi_z^\perp)_{\mathrm{sm}})\;,\\ \zeta_{\mathrm{la}}(1,z)&=\lim_{t\downarrow0}\operatorname{Str}\big({\eta\wedge}\,D_z^{-1}e^{-t\Delta_z}P_{z,\mathrm{la}}\big). \end{align*} $$
$$ \begin{align*} \zeta_{\mathrm{sm}}(1,z)&=\operatorname{Str}({\eta\wedge}\,D_z^{-1}(\Pi_z^\perp)_{\mathrm{sm}})\;,\\ \zeta_{\mathrm{la}}(1,z)&=\lim_{t\downarrow0}\operatorname{Str}\big({\eta\wedge}\,D_z^{-1}e^{-t\Delta_z}P_{z,\mathrm{la}}\big). \end{align*} $$
5.2. Truncated heat invariants of perturbed operators
For
![]() $k=0,\dots ,n$
, let
$k=0,\dots ,n$
, let
![]() $K^{\prime }_{z,k,t}(x,y)$
and
$K^{\prime }_{z,k,t}(x,y)$
and
![]() $\widetilde K_{z,k,t}(x,y)$
denote the Schwartz kernels of
$\widetilde K_{z,k,t}(x,y)$
denote the Schwartz kernels of
![]() $e^{-t\Delta _{z,k}}\Pi _z^\perp $
and
$e^{-t\Delta _{z,k}}\Pi _z^\perp $
and
![]() $e^{-t\Delta _{z,k}}P_{z,\mathrm {la},k}$
, respectively. According to Section 3.1, their restrictions to the diagonal have asymptotic expansions (as
$e^{-t\Delta _{z,k}}P_{z,\mathrm {la},k}$
, respectively. According to Section 3.1, their restrictions to the diagonal have asymptotic expansions (as
![]() $t\downarrow 0$
),
$t\downarrow 0$
),
 $$ \begin{align} K^{\prime}_{z,k,t}(x,x)\sim\sum_{l=0}^\infty e^{\prime}_{k,l}(x,z)t^{(l-n)/2}\;,\quad \widetilde K_{z,k,t}(x,x)\sim\sum_{l=0}^\infty\tilde e_{k,l}(x,z)t^{(l-n)/2}. \end{align} $$
$$ \begin{align} K^{\prime}_{z,k,t}(x,x)\sim\sum_{l=0}^\infty e^{\prime}_{k,l}(x,z)t^{(l-n)/2}\;,\quad \widetilde K_{z,k,t}(x,x)\sim\sum_{l=0}^\infty\tilde e_{k,l}(x,z)t^{(l-n)/2}. \end{align} $$
We have
 $$ \begin{align} e^{\prime}_{k,l}(x,z)&= \begin{cases} e_{k,l}(x,z) & \text{if}\ l<n\\ e_{k,n}(x,z)-\beta_z^k & \text{if}\ l=n\;, \end{cases}\nonumber\\ \tilde e_{k,l}(x,z)&= \begin{cases} e_{k,l}(x,z) & \text{if}\ l<n\\ e_{k,n}(x,z)-H_{z,k,0}(x,x) & \text{if}\ l=n\;, \end{cases} \end{align} $$
$$ \begin{align} e^{\prime}_{k,l}(x,z)&= \begin{cases} e_{k,l}(x,z) & \text{if}\ l<n\\ e_{k,n}(x,z)-\beta_z^k & \text{if}\ l=n\;, \end{cases}\nonumber\\ \tilde e_{k,l}(x,z)&= \begin{cases} e_{k,l}(x,z) & \text{if}\ l<n\\ e_{k,n}(x,z)-H_{z,k,0}(x,x) & \text{if}\ l=n\;, \end{cases} \end{align} $$
where
![]() $H_{z,k,t}(x,y)$
is the Schwartz kernel of
$H_{z,k,t}(x,y)$
is the Schwartz kernel of
![]() $e^{-t\Delta _{z,k}}P_{z,\mathrm {sm},k}$
, which is defined for all
$e^{-t\Delta _{z,k}}P_{z,\mathrm {sm},k}$
, which is defined for all
![]() $t\in \mathbb {R}$
and is smooth. We also have asymptotic expansions
$t\in \mathbb {R}$
and is smooth. We also have asymptotic expansions
 $$ \begin{align} h^{\prime}_k(t,z)&:=\operatorname{Tr}\big(e^{-t\Delta_{z,k}}\Pi_z^\perp\big)\sim\sum_{l=0}^\infty a^{\prime}_{k,l}(z)t^{(l-n)/2},\quad\, \end{align} $$
$$ \begin{align} h^{\prime}_k(t,z)&:=\operatorname{Tr}\big(e^{-t\Delta_{z,k}}\Pi_z^\perp\big)\sim\sum_{l=0}^\infty a^{\prime}_{k,l}(z)t^{(l-n)/2},\quad\, \end{align} $$
 $$ \begin{align} \tilde h_k(t,z)&:=\operatorname{Tr}\big(e^{-t\Delta_{z,k}}P_{z,\mathrm{la},k}\big)\sim\sum_{l=0}^\infty\tilde a_{k,l}(z)t^{(l-n)/2}. \end{align} $$
$$ \begin{align} \tilde h_k(t,z)&:=\operatorname{Tr}\big(e^{-t\Delta_{z,k}}P_{z,\mathrm{la},k}\big)\sim\sum_{l=0}^\infty\tilde a_{k,l}(z)t^{(l-n)/2}. \end{align} $$
By Equations (3.4), (3.5) and (3.9),
 $$ \begin{align} a^{\prime}_{k,l}(z)&=\int_M\operatorname{str} e^{\prime}_{k,l}(x,z)\,\operatorname{dvol}(x) = \begin{cases} a_{k,l}(z) & \text{if}\ l<n\\ a_{k,l}(z)-\beta_z^k & \text{if}\ l=n. \end{cases} \end{align} $$
$$ \begin{align} a^{\prime}_{k,l}(z)&=\int_M\operatorname{str} e^{\prime}_{k,l}(x,z)\,\operatorname{dvol}(x) = \begin{cases} a_{k,l}(z) & \text{if}\ l<n\\ a_{k,l}(z)-\beta_z^k & \text{if}\ l=n. \end{cases} \end{align} $$
 $$ \begin{align} \tilde a_{k,l}(z)&=\int_M\operatorname{str}\tilde e_{k,l}(x,z)\,\operatorname{dvol}(x)= \begin{cases} a_{k,l}(z) & \text{if}\ l<n\\ a_{k,l}(z)-\dim E_{z,\mathrm{sm}}^k & \text{if}\ l=n. \end{cases} \end{align} $$
$$ \begin{align} \tilde a_{k,l}(z)&=\int_M\operatorname{str}\tilde e_{k,l}(x,z)\,\operatorname{dvol}(x)= \begin{cases} a_{k,l}(z) & \text{if}\ l<n\\ a_{k,l}(z)-\dim E_{z,\mathrm{sm}}^k & \text{if}\ l=n. \end{cases} \end{align} $$
The operators
![]() $e^{-t\Delta _z}\Pi _z^\perp \mathsf {w}$
and
$e^{-t\Delta _z}\Pi _z^\perp \mathsf {w}$
and
![]() $e^{-t\Delta _z}P_{z,\mathrm {la}}\mathsf {w}$
have Schwartz kernels
$e^{-t\Delta _z}P_{z,\mathrm {la}}\mathsf {w}$
have Schwartz kernels
 $$\begin{align*}K^{\prime}_{z,t}(x,y)=\sum_{k=0}^n(-1)^kK^{\prime}_{z,k,t}(x,y)\;,\quad \widetilde K_{z,t}(x,y)=\sum_{k=0}^n(-1)^k\widetilde K_{z,k,t}(x,y)\;, \end{align*}$$
$$\begin{align*}K^{\prime}_{z,t}(x,y)=\sum_{k=0}^n(-1)^kK^{\prime}_{z,k,t}(x,y)\;,\quad \widetilde K_{z,t}(x,y)=\sum_{k=0}^n(-1)^k\widetilde K_{z,k,t}(x,y)\;, \end{align*}$$
with induced asymptotic expansions
 $$\begin{align*}K^{\prime}_{z,t}(x,x)\sim\sum_{l=0}^\infty e^{\prime}_l(x,z)t^{(l-n)/2}\;,\quad \widetilde K_{z,t}(x,x)\sim\sum_{l=0}^\infty\tilde e_l(x,z)t^{(l-n)/2}\;, \end{align*}$$
$$\begin{align*}K^{\prime}_{z,t}(x,x)\sim\sum_{l=0}^\infty e^{\prime}_l(x,z)t^{(l-n)/2}\;,\quad \widetilde K_{z,t}(x,x)\sim\sum_{l=0}^\infty\tilde e_l(x,z)t^{(l-n)/2}\;, \end{align*}$$
where
 $$ \begin{gather*} e^{\prime}_l(x,z)=\sum_{k=0}^n(-1)^ke^{\prime}_{k,l}(x,z)\;,\quad \tilde e_l(x,z)=\sum_{k=0}^n(-1)^k\tilde e_{k,l}(x,z). \end{gather*} $$
$$ \begin{gather*} e^{\prime}_l(x,z)=\sum_{k=0}^n(-1)^ke^{\prime}_{k,l}(x,z)\;,\quad \tilde e_l(x,z)=\sum_{k=0}^n(-1)^k\tilde e_{k,l}(x,z). \end{gather*} $$
We also have induced asymptotic expansions,
 $$ \begin{gather*} h'(t,z):=\operatorname{Str}\big(e^{-t\Delta_z}\Pi_z^\perp\big)\sim\sum_{l=0}^\infty a^{\prime}_l(z)t^{(l-n)/2}\;,\\ \tilde h(t,z):=\operatorname{Str}\big(e^{-t\Delta_z}P_{z,\mathrm{la}}\big)\sim\sum_{l=0}^\infty\tilde a_l(z)t^{(l-n)/2}\;, \end{gather*} $$
$$ \begin{gather*} h'(t,z):=\operatorname{Str}\big(e^{-t\Delta_z}\Pi_z^\perp\big)\sim\sum_{l=0}^\infty a^{\prime}_l(z)t^{(l-n)/2}\;,\\ \tilde h(t,z):=\operatorname{Str}\big(e^{-t\Delta_z}P_{z,\mathrm{la}}\big)\sim\sum_{l=0}^\infty\tilde a_l(z)t^{(l-n)/2}\;, \end{gather*} $$
where
 $$\begin{align*}a^{\prime}_l(z)=\sum_{k=0}^n(-1)^ka^{\prime}_{k,l}(z)\;,\quad \tilde a_l(z)=\sum_{k=0}^n(-1)^k\tilde a_{k,l}(z). \end{align*}$$
$$\begin{align*}a^{\prime}_l(z)=\sum_{k=0}^n(-1)^ka^{\prime}_{k,l}(z)\;,\quad \tilde a_l(z)=\sum_{k=0}^n(-1)^k\tilde a_{k,l}(z). \end{align*}$$
If
![]() $\mu \gg 0$
, by Equation (2.9), Corollary 4.9 and Theorem 4.10,
$\mu \gg 0$
, by Equation (2.9), Corollary 4.9 and Theorem 4.10,
![]() $e^{\prime }_{k,l}(x,z)$
and
$e^{\prime }_{k,l}(x,z)$
and
![]() $\tilde e_{k,l}(x,z)$
depend smoothly on z (Section 3.1), and therefore so do
$\tilde e_{k,l}(x,z)$
depend smoothly on z (Section 3.1), and therefore so do
![]() $h^{\prime }_k(t,z)$
,
$h^{\prime }_k(t,z)$
,
![]() $\tilde h_k(t,z)$
,
$\tilde h_k(t,z)$
,
![]() $a^{\prime }_{k,l}(z)$
,
$a^{\prime }_{k,l}(z)$
,
![]() $\tilde a_{k,l}(z)$
,
$\tilde a_{k,l}(z)$
,
![]() $e^{\prime }_l(x,z)$
,
$e^{\prime }_l(x,z)$
,
![]() $\tilde e_l(x,z)$
,
$\tilde e_l(x,z)$
,
![]() $h'(t,z)$
,
$h'(t,z)$
,
![]() $\tilde h(t,z)$
,
$\tilde h(t,z)$
,
![]() $a^{\prime }_l(z)$
and
$a^{\prime }_l(z)$
and
![]() $\tilde a_l(z)$
.
$\tilde a_l(z)$
.
5.3. Truncated derived heat invariants of perturbed operators
For
![]() $k=0,\dots ,n$
and
$k=0,\dots ,n$
and
![]() $j=1,2$
, let
$j=1,2$
, let
Lemma 5.3. We have
 $$\begin{align*}h_{k+1}^1(t,z)=h_k^2(t,z)=\sum_{p=0}^k(-1)^{k-p}h^{\prime}_p(t,z) =\sum_{q=k+1}^n(-1)^{q-k-1}h^{\prime}_q(t,z). \end{align*}$$
$$\begin{align*}h_{k+1}^1(t,z)=h_k^2(t,z)=\sum_{p=0}^k(-1)^{k-p}h^{\prime}_p(t,z) =\sum_{q=k+1}^n(-1)^{q-k-1}h^{\prime}_q(t,z). \end{align*}$$
Proof. This follows by induction on k, using that
The last equality holds because the diagram of Equation (2.7) is commutative.
Let
 $$ \begin{gather*} h^j(t,z)=\operatorname{Str}\big(e^{-t\Delta_z}\Pi^j_z\big)=\sum_{k=0}^n(-1)^kh^j_k(t,z)\;,\\ \tilde h^j(t,z)=\operatorname{Str}\big(e^{-t\Delta_z}\Pi^j_{z,\mathrm{la}}\big)=\sum_{k=0}^n(-1)^k\tilde h^j_k(t,z). \end{gather*} $$
$$ \begin{gather*} h^j(t,z)=\operatorname{Str}\big(e^{-t\Delta_z}\Pi^j_z\big)=\sum_{k=0}^n(-1)^kh^j_k(t,z)\;,\\ \tilde h^j(t,z)=\operatorname{Str}\big(e^{-t\Delta_z}\Pi^j_{z,\mathrm{la}}\big)=\sum_{k=0}^n(-1)^k\tilde h^j_k(t,z). \end{gather*} $$
Thus,
Corollary 5.4. We have
![]() $h'(t,z)=0$
.
$h'(t,z)=0$
.
Corollary 5.5. We have
 $$\begin{align*}h^1(t,z)=-h^2(t,z)=\sum_{k=0}^n(-1)^kkh^{\prime}_k(t,z)=\operatorname{Str}\big({\mathsf{N}} e^{-t\Delta_z}\Pi_z^\perp\big). \end{align*}$$
$$\begin{align*}h^1(t,z)=-h^2(t,z)=\sum_{k=0}^n(-1)^kkh^{\prime}_k(t,z)=\operatorname{Str}\big({\mathsf{N}} e^{-t\Delta_z}\Pi_z^\perp\big). \end{align*}$$
Proof. Corollary 5.4 and Equation (5.7) give the first equality. By Lemma 5.3 and Corollary 5.4,
 $$ \begin{align*} h^1(t,z)&=\sum_{k=0}^n(-1)^k\sum_{q=k}^n(-1)^{q-k}h^{\prime}_q(t,z)=\sum_{q=0}^n(-1)^q(q+1)h^{\prime}_q(t,z)\\ &=h'(t,z)+\sum_{q=0}^n(-1)^qqh^{\prime}_q(t,z)=\sum_{q=0}^n(-1)^qqh^{\prime}_q(t,z). \; \end{align*} $$
$$ \begin{align*} h^1(t,z)&=\sum_{k=0}^n(-1)^k\sum_{q=k}^n(-1)^{q-k}h^{\prime}_q(t,z)=\sum_{q=0}^n(-1)^q(q+1)h^{\prime}_q(t,z)\\ &=h'(t,z)+\sum_{q=0}^n(-1)^qqh^{\prime}_q(t,z)=\sum_{q=0}^n(-1)^qqh^{\prime}_q(t,z). \; \end{align*} $$
Applying Equation (5.3) and Lemma 5.3, we get
 $$ \begin{align} h^j_k(t,z)\sim\sum_{l=0}^\infty a_{k,l}^j(z)t^{(l-n)/2}\;,\quad h^j(t,z)\sim\sum_{l=0}^\infty a^j_l(z)t^{(l-n)/2}\;, \end{align} $$
$$ \begin{align} h^j_k(t,z)\sim\sum_{l=0}^\infty a_{k,l}^j(z)t^{(l-n)/2}\;,\quad h^j(t,z)\sim\sum_{l=0}^\infty a^j_l(z)t^{(l-n)/2}\;, \end{align} $$
where
 $$ \begin{gather*} a^1_{k+1,l}(z)=a^2_{k,l}(z)=\sum_{p=0}^k(-1)^{k-p}a^{\prime}_{p,l}(t,z) =\sum_{q=k+1}^n(-1)^{q-k-1}a^{\prime}_{q,l}(t,z)\;,\\ a^1_l(z)=-a^2_l(z)=\sum_{k=0}^n(-1)^kka^{\prime}_{k,l}(z). \end{gather*} $$
$$ \begin{gather*} a^1_{k+1,l}(z)=a^2_{k,l}(z)=\sum_{p=0}^k(-1)^{k-p}a^{\prime}_{p,l}(t,z) =\sum_{q=k+1}^n(-1)^{q-k-1}a^{\prime}_{q,l}(t,z)\;,\\ a^1_l(z)=-a^2_l(z)=\sum_{k=0}^n(-1)^kka^{\prime}_{k,l}(z). \end{gather*} $$
Lemma 5.3, Corollary 5.4 and Equation (5.8) have obvious versions for
![]() $\tilde h^j_k(t,z)$
and
$\tilde h^j_k(t,z)$
and
![]() $\tilde h^j(t,z)$
, with similar proofs. The coefficients of the corresponding asymptotic expansions are denoted by
$\tilde h^j(t,z)$
, with similar proofs. The coefficients of the corresponding asymptotic expansions are denoted by
![]() $\tilde a^j_{k,l}(z)$
and
$\tilde a^j_{k,l}(z)$
and
![]() $\tilde a^j_l(z)$
.
$\tilde a^j_l(z)$
.
Corollary 5.7. For all
![]() $l\le n$
and
$l\le n$
and
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
![]() $a^1_l(z)$
and
$a^1_l(z)$
and
![]() $\tilde a^1_l(z)$
are independent of z.
$\tilde a^1_l(z)$
are independent of z.
5.4. Zeta function versus theta function
Consider also the meromorphic function
called theta function of
![]() $\Delta _z$
, and write
$\Delta _z$
, and write
where
By Corollary 5.5,
 $$ \begin{align} -\zeta(s,\Delta_z,\Pi_z^1\mathsf{w})&=\zeta(s,\Delta_z,\Pi_z^2\mathsf{w})=\theta(s,z)\;,\nonumber\\ -\zeta_{\mathrm{sm/la}}(s,\Delta_z,\Pi_z^1\mathsf{w})&=\zeta_{\mathrm{sm/la}}(s,\Delta_z,\Pi_z^2\mathsf{w})=\theta_{\mathrm{sm/la}}(s,z). \end{align} $$
$$ \begin{align} -\zeta(s,\Delta_z,\Pi_z^1\mathsf{w})&=\zeta(s,\Delta_z,\Pi_z^2\mathsf{w})=\theta(s,z)\;,\nonumber\\ -\zeta_{\mathrm{sm/la}}(s,\Delta_z,\Pi_z^1\mathsf{w})&=\zeta_{\mathrm{sm/la}}(s,\Delta_z,\Pi_z^2\mathsf{w})=\theta_{\mathrm{sm/la}}(s,z). \end{align} $$
Recall that
![]() $\zeta (s,z)$
is smooth at
$\zeta (s,z)$
is smooth at
![]() $s=1$
(Corollary 3.9). Moreover,
$s=1$
(Corollary 3.9). Moreover,
![]() $\theta (s,z)$
is smooth at
$\theta (s,z)$
is smooth at
![]() $s=0$
[Reference Seeley66]. The same is true for
$s=0$
[Reference Seeley66]. The same is true for
![]() $\zeta _{\mathrm {la}}(s,z)$
and
$\zeta _{\mathrm {la}}(s,z)$
and
![]() $\theta _{\mathrm {la}}(s,z)$
.
$\theta _{\mathrm {la}}(s,z)$
.
Proposition 5.8. If
![]() $\mu \gg 0$
, then
$\mu \gg 0$
, then
Proof. Recall that a dot may be used to denote
![]() $\partial _z$
. Like in Equation (4.29),
$\partial _z$
. Like in Equation (4.29),
Therefore, since
![]() $\Pi ^1_z$
and
$\Pi ^1_z$
and
![]() $(\Pi ^1_z)^\perp $
commute with
$(\Pi ^1_z)^\perp $
commute with
![]() $\Delta _z^{-s}$
and
$\Delta _z^{-s}$
and
![]() $P_{z,\mathrm {la}}$
, for
$P_{z,\mathrm {la}}$
, for
![]() $\Re s\gg 0$
,
$\Re s\gg 0$
,
yielding
![]() $\zeta _{\mathrm {la}}(s,\Delta _z,\dot \Pi ^1_z\mathsf {w})=0$
for all s because this is a meromorphic function. Hence, since
$\zeta _{\mathrm {la}}(s,\Delta _z,\dot \Pi ^1_z\mathsf {w})=0$
for all s because this is a meromorphic function. Hence, since
![]() $\Delta _z$
and
$\Delta _z$
and
![]() $\Pi ^1_{z,\mathrm {la}}\mathsf {w}$
commute, Proposition 3.1 (i),(v) gives
$\Pi ^1_{z,\mathrm {la}}\mathsf {w}$
commute, Proposition 3.1 (i),(v) gives
Next, by Equation (2.4),
But, since
![]() $\Pi ^1_z\delta _z=0$
,
$\Pi ^1_z\delta _z=0$
,
From Equations (5.11)–(5.14) and Proposition 3.1 (i), we get
 $$ \begin{align*} \partial_z\theta_{\mathrm{la}}(s,z)&=-\partial_z\zeta_{\mathrm{la}}(s,\Delta_z,\Pi^1_z\mathsf{w}) =s\operatorname{Str}\big({\eta\wedge}\,\delta_z\Delta_z^{-s-1}\Pi^1_{z,\mathrm{la}}\big)\\ &=s\operatorname{Str}\big({\eta\wedge}\,D_z\Delta_z^{-s-1}\Pi^1_{z,\mathrm{la}}\big) =s\zeta_{\mathrm{la}}(s+1,z). \; \end{align*} $$
$$ \begin{align*} \partial_z\theta_{\mathrm{la}}(s,z)&=-\partial_z\zeta_{\mathrm{la}}(s,\Delta_z,\Pi^1_z\mathsf{w}) =s\operatorname{Str}\big({\eta\wedge}\,\delta_z\Delta_z^{-s-1}\Pi^1_{z,\mathrm{la}}\big)\\ &=s\operatorname{Str}\big({\eta\wedge}\,D_z\Delta_z^{-s-1}\Pi^1_{z,\mathrm{la}}\big) =s\zeta_{\mathrm{la}}(s+1,z). \; \end{align*} $$
Remark 5.9. In the case where
![]() $\eta $
is a Morse form and
$\eta $
is a Morse form and
![]() $\mu \gg 0$
, the regularity of
$\mu \gg 0$
, the regularity of
![]() $\zeta (s,z)$
indicated in Remark 3.10 also follows from Corollary 5.7 and Proposition 5.8.
$\zeta (s,z)$
indicated in Remark 3.10 also follows from Corollary 5.7 and Proposition 5.8.
Corollary 5.10. If
![]() $\mu \gg 0$
, then Equation (1.6) is true.
$\mu \gg 0$
, then Equation (1.6) is true.
5.5. The case of the differential of a Morse function
Let us consider the special case where
![]() $\eta =dh$
for a Morse function h. The following four results follow like Lemma 3.12 and Corollaries 3.13 to 3.15.
$\eta =dh$
for a Morse function h. The following four results follow like Lemma 3.12 and Corollaries 3.13 to 3.15.
Lemma 5.11. For
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
 $$ \begin{align*} \operatorname{Str}\big({\eta\wedge}\,d_z^{-1}\Pi^1_{z,\mathrm{sm}}\big)&=-\operatorname{Str}\big(h\,(\Pi_z^\perp)_{\mathrm{sm}}\big)\;,\\ \operatorname{Str}\big({\eta\wedge}\,d_z^{-1}e^{-t\Delta_z}\Pi^1_{z,\mathrm{la}}\big)&=-\operatorname{Str}\big(h\,e^{-t\Delta_z}P_{z,\mathrm{la}}\big). \end{align*} $$
$$ \begin{align*} \operatorname{Str}\big({\eta\wedge}\,d_z^{-1}\Pi^1_{z,\mathrm{sm}}\big)&=-\operatorname{Str}\big(h\,(\Pi_z^\perp)_{\mathrm{sm}}\big)\;,\\ \operatorname{Str}\big({\eta\wedge}\,d_z^{-1}e^{-t\Delta_z}\Pi^1_{z,\mathrm{la}}\big)&=-\operatorname{Str}\big(h\,e^{-t\Delta_z}P_{z,\mathrm{la}}\big). \end{align*} $$
Corollary 5.12. For
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
 $$ \begin{align*} \zeta_{\mathrm{sm}}(1,z)&=-\operatorname{Str}\big(h\,(\Pi_z^\perp)_{\mathrm{sm}}\big)\;,\\ \zeta_{\mathrm{la}}(1,z)&=-\lim_{t\downarrow0}\operatorname{Str}\big(h\,e^{-t\Delta_z}P_{z,\mathrm{la}}\big). \end{align*} $$
$$ \begin{align*} \zeta_{\mathrm{sm}}(1,z)&=-\operatorname{Str}\big(h\,(\Pi_z^\perp)_{\mathrm{sm}}\big)\;,\\ \zeta_{\mathrm{la}}(1,z)&=-\lim_{t\downarrow0}\operatorname{Str}\big(h\,e^{-t\Delta_z}P_{z,\mathrm{la}}\big). \end{align*} $$
Corollary 5.13. If
![]() $\mu \gg 0$
, then
$\mu \gg 0$
, then
![]() $\zeta _{\mathrm {sm/la}}(1,z)\in \mathbb {R}$
.
$\zeta _{\mathrm {sm/la}}(1,z)\in \mathbb {R}$
.
Corollary 5.14. If M is oriented and
![]() $|\mu |\gg 0$
, then
$|\mu |\gg 0$
, then
Corollary 5.15. The value
![]() $\zeta _{\mathrm {sm}}(1,z)$
is uniformly bounded on z for
$\zeta _{\mathrm {sm}}(1,z)$
is uniformly bounded on z for
![]() $\mu \gg 0$
.
$\mu \gg 0$
.
Proof. The operator
![]() $h\,(\Pi _z^\perp )_{\mathrm {sm}}$
is uniformly bounded and, for
$h\,(\Pi _z^\perp )_{\mathrm {sm}}$
is uniformly bounded and, for
![]() $\mu \gg 0$
, has uniformly bounded rank. So
$\mu \gg 0$
, has uniformly bounded rank. So
![]() $\operatorname {Str}(h\,(\Pi _z^\perp )_{\mathrm {sm}})$
is uniformly bounded on z for
$\operatorname {Str}(h\,(\Pi _z^\perp )_{\mathrm {sm}})$
is uniformly bounded on z for
![]() $\mu \gg 0$
, and therefore the result follows from Corollary 5.12.
$\mu \gg 0$
, and therefore the result follows from Corollary 5.12.
Theorem 5.16. The following limit holds uniformly on
![]() $\nu $
:
$\nu $
:
 $$\begin{align*}\lim_{\mu\to+\infty}\zeta_{\mathrm{la}}(1,z)=-\int_Mh\,e(M,\nabla^M)\,\operatorname{dvol} +\sum_{p\in\mathcal{X}}^n(-1)^{\operatorname{ind}(p)}h(p). \end{align*}$$
$$\begin{align*}\lim_{\mu\to+\infty}\zeta_{\mathrm{la}}(1,z)=-\int_Mh\,e(M,\nabla^M)\,\operatorname{dvol} +\sum_{p\in\mathcal{X}}^n(-1)^{\operatorname{ind}(p)}h(p). \end{align*}$$
Proof. By Equations (5.1) and (5.2), Theorem 3.2 and Corollary 5.12, for
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
 $$ \begin{align*} \zeta_{\mathrm{la}}(1,z)&=-\lim_{t\downarrow0}\operatorname{Str}\big(h\,e^{-t\Delta_z}P_{z,\mathrm{la}}\big) =-\int_Mh(x)\,\operatorname{str}\tilde e_n(x,z)\,\operatorname{dvol}(x)\\ &=-\int_Mh(x)\,\operatorname{str} e_n(x,z)\,\operatorname{dvol}(x)+\operatorname{Str}(hP_{z,\mathrm{sm}})\\ &=-\int_Mh\,e(M,\nabla^M)\,\operatorname{dvol}+\operatorname{Str}(hP_{z,\mathrm{sm}}). \end{align*} $$
$$ \begin{align*} \zeta_{\mathrm{la}}(1,z)&=-\lim_{t\downarrow0}\operatorname{Str}\big(h\,e^{-t\Delta_z}P_{z,\mathrm{la}}\big) =-\int_Mh(x)\,\operatorname{str}\tilde e_n(x,z)\,\operatorname{dvol}(x)\\ &=-\int_Mh(x)\,\operatorname{str} e_n(x,z)\,\operatorname{dvol}(x)+\operatorname{Str}(hP_{z,\mathrm{sm}})\\ &=-\int_Mh\,e(M,\nabla^M)\,\operatorname{dvol}+\operatorname{Str}(hP_{z,\mathrm{sm}}). \end{align*} $$
According to Corollary 4.9, the elements
![]() $P_{z,\mathrm {sm}} e_{p,z}$
(
$P_{z,\mathrm {sm}} e_{p,z}$
(
![]() $p\in \mathcal {X}$
) form a base of
$p\in \mathcal {X}$
) form a base of
![]() $E_{z,\mathrm {sm}}^k$
when
$E_{z,\mathrm {sm}}^k$
when
![]() $\mu \gg 0$
. Applying the Gram–Schmidt process to this base, we get an orthonormal frame
$\mu \gg 0$
. Applying the Gram–Schmidt process to this base, we get an orthonormal frame
![]() $\tilde e_{p,z}$
(
$\tilde e_{p,z}$
(
![]() $p\in \mathcal {X}$
) of
$p\in \mathcal {X}$
) of
![]() $E_{z,\mathrm {sm}}$
. By Proposition 4.7 for
$E_{z,\mathrm {sm}}$
. By Proposition 4.7 for
![]() $m=0$
and Equations (4.8)–(4.11),
$m=0$
and Equations (4.8)–(4.11),
Hence,
 $$\begin{align*}\lim_{\mu\to+\infty}\operatorname{Str}(hP_{z,\mathrm{sm}})=\sum_{k=0}^n(-1)^k\sum_{p\in\mathcal{X}_k}h(p). \; \end{align*}$$
$$\begin{align*}\lim_{\mu\to+\infty}\operatorname{Str}(hP_{z,\mathrm{sm}})=\sum_{k=0}^n(-1)^k\sum_{p\in\mathcal{X}_k}h(p). \; \end{align*}$$
6. The small complex versus the Morse complex
6.1. Preliminaries on Morse and Smale vector fields
6.1.1. Vector fields with Morse-type zeros
Let X be a real smooth vector field on M with flow
![]() $\phi =\{\phi ^t\}$
. Let
$\phi =\{\phi ^t\}$
. Let
![]() $\mathcal {Y}=\operatorname {Zero}(X)$
denote the set of zeros of X (or rest points
$\mathcal {Y}=\operatorname {Zero}(X)$
denote the set of zeros of X (or rest points
![]() $\phi $
). It is said that a zero p of X is of Morse type with (Morse) index of
$\phi $
). It is said that a zero p of X is of Morse type with (Morse) index of
![]() $\operatorname {ind}(p)$
if, using the notation of Equation (4.2),
$\operatorname {ind}(p)$
if, using the notation of Equation (4.2),
 $$ \begin{align} X=-\sum_{j=1}^n\epsilon_{p,j}x_p^j\,\frac{\partial}{\partial x_p^j} \end{align} $$
$$ \begin{align} X=-\sum_{j=1}^n\epsilon_{p,j}x_p^j\,\frac{\partial}{\partial x_p^j} \end{align} $$
on the domain
![]() $U_p$
of some coordinates
$U_p$
of some coordinates
![]() $x_p=(x_p^1,\dots ,x_p^n)$
at p, also called Morse coordinates. This condition means that
$x_p=(x_p^1,\dots ,x_p^n)$
at p, also called Morse coordinates. This condition means that
![]() $X=-\operatorname {grad}_gh_{X,p}$
on
$X=-\operatorname {grad}_gh_{X,p}$
on
![]() $U_p$
, where
$U_p$
, where
![]() $h_{X,p}$
and g are given on
$h_{X,p}$
and g are given on
![]() $U_p$
by the center and right-hand side of Equations (4.1) and (4.3). The coordinates
$U_p$
by the center and right-hand side of Equations (4.1) and (4.3). The coordinates
![]() $x_p$
used in Equation (6.1) are not unique; that expression is invariant by taking positive multiples of the coordinates (contrary to the expressions of Equations (4.1), (4.3) and (4.4)). But
$x_p$
used in Equation (6.1) are not unique; that expression is invariant by taking positive multiples of the coordinates (contrary to the expressions of Equations (4.1), (4.3) and (4.4)). But
![]() $\operatorname {ind}(p)$
is independent of
$\operatorname {ind}(p)$
is independent of
![]() $x_p$
. Note that the Hopf index of
$x_p$
. Note that the Hopf index of
![]() $-X$
at p is
$-X$
at p is
![]() $(-1)^{\operatorname {ind}(p)}$
.
$(-1)^{\operatorname {ind}(p)}$
.
Let us consider
![]() $\eta \in Z^1(M,\mathbb R)$
and use the notation of Section 4.1. For
$\eta \in Z^1(M,\mathbb R)$
and use the notation of Section 4.1. For
![]() $p\in \mathcal {X}\cap \mathcal {Y}$
, if Equations (4.3), (4.4) and (6.1) hold with the same coordinates, then
$p\in \mathcal {X}\cap \mathcal {Y}$
, if Equations (4.3), (4.4) and (6.1) hold with the same coordinates, then
![]() $\eta $
and g are said to be in standard form with respect to X around p. In this case,
$\eta $
and g are said to be in standard form with respect to X around p. In this case,
![]() $C\eta $
and
$C\eta $
and
![]() $Cg$
(
$Cg$
(
![]() $C>0$
) are also in standard form with respect to X around p; indeed,
$C>0$
) are also in standard form with respect to X around p; indeed,
![]() $C\eta $
, X and
$C\eta $
, X and
![]() $Cg$
satisfy Equations (4.3), (4.4) and (6.1) with the coordinates
$Cg$
satisfy Equations (4.3), (4.4) and (6.1) with the coordinates
![]() $\sqrt {C}x_p$
. If
$\sqrt {C}x_p$
. If
![]() $\mathcal {X}=\mathcal {Y}$
, and
$\mathcal {X}=\mathcal {Y}$
, and
![]() $\eta $
and g are in standard form with respect to X around every
$\eta $
and g are in standard form with respect to X around every
![]() $p\in \mathcal {X}$
, then
$p\in \mathcal {X}$
, then
![]() $\eta $
and g are said to be in standard form with respect to X. This concept is also applied to any Morse function h on M referring to
$\eta $
and g are said to be in standard form with respect to X. This concept is also applied to any Morse function h on M referring to
![]() $dh$
and g. The reference to g may be omitted in this terminology.
$dh$
and g. The reference to g may be omitted in this terminology.
Unless otherwise indicated, we assume from now on that X has Morse-type zeros. Then
![]() $\mathcal {Y}$
is finite, and the sets
$\mathcal {Y}$
is finite, and the sets
![]() $\mathcal {Y}_k$
,
$\mathcal {Y}_k$
,
![]() $\mathcal {Y}_+$
and
$\mathcal {Y}_+$
and
![]() $\mathcal {Y}_{<k}$
are defined like in Section 4.1.
$\mathcal {Y}_{<k}$
are defined like in Section 4.1.
6.1.2. Stable/unstable manifolds
For
![]() $k=0,\dots ,n$
and
$k=0,\dots ,n$
and
![]() $p\in \mathcal {Y}_k$
, the stable/unstable manifolds of p are smooth injective immersions,
$p\in \mathcal {Y}_k$
, the stable/unstable manifolds of p are smooth injective immersions,
![]() $\iota ^\pm _p:W^\pm _p\to M$
, where the images
$\iota ^\pm _p:W^\pm _p\to M$
, where the images
![]() $\iota ^\pm _p(W^\pm _p)$
consist of the points satisfying
$\iota ^\pm _p(W^\pm _p)$
consist of the points satisfying
![]() $\phi ^t(x)\to p$
as
$\phi ^t(x)\to p$
as
![]() $t\to \pm \infty $
, and the manifolds
$t\to \pm \infty $
, and the manifolds
![]() $W^+_p$
and
$W^+_p$
and
![]() $W^-_p$
are diffeomorphic to
$W^-_p$
are diffeomorphic to
![]() $\mathbb {R}^{n-k}$
and
$\mathbb {R}^{n-k}$
and
![]() $\mathbb {R}^k$
, respectively [Reference Smale70, Theorem 9.1]. In particular,
$\mathbb {R}^k$
, respectively [Reference Smale70, Theorem 9.1]. In particular,
![]() $p\in \iota ^\pm _p(W^\pm _p)$
, and the maps
$p\in \iota ^\pm _p(W^\pm _p)$
, and the maps
![]() $\iota ^+_p$
and
$\iota ^+_p$
and
![]() $\iota ^-_p$
meet transversely at p. Let
$\iota ^-_p$
meet transversely at p. Let
![]() $p^\pm =(\iota ^\pm _p)^{-1}(p)$
. Assume every
$p^\pm =(\iota ^\pm _p)^{-1}(p)$
. Assume every
![]() $U_p$
is connected, and let
$U_p$
is connected, and let
![]() $U^\pm _p$
be the connected component of
$U^\pm _p$
be the connected component of
![]() $(\iota ^\pm _p)^{-1}(U_p)$
that contains
$(\iota ^\pm _p)^{-1}(U_p)$
that contains
![]() $p^\pm $
. The restriction
$p^\pm $
. The restriction
![]() $\iota ^\pm _p:U^\pm _p\to (x_p^\pm )^{-1}(0)$
is a diffeomorphism, and therefore
$\iota ^\pm _p:U^\pm _p\to (x_p^\pm )^{-1}(0)$
is a diffeomorphism, and therefore
![]() $(U^\pm _p,x^\pm _p\iota ^\pm _p)$
is a chart of
$(U^\pm _p,x^\pm _p\iota ^\pm _p)$
is a chart of
![]() $W^\pm _p$
at
$W^\pm _p$
at
![]() $p^\pm $
.
$p^\pm $
.
6.1.3. Gradient-like vector fields
Given a Morse function h on M in standard form with respect to X, we have
![]() $X=-\operatorname {grad}_gh$
on M for some Riemannian metric g if and only if
$X=-\operatorname {grad}_gh$
on M for some Riemannian metric g if and only if
![]() $Xh<0$
on
$Xh<0$
on
![]() $M\setminus \mathcal {Y}$
[Reference Burghelea, Friedlander and Kappeler16, Lemma 2.1], [Reference Laudenbach40, Section 6.1.3]; in this case, X is said to be gradient-like (with respect to h). If X is gradient-like, then the maps
$M\setminus \mathcal {Y}$
[Reference Burghelea, Friedlander and Kappeler16, Lemma 2.1], [Reference Laudenbach40, Section 6.1.3]; in this case, X is said to be gradient-like (with respect to h). If X is gradient-like, then the maps
![]() $\iota ^\pm _p$
are embeddings [Reference Smale68, Lemma 3.8], [Reference Burghelea, Friedlander and Kappeler16, Lemma 2.2], and their images cover M [Reference Smale69, Theorem B and Lemma 1.1], [Reference Burghelea, Friedlander and Kappeler16, Corollary 2.5]. Thus, in this case, the
$\iota ^\pm _p$
are embeddings [Reference Smale68, Lemma 3.8], [Reference Burghelea, Friedlander and Kappeler16, Lemma 2.2], and their images cover M [Reference Smale69, Theorem B and Lemma 1.1], [Reference Burghelea, Friedlander and Kappeler16, Corollary 2.5]. Thus, in this case, the
![]() $\alpha $
- and
$\alpha $
- and
![]() $\omega $
-limits of the orbits of X are zero points, we can write
$\omega $
-limits of the orbits of X are zero points, we can write
![]() $W^\pm _p=\iota ^\pm _p(W^\pm _p)$
and
$W^\pm _p=\iota ^\pm _p(W^\pm _p)$
and
![]() $p^\pm =p$
, and
$p^\pm =p$
, and
![]() $\iota ^\pm _p$
becomes the inclusion map.
$\iota ^\pm _p$
becomes the inclusion map.
Unless otherwise indicated, we also assume in the rest of the paper that X is gradient-like.
6.1.4. Smale vector fields
X is said to be Smale if
![]() $W^+_p\pitchfork W^-_q$
for all
$W^+_p\pitchfork W^-_q$
for all
![]() $p,q\in \mathcal {Y}$
. Then
$p,q\in \mathcal {Y}$
. Then
![]() $\mathcal {M}(p,q):=W^+_p\cap W^-_q$
is a
$\mathcal {M}(p,q):=W^+_p\cap W^-_q$
is a
![]() $\phi $
-saturated smooth submanifold of dimension
$\phi $
-saturated smooth submanifold of dimension
![]() $\operatorname {ind}(p)-\operatorname {ind}(q)$
. If
$\operatorname {ind}(p)-\operatorname {ind}(q)$
. If
![]() $p=q$
, we have
$p=q$
, we have
![]() $\mathcal {M}(p,p)=\{p\}$
; in this case, define
$\mathcal {M}(p,p)=\{p\}$
; in this case, define
![]() $\mathcal {T}(p,p)=\emptyset $
. If
$\mathcal {T}(p,p)=\emptyset $
. If
![]() $p\ne q$
, the induced
$p\ne q$
, the induced
![]() $\mathbb {R}$
-action on
$\mathbb {R}$
-action on
![]() $\mathcal {M}(p,q)$
is free and proper; in this case, define
$\mathcal {M}(p,q)$
is free and proper; in this case, define
![]() $\mathcal {T}(p,q)=\mathcal {M}(p,q)/\mathbb {R}$
, which is a smooth manifold of dimension
$\mathcal {T}(p,q)=\mathcal {M}(p,q)/\mathbb {R}$
, which is a smooth manifold of dimension
![]() $\operatorname {ind}(p)-\operatorname {ind}(q)-1$
. The elements of
$\operatorname {ind}(p)-\operatorname {ind}(q)-1$
. The elements of
![]() $\mathcal {T}(p,q)$
are the (unparameterized) trajectories with
$\mathcal {T}(p,q)$
are the (unparameterized) trajectories with
![]() $\alpha $
-limit p and
$\alpha $
-limit p and
![]() $\omega $
-limit q, which are oriented by X. If
$\omega $
-limit q, which are oriented by X. If
![]() $\operatorname {ind}(p)\le \operatorname {ind}(q)$
, then
$\operatorname {ind}(p)\le \operatorname {ind}(q)$
, then
![]() $\mathcal {T}(p,q)=\emptyset $
. If
$\mathcal {T}(p,q)=\emptyset $
. If
![]() $\operatorname {ind}(p)-\operatorname {ind}(q)=1$
, then
$\operatorname {ind}(p)-\operatorname {ind}(q)=1$
, then
![]() $\mathcal {T}(p,q)$
consists of isolated points, each of them representing a trajectory in M. Let
$\mathcal {T}(p,q)$
consists of isolated points, each of them representing a trajectory in M. Let
 $$\begin{align*}\mathcal{T}=\bigcup_{p,q\in\mathcal{X}}\mathcal{T}(p,q)\;,\quad\mathcal{T}^1_p=\bigcup_{q\in\mathcal{X}_{\operatorname{ind}(p)-1}}\mathcal{T}(p,q)\;,\quad\mathcal{T}^1_k=\bigcup_{p\in\mathcal{X}_k}\mathcal{T}^1_p\;,\quad\mathcal{T}^1=\bigcup_{k=0}^n\mathcal{T}^1_k. \end{align*}$$
$$\begin{align*}\mathcal{T}=\bigcup_{p,q\in\mathcal{X}}\mathcal{T}(p,q)\;,\quad\mathcal{T}^1_p=\bigcup_{q\in\mathcal{X}_{\operatorname{ind}(p)-1}}\mathcal{T}(p,q)\;,\quad\mathcal{T}^1_k=\bigcup_{p\in\mathcal{X}_k}\mathcal{T}^1_p\;,\quad\mathcal{T}^1=\bigcup_{k=0}^n\mathcal{T}^1_k. \end{align*}$$
The elements of
![]() $\mathcal {T}^1$
are called instantons.Footnote 1
$\mathcal {T}^1$
are called instantons.Footnote 1
X can be
![]() $C^\infty $
-approximated by gradient-like Smale vector fields that agree with X around
$C^\infty $
-approximated by gradient-like Smale vector fields that agree with X around
![]() $\mathcal {X}$
[Reference Burghelea and Haller20, Proposition 2.4] (this follows from [Reference Smale69, Theorem A]). A well-known consequence is that, for any Morse function h, there is a
$\mathcal {X}$
[Reference Burghelea and Haller20, Proposition 2.4] (this follows from [Reference Smale69, Theorem A]). A well-known consequence is that, for any Morse function h, there is a
![]() $C^\infty $
-dense set of Riemannian metrics g on M such that
$C^\infty $
-dense set of Riemannian metrics g on M such that
![]() $-\operatorname {grad}_gh$
is Smale; this density is also true in the subspace of metrics that are Euclidean with respect to Morse coordinates on given neighborhoods of the critical points.
$-\operatorname {grad}_gh$
is Smale; this density is also true in the subspace of metrics that are Euclidean with respect to Morse coordinates on given neighborhoods of the critical points.
Unless otherwise indicated, besides the above conditions, we assume from now on that X is Smale; that is, we assume (b) (Section 1.1).
6.1.5. Lyapunov forms
Any
![]() $\eta \in Z^1(M,\mathbb {R})$
is said to be Lyapunov for X if
$\eta \in Z^1(M,\mathbb {R})$
is said to be Lyapunov for X if
![]() $\eta (X)<0$
on
$\eta (X)<0$
on
![]() $M\setminus \mathcal {Y}$
[Reference Burghelea and Haller20, Definition 2.3]. Note that this condition implies that
$M\setminus \mathcal {Y}$
[Reference Burghelea and Haller20, Definition 2.3]. Note that this condition implies that
![]() $\operatorname {Zero}(\eta )=\mathcal {Y}$
. By (b), every class in
$\operatorname {Zero}(\eta )=\mathcal {Y}$
. By (b), every class in
![]() $H^1(M,\mathbb {R})$
has a representative
$H^1(M,\mathbb {R})$
has a representative
![]() $\eta $
which is Lyapunov for X and
$\eta $
which is Lyapunov for X and
![]() $\eta ^\sharp =-X$
for some Riemannian metric g on M, with
$\eta ^\sharp =-X$
for some Riemannian metric g on M, with
![]() $\eta $
and g in standard form with respect to X [Reference Burghelea and Haller18, Proposition 16 (i)], [Reference Burghelea and Haller20, Observations 2.5 and 2.6], [Reference Harvey and Minervini34, Lemma 3.7], [Reference Laudenbach40, Section 6.1.3].
$\eta $
and g in standard form with respect to X [Reference Burghelea and Haller18, Proposition 16 (i)], [Reference Burghelea and Haller20, Observations 2.5 and 2.6], [Reference Harvey and Minervini34, Lemma 3.7], [Reference Laudenbach40, Section 6.1.3].
6.1.6. Completion of the unstable manifolds
Proposition 6.1 ([Reference Bismut, Zhang and Laudenbach10, Appendix by F. Laudenbach, Proposition 2], [Reference Latour39, Chapter 2], [Reference Burghelea15, Theorem 2.1], [Reference Burghelea and Haller17, Theorem 1], [Reference Burghelea, Friedlander and Kappeler16, Theorem 4.4], [Reference Laudenbach40, Sections A.2 and A.8], [Reference Minervini52, Corollary 2.3.2])
The following holds for every
![]() $p\in \mathcal {Y}_k\ (k=0,\dots ,n)$
:
$p\in \mathcal {Y}_k\ (k=0,\dots ,n)$
:
-
(i)
 $\overline {W^-_p}$
is a
$\overline {W^-_p}$
is a
 $C^1$
submanifold with conic singularitiesFootnote 2 and a Whitney stratified subspaceFootnote 3. Its strata are the submanifolds
$C^1$
submanifold with conic singularitiesFootnote 2 and a Whitney stratified subspaceFootnote 3. Its strata are the submanifolds
 $W^-_q$
for
$W^-_q$
for
 $q\in \mathcal {Y}_{<k}$
with
$q\in \mathcal {Y}_{<k}$
with
 $\mathcal {T}(p,q)\ne \emptyset $
. As a consequence,
$\mathcal {T}(p,q)\ne \emptyset $
. As a consequence,
 $W^-_p$
has finite volume, and if
$W^-_p$
has finite volume, and if $$\begin{align*}\overline{W^-_q}\cap\overline{W^-_p}\subset\bigcup_{x\in\mathcal{Y}_{<k}}W_x^- \end{align*}$$
$$\begin{align*}\overline{W^-_q}\cap\overline{W^-_p}\subset\bigcup_{x\in\mathcal{Y}_{<k}}W_x^- \end{align*}$$
 $q\ne p$
in
$q\ne p$
in
 $\mathcal {Y}_k$
; in particular,
$\mathcal {Y}_k$
; in particular,
 $p\notin \overline {W^-_q}$
.
$p\notin \overline {W^-_q}$
.
-
(ii) There is a compact k-manifold with cornersFootnote 4
 $\widehat W^-_p$
whose l-cornerFootnote 5 is In particular, the interior of
$\widehat W^-_p$
whose l-cornerFootnote 5 is In particular, the interior of $$\begin{align*}\partial_l\widehat W^-_p=\bigsqcup_{(q_0,\dots,q_l)\in\{p\}\times\mathcal{Y}^l}\bigg(\prod_{j=1}^l\mathcal{T}(q_{j-1},q_j)\bigg)\times W_{q_l}^- \quad(0\le l\le k). \end{align*}$$
$$\begin{align*}\partial_l\widehat W^-_p=\bigsqcup_{(q_0,\dots,q_l)\in\{p\}\times\mathcal{Y}^l}\bigg(\prod_{j=1}^l\mathcal{T}(q_{j-1},q_j)\bigg)\times W_{q_l}^- \quad(0\le l\le k). \end{align*}$$
 $\widehat W^-_p$
is
$\widehat W^-_p$
is
 $\partial _0\widehat W^-_p=W^-_p$
, and the set
$\partial _0\widehat W^-_p=W^-_p$
, and the set
 $\mathcal {T}(p,q)$
is finite if
$\mathcal {T}(p,q)$
is finite if
 $q\in \mathcal {Y}_{k-1}$
.
$q\in \mathcal {Y}_{k-1}$
.
-
(iii) There is a smooth map
 $\hat \iota ^-_p:\widehat W^-_p\to M$
whose restriction to every component of
$\hat \iota ^-_p:\widehat W^-_p\to M$
whose restriction to every component of
 $\partial _l\widehat W^-_p$
is given by the factor projection to
$\partial _l\widehat W^-_p$
is given by the factor projection to
 $W_{q_l}^-$
, according to (ii). In particular,
$W_{q_l}^-$
, according to (ii). In particular,
 $\hat \iota ^-_p=\iota ^-_p$
on
$\hat \iota ^-_p=\iota ^-_p$
on
 $W^-_p$
, and
$W^-_p$
, and
 $\hat \iota _p^-:\widehat W^-_p\to \overline {W^-_p}$
is a stratified map.
$\hat \iota _p^-:\widehat W^-_p\to \overline {W^-_p}$
is a stratified map.
By Proposition 6.1 (i), we can choose the open sets
![]() $U_p$
(
$U_p$
(
![]() $p\in \mathcal {Y}_k$
,
$p\in \mathcal {Y}_k$
,
![]() $k=0,\dots ,n$
) so small that
$k=0,\dots ,n$
) so small that
![]() $U_p\cap \overline {W^-_q}=\emptyset $
if
$U_p\cap \overline {W^-_q}=\emptyset $
if
![]() $q\ne p$
in
$q\ne p$
in
![]() $\mathcal {Y}_k$
.
$\mathcal {Y}_k$
.
For every
![]() $q\in \mathcal {Y}_{k-1}$
and
$q\in \mathcal {Y}_{k-1}$
and
![]() $\gamma \in \mathcal {T}(p,q)$
, the closure
$\gamma \in \mathcal {T}(p,q)$
, the closure
![]() $\bar \gamma $
in M is a compact oriented submanifold with boundary of dimension one, and
$\bar \gamma $
in M is a compact oriented submanifold with boundary of dimension one, and
![]() $\partial \bar \gamma =\{p,q\}$
. We may also consider
$\partial \bar \gamma =\{p,q\}$
. We may also consider
![]() $\bar \gamma $
as the closure of
$\bar \gamma $
as the closure of
![]() $\gamma $
in
$\gamma $
in
![]() $\widehat W^-_p$
.
$\widehat W^-_p$
.
6.2. Preliminaries on the Morse complex
6.2.1. The Morse complex when M is oriented
For reasons of clarity, assume first that M is oriented. Fix an orientation
![]() $\mathcal {O}_p^-$
of every unstable manifold
$\mathcal {O}_p^-$
of every unstable manifold
![]() $W^-_p$
(
$W^-_p$
(
![]() $p\in \mathcal {Y}_k$
,
$p\in \mathcal {Y}_k$
,
![]() $k=0,\dots ,n$
), which can be also considered as an orientation of
$k=0,\dots ,n$
), which can be also considered as an orientation of
![]() $\widehat W^-_p$
. Then
$\widehat W^-_p$
. Then
![]() $W^-_p\equiv (W^-_p,\mathcal {O}^-_p)$
defines a current of dimension k on M, also denoted by
$W^-_p\equiv (W^-_p,\mathcal {O}^-_p)$
defines a current of dimension k on M, also denoted by
![]() $W^-_p$
; namely, for
$W^-_p$
; namely, for
![]() $\alpha \in \Omega ^k(M)$
,
$\alpha \in \Omega ^k(M)$
,
 $$ \begin{align} \langle W^-_p,\alpha\rangle=\int_{W^-_p}\alpha=\int_{\widehat W^-_p}(\hat\iota_p^-)^*\alpha. \end{align} $$
$$ \begin{align} \langle W^-_p,\alpha\rangle=\int_{W^-_p}\alpha=\int_{\widehat W^-_p}(\hat\iota_p^-)^*\alpha. \end{align} $$
Let
![]() $\partial _1\mathcal {O}_p^-$
be the orientation of
$\partial _1\mathcal {O}_p^-$
be the orientation of
![]() $\partial _1\widehat W^-_p$
induced by
$\partial _1\widehat W^-_p$
induced by
![]() $\mathcal {O}_p^-$
like in the Stokes’ theorem; precisely, it is determined by
$\mathcal {O}_p^-$
like in the Stokes’ theorem; precisely, it is determined by
![]() $\mathcal {O}_p^-=\nu _p^-\otimes \partial _1\mathcal {O}_p^-$
along
$\mathcal {O}_p^-=\nu _p^-\otimes \partial _1\mathcal {O}_p^-$
along
![]() $\partial _1\widehat W^-_p$
for any outward-pointing normal vector
$\partial _1\widehat W^-_p$
for any outward-pointing normal vector
![]() $\nu _p^-$
. The restriction of
$\nu _p^-$
. The restriction of
![]() $\partial _1\mathcal {O}_p^-$
to every component
$\partial _1\mathcal {O}_p^-$
to every component
![]() $\mathcal {T}(p,q)\times W^-_q$
(
$\mathcal {T}(p,q)\times W^-_q$
(
![]() $q\in \mathcal {Y}_{k'}$
) of
$q\in \mathcal {Y}_{k'}$
) of
![]() $\partial _1\widehat W^-_p$
is of the form
$\partial _1\widehat W^-_p$
is of the form
![]() $\mathcal {O}_{p,q}\otimes \mathcal {O}_q^-$
for a unique orientation
$\mathcal {O}_{p,q}\otimes \mathcal {O}_q^-$
for a unique orientation
![]() $\mathcal {O}_{p,q}$
of
$\mathcal {O}_{p,q}$
of
![]() $\mathcal {T}(p,q)$
. If
$\mathcal {T}(p,q)$
. If
![]() $k'=k-1$
, then
$k'=k-1$
, then
![]() $\mathcal {O}_{p,q}$
can be represented by a unique function
$\mathcal {O}_{p,q}$
can be represented by a unique function
![]() $\epsilon _{p,q}:\mathcal {T}(p,q)\to \{\pm 1\}$
; combining these functions, we get a map
$\epsilon _{p,q}:\mathcal {T}(p,q)\to \{\pm 1\}$
; combining these functions, we get a map
![]() $\epsilon :\mathcal {T}^1\to \{\pm 1\}$
. By the descriptions of
$\epsilon :\mathcal {T}^1\to \{\pm 1\}$
. By the descriptions of
![]() $\partial _1\widehat W^-_p$
and
$\partial _1\widehat W^-_p$
and
![]() $\hat \iota ^-_p:\partial _1\widehat W^-_p\to M$
, and by the Stokes’ theorem for manifolds with corners, we have [Reference Bismut, Zhang and Laudenbach10, Appendix by F. Laudenbach], [Reference Harvey and Minervini34, Remark 1.9], [Reference Burghelea, Friedlander and Kappeler16, Theorem 3.6 and Proposition 5.3], [Reference Laudenbach40, Section 6.5.3]
$\hat \iota ^-_p:\partial _1\widehat W^-_p\to M$
, and by the Stokes’ theorem for manifolds with corners, we have [Reference Bismut, Zhang and Laudenbach10, Appendix by F. Laudenbach], [Reference Harvey and Minervini34, Remark 1.9], [Reference Burghelea, Friedlander and Kappeler16, Theorem 3.6 and Proposition 5.3], [Reference Laudenbach40, Section 6.5.3]
 $$ \begin{align} \partial W^-_p=\sum_{q\in\mathcal{Y}_{k-1},\ \gamma\in\mathcal{T}(p,q)}\epsilon(\gamma)\,W^-_q. \end{align} $$
$$ \begin{align} \partial W^-_p=\sum_{q\in\mathcal{Y}_{k-1},\ \gamma\in\mathcal{T}(p,q)}\epsilon(\gamma)\,W^-_q. \end{align} $$
Thus, the currents
![]() $W^-_p$
(
$W^-_p$
(
![]() $p\in \mathcal {X}$
) generate over
$p\in \mathcal {X}$
) generate over
![]() $\mathbb {C}$
a finite-dimensional subcomplex
$\mathbb {C}$
a finite-dimensional subcomplex
![]() $(C_\bullet (X,W^-),\partial )$
of the complex
$(C_\bullet (X,W^-),\partial )$
of the complex
![]() $(\Omega (M)',\partial )$
of currents on M, called the Morse complex. The simpler notation
$(\Omega (M)',\partial )$
of currents on M, called the Morse complex. The simpler notation
![]() $\mathbf {C}_\bullet =\mathbf {C}_\bullet (X)=C_\bullet (X,W^-)$
may be also used. Moreover,
$\mathbf {C}_\bullet =\mathbf {C}_\bullet (X)=C_\bullet (X,W^-)$
may be also used. Moreover,
![]() $\mathbf {C}_\bullet \hookrightarrow \Omega (M)'$
is a quasi-isomorphism,Footnote 6
$\mathbf {C}_\bullet \hookrightarrow \Omega (M)'$
is a quasi-isomorphism,Footnote 6
![]() $H_\bullet (\mathbf {C}_\bullet ,\partial )\cong H_\bullet (M,\mathbb {C})$
[Reference Thom71, Reference Smale67, Reference Milnor51] (see also [Reference Floer29, Reference Schwarz64, Reference Schwarz65], [Reference Helffer and Sjöstrand35, Theorem 0.1], [Reference Bismut, Zhang and Laudenbach10, Appendix by F. Laudenbach, Proposition 7], [Reference Laudenbach40, Section 6.6.5]).
$H_\bullet (\mathbf {C}_\bullet ,\partial )\cong H_\bullet (M,\mathbb {C})$
[Reference Thom71, Reference Smale67, Reference Milnor51] (see also [Reference Floer29, Reference Schwarz64, Reference Schwarz65], [Reference Helffer and Sjöstrand35, Theorem 0.1], [Reference Bismut, Zhang and Laudenbach10, Appendix by F. Laudenbach, Proposition 7], [Reference Laudenbach40, Section 6.6.5]).
Let
![]() $(C_\bullet (X,W^+),\partial )=(C_\bullet (-X,W^-),\partial )$
, involving the stable Morse cells
$(C_\bullet (X,W^+),\partial )=(C_\bullet (-X,W^-),\partial )$
, involving the stable Morse cells
![]() $W^+_p$
. If M is oriented by
$W^+_p$
. If M is oriented by
![]() $\mathcal {O}_M$
and the orientation
$\mathcal {O}_M$
and the orientation
![]() $\mathcal {O}_p^+$
of every
$\mathcal {O}_p^+$
of every
![]() $W^+_p$
is chosen so that
$W^+_p$
is chosen so that
![]() $\mathcal {O}_p^+\otimes \mathcal {O}_p^-=\mathcal {O}_M$
at p, then the canonical pairing
$\mathcal {O}_p^+\otimes \mathcal {O}_p^-=\mathcal {O}_M$
at p, then the canonical pairing
satisfies [Reference Laudenbach40, Section 6.6.2]
6.2.2. The Morse complex when M may not be oriented
When M is not assumed to be oriented, the concepts of Section 6.2.1 can be extended as follows. We fix an orientation
![]() $N\mathcal {O}_p^-$
of every normal bundle
$N\mathcal {O}_p^-$
of every normal bundle
![]() $NW^-_p$
, which can be also considered as an orientation of
$NW^-_p$
, which can be also considered as an orientation of
![]() $N\widehat W^-_p$
(the normal bundle of the immersion
$N\widehat W^-_p$
(the normal bundle of the immersion
![]() $\hat \iota _p^-$
). Then we can consider
$\hat \iota _p^-$
). Then we can consider
![]() $W^-_p\equiv (W^-_p,N\mathcal {O}^-_p)\in \Omega ^k(M,o(M))'$
, by using
$W^-_p\equiv (W^-_p,N\mathcal {O}^-_p)\in \Omega ^k(M,o(M))'$
, by using
![]() $N\mathcal {O}_p^-\otimes \alpha $
as integrand in Equation (6.2) for every
$N\mathcal {O}_p^-\otimes \alpha $
as integrand in Equation (6.2) for every
![]() $\alpha \in \Omega ^k(M,o(M))$
; note that
$\alpha \in \Omega ^k(M,o(M))$
; note that
![]() $N\mathcal {O}_p^-\otimes \alpha \in \Omega ^k(\widehat W^-_p,o(\widehat W^-_p))=\Omega ^k(\widehat W^-_p)$
. With the notation of Section 6.2.1,
$N\mathcal {O}_p^-\otimes \alpha \in \Omega ^k(\widehat W^-_p,o(\widehat W^-_p))=\Omega ^k(\widehat W^-_p)$
. With the notation of Section 6.2.1,
![]() $\partial _1N\mathcal {O}_p^-:=N\mathcal {O}_p^-\otimes \nu _p^-$
describes an orientation of
$\partial _1N\mathcal {O}_p^-:=N\mathcal {O}_p^-\otimes \nu _p^-$
describes an orientation of
![]() $N\partial _1\widehat W^-_p$
, and the Stokes theorem has the extension (see [Reference Bott and Tu13, Theorem 7.7] for the case without boundary)
$N\partial _1\widehat W^-_p$
, and the Stokes theorem has the extension (see [Reference Bott and Tu13, Theorem 7.7] for the case without boundary)
 $$ \begin{align} \int_{\widehat W^-_p}N\mathcal{O}_p^-\otimes d\beta=\int_{\partial_1\widehat W^-_p}\partial_1N\mathcal{O}_p^-\otimes\beta\quad \big(\beta\in\Omega^{k-1}(M,o(M))\big). \end{align} $$
$$ \begin{align} \int_{\widehat W^-_p}N\mathcal{O}_p^-\otimes d\beta=\int_{\partial_1\widehat W^-_p}\partial_1N\mathcal{O}_p^-\otimes\beta\quad \big(\beta\in\Omega^{k-1}(M,o(M))\big). \end{align} $$
If M is oriented by
![]() $O_M$
, then
$O_M$
, then
![]() $N\mathcal {O}_p^-$
and
$N\mathcal {O}_p^-$
and
![]() $\mathcal {O}_p^-$
determine each other by the condition
$\mathcal {O}_p^-$
determine each other by the condition
![]() $O_M=N\mathcal {O}_p^-\otimes \mathcal {O}_p^-$
. Then
$O_M=N\mathcal {O}_p^-\otimes \mathcal {O}_p^-$
. Then
![]() $\partial _1N\mathcal {O}_p^-$
and
$\partial _1N\mathcal {O}_p^-$
and
![]() $\partial _1\mathcal {O}_p^-$
determine each other in the same way:
$\partial _1\mathcal {O}_p^-$
determine each other in the same way:
So Equation (6.6) agrees with the usual Stokes’ theorem in this way.
If M is not oriented, by using local orientations of M, the above argument shows that Equation (6.6) also agrees with the usual Stokes’ theorem for
![]() $o(M)$
-valued forms
$o(M)$
-valued forms
![]() $\beta $
with small enough support. Then, like in Section 6.2.1, we get the same map
$\beta $
with small enough support. Then, like in Section 6.2.1, we get the same map
![]() $\epsilon :\mathcal {T}^1\to \{\pm 1\}$
, and therefore the same definition of
$\epsilon :\mathcal {T}^1\to \{\pm 1\}$
, and therefore the same definition of
![]() $(\mathbf {C}_\bullet ,\partial )$
.
$(\mathbf {C}_\bullet ,\partial )$
.
6.2.3. The dual Morse complex
Let
![]() $C^k(X,W^-)=(\mathbf {C}_k)^*\equiv \mathbb {C}^{\mathcal {Y}_k}$
(
$C^k(X,W^-)=(\mathbf {C}_k)^*\equiv \mathbb {C}^{\mathcal {Y}_k}$
(
![]() $k=0,\dots ,n$
) and
$k=0,\dots ,n$
) and
![]() $\mathbf {d}=\partial ^*$
. The simpler notation
$\mathbf {d}=\partial ^*$
. The simpler notation
![]() $\mathbf {C}^{\bullet }=\mathbf {C}^{\bullet }(X)$
will be preferred. It is said that
$\mathbf {C}^{\bullet }=\mathbf {C}^{\bullet }(X)$
will be preferred. It is said that
![]() $(\mathbf {C}^{\bullet },\mathbf {d})$
is the dual Morse complex. Boldface notation is also used for elements of
$(\mathbf {C}^{\bullet },\mathbf {d})$
is the dual Morse complex. Boldface notation is also used for elements of
![]() $\mathbf {C}^{\bullet }$
and other operators on
$\mathbf {C}^{\bullet }$
and other operators on
![]() $\mathbf {C}^{\bullet }$
. Let
$\mathbf {C}^{\bullet }$
. Let
![]() $\mathbf {e}_p$
(
$\mathbf {e}_p$
(
![]() $p\in \mathcal {Y}$
) denote the elements of the canonical base of
$p\in \mathcal {Y}$
) denote the elements of the canonical base of
![]() $\mathbf {C}^{\bullet }$
, determined by
$\mathbf {C}^{\bullet }$
, determined by
![]() $\mathbf {e}_p(q)=\delta _{pq}$
. By Equation (6.3), for
$\mathbf {e}_p(q)=\delta _{pq}$
. By Equation (6.3), for
![]() $q\in \mathcal {Y}_{k-1}$
,
$q\in \mathcal {Y}_{k-1}$
,
 $$ \begin{align} \mathbf{d}\mathbf{e}_q=\sum_{p\in\mathcal{Y}_k,\ \gamma\in\mathcal{T}(p,q)}\epsilon(\gamma)\,\mathbf{e}_p. \end{align} $$
$$ \begin{align} \mathbf{d}\mathbf{e}_q=\sum_{p\in\mathcal{Y}_k,\ \gamma\in\mathcal{T}(p,q)}\epsilon(\gamma)\,\mathbf{e}_p. \end{align} $$
Comparing Equations (6.3) and (6.7), we see that
![]() $(C^{\bullet }(X,W^-),\mathbf {d})\equiv (C_\bullet (-X,W^+),\partial )$
. Thus, from now on,
$(C^{\bullet }(X,W^-),\mathbf {d})\equiv (C_\bullet (-X,W^+),\partial )$
. Thus, from now on,
![]() $(\mathbf {C}^{\bullet },\mathbf {d})$
will be also called a Morse complex. If M is oriented, it also follows from Equations (6.4) and (6.5) that
$(\mathbf {C}^{\bullet },\mathbf {d})$
will be also called a Morse complex. If M is oriented, it also follows from Equations (6.4) and (6.5) that
![]() $(C^{\bullet }(X,W^-),\mathsf {w}\mathbf {d})\equiv (C_{n-\bullet }(X,W^+),\partial )$
.
$(C^{\bullet }(X,W^-),\mathsf {w}\mathbf {d})\equiv (C_{n-\bullet }(X,W^+),\partial )$
.
6.2.4. The perturbed Morse complex
Take any
![]() $\eta \in Z^1(M,\mathbb {R})$
defining a class
$\eta \in Z^1(M,\mathbb {R})$
defining a class
![]() $\xi \in H^1(M,\mathbb {R})$
(there is no need of any condition on
$\xi \in H^1(M,\mathbb {R})$
(there is no need of any condition on
![]() $\eta $
or g in Sections 6.2.4 to 6.2.6). For reasons of brevity, write
$\eta $
or g in Sections 6.2.4 to 6.2.6). For reasons of brevity, write
![]() $\eta (\gamma )=\int _\gamma \eta $
for every
$\eta (\gamma )=\int _\gamma \eta $
for every
![]() $\gamma \in \mathcal {T}^1$
. According to [Reference Burghelea and Haller17, Reference Burghelea and Haller18, Reference Burghelea and Haller20],
$\gamma \in \mathcal {T}^1$
. According to [Reference Burghelea and Haller17, Reference Burghelea and Haller18, Reference Burghelea and Haller20],
![]() $(\mathbf {C}^{\bullet },\mathbf {d})$
has an analog of the Witten’s perturbation,
$(\mathbf {C}^{\bullet },\mathbf {d})$
has an analog of the Witten’s perturbation,
![]() $(\mathbf {C}^{\bullet },\mathbf {d}_z=\mathbf {d}_{z\eta })$
(
$(\mathbf {C}^{\bullet },\mathbf {d}_z=\mathbf {d}_{z\eta })$
(
![]() $z\in \mathbb {C}$
), where, for
$z\in \mathbb {C}$
), where, for
![]() $q\in \mathcal {Y}_{k-1}$
(
$q\in \mathcal {Y}_{k-1}$
(
![]() $k=1,\dots ,n$
),
$k=1,\dots ,n$
),
 $$ \begin{align} \mathbf{d}_z\mathbf{e}_q=\sum_{p\in\mathcal{Y}_k,\ \gamma\in\mathcal{T}(p,q)}\epsilon(\gamma)e^{z\eta(\gamma)}\mathbf{e}_p. \end{align} $$
$$ \begin{align} \mathbf{d}_z\mathbf{e}_q=\sum_{p\in\mathcal{Y}_k,\ \gamma\in\mathcal{T}(p,q)}\epsilon(\gamma)e^{z\eta(\gamma)}\mathbf{e}_p. \end{align} $$
If
![]() $\eta =dh$
for some
$\eta =dh$
for some
![]() $h\in C^\infty (M,\mathbb {R})$
, then
$h\in C^\infty (M,\mathbb {R})$
, then
![]() $\mathbf {d}_z=e^{-zh}\mathbf {d} e^{zh}$
on
$\mathbf {d}_z=e^{-zh}\mathbf {d} e^{zh}$
on
![]() $\mathbf {C}^{\bullet }$
because
$\mathbf {C}^{\bullet }$
because
![]() $\eta (\gamma )=h(q)-h(p)$
for
$\eta (\gamma )=h(q)-h(p)$
for
![]() $p\in \mathcal {Y}_k$
,
$p\in \mathcal {Y}_k$
,
![]() $q\in \mathcal {Y}_{k-1}$
and
$q\in \mathcal {Y}_{k-1}$
and
![]() $\gamma \in \mathcal {T}(p,q)$
; here,
$\gamma \in \mathcal {T}(p,q)$
; here,
![]() $e^{\pm zh}$
also denotes the operator of multiplication by the restriction of this function to
$e^{\pm zh}$
also denotes the operator of multiplication by the restriction of this function to
![]() $\mathcal {Y}$
. It will be said that
$\mathcal {Y}$
. It will be said that
![]() $(\mathbf {C}^{\bullet },\mathbf {d}_z)$
(
$(\mathbf {C}^{\bullet },\mathbf {d}_z)$
(
![]() $z\in \mathbb {C}$
) is the perturbed dual Morse complex defined by X and
$z\in \mathbb {C}$
) is the perturbed dual Morse complex defined by X and
![]() $\eta $
. A perturbation
$\eta $
. A perturbation
![]() $(\mathbf {C}_\bullet ,\partial ^z)$
is similarly defined, multiplying by
$(\mathbf {C}_\bullet ,\partial ^z)$
is similarly defined, multiplying by
![]() $e^{z\eta (\gamma )}$
the terms of the right-hand side of Equation (6.3).
$e^{z\eta (\gamma )}$
the terms of the right-hand side of Equation (6.3).
Since
![]() $W^-_p$
(
$W^-_p$
(
![]() $p\in \mathcal {Y}_k$
,
$p\in \mathcal {Y}_k$
,
![]() $k=0,\dots ,n$
) is diffeomorphic to
$k=0,\dots ,n$
) is diffeomorphic to
![]() $\mathbb {R}^k$
, there is a unique
$\mathbb {R}^k$
, there is a unique
![]() $h_{\eta ,p}^-\in C^\infty (W^-_p,\mathbb {R})$
such that
$h_{\eta ,p}^-\in C^\infty (W^-_p,\mathbb {R})$
such that
![]() $h_{\eta ,p}^-(\hat p^-)=0$
and
$h_{\eta ,p}^-(\hat p^-)=0$
and
![]() $dh_{\eta ,p}^-=(\iota _p^-)^*\eta $
, where
$dh_{\eta ,p}^-=(\iota _p^-)^*\eta $
, where
![]() $\hat p^-\in W_p^-\subset \widehat W_p^-$
is determined by
$\hat p^-\in W_p^-\subset \widehat W_p^-$
is determined by
![]() $\iota _p^-(\hat p^-)=p$
. Indeed,
$\iota _p^-(\hat p^-)=p$
. Indeed,
![]() $h_{\eta ,p}^-$
has a smooth extension
$h_{\eta ,p}^-$
has a smooth extension
![]() $\hat h_{\eta ,p}^-$
to
$\hat h_{\eta ,p}^-$
to
![]() $\widehat W^-_p$
because
$\widehat W^-_p$
because
![]() $\widehat W^-_p$
is contractile. By Proposition 6.1 (ii), for all
$\widehat W^-_p$
is contractile. By Proposition 6.1 (ii), for all
![]() $q\in \mathcal {Y}_{k-1}$
and
$q\in \mathcal {Y}_{k-1}$
and
![]() $\gamma \in \mathcal {T}(p,q)$
, we have
$\gamma \in \mathcal {T}(p,q)$
, we have
![]() $\hat h_{\eta ,p}^-(\gamma ,\hat q^-)=\eta (\gamma )$
at
$\hat h_{\eta ,p}^-(\gamma ,\hat q^-)=\eta (\gamma )$
at
![]() $(\gamma ,\hat q^-)\in \{\gamma \}\times \widehat W^-_q\subset \partial _1\widehat W^-_p$
. Therefore,
$(\gamma ,\hat q^-)\in \{\gamma \}\times \widehat W^-_q\subset \partial _1\widehat W^-_p$
. Therefore,
![]() $\hat h_{\eta ,q}^-$
corresponds to the restriction of
$\hat h_{\eta ,q}^-$
corresponds to the restriction of
![]() $\hat h_{\eta ,p}^--\eta (\gamma )$
via the canonical diffeomorphism
$\hat h_{\eta ,p}^--\eta (\gamma )$
via the canonical diffeomorphism
![]() $\widehat W^-_q\approx \{\gamma \}\times \widehat W^-_q$
.
$\widehat W^-_q\approx \{\gamma \}\times \widehat W^-_q$
.
According to [Reference Burghelea and Haller17, Proposition 4], [Reference Burghelea and Haller18, Proposition 10], [Reference Burghelea and Haller20, Propositions 2.15 and 2.16 and Section 6.2], a surjective homomorphism of complexes,
is defined by
 $$\begin{align*}\Phi_z(\omega)(p)=\int_{W^-_p}e^{zh_{\eta,p}^-}\omega=\int_{\widehat W^-_p}e^{z\hat h_{\eta,p}^-}(\hat\iota_p^-)^*\omega. \end{align*}$$
$$\begin{align*}\Phi_z(\omega)(p)=\int_{W^-_p}e^{zh_{\eta,p}^-}\omega=\int_{\widehat W^-_p}e^{z\hat h_{\eta,p}^-}(\hat\iota_p^-)^*\omega. \end{align*}$$
Moreover,
![]() $\Phi _z$
is a quasi-isomorphism for all
$\Phi _z$
is a quasi-isomorphism for all
![]() $z\in \mathbb {C}$
[Reference Bismut, Zhang and Laudenbach10, Proposition 7 in the Appendix by F. Laudenbach] (see also [Reference Bismut, Zhang and Laudenbach10, Theorem 2.9], [Reference Bismut and Zhang11, Theorem 1.6], [Reference Burghelea and Haller20, Proposition 2.17 and Section 6.2]). If
$z\in \mathbb {C}$
[Reference Bismut, Zhang and Laudenbach10, Proposition 7 in the Appendix by F. Laudenbach] (see also [Reference Bismut, Zhang and Laudenbach10, Theorem 2.9], [Reference Bismut and Zhang11, Theorem 1.6], [Reference Burghelea and Haller20, Proposition 2.17 and Section 6.2]). If
![]() $\eta $
and g satisfy (a), then, by Equation (4.13),
$\eta $
and g satisfy (a), then, by Equation (4.13),
is also a quasi-isomorphism. Since a direct adaptation of [Reference Burghelea and Haller18, Appendix A] shows that, for
![]() $k=0,\dots ,n$
,
$k=0,\dots ,n$
,
![]() $\dim H^k(\mathbf {C}^{\bullet },\mathbf {d}_z)$
is independent of
$\dim H^k(\mathbf {C}^{\bullet },\mathbf {d}_z)$
is independent of
![]() $z\in \mathbb {C}$
with
$z\in \mathbb {C}$
with
![]() $|\mu |\gg 0$
, we get Equation (2.9) because any
$|\mu |\gg 0$
, we get Equation (2.9) because any
![]() $\xi \in H^1(M,\mathbb {R})$
is represented by a Morse form.
$\xi \in H^1(M,\mathbb {R})$
is represented by a Morse form.
6.2.5. Morse complex with coefficients in a flat vector bundle
With more generality, for a flat vector bundle F, we may consider
![]() $(C^{\bullet }(X,W^-,F),\mathbf {d}^F)$
, where
$(C^{\bullet }(X,W^-,F),\mathbf {d}^F)$
, where
![]() $C^k(X,W^-,F)=\bigoplus _{p\in \mathcal {Y}_k}F_p$
, and
$C^k(X,W^-,F)=\bigoplus _{p\in \mathcal {Y}_k}F_p$
, and
![]() $\mathbf {d}^F\mathbf {e}$
(
$\mathbf {d}^F\mathbf {e}$
(
![]() $\mathbf {e}\in F_q$
,
$\mathbf {e}\in F_q$
,
![]() $q\in \mathcal {Y}_{k-1}$
) is defined like in the right-hand side of Equation (6.7), replacing
$q\in \mathcal {Y}_{k-1}$
) is defined like in the right-hand side of Equation (6.7), replacing
![]() $\mathbf {e}_p$
with the parallel transport of
$\mathbf {e}_p$
with the parallel transport of
![]() $\mathbf {e}$
along
$\mathbf {e}$
along
![]() $\bar \gamma ^{-1}$
[Reference Bismut, Zhang and Laudenbach10, Section 1c)]. This is the dual of the complex
$\bar \gamma ^{-1}$
[Reference Bismut, Zhang and Laudenbach10, Section 1c)]. This is the dual of the complex
![]() $(C_\bullet (X,W^-,F^*),\partial ^{F^*})$
, where
$(C_\bullet (X,W^-,F^*),\partial ^{F^*})$
, where
![]() $C_k(X,W^-,F^*)=\bigoplus _{p\in \mathcal {Y}_k}F_p^*$
, and
$C_k(X,W^-,F^*)=\bigoplus _{p\in \mathcal {Y}_k}F_p^*$
, and
![]() $\partial ^Ff$
(
$\partial ^Ff$
(
![]() $f\in F_p^*$
,
$f\in F_p^*$
,
![]() $p\in \mathcal {X}_k$
) is defined like in the right-hand side of Equation (6.3), replacing
$p\in \mathcal {X}_k$
) is defined like in the right-hand side of Equation (6.3), replacing
![]() $W^-_q$
with the parallel transport of f along
$W^-_q$
with the parallel transport of f along
![]() $\bar \gamma $
. A quasi-isomorphism
$\bar \gamma $
. A quasi-isomorphism
can be defined like
![]() $\Phi _z$
[Reference Bismut, Zhang and Laudenbach10, Theorem 2.9], using the isomorphism
$\Phi _z$
[Reference Bismut, Zhang and Laudenbach10, Theorem 2.9], using the isomorphism
given by the parallel transport of
![]() $(\hat \iota ^-_p)^*F$
. If
$(\hat \iota ^-_p)^*F$
. If
![]() $F=\mathcal {L}^z$
(Section 2.1.4), then
$F=\mathcal {L}^z$
(Section 2.1.4), then
6.2.6. Hodge theory of the Morse complex
Consider the Hermitian scalar product on
![]() $\mathbf {C}^{\bullet }$
so that the canonical base
$\mathbf {C}^{\bullet }$
so that the canonical base
![]() $\mathbf {e}_p$
(
$\mathbf {e}_p$
(
![]() $p\in \mathcal {Y}$
) is orthonormal. All operators induced by
$p\in \mathcal {Y}$
) is orthonormal. All operators induced by
![]() $\mathbf {d}_z$
and this Hermitian structure are called perturbed Morse operators. For instance, besides
$\mathbf {d}_z$
and this Hermitian structure are called perturbed Morse operators. For instance, besides
![]() $\mathbf {d}_z$
, we have the perturbed Morse operators
$\mathbf {d}_z$
, we have the perturbed Morse operators
In particular, it will be said that
![]() $\boldsymbol {\Delta }_z$
is the perturbed Morse Laplacian, and its eigenvalues will be called perturbed Morse eigenvalues. If
$\boldsymbol {\Delta }_z$
is the perturbed Morse Laplacian, and its eigenvalues will be called perturbed Morse eigenvalues. If
![]() $z=0$
, we omit the subscript ‘z’ and the word ‘perturbed’. From Equation (6.8), we easily get
$z=0$
, we omit the subscript ‘z’ and the word ‘perturbed’. From Equation (6.8), we easily get
 $$ \begin{align} \boldsymbol{\delta}_z\mathbf{e}_p=\sum_{q\in\mathcal{Y}_{k-1},\ \gamma\in\mathcal{T}(p,q)}e^{\bar z\eta(\gamma)}\epsilon(\gamma)\,\mathbf{e}_q\;, \end{align} $$
$$ \begin{align} \boldsymbol{\delta}_z\mathbf{e}_p=\sum_{q\in\mathcal{Y}_{k-1},\ \gamma\in\mathcal{T}(p,q)}e^{\bar z\eta(\gamma)}\epsilon(\gamma)\,\mathbf{e}_q\;, \end{align} $$
for
![]() $p\in \mathcal {Y}_k$
. We also have
$p\in \mathcal {Y}_k$
. We also have
 $$ \begin{gather*} \mathbf{C}^{\bullet}=\ker\boldsymbol{\Delta}_z\oplus\operatorname{im}\mathbf{d}_z\oplus\operatorname{im}\boldsymbol{\delta}_z\;,\\ \ker\boldsymbol{\Delta}_z=\ker\mathbf{D}_z=\ker\mathbf{d}_z\cap\ker\boldsymbol{\delta}_z\;,\quad \operatorname{im}\boldsymbol{\Delta}_z=\operatorname{im}\mathbf{D}_z=\operatorname{im}\mathbf{d}_z\oplus\operatorname{im}\boldsymbol{\delta}_z. \end{gather*} $$
$$ \begin{gather*} \mathbf{C}^{\bullet}=\ker\boldsymbol{\Delta}_z\oplus\operatorname{im}\mathbf{d}_z\oplus\operatorname{im}\boldsymbol{\delta}_z\;,\\ \ker\boldsymbol{\Delta}_z=\ker\mathbf{D}_z=\ker\mathbf{d}_z\cap\ker\boldsymbol{\delta}_z\;,\quad \operatorname{im}\boldsymbol{\Delta}_z=\operatorname{im}\mathbf{D}_z=\operatorname{im}\mathbf{d}_z\oplus\operatorname{im}\boldsymbol{\delta}_z. \end{gather*} $$
The orthogonal projections of
![]() $\mathbf {C}^{\bullet }$
to
$\mathbf {C}^{\bullet }$
to
![]() $\ker \boldsymbol {\Delta }_z$
,
$\ker \boldsymbol {\Delta }_z$
,
![]() $\operatorname {im}\mathbf {d}_z$
and
$\operatorname {im}\mathbf {d}_z$
and
![]() $\operatorname {im}\boldsymbol {\delta }_z$
are denoted by
$\operatorname {im}\boldsymbol {\delta }_z$
are denoted by
![]() $\boldsymbol {\Pi }_z=\boldsymbol {\Pi }^0_z$
,
$\boldsymbol {\Pi }_z=\boldsymbol {\Pi }^0_z$
,
![]() $\boldsymbol {\Pi }_z^1$
and
$\boldsymbol {\Pi }_z^1$
and
![]() $\boldsymbol {\Pi }_z^2$
, respectively. The compositions
$\boldsymbol {\Pi }_z^2$
, respectively. The compositions
![]() $\mathbf {d}_z^{-1}\boldsymbol {\Pi }_z^1$
,
$\mathbf {d}_z^{-1}\boldsymbol {\Pi }_z^1$
,
![]() $\boldsymbol {\delta }_z^{-1}\boldsymbol {\Pi }_z^2$
and
$\boldsymbol {\delta }_z^{-1}\boldsymbol {\Pi }_z^2$
and
![]() $\mathbf {D}_z^{-1}\boldsymbol {\Pi }_z^\perp $
are defined like in Section 2.1.2, and there is an obvious version of the commutative diagram of Equation (2.7).
$\mathbf {D}_z^{-1}\boldsymbol {\Pi }_z^\perp $
are defined like in Section 2.1.2, and there is an obvious version of the commutative diagram of Equation (2.7).
6.3. The small complex versus the Morse complex
Our main objects of interest are the form
![]() $\eta \in Z^1(M;\mathbb {R})$
and the Riemannian metric g; X plays an auxiliary role. As indicated in Section 6.1.5, by (b), we can choose some
$\eta \in Z^1(M;\mathbb {R})$
and the Riemannian metric g; X plays an auxiliary role. As indicated in Section 6.1.5, by (b), we can choose some
![]() $\eta \in \xi $
and g satisfying (a) and (c) (Section 1.1). Thus, unless otherwise indicated, assume from now on that X,
$\eta \in \xi $
and g satisfying (a) and (c) (Section 1.1). Thus, unless otherwise indicated, assume from now on that X,
![]() $\eta $
and g satisfy (c), besides (a) and (b). In particular,
$\eta $
and g satisfy (c), besides (a) and (b). In particular,
![]() $\mathcal {Y}=\operatorname {Zero}(\eta )$
.
$\mathcal {Y}=\operatorname {Zero}(\eta )$
.
For every
![]() $p\in \mathcal {Y}$
, consider the functions
$p\in \mathcal {Y}$
, consider the functions
![]() $h_{\eta ,p}$
,
$h_{\eta ,p}$
,
![]() $h_{X,p}$
,
$h_{X,p}$
,
![]() $h_{\eta ,p}^-$
and
$h_{\eta ,p}^-$
and
![]() $\hat h_{\eta ,p}^-$
defined in Sections 4.1, 6.1.1 and 6.2.4. By (c), we have
$\hat h_{\eta ,p}^-$
defined in Sections 4.1, 6.1.1 and 6.2.4. By (c), we have
 $$ \begin{align} h_{\eta,p} &=h_{X,p}\qquad\qquad\qquad\text{on}\quad U_p\;,\nonumber\\ h_{\eta,p}^- &=h_{\eta,p}=-\frac12|x_p^-|^2\quad \ \text{on}\quad U_p^-, \end{align} $$
$$ \begin{align} h_{\eta,p} &=h_{X,p}\qquad\qquad\qquad\text{on}\quad U_p\;,\nonumber\\ h_{\eta,p}^- &=h_{\eta,p}=-\frac12|x_p^-|^2\quad \ \text{on}\quad U_p^-, \end{align} $$
From now on, the subscripts X and
![]() $\eta $
will be dropped from the notation of these functions.
$\eta $
will be dropped from the notation of these functions.
Continuing with the notation of Section 6.2.4, let
![]() $J_z:\mathbf {C}^{\bullet }\to E_z$
be the
$J_z:\mathbf {C}^{\bullet }\to E_z$
be the
![]() $\mathbb {C}$
-linear isometry given by
$\mathbb {C}$
-linear isometry given by
![]() $J_z(\mathbf {e}_p)= e_{p,z}$
, and let
$J_z(\mathbf {e}_p)= e_{p,z}$
, and let
![]() $\Psi _z=P_{z,\mathrm { sm}}J_z:\mathbf {C}^{\bullet }\to E_{z,\mathrm {sm}}$
, which is an isomorphism for
$\Psi _z=P_{z,\mathrm { sm}}J_z:\mathbf {C}^{\bullet }\to E_{z,\mathrm {sm}}$
, which is an isomorphism for
![]() $\mu \gg 0$
(Corollary 4.9). By Proposition 4.7,
$\mu \gg 0$
(Corollary 4.9). By Proposition 4.7,
for all
![]() $\mathbf {e}\in \mathbf {C}^{\bullet }$
. Using polarization (see, e.g., [Reference Kato37, Section I.6.2]) and conjugation, this means that, as
$\mathbf {e}\in \mathbf {C}^{\bullet }$
. Using polarization (see, e.g., [Reference Kato37, Section I.6.2]) and conjugation, this means that, as
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Notation 6.2. Consider functions
![]() $u(z)$
and
$u(z)$
and
![]() $v(z)$
(
$v(z)$
(
![]() $z\in \mathbb {C})$
with values in Banach spaces. The notation
$z\in \mathbb {C})$
with values in Banach spaces. The notation
![]() $u(z)\asymp _0 v(z)$
(
$u(z)\asymp _0 v(z)$
(
![]() $\mu \to \pm \infty $
) means
$\mu \to \pm \infty $
) means
This notation may be used even when the Banach spaces depend on z.
Theorem 6.3 (Cf. [Reference Bismut and Zhang11, Theorem 6.11], [Reference Zhang75, Theorem 6.9], [Reference Burghelea and Haller17, Theorem 4])
For every
![]() $\tau \in \mathbb {R}$
, as
$\tau \in \mathbb {R}$
, as
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
 $$\begin{align*}\Phi_{z+\tau}\Psi_z \asymp_0\Big(\frac{\pi}{\mu+\tau/2}\Big)^{{\mathsf{N}}/2}\Big(\frac{\mu}{\pi}\Big)^{n/4}. \end{align*}$$
$$\begin{align*}\Phi_{z+\tau}\Psi_z \asymp_0\Big(\frac{\pi}{\mu+\tau/2}\Big)^{{\mathsf{N}}/2}\Big(\frac{\mu}{\pi}\Big)^{n/4}. \end{align*}$$
Proof. We adapt the proof of [Reference Zhang75, Theorem 6.9] to the case of complex parameter. For every
![]() $p\in \mathcal {Y}_k$
,
$p\in \mathcal {Y}_k$
,
 $$ \begin{align} \Phi_{z+\tau}\Psi_z\mathbf{e}_p=\sum_{q\in\mathcal{Y}_k}\mathbf{e}_q \int_{\widehat W^-_q}e^{(z+\tau)\hat h_q^-}(\hat\iota_q^-)^*P_{z,\mathrm{sm}} e_{p,z}. \end{align} $$
$$ \begin{align} \Phi_{z+\tau}\Psi_z\mathbf{e}_p=\sum_{q\in\mathcal{Y}_k}\mathbf{e}_q \int_{\widehat W^-_q}e^{(z+\tau)\hat h_q^-}(\hat\iota_q^-)^*P_{z,\mathrm{sm}} e_{p,z}. \end{align} $$
Then the result follows by checking the asymptotics of these integrals using the compactness of
![]() $\widehat W^-_q$
.
$\widehat W^-_q$
.
In the case
![]() $q=p$
, by Equation (6.11) and Corollary 4.8,
$q=p$
, by Equation (6.11) and Corollary 4.8,
 $$\begin{align*}\int_{\widehat W^-_p}e^{(z+\tau)\hat h_p^-}(\hat\iota_p^-)^*(P_{z,\mathrm{sm}}-1) e_{p,z}\asymp_00. \end{align*}$$
$$\begin{align*}\int_{\widehat W^-_p}e^{(z+\tau)\hat h_p^-}(\hat\iota_p^-)^*(P_{z,\mathrm{sm}}-1) e_{p,z}\asymp_00. \end{align*}$$
But, by Proposition 4.1 (iii) and Equations (4.8)–(4.11) and (6.10),
 $$ \begin{align} \int_{\widehat W^-_p}e^{(z+\tau)\hat h_p^-}(\hat\iota_p^-)^* e_{p,z} &=\int_{\widehat W^-_p}e^{(z+\tau)\hat h_p^-}(\hat\iota_p^-)^*\big(e^{-i\nu h_p}e_{p,\mu}\big)\nonumber\\ &=\int_{\widehat W^-_p}e^{(\mu+\tau)\hat h_p^-}(\hat\iota_p^-)^*e_{p,\mu} =\frac1{a_\mu}\Big(\int_{-2r}^{2r}\rho(x)e^{-(2\mu+\tau)x^2/2}\,dx\Big)^k \nonumber\\ &=\Big(\frac{\pi}{\mu+\tau/2}\Big)^{k/2}\Big(\frac\mu\pi\Big)^{n/4}\big(1+O\big(e^{-c\mu}\big)\big). \end{align} $$
$$ \begin{align} \int_{\widehat W^-_p}e^{(z+\tau)\hat h_p^-}(\hat\iota_p^-)^* e_{p,z} &=\int_{\widehat W^-_p}e^{(z+\tau)\hat h_p^-}(\hat\iota_p^-)^*\big(e^{-i\nu h_p}e_{p,\mu}\big)\nonumber\\ &=\int_{\widehat W^-_p}e^{(\mu+\tau)\hat h_p^-}(\hat\iota_p^-)^*e_{p,\mu} =\frac1{a_\mu}\Big(\int_{-2r}^{2r}\rho(x)e^{-(2\mu+\tau)x^2/2}\,dx\Big)^k \nonumber\\ &=\Big(\frac{\pi}{\mu+\tau/2}\Big)^{k/2}\Big(\frac\mu\pi\Big)^{n/4}\big(1+O\big(e^{-c\mu}\big)\big). \end{align} $$
(When
![]() $\tau =0$
, the last equality is the same as [Reference Zhang75, Eq. (6.30)].)
$\tau =0$
, the last equality is the same as [Reference Zhang75, Eq. (6.30)].)
For
![]() $q\ne p$
in
$q\ne p$
in
![]() $\mathcal {Y}_k$
, since
$\mathcal {Y}_k$
, since
![]() $e_{p,z}=0$
on
$e_{p,z}=0$
on
![]() $\overline {W^-_q}$
because
$\overline {W^-_q}$
because
![]() $U_p\cap \overline {W^-_q}=\emptyset $
(Section 6.1.6), like in the previous case, we get
$U_p\cap \overline {W^-_q}=\emptyset $
(Section 6.1.6), like in the previous case, we get
 $$\begin{align*}\int_{\widehat W^-_q}e^{(z+\tau)\hat h_q^-}(\hat\iota_q^-)^*P_{z,\mathrm{sm}} e_{p,z}\asymp_00. \; \end{align*}$$
$$\begin{align*}\int_{\widehat W^-_q}e^{(z+\tau)\hat h_q^-}(\hat\iota_q^-)^*P_{z,\mathrm{sm}} e_{p,z}\asymp_00. \; \end{align*}$$
Corollary 6.4. For every
![]() $\tau \in \mathbb {R}$
, if
$\tau \in \mathbb {R}$
, if
![]() $\mu \gg 0$
, then
$\mu \gg 0$
, then
![]() $\Phi _{z+\tau }:E_{z,\mathrm {sm}}\to \mathbf {C}^{\bullet }$
is a linearFootnote 7 isomorphism.
$\Phi _{z+\tau }:E_{z,\mathrm {sm}}\to \mathbf {C}^{\bullet }$
is a linearFootnote 7 isomorphism.
Remark 6.5. The argument of the proof of Theorem 6.3 shows that
So
![]() $\Phi _z:E_z\to \mathbf {C}^{\bullet }$
is an isomorphism for
$\Phi _z:E_z\to \mathbf {C}^{\bullet }$
is an isomorphism for
![]() $\mu \gg 0$
(see also [Reference Burghelea and Haller20, Lemma 5.2]).
$\mu \gg 0$
(see also [Reference Burghelea and Haller20, Lemma 5.2]).
Let
Corollary 6.6. Consider
![]() $\widetilde \Psi _z^*:E_{z,\mathrm {sm}}\to \mathbf {C}^{\bullet }$
. As
$\widetilde \Psi _z^*:E_{z,\mathrm {sm}}\to \mathbf {C}^{\bullet }$
. As
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Proof. This is a direct consequence of Equation (6.12).
Corollary 6.7. For any
![]() $\tau \in \mathbb {R}$
, consider
$\tau \in \mathbb {R}$
, consider
![]() $\Phi _{z+\tau }:E_{z,\mathrm {sm}}\to \mathbf {C}^{\bullet }$
. As
$\Phi _{z+\tau }:E_{z,\mathrm {sm}}\to \mathbf {C}^{\bullet }$
. As
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
 $$\begin{align*}\Phi_{z+\tau}\widetilde\Psi_z\asymp_0\Big(\frac{\mu}{\mu+\tau/2}\Big)^{{\mathsf{N}}/2}\;,\quad \widetilde\Psi_z\Phi_{z+\tau}\asymp_0\Big(\frac{\mu}{\mu+\tau/2}\Big)^{{\mathsf{N}}/2}. \end{align*}$$
$$\begin{align*}\Phi_{z+\tau}\widetilde\Psi_z\asymp_0\Big(\frac{\mu}{\mu+\tau/2}\Big)^{{\mathsf{N}}/2}\;,\quad \widetilde\Psi_z\Phi_{z+\tau}\asymp_0\Big(\frac{\mu}{\mu+\tau/2}\Big)^{{\mathsf{N}}/2}. \end{align*}$$
Proof. The first relation is a restatement of Theorem 6.3. The second relation follows by conjugating the first one by
![]() $\widetilde \Psi _z$
and using Corollary 6.6.
$\widetilde \Psi _z$
and using Corollary 6.6.
Corollary 6.8. As
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
![]() $\widetilde \Psi _z^{-1}\asymp _0\Phi _z$
on
$\widetilde \Psi _z^{-1}\asymp _0\Phi _z$
on
![]() $E_{z,\mathrm {sm}}$
.
$E_{z,\mathrm {sm}}$
.
Proof. By Corollaries 6.6 and 6.7, on
![]() $E_{z,\mathrm {sm}}$
,
$E_{z,\mathrm {sm}}$
,
In the rest of this section, consider
![]() $\Phi _z:E_{z,\mathrm {sm}}\to \mathbf {C}^{\bullet }$
unless otherwise indicated.
$\Phi _z:E_{z,\mathrm {sm}}\to \mathbf {C}^{\bullet }$
unless otherwise indicated.
Corollary 6.9. As
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Proof. We show the first relation, the other one being similar. By Corollaries 6.6 and 6.8, on
![]() $E_{z,\mathrm {sm}}$
,
$E_{z,\mathrm {sm}}$
,
Corollary 6.10. As
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Proof. By Corollaries 6.7 and 6.9,
Corollary 6.11. For every
![]() $\tau \in \mathbb {R}$
, as
$\tau \in \mathbb {R}$
, as
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
 $$\begin{align*}\Phi_{z+\tau}P_{z+\tau,\mathrm{sm}}\widetilde\Psi_z\asymp_0\Big(\frac{\mu}{\mu+\tau/2}\Big)^{{\mathsf{N}}/2} +O\big(\mu^{-1}\big). \end{align*}$$
$$\begin{align*}\Phi_{z+\tau}P_{z+\tau,\mathrm{sm}}\widetilde\Psi_z\asymp_0\Big(\frac{\mu}{\mu+\tau/2}\Big)^{{\mathsf{N}}/2} +O\big(\mu^{-1}\big). \end{align*}$$
Proof. By Corollaries 6.7, 6.6 and 6.9 and Proposition 4.19,
 $$ \begin{align*} \Phi_{z+\tau}P_{z+\tau,\mathrm{sm}}\widetilde\Psi_z &=\Phi_{z+\tau}(P_{z+\tau,\mathrm{sm}}-P_{z,\mathrm{sm}})\widetilde\Psi_z+\Phi_{z+\tau}\widetilde\Psi_z\\ &\asymp_0 O\big(\mu^{-1}\big)+\Big(\frac{\mu}{\mu+\tau/2}\Big)^{{\mathsf{N}}/2}. \; \end{align*} $$
$$ \begin{align*} \Phi_{z+\tau}P_{z+\tau,\mathrm{sm}}\widetilde\Psi_z &=\Phi_{z+\tau}(P_{z+\tau,\mathrm{sm}}-P_{z,\mathrm{sm}})\widetilde\Psi_z+\Phi_{z+\tau}\widetilde\Psi_z\\ &\asymp_0 O\big(\mu^{-1}\big)+\Big(\frac{\mu}{\mu+\tau/2}\Big)^{{\mathsf{N}}/2}. \; \end{align*} $$
Corollary 6.12. As
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Proof. By Theorem 4.10 and Corollary 6.7,
Now, taking adjoints and using Corollaries 6.6, 6.9 and 6.10, we obtain
Let
![]() $\widetilde {\boldsymbol {\Pi }}_z=\widetilde {\boldsymbol {\Pi }}^0_z$
,
$\widetilde {\boldsymbol {\Pi }}_z=\widetilde {\boldsymbol {\Pi }}^0_z$
,
![]() $\widetilde {\boldsymbol {\Pi }}^1_z$
and
$\widetilde {\boldsymbol {\Pi }}^1_z$
and
![]() $\widetilde {\boldsymbol {\Pi }}^2_z$
be the orthogonal projections of
$\widetilde {\boldsymbol {\Pi }}^2_z$
be the orthogonal projections of
![]() $\mathbf {C}^{\bullet }$
to
$\mathbf {C}^{\bullet }$
to
![]() $\Phi _z(\ker \Delta _{z,\mathrm {sm}})$
,
$\Phi _z(\ker \Delta _{z,\mathrm {sm}})$
,
![]() $\Phi _z(\operatorname {im} d_{z,\mathrm {sm}})$
and
$\Phi _z(\operatorname {im} d_{z,\mathrm {sm}})$
and
![]() $\Phi _z(\operatorname {im}\delta _{z,\mathrm {sm}})$
, respectively. Note that
$\Phi _z(\operatorname {im}\delta _{z,\mathrm {sm}})$
, respectively. Note that
![]() $\widetilde {\boldsymbol {\Pi }}^1_z=\widetilde {\boldsymbol {\Pi }}^1_z\boldsymbol {\Pi }^1_z$
.
$\widetilde {\boldsymbol {\Pi }}^1_z=\widetilde {\boldsymbol {\Pi }}^1_z\boldsymbol {\Pi }^1_z$
.
Corollary 6.13. For
![]() $j=0,1,2$
, as
$j=0,1,2$
, as
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Proof. We only prove the case of
![]() $\widetilde {\boldsymbol {\Pi }}^2_z$
, the other cases being similar. Let
$\widetilde {\boldsymbol {\Pi }}^2_z$
, the other cases being similar. Let
![]() $\alpha _{z,1},\dots ,\alpha _{z,p_z}$
be an orthonormal frame of
$\alpha _{z,1},\dots ,\alpha _{z,p_z}$
be an orthonormal frame of
![]() $\delta _z(E_{z,\mathrm {sm}}^{k+1})$
. So
$\delta _z(E_{z,\mathrm {sm}}^{k+1})$
. So
![]() $\Phi _z\alpha _{z,1},\dots ,\Phi _z\alpha _{z,p_z}$
is a base of
$\Phi _z\alpha _{z,1},\dots ,\Phi _z\alpha _{z,p_z}$
is a base of
![]() $\Phi _z\delta _z(E_{z,\mathrm {sm}}^{k+1})$
for
$\Phi _z\delta _z(E_{z,\mathrm {sm}}^{k+1})$
for
![]() $\mu \gg 0$
by Corollary 6.4. Applying the Gram–Schmidt process to this base, we get an orthonormal base
$\mu \gg 0$
by Corollary 6.4. Applying the Gram–Schmidt process to this base, we get an orthonormal base
![]() $\mathbf {f}_{z,1},\dots ,\mathbf {f}_{z,p_z}$
of
$\mathbf {f}_{z,1},\dots ,\mathbf {f}_{z,p_z}$
of
![]() $\Phi _z\delta _z(E_{z,\mathrm {sm}}^{k+1})$
. By Corollary 6.9,
$\Phi _z\delta _z(E_{z,\mathrm {sm}}^{k+1})$
. By Corollary 6.9,
for
![]() $1\le a,b\le p_z$
. So
$1\le a,b\le p_z$
. So
Hence, by Corollary 6.9, for any
![]() $\beta \in E_{z,\mathrm {sm}}^k$
,
$\beta \in E_{z,\mathrm {sm}}^k$
,
 $$ \begin{align*} \widetilde{\boldsymbol{\Pi}}^2_z\Phi_z\beta&=\sum_{a=1}^{p_z}\langle\Phi_z\beta,\mathbf{f}_{z,a}\rangle\mathbf{f}_{z,a} \asymp_0\Big(\frac\mu\pi\Big)^{k-n/2}\sum_{a=1}^{p_z}\langle\Phi_z\beta,\Phi_z\alpha_{z,a}\rangle\Phi_z\alpha_{z,a}\\ &\asymp_0\sum_{a=1}^m\langle\beta,\alpha_{z,a}\rangle\Phi_z\alpha_{z,a} =\Phi_z\Pi^2_{z,\mathrm{sm}}\beta. \end{align*} $$
$$ \begin{align*} \widetilde{\boldsymbol{\Pi}}^2_z\Phi_z\beta&=\sum_{a=1}^{p_z}\langle\Phi_z\beta,\mathbf{f}_{z,a}\rangle\mathbf{f}_{z,a} \asymp_0\Big(\frac\mu\pi\Big)^{k-n/2}\sum_{a=1}^{p_z}\langle\Phi_z\beta,\Phi_z\alpha_{z,a}\rangle\Phi_z\alpha_{z,a}\\ &\asymp_0\sum_{a=1}^m\langle\beta,\alpha_{z,a}\rangle\Phi_z\alpha_{z,a} =\Phi_z\Pi^2_{z,\mathrm{sm}}\beta. \end{align*} $$
This shows the first relation of the statement because
![]() $\dim E_{z,\mathrm {sm}}^k<\infty $
. Then the other stated relations follow using Corollaries 6.6, 6.7 and 6.9.
$\dim E_{z,\mathrm {sm}}^k<\infty $
. Then the other stated relations follow using Corollaries 6.6, 6.7 and 6.9.
According to Corollary 6.4, in the following corollaries, we take
![]() $\mu \gg 0$
so that
$\mu \gg 0$
so that
![]() $\Phi _z:E_{z,\mathrm {sm}}\to \mathbf {C}^{\bullet }$
is an isomorphism.
$\Phi _z:E_{z,\mathrm {sm}}\to \mathbf {C}^{\bullet }$
is an isomorphism.
Corollary 6.14. As
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Proof. By Corollary 6.9, for
![]() $\mathbf {e}\in \mathbf {C}^k$
with
$\mathbf {e}\in \mathbf {C}^k$
with
![]() $\|\mathbf {e}\|=1$
,
$\|\mathbf {e}\|=1$
,
yielding the first stated relation. The second one has a similar proof.
Corollary 6.15. As
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Proof. By Corollaries 6.9 and 6.14,
Corollary 6.16. We have
![]() $\widetilde {\boldsymbol {\Pi }}^1_z=\boldsymbol {\Pi }^1_z$
for
$\widetilde {\boldsymbol {\Pi }}^1_z=\boldsymbol {\Pi }^1_z$
for
![]() $\mu \gg 0$
, and
$\mu \gg 0$
, and
![]() $\widetilde {\boldsymbol {\Pi }}^2_z\asymp _0\boldsymbol {\Pi }^2_z$
as
$\widetilde {\boldsymbol {\Pi }}^2_z\asymp _0\boldsymbol {\Pi }^2_z$
as
![]() $\mu \to +\infty $
.
$\mu \to +\infty $
.
Proof. Since
![]() $\Phi _z(\operatorname {im} d_{z,\mathrm {sm}})=\operatorname {im}\mathbf {d}_z$
for
$\Phi _z(\operatorname {im} d_{z,\mathrm {sm}})=\operatorname {im}\mathbf {d}_z$
for
![]() $\mu \gg 0$
, we get
$\mu \gg 0$
, we get
![]() $\widetilde {\boldsymbol {\Pi }}^1_z=\boldsymbol {\Pi }^1_z$
.
$\widetilde {\boldsymbol {\Pi }}^1_z=\boldsymbol {\Pi }^1_z$
.
To prove
![]() $\widetilde {\boldsymbol {\Pi }}^2_z\asymp _0\boldsymbol {\Pi }^2_z$
as
$\widetilde {\boldsymbol {\Pi }}^2_z\asymp _0\boldsymbol {\Pi }^2_z$
as
![]() $\mu \to +\infty $
, consider the notation of the proof of Corollary 6.13. We have
$\mu \to +\infty $
, consider the notation of the proof of Corollary 6.13. We have
![]() $\alpha _{z,a}=\delta _z\beta _{z,a}$
(
$\alpha _{z,a}=\delta _z\beta _{z,a}$
(
![]() $a=1,\dots ,p_z$
) for some base
$a=1,\dots ,p_z$
) for some base
![]() $\beta _{z,1},\dots ,\beta _{z,p_z}$
of
$\beta _{z,1},\dots ,\beta _{z,p_z}$
of
![]() $\operatorname {im} d_{z,\mathrm {sm},k}$
. Hence, by Corollaries 6.7, 6.9 and 6.12,
$\operatorname {im} d_{z,\mathrm {sm},k}$
. Hence, by Corollaries 6.7, 6.9 and 6.12,
and
![]() $\boldsymbol {\delta }_z\Phi _z\beta _{z,1},\dots ,\boldsymbol {\delta }_z\Phi _z\beta _{z,p_z}$
is a base of
$\boldsymbol {\delta }_z\Phi _z\beta _{z,1},\dots ,\boldsymbol {\delta }_z\Phi _z\beta _{z,p_z}$
is a base of
![]() $\operatorname {im}\boldsymbol {\delta }_{z,k+1}$
. Applying the Gram–Schmidt process to this base, we get an orthonormal base
$\operatorname {im}\boldsymbol {\delta }_{z,k+1}$
. Applying the Gram–Schmidt process to this base, we get an orthonormal base
![]() $\mathbf {g}_{z,1},\dots ,\mathbf {g}_{z,p_z}$
of
$\mathbf {g}_{z,1},\dots ,\mathbf {g}_{z,p_z}$
of
![]() $\operatorname {im}\boldsymbol {\delta }_{z,k+1}$
satisfying
$\operatorname {im}\boldsymbol {\delta }_{z,k+1}$
satisfying
![]() $\mathbf {g}_{z,a}\asymp _0\mathbf {f}_{z,a}$
by Equation (6.15). Then, for any
$\mathbf {g}_{z,a}\asymp _0\mathbf {f}_{z,a}$
by Equation (6.15). Then, for any
![]() $\mathbf {e}\in \mathbf {C}^k$
with
$\mathbf {e}\in \mathbf {C}^k$
with
![]() $\|\mathbf {e}\|=1$
,
$\|\mathbf {e}\|=1$
,
 $$\begin{align*}\widetilde{\boldsymbol{\Pi}}^2_z\mathbf{e}=\sum_{a=1}^{p_z}\langle\mathbf{e},\mathbf{g}_{z,a}\rangle\mathbf{g}_{z,a} \asymp_0\sum_{a=1}^{p_z}\langle\mathbf{e},\mathbf{f}_{z,a}\rangle\mathbf{f}_{z,a} =\boldsymbol{\Pi}^2_z\mathbf{e}. \; \end{align*}$$
$$\begin{align*}\widetilde{\boldsymbol{\Pi}}^2_z\mathbf{e}=\sum_{a=1}^{p_z}\langle\mathbf{e},\mathbf{g}_{z,a}\rangle\mathbf{g}_{z,a} \asymp_0\sum_{a=1}^{p_z}\langle\mathbf{e},\mathbf{f}_{z,a}\rangle\mathbf{f}_{z,a} =\boldsymbol{\Pi}^2_z\mathbf{e}. \; \end{align*}$$
Corollary 6.17. We have
Proof. The first equality follows like the first relation of Corollary 6.12, using
![]() $\Phi _z^{-1}$
instead of
$\Phi _z^{-1}$
instead of
![]() $\widetilde \Psi _z$
. To prove the second one, take any
$\widetilde \Psi _z$
. To prove the second one, take any
![]() $\alpha \in \operatorname {im} d_{z,\mathrm {sm}}$
. Since
$\alpha \in \operatorname {im} d_{z,\mathrm {sm}}$
. Since
with
![]() $\Pi ^2_{z,\mathrm {sm}}\Phi _z^{-1}\mathbf {d}_z^{-1}\Phi _z\alpha \in \operatorname {im}\delta _{z,\mathrm {sm}}$
, we obtain
$\Pi ^2_{z,\mathrm {sm}}\Phi _z^{-1}\mathbf {d}_z^{-1}\Phi _z\alpha \in \operatorname {im}\delta _{z,\mathrm {sm}}$
, we obtain
6.4. Derivatives of some homomorphisms
Theorem 6.18. As
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Proof. By Equation (6.13),
 $$ \begin{align} \partial_z(\Phi_z\Psi_z\mathbf{e}_p)= \sum_{q\in\mathcal{Y}_k}\mathbf{e}_q \bigg(\int_{\widehat W^-_q}\hat h_q^-e^{z\hat h_q^-}(\hat\iota_q^-)^*P_{z,\mathrm{sm}} e_{p,z} +\int_{\widehat W^-_q}e^{z\hat h_q^-}(\hat\iota_q^-)^*\partial_z(P_{z,\mathrm{sm}} e_{p,z})\bigg)\;, \end{align} $$
$$ \begin{align} \partial_z(\Phi_z\Psi_z\mathbf{e}_p)= \sum_{q\in\mathcal{Y}_k}\mathbf{e}_q \bigg(\int_{\widehat W^-_q}\hat h_q^-e^{z\hat h_q^-}(\hat\iota_q^-)^*P_{z,\mathrm{sm}} e_{p,z} +\int_{\widehat W^-_q}e^{z\hat h_q^-}(\hat\iota_q^-)^*\partial_z(P_{z,\mathrm{sm}} e_{p,z})\bigg)\;, \end{align} $$
for every
![]() $p\in \mathcal {Y}_k$
(
$p\in \mathcal {Y}_k$
(
![]() $k=0,\dots ,n$
). We estimate each of these integrals.
$k=0,\dots ,n$
). We estimate each of these integrals.
Like in the proof of Theorem 6.3, we get, for any
![]() $q\ne p$
in
$q\ne p$
in
![]() $\mathcal {Y}_k$
,
$\mathcal {Y}_k$
,
 $$ \begin{align} \int_{\widehat W^-_p}\hat h_p^-e^{z\hat h_p^-}(\hat\iota_p^-)^*(P_{z,\mathrm{sm}}-1) e_{p,z} &\asymp_00\;, \end{align} $$
$$ \begin{align} \int_{\widehat W^-_p}\hat h_p^-e^{z\hat h_p^-}(\hat\iota_p^-)^*(P_{z,\mathrm{sm}}-1) e_{p,z} &\asymp_00\;, \end{align} $$
 $$ \begin{align} \int_{\widehat W^-_q}\hat h_q^-e^{z\hat h_q^-}(\hat\iota_q^-)^*P_{z,\mathrm{sm}} e_{p,z} &\asymp_00. \end{align} $$
$$ \begin{align} \int_{\widehat W^-_q}\hat h_q^-e^{z\hat h_q^-}(\hat\iota_q^-)^*P_{z,\mathrm{sm}} e_{p,z} &\asymp_00. \end{align} $$
Moreover, by Proposition 4.1 (iii) and Equations (4.8)–(4.11) and (4.30),
 $$ \begin{align} \int_{\widehat W^-_p}\hat h_p^-e^{z\hat h_p^-}(\hat\iota_p^-)^*e_{p,z} & =-\frac k{2a_\mu}\bigg(\int_{-2r}^{2r}\rho(x)e^{-\mu x^2/2}\,dx\bigg)^{k-1} \int_{-2r}^{2r}\rho(x)x^2e^{-\mu x^2/2}\,dx \nonumber\\ &=-\frac k{4\mu}\Big(\frac\pi\mu\Big)^{\frac k2-\frac n4}+O(e^{-c\mu}). \end{align} $$
$$ \begin{align} \int_{\widehat W^-_p}\hat h_p^-e^{z\hat h_p^-}(\hat\iota_p^-)^*e_{p,z} & =-\frac k{2a_\mu}\bigg(\int_{-2r}^{2r}\rho(x)e^{-\mu x^2/2}\,dx\bigg)^{k-1} \int_{-2r}^{2r}\rho(x)x^2e^{-\mu x^2/2}\,dx \nonumber\\ &=-\frac k{4\mu}\Big(\frac\pi\mu\Big)^{\frac k2-\frac n4}+O(e^{-c\mu}). \end{align} $$
On the other hand, by Equation (6.11) and Proposition 4.26,
 $$\begin{align*}\int_{\widehat W^-_q}e^{z\hat h_q^-}(\hat\iota_q^-)^*\partial_z(P_{z,\mathrm{sm}}e_{p,z}-e_{p,z}) \asymp_00\;, \end{align*}$$
$$\begin{align*}\int_{\widehat W^-_q}e^{z\hat h_q^-}(\hat\iota_q^-)^*\partial_z(P_{z,\mathrm{sm}}e_{p,z}-e_{p,z}) \asymp_00\;, \end{align*}$$
for all
![]() $q\in \mathcal {Y}_k$
. In the case
$q\in \mathcal {Y}_k$
. In the case
![]() $q=p$
, by Equation (6.14) and Lemma 4.24,
$q=p$
, by Equation (6.14) and Lemma 4.24,
 $$ \begin{align} \int_{\widehat W^-_p}e^{z\hat h_p^-}(\hat\iota_p^-)^*\partial_ze_{p,z} &=\Big(\frac n{8\mu}+O(e^{-c\mu})\Big)\int_{\widehat W^-_p}e^{z\hat h_p^-}(\hat\iota_p^-)^*e_{p,z} \nonumber\\ &=\Big(\frac n{8\mu}+O(e^{-c\mu})\Big)\bigg(\Big(\frac \pi\mu\Big)^{\frac k2-\frac n4}+O(e^{-c\mu})\bigg)\nonumber\\ & =\frac n{8\mu}\Big(\frac \pi\mu\Big)^{\frac k2-\frac n4}+O(e^{-c\mu}). \end{align} $$
$$ \begin{align} \int_{\widehat W^-_p}e^{z\hat h_p^-}(\hat\iota_p^-)^*\partial_ze_{p,z} &=\Big(\frac n{8\mu}+O(e^{-c\mu})\Big)\int_{\widehat W^-_p}e^{z\hat h_p^-}(\hat\iota_p^-)^*e_{p,z} \nonumber\\ &=\Big(\frac n{8\mu}+O(e^{-c\mu})\Big)\bigg(\Big(\frac \pi\mu\Big)^{\frac k2-\frac n4}+O(e^{-c\mu})\bigg)\nonumber\\ & =\frac n{8\mu}\Big(\frac \pi\mu\Big)^{\frac k2-\frac n4}+O(e^{-c\mu}). \end{align} $$
In the case
![]() $q\ne p$
, using Lemma 4.24 and arguing again like in the proof of Theorem 6.3, we get
$q\ne p$
, using Lemma 4.24 and arguing again like in the proof of Theorem 6.3, we get
 $$ \begin{align} \int_{\widehat W^-_q}e^{z\hat h_q^-}(\hat\iota_q^-)^*\partial_ze_{p,z}\asymp_00\quad(\mu\to+\infty). \end{align} $$
$$ \begin{align} \int_{\widehat W^-_q}e^{z\hat h_q^-}(\hat\iota_q^-)^*\partial_ze_{p,z}\asymp_00\quad(\mu\to+\infty). \end{align} $$
Now, the result for
![]() $\partial _z$
follows from Equations (6.16)–(6.19), (6.20) and (6.21).
$\partial _z$
follows from Equations (6.16)–(6.19), (6.20) and (6.21).
If we consider
![]() $\partial _{\bar z}$
, the proof has to be modified as follows. In the analogue of Equation (6.16), the first term of the right-hand side must be removed. In the analogue of Lemma 4.24, we get
$\partial _{\bar z}$
, the proof has to be modified as follows. In the analogue of Equation (6.16), the first term of the right-hand side must be removed. In the analogue of Lemma 4.24, we get
![]() $|x_p^-|^2$
instead of
$|x_p^-|^2$
instead of
![]() $|x_p^+|^2$
by the right-hand side of Equations (4.1) and (4.33). So
$|x_p^+|^2$
by the right-hand side of Equations (4.1) and (4.33). So
![]() $\partial _{\bar z}(\Phi _z\Psi _z)$
has the same final expression as
$\partial _{\bar z}(\Phi _z\Psi _z)$
has the same final expression as
![]() $\partial _z(\Phi _z\Psi _z)$
by Equation (6.19).
$\partial _z(\Phi _z\Psi _z)$
by Equation (6.19).
Theorem 6.19. As
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Proof. We only show the case of
![]() $\partial _z$
. Consider
$\partial _z$
. Consider
![]() $P_{z,\mathrm {sm}}:E_z\to E_{z,\mathrm {sm}}$
, whose adjoint is
$P_{z,\mathrm {sm}}:E_z\to E_{z,\mathrm {sm}}$
, whose adjoint is
![]() $P_z:E_{z,\mathrm {sm}}\to E_z$
. Then, since
$P_z:E_{z,\mathrm {sm}}\to E_z$
. Then, since
![]() $J_z:\mathbf {C}^{\bullet }\to E_z$
is an isometry,
$J_z:\mathbf {C}^{\bullet }\to E_z$
is an isometry,
It follows that, for every
![]() $p\in \mathcal {Y}_k$
(
$p\in \mathcal {Y}_k$
(
![]() $k=0,\dots ,n$
),
$k=0,\dots ,n$
),
Therefore,
 $$ \begin{align*} & \partial_z(\Psi_z^*\Psi_z)\mathbf{e}_p\\ &\quad =\sum_{q\in\mathcal{Y}_k}\big(\langle\partial_z(P_{z,\mathrm{sm}})e_{p,z},e_{q,z}\rangle +\langle P_{z,\mathrm{sm}}\partial_z(e_{p,z}),e_{q,z}\rangle +\langle P_{z,\mathrm{sm}}e_{p,z},\partial_{\bar z}(e_{q,z})\rangle\big)\mathbf{e}_q. \end{align*} $$
$$ \begin{align*} & \partial_z(\Psi_z^*\Psi_z)\mathbf{e}_p\\ &\quad =\sum_{q\in\mathcal{Y}_k}\big(\langle\partial_z(P_{z,\mathrm{sm}})e_{p,z},e_{q,z}\rangle +\langle P_{z,\mathrm{sm}}\partial_z(e_{p,z}),e_{q,z}\rangle +\langle P_{z,\mathrm{sm}}e_{p,z},\partial_{\bar z}(e_{q,z})\rangle\big)\mathbf{e}_q. \end{align*} $$
Then, by Propositions 4.19 and 4.23, Lemma 4.24 and its analogue for
![]() $\partial _{\bar z}$
,
$\partial _{\bar z}$
,
 $$ \begin{align*} \partial_z(\Psi_z^*\Psi_z)\mathbf{e}_p &=O\big(\mu^{-1}\big)+\Big(\frac n{8\mu}-\frac12\big\langle|x_p^+|^2e_{p,z},e_{p,z}\big\rangle\Big)\mathbf{e}_p +O\big(e^{-c\mu}\big)\\ &=\Big(\frac n{8\mu}-\frac12\big\langle|x_p^+|^2e_{p,z},e_{p,z}\big\rangle\Big)\mathbf{e}_p+O\big(\mu^{-1}\big). \end{align*} $$
$$ \begin{align*} \partial_z(\Psi_z^*\Psi_z)\mathbf{e}_p &=O\big(\mu^{-1}\big)+\Big(\frac n{8\mu}-\frac12\big\langle|x_p^+|^2e_{p,z},e_{p,z}\big\rangle\Big)\mathbf{e}_p +O\big(e^{-c\mu}\big)\\ &=\Big(\frac n{8\mu}-\frac12\big\langle|x_p^+|^2e_{p,z},e_{p,z}\big\rangle\Big)\mathbf{e}_p+O\big(\mu^{-1}\big). \end{align*} $$
But, by Equations (4.11) and (4.30),
 $$ \begin{align*} \big\langle|x_p|^2e_{p,z},e_{p,z}\big\rangle &=\Big(\int_{-2r}^{2r}\rho(x)^2e^{-\mu x^2}\,dx\Big)^{n-1}(n-k)\int_{-2r}^{2r}y^2\rho(y)^2e^{-\mu y^2}\,dy\\ &=\frac{n-k}{2\mu}\Big(\frac\pi\mu\Big)^{\frac n2}+O\big(e^{-c\mu}\big). \end{align*} $$
$$ \begin{align*} \big\langle|x_p|^2e_{p,z},e_{p,z}\big\rangle &=\Big(\int_{-2r}^{2r}\rho(x)^2e^{-\mu x^2}\,dx\Big)^{n-1}(n-k)\int_{-2r}^{2r}y^2\rho(y)^2e^{-\mu y^2}\,dy\\ &=\frac{n-k}{2\mu}\Big(\frac\pi\mu\Big)^{\frac n2}+O\big(e^{-c\mu}\big). \end{align*} $$
Hence,
yielding the stated expression for
![]() $\partial _z\big (\Psi _z^*\Psi _z)$
.
$\partial _z\big (\Psi _z^*\Psi _z)$
.
Now, arguing like in the proof of Equation (4.27) and using Equation (6.12), we get
 $$ \begin{align*} \partial_z\big((\Psi_z^*\Psi_z)^{-1}\big) &=-(\Psi_z^*\Psi_z)^{-1}\partial_z(\Psi_z^*\Psi_z)(\Psi_z^*\Psi_z)^{-1}\\ &=-\big(1+O\big(e^{-c\mu}\big)\big)O\big(\mu^{-1}\big)\big(1+O\big(e^{-c\mu}\big)\big) =O\big(\mu^{-1}\big). \; \end{align*} $$
$$ \begin{align*} \partial_z\big((\Psi_z^*\Psi_z)^{-1}\big) &=-(\Psi_z^*\Psi_z)^{-1}\partial_z(\Psi_z^*\Psi_z)(\Psi_z^*\Psi_z)^{-1}\\ &=-\big(1+O\big(e^{-c\mu}\big)\big)O\big(\mu^{-1}\big)\big(1+O\big(e^{-c\mu}\big)\big) =O\big(\mu^{-1}\big). \; \end{align*} $$
7. Asymptotics of the large zeta invariant
7.1. Preliminaries on Quillen metrics
7.1.1. Case of a finite-dimensional complex
All vector spaces considered here are over
![]() $\mathbb {C}$
. For a line
$\mathbb {C}$
. For a line
![]() $\lambda $
, its dual
$\lambda $
, its dual
![]() $\lambda ^*$
is also denoted by
$\lambda ^*$
is also denoted by
![]() $\lambda ^{-1}$
. For a vector space V of finite dimension, recall that
$\lambda ^{-1}$
. For a vector space V of finite dimension, recall that
![]() $\det V=\bigwedge ^{\dim V}V$
. For a graded vector space
$\det V=\bigwedge ^{\dim V}V$
. For a graded vector space
![]() $V^{\bullet }$
of finite dimension, let
$V^{\bullet }$
of finite dimension, let
![]() $\det V^{\bullet }=\bigotimes _k(\det V^k)^{(-1)^k}$
.
$\det V^{\bullet }=\bigotimes _k(\det V^k)^{(-1)^k}$
.
Now, consider a finite-dimensional cochain complex
![]() $(V^{\bullet },\partial )$
, whose cohomology is denoted by
$(V^{\bullet },\partial )$
, whose cohomology is denoted by
![]() $H^{\bullet }(V)$
. Then there is a canonical isomorphism [Reference Knudsen and Mumford38], [Reference Bismut, Gillet and Soulé8, Section 1 a)]
$H^{\bullet }(V)$
. Then there is a canonical isomorphism [Reference Knudsen and Mumford38], [Reference Bismut, Gillet and Soulé8, Section 1 a)]
Given a Hermitian metric on
![]() $V^{\bullet }$
so that the homogeneous components
$V^{\bullet }$
so that the homogeneous components
![]() $V^k$
are orthogonal one another, the corresponding norm
$V^k$
are orthogonal one another, the corresponding norm
![]() $\|\ \|_{V^{\bullet }}$
on
$\|\ \|_{V^{\bullet }}$
on
![]() $V^{\bullet }$
induces a metric
$V^{\bullet }$
induces a metric
![]() $\|\ \|_{\det V^{\bullet }}$
on
$\|\ \|_{\det V^{\bullet }}$
on
![]() $\det V^{\bullet }$
, which corresponds to a metric
$\det V^{\bullet }$
, which corresponds to a metric
![]() $\|\ \|_{\det H^{\bullet }(V)}$
on
$\|\ \|_{\det H^{\bullet }(V)}$
on
![]() $\det H^{\bullet }(V)$
via Equation (7.1).
$\det H^{\bullet }(V)$
via Equation (7.1).
On the other hand, consider the induced Laplacian,
![]() $\square =(\partial +\partial ^*)^2=\partial \partial ^*+\partial ^*\partial $
, whose kernel is a graded vector subspace
$\square =(\partial +\partial ^*)^2=\partial \partial ^*+\partial ^*\partial $
, whose kernel is a graded vector subspace
![]() $\mathcal {H}^{\bullet }$
. Then finite-dimensional Hodge theory gives an isomorphism
$\mathcal {H}^{\bullet }$
. Then finite-dimensional Hodge theory gives an isomorphism
![]() $H^{\bullet }(V)\cong \mathcal {H}^{\bullet }$
, which induces an isomorphism
$H^{\bullet }(V)\cong \mathcal {H}^{\bullet }$
, which induces an isomorphism
The restriction of
![]() $\|\ \|_{V^{\bullet }}$
to
$\|\ \|_{V^{\bullet }}$
to
![]() $\mathcal {H}^{\bullet }$
induces a metric
$\mathcal {H}^{\bullet }$
induces a metric
![]() $\|\ \|_{\det \mathcal {H}^{\bullet }}$
on
$\|\ \|_{\det \mathcal {H}^{\bullet }}$
on
![]() $\det \mathcal {H}^{\bullet }$
, which corresponds to another metric
$\det \mathcal {H}^{\bullet }$
, which corresponds to another metric
![]() $|\ |_{\det H^{\bullet }(V)}$
on
$|\ |_{\det H^{\bullet }(V)}$
on
![]() $\det H^{\bullet }(V)$
via Equation (7.2).
$\det H^{\bullet }(V)$
via Equation (7.2).
Let
![]() $\square '$
denote the restriction
$\square '$
denote the restriction
![]() $\square :\operatorname {im}\square \to \operatorname {im}\square $
. For
$\square :\operatorname {im}\square \to \operatorname {im}\square $
. For
![]() $s\in \mathbb {C}$
, let
$s\in \mathbb {C}$
, let
This defines a holomorphic function on
![]() $\mathbb {C}$
. Then the above metrics on
$\mathbb {C}$
. Then the above metrics on
![]() $\det H^{\bullet }(V)$
satisfy [Reference Bismut, Gillet and Soulé8, Proposition 1.5], [Reference Bismut, Zhang and Laudenbach10, Theorem 1.1], [Reference Bismut and Zhang11, Theorem 1.4]
$\det H^{\bullet }(V)$
satisfy [Reference Bismut, Gillet and Soulé8, Proposition 1.5], [Reference Bismut, Zhang and Laudenbach10, Theorem 1.1], [Reference Bismut and Zhang11, Theorem 1.4]
If
![]() $ H^{\bullet }(V)=0$
, then
$ H^{\bullet }(V)=0$
, then
![]() $\det H^{\bullet }(V)\equiv \mathbb {C}$
is canonically generated by 1, and we have
$\det H^{\bullet }(V)\equiv \mathbb {C}$
is canonically generated by 1, and we have
![]() $\|1\|_{\det H^{\bullet }(V)}=e^{\theta '(0)/2}$
. Using the orthogonal projection
$\|1\|_{\det H^{\bullet }(V)}=e^{\theta '(0)/2}$
. Using the orthogonal projection
![]() $\Pi ^1:V\to \operatorname {im}\partial $
, we can write Equation (7.3) as
$\Pi ^1:V\to \operatorname {im}\partial $
, we can write Equation (7.3) as
Let
![]() $(\widetilde V^{\bullet },\tilde \partial )$
be another finite-dimensional cochain complex, endowed with a Hermitian metric so that the homogeneous components are orthogonal to each other, and let
$(\widetilde V^{\bullet },\tilde \partial )$
be another finite-dimensional cochain complex, endowed with a Hermitian metric so that the homogeneous components are orthogonal to each other, and let
![]() $\phi :(V,\partial )\to (\widetilde V^{\bullet },\tilde \partial )$
be an isomorphism of cochain complexes, which may not be unitary. Then (see the proof of [Reference Bismut and Zhang11, Theorem 6.17])
$\phi :(V,\partial )\to (\widetilde V^{\bullet },\tilde \partial )$
be an isomorphism of cochain complexes, which may not be unitary. Then (see the proof of [Reference Bismut and Zhang11, Theorem 6.17])
 $$ \begin{align} \log\bigg(\frac{\|\ \|_{\det H^{\bullet}(\widetilde V)}}{\|\ \|_{\det H^{\bullet}(V)}}\bigg)^2=\operatorname{Str}(\log(\phi^*\phi)). \end{align} $$
$$ \begin{align} \log\bigg(\frac{\|\ \|_{\det H^{\bullet}(\widetilde V)}}{\|\ \|_{\det H^{\bullet}(V)}}\bigg)^2=\operatorname{Str}(\log(\phi^*\phi)). \end{align} $$
7.1.2. Case of an elliptic complex
Some of the concepts of Section 7.1.1 extend to the case where
![]() $V^{\bullet }=C^\infty (M;E^{\bullet })$
, for some graded Hermitian vector bundle
$V^{\bullet }=C^\infty (M;E^{\bullet })$
, for some graded Hermitian vector bundle
![]() $E^{\bullet }$
over M, and
$E^{\bullet }$
over M, and
![]() $\partial $
is an elliptic differential complex of order one. Then
$\partial $
is an elliptic differential complex of order one. Then
![]() $\det H^{\bullet }(V)$
is defined because
$\det H^{\bullet }(V)$
is defined because
![]() $\dim H^{\bullet }(V)<\infty $
. Moreover, Hodge theory for the Laplacian
$\dim H^{\bullet }(V)<\infty $
. Moreover, Hodge theory for the Laplacian
![]() $\square $
gives the isomorphism (7.2). Thus, at least the norm
$\square $
gives the isomorphism (7.2). Thus, at least the norm
![]() $|\ |_{\det H^{\bullet }(V)}$
is defined in this setting. Now, the expression (7.3) only defines
$|\ |_{\det H^{\bullet }(V)}$
is defined in this setting. Now, the expression (7.3) only defines
![]() $\theta (s)=\theta (s,\square )$
when
$\theta (s)=\theta (s,\square )$
when
![]() $\Re s>n/2$
, but it has a meromorphic extension to
$\Re s>n/2$
, but it has a meromorphic extension to
![]() $\mathbb {C}$
, denoted in the same way; indeed, Equation (7.3) becomes
$\mathbb {C}$
, denoted in the same way; indeed, Equation (7.3) becomes
for
![]() $\Re s>n/2$
, and therefore this equality also holds for the meromorphic extensions. Furthermore,
$\Re s>n/2$
, and therefore this equality also holds for the meromorphic extensions. Furthermore,
![]() $\theta (s)$
is smooth at
$\theta (s)$
is smooth at
![]() $s=0$
[Reference Seeley66], and
$s=0$
[Reference Seeley66], and
![]() $\theta '(0)$
can be considered as a renormalized version of the supertrace of the operator
$\theta '(0)$
can be considered as a renormalized version of the supertrace of the operator
![]() ${\mathsf {N}}\log (\square ')$
, which is not of trace class. Thus, the right-hand side of Equation (7.4) is defined in this way and plays the role of an analytic version of the metric
${\mathsf {N}}\log (\square ')$
, which is not of trace class. Thus, the right-hand side of Equation (7.4) is defined in this way and plays the role of an analytic version of the metric
![]() $\|\ \|_{\det H^{\bullet }(V)}$
, which is not directly defined. This kind of metrics were introduced by D. Quillen [Reference Quillen60] for the case of the Dolbeault complex. The expression (7.5) also holds in this case for
$\|\ \|_{\det H^{\bullet }(V)}$
, which is not directly defined. This kind of metrics were introduced by D. Quillen [Reference Quillen60] for the case of the Dolbeault complex. The expression (7.5) also holds in this case for
![]() $\Re s\gg 0$
; in fact, it becomes
$\Re s\gg 0$
; in fact, it becomes
where this zeta function can be shown to define a meromorphic function on
![]() $\mathbb {C}$
, even though
$\mathbb {C}$
, even though
![]() $\Pi ^1$
is not a differential operator, and this equality holds as meromorphic functions.
$\Pi ^1$
is not a differential operator, and this equality holds as meromorphic functions.
7.1.3. Reidemeister, Milnor and Ray–Singer metrics
Let F be a flat vector bundle over M, defined by a representation
![]() $\rho $
of
$\rho $
of
![]() $\pi _1M$
, and let
$\pi _1M$
, and let
![]() $\nabla ^F$
denote its covariant derivative. Consider a smooth triangulation K of M and the corresponding cochain complex
$\nabla ^F$
denote its covariant derivative. Consider a smooth triangulation K of M and the corresponding cochain complex
![]() $C^{\bullet }(K,F)$
with coefficients in F, whose cohomology is isomorphic to
$C^{\bullet }(K,F)$
with coefficients in F, whose cohomology is isomorphic to
![]() $H^{\bullet }(M,F)$
via the quasi-isomorphism
$H^{\bullet }(M,F)$
via the quasi-isomorphism
defined by integration of differential forms on smooth simplices. Given a Hermitian structure
![]() $g^F$
on F, its restriction to the fibers over the barycenters of the simplices induces a metric on
$g^F$
on F, its restriction to the fibers over the barycenters of the simplices induces a metric on
![]() $C^{\bullet }(K,F)$
, and the concepts of Section 7.1.1 can be applied. In this case, the left-hand side of Equation (7.4) is called the Reidemeister metric, denoted by
$C^{\bullet }(K,F)$
, and the concepts of Section 7.1.1 can be applied. In this case, the left-hand side of Equation (7.4) is called the Reidemeister metric, denoted by
![]() $\|\ \|^{\mathrm {R}}_{\det H^{\bullet }(M,F)}$
.
$\|\ \|^{\mathrm {R}}_{\det H^{\bullet }(M,F)}$
.
If
![]() $\nabla ^Fg^F=0$
(
$\nabla ^Fg^F=0$
(
![]() $\rho $
is unitary) and
$\rho $
is unitary) and
![]() $H^{\bullet }(M,F)=0$
, then the Reidemeister torsion
$H^{\bullet }(M,F)=0$
, then the Reidemeister torsion
![]() $\tau _M(\rho )$
is defined using K, and it is a topological invariant of M [Reference Franz30, Reference Reidemeister62, Reference de Rham23]. Moreover,
$\tau _M(\rho )$
is defined using K, and it is a topological invariant of M [Reference Franz30, Reference Reidemeister62, Reference de Rham23]. Moreover,
![]() $\tau _M(\rho )=\|1\|^{\mathrm {R}}_{\det H^{\bullet }(M,F)}$
is the exponential factor of the right-hand side of Equation (7.4) [Reference Ray and Singer61, Proposition 1.7]. If we only assume
$\tau _M(\rho )=\|1\|^{\mathrm {R}}_{\det H^{\bullet }(M,F)}$
is the exponential factor of the right-hand side of Equation (7.4) [Reference Ray and Singer61, Proposition 1.7]. If we only assume
![]() $\nabla ^Fg^F=0$
, then
$\nabla ^Fg^F=0$
, then
![]() $\|\ \|^{\mathrm {R}}_{\det H^{\bullet }(M,F)}$
is still a topological invariant of M.
$\|\ \|^{\mathrm {R}}_{\det H^{\bullet }(M,F)}$
is still a topological invariant of M.
Next, given a vector field X on M satisfying (b),
![]() $H^{\bullet }(M,F)$
is also isomorphic to the cohomology of
$H^{\bullet }(M,F)$
is also isomorphic to the cohomology of
![]() $(C^{\bullet }(-X,W^-,F),\mathbf {d}^F)$
via the quasi-isomorphism
$(C^{\bullet }(-X,W^-,F),\mathbf {d}^F)$
via the quasi-isomorphism
This complex has a metric induced by
![]() $g^F$
, like in Section 6.2.4, and the concepts of Section 7.1.1 can be also applied. In this case, the left-hand side of Equation (7.4) is called the Milnor metric, denoted by
$g^F$
, like in Section 6.2.4, and the concepts of Section 7.1.1 can be also applied. In this case, the left-hand side of Equation (7.4) is called the Milnor metric, denoted by
![]() $\|\ \|^{\mathrm {M},-X}_{\det H^{\bullet }(M,F)}$
, and the metric factor of the right-hand side of Equation (7.4) is denoted by
$\|\ \|^{\mathrm {M},-X}_{\det H^{\bullet }(M,F)}$
, and the metric factor of the right-hand side of Equation (7.4) is denoted by
![]() $|\ |^{\mathrm {M},-X}_{\det H^{\bullet }(M,F)}$
. If
$|\ |^{\mathrm {M},-X}_{\det H^{\bullet }(M,F)}$
. If
![]() $\nabla ^Fg^F=0$
, then
$\nabla ^Fg^F=0$
, then
![]() $\|\ \|^{\mathrm {M},-X}_{\det H^{\bullet }(M,F)}=\|\ \|^{\mathrm {R}}_{\det H^{\bullet }(M,F)}$
[Reference Milnor50, Theorem 9.3].
$\|\ \|^{\mathrm {M},-X}_{\det H^{\bullet }(M,F)}=\|\ \|^{\mathrm {R}}_{\det H^{\bullet }(M,F)}$
[Reference Milnor50, Theorem 9.3].
Finally, the concepts of Section 7.1.2 can be applied to
![]() $(\Omega (M,F),d^F)$
, whose cohomology is again
$(\Omega (M,F),d^F)$
, whose cohomology is again
![]() $H^{\bullet }(M,F)$
. In this case, the right-hand side of Equation (7.4) is called the Ray–Singer metric, denoted by
$H^{\bullet }(M,F)$
. In this case, the right-hand side of Equation (7.4) is called the Ray–Singer metric, denoted by
![]() $\|\ \|^{\mathrm {RS}}_{\det H^{\bullet }(M,F)}$
, and the metric factor of the right-hand side of Equation (7.4) is denoted by
$\|\ \|^{\mathrm {RS}}_{\det H^{\bullet }(M,F)}$
, and the metric factor of the right-hand side of Equation (7.4) is denoted by
![]() $|\ |^{\mathrm {RS}}_{\det H^{\bullet }(M,F)}$
. If
$|\ |^{\mathrm {RS}}_{\det H^{\bullet }(M,F)}$
. If
![]() $H^{\bullet }(M,F)=0$
, then the exponential factor of the right-hand side of Equation (7.4) is called the analytic torsion or Ray–Singer torsion, denoted by
$H^{\bullet }(M,F)=0$
, then the exponential factor of the right-hand side of Equation (7.4) is called the analytic torsion or Ray–Singer torsion, denoted by
![]() $T_M(\rho )$
. These concepts were introduced by Ray and Singer [Reference Ray and Singer61], who conjectured that
$T_M(\rho )$
. These concepts were introduced by Ray and Singer [Reference Ray and Singer61], who conjectured that
![]() $T_M(\rho )=\tau _M(\rho )$
if
$T_M(\rho )=\tau _M(\rho )$
if
![]() $\nabla ^Fg^F=0$
and
$\nabla ^Fg^F=0$
and
![]() $H^{\bullet }(M,F)=0$
. Independent proofs of this conjecture were given by Cheeger [Reference Cheeger21] and Müller [Reference Müller54]. This conjecture still holds true if the induced Hermitian structure
$H^{\bullet }(M,F)=0$
. Independent proofs of this conjecture were given by Cheeger [Reference Cheeger21] and Müller [Reference Müller54]. This conjecture still holds true if the induced Hermitian structure
![]() $g^{\det F}$
on
$g^{\det F}$
on
![]() $\det F$
is flat, as shown at the same time by Bismut and Zhang [Reference Bismut, Zhang and Laudenbach10] and Müller [Reference Müller54]. Actually, in [10], Bismut and Zhang reformulated the conjecture in the form
$\det F$
is flat, as shown at the same time by Bismut and Zhang [Reference Bismut, Zhang and Laudenbach10] and Müller [Reference Müller54]. Actually, in [10], Bismut and Zhang reformulated the conjecture in the form
![]() $\|\ \|^{\mathrm {RS}}_{\det H^{\bullet }(M,F)}=\|\ \|^{\mathrm {R}}_{\det H^{\bullet }(M,F)}$
. Moreover, they also considered the case where
$\|\ \|^{\mathrm {RS}}_{\det H^{\bullet }(M,F)}=\|\ \|^{\mathrm {R}}_{\det H^{\bullet }(M,F)}$
. Moreover, they also considered the case where
![]() $g^{\det F}$
is not assumed to be flat [Reference Bismut, Zhang and Laudenbach10, Reference Bismut and Zhang11], extending the above results by introducing an additional term. The first ingredient of this extra term is the 1-form
$g^{\det F}$
is not assumed to be flat [Reference Bismut, Zhang and Laudenbach10, Reference Bismut and Zhang11], extending the above results by introducing an additional term. The first ingredient of this extra term is the 1-form
which vanishes if and only if
![]() $g^{\det F}$
is flat. Moreover,
$g^{\det F}$
is flat. Moreover,
![]() $\theta (F,g^F)$
is closed and its cohomology class of
$\theta (F,g^F)$
is closed and its cohomology class of
![]() $\theta (F,g^F)$
is independent of the choice of
$\theta (F,g^F)$
is independent of the choice of
![]() $g^F$
[Reference Bismut, Zhang and Laudenbach10, Proposition 4.6]; this class measures the obstruction to the existence of a flat Hermitian structure on
$g^F$
[Reference Bismut, Zhang and Laudenbach10, Proposition 4.6]; this class measures the obstruction to the existence of a flat Hermitian structure on
![]() $\det F$
.
$\det F$
.
Let
![]() $e(M,\nabla ^M)$
be the representative of the Euler class of M given by the Chern–Weil theory using
$e(M,\nabla ^M)$
be the representative of the Euler class of M given by the Chern–Weil theory using
![]() $g^M$
; it belongs to
$g^M$
; it belongs to
![]() $\Omega ^n(M,o(M))$
because M may not be oriented. Let
$\Omega ^n(M,o(M))$
because M may not be oriented. Let
![]() $\psi (M,\nabla ^M)$
be the current of degree
$\psi (M,\nabla ^M)$
be the current of degree
![]() $n-1$
on
$n-1$
on
![]() $TM$
constructed in [Reference Mathai and Quillen44] (see also [Reference Bismut, Gillet and Soulé9, Section 3], [Reference Bismut, Zhang and Laudenbach10, Section 3], [Reference Burghelea and Haller19, Section 2], [Reference Burghelea and Haller20, Section 4]). Identify the image of the zero section of
$TM$
constructed in [Reference Mathai and Quillen44] (see also [Reference Bismut, Gillet and Soulé9, Section 3], [Reference Bismut, Zhang and Laudenbach10, Section 3], [Reference Burghelea and Haller19, Section 2], [Reference Burghelea and Haller20, Section 4]). Identify the image of the zero section of
![]() $TM$
with M, and identify the conormal bundle of M in
$TM$
with M, and identify the conormal bundle of M in
![]() $TM$
with
$TM$
with
![]() $T^*M$
. Let
$T^*M$
. Let
![]() $\delta _M$
be the current on
$\delta _M$
be the current on
![]() $TM$
defined by integration on M, and let
$TM$
defined by integration on M, and let
![]() $\pi :TM\to M$
be the vector bundle projection.
$\pi :TM\to M$
be the vector bundle projection.
Proposition 7.1 (Bismut–Zhang [Reference Bismut, Zhang and Laudenbach10, Theorem 3.7])
The following holds:
-
(i) For any smooth function
 $\lambda :TM\to \mathbb {R}^\pm $
, under the mapping
$\lambda :TM\to \mathbb {R}^\pm $
, under the mapping
 $v\mapsto \lambda v$
,
$v\mapsto \lambda v$
,
 $\psi (M,\nabla ^M)$
is changed into
$\psi (M,\nabla ^M)$
is changed into
 $(\pm 1)^n\psi (M,\nabla ^M)$
.
$(\pm 1)^n\psi (M,\nabla ^M)$
. -
(ii) The current
 $\psi (M,\nabla ^M)$
is locally integrable, and its wave front set is contained in
$\psi (M,\nabla ^M)$
is locally integrable, and its wave front set is contained in
 $T^*M$
. Thus,
$T^*M$
. Thus,
 $\psi (M,\nabla ^M)$
is smooth on
$\psi (M,\nabla ^M)$
is smooth on
 $TM\setminus M$
.
$TM\setminus M$
. -
(iii) The restriction of
 $-\psi (M,\nabla ^M)$
to the fibers of
$-\psi (M,\nabla ^M)$
to the fibers of
 $TM\setminus M$
coincides with the solid angle defined by
$TM\setminus M$
coincides with the solid angle defined by
 $g^M$
.
$g^M$
. -
(iv) We have
 $$\begin{align*}d\psi(M,\nabla^M)=\pi^*e(M,\nabla^M)-\delta_M. \end{align*}$$
$$\begin{align*}d\psi(M,\nabla^M)=\pi^*e(M,\nabla^M)-\delta_M. \end{align*}$$
Remark 7.2. In Proposition 7.1, observe that (i) and (iv) are compatible because
![]() $e(M,\nabla ^M)=0$
if n is odd. By (ii)–(iv), the restriction of
$e(M,\nabla ^M)=0$
if n is odd. By (ii)–(iv), the restriction of
![]() $\psi (M,\nabla ^M)$
to
$\psi (M,\nabla ^M)$
to
![]() $TM\setminus M$
is induced by a smooth differential form on the sphere bundle which transgresses
$TM\setminus M$
is induced by a smooth differential form on the sphere bundle which transgresses
![]() $e(M,\nabla ^M)$
(such a differential form was already defined and used in [Reference Chern22]).
$e(M,\nabla ^M)$
(such a differential form was already defined and used in [Reference Chern22]).
Theorem 7.3 (Bismut–Zhang [Reference Bismut, Zhang and Laudenbach10, Theorem 0.2], [Reference Bismut and Zhang11, Theorem 0.2])
We have
 $$\begin{align*}\log\Bigg(\frac{\|\ \|^{\mathrm{RS}}_{\det H^{\bullet}(M,F)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}(M,F)}}\Bigg)^2 =-\int_M\theta(F,g^F)\wedge(-X)^*\psi(M,\nabla^M). \end{align*}$$
$$\begin{align*}\log\Bigg(\frac{\|\ \|^{\mathrm{RS}}_{\det H^{\bullet}(M,F)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}(M,F)}}\Bigg)^2 =-\int_M\theta(F,g^F)\wedge(-X)^*\psi(M,\nabla^M). \end{align*}$$
Remark 7.4. By (b),
![]() $X=-\operatorname {grad}_{g'}h$
for some Morse function h and some Riemannian metric
$X=-\operatorname {grad}_{g'}h$
for some Morse function h and some Riemannian metric
![]() $g'$
on M, which may not be the given metric
$g'$
on M, which may not be the given metric
![]() $g^M$
. If we fix h, the right-hand side of the equality in Theorem 7.3 is independent of the choice of X satisfying
$g^M$
. If we fix h, the right-hand side of the equality in Theorem 7.3 is independent of the choice of X satisfying
![]() $X=-\operatorname {grad}_{g'}h$
for some
$X=-\operatorname {grad}_{g'}h$
for some
![]() $g'$
[Reference Bismut, Zhang and Laudenbach10, Proposition 6.1].
$g'$
[Reference Bismut, Zhang and Laudenbach10, Proposition 6.1].
Theorem 7.3 will be applied to the case of the flat complex line bundle
![]() $\mathcal {L}^z$
with a Hermitian structure
$\mathcal {L}^z$
with a Hermitian structure
![]() $g^{\mathcal {L}^z}$
(Section 2.1.2). By Equations (2.13) and (7.7),
$g^{\mathcal {L}^z}$
(Section 2.1.2). By Equations (2.13) and (7.7),
7.2. Asymptotics of the large zeta invariant
We prove Theorem 1.2 (i) here. With the notation of Section 7.1.2, consider the meromorphic function
![]() $\theta (s,z)=\theta (s,\Delta _z)$
, also defined in Equation (5.9), as well as its components
$\theta (s,z)=\theta (s,\Delta _z)$
, also defined in Equation (5.9), as well as its components
![]() $\theta _{\mathrm {sm/la}}(s,z)$
defined in Equation (5.10). Consider also the current
$\theta _{\mathrm {sm/la}}(s,z)$
defined in Equation (5.10). Consider also the current
![]() $\psi (M,\nabla ^M)$
of degree
$\psi (M,\nabla ^M)$
of degree
![]() $n-1$
on
$n-1$
on
![]() $TM$
(Section 7.1.3). By Proposition 7.1 (i),
$TM$
(Section 7.1.3). By Proposition 7.1 (i),
Notation 7.5. Let
![]() $\asymp _1$
be defined like
$\asymp _1$
be defined like
![]() $\asymp _0$
in Notation 6.2, using
$\asymp _0$
in Notation 6.2, using
![]() $O(|\mu |^{-1})$
instead of
$O(|\mu |^{-1})$
instead of
![]() $O(e^{-c|\mu |})$
.
$O(e^{-c|\mu |})$
.
Take some Morse function h on M such that
![]() $Xh<0$
on
$Xh<0$
on
![]() $M\setminus \mathcal {Y}$
, and h is in standard form with respect to X. Then
$M\setminus \mathcal {Y}$
, and h is in standard form with respect to X. Then
![]() $X=-\operatorname {grad}_{g'}h$
for some Riemannian metric
$X=-\operatorname {grad}_{g'}h$
for some Riemannian metric
![]() $g'$
(Section 6.1.3), which may not be the given metric g. Consider the flat complex line bundle
$g'$
(Section 6.1.3), which may not be the given metric g. Consider the flat complex line bundle
![]() $\mathcal {L}_{z\eta -dh}$
with the Hermitian structure
$\mathcal {L}_{z\eta -dh}$
with the Hermitian structure
![]() $g^{\mathcal {L}_{z\eta -dh}}$
(Section 2.1.2). Note that
$g^{\mathcal {L}_{z\eta -dh}}$
(Section 2.1.2). Note that
![]() $\mathbf {d}^{\mathcal {L}_{z\eta -dh}}_{dh}\equiv \mathbf {d}_{z\eta }$
on
$\mathbf {d}^{\mathcal {L}_{z\eta -dh}}_{dh}\equiv \mathbf {d}_{z\eta }$
on
![]() $C^{\bullet }(X,W^-,\mathcal {L}_{z\eta -dh})\equiv \mathbf {C}^{\bullet }(X)$
. So, by Equation (7.8), Theorem 7.3 and Remark 7.4,
$C^{\bullet }(X,W^-,\mathcal {L}_{z\eta -dh})\equiv \mathbf {C}^{\bullet }(X)$
. So, by Equation (7.8), Theorem 7.3 and Remark 7.4,
 $$ \begin{align} \log\frac{\|\ \|^{\mathrm{RS}}_{\det H^{\bullet}_z(M)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}_z(M)}} =\int_M(\mu\eta-dh)\wedge (-X)^*\psi(M,\nabla^M)\;, \end{align} $$
$$ \begin{align} \log\frac{\|\ \|^{\mathrm{RS}}_{\det H^{\bullet}_z(M)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}_z(M)}} =\int_M(\mu\eta-dh)\wedge (-X)^*\psi(M,\nabla^M)\;, \end{align} $$
where
![]() $H^{\bullet }_z(M)=H^{\bullet }_{z\eta }(M)$
. With the notation of Section 7.1.3, let
$H^{\bullet }_z(M)=H^{\bullet }_{z\eta }(M)$
. With the notation of Section 7.1.3, let
By Equation (7.4),
 $$ \begin{align} \log\frac{\|\ \|^{\mathrm{RS}}_{\det H^{\bullet}_z(M)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}_z(M)}} =\log\frac{\|\ \|^{\mathrm{RS,sm}}_{\det H^{\bullet}_z(M)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}_z(M)}} +\frac{\theta_{\mathrm{la}}'(0,z)}{2}. \end{align} $$
$$ \begin{align} \log\frac{\|\ \|^{\mathrm{RS}}_{\det H^{\bullet}_z(M)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}_z(M)}} =\log\frac{\|\ \|^{\mathrm{RS,sm}}_{\det H^{\bullet}_z(M)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}_z(M)}} +\frac{\theta_{\mathrm{la}}'(0,z)}{2}. \end{align} $$
By Equation (7.6) and Corollary 6.4, for
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
 $$ \begin{align} \log\Bigg(\frac{\|\ \|^{\mathrm{RS,sm}}_{\det H^{\bullet}_z(M)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}_z(M)}}\Bigg)^2 &=-\operatorname{Str}(\log(\Phi_z^*\Phi_z))=-\operatorname{Str}\big(\log\big(\Psi_z^{-1}\Phi_z^*\Phi_z\Psi_z\big)\big)\nonumber\\ &=-\operatorname{Str}\big(\log\big((\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)\big). \end{align} $$
$$ \begin{align} \log\Bigg(\frac{\|\ \|^{\mathrm{RS,sm}}_{\det H^{\bullet}_z(M)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}_z(M)}}\Bigg)^2 &=-\operatorname{Str}(\log(\Phi_z^*\Phi_z))=-\operatorname{Str}\big(\log\big(\Psi_z^{-1}\Phi_z^*\Phi_z\Psi_z\big)\big)\nonumber\\ &=-\operatorname{Str}\big(\log\big((\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)\big). \end{align} $$
From Equation (6.12) and Theorems 6.3, 6.18 and 6.19, we obtain
 $$ \begin{align*} \big((\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)^{-1} &=\Big(\frac{\pi}{\mu}\Big)^{\frac n2-{\mathsf{N}}}+O\big(e^{-c\mu}\big)\;,\\ \partial_z\big(\!(\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)\! &=\partial_z\big(\!(\Psi_z^*\Psi_z)^{-1}\big)(\Phi_z\Psi_z)^*\Phi_z\Psi_z +\! (\Psi_z^*\Psi_z)^{-1}(\partial_{\bar z}(\Phi_z\Psi_z)\!)^*\Phi_z\!\Psi_z\\ &\phantom{={}}{}+(\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\partial_z(\Phi_z\Psi_z)\\ &\asymp_0\bigg(O\big(\mu^{-1}\big)+\Big(\frac n{4\mu}-\frac {\mathsf{N}}{2\mu}\Big)\bigg)\Big(\frac{\pi}{\mu}\Big)^{{\mathsf{N}}-\frac n2}. \end{align*} $$
$$ \begin{align*} \big((\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)^{-1} &=\Big(\frac{\pi}{\mu}\Big)^{\frac n2-{\mathsf{N}}}+O\big(e^{-c\mu}\big)\;,\\ \partial_z\big(\!(\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)\! &=\partial_z\big(\!(\Psi_z^*\Psi_z)^{-1}\big)(\Phi_z\Psi_z)^*\Phi_z\Psi_z +\! (\Psi_z^*\Psi_z)^{-1}(\partial_{\bar z}(\Phi_z\Psi_z)\!)^*\Phi_z\!\Psi_z\\ &\phantom{={}}{}+(\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\partial_z(\Phi_z\Psi_z)\\ &\asymp_0\bigg(O\big(\mu^{-1}\big)+\Big(\frac n{4\mu}-\frac {\mathsf{N}}{2\mu}\Big)\bigg)\Big(\frac{\pi}{\mu}\Big)^{{\mathsf{N}}-\frac n2}. \end{align*} $$
So
 $$ \begin{align*} & \partial_z\operatorname{Str}\big(\log\big((\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)\big)\\ &\quad =\operatorname{Str}\big((\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)^{-1} \partial_z\big((\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)\\ &\quad =O\big(\mu^{-1}\big)+\operatorname{Str}\Big(\frac n{4\mu}-\frac {\mathsf{N}}{2\mu}\Big)+O\big(e^{-c\mu}\big) =O\big(\mu^{-1}\big). \end{align*} $$
$$ \begin{align*} & \partial_z\operatorname{Str}\big(\log\big((\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)\big)\\ &\quad =\operatorname{Str}\big((\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)^{-1} \partial_z\big((\Psi_z^*\Psi_z)^{-1}(\Phi_z\Psi_z)^*\Phi_z\Psi_z\big)\\ &\quad =O\big(\mu^{-1}\big)+\operatorname{Str}\Big(\frac n{4\mu}-\frac {\mathsf{N}}{2\mu}\Big)+O\big(e^{-c\mu}\big) =O\big(\mu^{-1}\big). \end{align*} $$
Then, by Equation (7.12),
 $$ \begin{align} \partial_z\log\frac{\|\ \|^{\mathrm{RS,sm}}_{\det H^{\bullet}_z(M)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}_z(M)}} =O\big(\mu^{-1}\big). \end{align} $$
$$ \begin{align} \partial_z\log\frac{\|\ \|^{\mathrm{RS,sm}}_{\det H^{\bullet}_z(M)}}{\|\ \|^{\mathrm{M},-X}_{\det H^{\bullet}_z(M)}} =O\big(\mu^{-1}\big). \end{align} $$
By taking the derivative with respect to z of both sides of Equation (7.10) and using Equations (7.11) and (7.13) and Corollary 5.10, we get
![]() $\zeta _{\mathrm {la}}(1,z)\asymp _1\mathbf {z}_{\mathrm {la}}$
, as stated in Theorem 1.2 (i).
$\zeta _{\mathrm {la}}(1,z)\asymp _1\mathbf {z}_{\mathrm {la}}$
, as stated in Theorem 1.2 (i).
Remark 7.6. In the case where
![]() $\eta =dh$
, Theorem 1.2 (i) agrees with Theorem 5.16. In fact, by Proposition 7.1 (iv), Theorem 1.2 (i) and the Stokes formula,
$\eta =dh$
, Theorem 1.2 (i) agrees with Theorem 5.16. In fact, by Proposition 7.1 (iv), Theorem 1.2 (i) and the Stokes formula,
 $$ \begin{align*} \zeta_{\mathrm{la}}(1,z)&\asymp_1-\int_Mh\,(-X)^*d\psi(M,\nabla^M) =-\int_Mh\,(-X)^*(\pi^*e(M,\nabla^M)-\delta_M)\\ &=-\int_Mh\,e(M,\nabla^M)+\sum_{p\in\mathcal{Y}}(-1)^{\operatorname{ind}(p)}h(p). \end{align*} $$
$$ \begin{align*} \zeta_{\mathrm{la}}(1,z)&\asymp_1-\int_Mh\,(-X)^*d\psi(M,\nabla^M) =-\int_Mh\,(-X)^*(\pi^*e(M,\nabla^M)-\delta_M)\\ &=-\int_Mh\,e(M,\nabla^M)+\sum_{p\in\mathcal{Y}}(-1)^{\operatorname{ind}(p)}h(p). \end{align*} $$
8. Asymptotics of the small zeta invariant
8.1. Condition on the integrals along instantons
Let
 $$ \begin{align*} \mathcal{M}_p&=\mathcal{M}_p(\eta,X)=-\max\{\,\eta(\gamma)\mid\gamma\in\mathcal{T}^1_p\,\}\quad\big(p\in\mathcal{Y}_+\big)\;,\\ \mathcal{M}_k&=\mathcal{M}_k(\eta,X)=\min_{p\in\mathcal{Y}_k}\mathcal{M}_p\quad(k=1,\dots,n). \end{align*} $$
$$ \begin{align*} \mathcal{M}_p&=\mathcal{M}_p(\eta,X)=-\max\{\,\eta(\gamma)\mid\gamma\in\mathcal{T}^1_p\,\}\quad\big(p\in\mathcal{Y}_+\big)\;,\\ \mathcal{M}_k&=\mathcal{M}_k(\eta,X)=\min_{p\in\mathcal{Y}_k}\mathcal{M}_p\quad(k=1,\dots,n). \end{align*} $$
Thus, (d) means that
![]() $\mathcal {M}_p=\mathcal {M}_k$
for all
$\mathcal {M}_p=\mathcal {M}_k$
for all
![]() $k=1,\dots ,n$
and
$k=1,\dots ,n$
and
![]() $p\in \mathcal {Y}_k$
. The following result will be proved in Appendix A.
$p\in \mathcal {Y}_k$
. The following result will be proved in Appendix A.
Theorem 8.1. For every
![]() $\xi \in H^1(M,\mathbb {R})$
and numbers
$\xi \in H^1(M,\mathbb {R})$
and numbers
![]() $a_n\ge \dots \ge a_1\gg 0$
or
$a_n\ge \dots \ge a_1\gg 0$
or
![]() $a_1\ge \dots \ge a_n\gg 0$
, there is some
$a_1\ge \dots \ge a_n\gg 0$
, there is some
![]() $\eta \in \xi $
, satisfying (a) and (c) with the given X and some metric g, such that
$\eta \in \xi $
, satisfying (a) and (c) with the given X and some metric g, such that
![]() $\mathcal {M}_p(\eta ,X)=a_k$
for all
$\mathcal {M}_p(\eta ,X)=a_k$
for all
![]() $k=1,\dots ,n$
and
$k=1,\dots ,n$
and
![]() $p\in \mathcal {Y}_k$
.
$p\in \mathcal {Y}_k$
.
Remark 8.2. If
![]() $\xi \ne 0$
, for
$\xi \ne 0$
, for
![]() $p\in \mathcal {Y}_k$
,
$p\in \mathcal {Y}_k$
,
![]() $q\in \mathcal {Y}_{k-1}$
and
$q\in \mathcal {Y}_{k-1}$
and
![]() $\gamma ,\delta \in \mathcal {T}(p,q)\subset \mathcal {T}^1_p$
, the period
$\gamma ,\delta \in \mathcal {T}(p,q)\subset \mathcal {T}^1_p$
, the period
![]() $\langle \xi ,\bar \gamma \bar \delta ^{-1}\rangle =\eta (\gamma )-\eta (\delta )$
may not be zero. Hence, it may not be possible to get
$\langle \xi ,\bar \gamma \bar \delta ^{-1}\rangle =\eta (\gamma )-\eta (\delta )$
may not be zero. Hence, it may not be possible to get
![]() $\eta (\gamma )=-a_k$
for all
$\eta (\gamma )=-a_k$
for all
![]() $\gamma \in \mathcal {T}^1_p$
, contrary to the case where
$\gamma \in \mathcal {T}^1_p$
, contrary to the case where
![]() $\xi =0$
.
$\xi =0$
.
From now on, we assume
![]() $\eta $
satisfies (d), besides (a) and (c). By Theorem 8.1, this is possible for any prescription of the class
$\eta $
satisfies (d), besides (a) and (c). By Theorem 8.1, this is possible for any prescription of the class
![]() $\xi =[\eta ]\in H^1(M,\mathbb {R})$
. Let
$\xi =[\eta ]\in H^1(M,\mathbb {R})$
. Let
![]() $a_k=\mathcal {M}_k(\eta ,X)$
(
$a_k=\mathcal {M}_k(\eta ,X)$
(
![]() $k=1,\dots ,n$
). Then
$k=1,\dots ,n$
). Then
![]() $-\eta $
also satisfies (a), (c) and (d) with
$-\eta $
also satisfies (a), (c) and (d) with
![]() $-X$
and g, and
$-X$
and g, and
![]() $\mathcal {M}_k(-\eta ,-X)=a_{n-k+1}$
. So, if M is oriented, by Corollaries 4.15 and 4.16,
$\mathcal {M}_k(-\eta ,-X)=a_{n-k+1}$
. So, if M is oriented, by Corollaries 4.15 and 4.16,
 $$ \begin{align} -\mathbf{z}_{\mathrm{sm}}(-\eta)=-\sum_{k=1}^n(-1)^k\big(1-e^{a_{n-k+1}}\big)m^1_{n-k+1}. \end{align} $$
$$ \begin{align} -\mathbf{z}_{\mathrm{sm}}(-\eta)=-\sum_{k=1}^n(-1)^k\big(1-e^{a_{n-k+1}}\big)m^1_{n-k+1}. \end{align} $$
8.2. Asymptotics of the perturbed Morse operators
Consider the notation of Section 6.2.4. By Equation (6.8),
for
![]() $k=1,\dots ,n$
, where
$k=1,\dots ,n$
, where
 $$ \begin{align} \mathbf{d}^{\prime}_{k-1}\mathbf{e}_q&=\sum_{p\in\mathcal{Y}_k,\ \gamma\in\mathcal{T}(p,q),\ \eta(\gamma)=-a_k}\epsilon(\gamma)\mathbf{e}_p\;, \end{align} $$
$$ \begin{align} \mathbf{d}^{\prime}_{k-1}\mathbf{e}_q&=\sum_{p\in\mathcal{Y}_k,\ \gamma\in\mathcal{T}(p,q),\ \eta(\gamma)=-a_k}\epsilon(\gamma)\mathbf{e}_p\;, \end{align} $$
 $$ \begin{align} \mathbf{d}^{\prime\prime}_{z,k-1}\mathbf{e}_q&=\sum_{p\in\mathcal{Y}_k,\ \gamma\in\mathcal{T}(p,q),\ \eta(\gamma)<-a_k}e^{z(a_k+\eta(\gamma))}\epsilon(\gamma)\mathbf{e}_p\;, \end{align} $$
$$ \begin{align} \mathbf{d}^{\prime\prime}_{z,k-1}\mathbf{e}_q&=\sum_{p\in\mathcal{Y}_k,\ \gamma\in\mathcal{T}(p,q),\ \eta(\gamma)<-a_k}e^{z(a_k+\eta(\gamma))}\epsilon(\gamma)\mathbf{e}_p\;, \end{align} $$
for
![]() $q\in \mathcal {Y}_{k-1}$
. Observe that
$q\in \mathcal {Y}_{k-1}$
. Observe that
So
Hence, the operator
![]() $\mathbf {d}'=\sum _k\mathbf {d}^{\prime }_k$
on
$\mathbf {d}'=\sum _k\mathbf {d}^{\prime }_k$
on
![]() $\mathbf {C}^{\bullet }$
satisfies
$\mathbf {C}^{\bullet }$
satisfies
![]() $(\mathbf {d}')^2=0$
. Taking adjoints in Equations (8.2)–(8.4) or using Equation (6.9), we also get
$(\mathbf {d}')^2=0$
. Taking adjoints in Equations (8.2)–(8.4) or using Equation (6.9), we also get
for
![]() $k=1,\dots ,n$
, where
$k=1,\dots ,n$
, where
 $$ \begin{align} \boldsymbol{\delta}^{\prime}_k\mathbf{e}_p&=\sum_{q\in\mathcal{Y}_{k-1},\ \gamma\in\mathcal{T}(p,q),\ \eta(\gamma)=-a_k} \epsilon(\gamma)\,\mathbf{e}_q,\qquad\qquad \end{align} $$
$$ \begin{align} \boldsymbol{\delta}^{\prime}_k\mathbf{e}_p&=\sum_{q\in\mathcal{Y}_{k-1},\ \gamma\in\mathcal{T}(p,q),\ \eta(\gamma)=-a_k} \epsilon(\gamma)\,\mathbf{e}_q,\qquad\qquad \end{align} $$
 $$ \begin{align} \boldsymbol{\delta}^{\prime\prime}_{z,k}\mathbf{e}_p&=\sum_{q\in\mathcal{Y}_{k-1},\ \gamma\in\mathcal{T}(p,q),\ \eta(\gamma)=-a_k}e ^{\bar z(a_k+\eta(\gamma))}\epsilon(\gamma)\mathbf{e}_q\;, \end{align} $$
$$ \begin{align} \boldsymbol{\delta}^{\prime\prime}_{z,k}\mathbf{e}_p&=\sum_{q\in\mathcal{Y}_{k-1},\ \gamma\in\mathcal{T}(p,q),\ \eta(\gamma)=-a_k}e ^{\bar z(a_k+\eta(\gamma))}\epsilon(\gamma)\mathbf{e}_q\;, \end{align} $$
for
![]() $p\in \mathcal {Y}_k$
. Moreover, Equation (8.5) yields
$p\in \mathcal {Y}_k$
. Moreover, Equation (8.5) yields
Let
![]() $\boldsymbol {\delta }'=\sum _k\boldsymbol {\delta }^{\prime }_k=(\mathbf {d}')^*$
, which satisfies
$\boldsymbol {\delta }'=\sum _k\boldsymbol {\delta }^{\prime }_k=(\mathbf {d}')^*$
, which satisfies
![]() $(\boldsymbol {\delta }')^2 = 0$
, and let
$(\boldsymbol {\delta }')^2 = 0$
, and let
We have
 $$ \begin{gather*} \mathbf{C}^{\bullet}=\ker\boldsymbol{\Delta}'\oplus\operatorname{im}\mathbf{d}'\oplus\operatorname{im}\boldsymbol{\delta}'\;,\\ \operatorname{im}\boldsymbol{\Delta}'=\operatorname{im}\mathbf{D}'=\operatorname{im}\mathbf{d}'\oplus\operatorname{im}\boldsymbol{\delta}'\;,\quad \ker\boldsymbol{\Delta}'=\ker\mathbf{D}'=\ker\mathbf{d}'\cap\ker\boldsymbol{\delta}'. \end{gather*} $$
$$ \begin{gather*} \mathbf{C}^{\bullet}=\ker\boldsymbol{\Delta}'\oplus\operatorname{im}\mathbf{d}'\oplus\operatorname{im}\boldsymbol{\delta}'\;,\\ \operatorname{im}\boldsymbol{\Delta}'=\operatorname{im}\mathbf{D}'=\operatorname{im}\mathbf{d}'\oplus\operatorname{im}\boldsymbol{\delta}'\;,\quad \ker\boldsymbol{\Delta}'=\ker\mathbf{D}'=\ker\mathbf{d}'\cap\ker\boldsymbol{\delta}'. \end{gather*} $$
The orthogonal projections of
![]() $\mathbf {C}^{\bullet }$
to
$\mathbf {C}^{\bullet }$
to
![]() $\ker \boldsymbol {\Delta }'$
,
$\ker \boldsymbol {\Delta }'$
,
![]() $\operatorname {im}\mathbf {d}'$
and
$\operatorname {im}\mathbf {d}'$
and
![]() $\operatorname {im}\boldsymbol {\delta }'$
are denoted by
$\operatorname {im}\boldsymbol {\delta }'$
are denoted by
![]() $\boldsymbol {\Pi }'=\boldsymbol {\Pi }^{\prime \,0}$
,
$\boldsymbol {\Pi }'=\boldsymbol {\Pi }^{\prime \,0}$
,
![]() $\boldsymbol {\Pi }^{\prime \,1}$
and
$\boldsymbol {\Pi }^{\prime \,1}$
and
![]() $\boldsymbol {\Pi }^{\prime \,2}$
, respectively. Like in Sections 2.1.2 and 6.2.6, the composition
$\boldsymbol {\Pi }^{\prime \,2}$
, respectively. Like in Sections 2.1.2 and 6.2.6, the composition
![]() $(\mathbf {d}')^{-1}\boldsymbol {\Pi }^{\prime \,1}$
is defined on
$(\mathbf {d}')^{-1}\boldsymbol {\Pi }^{\prime \,1}$
is defined on
![]() $\mathbf {C}^{\bullet }$
. From Equations (8.5) and (8.9), we easily get that, as
$\mathbf {C}^{\bullet }$
. From Equations (8.5) and (8.9), we easily get that, as
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
By Equations (8.5) and (8.9), on
![]() $\operatorname {im}\boldsymbol {\delta }_{z,k}\oplus \operatorname {im}\mathbf {d}_{z,k-1}$
,
$\operatorname {im}\boldsymbol {\delta }_{z,k}\oplus \operatorname {im}\mathbf {d}_{z,k-1}$
,
Proposition 8.3. For
![]() $k=0,\dots ,n$
and
$k=0,\dots ,n$
and
![]() $\mu \gg 0$
, the spectrum of
$\mu \gg 0$
, the spectrum of
![]() $\boldsymbol {\Delta }_z$
on
$\boldsymbol {\Delta }_z$
on
![]() $\operatorname {im}\boldsymbol {\delta }_{z,k}\oplus \operatorname {im}\mathbf {d}_{z,k-1}$
is contained in an interval of the form
$\operatorname {im}\boldsymbol {\delta }_{z,k}\oplus \operatorname {im}\mathbf {d}_{z,k-1}$
is contained in an interval of the form
Proof. The positive eigenvalues of
![]() $\boldsymbol {\Delta }'$
are contained in an interval
$\boldsymbol {\Delta }'$
are contained in an interval
![]() $[C_0,C^{\prime }_0]$
(
$[C_0,C^{\prime }_0]$
(
![]() $C^{\prime }_0\ge C_0>0$
). By Equation (8.12), for
$C^{\prime }_0\ge C_0>0$
). By Equation (8.12), for
![]() $\mu \gg 0$
and
$\mu \gg 0$
and
![]() $\mathbf {e}\in \operatorname {im}\boldsymbol {\delta }_{z,k}\oplus \operatorname {im}\mathbf {d}_{z,k-1}$
,
$\mathbf {e}\in \operatorname {im}\boldsymbol {\delta }_{z,k}\oplus \operatorname {im}\mathbf {d}_{z,k-1}$
,
 $$ \begin{align*} \langle\boldsymbol{\Delta}_z\mathbf{e},\mathbf{e}\rangle &\ge e^{2a_k\mu}\langle\boldsymbol{\Delta}'\mathbf{e},\mathbf{e}\rangle-C_1e^{-(2a_k+c)\mu}\|\mathbf{e}\|^2 \ge\big(C_0e^{-2a_k\mu}-C_1e^{-(2a_k+c)\mu}\big)\|\mathbf{e}\|^2\;,\\ \langle\boldsymbol{\Delta}_z\mathbf{e},\mathbf{e}\rangle &\le e^{2a_k\mu}\langle\boldsymbol{\Delta}'\mathbf{e},\mathbf{e}\rangle+C_1e^{-(2a_k+c)\mu}\|\mathbf{e}\|^2 \le\big(C^{\prime}_0e^{-2a_k\mu}+C_1e^{-(2a_k+c)\mu}\big)\|\mathbf{e}\|^2. \end{align*} $$
$$ \begin{align*} \langle\boldsymbol{\Delta}_z\mathbf{e},\mathbf{e}\rangle &\ge e^{2a_k\mu}\langle\boldsymbol{\Delta}'\mathbf{e},\mathbf{e}\rangle-C_1e^{-(2a_k+c)\mu}\|\mathbf{e}\|^2 \ge\big(C_0e^{-2a_k\mu}-C_1e^{-(2a_k+c)\mu}\big)\|\mathbf{e}\|^2\;,\\ \langle\boldsymbol{\Delta}_z\mathbf{e},\mathbf{e}\rangle &\le e^{2a_k\mu}\langle\boldsymbol{\Delta}'\mathbf{e},\mathbf{e}\rangle+C_1e^{-(2a_k+c)\mu}\|\mathbf{e}\|^2 \le\big(C^{\prime}_0e^{-2a_k\mu}+C_1e^{-(2a_k+c)\mu}\big)\|\mathbf{e}\|^2. \end{align*} $$
Then result follows taking
![]() $0<C<C_0$
and
$0<C<C_0$
and
![]() $C'>C^{\prime }_0$
.
$C'>C^{\prime }_0$
.
8.3. Estimates of the nonzero small spectrum
Theorem 8.4. If
![]() $\mu \gg 0$
, the spectrum of
$\mu \gg 0$
, the spectrum of
![]() $\Delta _{z,\mathrm {sm}}$
on
$\Delta _{z,\mathrm {sm}}$
on
![]() $\operatorname {im}\delta _{z,\mathrm {sm},k}\oplus \operatorname {im} d_{z,\mathrm {sm},k-1}$
is contained in an interval of the form
$\operatorname {im}\delta _{z,\mathrm {sm},k}\oplus \operatorname {im} d_{z,\mathrm {sm},k-1}$
is contained in an interval of the form
Proof. By the commutativity of the diagram of Equation (2.7), for every eigenvalue
![]() $\lambda $
of
$\lambda $
of
![]() $\Delta _{z,\mathrm {sm}}$
on
$\Delta _{z,\mathrm {sm}}$
on
![]() $\operatorname {im}\delta _{z,\mathrm {sm},k}\oplus \operatorname {im} d_{z,\mathrm { sm},k-1}$
, there are normalized
$\operatorname {im}\delta _{z,\mathrm {sm},k}\oplus \operatorname {im} d_{z,\mathrm { sm},k-1}$
, there are normalized
![]() $\lambda $
-eigenforms,
$\lambda $
-eigenforms,
![]() $e\in \operatorname {im}\delta _{z,\mathrm {sm},k}$
and
$e\in \operatorname {im}\delta _{z,\mathrm {sm},k}$
and
![]() $e'\in \operatorname {im} d_{z,\mathrm {sm},k-1}$
so that
$e'\in \operatorname {im} d_{z,\mathrm {sm},k-1}$
so that
![]() $d_ze=\lambda ^{1/2}e'$
and
$d_ze=\lambda ^{1/2}e'$
and
![]() $\delta _ze'=\lambda ^{1/2}e$
. So the maximum and minimum of the spectrum of
$\delta _ze'=\lambda ^{1/2}e$
. So the maximum and minimum of the spectrum of
![]() $\Delta _{z,\mathrm {sm}}$
on
$\Delta _{z,\mathrm {sm}}$
on
![]() $\operatorname {im}\delta _{z,\mathrm {sm},k}\oplus \operatorname {im} d_{z,\mathrm {sm},k-1}$
is
$\operatorname {im}\delta _{z,\mathrm {sm},k}\oplus \operatorname {im} d_{z,\mathrm {sm},k-1}$
is
![]() $\|d_{z,\mathrm {sm},k-1}\|^2$
and
$\|d_{z,\mathrm {sm},k-1}\|^2$
and
![]() $\|d_{z,\mathrm {sm},k-1}^{-1}\Pi ^1_{z,\mathrm {sm},k}\|^{-2}$
, respectively. Similarly, the maximum and minimum of the spectrum of
$\|d_{z,\mathrm {sm},k-1}^{-1}\Pi ^1_{z,\mathrm {sm},k}\|^{-2}$
, respectively. Similarly, the maximum and minimum of the spectrum of
![]() $\boldsymbol {\Delta }_z$
on
$\boldsymbol {\Delta }_z$
on
![]() $\operatorname {im}\boldsymbol {\delta }_{z,k}\oplus \operatorname {im}\mathbf {d}_{z,k-1}$
is
$\operatorname {im}\boldsymbol {\delta }_{z,k}\oplus \operatorname {im}\mathbf {d}_{z,k-1}$
is
![]() $\|\mathbf {d}_{z,k-1}\|^2$
and
$\|\mathbf {d}_{z,k-1}\|^2$
and
![]() $\|\mathbf {d}_{z,k-1}^{-1}\boldsymbol {\Pi }^1_{z,k}\|^{-2}$
, respectively. Then the result follows from Corollaries 6.9, 6.14 and 6.17 and Proposition 8.3:
$\|\mathbf {d}_{z,k-1}^{-1}\boldsymbol {\Pi }^1_{z,k}\|^{-2}$
, respectively. Then the result follows from Corollaries 6.9, 6.14 and 6.17 and Proposition 8.3:
 $$ \begin{align*} \begin{aligned} \|d_{z,\mathrm{sm},k-1}\|^2 &\le\|\Phi_{z,k}^{-1}\|^2\|\mathbf{d}_{z,k-1}\|^2\|\Phi_{z,k-1}\|^2\\ &\le\Big(\Big(\frac\mu\pi\Big)^{k-\frac n2}+O\big(e^{-c\mu}\big)\Big)C^{\prime}_0e^{-2a_k\mu} \Big(\Big(\frac\pi\mu\Big)^{k-1-\frac n2}+O\big(e^{-c\mu}\big)\Big)\\ &\le C'\mu e^{-2a_k\mu}\;, \end{aligned}\\ \begin{aligned} \|d_{z,\mathrm{sm},k-1}^{-1}\Pi^1_{z,\mathrm{sm},k-1}\|^{-2} &\ge\|\Phi_{z,k-1}^{-1}\|^{-2}\|\mathbf{d}_{z,k-1}^{-1}\boldsymbol{\Pi}^1_{z,k}\|^{-2}\|\Phi_{z,k}\|^{-2}\\ &\ge\Big(\Big(\frac\pi\mu\Big)^{k-1-\frac n2}+O\big(e^{-c\mu}\big)\Big)C_0e^{-2a_k\mu} \Big(\Big(\frac\mu\pi\Big)^{k-\frac n2}+O\big(e^{-c\mu}\big)\Big)\\ &\ge C\mu e^{-2a_k\mu}. \; \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|d_{z,\mathrm{sm},k-1}\|^2 &\le\|\Phi_{z,k}^{-1}\|^2\|\mathbf{d}_{z,k-1}\|^2\|\Phi_{z,k-1}\|^2\\ &\le\Big(\Big(\frac\mu\pi\Big)^{k-\frac n2}+O\big(e^{-c\mu}\big)\Big)C^{\prime}_0e^{-2a_k\mu} \Big(\Big(\frac\pi\mu\Big)^{k-1-\frac n2}+O\big(e^{-c\mu}\big)\Big)\\ &\le C'\mu e^{-2a_k\mu}\;, \end{aligned}\\ \begin{aligned} \|d_{z,\mathrm{sm},k-1}^{-1}\Pi^1_{z,\mathrm{sm},k-1}\|^{-2} &\ge\|\Phi_{z,k-1}^{-1}\|^{-2}\|\mathbf{d}_{z,k-1}^{-1}\boldsymbol{\Pi}^1_{z,k}\|^{-2}\|\Phi_{z,k}\|^{-2}\\ &\ge\Big(\Big(\frac\pi\mu\Big)^{k-1-\frac n2}+O\big(e^{-c\mu}\big)\Big)C_0e^{-2a_k\mu} \Big(\Big(\frac\mu\pi\Big)^{k-\frac n2}+O\big(e^{-c\mu}\big)\Big)\\ &\ge C\mu e^{-2a_k\mu}. \; \end{aligned} \end{align*} $$
8.4. Asymptotics of the small zeta invariant
Theorem 1.2 (ii) is proved here.
Theorem 8.5. As
![]() $\mu \to +\infty $
,
$\mu \to +\infty $
,
Proof. Consider the notation of Sections 6.3 and 8.2. By Corollaries 6.13 and 6.16, for
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
For brevity, let
![]() $S_z=\Phi _z\widetilde \Psi _{z-1}$
and
$S_z=\Phi _z\widetilde \Psi _{z-1}$
and
![]() $T_z=\Phi _{z-1}P_{z-1,\mathrm {sm}}\widetilde \Psi _z$
on
$T_z=\Phi _{z-1}P_{z-1,\mathrm {sm}}\widetilde \Psi _z$
on
![]() $\mathbf {C}^{\bullet }$
. By Corollaries 6.9 and 6.13,
$\mathbf {C}^{\bullet }$
. By Corollaries 6.9 and 6.13,
Moreover, by Proposition 4.19 and Corollary 6.7, and the definitions of
![]() $\Psi _z$
and
$\Psi _z$
and
![]() $\widetilde \Psi _z$
, considered as maps
$\widetilde \Psi _z$
, considered as maps
![]() $\mathbf {C}^{\bullet }\to L^2(M;\Lambda )$
, we get
$\mathbf {C}^{\bullet }\to L^2(M;\Lambda )$
, we get
 $$ \begin{align} \widetilde\Psi_zS_z=\widetilde\Psi_z\Phi_zP_{z-1,\mathrm{sm}}\widetilde\Psi_{z-1} \asymp_1\widetilde\Psi_z\Phi_zP_{z,\mathrm{sm}}\widetilde\Psi_{z-1}\nonumber\\ \asymp_1P_{z,\mathrm{sm}}\widetilde\Psi_{z-1}\asymp_1P_{z-1,\mathrm{sm}}\widetilde\Psi_{z-1}=\widetilde\Psi_{z-1}. \end{align} $$
$$ \begin{align} \widetilde\Psi_zS_z=\widetilde\Psi_z\Phi_zP_{z-1,\mathrm{sm}}\widetilde\Psi_{z-1} \asymp_1\widetilde\Psi_z\Phi_zP_{z,\mathrm{sm}}\widetilde\Psi_{z-1}\nonumber\\ \asymp_1P_{z,\mathrm{sm}}\widetilde\Psi_{z-1}\asymp_1P_{z-1,\mathrm{sm}}\widetilde\Psi_{z-1}=\widetilde\Psi_{z-1}. \end{align} $$
By Equations (8.5), (8.10), (8.11), and (8.13)–(8.15); Proposition 8.3; and Corollaries 4.20, 6.6, 6.7, 6.9, 6.11, 6.13 and 6.15 to 6.17; and Theorem 8.4,
 $$ \begin{align*} e^{a_k}\Pi^1_{z,\mathrm{sm},k}&\asymp_0 e^{a_k}\widetilde\Psi_z\boldsymbol{\Pi}^1_{z,k}\Phi_{z,\mathrm{sm}} \asymp_1 e^{a_k}\widetilde\Psi_z\boldsymbol{\Pi}^{\prime\,1}_k\Phi_{z,\mathrm{sm}}\\ &=e^{a_k}\widetilde\Psi_z\mathbf{d}^{\prime}_{k-1}(\mathbf{d}^{\prime}_{k-1})^{-1}\boldsymbol{\Pi}^{\prime\,1}_k\Phi_{z,\mathrm{sm}}\\ &\asymp_1 e^{a_k}\widetilde\Psi_zS_z\mathbf{d}^{\prime}_{k-1}T_z(\mathbf{d}^{\prime}_{k-1})^{-1}\boldsymbol{\Pi}^{\prime\,1}_k\Phi_{z,\mathrm{sm}}\\ &\asymp_1 e^{a_k}\widetilde\Psi_{z-1}\mathbf{d}^{\prime}_{k-1}T_z(\mathbf{d}^{\prime}_{k-1})^{-1}\boldsymbol{\Pi}^{\prime\,1}_k\Phi_{z,\mathrm{sm}}\\ &\asymp_1 e^{a_k}\widetilde\Psi_{z-1}e^{a_k(z-1)}\mathbf{d}_{z-1,k-1}T_z e^{-a_kz}\mathbf{d}_{z,k-1}^{-1}\boldsymbol{\Pi}^1_{z,k}\Phi_{z,\mathrm{sm}}\\ &=\widetilde\Psi_{z-1}\mathbf{d}_{z-1,k-1}T_z\mathbf{d}_{z,k-1}^{-1}\boldsymbol{\Pi}^1_{z,k}\Phi_{z,\mathrm{sm}}\\ &\asymp_0\widetilde\Psi_{z-1}\mathbf{d}_{z-1,k-1}T_z\widetilde{\boldsymbol{\Pi}}^2_{z,k-1} \mathbf{d}_{z,k-1}^{-1}\widetilde{\boldsymbol{\Pi}}^1_{z,k}\Phi_{z,\mathrm{sm}}\\ &\asymp_0\widetilde\Psi_{z-1}\mathbf{d}_{z-1,k-1}\Phi_{z-1}P_{z-1,\mathrm{sm}}\Pi^2_{z,k-1}\widetilde\Psi_z\mathbf{d}_{z,k-1}^{-1}\Phi_z\Pi^1_{z,\mathrm{sm}}\\ &\asymp_0\widetilde\Psi_{z-1}\mathbf{d}_{z-1,k-1}\Phi_{z-1}P_{z-1,\mathrm{sm}}\Pi^2_{z,k-1}\Phi_z^{-1}\mathbf{d}_{z,k-1}^{-1}\Phi_z\Pi^1_{z,\mathrm{sm}}\\ &=\widetilde\Psi_{z-1}\Phi_{z-1}d_{z-1,\mathrm{sm},k-1}d_{z,\mathrm{sm},k-1}^{-1}\Pi^1_{z,\mathrm{sm},k} \asymp_0 d_{z-1}d_z^{-1}\Pi^1_{z,\mathrm{sm},k}. \end{align*} $$
$$ \begin{align*} e^{a_k}\Pi^1_{z,\mathrm{sm},k}&\asymp_0 e^{a_k}\widetilde\Psi_z\boldsymbol{\Pi}^1_{z,k}\Phi_{z,\mathrm{sm}} \asymp_1 e^{a_k}\widetilde\Psi_z\boldsymbol{\Pi}^{\prime\,1}_k\Phi_{z,\mathrm{sm}}\\ &=e^{a_k}\widetilde\Psi_z\mathbf{d}^{\prime}_{k-1}(\mathbf{d}^{\prime}_{k-1})^{-1}\boldsymbol{\Pi}^{\prime\,1}_k\Phi_{z,\mathrm{sm}}\\ &\asymp_1 e^{a_k}\widetilde\Psi_zS_z\mathbf{d}^{\prime}_{k-1}T_z(\mathbf{d}^{\prime}_{k-1})^{-1}\boldsymbol{\Pi}^{\prime\,1}_k\Phi_{z,\mathrm{sm}}\\ &\asymp_1 e^{a_k}\widetilde\Psi_{z-1}\mathbf{d}^{\prime}_{k-1}T_z(\mathbf{d}^{\prime}_{k-1})^{-1}\boldsymbol{\Pi}^{\prime\,1}_k\Phi_{z,\mathrm{sm}}\\ &\asymp_1 e^{a_k}\widetilde\Psi_{z-1}e^{a_k(z-1)}\mathbf{d}_{z-1,k-1}T_z e^{-a_kz}\mathbf{d}_{z,k-1}^{-1}\boldsymbol{\Pi}^1_{z,k}\Phi_{z,\mathrm{sm}}\\ &=\widetilde\Psi_{z-1}\mathbf{d}_{z-1,k-1}T_z\mathbf{d}_{z,k-1}^{-1}\boldsymbol{\Pi}^1_{z,k}\Phi_{z,\mathrm{sm}}\\ &\asymp_0\widetilde\Psi_{z-1}\mathbf{d}_{z-1,k-1}T_z\widetilde{\boldsymbol{\Pi}}^2_{z,k-1} \mathbf{d}_{z,k-1}^{-1}\widetilde{\boldsymbol{\Pi}}^1_{z,k}\Phi_{z,\mathrm{sm}}\\ &\asymp_0\widetilde\Psi_{z-1}\mathbf{d}_{z-1,k-1}\Phi_{z-1}P_{z-1,\mathrm{sm}}\Pi^2_{z,k-1}\widetilde\Psi_z\mathbf{d}_{z,k-1}^{-1}\Phi_z\Pi^1_{z,\mathrm{sm}}\\ &\asymp_0\widetilde\Psi_{z-1}\mathbf{d}_{z-1,k-1}\Phi_{z-1}P_{z-1,\mathrm{sm}}\Pi^2_{z,k-1}\Phi_z^{-1}\mathbf{d}_{z,k-1}^{-1}\Phi_z\Pi^1_{z,\mathrm{sm}}\\ &=\widetilde\Psi_{z-1}\Phi_{z-1}d_{z-1,\mathrm{sm},k-1}d_{z,\mathrm{sm},k-1}^{-1}\Pi^1_{z,\mathrm{sm},k} \asymp_0 d_{z-1}d_z^{-1}\Pi^1_{z,\mathrm{sm},k}. \end{align*} $$
Therefore,
Theorem 1.2 (ii) follows from Corollaries 4.9 and 5.2 and Theorem 8.5.
9. Prescription of the asymptotics of the zeta invariant
We prove Theorem 1.3 here. By Theorem 8.1, given
![]() $a\gg 0$
, there is some
$a\gg 0$
, there is some
![]() $\eta _0\in \xi $
and some metric g satisfying (a) and (d) with the given X and so that
$\eta _0\in \xi $
and some metric g satisfying (a) and (d) with the given X and so that
![]() $\mathcal {M}_k(\eta _0,X)=a$
for all
$\mathcal {M}_k(\eta _0,X)=a$
for all
![]() $k=1,\dots ,n$
. Using the notation of Section 4.1, we are going to modify
$k=1,\dots ,n$
. Using the notation of Section 4.1, we are going to modify
![]() $\eta _0$
only in every
$\eta _0$
only in every
![]() $U_p$
for
$U_p$
for
![]() $p\in \mathcal {Y}_0\cup \mathcal {Y}_n$
.
$p\in \mathcal {Y}_0\cup \mathcal {Y}_n$
.
Fix any
![]() $\epsilon>0$
such that, for every
$\epsilon>0$
such that, for every
![]() $p\in \mathcal {Y}_0\cup \mathcal {Y}_n$
, the open ball
$p\in \mathcal {Y}_0\cup \mathcal {Y}_n$
, the open ball
![]() $B(p,3\epsilon )$
is contained in
$B(p,3\epsilon )$
is contained in
![]() $U_p$
. Let
$U_p$
. Let
Take a smooth function
![]() $\sigma :[0,3\epsilon ]\to [0,1]$
so that
$\sigma :[0,3\epsilon ]\to [0,1]$
so that
Let
![]() $f_j\in C^\infty (M,\mathbb {R})$
(
$f_j\in C^\infty (M,\mathbb {R})$
(
![]() $j=0,n$
) be the extension by zero of the combination of the functions
$j=0,n$
) be the extension by zero of the combination of the functions
![]() $\sigma (|x_p|)\in C^\infty _{\mathrm {c}}(B(p,3\epsilon ),\mathbb {R})$
(
$\sigma (|x_p|)\in C^\infty _{\mathrm {c}}(B(p,3\epsilon ),\mathbb {R})$
(
![]() $p\in \mathcal {Y}_j$
). We have
$p\in \mathcal {Y}_j$
). We have
For any
![]() $c_0,c_n\ge 0$
, let
$c_0,c_n\ge 0$
, let
![]() $\eta =\eta (c_0,c_n)=\eta _0-c_0\,df_0+c_n\,df_n$
. This closed 1-form satisfies (a) and (d) with X and g, and we have
$\eta =\eta (c_0,c_n)=\eta _0-c_0\,df_0+c_n\,df_n$
. This closed 1-form satisfies (a) and (d) with X and g, and we have
Hence, by Corollary 4.15,
By (a),
![]() $e(M,\nabla ^M)=0$
on every
$e(M,\nabla ^M)=0$
on every
![]() $U_p$
(
$U_p$
(
![]() $p\in \mathcal {Y}$
). So, using the Stokes formula,
$p\in \mathcal {Y}$
). So, using the Stokes formula,
 $$ \begin{align} \mathbf{z}_{\mathrm{la}}(\eta)-\mathbf{z}_{\mathrm{la}}(\eta_0) &=\int_M(c_n\,df_n-c_0\,df_0)\wedge (-X)^*\psi(M,\nabla^M)\nonumber\\ &=\int_M(c_0f_0-c_nf_n)\,(-X)^*d\psi(M,\nabla^M)\nonumber\\ &=\int_M(c_0f_0-c_nf_n)\,e(M,\nabla^M)-\sum_{p\in\mathcal{Y}}(-1)^{\operatorname{ind}(p)}(c_0f_0-c_nf_n)(p)\nonumber\\ &=(-1)^nc_n|\mathcal{Y}_n|-c_0|\mathcal{Y}_0|. \end{align} $$
$$ \begin{align} \mathbf{z}_{\mathrm{la}}(\eta)-\mathbf{z}_{\mathrm{la}}(\eta_0) &=\int_M(c_n\,df_n-c_0\,df_0)\wedge (-X)^*\psi(M,\nabla^M)\nonumber\\ &=\int_M(c_0f_0-c_nf_n)\,(-X)^*d\psi(M,\nabla^M)\nonumber\\ &=\int_M(c_0f_0-c_nf_n)\,e(M,\nabla^M)-\sum_{p\in\mathcal{Y}}(-1)^{\operatorname{ind}(p)}(c_0f_0-c_nf_n)(p)\nonumber\\ &=(-1)^nc_n|\mathcal{Y}_n|-c_0|\mathcal{Y}_0|. \end{align} $$
Combining Equations (9.1) and (9.2), we obtain
Using local changes of X and applying [Reference Smale69, Lemmas 1.1 and 1.2], we can increase
![]() $|\mathcal {Y}_0|$
or
$|\mathcal {Y}_0|$
or
![]() $|\mathcal {Y}_n|$
as much as desired. By Lemma 4.12 and Equation (4.21), we have
$|\mathcal {Y}_n|$
as much as desired. By Lemma 4.12 and Equation (4.21), we have
which can be increased as much as desired. So, if n is even (resp., odd), given any
![]() $\tau \in \mathbb {R}$
(resp.,
$\tau \in \mathbb {R}$
(resp.,
![]() $\tau \gg 0$
), we get
$\tau \gg 0$
), we get
![]() $\mathbf {z}(\eta (c_0,c_n))=\tau $
for some
$\mathbf {z}(\eta (c_0,c_n))=\tau $
for some
![]() $c_0,c_n\ge 0$
.
$c_0,c_n\ge 0$
.
Now, assume n is even. To prove that
![]() $\pm \mathbf {z}(\pm \eta )=\tau $
, by Equations (7.9), (9.1) and (9.2), it is enough to prove that we can choose
$\pm \mathbf {z}(\pm \eta )=\tau $
, by Equations (7.9), (9.1) and (9.2), it is enough to prove that we can choose
![]() $|\mathcal {Y}_0|$
,
$|\mathcal {Y}_0|$
,
![]() $|\mathcal {Y}_n|$
,
$|\mathcal {Y}_n|$
,
![]() $c_0$
and
$c_0$
and
![]() $c_n$
so that
$c_n$
so that
 $$ \begin{align*} \mathbf{z}_{\mathrm{sm}}(\eta) &=\mathbf{z}_{\mathrm{sm}}(\eta_0) +e^a(e^{c_0}-1)m^1_1+e^a(1-e^{c_n})m^1_n=0,\\ \mathbf{z}_{\mathrm{la}}(\eta) &=\mathbf{z}_{\mathrm{la}}(\eta_0) +c_n|\mathcal{Y}_n|-c_0|\mathcal{Y}_0|=\tau. \end{align*} $$
$$ \begin{align*} \mathbf{z}_{\mathrm{sm}}(\eta) &=\mathbf{z}_{\mathrm{sm}}(\eta_0) +e^a(e^{c_0}-1)m^1_1+e^a(1-e^{c_n})m^1_n=0,\\ \mathbf{z}_{\mathrm{la}}(\eta) &=\mathbf{z}_{\mathrm{la}}(\eta_0) +c_n|\mathcal{Y}_n|-c_0|\mathcal{Y}_0|=\tau. \end{align*} $$
Using Equation (9.3) and writing
![]() $u=-e^{-a}\mathbf {z}_{\mathrm {sm}}(\eta _0)$
and
$u=-e^{-a}\mathbf {z}_{\mathrm {sm}}(\eta _0)$
and
![]() $v=\tau -\mathbf {z}_{\mathrm {la}}(\eta _0)$
, the above system becomes
$v=\tau -\mathbf {z}_{\mathrm {la}}(\eta _0)$
, the above system becomes
 $$ \begin{align*} (e^{c_0}-1)(|\mathcal{Y}_0|-\beta_{\mathrm{No}}^0)+(1-e^{c_n})(|\mathcal{Y}_n|-\beta_{\mathrm{No}}^n) &=u,\\ c_n|\mathcal{Y}_n|-c_0|\mathcal{Y}_0| &=v. \end{align*} $$
$$ \begin{align*} (e^{c_0}-1)(|\mathcal{Y}_0|-\beta_{\mathrm{No}}^0)+(1-e^{c_n})(|\mathcal{Y}_n|-\beta_{\mathrm{No}}^n) &=u,\\ c_n|\mathcal{Y}_n|-c_0|\mathcal{Y}_0| &=v. \end{align*} $$
The following result states that these equalities are satisfied by some
![]() $c_0,c_n\ge 0$
and
$c_0,c_n\ge 0$
and
![]() $|\mathcal {Y}_0|,|\mathcal {Y}_n|\gg 0$
.
$|\mathcal {Y}_0|,|\mathcal {Y}_n|\gg 0$
.
Lemma 9.1. Given
![]() $u,v\in \mathbb {R}$
and
$u,v\in \mathbb {R}$
and
![]() $\beta ,\gamma \ge 0$
, there are
$\beta ,\gamma \ge 0$
, there are
![]() $c,d\ge 0$
and integers
$c,d\ge 0$
and integers
![]() $p,q\gg 0$
such that
$p,q\gg 0$
such that
 $$ \begin{align*} (e^c-1)(p-\beta)+(1-e^d)(q-\gamma) &=u,\\ dq-cp&=v. \end{align*} $$
$$ \begin{align*} (e^c-1)(p-\beta)+(1-e^d)(q-\gamma) &=u,\\ dq-cp&=v. \end{align*} $$
Proof. Taking
![]() $q>0$
, we get
$q>0$
, we get
Thus,
![]() $cp+v\ge 0$
; that is,
$cp+v\ge 0$
; that is,
![]() $c\ge -v/p$
. Let
$c\ge -v/p$
. Let
We have to find integers
![]() $p,q\gg 0$
and
$p,q\gg 0$
and
![]() $c\ge 0,-v/p$
such that
$c\ge 0,-v/p$
such that
![]() $F_{p,q}(c)=u$
.
$F_{p,q}(c)=u$
.
Observe that
Note also that, if
![]() $(c,d,p,q)$
is a solution for some
$(c,d,p,q)$
is a solution for some
![]() $(u,v, \beta , \gamma )$
, then
$(u,v, \beta , \gamma )$
, then
![]() $(d,c,q,p)$
is a solution for
$(d,c,q,p)$
is a solution for
![]() $(-u,-v, \gamma ,\beta )$
. So it is sufficient to consider the case
$(-u,-v, \gamma ,\beta )$
. So it is sufficient to consider the case
![]() $v\geq 0$
. In this case, c can reach
$v\geq 0$
. In this case, c can reach
![]() $0$
and
$0$
and
which is independent of p. Choose
![]() $q\gg \beta ,\gamma $
; thus,
$q\gg \beta ,\gamma $
; thus,
![]() $F_{p,q}(0)\le 0$
. If
$F_{p,q}(0)\le 0$
. If
![]() $u\ge F_{p,q}(0)$
, take p so that
$u\ge F_{p,q}(0)$
, take p so that
![]() $\beta \ll p<q$
, yielding
$\beta \ll p<q$
, yielding
![]() $u\in \operatorname {im} F_{p,q}$
by Equation (9.4). If
$u\in \operatorname {im} F_{p,q}$
by Equation (9.4). If
![]() $u<F_{p,q}(0)$
, take
$u<F_{p,q}(0)$
, take
![]() $p>q$
, yielding
$p>q$
, yielding
![]() $u\in \operatorname {im} F_{p,q}$
by Equation (9.5).
$u\in \operatorname {im} F_{p,q}$
by Equation (9.5).
10. The switch of the order of integration
The proof of Theorem 1.4 is given in this section. Let
![]() $\mathcal {S}$
be the Schwartz space on
$\mathcal {S}$
be the Schwartz space on
![]() $\mathbb {R}$
. Recall that the space of tempered distributions is the continuous dual space
$\mathbb {R}$
. Recall that the space of tempered distributions is the continuous dual space
![]() $\mathcal {S}'$
, with the strong topology. Suppose first that Equation (1.7) is used as definition of
$\mathcal {S}'$
, with the strong topology. Suppose first that Equation (1.7) is used as definition of
![]() $Z_\mu $
. By Theorems 1.1 and 1.2, the expression (1.7) defines a tempered distribution
$Z_\mu $
. By Theorems 1.1 and 1.2, the expression (1.7) defines a tempered distribution
![]() $Z_\mu $
for
$Z_\mu $
for
![]() $\mu \gg 0$
. Moreover, using also the formula of the inverse Fourier transform, we get, for
$\mu \gg 0$
. Moreover, using also the formula of the inverse Fourier transform, we get, for
![]() $f\in \mathcal {S}$
,
$f\in \mathcal {S}$
,
 $$\begin{align*}\langle Z_\mu,f\rangle=\frac{1}{2\pi}\int_{-\infty}^\infty\zeta(1,z)\,\hat f(\nu)\,d\nu \to\frac{\mathbf{z}}{2\pi}\int_{-\infty}^\infty\hat f(\nu)\,d\nu =\mathbf{z} f(0)\;, \end{align*}$$
$$\begin{align*}\langle Z_\mu,f\rangle=\frac{1}{2\pi}\int_{-\infty}^\infty\zeta(1,z)\,\hat f(\nu)\,d\nu \to\frac{\mathbf{z}}{2\pi}\int_{-\infty}^\infty\hat f(\nu)\,d\nu =\mathbf{z} f(0)\;, \end{align*}$$
as
![]() $\mu \to +\infty $
, uniformly on
$\mu \to +\infty $
, uniformly on
![]() $\nu $
. For every
$\nu $
. For every
![]() $C>0$
, this convergence is also uniform on
$C>0$
, this convergence is also uniform on
![]() $f\in \mathcal {S}$
with
$f\in \mathcal {S}$
with
![]() $|\hat f(\nu )|,|\nu ^2\hat f(\nu )|\le C$
. So
$|\hat f(\nu )|,|\nu ^2\hat f(\nu )|\le C$
. So
![]() $Z_\mu \to \mathbf {z}\delta _0$
in
$Z_\mu \to \mathbf {z}\delta _0$
in
![]() $\mathcal {S}'$
as
$\mathcal {S}'$
as
![]() $\mu \to +\infty $
. To get Theorem 1.4, it only remains to prove the following.
$\mu \to +\infty $
. To get Theorem 1.4, it only remains to prove the following.
Theorem 10.1. Both Equations (1.4) and (1.7) define the same tempered distribution
![]() $Z_\mu $
for
$Z_\mu $
for
![]() $\mu \gg 0$
.
$\mu \gg 0$
.
Proposition 10.2. For
![]() $\mu \gg 0$
,
$\mu \gg 0$
,
![]() $t>0$
and
$t>0$
and
![]() $f\in \mathcal {S}$
,
$f\in \mathcal {S}$
,
 $$\begin{align*}\int_{-\infty}^\infty\int_t^\infty\big|\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\big|\,|\hat f(\nu)|\,du\,d\nu<\infty. \end{align*}$$
$$\begin{align*}\int_{-\infty}^\infty\int_t^\infty\big|\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\big|\,|\hat f(\nu)|\,du\,d\nu<\infty. \end{align*}$$
Proof. By [Reference Dunford and Schwartz26, Corollary XI.9.8 and Lemma XI.9.9 (d)],
 $$ \begin{align*} \big|\operatorname{Str}\big({\eta\wedge}\,\delta_{z}e^{-u\Delta_z}\big)\big| &\le\big|{\eta\wedge}\,\delta_{z}e^{-u\Delta_z}\big|_1 \le\|{\eta\wedge}\|\,\big|\delta_{z}e^{-u\Delta_z}\big|_1\\ &=\|\eta\|_{L^\infty}\,\operatorname{Tr}\big((d_{z}\delta_{z})^{1/2}e^{-u\Delta_z}\big) \le\|\eta\|_{L^\infty}\,\operatorname{Tr}\big(\Delta_{z}^{1/2}e^{-u\Delta_z}\big)\;, \end{align*} $$
$$ \begin{align*} \big|\operatorname{Str}\big({\eta\wedge}\,\delta_{z}e^{-u\Delta_z}\big)\big| &\le\big|{\eta\wedge}\,\delta_{z}e^{-u\Delta_z}\big|_1 \le\|{\eta\wedge}\|\,\big|\delta_{z}e^{-u\Delta_z}\big|_1\\ &=\|\eta\|_{L^\infty}\,\operatorname{Tr}\big((d_{z}\delta_{z})^{1/2}e^{-u\Delta_z}\big) \le\|\eta\|_{L^\infty}\,\operatorname{Tr}\big(\Delta_{z}^{1/2}e^{-u\Delta_z}\big)\;, \end{align*} $$
where
![]() $|\ |_1$
denotes the trace norm. Hence,
$|\ |_1$
denotes the trace norm. Hence,
 $$ \begin{align*} \int_t^\infty\big|\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\big|\,du &\le\|\eta\|_{L^\infty}\int_t^\infty \operatorname{Tr}\big(\Delta_{z}^{1/2}e^{-u\Delta_z}\big)\,du\\ &=\|\eta\|_{L^\infty} \operatorname{Tr}\big(\Delta_{z}^{-1/2}e^{-t\Delta_z}\Pi_z^\perp\big). \end{align*} $$
$$ \begin{align*} \int_t^\infty\big|\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\big|\,du &\le\|\eta\|_{L^\infty}\int_t^\infty \operatorname{Tr}\big(\Delta_{z}^{1/2}e^{-u\Delta_z}\big)\,du\\ &=\|\eta\|_{L^\infty} \operatorname{Tr}\big(\Delta_{z}^{-1/2}e^{-t\Delta_z}\Pi_z^\perp\big). \end{align*} $$
The operator
![]() $(1+\Delta )^{-N}$
is of trace class for any
$(1+\Delta )^{-N}$
is of trace class for any
![]() $N>n$
. Therefore,
$N>n$
. Therefore,
By Corollary 2.3 and Theorem 8.4, for
![]() $\mu \gg 0$
and
$\mu \gg 0$
and
![]() $\alpha \in L^2(M;\Lambda )$
,
$\alpha \in L^2(M;\Lambda )$
,
 $$ \begin{align*} &\big\|(1+\Delta)^{N}\Delta_{z}^{-1/2}e^{-t\Delta_z}\Pi_z^\perp\alpha \big\|\\ &\quad \le C_0 \big\|\Delta_{z}^{-1/2}e^{-t\Delta_z}\Pi_z^\perp\alpha \big\|_{2N} \le C_1|z|^{2N} \big\|\Delta_{z}^{-1/2}e^{-t\Delta_z}\Pi_z^\perp\alpha \big\|_{2N,z}\\ &\quad = C_2 |z|^{2N} \sum_{k=0}^{2N}\big\|D_z^k\Delta_{z}^{-1/2}e^{-t\Delta_z}\Pi_z^\perp\alpha \big\| \le C_3|z|^{2N}\sum_{k=0}^{2N}\frac1{t^{k/2}}\big\|\Delta_{z}^{-1/2}\Pi_z^\perp\alpha \big\|\\ &\quad \le C|z|^{2N}\big(1+t^{-N}\big)e^{c \mu}\|\alpha\|. \end{align*} $$
$$ \begin{align*} &\big\|(1+\Delta)^{N}\Delta_{z}^{-1/2}e^{-t\Delta_z}\Pi_z^\perp\alpha \big\|\\ &\quad \le C_0 \big\|\Delta_{z}^{-1/2}e^{-t\Delta_z}\Pi_z^\perp\alpha \big\|_{2N} \le C_1|z|^{2N} \big\|\Delta_{z}^{-1/2}e^{-t\Delta_z}\Pi_z^\perp\alpha \big\|_{2N,z}\\ &\quad = C_2 |z|^{2N} \sum_{k=0}^{2N}\big\|D_z^k\Delta_{z}^{-1/2}e^{-t\Delta_z}\Pi_z^\perp\alpha \big\| \le C_3|z|^{2N}\sum_{k=0}^{2N}\frac1{t^{k/2}}\big\|\Delta_{z}^{-1/2}\Pi_z^\perp\alpha \big\|\\ &\quad \le C|z|^{2N}\big(1+t^{-N}\big)e^{c \mu}\|\alpha\|. \end{align*} $$
Thus, since
![]() $f\in \mathcal {S}$
,
$f\in \mathcal {S}$
,
 $$ \begin{align*} & \int_{-\infty}^\infty\int_t^\infty\big|\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\big|\,|\hat f(\nu)|\,du\,d\nu\\ &\quad \le C\|\eta\|_{L^\infty}\big|(1+\Delta)^{-N}\big|_1\big(1+t^{-N}\big)e^{c \mu} \int_{-\infty}^\infty|z|^{2N}|\hat f(\nu)|\,d\nu<\infty. \; \end{align*} $$
$$ \begin{align*} & \int_{-\infty}^\infty\int_t^\infty\big|\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\big|\,|\hat f(\nu)|\,du\,d\nu\\ &\quad \le C\|\eta\|_{L^\infty}\big|(1+\Delta)^{-N}\big|_1\big(1+t^{-N}\big)e^{c \mu} \int_{-\infty}^\infty|z|^{2N}|\hat f(\nu)|\,d\nu<\infty. \; \end{align*} $$
Proof of Theorem 10.1
We compute
 $$ \begin{align*} & -\frac{1}{2\pi}\int_{-\infty}^\infty\lim_{t\downarrow0}\operatorname{Str}\left({\eta\wedge}\,d_z^{-1}e^{-t\Delta_z}\Pi_z^1\right)\, \hat f(\nu)\,d\nu\\ &\quad =-\frac{1}{2\pi}\lim_{t\downarrow0}\int_{-\infty}^\infty\operatorname{Str}\big({\eta\wedge}\,d_z^{-1}e^{-t\Delta_z}\Pi_z^1\big)\,\hat f(\nu)\,d\nu\\ &\quad =\frac{1}{2\pi}\lim_{t\downarrow0}\int_{-\infty}^\infty\int_t^\infty\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\,\hat f(\nu)\,du\,d\nu\\ &\quad =\frac{1}{2\pi}\lim_{t\downarrow0}\int_t^\infty\int_{-\infty}^\infty\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\,\hat f(\nu)\,d\nu\,du\\ &\quad =\frac{1}{2\pi}\int_0^\infty\int_{-\infty}^\infty\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\,\hat f(\nu)\,d\nu\,du. \; \end{align*} $$
$$ \begin{align*} & -\frac{1}{2\pi}\int_{-\infty}^\infty\lim_{t\downarrow0}\operatorname{Str}\left({\eta\wedge}\,d_z^{-1}e^{-t\Delta_z}\Pi_z^1\right)\, \hat f(\nu)\,d\nu\\ &\quad =-\frac{1}{2\pi}\lim_{t\downarrow0}\int_{-\infty}^\infty\operatorname{Str}\big({\eta\wedge}\,d_z^{-1}e^{-t\Delta_z}\Pi_z^1\big)\,\hat f(\nu)\,d\nu\\ &\quad =\frac{1}{2\pi}\lim_{t\downarrow0}\int_{-\infty}^\infty\int_t^\infty\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\,\hat f(\nu)\,du\,d\nu\\ &\quad =\frac{1}{2\pi}\lim_{t\downarrow0}\int_t^\infty\int_{-\infty}^\infty\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\,\hat f(\nu)\,d\nu\,du\\ &\quad =\frac{1}{2\pi}\int_0^\infty\int_{-\infty}^\infty\operatorname{Str}\big({\eta\wedge}\,\delta_ze^{-u\Delta_z}\big)\,\hat f(\nu)\,d\nu\,du. \; \end{align*} $$
Here, the first equality is given by the Lebesgue’s dominated convergence theorem, whose hypothesis is satisfied because
![]() $\hat f\in \mathcal {S}$
and
$\hat f\in \mathcal {S}$
and
![]() $|\operatorname {Str}({\eta \wedge }\,d_z^{-1}e^{-t\Delta _z}\Pi _z^1)|\le C$
for all
$|\operatorname {Str}({\eta \wedge }\,d_z^{-1}e^{-t\Delta _z}\Pi _z^1)|\le C$
for all
![]() $t>0$
,
$t>0$
,
![]() $|\mu |\gg 0$
and
$|\mu |\gg 0$
and
![]() $\nu \in \mathbb {R}$
by Theorems 1.1 and 1.2. The third equality is given by Fubini’s theorem, whose hypothesis is satisfied by Proposition 10.2.
$\nu \in \mathbb {R}$
by Theorems 1.1 and 1.2. The third equality is given by Fubini’s theorem, whose hypothesis is satisfied by Proposition 10.2.
A Integrals along instantons
Theorem 8.1 is proved here. We show the case where
![]() $a_n\ge \dots \ge a_1\gg 0$
. Then the case where
$a_n\ge \dots \ge a_1\gg 0$
. Then the case where
![]() $a_1\ge \dots \ge a_n\gg 0$
follows by using
$a_1\ge \dots \ge a_n\gg 0$
follows by using
![]() $-X$
and
$-X$
and
![]() $-\xi $
.
$-\xi $
.
By [Reference Smale69, Theorem B], there is some Morse function h on M such that
![]() $h(\mathcal {Y}_k)=\{k\}$
(
$h(\mathcal {Y}_k)=\{k\}$
(
![]() $k=0,\dots ,n$
),
$k=0,\dots ,n$
),
![]() $Xh<0$
on
$Xh<0$
on
![]() $M\setminus \mathcal {Y}$
, and h is in standard form with respect to X; in particular,
$M\setminus \mathcal {Y}$
, and h is in standard form with respect to X; in particular,
![]() $\operatorname {Crit}_k(h)=\mathcal {Y}_k$
. Now, we proceed like in the proof of [Reference Burghelea and Haller18, Proposition 16 (i)]. Since
$\operatorname {Crit}_k(h)=\mathcal {Y}_k$
. Now, we proceed like in the proof of [Reference Burghelea and Haller18, Proposition 16 (i)]. Since
![]() $\mathcal {Y}$
is finite, there is some
$\mathcal {Y}$
is finite, there is some
![]() $\eta '\in \xi $
such that
$\eta '\in \xi $
such that
![]() $\eta '=0$
on some open neighborhood
$\eta '=0$
on some open neighborhood
![]() $U_p$
of every
$U_p$
of every
![]() $p\in \mathcal {Y}$
. Let
$p\in \mathcal {Y}$
. Let
![]() $U_k=\bigcup _{p\in \mathcal {Y}_k}U_p$
and
$U_k=\bigcup _{p\in \mathcal {Y}_k}U_p$
and
![]() $U=\bigcup _kU_k$
. We can assume
$U=\bigcup _kU_k$
. We can assume
![]() $h(U_k)\subset (k-1/4,k+1/4)$
for all
$h(U_k)\subset (k-1/4,k+1/4)$
for all
![]() $k=0,\dots ,n$
. If
$k=0,\dots ,n$
. If
![]() $C\gg 0$
, then the representative
$C\gg 0$
, then the representative
![]() $\eta ":=\eta '+C\,dh$
of
$\eta ":=\eta '+C\,dh$
of
![]() $\xi $
satisfies
$\xi $
satisfies
![]() $\eta "(X)<0$
on
$\eta "(X)<0$
on
![]() $M\setminus \mathcal {Y}$
.
$M\setminus \mathcal {Y}$
.
For
![]() $k=0,\dots ,n$
, let
$k=0,\dots ,n$
, let
![]() $I_k^\pm \subset \mathbb {R}$
be the closed interval with boundary points
$I_k^\pm \subset \mathbb {R}$
be the closed interval with boundary points
![]() $k\pm 1/4$
and
$k\pm 1/4$
and
![]() $k\pm 1/2$
. Since there are no critical values of h in
$k\pm 1/2$
. Since there are no critical values of h in
![]() $I_k^\pm $
, every
$I_k^\pm $
, every
![]() $T_k^\pm :=h^{-1}(I_k^\pm )$
is compact submanifold with boundary of dimension n, every
$T_k^\pm :=h^{-1}(I_k^\pm )$
is compact submanifold with boundary of dimension n, every
![]() $\Sigma _k^\pm :=h^{-1}(k\pm 1/2)$
is a closed submanifold of codimension
$\Sigma _k^\pm :=h^{-1}(k\pm 1/2)$
is a closed submanifold of codimension
![]() $1$
, and there are identities
$1$
, and there are identities
![]() $T_k^\pm \equiv \Sigma _k^\pm \times I_k^\pm $
given by
$T_k^\pm \equiv \Sigma _k^\pm \times I_k^\pm $
given by
![]() $x\equiv (\pi _k^\pm (x),h(x))$
(
$x\equiv (\pi _k^\pm (x),h(x))$
(
![]() $x\in T_k^\pm $
), where
$x\in T_k^\pm $
), where
![]() $\pi _k^\pm (x)$
is the unique point of
$\pi _k^\pm (x)$
is the unique point of
![]() $\Sigma _k^\pm $
that meets the
$\Sigma _k^\pm $
that meets the
![]() $\phi $
-orbit of x. Of course,
$\phi $
-orbit of x. Of course,
![]() $\Sigma _k^-=\Sigma _{k-1}^+$
(
$\Sigma _k^-=\Sigma _{k-1}^+$
(
![]() $k=1,\dots ,n$
) and
$k=1,\dots ,n$
) and
![]() $T_0^-=\Sigma _0^-=T_n^+=\Sigma _n^+=\emptyset $
. (See Figure 1.)
$T_0^-=\Sigma _0^-=T_n^+=\Sigma _n^+=\emptyset $
. (See Figure 1.)

Figure 1 A representation of the sets
![]() $T_k^\pm $
,
$T_k^\pm $
,
![]() $\Sigma _k^\pm $
,
$\Sigma _k^\pm $
,
![]() $T_{k-1}^+$
and
$T_{k-1}^+$
and
![]() $T_{k+1}^-$
, taking
$T_{k+1}^-$
, taking
![]() $\mathcal {Y}_k=\{p\}$
.
$\mathcal {Y}_k=\{p\}$
.
We have
![]() $\Sigma _k^\pm \pitchfork \iota _p^\pm (W^\pm _p)$
for
$\Sigma _k^\pm \pitchfork \iota _p^\pm (W^\pm _p)$
for
![]() $p\in \mathcal {Y}_k$
. Let
$p\in \mathcal {Y}_k$
. Let
![]() $K_p^\pm =\Sigma _k^\pm \cap \iota _p^\pm (W^\pm _p)$
and
$K_p^\pm =\Sigma _k^\pm \cap \iota _p^\pm (W^\pm _p)$
and
![]() $K_k^\pm =\bigcup _{p\in \mathcal {Y}_k}K_p^\pm $
, which are closed submanifolds of
$K_k^\pm =\bigcup _{p\in \mathcal {Y}_k}K_p^\pm $
, which are closed submanifolds of
![]() $\Sigma _k^\pm $
;
$\Sigma _k^\pm $
;
![]() $K_k^-$
is of codimension k in
$K_k^-$
is of codimension k in
![]() $\Sigma _k^-$
, and
$\Sigma _k^-$
, and
![]() $K_k^+$
of codimension
$K_k^+$
of codimension
![]() $n-k$
in
$n-k$
in
![]() $\Sigma _k^+$
. Since the
$\Sigma _k^+$
. Since the
![]() $\alpha $
- and
$\alpha $
- and
![]() $\omega $
-limits of the orbits of X are zero points, the orbit of
$\omega $
-limits of the orbits of X are zero points, the orbit of
![]() $\phi $
through every point
$\phi $
through every point
![]() $x\in \Sigma _k^+\setminus K_k^+$
meets
$x\in \Sigma _k^+\setminus K_k^+$
meets
![]() $\Sigma _k^-\setminus K_k^-$
at a unique point
$\Sigma _k^-\setminus K_k^-$
at a unique point
![]() $\psi _k(x):=\phi ^{\tau _k(x)}(x)$
(
$\psi _k(x):=\phi ^{\tau _k(x)}(x)$
(
![]() $\tau _k(x)>0$
). This defines a diffeomorphism
$\tau _k(x)>0$
). This defines a diffeomorphism
![]() $\psi _k:\Sigma _k^+\setminus K_k^+\to \Sigma _k^-\setminus K_k^-$
and a smooth function
$\psi _k:\Sigma _k^+\setminus K_k^+\to \Sigma _k^-\setminus K_k^-$
and a smooth function
![]() $\tau _k:\Sigma _k^+\setminus K_k^+\to \mathbb {R}^+$
. Moreover, the sets
$\tau _k:\Sigma _k^+\setminus K_k^+\to \mathbb {R}^+$
. Moreover, the sets
![]() $K_p^\pm $
(
$K_p^\pm $
(
![]() $p\in \mathcal {Y}_k$
) have corresponding open neighborhoods
$p\in \mathcal {Y}_k$
) have corresponding open neighborhoods
![]() $V_p^\pm $
in
$V_p^\pm $
in
![]() $\Sigma _k^\pm $
, with disjoint closures, such that
$\Sigma _k^\pm $
, with disjoint closures, such that
![]() $\psi _k(V_p^+\setminus K_p^+)=V_p^-\setminus K_p^-$
. Take smooth functions
$\psi _k(V_p^+\setminus K_p^+)=V_p^-\setminus K_p^-$
. Take smooth functions
![]() $\lambda _p^\pm $
(
$\lambda _p^\pm $
(
![]() $p\in \mathcal {Y}_k)$
on
$p\in \mathcal {Y}_k)$
on
![]() $\Sigma _k^\pm $
so that
$\Sigma _k^\pm $
so that
![]() $0\le \lambda _p^\pm \le 1$
,
$0\le \lambda _p^\pm \le 1$
,
![]() $\operatorname {supp}\lambda _p^\pm \subset V_p^\pm $
,
$\operatorname {supp}\lambda _p^\pm \subset V_p^\pm $
,
![]() $\lambda _p^\pm =1$
on
$\lambda _p^\pm =1$
on
![]() $K_p^\pm $
and
$K_p^\pm $
and
![]() $\lambda _p^+=\psi _k^*\lambda _p^-$
on
$\lambda _p^+=\psi _k^*\lambda _p^-$
on
![]() $\Sigma _k^+\setminus K_k^+$
. Moreover, let
$\Sigma _k^+\setminus K_k^+$
. Moreover, let
 $$ \begin{align*} \widetilde T_k&=h^{-1}([k-1/2,k+1/2])\;,\quad \widetilde K_p=\widetilde T_k\cap\big(\iota_p^+(W^+_p)\cup\iota_p^-(W^-_p)\big)\;,\\ \widetilde V_p&=\{\,\phi^t(x)\mid x\in V_p^+\setminus K_p^+,\ 0\le t\le\tau_k(x)\,\}\cup\widetilde K_p\;,\\ \widetilde K_k&=\bigcup_{p\in\mathcal{Y}_k}\widetilde K_p\;,\quad \widetilde V_k=\bigcup_{p\in\mathcal{Y}_k}\widetilde V_p\;,\quad M_k=h^{-1}((-\infty,k+1/2]). \end{align*} $$
$$ \begin{align*} \widetilde T_k&=h^{-1}([k-1/2,k+1/2])\;,\quad \widetilde K_p=\widetilde T_k\cap\big(\iota_p^+(W^+_p)\cup\iota_p^-(W^-_p)\big)\;,\\ \widetilde V_p&=\{\,\phi^t(x)\mid x\in V_p^+\setminus K_p^+,\ 0\le t\le\tau_k(x)\,\}\cup\widetilde K_p\;,\\ \widetilde K_k&=\bigcup_{p\in\mathcal{Y}_k}\widetilde K_p\;,\quad \widetilde V_k=\bigcup_{p\in\mathcal{Y}_k}\widetilde V_p\;,\quad M_k=h^{-1}((-\infty,k+1/2]). \end{align*} $$
Thus,
![]() $M_k=\widetilde T_0\cup \dots \cup \widetilde T_k$
. Note that
$M_k=\widetilde T_0\cup \dots \cup \widetilde T_k$
. Note that
![]() $\widetilde T_k$
and
$\widetilde T_k$
and
![]() $M_k$
are compact submanifolds with boundary of dimension n, and every
$M_k$
are compact submanifolds with boundary of dimension n, and every
![]() $\widetilde V_p$
(resp.,
$\widetilde V_p$
(resp.,
![]() $\widetilde K_p$
) is open (resp., closed) in
$\widetilde K_p$
) is open (resp., closed) in
![]() $\widetilde T_k$
. We also get smooth functions
$\widetilde T_k$
. We also get smooth functions
![]() $\tilde \lambda _p$
(
$\tilde \lambda _p$
(
![]() $p\in \mathcal {Y}_k$
) on
$p\in \mathcal {Y}_k$
) on
![]() $\widetilde T_k$
determined by the condition
$\widetilde T_k$
determined by the condition
![]() $\tilde \lambda _p(\phi ^t(x))=\lambda _p^+(x)$
for all
$\tilde \lambda _p(\phi ^t(x))=\lambda _p^+(x)$
for all
![]() $x\in \Sigma _k^+\setminus K_k^+$
and
$x\in \Sigma _k^+\setminus K_k^+$
and
![]() $0\le t\le \tau _k(x)$
. They satisfy
$0\le t\le \tau _k(x)$
. They satisfy
![]() $0\le \tilde \lambda _p\le 1$
,
$0\le \tilde \lambda _p\le 1$
,
![]() $\operatorname {supp}\tilde \lambda _p\subset \widetilde V_p$
and
$\operatorname {supp}\tilde \lambda _p\subset \widetilde V_p$
and
![]() $\tilde \lambda _p=1$
on
$\tilde \lambda _p=1$
on
![]() $\widetilde K_p$
.
$\widetilde K_p$
.
Let
 $$ \begin{align*} A_p &=\max\{\,|\eta'(\gamma)|\mid\gamma\in\mathcal{T}^1_p\,\}\quad\big(p\in\mathcal{Y}_+\big)\;,\\ A_k &=\max_{p\in\mathcal{Y}_k}A_p\quad(k=1,\dots,n)\;,\quad A=\max\{A_1,\dots,A_n\}. \end{align*} $$
$$ \begin{align*} A_p &=\max\{\,|\eta'(\gamma)|\mid\gamma\in\mathcal{T}^1_p\,\}\quad\big(p\in\mathcal{Y}_+\big)\;,\\ A_k &=\max_{p\in\mathcal{Y}_k}A_p\quad(k=1,\dots,n)\;,\quad A=\max\{A_1,\dots,A_n\}. \end{align*} $$
We can suppose
![]() $C>A$
and
$C>A$
and
![]() $a_1>C+A>0$
. For
$a_1>C+A>0$
. For
![]() $p\in \mathcal {Y}_k$
,
$p\in \mathcal {Y}_k$
,
![]() $q\in \mathcal {Y}_{k-1}$
and
$q\in \mathcal {Y}_{k-1}$
and
![]() $\gamma \in \mathcal {T}(p,q)$
,
$\gamma \in \mathcal {T}(p,q)$
,
Therefore,
Claim 1. For
![]() $k=0,\dots ,n$
, there is a smooth function
$k=0,\dots ,n$
, there is a smooth function
![]() $f_k$
on M such that
$f_k$
on M such that
The statement follows directly from Claim 1 taking
![]() $\eta =\eta "+df_n$
. So we only have to prove this assertion.
$\eta =\eta "+df_n$
. So we only have to prove this assertion.
We proceed by induction on k. For
![]() $k=0$
, we choose
$k=0$
, we choose
![]() $f_0=0$
. Then Equation (A.4) is vacuous, Equations (A.2) and (A.3) are trivial and Equation (A.5) is given by Equation (A.1).
$f_0=0$
. Then Equation (A.4) is vacuous, Equations (A.2) and (A.3) are trivial and Equation (A.5) is given by Equation (A.1).
Now, take any
![]() $k\ge 1$
and assume
$k\ge 1$
and assume
![]() $f_{k-1}$
is defined and satisfies Equations (A.2)–(A.5). Let
$f_{k-1}$
is defined and satisfies Equations (A.2)–(A.5). Let
 $$ \begin{align} b_p&=-\max\{\,(\eta"+df_{k-1})(\gamma)\mid\gamma\in\mathcal{T}^1_p\,\}\quad(p\in\mathcal{Y}_k)\;,\\ b_k&=\min\{\,b_p\mid p\in\mathcal{Y}_k\,\}. \nonumber \end{align} $$
$$ \begin{align} b_p&=-\max\{\,(\eta"+df_{k-1})(\gamma)\mid\gamma\in\mathcal{T}^1_p\,\}\quad(p\in\mathcal{Y}_k)\;,\\ b_k&=\min\{\,b_p\mid p\in\mathcal{Y}_k\,\}. \nonumber \end{align} $$
For every
![]() $p\in \mathcal {Y}_k$
, we have
$p\in \mathcal {Y}_k$
, we have
![]() $b_p<a_{k-1}\le a_k$
because
$b_p<a_{k-1}\le a_k$
because
![]() $f_{k-1}$
satisfies Equation (A.5). So there is a smooth function
$f_{k-1}$
satisfies Equation (A.5). So there is a smooth function
![]() $h_p^-$
on
$h_p^-$
on
![]() $I_k^-$
such that
$I_k^-$
such that
![]() $(h_p^-)'\ge 0$
,
$(h_p^-)'\ge 0$
,
![]() $h_p^-=0$
around
$h_p^-=0$
around
![]() $k-1/2$
, and
$k-1/2$
, and
![]() $h_p^-=a_k-b_p$
around
$h_p^-=a_k-b_p$
around
![]() $k-1/4$
. Let
$k-1/4$
. Let
![]() $\tilde h_p^-$
be the function on
$\tilde h_p^-$
be the function on
![]() $V_p^-\times I_k^-\subset \Sigma _k^-\times I_k^-\equiv T_k^-$
given by
$V_p^-\times I_k^-\subset \Sigma _k^-\times I_k^-\equiv T_k^-$
given by
![]() $\tilde h_p^-(x,s)=h_p^-(s)$
. We have
$\tilde h_p^-(x,s)=h_p^-(s)$
. We have
![]() $\tilde h_p^-=0$
around
$\tilde h_p^-=0$
around
![]() $V_p^-\times \{k-1/2\}$
and
$V_p^-\times \{k-1/2\}$
and
![]() $\tilde h_p^-=a_k-b_p$
around
$\tilde h_p^-=a_k-b_p$
around
![]() $V_p^-\times \{k-1/4\}$
. Thus,
$V_p^-\times \{k-1/4\}$
. Thus,
![]() $\tilde h_p^-$
has a smooth extension to
$\tilde h_p^-$
has a smooth extension to
![]() $\widetilde V_p$
, also denoted by
$\widetilde V_p$
, also denoted by
![]() $\tilde h_p^-$
, which is equal to
$\tilde h_p^-$
, which is equal to
![]() $a_k-b_p$
on
$a_k-b_p$
on
![]() $\widetilde V_p\setminus T_k^-$
. The function
$\widetilde V_p\setminus T_k^-$
. The function
![]() $\tilde \lambda _p\tilde h_p^-$
on
$\tilde \lambda _p\tilde h_p^-$
on
![]() $\widetilde V_p$
can be extended by zero to get a smooth function on
$\widetilde V_p$
can be extended by zero to get a smooth function on
![]() $\widetilde T_k$
, also denoted by
$\widetilde T_k$
, also denoted by
![]() $\tilde \lambda _p\tilde h_p^-$
. Let
$\tilde \lambda _p\tilde h_p^-$
. Let
![]() $\tilde h_k^-=\sum _{p\in \mathcal {Y}_k}\tilde \lambda _p\tilde h_p^-$
on
$\tilde h_k^-=\sum _{p\in \mathcal {Y}_k}\tilde \lambda _p\tilde h_p^-$
on
![]() $\widetilde T_k$
.
$\widetilde T_k$
.
On the other hand, let
![]() $\rho _k$
be a smooth function on
$\rho _k$
be a smooth function on
![]() $I_k^+$
such that
$I_k^+$
such that
![]() $\rho _k'\ge 0$
,
$\rho _k'\ge 0$
,
![]() $\rho _k=0$
around
$\rho _k=0$
around
![]() $k+1/4$
and
$k+1/4$
and
![]() $\rho _k=1$
around
$\rho _k=1$
around
![]() $k+1/2$
. Let
$k+1/2$
. Let
![]() $\tilde \rho _k$
be the smooth function on
$\tilde \rho _k$
be the smooth function on
![]() $T_k^+\equiv \Sigma _k^+\times I_k^+$
given by
$T_k^+\equiv \Sigma _k^+\times I_k^+$
given by
![]() $\tilde \rho _k(x,s)=\rho _k(s)$
, and let
$\tilde \rho _k(x,s)=\rho _k(s)$
, and let
on
![]() $T_k^+$
. This smooth function is equal to
$T_k^+$
. This smooth function is equal to
![]() $\tilde h_k^-$
around
$\tilde h_k^-$
around
![]() $\Sigma _k^+\times \{k+1/4\}$
, and is equal to
$\Sigma _k^+\times \{k+1/4\}$
, and is equal to
![]() $a_k-b_k$
around
$a_k-b_k$
around
![]() $\Sigma _k^+\times \{k+1/2\}\equiv \Sigma _k^+$
. So the functions,
$\Sigma _k^+\times \{k+1/2\}\equiv \Sigma _k^+$
. So the functions,
![]() $\tilde h_k^-$
on
$\tilde h_k^-$
on
![]() $\widetilde T_k\setminus T_k^+$
and
$\widetilde T_k\setminus T_k^+$
and
![]() $\tilde h_k^+$
on
$\tilde h_k^+$
on
![]() $T_k^+$
, can be combined to produce a smooth function
$T_k^+$
, can be combined to produce a smooth function
![]() $\tilde h_k$
on
$\tilde h_k$
on
![]() $\widetilde T_k$
. Since
$\widetilde T_k$
. Since
![]() $\tilde h_k=0$
around
$\tilde h_k=0$
around
![]() $\Sigma _k^-$
and
$\Sigma _k^-$
and
![]() $\tilde h_k=a_k-b_k$
around
$\tilde h_k=a_k-b_k$
around
![]() $\Sigma _k^+$
, there is a smooth extension of
$\Sigma _k^+$
, there is a smooth extension of
![]() $\tilde h_k$
to M, also denoted by
$\tilde h_k$
to M, also denoted by
![]() $\tilde h_k$
, which is constant on
$\tilde h_k$
, which is constant on
![]() $M\setminus \widetilde T_k$
.
$M\setminus \widetilde T_k$
.
Let
![]() $f_k=f_{k-1}+\tilde h_k$
on M. This smooth function satisfies Equation (A.2) because
$f_k=f_{k-1}+\tilde h_k$
on M. This smooth function satisfies Equation (A.2) because
![]() $f_{k-1}$
satisfies Equation (A.2), and X induces the opposite of the standard orientation on every fiber
$f_{k-1}$
satisfies Equation (A.2), and X induces the opposite of the standard orientation on every fiber
![]() $\{x\}\times I_k^\pm \equiv I_k^\pm $
of
$\{x\}\times I_k^\pm \equiv I_k^\pm $
of
![]() $T_k^\pm $
(
$T_k^\pm $
(
![]() $x\in \Sigma _k^\pm $
). It also satisfies Equations (A.3) and (A.4) for
$x\in \Sigma _k^\pm $
). It also satisfies Equations (A.3) and (A.4) for
![]() $p\in \mathcal {Y}_l$
with
$p\in \mathcal {Y}_l$
with
![]() $1\le l<k$
because
$1\le l<k$
because
![]() $f_{k-1}$
satisfies these properties and
$f_{k-1}$
satisfies these properties and
![]() $d\tilde h_k$
is supported in the interior of
$d\tilde h_k$
is supported in the interior of
![]() $\widetilde T_k$
.
$\widetilde T_k$
.
Next, take any
![]() $p\in \mathcal {Y}_k$
,
$p\in \mathcal {Y}_k$
,
![]() $q\in \mathcal {Y}_{k-1}$
and
$q\in \mathcal {Y}_{k-1}$
and
![]() $\gamma \in \mathcal {T}(p,q)\subset \mathcal {T}^1_p$
. We have
$\gamma \in \mathcal {T}(p,q)\subset \mathcal {T}^1_p$
. We have
![]() $\gamma \cap T_k^-\equiv \{x\}\times I_k^-$
for some
$\gamma \cap T_k^-\equiv \{x\}\times I_k^-$
for some
![]() $x\in K_p^-\cap K_q^+\subset \Sigma _k^-=\Sigma _{k-1}^+$
, and the orientation of
$x\in K_p^-\cap K_q^+\subset \Sigma _k^-=\Sigma _{k-1}^+$
, and the orientation of
![]() $\gamma \cap T_k^-$
agrees with the opposite of the standard orientation of
$\gamma \cap T_k^-$
agrees with the opposite of the standard orientation of
![]() $\{x\}\times I_k^-\equiv I_k^-$
. Then
$\{x\}\times I_k^-\equiv I_k^-$
. Then
 $$ \begin{align*} (\eta"+df_k)(\gamma)&=(\eta"+df_{k-1}+d\tilde h_k)(\gamma)\le-b_p+\lambda_p^-(x)d\tilde h_p^-(\gamma)\\ &=-b_p-\int_{I_k^-}dh_p^-=-b_p-(a_k-b_p)=-a_k. \end{align*} $$
$$ \begin{align*} (\eta"+df_k)(\gamma)&=(\eta"+df_{k-1}+d\tilde h_k)(\gamma)\le-b_p+\lambda_p^-(x)d\tilde h_p^-(\gamma)\\ &=-b_p-\int_{I_k^-}dh_p^-=-b_p-(a_k-b_p)=-a_k. \end{align*} $$
Here, the equality holds when the maximum of Equation (A.6) is achieved at
![]() $\gamma $
. Hence,
$\gamma $
. Hence,
![]() $f_k$
also satisfies Equation (A.4) for
$f_k$
also satisfies Equation (A.4) for
![]() $p\in \mathcal {Y}_k$
.
$p\in \mathcal {Y}_k$
.
Finally, take any
![]() $p\in \mathcal {Y}_k$
,
$p\in \mathcal {Y}_k$
,
![]() $u\in \mathcal {Y}_{k+1}$
and
$u\in \mathcal {Y}_{k+1}$
and
![]() $\delta \in \mathcal {T}(u,p)\subset \mathcal {T}^1_u\subset \mathcal {T}^1_{k+1}$
. Thus,
$\delta \in \mathcal {T}(u,p)\subset \mathcal {T}^1_u\subset \mathcal {T}^1_{k+1}$
. Thus,
![]() $\delta \cap T_k^+\equiv \{y\}\times I_k^+$
for some
$\delta \cap T_k^+\equiv \{y\}\times I_k^+$
for some
![]() $y\in K_p^+\cap K_u^-\subset \Sigma _k^+=\Sigma _{k+1}^-$
, and the orientation of
$y\in K_p^+\cap K_u^-\subset \Sigma _k^+=\Sigma _{k+1}^-$
, and the orientation of
![]() $\delta \cap T_k^+$
agrees with the opposite of the standard orientation of
$\delta \cap T_k^+$
agrees with the opposite of the standard orientation of
![]() $\{y\}\times I_k^+\equiv I_k^+$
. Then
$\{y\}\times I_k^+\equiv I_k^+$
. Then
 $$ \begin{align*} (\eta"+df_k)(\delta)&=(\eta"+df_{k-1}+d\tilde h_k)(\delta) =\eta"(\delta)+d\tilde h_k^+(\delta)\\ &=\eta"(\delta)+\big(\tilde h_k^-(y)-(a_k-b_k)\big)\int_{I_k^-}d\rho_k\\ &=\eta"(\delta)+\tilde\lambda_p(y)\tilde h_p^-(y)+b_k-a_k\\ &=\eta"(\delta)+a_k-b_p+b_k-a_k=\eta"(\delta)+b_k-b_p \ge\eta"(\delta)>-a_k\;, \end{align*} $$
$$ \begin{align*} (\eta"+df_k)(\delta)&=(\eta"+df_{k-1}+d\tilde h_k)(\delta) =\eta"(\delta)+d\tilde h_k^+(\delta)\\ &=\eta"(\delta)+\big(\tilde h_k^-(y)-(a_k-b_k)\big)\int_{I_k^-}d\rho_k\\ &=\eta"(\delta)+\tilde\lambda_p(y)\tilde h_p^-(y)+b_k-a_k\\ &=\eta"(\delta)+a_k-b_p+b_k-a_k=\eta"(\delta)+b_k-b_p \ge\eta"(\delta)>-a_k\;, \end{align*} $$
where the second equality is true because
![]() $f_{k-1}$
satisfies Equation (A.3), and the last inequality holds by Equation (A.1). So
$f_{k-1}$
satisfies Equation (A.3), and the last inequality holds by Equation (A.1). So
![]() $f_k$
satisfies Equation (A.5).
$f_k$
satisfies Equation (A.5).
Acknowledgements
We thank the referee for constructive comments improving several results.
Competing Interest
The author declares none.