Article contents
RAMSEY GROWTH IN SOME NIP STRUCTURES
Published online by Cambridge University Press: 19 February 2019
Abstract
We investigate bounds in Ramsey’s theorem for relations definable in NIP structures. Applying model-theoretic methods to finitary combinatorics, we generalize a theorem of Bukh and Matousek (Duke Mathematical Journal 163(12) (2014), 2243–2270) from the semialgebraic case to arbitrary polynomially bounded  $o$-minimal expansions of
$o$-minimal expansions of 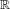 $\mathbb{R}$, and show that it does not hold in
$\mathbb{R}$, and show that it does not hold in 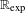 $\mathbb{R}_{\exp }$. This provides a new combinatorial characterization of polynomial boundedness for
$\mathbb{R}_{\exp }$. This provides a new combinatorial characterization of polynomial boundedness for  $o$-minimal structures. We also prove an analog for relations definable in
$o$-minimal structures. We also prove an analog for relations definable in  $P$-minimal structures, in particular for the field of the
$P$-minimal structures, in particular for the field of the 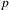 $p$-adics. Generalizing Conlon et al. (Transactions of the American Mathematical Society 366(9) (2014), 5043–5065), we show that in distal structures the upper bound for
$p$-adics. Generalizing Conlon et al. (Transactions of the American Mathematical Society 366(9) (2014), 5043–5065), we show that in distal structures the upper bound for 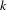 $k$-ary definable relations is given by the exponential tower of height
$k$-ary definable relations is given by the exponential tower of height  $k-1$.
$k-1$.
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 1 , January 2021 , pp. 1 - 29
- Copyright
- © Cambridge University Press 2019
References
- 1
- Cited by


