Article contents
DENSITY RESULTS FOR SPECIALIZATION SETS OF GALOIS COVERS
Published online by Cambridge University Press: 25 October 2019
Abstract
We provide evidence for this conclusion: given a finite Galois cover 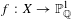 $f:X\rightarrow \mathbb{P}_{\mathbb{Q}}^{1}$ of group
$f:X\rightarrow \mathbb{P}_{\mathbb{Q}}^{1}$ of group 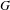 $G$, almost all (in a density sense) realizations of
$G$, almost all (in a density sense) realizations of 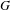 $G$ over
$G$ over 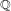 $\mathbb{Q}$ do not occur as specializations of
$\mathbb{Q}$ do not occur as specializations of 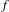 $f$. We show that this holds if the number of branch points of
$f$. We show that this holds if the number of branch points of 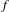 $f$ is sufficiently large, under the abc-conjecture and, possibly, the lower bound predicted by the Malle conjecture for the number of Galois extensions of
$f$ is sufficiently large, under the abc-conjecture and, possibly, the lower bound predicted by the Malle conjecture for the number of Galois extensions of 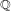 $\mathbb{Q}$ of given group and bounded discriminant. This widely extends a result of Granville on the lack of
$\mathbb{Q}$ of given group and bounded discriminant. This widely extends a result of Granville on the lack of 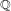 $\mathbb{Q}$-rational points on quadratic twists of hyperelliptic curves over
$\mathbb{Q}$-rational points on quadratic twists of hyperelliptic curves over 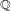 $\mathbb{Q}$ with large genus, under the abc-conjecture (a diophantine reformulation of the case
$\mathbb{Q}$ with large genus, under the abc-conjecture (a diophantine reformulation of the case 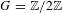 $G=\mathbb{Z}/2\mathbb{Z}$ of our result). As a further evidence, we exhibit a few finite groups
$G=\mathbb{Z}/2\mathbb{Z}$ of our result). As a further evidence, we exhibit a few finite groups  $G$ for which the above conclusion holds unconditionally for almost all covers of
$G$ for which the above conclusion holds unconditionally for almost all covers of 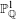 $\mathbb{P}_{\mathbb{Q}}^{1}$ of group
$\mathbb{P}_{\mathbb{Q}}^{1}$ of group 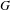 $G$. We also introduce a local–global principle for specializations of Galois covers
$G$. We also introduce a local–global principle for specializations of Galois covers 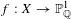 $f:X\rightarrow \mathbb{P}_{\mathbb{Q}}^{1}$ and show that it often fails if
$f:X\rightarrow \mathbb{P}_{\mathbb{Q}}^{1}$ and show that it often fails if 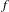 $f$ has abelian Galois group and sufficiently many branch points, under the abc-conjecture. On the one hand, such a local–global conclusion underscores the ‘smallness’ of the specialization set of a Galois cover of
$f$ has abelian Galois group and sufficiently many branch points, under the abc-conjecture. On the one hand, such a local–global conclusion underscores the ‘smallness’ of the specialization set of a Galois cover of 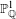 $\mathbb{P}_{\mathbb{Q}}^{1}$. On the other hand, it allows to generate conditionally ‘many’ curves over
$\mathbb{P}_{\mathbb{Q}}^{1}$. On the other hand, it allows to generate conditionally ‘many’ curves over 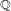 $\mathbb{Q}$ failing the Hasse principle, thus generalizing a recent result of Clark and Watson devoted to the hyperelliptic case.
$\mathbb{Q}$ failing the Hasse principle, thus generalizing a recent result of Clark and Watson devoted to the hyperelliptic case.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 5 , September 2021 , pp. 1455 - 1496
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2019. Published by Cambridge University Press
References
- 3
- Cited by


