Article contents
RELATIVE UNITARY RZ-SPACES AND THE ARITHMETIC FUNDAMENTAL LEMMA
Published online by Cambridge University Press: 24 March 2020
Abstract
We prove a comparison isomorphism between certain moduli spaces of 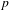 $p$-divisible groups and strict
$p$-divisible groups and strict 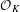 ${\mathcal{O}}_{K}$-modules (RZ-spaces). Both moduli problems are of PEL-type (polarization, endomorphism, level structure) and the difficulty lies in relating polarized
${\mathcal{O}}_{K}$-modules (RZ-spaces). Both moduli problems are of PEL-type (polarization, endomorphism, level structure) and the difficulty lies in relating polarized 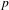 $p$-divisible groups and polarized strict
$p$-divisible groups and polarized strict 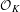 ${\mathcal{O}}_{K}$-modules. We use the theory of relative displays and frames, as developed by Ahsendorf, Lau and Zink, to translate this into a problem in linear algebra. As an application of these results, we verify new cases of the arithmetic fundamental lemma (AFL) of Wei Zhang: The comparison isomorphism yields an explicit description of certain cycles that play a role in the AFL. This allows, under certain conditions, to reduce the AFL identity in question to an AFL identity in lower dimension.
${\mathcal{O}}_{K}$-modules. We use the theory of relative displays and frames, as developed by Ahsendorf, Lau and Zink, to translate this into a problem in linear algebra. As an application of these results, we verify new cases of the arithmetic fundamental lemma (AFL) of Wei Zhang: The comparison isomorphism yields an explicit description of certain cycles that play a role in the AFL. This allows, under certain conditions, to reduce the AFL identity in question to an AFL identity in lower dimension.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 1 , January 2022 , pp. 241 - 301
- Copyright
- © The Author(s) 2020. Published by Cambridge University Press
References
- 6
- Cited by

