Article contents
REMARKS ON BIANCHI SUMS AND PONTRJAGIN CLASSES
Published online by Cambridge University Press: 24 September 2014
Abstract
We use the exterior and composition products of doubleforms together with the alternating operator to reformulate Pontrjagin classes and all Pontrjagin numbers in terms of the Riemannian curvature. We show that the alternating operator is obtained by a succession of applications of the first Bianchi sum and we prove some useful identities relating the previous four operations on double forms. As an application, we prove that for a  $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-conformally flat manifold of dimension
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-conformally flat manifold of dimension 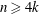 $n\geq 4k$, the Pontrjagin classes
$n\geq 4k$, the Pontrjagin classes 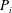 $P_i$ vanish for any
$P_i$ vanish for any 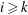 $i\geq k$. Finally, we study the equality case in an inequality of Thorpe between the Euler–Poincaré characteristic and the
$i\geq k$. Finally, we study the equality case in an inequality of Thorpe between the Euler–Poincaré characteristic and the 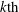 $k{\rm th}$ Pontrjagin number of a
$k{\rm th}$ Pontrjagin number of a 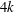 $4k$-dimensional Thorpe manifold.
$4k$-dimensional Thorpe manifold.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 97 , Issue 3 , December 2014 , pp. 365 - 382
- Copyright
- Copyright © 2014 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by

