Article contents
ONE-POINT CONNECTIFICATIONS
Published online by Cambridge University Press: 09 January 2015
Abstract
A space 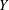 $Y$ is called an extension of a space
$Y$ is called an extension of a space 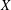 $X$ if
$X$ if 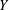 $Y$ contains
$Y$ contains 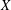 $X$ as a dense subspace. An extension
$X$ as a dense subspace. An extension 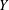 $Y$ of
$Y$ of 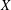 $X$ is called a one-point extension if
$X$ is called a one-point extension if 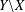 $Y\setminus X$ is a singleton. Compact extensions are called compactifications and connected extensions are called connectifications. It is well known that every locally compact noncompact space has a one-point compactification (known as the Alexandroff compactification) obtained by adding a point at infinity. A locally connected disconnected space, however, may fail to have a one-point connectification. It is indeed a long-standing question of Alexandroff to characterize spaces which have a one-point connectification. Here we prove that in the class of completely regular spaces, a locally connected space has a one-point connectification if and only if it contains no compact component.
$Y\setminus X$ is a singleton. Compact extensions are called compactifications and connected extensions are called connectifications. It is well known that every locally compact noncompact space has a one-point compactification (known as the Alexandroff compactification) obtained by adding a point at infinity. A locally connected disconnected space, however, may fail to have a one-point connectification. It is indeed a long-standing question of Alexandroff to characterize spaces which have a one-point connectification. Here we prove that in the class of completely regular spaces, a locally connected space has a one-point connectification if and only if it contains no compact component.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.
References
- 3
- Cited by

