Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Picavet-L’Hermitte, Martine
2003.
Some remarks on half-factorial orders.
Rendiconti del Circolo Matematico di Palermo,
Vol. 52,
Issue. 2,
p.
297.
Garcia, Stephan Ramon
O’Neill, Christopher
and
Yih, Samuel
2019.
Factorization length distribution for affine semigroups I: Numerical semigroups with three generators.
European Journal of Combinatorics,
Vol. 78,
Issue. ,
p.
190.

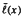 and
and 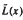 on
on 