Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brenton, Lawrence
and
Joo, Mi-Kyung
1995.
On the System of Congruences Π
j≠i
n
j
≡ 1 mod
n
i
.
The Fibonacci Quarterly,
Vol. 33,
Issue. 3,
p.
258.
Brenton, Lawrence
2001.
Homologically simple singularities.
Classical and Quantum Gravity,
Vol. 18,
Issue. 2,
p.
325.
Brenton, Lawrence
and
Vasiliu, Ana
2002.
Znam's Problem.
Mathematics Magazine,
Vol. 75,
Issue. 1,
p.
3.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
209.
DOMARATZKI, MICHAEL
ELLUL, KEITH
SHALLIT, JEFFREY
and
WANG, MING-WEI
2005.
NON-UNIQUENESS AND RADIUS OF CYCLIC UNARY NFAs.
International Journal of Foundations of Computer Science,
Vol. 16,
Issue. 05,
p.
883.
Arce-Nazario, R.
Castro, F.
and
Figueroa, R.
2013.
On the number of solutions of∑i=1111xi=1in distinct odd natural numbers.
Journal of Number Theory,
Vol. 133,
Issue. 6,
p.
2036.

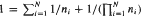 and discuss techniques for generating solutions. By examining a quadratic recurrence relation modulo a family of primes we have found some 500 new infinite sequences of solutions. We also initiate an investigation of the randomness of the distribution of solutions, and show that there are infinitely many solutions not generated by the aforementioned technique.
and discuss techniques for generating solutions. By examining a quadratic recurrence relation modulo a family of primes we have found some 500 new infinite sequences of solutions. We also initiate an investigation of the randomness of the distribution of solutions, and show that there are infinitely many solutions not generated by the aforementioned technique.