Article contents
IRREDUCIBLE QUASIORDERS OF MONOUNARY ALGEBRAS
Published online by Cambridge University Press: 01 March 2013
Abstract
Rooted monounary algebras can be considered as an algebraic counterpart of directed rooted trees. We work towards a characterization of the lattice of compatible quasiorders by describing its join- and meet-irreducible elements. We introduce the limit 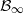 $\cB _\infty $ of all
$\cB _\infty $ of all 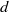 $d$-dimensional Boolean cubes
$d$-dimensional Boolean cubes 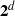 $\Two ^d$ as a monounary algebra; then the natural order on
$\Two ^d$ as a monounary algebra; then the natural order on 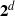 $\Two ^d$ is meet-irreducible. Our main result is that any completely meet-irreducible quasiorder of a rooted algebra is a homomorphic preimage of the natural partial order (or its inverse) of a suitable subalgebra of
$\Two ^d$ is meet-irreducible. Our main result is that any completely meet-irreducible quasiorder of a rooted algebra is a homomorphic preimage of the natural partial order (or its inverse) of a suitable subalgebra of 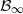 $\cB _\infty $. For a partial order, it is known that complete meet-irreducibility means that the corresponding partially ordered structure is subdirectly irreducible. For a rooted monounary algebra it is shown that this property implies that the unary operation has finitely many nontrivial kernel classes and its graph is a binary tree.
$\cB _\infty $. For a partial order, it is known that complete meet-irreducibility means that the corresponding partially ordered structure is subdirectly irreducible. For a rooted monounary algebra it is shown that this property implies that the unary operation has finitely many nontrivial kernel classes and its graph is a binary tree.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 93 , Issue 3 , December 2012 , pp. 259 - 276
- Copyright
- Copyright © 2013 Australian Mathematical Publishing Association Inc.
References
- 3
- Cited by

