Article contents
INTEGRAL MEANS AND DIRICHLET INTEGRAL FOR CERTAIN CLASSES OF ANALYTIC FUNCTIONS
Published online by Cambridge University Press: 16 July 2015
Abstract
For a normalized analytic function 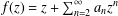 $f(z)=z+\sum _{n=2}^{\infty }a_{n}z^{n}$ in the unit disk
$f(z)=z+\sum _{n=2}^{\infty }a_{n}z^{n}$ in the unit disk 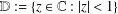 $\mathbb{D}:=\{z\in \mathbb{C}:|z|<1\}$, the estimate of the integral means
$\mathbb{D}:=\{z\in \mathbb{C}:|z|<1\}$, the estimate of the integral means 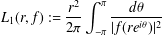 $$\begin{eqnarray}L_{1}(r,f):=\frac{r^{2}}{2{\it\pi}}\int _{-{\it\pi}}^{{\it\pi}}\frac{d{\it\theta}}{|f(re^{i{\it\theta}})|^{2}}\end{eqnarray}$$
$$\begin{eqnarray}L_{1}(r,f):=\frac{r^{2}}{2{\it\pi}}\int _{-{\it\pi}}^{{\it\pi}}\frac{d{\it\theta}}{|f(re^{i{\it\theta}})|^{2}}\end{eqnarray}$$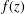 $f(z)$ are nonvanishing in the punctured unit disk
$f(z)$ are nonvanishing in the punctured unit disk 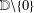 $\mathbb{D}\setminus \{0\}$. Let
$\mathbb{D}\setminus \{0\}$. Let 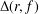 ${\rm\Delta}(r,f)$ denote the area of the image of the subdisk
${\rm\Delta}(r,f)$ denote the area of the image of the subdisk 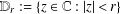 $\mathbb{D}_{r}:=\{z\in \mathbb{C}:|z|<r\}$ under
$\mathbb{D}_{r}:=\{z\in \mathbb{C}:|z|<r\}$ under 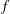 $f$, where
$f$, where 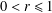 $0<r\leq 1$. In this paper, we solve two extremal problems of finding the maximum value of
$0<r\leq 1$. In this paper, we solve two extremal problems of finding the maximum value of 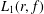 $L_{1}(r,f)$ and
$L_{1}(r,f)$ and 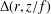 ${\rm\Delta}(r,z/f)$ as a function of
${\rm\Delta}(r,z/f)$ as a function of  $r$ when
$r$ when 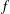 $f$ belongs to the class of
$f$ belongs to the class of 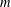 $m$-fold symmetric starlike functions of complex order defined by a subordination relation. One of the particular cases of the latter problem includes the solution to a conjecture of Yamashita, which was settled recently by Obradović et al. [‘A proof of Yamashita’s conjecture on area integral’, Comput. Methods Funct. Theory13 (2013), 479–492].
$m$-fold symmetric starlike functions of complex order defined by a subordination relation. One of the particular cases of the latter problem includes the solution to a conjecture of Yamashita, which was settled recently by Obradović et al. [‘A proof of Yamashita’s conjecture on area integral’, Comput. Methods Funct. Theory13 (2013), 479–492].
Keywords
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 99 , Issue 3 , December 2015 , pp. 315 - 333
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by

