Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhou, Sanming
2009.
A Class of Arc-Transitive Cayley Graphs as Models for Interconnection Networks.
SIAM Journal on Discrete Mathematics,
Vol. 23,
Issue. 2,
p.
694.
Thomson, Alison
and
Zhou, Sanming
2010.
Gossiping and routing in undirected triple-loop networks.
Networks,
Vol. 55,
Issue. 4,
p.
341.
Zhou, Jin-Xin
2011.
The automorphism group of the alternating group graph.
Applied Mathematics Letters,
Vol. 24,
Issue. 2,
p.
229.
Fang, Xin Gui
and
Zhou, Sanming
2012.
Gossiping and routing in second-kind Frobenius graphs.
European Journal of Combinatorics,
Vol. 33,
Issue. 6,
p.
1001.
Thomson, Alison
and
Zhou, Sanming
2014.
Frobenius circulant graphs of valency six, Eisenstein–Jacobi networks, and hexagonal meshes.
European Journal of Combinatorics,
Vol. 38,
Issue. ,
p.
61.
Thomson, Alison
and
Zhou, Sanming
2014.
Rotational circulant graphs.
Discrete Applied Mathematics,
Vol. 162,
Issue. ,
p.
296.
Sun, Yuefang
2015.
Advances in Global Optimization.
Vol. 95,
Issue. ,
p.
109.
Gan, Heng-Soon
Mokhtar, Hamid
and
Zhou, Sanming
2015.
Forwarding and optical indices of 4-regular circulant networks.
Journal of Discrete Algorithms,
Vol. 35,
Issue. ,
p.
27.
Sun, Yuefang
and
Zhou, Sanming
2016.
Tree Connectivities of Cayley Graphs on Abelian Groups with Small Degrees.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 39,
Issue. 4,
p.
1673.
MOKHTAR, HAMID
2017.
Cube-Connected Circulants as Efficient Models for Interconnection Networks.
Journal of Interconnection Networks,
Vol. 17,
Issue. 03n04,
p.
1741007.
Mokhtar, Hamid
and
Zhou, Sanming
2017.
Recursive cubes of rings as models for interconnection networks.
Discrete Applied Mathematics,
Vol. 217,
Issue. ,
p.
639.
MOKHTAR, HAMID
2017.
A FEW FAMILIES OF CAYLEY GRAPHS AND THEIR EFFICIENCY AS COMMUNICATION NETWORKS.
Bulletin of the Australian Mathematical Society,
Vol. 95,
Issue. 3,
p.
518.
HSU, D. F.
and
ZHOU, SANMING
2018.
RESOLVABLE MENDELSOHN DESIGNS AND FINITE FROBENIUS GROUPS.
Bulletin of the Australian Mathematical Society,
Vol. 98,
Issue. 1,
p.
1.
Zhou, Sanming
2019.
Cyclotomic graphs and perfect codes.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 3,
p.
931.
Mokhtar, Hamid
2020.
Cube-connected circulants: Bisection width, Wiener and forwarding indices.
Discrete Applied Mathematics,
Vol. 272,
Issue. ,
p.
48.
Monakhova, Emilia
and
Monakhov, Oleg
2021.
A Generalized Routing Algorithm for a Family of Optimal 2D Circulant Networks Based on Relative Addressing.
p.
55.
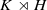 such that S=aH for some a∈K with 〈aH〉=K, where H is of even order or a is an involution. It is known that such graphs admit ‘perfect’ routing and gossiping schemes. A circulant graph is a Cayley graph on a cyclic group of order at least three. Since circulant graphs are widely used as models for interconnection networks, it is thus highly desirable to characterize those which are Frobenius of the first kind. In this paper we first give such a characterization for connected 4-valent circulant graphs, and then describe optimal routing and gossiping schemes for those which are first kind Frobenius graphs. Examples of such graphs include the 4-valent circulant graph with a given diameter and maximum possible order.
such that S=aH for some a∈K with 〈aH〉=K, where H is of even order or a is an involution. It is known that such graphs admit ‘perfect’ routing and gossiping schemes. A circulant graph is a Cayley graph on a cyclic group of order at least three. Since circulant graphs are widely used as models for interconnection networks, it is thus highly desirable to characterize those which are Frobenius of the first kind. In this paper we first give such a characterization for connected 4-valent circulant graphs, and then describe optimal routing and gossiping schemes for those which are first kind Frobenius graphs. Examples of such graphs include the 4-valent circulant graph with a given diameter and maximum possible order.
