In recent years there has been a proliferation of logics which extend first-order logic, e.g., logics with infinite sentences, logics with cardinal quantifiers such as “there exist infinitely many…” and “there exist uncountably many…”, and a weak second-order logic with variables and quantifiers for finite sets of individuals. It is well known that first-order logic has a limited ability to express many of the concepts studied by mathematicians, e.g., the concept of a wellordering. However, first-order logic, being among the simplest logics with applications to mathematics, does have an extensively developed and well understood model theory. On the other hand, full second-order logic has all the expressive power needed to do mathematics, but has an unworkable model theory. Indeed, the search for a logic with a semantics complex enough to say something, yet at the same time simple enough to say something about, accounts for the proliferation of logics mentioned above. In this paper, a number of proposed strengthenings of first-order logic are examined with respect to their relative expressive power, i.e., given two logics, what concepts can be expressed in one but not the other?

For the most part, the notation is standard. Most of the notation is either explained in the text or can be found in the book [2] of Chang and Keisler. Some notational conventions used throughout the text are listed below: the empty set is denoted by ∅.

The central notion of this paper is that of a (conjunctive) game-sentence, i.e., a sentence of the form

where the indices ki, ji range over given countable sets and the matrix conjuncts are, say, open -formulas. Such game sentences were first considered, independently, by Svenonius [19], Moschovakis [13]—[15] and Vaught [20]. Other references are [1], [3]—[5], [10]—[12]. The following normal form theorem was proved by Vaught (and, in less general forms, by his predecessors).

Theorem 0.1. Let L = L0(R). For every -sentence ϕ there is an L0-game sentence Θ such that ⊨′ ∃Rϕ ↔ Θ.

(A word about the notations: L0(R) denotes the language obtained from L0 by adding to it the sequence R of logical symbols which do not belong to L0; “⊨′α” means that α is true in all countable models.)

0.1 can be restated as follows.

Theorem 0.1′. For every-sentence ϕ there is an L0-game sentence Θ such that ⊨ϕ → Θ and for any-sentence ϕ if ⊨ϕ → ϕ and L′ ⋂ L ⊆ L0, then ⊨ Θ → ϕ.

(We sketch the proof of the equivalence between 0.1 and 0.1′.

0.1 implies 0.1′. This is obvious once we realize that game sentences and their negations satisfy the downward Löwenheim-Skolem theorem and hence, ⊨′α is equivalent to ⊨α whenever α is a boolean combination of and game sentences.

This is the first part of a two part work on the monadic theory of short orders (embedding neither ω1 nor ω1*. This part provides the technical groundwork for decidability results. Other applications are possible.

In this paper the canonical modal logics, a kind of complete modal logics introduced in K. Fine [4] and R. I. Goldblatt [5], will be characterized semantically using the concept of an ultrafilter extension, an operation on frames inspired by the algebraic theory of modal logic. Theorem 8 of R. I. Goldblatt and S. K. Thomason [6] characterizing the modally definable Σ⊿-elementary classes of frames will follow as a corollary. A second corollary is Theorem 2 of [4] which states that any complete modal logic defining a Σ⊿-elementary class of frames is canonical.

The main tool in obtaining these results is the duality between modal algebras and general frames developed in R. I. Goldblatt [5]. The relevant notions and results from this theory will be stated in §2. The concept of a canonical modal logic is introduced and motivated in §3, which also contains the above-mentioned theorems. In §4, a kind of appendix to the preceding discussion, preservation of first-order sentences under ultrafilter extensions (and some other relevant operations on frames) is discussed.

The modal language to be considered here has an infinite supply of proposition letters (p, q, r, …), a propositional constant ⊥ (the so-called falsum, standing for a fixed contradiction), the usual Boolean operators ¬ (not), ∨ (or), ∨ (and), → (if … then …), and ↔ (if and only if)—with ¬ and ∨ regarded as primitives—and the two unary modal operators ◇ (possibly) and □ (necessarily)— ◇ being regarded as primitive. Modal formulas will be denoted by lower case Greek letters, sets of formulas by Greek capitals.

A well-known result of Vaught's is that no complete theory has exactly two nonisomorphic countable models. The main result of this paper is that there is a complete decidable theory with exactly two nonisomorphic decidable models.

A model is decidable if it has a decidable satisfaction predicate. To be more precise, let T be a decidable theory, let {θn∣n < ω} be an effective enumeration of all formulas in L(T), and let be a countable model of T. For any indexing E = {ai∣ i < ω} of ∣∣, and any formula ϕ ∈ L(T), let ‘ϕE’ denote the result of substituting ‘ai’ for every free occurrence of ‘xi’ in ϕ, i < ω. Then is decidable just in case, for some indexing E of ∣∣, {n ∣ ⊨ θnE} is a recursive set of integers. It is easy to show that the decidability of a model does not depend on the choice of the effective enumeration of the formulas in L(T); we omit details. By a simple ‘effectivization’ of Henkin's proof of the completeness theorem (see Chang [1]) we have

Fact 1. Every decidable consistent theory has a decidable model.

Assume next that T is a complete decidable theory and {θn ∣ n < ω} is an effective enumeration of all formulas of L(T).

Consistency properties and their model existence theorems have provided an important method of constructing models for fragments of L∞ω. In [E] Ellentuck extended this construction to Suslin logic. One of his extensions, the Borel consistency property, has its extra rule based not on the semantic interpretation of the extra symbols but rather on a theorem of Sierpinski about the classical operation . In this paper we extend that consistency property to the game logic LG and use it to show how one can extend results about and its countable fragments to LG and certain of its countable fragments. The particular formation of LG which we use will allow in the game quantifier infinite alternation of countable conjunctions and disjunctions as well as infinite alternation of quantifiers. In this way LG can be viewed as an extension of Suslin logic.

Vaught's “*-transform method” is applied to derive a global definability theorem of M. Makkai from a classical theorem of Lusin.

We analyse here the monadic theory of the rational order, the monadic theory of the real line with quantification over “small” subsets and models of these theories. We prove that the results are in some sense the best possible.

In recent years model theorists have been studying various sheaf-theoretic notions as they apply to model theory. For quite a while however, a sheaf of structures was considered to be just a local homeomorphism between topological spaces such that each stalk Sx = p−1(x) is a model-theoretic structure and such that certain maps are continuous. Some of the model-theoretic work done with this notion of a sheaf of structures are the papers by Carson [2] and Macintyre [7]. Soon came the idea of considering a sheaf of structures not just as a collection of structures glued together in some continuous way, but rather as some sort of generalized structure. A significant model-theoretic study of sheaves in this new sense became possible only after the development of the theory of topoi. As F.W. Lawvere pointed out in [6], this represents the advance of mathematics (in our case the advance of model theory) from metaphysics to dialectics.

A topos is the rather ingenious evolution of the notion of a Grothendieck topos [13]. It provides us with the idea that an object of a topos (e.g. the topos of sheaves over a topological space) may be thought of as a generalized set. Furthermore, all first-order logical operations have an interpretation in a topos, hence we may talk about generalized structures. Angus Macintyre suggested that some of his model-theoretic results about sheaves of structures may be understood better and perhaps simplified by doing model theory inside a topos of sheaves.

Solovay proved in 1967 that the axiom of determinateness implies that the filter C generated by closed and unbounded subsets of ω1 is an ultrafilter. It has long been conjectured that a significant part of the theory of the axiom of determinateness should be provable from the hypothesis that C is an ultrafilter, but even the first step of finding inner models with several measurable cardinals has proved elusive. In this paper we show that such models exist. Much of our proof is a modification of Kunen's proof in [3] of the same conclusion from the existence of a measurable cardinal κ such that 2κ > κ+.

Since no proof of Solovay's result seems to have been published, we insert a proof here. We want to show that for any set x ⊂ ω1 there is a closed, unbounded set either contained in or disjoint from x. By the lemma of [4] there is a Turing degree d such that either ω1e Є x for all degrees e ≥T d or ω1e ∉ x for all degrees e ≥T d. By a theorem of Sacks [1], [5] every d-admissible is ω1e for some e ≥T d, so it is enough to show that there is a closed, unbounded set of d-admissibles. Let a ⊂ ω have degree d; then is such a set.

The language LA(Ⅎ) is formed by adding the quantifier Ⅎx, “few x”, to the infinitary logic LA on an admissible set A. A complete axiomatization is obtained for models whose universe is the set of ordinals of A and where Ⅎx is interpreted as there exist A-finitely many x. For well-behaved A, every consistent sentence has a model with an A-recursive diagram. A principal tool is forcing for LA(Ⅎ).

We present a number of results involving almost disjoint sets and Martin's axiom. Included is an example, due to K. Kunen, of a c.c.c. partial order without property K whose product with every c.c.c. partial order is c.c.c.

For L a countable first-order language, let L(Q) be logic with the quantifier Qx which means “there exist uncountably many x”. We assume a little familiarity with Keisler's paper [8]. One finds there completeness and compactness theorems for L(Q), as well as an omitting types theorem: a syntactic condition is given for a consistent countable theory to have a model satisfying ∀x⋁Σ(x), where Σ is a countable set of formulas of L(Q). (See also Chang and Keisler [3] for the first-order omitting types theorem, due to Henkin and Orey.) An analogous theorem is proved in Barwise, Kaufmann, and Makkai [1] and in Kaufmann [6] for stationary logic. However, a more general theorem than just an anlaogue to Keisler's is proved there. Conditions are given which are sufficient for a theory T to have models satisfying sentences such as aas1aas2 … aasn⋁Σ(s1, … sn), ∀xaas ∨ Σ(x, s), and so forth. Bruce [2] had asked whether such a theorem can be proved for L(Q). with “aa” replaced by “Q*”, where Q* is ¬Q¬ (“for all but countably many”).

In [5] Henkin defined a quantifier, which we shall denote by QH: linking four variables in one formula. This quantifier is related to the notion of formulas in which the usual universal and existential quantifiers occur but are not linearly ordered. The original definition of QH was

Here (QHx1x2y1y2)φ is true if for every x1 there exists y1 such that for every x2 there exists y2, whose choice depends only on x2 not on x1 and y1 such that φ(x14, x2, y1, y2). Another way of writing this is

In [5] it was observed that the logic L(QH) obtained by adjoining QH defined as in (1) is more powerful than first-order logic. In particular, it turned out that the quantifier “there exist infinitely many” denoted Q0 was definable from QH because

We improve a general theorem of J. A. Makowsky which characterizes, for a wide class of languages, those sentences θ such that both Mod(θ) and Mod(¬θ) are closed under unions of chains.

Let T be a complete countable first-order theory such that every ultrapower of a model of T is saturated. If T has a model omitting a type p in every cardinality < ℶ′, then T has a model omitting p in every cardinality. There is also a related theorem, and an example showing the ℶ′ cannot be improved.

In order to prove that the Scott's interpolation theorem fails in Lω1ω, H. Africk proved the following lemma in [1]. (See [1] for notations.)

Africk's Lemma. Suppose that and 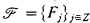. Then every 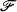-sentence in Lω1ω is equivalent to a sentence of the form 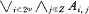and a sentence of the form 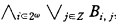, where Ai,j, Bi,j, are Fj-sentences and there are only countable distinct Ai,j or Bi,j together.

But this lemma is false as is shown in the following: Suppose that Z = {0,1}, Fj = {Pk,j}k⊂ω and 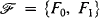. Let A be the sentence ⋀k⊂ω(∀xPk,0(x) ∨ ∀xPk,1(x)). If Africk's Lemma is true, then there are countably many Fj-sentences 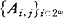, such that A is equivalent to 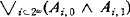Since 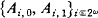is countable, there are only countably many distinct pairs (Ai,0, Ai,1). So, we get a countable set {(Bi,0, Bi,1)}i⊂ω, such that A is equivalent to ⋁ik⊂ω(Bk,0 ∧ Bk,1). Since Bk,0 ∧ Bk,1 → ∀xPk,0(x) ∨ ∀xPk,1 is l-valid(i.e. valid in all first-order structures of cardinality 1) for every k ϵ ω, we have that either Bk,0 → ∀xPk,0(x) is 1-valid or Bk,0 → ∀xPk,1(x) is 1-valid. 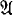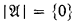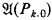Let I be the set of all the k ϵ ω such that Bk,0 → ∀xPk,0(x) is 1-valid and the first-order structure defined by , , 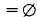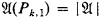if k ϵ I and 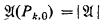, 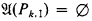if k ∉ I.

For general information on bar recursion the reader should consult the papers of Spector [8], where it was introduced, Howard [2] and Tait [11]. In this note we shall prove that the terms of Gödel's theory T(in its extensional version of Spector [8]) are closed under the rule BR0,1 of bar recursion of types 0 and 1. Our method of proof is based on the notion of an infinite term introduced by Tait [9]. The main tools of the proof are (i) the normalization theorem for (notations for) infinite terms and (ii) valuation functionals. Both are elaborated in [6]; for brevity some familiarity with this paper is assumed here. Using (i) and (ii) we reduce BR0,1 to ξ-recursion with ξ < ε0. From this the result follows by work of Tait [10], who gave a reduction of 2ξ-recursion to ξ-recursion at a higher type. At the end of the paper we discuss a perhaps more natural variant of bar recursion introduced by Kreisel in [4].

Related results are due to Kreisel (in his appendix to [8]), who obtains results which imply, using the reduction given by Howard [2] of the constant of bar recursion of type τ to the rule of bar recursion of type (0 → τ) → τ, that T is not closed under the rule of bar recursion of a type of level ≥ 2, to Diller [1], who gave a reduction of BR0,1 to ξ-recursion with ξ bounded by the least ω-critical number, and to Howard [3], who gave an ordinal analysis of the constant of bar recursion of type 0. I am grateful to H. Barendregt, W. Howard and G. Kreisel for many useful comments and discussions.

Beth's Definability Theorem, and consequently the Interpolation Lemma, fail for the version of quantified S5 that is presented in Kripke's [6]. These failures persist when the constant domain axiom-scheme ∀x□φ ≡ □∀xφ is added to S5 or, indeed, to any weaker extension of quantificational K.

§1 reviews some standard material on quantificational modal logic. This is in contrast to quantified intermediate logics for, as Gabbay [6] has shown, the Interpolation Lemma holds for the logic CD with constant domains and for several of its extensions. §§2—4 establish the negative results for the systems based upon S5. §5 establishes a more general negative result and, finally, §6 considers some positive results and open problems. A basic knowledge of classical and modal quantificational logic is presupposed.

Let me briefly review the relevant model theory for quantified modal logic. Further details can be found in [3] or [7].

The language is obtained from the language for classical first-order logic with identity by adding a unary operator □ for necessity. The atomic formula ‘Ex’ is used as an abbreviation for ‘∃y(y = x)’ and may be read as ‘x exists’.

Let M be a countable algebraically closed group, κ an uncountable cardinal. We will prove in this paper the following theorems.

Theorem 1. There is an algebraically closed group N of cardinality κ which is ∞ – ω-equivalent to M.

Theorem 2. There is an algebraically closed group N of cardinality κ which is ∞ – ω-equivalent to M, and contains a free abelian group of cardinality κ.

Theorem 3. There are 2κ nonisomorphic algebraically closed groups of cardinality κ which are ∞ – ω-equivalent to M.

Theorem 4. There is an algebraically closed group N of cardinality κ which is ∞ – ω-equivalent to M and satisfies: Every subgroup of N of uncountable reqular cardinality contains a free subgroup of the same cardinality.

Theorems 2 and 4 illustrate Theorem 3 by exhibiting two groups N ≡ ∞ωM of cardinality κ which are nonisomorphic by obvious reasons. We state and prove Theorem 1 separately in order to give an easy example of our principal tool: the use of automorphisms instead of indiscernibles (see §2).