We say that a ring admits elimination of quantifiers, if in the language of rings, {0, 1, +, ·}, the complete theory of R admits elimination of quantifiers.
Theorem 1. Let D be a division ring. Then D admits elimination of quantifiers if and only if D is an algebraically closed or finite field.
A ring is prime if it satisfies the sentence: ∀x∀y∃z (x =0 ∨ y = 0∨ xzy ≠ 0).
Theorem 2. If R is a prime ring with an infinite center and R admits elimination of quantifiers, then R is an algebraically closed field.
Let 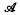 be the class of finite fields. Let
be the class of finite fields. Let 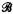 be the class of 2 × 2 matrix rings over a field with a prime number of elements. Let
be the class of 2 × 2 matrix rings over a field with a prime number of elements. Let 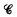 be the class of rings of the form GF(pn)⊕GF(pk) such that either n = k or g.c.d. (n, k) = 1. Let
be the class of rings of the form GF(pn)⊕GF(pk) such that either n = k or g.c.d. (n, k) = 1. Let 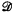 be the set of ordered pairs (f, Q) where Q is a finite set of primes and
be the set of ordered pairs (f, Q) where Q is a finite set of primes and 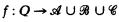 such that the characteristic of the ring f(q) is q. Finally, let
such that the characteristic of the ring f(q) is q. Finally, let 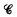 be the class of rings of the form ⊕q ∈ Qf(q), for some (f, Q) in
be the class of rings of the form ⊕q ∈ Qf(q), for some (f, Q) in 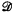 .
.
Theorem 3. Let R be a finite ring without nonzero trivial ideals. Then R admits elimination of quantifiers if and only if R belongs to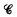 .
.
Theorem 4. Let R be a ring with the descending chain condition of left ideals and without nonzero trivial ideals. Then R admits elimination of quantifiers if and only if R is an algebraically closed field or R belongs to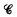 .
.
In contrast to Theorems 2 and 4, we have
Theorem 5. If R is an atomless p-ring, then R is finite, commutative, has no nonzero trivial ideals and admits elimination of quantifiers, but is not prime and does not have the descending chain condition.
We also generalize Theorems 1, 2 and 4 to alternative rings.