Hostname: page-component-7dd5485656-zklqj Total loading time: 0 Render date: 2025-10-29T23:24:43.446Z Has data issue: false hasContentIssue false
  • English
  • Français

Sticky Brownian motion as the limit of storage processes

Published online by Cambridge University Press:  14 July 2016

J. Michael Harrison  and
Austin J. Lemoine
J. Michael Harrison*
Affiliation:
Stanford University
Austin J. Lemoine*
Affiliation:
Systems Control, Inc.
*
∗ Postal address: Graduate School of Business, Stanford University, Stanford, CA 94305, U.S.A.
∗∗ Postal address: Systems Control Inc., 1801 Page Mill Rd., Palo Alto, CA 94304, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

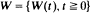The paper considers a modified storage process with state space [0,∞). Away from the origin, W behaves like an ordinary storage process with constant release rate and finite jump intensity A. In state 0, however, the jump intensity falls to 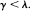It is shown that W can be obtained by applying first a reflection mapping and then a random change of time scale to a compound Poisson process with drift. When these same two transformations are applied to Brownian motion, one obtains sticky (or slowly reflected) Brownian motion W∗ on [0,∞). Thus W∗ is the natural diffusion approximation for W, and it is shown that W converges in distribution to W∗ under appropriate conditions. The boundary behavior of W∗ is discussed, its infinitesimal generator is calculated and its stationary distribution (which has an atom at the origin) is computed.

Keywords

STORAGE PROCESSESBROWNIAN MOTIONREFLECTING BARRIERSDIFFUSION PROCESSESSTICKY BROWNIAN MOTIONLIMIT THEOREM

Information

Type
Research Papers
Information
Journal of Applied Probability , Volume 18 , Issue 1 , March 1981 , pp. 216 - 226
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1] Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
[2] Breiman, L. (1968) Probability. Addison-Wesley, Reading, Mass.Google Scholar
[3] Freedman, D. (1971) Brownian Motion and Diffusion. Holden-Day, San Francisco.Google Scholar
[4] Gaver, D. P. and Shedler, G. S. (1973) Processor utilization in multiprogramming systems via diffusion approximations. Operat. Res. 21, 569–576.Google Scholar
[5] Gelenbe, E. (1975) On approximate computer system models. J. Assoc. Comput. Mach. 22, 261–269.Google Scholar
[6] Harrison, J. M. (1977) Ruin problems with compounding assets. Stoch. Proc. Appl. 5, 67–79.Google Scholar
[7] Harrison, J. M. and Resnick, S. I. (1976) The stationary distribution and first exit probabilities of a storage process with general release rule. Math. Operat. Res. 4, 347–358.CrossRefGoogle Scholar
[8] Kunita, H. and Watanabe, S. (1967) On square integrable martingales. Nagoya Math. J. 30, 209–245.CrossRefGoogle Scholar
[9] Lemoine, A. J. (1975) Limit theorems for generalized single server queues: the exceptional system. SIAM J. Appl. Math. 28, 596–606.CrossRefGoogle Scholar
[10] Moran, P. A. P. (1956) A probability theory of a dam with continuous release. Quart. Math. J. 7, 310–377.Google Scholar
[11] Takács, L. (1962) Introduction to the Theory of Queues. Oxford University Press, New York.Google Scholar