Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lefebvre, Nans
2015.
Theory and Applications of Models of Computation.
Vol. 9076,
Issue. ,
p.
177.
SALEZ, JUSTIN
2016.
The Interpolation Method for Random Graphs with Prescribed Degrees.
Combinatorics, Probability and Computing,
Vol. 25,
Issue. 3,
p.
436.
Janson, Svante
Luczak, Malwina
Windridge, Peter
and
House, Thomas
2017.
Near-critical SIR epidemic on a random graph with given degrees.
Journal of Mathematical Biology,
Vol. 74,
Issue. 4,
p.
843.
Bermolen, Paola
Jonckheere, Matthieu
and
Moyal, Pascal
2017.
The jamming constant of uniform random graphs.
Stochastic Processes and their Applications,
Vol. 127,
Issue. 7,
p.
2138.
FEDERICO, LORENZO
and
VAN DER HOFSTAD, REMCO
2017.
Critical Window for Connectivity in the Configuration Model.
Combinatorics, Probability and Computing,
Vol. 26,
Issue. 5,
p.
660.
Cai, Xing Shi
and
Devroye, Luc
2017.
The graph structure of a deterministic automaton chosen at random.
Random Structures & Algorithms,
Vol. 51,
Issue. 3,
p.
428.
Brightwell, Graham
Janson, Svante
and
Luczak, Malwina
2017.
The Greedy Independent Set in a Random Graph with Given Degrees.
Random Structures & Algorithms,
Vol. 51,
Issue. 4,
p.
565.
Avena, Luca
Güldaş, Hakan
van der Hofstad, Remco
and
den Hollander, Frank
2018.
Mixing times of random walks on dynamic configuration models.
The Annals of Applied Probability,
Vol. 28,
Issue. 4,
Lelarge, Marc
and
Oulamara, Mendes
2018.
Replica Bounds by Combinatorial Interpolation for Diluted Spin Systems.
Journal of Statistical Physics,
Vol. 173,
Issue. 3-4,
p.
917.
Ahlberg, Daniel
Deijfen, Maria
and
Janson, Svante
2019.
Competing first passage percolation on random graphs with finite variance degrees.
Random Structures & Algorithms,
Vol. 55,
Issue. 3,
p.
545.
van der Hofstad, Remco
Janson, Svante
and
Luczak, Malwina
2019.
Component structure of the configuration model: Barely supercritical case.
Random Structures & Algorithms,
Vol. 55,
Issue. 1,
p.
3.
Angel, Omer
van der Hofstad, Remco
and
Holmgren, Cecilia
2019.
Limit laws for self-loops and multiple edges in the configuration model.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 55,
Issue. 3,
Demaine, Erik D.
Reidl, Felix
Rossmanith, Peter
Sánchez Villaamil, Fernando
Sikdar, Somnath
and
Sullivan, Blair D.
2019.
Structural sparsity of complex networks: Bounded expansion in random models and real-world graphs.
Journal of Computer and System Sciences,
Vol. 105,
Issue. ,
p.
199.
Janson, Svante
2020.
Asymptotic normality in random graphs with given vertex degrees.
Random Structures & Algorithms,
Vol. 56,
Issue. 4,
p.
1070.
van der Hofstad, Remco
van der Hoorn, Pim
Litvak, Nelly
and
Stegehuis, Clara
2020.
Limit theorems for assortativity and clustering in null models for scale-free networks.
Advances in Applied Probability,
Vol. 52,
Issue. 4,
p.
1035.
Janson, Svante
2020.
Random graphs with given vertex degrees and switchings.
Random Structures & Algorithms,
Vol. 57,
Issue. 1,
p.
3.
Ball, Frank
2021.
Central limit theorems for SIR epidemics and percolation on configuration model random graphs.
The Annals of Applied Probability,
Vol. 31,
Issue. 5,
Shafie, Termeh
and
Schoch, David
2021.
Multiplexity analysis of networks using multigraph representations.
Statistical Methods & Applications,
Vol. 30,
Issue. 5,
p.
1425.
Can, Van Hao
van der Hofstad, Remco
and
Kumagai, Takashi
2021.
Glauber dynamics for Ising models on random
regular graphs: cut-off and metastability
.
Latin American Journal of Probability and Mathematical Statistics,
Vol. 18,
Issue. 1,
p.
1441.
Galanis, Andreas
Goldberg, Leslie Ann
and
Stewart, James
2022.
Fast mixing via polymers for random graphs with unbounded degree.
Information and Computation,
Vol. 285,
Issue. ,
p.
104894.

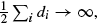 the probability that the multigraph is simple stays away from 0 if and only if
the probability that the multigraph is simple stays away from 0 if and only if 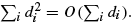 The new proof uses the method of moments, which makes it possible to use it in some applications concerning convergence in distribution. Corresponding results for bipartite graphs are included.
The new proof uses the method of moments, which makes it possible to use it in some applications concerning convergence in distribution. Corresponding results for bipartite graphs are included.