Article contents
Prevalence of deficiency-zero reaction networks in an Erdös–Rényi framework
Published online by Cambridge University Press: 28 January 2022
Abstract
Reaction networks are commonly used within the mathematical biology and mathematical chemistry communities to model the dynamics of interacting species. These models differ from the typical graphs found in random graph theory since their vertices are constructed from elementary building blocks, i.e. the species. We consider these networks in an Erdös–Rényi framework and, under suitable assumptions, derive a threshold function for the network to have a deficiency of zero, which is a property of great interest in the reaction network community. Specifically, if the number of species is denoted by n and the edge probability by 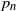 $p_n$, then we prove that the probability of a random binary network being deficiency zero converges to 1 if
$p_n$, then we prove that the probability of a random binary network being deficiency zero converges to 1 if 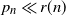 $p_n\ll r(n)$ as
$p_n\ll r(n)$ as 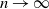 $n \to \infty$, and converges to 0 if
$n \to \infty$, and converges to 0 if 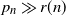 $p_n \gg r(n)$ as
$p_n \gg r(n)$ as 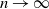 $n \to \infty$, where
$n \to \infty$, where 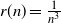 $r(n)=\frac{1}{n^3}$.
$r(n)=\frac{1}{n^3}$.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 6
- Cited by


