Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dabye, Ali S.
Farinetto, Christian
and
Kutoyants, Yury A.
2003.
On Bayesian estimators in misspecified change-point problems for Poisson process.
Statistics & Probability Letters,
Vol. 61,
Issue. 1,
p.
17.
Kutoyants, Y. A.
2009.
On properties of estimators in nonregular situations for Poisson processes.
Journal of Mathematical Sciences,
Vol. 163,
Issue. 3,
p.
213.
Hang, Ngai
and
Kutoyants, Yury A.
2010.
Recent Developments of Threshold Estimation for Nonlinear Time Series.
JOURNAL OF THE JAPAN STATISTICAL SOCIETY,
Vol. 40,
Issue. 2,
p.
277.
Tercero-Gómez, Víctor G.
Cordero-Franco, Alvaro
Pérez-Blanco, Angel
and
Hernández-Luna, Alberto
2014.
A Self-Starting CUSUM Chart Combined with a Maximum Likelihood Estimator for the Time of a Detected Shift in the Process Mean.
Quality and Reliability Engineering International,
Vol. 30,
Issue. 4,
p.
591.
Farinetto, Christian
2017.
On hypothesis tests in misspecified change-point problems for a Poisson process.
Communications in Statistics - Theory and Methods,
Vol. 46,
Issue. 20,
p.
10103.

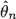 of
of 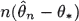 converges in law and in
converges in law and in 