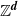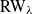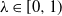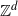Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Amina, Sabir
and
Mairemunisa, Abudusaimaiti
2024.
Stepwise Alternating Direction Implicit Method of the Three Dimensional Convective-Diffusion Equation.
Annals of Mathematics and Physics,
Vol. 7,
Issue. 3,
p.
248.