Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rey, William J. J.
1983.
Introduction to Robust and Quasi-Robust Statistical Methods.
p.
207.
Galambos, Janos
1984.
Nonparametric Methods.
Vol. 4,
Issue. ,
p.
359.
Simiu, Emil
Leigh, Stefan D.
and
Nolan, William A.
1986.
Environmental Load Direction and Reliability Bounds.
Journal of Structural Engineering,
Vol. 112,
Issue. 5,
p.
1199.
Recsei, Elaine
and
Seneta, E.
1987.
Bonferroni-type inequalities.
Advances in Applied Probability,
Vol. 19,
Issue. 02,
p.
508.
1988.
Extreme Value Theory in Engineering.
p.
341.
Lau, Tai-shing
1989.
Moment inequalities.
Statistics & Probability Letters,
Vol. 8,
Issue. 1,
p.
9.
Sibuya, Masaaki
1991.
Bonferroni-type inequalities; Chebyshev-type inequalities for the distributions on [0, n].
Annals of the Institute of Statistical Mathematics,
Vol. 43,
Issue. 2,
p.
261.
Kounias, S.
and
Sotirakoglou, K.
1993.
Upper and lower bounds for the probability that r events occur.
Optimization,
Vol. 27,
Issue. 1-2,
p.
63.
Galambos, Janos
and
Simonelli, Italo
1996.
An extension of the method of polynomials and a new reduction formula for Bonferroni-type inequalities.
Statistics & Probability Letters,
Vol. 28,
Issue. 2,
p.
147.
Frolov, A. N.
2019.
On Bounds for Probabilities of Combinations of Events, the Jordan Formula, and the Bonferroni Inequalities.
Vestnik St. Petersburg University, Mathematics,
Vol. 52,
Issue. 2,
p.
178.

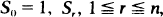 be the sum of the probabilities of all
be the sum of the probabilities of all 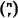 intersections of r events, and
intersections of r events, and 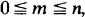 and
and 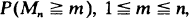 equal to partial sums of series of the form
equal to partial sums of series of the form 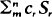 which give the exact probabilities. These inequalities have recently been extended by J. Galambos to give sharper bounds.
which give the exact probabilities. These inequalities have recently been extended by J. Galambos to give sharper bounds.