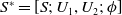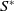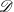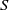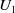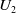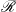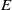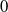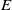1. Introduction
Higman et al. [Reference Higman, Neumann and Neumann10] introduced the concept of an HNN extension of a group. In combinatorial group theory, HNN extensions play an important role in algorithmic problems.
Yamamura [Reference Yamamura20] showed the usefulness of HNN extensions in the variety of inverse semigroups by proving the undecidability of any Markov property and the undecidability of several non-Markov properties. Jajcayová introduced lower bounded HNN extensions in [12], mirroring the definition of lower bounded amalgams of inverse semigroups given in Bennett [Reference Bennett3] and [Reference Bennett4]. It was proved in Jajcayová [Reference Jajcayová13] that an HNN extension of a free inverse semigroup with finitely generated subsemigroups has decidable word problem.
HNN extensions of a finite inverse semigroup have been considered by Cherubini and Rodaro [Reference Cherubini and Rodaro6], showing that an HNN extension of a finite inverse semigroup has decidable word problem. More recently, Ayyash and Cherubini [Reference Ayyash1] and [Reference Ayyash and Cherubini2] give necessary and sufficient conditions for an HNN extension of a finite inverse semigroup or a lower bounded HNN extension to be completely semisimple. Ayyash [Reference Ayyash1] also described the maximal subgroups in the finite case.
In the current paper, we use Bass-Serre theory to describe the maximal subgroups of a lower bounded HNN extension
![]() $S^*$
containing the idempotents of
$S^*$
containing the idempotents of
![]() $S$
(Theorem 4.4). The maximal subgroups are the fundamental groups of graph of groups constructed from
$S$
(Theorem 4.4). The maximal subgroups are the fundamental groups of graph of groups constructed from
![]() $\mathcal{D}$
-classes and maximal subgroups of
$\mathcal{D}$
-classes and maximal subgroups of
![]() $S$
. All other maximal subgroups of
$S$
. All other maximal subgroups of
![]() $S^*$
are isomorphic to subgroups of
$S^*$
are isomorphic to subgroups of
![]() $S$
(Theorem 4.6). Conditions are given for
$S$
(Theorem 4.6). Conditions are given for
![]() $S^*$
to have finite
$S^*$
to have finite
![]() $\mathcal{R}$
-classes (Theorem 4.16). Conditions are given for
$\mathcal{R}$
-classes (Theorem 4.16). Conditions are given for
![]() $S^*$
to be
$S^*$
to be
![]() $E$
-unitary and
$E$
-unitary and
![]() $0$
-
$0$
-
![]() $E$
-unitary (Theorem 4.19). We show that the HNN extension of a polycyclic inverse monoid can be
$E$
-unitary (Theorem 4.19). We show that the HNN extension of a polycyclic inverse monoid can be
![]() $0$
-
$0$
-
![]() $E$
-unitary, with group of units isomorphic to a free group and all other maximal subgroups are trivial.
$E$
-unitary, with group of units isomorphic to a free group and all other maximal subgroups are trivial.
2. Preliminaries
A semigroup
![]() $S$
is an inverse semigroup if for all
$S$
is an inverse semigroup if for all
![]() $s \in S$
there is a unique element
$s \in S$
there is a unique element
![]() $s^{-1}$
, the inverse of
$s^{-1}$
, the inverse of
![]() $s$
, such that
$s$
, such that
![]() $s s^{-1} s = s$
and
$s s^{-1} s = s$
and
![]() $s^{-1} s s^{-1} = s^{ -1 }$
. The semilattice of idempotents of
$s^{-1} s s^{-1} = s^{ -1 }$
. The semilattice of idempotents of
![]() $S$
is the set
$S$
is the set
![]() $E( S ) = \{ e \in S \;:\; e^2 = e \}$
. The natural partial order
$E( S ) = \{ e \in S \;:\; e^2 = e \}$
. The natural partial order
![]() $\leq$
of
$\leq$
of
![]() $S$
is defined by
$S$
is defined by
![]() $a \leq b$
if and only if
$a \leq b$
if and only if
![]() $a = eb$
, for some
$a = eb$
, for some
![]() $e \in E( S )$
, for
$e \in E( S )$
, for
![]() $a, b \in S$
. A subsemigroup
$a, b \in S$
. A subsemigroup
![]() $U$
of
$U$
of
![]() $S$
is an inverse subsemigroup if
$S$
is an inverse subsemigroup if
![]() $u^{-1} \in U$
, for all
$u^{-1} \in U$
, for all
![]() $u \in U$
. For inverse semigroups, see Howie [Reference Howie11], Petrich [Reference Petrich18], and Lawson [Reference Lawson16].
$u \in U$
. For inverse semigroups, see Howie [Reference Howie11], Petrich [Reference Petrich18], and Lawson [Reference Lawson16].
A presentation for an inverse semigroup
![]() $S$
is a pair
$S$
is a pair
![]() $\langle X \mid R \rangle$
, where
$\langle X \mid R \rangle$
, where
![]() $X$
is a non-empty set and
$X$
is a non-empty set and
![]() $R$
is a binary relation on
$R$
is a binary relation on
![]() $( X \cup X^{-1} )^+$
, with
$( X \cup X^{-1} )^+$
, with
![]() $S \cong ( X \cup X^{-1} )^+/ \tau$
, where
$S \cong ( X \cup X^{-1} )^+/ \tau$
, where
![]() $\tau$
is the congruence generated by
$\tau$
is the congruence generated by
![]() $R$
and the Vagner congruence
$R$
and the Vagner congruence
![]() $\rho$
. We then say
$\rho$
. We then say
![]() $S$
is presented by the generators
$S$
is presented by the generators
![]() $X$
and relations
$X$
and relations
![]() $R$
, written
$R$
, written
![]() $S = Inv \langle X \mid R \rangle$
.
$S = Inv \langle X \mid R \rangle$
.
We study
![]() $\langle X \mid R \rangle$
by considering the Schützenberger automaton
$\langle X \mid R \rangle$
by considering the Schützenberger automaton
![]() $\mathcal{A} ( X, R, w )$
of
$\mathcal{A} ( X, R, w )$
of
![]() $w$
, for
$w$
, for
![]() $w \in ( X \cup X^{-1} )^+$
. The automaton
$w \in ( X \cup X^{-1} )^+$
. The automaton
![]() $\mathcal{A} ( X, R, w )$
has underlying graph
$\mathcal{A} ( X, R, w )$
has underlying graph
![]() $S\Gamma ( X, R, w )$
, with vertices
$S\Gamma ( X, R, w )$
, with vertices
![]() $R_{w \tau }$
, the
$R_{w \tau }$
, the
![]() $\mathcal{R}$
-class of
$\mathcal{R}$
-class of
![]() $S$
containing
$S$
containing
![]() $w \tau$
, and an edge from
$w \tau$
, and an edge from
![]() $s$
to
$s$
to
![]() $t$
labeled by
$t$
labeled by
![]() $y$
, for
$y$
, for
![]() $s, t \in R_{w \tau }$
and
$s, t \in R_{w \tau }$
and
![]() $y \in X \cup X^{-1}$
where
$y \in X \cup X^{-1}$
where
![]() $s \cdot y \tau = t$
in
$s \cdot y \tau = t$
in
![]() $S$
. The initial state is
$S$
. The initial state is
![]() $ww^{-1} \tau$
and the terminal state is
$ww^{-1} \tau$
and the terminal state is
![]() $w \tau$
. We also denote
$w \tau$
. We also denote
![]() $\langle X \mid R \rangle$
,
$\langle X \mid R \rangle$
,
![]() $S \Gamma ( X, R, w )$
,
$S \Gamma ( X, R, w )$
,
![]() $\mathcal{A} ( X, R, w )$
by
$\mathcal{A} ( X, R, w )$
by
![]() $\langle S \rangle$
,
$\langle S \rangle$
,
![]() $S \Gamma ( S, w )$
,
$S \Gamma ( S, w )$
,
![]() $\mathcal{A} ( S, w )$
, respectively. For presentations, see Stephen [Reference Stephen19].
$\mathcal{A} ( S, w )$
, respectively. For presentations, see Stephen [Reference Stephen19].
For any non-empty set
![]() $X$
, an inverse word graph
$X$
, an inverse word graph
![]() $\Gamma$
over
$\Gamma$
over
![]() $X$
is a connected graph with edges labeled over the set
$X$
is a connected graph with edges labeled over the set
![]() $X \cup X^{-1}$
, such that for any edge from
$X \cup X^{-1}$
, such that for any edge from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
labeled by
$v_2$
labeled by
![]() $y$
, there is an inverse edge from
$y$
, there is an inverse edge from
![]() $v_2$
to
$v_2$
to
![]() $v_1$
labeled by
$v_1$
labeled by
![]() $y^{-1}$
. The inverse word graph
$y^{-1}$
. The inverse word graph
![]() $\Gamma$
is deterministic if no two distinct edges have the same initial vertex and label. We denote the vertex and edge by
$\Gamma$
is deterministic if no two distinct edges have the same initial vertex and label. We denote the vertex and edge by
![]() $V( \Gamma )$
and
$V( \Gamma )$
and
![]() $E( \Gamma )$
, respectively.
$E( \Gamma )$
, respectively.
A (birooted) inverse automaton over
![]() $X$
is a triple
$X$
is a triple
![]() $\mathcal{A} = ( \alpha, \Gamma, \beta )$
, where
$\mathcal{A} = ( \alpha, \Gamma, \beta )$
, where
![]() $\Gamma$
is an inverse word graph over
$\Gamma$
is an inverse word graph over
![]() $X$
and
$X$
and
![]() $\alpha$
,
$\alpha$
,
![]() $\beta$
are vertices, called the initial and terminal roots of
$\beta$
are vertices, called the initial and terminal roots of
![]() $\mathcal{A}$
, respectively. The language
$\mathcal{A}$
, respectively. The language
![]() $L [ \mathcal{A} ]$
of the automaton
$L [ \mathcal{A} ]$
of the automaton
![]() $\mathcal{A}$
is the set of all words labeling paths from
$\mathcal{A}$
is the set of all words labeling paths from
![]() $\alpha$
to
$\alpha$
to
![]() $\beta$
. An inverse automaton
$\beta$
. An inverse automaton
![]() $\mathcal{A}$
over
$\mathcal{A}$
over
![]() $X$
is called an approximate automaton of
$X$
is called an approximate automaton of
![]() $\mathcal{A} ( X, R, w )$
if
$\mathcal{A} ( X, R, w )$
if
![]() $L [ \mathcal{A} ] \subseteq L [ \mathcal{A} ( X, R, w ) ]$
, and there is some word
$L [ \mathcal{A} ] \subseteq L [ \mathcal{A} ( X, R, w ) ]$
, and there is some word
![]() $w_1 \in L [ \mathcal{A} ]$
with
$w_1 \in L [ \mathcal{A} ]$
with
![]() $w_1 = w$
in
$w_1 = w$
in
![]() $S = Inv \langle X \mid R \rangle$
, written
$S = Inv \langle X \mid R \rangle$
, written
![]() $\mathcal{A} \leadsto \mathcal{A} ( X, R, w )$
. The notation
$\mathcal{A} \leadsto \mathcal{A} ( X, R, w )$
. The notation
![]() $\cong$
is used to indicate when two inverse word graphs (automata) are isomorphic.
$\cong$
is used to indicate when two inverse word graphs (automata) are isomorphic.
If
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Gamma _1$
are disjoint inverse word graphs,
$\Gamma _1$
are disjoint inverse word graphs,
![]() $v_1, v_2 \in V( \Gamma )$
and
$v_1, v_2 \in V( \Gamma )$
and
![]() $\alpha _1, \beta _1 \in V( \Gamma _1 )$
then we sew on
$\alpha _1, \beta _1 \in V( \Gamma _1 )$
then we sew on
![]() $( \alpha _1, \Gamma _1, \beta _1 )$
from
$( \alpha _1, \Gamma _1, \beta _1 )$
from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
by taking the quotient of
$v_2$
by taking the quotient of
![]() $\Gamma \cup \Gamma _1$
by the
$\Gamma \cup \Gamma _1$
by the
![]() $V$
-equivalence generated by
$V$
-equivalence generated by
![]() $\{ ( v_1, \alpha _1 ), ( v_2, \beta _1 ) \}$
. The linear automaton of
$\{ ( v_1, \alpha _1 ), ( v_2, \beta _1 ) \}$
. The linear automaton of
![]() $w = z_1z_2 \cdots z_n \in ( X \cup X^{-1} )^+$
, for
$w = z_1z_2 \cdots z_n \in ( X \cup X^{-1} )^+$
, for
![]() $z_k \in X \cup X^{-1}$
, is the inverse automaton with vertices
$z_k \in X \cup X^{-1}$
, is the inverse automaton with vertices
![]() $v_0 = \alpha _w$
,
$v_0 = \alpha _w$
,
![]() $v_1$
,
$v_1$
,
![]() $\ldots$
,
$\ldots$
,
![]() $v_{n-1}$
,
$v_{n-1}$
,
![]() $v_n = \beta _w$
and edges
$v_n = \beta _w$
and edges
![]() $v_{k-1} \rightarrow ^{ z_k } v_k$
,
$v_{k-1} \rightarrow ^{ z_k } v_k$
,
![]() $v_k \rightarrow ^{ z^{-1}_k } v_{k-1}$
, for
$v_k \rightarrow ^{ z^{-1}_k } v_{k-1}$
, for
![]() $k = 1, 2, \ldots, n$
. If
$k = 1, 2, \ldots, n$
. If
![]() $( r, s )$
is a relation in
$( r, s )$
is a relation in
![]() $R$
and there is a path
$R$
and there is a path
![]() $v_1 \rightarrow ^r v_2$
in
$v_1 \rightarrow ^r v_2$
in
![]() $\Gamma$
, with no path
$\Gamma$
, with no path
![]() $v_1 \rightarrow ^s v_2$
, then we perform an elementary expansion, relative to
$v_1 \rightarrow ^s v_2$
, then we perform an elementary expansion, relative to
![]() $\langle X \mid R \rangle$
, by sewing on the linear automaton of
$\langle X \mid R \rangle$
, by sewing on the linear automaton of
![]() $s$
from
$s$
from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
. A deterministic inverse word graph (automaton) over
$v_2$
. A deterministic inverse word graph (automaton) over
![]() $X$
is closed relative to
$X$
is closed relative to
![]() $\langle X \mid R \rangle$
if no elementary expansion can be performed.
$\langle X \mid R \rangle$
if no elementary expansion can be performed.
If
![]() $\Gamma$
is an inverse graph over
$\Gamma$
is an inverse graph over
![]() $X$
, then we say there is a path from vertex
$X$
, then we say there is a path from vertex
![]() $v_1$
to vertex
$v_1$
to vertex
![]() $v_2$
labeled by
$v_2$
labeled by
![]() $s \in S$
, written
$s \in S$
, written
![]() $v_1 \rightarrow ^s v_2$
, if there is a path
$v_1 \rightarrow ^s v_2$
, if there is a path
![]() $v_1 \rightarrow ^w v_2$
, for some
$v_1 \rightarrow ^w v_2$
, for some
![]() $w \in ( X \cup X^{-1} )^+$
such that
$w \in ( X \cup X^{-1} )^+$
such that
![]() $w \tau = s$
in
$w \tau = s$
in
![]() $S$
. If
$S$
. If
![]() $\Gamma$
is closed, relative to
$\Gamma$
is closed, relative to
![]() $\langle X \mid R \rangle$
, and we have a path
$\langle X \mid R \rangle$
, and we have a path
![]() $v_1 \rightarrow ^w v_2$
, for some
$v_1 \rightarrow ^w v_2$
, for some
![]() $w \in ( X \cup X^{-1} )^+$
with
$w \in ( X \cup X^{-1} )^+$
with
![]() $w \tau = s$
, then we also have a path
$w \tau = s$
, then we also have a path
![]() $v_1 \rightarrow ^y v_2$
, for any
$v_1 \rightarrow ^y v_2$
, for any
![]() $y \in ( X \cup X^{-1} )^+$
with
$y \in ( X \cup X^{-1} )^+$
with
![]() $y \tau \geq s$
.
$y \tau \geq s$
.
3. HNN extensions of inverse semigroups
The theory of lower bounded HNN extensions has been generalized by the authors in [Reference Bennett and Jajcayová5]. An inverse subsemigroup
![]() $U$
is called lower bounded in
$U$
is called lower bounded in
![]() $S$
if, for any
$S$
if, for any
![]() $u \in U$
and
$u \in U$
and
![]() $e \in E( S )$
with
$e \in E( S )$
with
![]() $u \geq e$
in
$u \geq e$
in
![]() $S$
, there exists
$S$
, there exists
![]() $f \in E( U )$
with
$f \in E( U )$
with
![]() $u \geq f \geq e$
in
$u \geq f \geq e$
in
![]() $S$
. The lower bounded inverse subsemigroup condition is illustrated in Fig. 1. We review some definitions and results from [Reference Bennett and Jajcayová5].
$S$
. The lower bounded inverse subsemigroup condition is illustrated in Fig. 1. We review some definitions and results from [Reference Bennett and Jajcayová5].

Figure 1. The lower bounded subsemigroup condition.
We consider an HNN extension
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
of an inverse semigroup
$S^* = [ S;\; U_1, U_2;\; \phi ]$
of an inverse semigroup
![]() $S$
where
$S$
where
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are inverse monoids that are lower bounded in
$U_2$
are inverse monoids that are lower bounded in
![]() $S$
, with respective identities
$S$
, with respective identities
![]() $e_1$
and
$e_1$
and
![]() $e_2$
, and
$e_2$
, and
![]() $\phi \;:\; U_1 \rightarrow U_2$
is an isomorphism. If
$\phi \;:\; U_1 \rightarrow U_2$
is an isomorphism. If
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are only inverse subsemigroups that are lower bounded in
$U_2$
are only inverse subsemigroups that are lower bounded in
![]() $S$
, then we can study the HNN extension
$S$
, then we can study the HNN extension
![]() $[ S' ;\; U'_{\!\!1}, U'_{\!\!2};\; \phi ' ]$
, where
$[ S' ;\; U'_{\!\!1}, U'_{\!\!2};\; \phi ' ]$
, where
![]() $S' = S \cup \{ 1 \}$
, the element
$S' = S \cup \{ 1 \}$
, the element
![]() $1$
is disjoint from
$1$
is disjoint from
![]() $S$
and is the identity of
$S$
and is the identity of
![]() $S \cup \{ 1 \}$
,
$S \cup \{ 1 \}$
,
![]() $U'_{\!\!1} = U_1 \cup \{ 1 \}$
and
$U'_{\!\!1} = U_1 \cup \{ 1 \}$
and
![]() $U'_{\!\!2} = U_2 \cup \{ 1 \}$
are inverse monoids that are lower bounded in
$U'_{\!\!2} = U_2 \cup \{ 1 \}$
are inverse monoids that are lower bounded in
![]() $S \cup \{ 1 \}$
and
$S \cup \{ 1 \}$
and
![]() $\phi '$
is the isomorphism
$\phi '$
is the isomorphism
![]() $U'_{\!\!1} \rightarrow U'_{\!\!2}$
induced by
$U'_{\!\!1} \rightarrow U'_{\!\!2}$
induced by
![]() $\phi \;:\; U_1 \rightarrow U_2$
and
$\phi \;:\; U_1 \rightarrow U_2$
and
![]() $1 \rightarrow 1$
.
$1 \rightarrow 1$
.
Let
![]() $S$
have inverse semigroup presentation
$S$
have inverse semigroup presentation
![]() $\langle X \mid R \rangle$
. We also denote this presentation for
$\langle X \mid R \rangle$
. We also denote this presentation for
![]() $S$
by
$S$
by
![]() $\langle S \rangle$
. Let
$\langle S \rangle$
. Let
![]() $t$
be disjoint from
$t$
be disjoint from
![]() $S$
. The free product
$S$
. The free product
![]() $S * FIS( t )$
in the variety of inverse semigroups has presentation
$S * FIS( t )$
in the variety of inverse semigroups has presentation
![]() $\langle X \cup \{ t \} \mid R \rangle$
, where
$\langle X \cup \{ t \} \mid R \rangle$
, where
![]() $FIS( t )$
is the free inverse semigroup on
$FIS( t )$
is the free inverse semigroup on
![]() $\{ t \}$
. We also denote this presentation for
$\{ t \}$
. We also denote this presentation for
![]() $S * FIS( t )$
by
$S * FIS( t )$
by
![]() $\langle S \cup \{ t \} \rangle$
. The HNN extension
$\langle S \cup \{ t \} \rangle$
. The HNN extension
![]() $S^*$
has inverse semigroup presentation
$S^*$
has inverse semigroup presentation
![]() $\langle X \cup \{ t \} \mid R \cup R^* \rangle$
, where
$\langle X \cup \{ t \} \mid R \cup R^* \rangle$
, where
![]() $R^*$
consists of the relations
$R^*$
consists of the relations
![]() $tt^{-1} = e_1$
,
$tt^{-1} = e_1$
,
![]() $t^{-1} t = e_2$
and
$t^{-1} t = e_2$
and
![]() $t^{-1} u t = ( u ) \phi$
, for
$t^{-1} u t = ( u ) \phi$
, for
![]() $u \in U_1$
. We also denote this presentation for
$u \in U_1$
. We also denote this presentation for
![]() $S^*$
by
$S^*$
by
![]() $\langle S^* \rangle$
. In [Reference Yamamura20], it was proved that
$\langle S^* \rangle$
. In [Reference Yamamura20], it was proved that
![]() $S$
is embedded into
$S$
is embedded into
![]() $S^*$
. The HNN extension is illustrated in Fig. 2. For
$S^*$
. The HNN extension is illustrated in Fig. 2. For
![]() $w \in ( X \cup X^{-1} )^*$
, we let
$w \in ( X \cup X^{-1} )^*$
, we let
![]() $S\Gamma ( S, w )$
and
$S\Gamma ( S, w )$
and
![]() $\mathcal{A}( S, w )$
denote the Schützenberger graph and automaton of
$\mathcal{A}( S, w )$
denote the Schützenberger graph and automaton of
![]() $w$
, respectively, relative to
$w$
, respectively, relative to
![]() $\langle S \rangle$
. For
$\langle S \rangle$
. For
![]() $w \in ( X \cup X^{-1} \cup \{ t, t^{-1} \} )^*$
, we let
$w \in ( X \cup X^{-1} \cup \{ t, t^{-1} \} )^*$
, we let
![]() $S\Gamma ( S^*, w )$
and
$S\Gamma ( S^*, w )$
and
![]() $\mathcal{A}( S^*, w )$
denote the Schützenberger graph and automaton of
$\mathcal{A}( S^*, w )$
denote the Schützenberger graph and automaton of
![]() $w$
, respectively, relative to
$w$
, respectively, relative to
![]() $\langle S^* \rangle$
.
$\langle S^* \rangle$
.

Figure 2. The HNN extensions
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
.
$S^* = [ S;\; U_1, U_2;\; \phi ]$
.
We briefly describe the algorithm given in [Reference Bennett and Jajcayová5] for constructing the Schützenberger automata of
![]() $S^*$
. Let
$S^*$
. Let
![]() $\Gamma$
be an inverse word graph over
$\Gamma$
be an inverse word graph over
![]() $X \cup \{ t \}$
. An
$X \cup \{ t \}$
. An
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma$
is a maximal connected subgraph with edges labeled over
$\Gamma$
is a maximal connected subgraph with edges labeled over
![]() $X \cup X^{-1}$
. A
$X \cup X^{-1}$
. A
![]() $\langle t \rangle$
-lobe of
$\langle t \rangle$
-lobe of
![]() $\Gamma$
is a maximal connected subgraph with edges labeled over
$\Gamma$
is a maximal connected subgraph with edges labeled over
![]() $\{ t, t^{-1} \}$
. The
$\{ t, t^{-1} \}$
. The
![]() $\langle S \rangle$
-lobe containing
$\langle S \rangle$
-lobe containing
![]() $v \in V ( \Gamma )$
is denoted by
$v \in V ( \Gamma )$
is denoted by
![]() $\Delta ( v )$
. Any path
$\Delta ( v )$
. Any path
![]() $v_1 \rightarrow ^t v_2$
is called a
$v_1 \rightarrow ^t v_2$
is called a
![]() $t$
-edge. If
$t$
-edge. If
![]() $v_1 \rightarrow ^t v_2$
is a
$v_1 \rightarrow ^t v_2$
is a
![]() $t$
-edge where
$t$
-edge where
![]() $v_1$
and
$v_1$
and
![]() $v_2$
belong to distinct
$v_2$
belong to distinct
![]() $\langle S \rangle$
-lobes
$\langle S \rangle$
-lobes
![]() $\Delta ( v_1 )$
and
$\Delta ( v_1 )$
and
![]() $\Delta ( v_2 )$
, respectively, then
$\Delta ( v_2 )$
, respectively, then
![]() $\Delta ( v_1 )$
and
$\Delta ( v_1 )$
and
![]() $\Delta ( v_2 )$
are called adjacent and we say
$\Delta ( v_2 )$
are called adjacent and we say
![]() $\Delta ( v_2 )$
is connected to
$\Delta ( v_2 )$
is connected to
![]() $\Delta ( v_1 )$
by a
$\Delta ( v_1 )$
by a
![]() $t$
-edge.
$t$
-edge.
An
![]() $\langle S \rangle$
-lobe path is a finite sequence of
$\langle S \rangle$
-lobe path is a finite sequence of
![]() $\langle S \rangle$
-lobes
$\langle S \rangle$
-lobes
![]() $\Delta _1, \Delta _2, \ldots, \Delta _n$
, where
$\Delta _1, \Delta _2, \ldots, \Delta _n$
, where
![]() $\Delta _k$
is adjacent to
$\Delta _k$
is adjacent to
![]() $\Delta _{k+1}$
, for
$\Delta _{k+1}$
, for
![]() $1\leq k \leq n-1$
. The
$1\leq k \leq n-1$
. The
![]() $\langle S \rangle$
-lobe path is reduced if it is not of the form
$\langle S \rangle$
-lobe path is reduced if it is not of the form
![]() $\Delta _1, \Delta _2, \Delta _1$
and the
$\Delta _1, \Delta _2, \Delta _1$
and the
![]() $\langle S \rangle$
-lobes are distinct, except possibly the first and last. There is a unique reduced
$\langle S \rangle$
-lobes are distinct, except possibly the first and last. There is a unique reduced
![]() $\langle S \rangle$
-lobe path between any two
$\langle S \rangle$
-lobe path between any two
![]() $\langle S \rangle$
-lobes if and only if there are no non-trivial reduced
$\langle S \rangle$
-lobes if and only if there are no non-trivial reduced
![]() $\langle S \rangle$
-lobe loops. The
$\langle S \rangle$
-lobe loops. The
![]() $\langle S \rangle$
-lobe graph of
$\langle S \rangle$
-lobe graph of
![]() $\Gamma$
is the graph with vertices consisting of the
$\Gamma$
is the graph with vertices consisting of the
![]() $\langle S \rangle$
-lobes of
$\langle S \rangle$
-lobes of
![]() $\Gamma$
and edges consisting of all pairs
$\Gamma$
and edges consisting of all pairs
![]() $( \Delta _1, \Delta _2 )$
of adjacent
$( \Delta _1, \Delta _2 )$
of adjacent
![]() $\langle S \rangle$
-lobes, where there is a
$\langle S \rangle$
-lobes, where there is a
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
from a vertex
$v_1 \rightarrow ^t v_2$
from a vertex
![]() $v_1$
of
$v_1$
of
![]() $\Delta _1$
to a vertex
$\Delta _1$
to a vertex
![]() $v_2$
of
$v_2$
of
![]() $\Delta _2$
. The
$\Delta _2$
. The
![]() $\langle S \rangle$
-lobe graph of
$\langle S \rangle$
-lobe graph of
![]() $\Gamma$
is a tree if and only if there are no non-trivial reduced
$\Gamma$
is a tree if and only if there are no non-trivial reduced
![]() $\langle S \rangle$
-lobe loops. An
$\langle S \rangle$
-lobe loops. An
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma$
is a called extremal if it is adjacent to precisely one other
$\Gamma$
is a called extremal if it is adjacent to precisely one other
![]() $\langle S \rangle$
-lobe.
$\langle S \rangle$
-lobe.
We say
![]() $\Gamma$
is
$\Gamma$
is
![]() $t$
-cactoid if it has finitely many
$t$
-cactoid if it has finitely many
![]() $\langle S \rangle$
-lobes, every
$\langle S \rangle$
-lobes, every
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
connects distinct
$v_1 \rightarrow ^t v_2$
connects distinct
![]() $\langle S \rangle$
-lobes, for any such
$\langle S \rangle$
-lobes, for any such
![]() $t$
-edge there are loops
$t$
-edge there are loops
![]() $v_1 \rightarrow ^{ e_1 } v_1$
and
$v_1 \rightarrow ^{ e_1 } v_1$
and
![]() $v_2 \rightarrow ^{ e_2 } v_2$
in
$v_2 \rightarrow ^{ e_2 } v_2$
in
![]() $\Gamma$
, where
$\Gamma$
, where
![]() $e_1$
and
$e_1$
and
![]() $e_2$
are the identities of
$e_2$
are the identities of
![]() $U_1$
and
$U_1$
and
![]() $U_2$
, respectively, adjacent
$U_2$
, respectively, adjacent
![]() $\langle S \rangle$
-lobes are connected by precisely one
$\langle S \rangle$
-lobes are connected by precisely one
![]() $t$
-edge and the
$t$
-edge and the
![]() $\langle S \rangle$
-lobe graph of
$\langle S \rangle$
-lobe graph of
![]() $\Gamma$
is a finite tree. An inverse automaton over
$\Gamma$
is a finite tree. An inverse automaton over
![]() $X \cup \{ t \}$
is
$X \cup \{ t \}$
is
![]() $t$
-cactoid if its underlying graph is.
$t$
-cactoid if its underlying graph is.
Construction 3.1. [Reference Bennett and Jajcayová5, Construction 3.5] Let
![]() $\mathcal{A}$
be a
$\mathcal{A}$
be a
![]() $t$
-cactoid inverse automaton over
$t$
-cactoid inverse automaton over
![]() $X \cup \{ t \}$
that is closed, relative to
$X \cup \{ t \}$
that is closed, relative to
![]() $\langle X \cup \{ t \} \mid R \rangle$
. Suppose
$\langle X \cup \{ t \} \mid R \rangle$
. Suppose
![]() $v_1 \rightarrow ^t v_2$
is a
$v_1 \rightarrow ^t v_2$
is a
![]() $t$
-edge of
$t$
-edge of
![]() $\mathcal{A}$
and we have a loop
$\mathcal{A}$
and we have a loop
![]() $v_1 \rightarrow ^f v_1$
in
$v_1 \rightarrow ^f v_1$
in
![]() $\Delta ( v_1 )$
, for some
$\Delta ( v_1 )$
, for some
![]() $f \in E( U_1 )$
, and no loop
$f \in E( U_1 )$
, and no loop
![]() $v_2 \rightarrow ^{ ( f ) \phi } v_2$
in
$v_2 \rightarrow ^{ ( f ) \phi } v_2$
in
![]() $\Delta ( v_2 )$
. Let
$\Delta ( v_2 )$
. Let
![]() $\mathcal{A}'$
be the closed form, relative to
$\mathcal{A}'$
be the closed form, relative to
![]() $\langle X \cup \{ t \} \mid R \rangle$
, of the automaton obtained from
$\langle X \cup \{ t \} \mid R \rangle$
, of the automaton obtained from
![]() $\mathcal{A}$
by sewing on the linear automaton of any word that defines
$\mathcal{A}$
by sewing on the linear automaton of any word that defines
![]() $( f ) \phi$
in
$( f ) \phi$
in
![]() $S$
at
$S$
at
![]() $v_2$
. The construction is illustrated in Fig. 3, where the circles represent
$v_2$
. The construction is illustrated in Fig. 3, where the circles represent
![]() $\langle S \rangle$
-lobes, the dots represent vertices of
$\langle S \rangle$
-lobes, the dots represent vertices of
![]() $\mathcal{A}$
, the arrows represent paths, and the dashed arrow represents the linear automaton of
$\mathcal{A}$
, the arrows represent paths, and the dashed arrow represents the linear automaton of
![]() $( f ) \phi$
. We have an analogous construction when we have a loop
$( f ) \phi$
. We have an analogous construction when we have a loop
![]() $v_2 \rightarrow ^{ ( f ) \phi } v_2$
in
$v_2 \rightarrow ^{ ( f ) \phi } v_2$
in
![]() $\Delta ( v_2 )$
, for some
$\Delta ( v_2 )$
, for some
![]() $f \in E( U_1 )$
, and no loop
$f \in E( U_1 )$
, and no loop
![]() $v_1 \rightarrow ^f v_1$
in
$v_1 \rightarrow ^f v_1$
in
![]() $\Delta ( v_1 )$
.
$\Delta ( v_1 )$
.

Figure 3. Construction 3.1 illustrated.
Construction 3.2. [Reference Bennett and Jajcayová5, Construction 3.12] Let
![]() $\mathcal{B} = ( \alpha _2, \Gamma _2, \beta _2 )$
be a
$\mathcal{B} = ( \alpha _2, \Gamma _2, \beta _2 )$
be a
![]() $t$
-cactoid inverse automaton over
$t$
-cactoid inverse automaton over
![]() $X \cup \{ t \}$
that is closed, relative to
$X \cup \{ t \}$
that is closed, relative to
![]() $\langle X \cup \{ t \} \mid R \rangle$
. Suppose there are
$\langle X \cup \{ t \} \mid R \rangle$
. Suppose there are
![]() $t$
-edges
$t$
-edges
![]() $v_1 \rightarrow ^t v_2$
,
$v_1 \rightarrow ^t v_2$
,
![]() $v_3 \rightarrow ^t v_4$
and paths
$v_3 \rightarrow ^t v_4$
and paths
![]() $v_1 \rightarrow ^u v_3$
,
$v_1 \rightarrow ^u v_3$
,
![]() $v_2 \rightarrow ^{ ( u ) \phi } v_5$
in
$v_2 \rightarrow ^{ ( u ) \phi } v_5$
in
![]() $\Gamma _2$
, for some
$\Gamma _2$
, for some
![]() $u \in U_1$
. The situation is illustrated in Fig. 4.
$u \in U_1$
. The situation is illustrated in Fig. 4.

Figure 4. Construction 3.2 illustrated.
Since the
![]() $\langle S \rangle$
-lobe graph of
$\langle S \rangle$
-lobe graph of
![]() $\Gamma _2$
is a tree, the unique reduced
$\Gamma _2$
is a tree, the unique reduced
![]() $\langle S \rangle$
-lobe path from an
$\langle S \rangle$
-lobe path from an
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma _2$
to
$\Gamma _2$
to
![]() $\Delta ( v_1 )$
either contains
$\Delta ( v_1 )$
either contains
![]() $\Delta ( v_2 )$
or does not. Let
$\Delta ( v_2 )$
or does not. Let
![]() $\Sigma _1$
be the subgraph of
$\Sigma _1$
be the subgraph of
![]() $\Gamma _2$
containing
$\Gamma _2$
containing
![]() $\Delta ( v_1 )$
and any
$\Delta ( v_1 )$
and any
![]() $\langle S \rangle$
-lobe where the unique reduced
$\langle S \rangle$
-lobe where the unique reduced
![]() $\langle S \rangle$
-lobe path to
$\langle S \rangle$
-lobe path to
![]() $\Delta ( v_1 )$
does not contain
$\Delta ( v_1 )$
does not contain
![]() $\Delta ( v_2 )$
, including all
$\Delta ( v_2 )$
, including all
![]() $t$
-edges connecting these
$t$
-edges connecting these
![]() $\langle S \rangle$
-lobes. Similarly, let
$\langle S \rangle$
-lobes. Similarly, let
![]() $\Sigma _2$
be the subgraph of
$\Sigma _2$
be the subgraph of
![]() $\Gamma _2$
containing
$\Gamma _2$
containing
![]() $\Delta ( v_2 )$
and any
$\Delta ( v_2 )$
and any
![]() $\langle S \rangle$
-lobe where the unique reduced
$\langle S \rangle$
-lobe where the unique reduced
![]() $\langle S \rangle$
-lobe path to
$\langle S \rangle$
-lobe path to
![]() $\Delta ( v_2 )$
does not contain
$\Delta ( v_2 )$
does not contain
![]() $\Delta ( v_1 )$
, including all
$\Delta ( v_1 )$
, including all
![]() $t$
-edges connecting these
$t$
-edges connecting these
![]() $\langle S \rangle$
-lobes. Thus
$\langle S \rangle$
-lobes. Thus
![]() $\Sigma _1 \cup \Sigma _2$
is equal to
$\Sigma _1 \cup \Sigma _2$
is equal to
![]() $\Gamma _2$
, minus the
$\Gamma _2$
, minus the
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
, and
$v_1 \rightarrow ^t v_2$
, and
![]() $\Sigma _1 \cap \Sigma _2 = \emptyset$
.
$\Sigma _1 \cap \Sigma _2 = \emptyset$
.
Let
![]() $\Sigma ^*_1$
and
$\Sigma ^*_1$
and
![]() $\Sigma ^*_2$
denote disjoint copies of
$\Sigma ^*_2$
denote disjoint copies of
![]() $\Sigma _1$
and
$\Sigma _1$
and
![]() $\Sigma _2$
, respectively. Let
$\Sigma _2$
, respectively. Let
![]() $\alpha ^*$
and
$\alpha ^*$
and
![]() $\beta ^*$
denote the unique respective images of
$\beta ^*$
denote the unique respective images of
![]() $\alpha _2$
and
$\alpha _2$
and
![]() $\beta _2$
in
$\beta _2$
in
![]() $\Sigma ^*_1 \cup \Sigma ^*_2$
. Then, let
$\Sigma ^*_1 \cup \Sigma ^*_2$
. Then, let
![]() $\eta$
denote the
$\eta$
denote the
![]() $V$
-equivalence on
$V$
-equivalence on
![]() $ \Sigma ^*_1 \cup \Sigma ^*_2$
generated by
$ \Sigma ^*_1 \cup \Sigma ^*_2$
generated by
![]() $\{ ( v_4, v_5 ) \}$
, letting
$\{ ( v_4, v_5 ) \}$
, letting
![]() $v_4$
and
$v_4$
and
![]() $v_5$
denote their unique images in
$v_5$
denote their unique images in
![]() $ \Sigma ^*_1 \cup \Sigma ^*_2$
. Put
$ \Sigma ^*_1 \cup \Sigma ^*_2$
. Put
![]() $\mathcal{C} = ( \alpha ^* \eta, ( \Sigma ^*_1 \cup \Sigma ^*_2 )/ \eta, \beta ^* \eta )$
. Let
$\mathcal{C} = ( \alpha ^* \eta, ( \Sigma ^*_1 \cup \Sigma ^*_2 )/ \eta, \beta ^* \eta )$
. Let
![]() $\mathcal{B}'$
denote the closed form of
$\mathcal{B}'$
denote the closed form of
![]() $\mathcal{C}$
, relative to
$\mathcal{C}$
, relative to
![]() $\langle X \cup \{ t \} \mid R \rangle$
.
$\langle X \cup \{ t \} \mid R \rangle$
.
We have an analogous construction if there are
![]() $t$
-edges
$t$
-edges
![]() $v_2 \rightarrow ^t v_1$
,
$v_2 \rightarrow ^t v_1$
,
![]() $v_4 \rightarrow ^t v_3$
and paths
$v_4 \rightarrow ^t v_3$
and paths
![]() $v_1 \rightarrow ^{ ( u ) \phi } v_3$
,
$v_1 \rightarrow ^{ ( u ) \phi } v_3$
,
![]() $v_2 \rightarrow ^u v_5$
in
$v_2 \rightarrow ^u v_5$
in
![]() $\Gamma _2$
, for some
$\Gamma _2$
, for some
![]() $u \in U_1$
.
$u \in U_1$
.
Let
![]() $\Gamma$
be an inverse word graph over
$\Gamma$
be an inverse word graph over
![]() $X \cup \{ t \}$
. The graph
$X \cup \{ t \}$
. The graph
![]() $\Gamma$
has the idempotent property if for every loop
$\Gamma$
has the idempotent property if for every loop
![]() $v \rightarrow ^s v$
in
$v \rightarrow ^s v$
in
![]() $\Gamma$
, where
$\Gamma$
, where
![]() $s \in S$
, there is a loop
$s \in S$
, there is a loop
![]() $v \rightarrow ^e v$
, for some
$v \rightarrow ^e v$
, for some
![]() $e \in E( S )$
with
$e \in E( S )$
with
![]() $s \geq e$
in
$s \geq e$
in
![]() $S$
. The graph
$S$
. The graph
![]() $\Gamma$
has the equality property if, for every
$\Gamma$
has the equality property if, for every
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
in
$v_1 \rightarrow ^t v_2$
in
![]() $\Gamma$
, connecting two distinct
$\Gamma$
, connecting two distinct
![]() $\langle S \rangle$
-lobes, there is a loop
$\langle S \rangle$
-lobes, there is a loop
![]() $v_1 \rightarrow ^u v_1$
in
$v_1 \rightarrow ^u v_1$
in
![]() $\Delta ( v_1 )$
if and only if there is a loop
$\Delta ( v_1 )$
if and only if there is a loop
![]() $v_2 \rightarrow ^{ ( u )\phi } v_2$
in
$v_2 \rightarrow ^{ ( u )\phi } v_2$
in
![]() $\Delta ( v_2 )$
, for all
$\Delta ( v_2 )$
, for all
![]() $u \in U_1$
.
$u \in U_1$
.
For an
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
of
$v_1 \rightarrow ^t v_2$
of
![]() $\Gamma$
, the set of related pairs of
$\Gamma$
, the set of related pairs of
![]() $v_1 \rightarrow ^t v_2$
consists of
$v_1 \rightarrow ^t v_2$
consists of
![]() $( v_1, v_2 )$
and all pairs
$( v_1, v_2 )$
and all pairs
![]() $( v_3, v_4 )$
of vertices for which we have a path
$( v_3, v_4 )$
of vertices for which we have a path
![]() $v_1 \rightarrow ^u v_3$
in
$v_1 \rightarrow ^u v_3$
in
![]() $\Delta ( v_1 )$
and a path
$\Delta ( v_1 )$
and a path
![]() $v_2 \rightarrow ^{( u ) \phi } v_4$
in
$v_2 \rightarrow ^{( u ) \phi } v_4$
in
![]() $\Delta ( v_2 )$
, for some
$\Delta ( v_2 )$
, for some
![]() $u \in U_1$
. If
$u \in U_1$
. If
![]() $( v_3, v_4 )$
is a related pair of
$( v_3, v_4 )$
is a related pair of
![]() $v_1 \rightarrow ^t v_2$
, then
$v_1 \rightarrow ^t v_2$
, then
![]() $v_3$
and
$v_3$
and
![]() $v_4$
are called its first and second coordinates, respectively. The graph
$v_4$
are called its first and second coordinates, respectively. The graph
![]() $\Gamma$
has the separation property if the related pairs of any two
$\Gamma$
has the separation property if the related pairs of any two
![]() $t$
-edges, connecting different pairs of
$t$
-edges, connecting different pairs of
![]() $\langle S \rangle$
-lobes, share no common first coordinates and no common second coordinates.
$\langle S \rangle$
-lobes, share no common first coordinates and no common second coordinates.
We say that a
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
of
$v_1 \rightarrow ^t v_2$
of
![]() $\Gamma$
has identified related pairs if there is a
$\Gamma$
has identified related pairs if there is a
![]() $t$
-edge
$t$
-edge
![]() $v_3 \rightarrow ^t v_4$
for every related pair
$v_3 \rightarrow ^t v_4$
for every related pair
![]() $( v_3, v_4 )$
of
$( v_3, v_4 )$
of
![]() $v_1 \rightarrow ^t v_2$
. If, in addition, the pair
$v_1 \rightarrow ^t v_2$
. If, in addition, the pair
![]() $( v_3, v_4 )$
is a related pair of
$( v_3, v_4 )$
is a related pair of
![]() $v_1 \rightarrow ^t v_2$
, for every
$v_1 \rightarrow ^t v_2$
, for every
![]() $t$
-edge
$t$
-edge
![]() $v_3 \rightarrow ^t v_4$
from
$v_3 \rightarrow ^t v_4$
from
![]() $\Delta ( v_1 )$
to
$\Delta ( v_1 )$
to
![]() $\Delta ( v_2 )$
, then we say
$\Delta ( v_2 )$
, then we say
![]() $\Delta ( v_1 )$
and
$\Delta ( v_1 )$
and
![]() $\Delta ( v_2 )$
are
$\Delta ( v_2 )$
are
![]() $t$
-saturated by
$t$
-saturated by
![]() $v_1 \rightarrow ^t v_2$
. The graph
$v_1 \rightarrow ^t v_2$
. The graph
![]() $\Gamma$
has the
$\Gamma$
has the
![]() $t$
-saturation property if any two adjacent
$t$
-saturation property if any two adjacent
![]() $\langle S \rangle$
-lobes are
$\langle S \rangle$
-lobes are
![]() $t$
-saturated by some
$t$
-saturated by some
![]() $t$
-edge.
$t$
-edge.
If
![]() $\Gamma$
has the equality property, then the related pairs of any
$\Gamma$
has the equality property, then the related pairs of any
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
define a partial one-one map between
$v_1 \rightarrow ^t v_2$
define a partial one-one map between
![]() $V( \Delta ( v_1 ) )$
and
$V( \Delta ( v_1 ) )$
and
![]() $V( \Delta ( v_2 ) )$
. If
$V( \Delta ( v_2 ) )$
. If
![]() $\Gamma$
has the equality and separation properties and
$\Gamma$
has the equality and separation properties and
![]() $v_1 \rightarrow ^t v_2$
is the only
$v_1 \rightarrow ^t v_2$
is the only
![]() $t$
-edge from
$t$
-edge from
![]() $\Delta ( v_1 )$
to
$\Delta ( v_1 )$
to
![]() $\Delta ( v_2 )$
, then we can
$\Delta ( v_2 )$
, then we can
![]() $t$
-saturate
$t$
-saturate
![]() $\Delta _1( v )$
and
$\Delta _1( v )$
and
![]() $\Delta _2( v )$
by sewing on a
$\Delta _2( v )$
by sewing on a
![]() $t$
-edge from
$t$
-edge from
![]() $v_3$
to
$v_3$
to
![]() $v_4$
, for every related pair
$v_4$
, for every related pair
![]() $( v_3, v_4 )$
of
$( v_3, v_4 )$
of
![]() $v_1 \rightarrow ^t v_2$
, other than
$v_1 \rightarrow ^t v_2$
, other than
![]() $( v_1, v_2 )$
. If
$( v_1, v_2 )$
. If
![]() $\Gamma$
has the equality and separation properties and there is precisely one
$\Gamma$
has the equality and separation properties and there is precisely one
![]() $t$
-edge connecting adjacent
$t$
-edge connecting adjacent
![]() $\langle S \rangle$
-lobes, then the
$\langle S \rangle$
-lobes, then the
![]() $t$
-saturated form of
$t$
-saturated form of
![]() $\Gamma$
is obtained by
$\Gamma$
is obtained by
![]() $t$
-saturating every pair of adjacent
$t$
-saturating every pair of adjacent
![]() $\langle S \rangle$
-lobes.
$\langle S \rangle$
-lobes.
The graph
![]() $\Gamma$
is
$\Gamma$
is
![]() $t$
-opuntoid if every
$t$
-opuntoid if every
![]() $t$
-edge connects two distinct
$t$
-edge connects two distinct
![]() $\langle S \rangle$
-lobes, the idempotent, equality and
$\langle S \rangle$
-lobes, the idempotent, equality and
![]() $t$
-saturation properties hold and there are no non-trivial reduced
$t$
-saturation properties hold and there are no non-trivial reduced
![]() $\langle S \rangle$
-lobe loops. A
$\langle S \rangle$
-lobe loops. A
![]() $t$
-subopuntoid subgraph of a
$t$
-subopuntoid subgraph of a
![]() $t$
-opuntoid graph
$t$
-opuntoid graph
![]() $\Gamma$
is a connected subgraph that is also
$\Gamma$
is a connected subgraph that is also
![]() $t$
-opuntoid and is formed by a collection of the
$t$
-opuntoid and is formed by a collection of the
![]() $\langle S \rangle$
-lobes of
$\langle S \rangle$
-lobes of
![]() $\Gamma$
. If
$\Gamma$
. If
![]() $\Gamma$
is
$\Gamma$
is
![]() $t$
-opuntoid, then a
$t$
-opuntoid, then a
![]() $v \in V( \Gamma )$
is a bud if there is a loop
$v \in V( \Gamma )$
is a bud if there is a loop
![]() $v \rightarrow ^f v$
in
$v \rightarrow ^f v$
in
![]() $\Delta ( v )$
, for some
$\Delta ( v )$
, for some
![]() $f \in E( U_1 )$
, and no
$f \in E( U_1 )$
, and no
![]() $t$
-edge
$t$
-edge
![]() $v \rightarrow ^t v'$
, or if there a loop
$v \rightarrow ^t v'$
, or if there a loop
![]() $v \rightarrow ^{ ( f ) \phi } v$
in
$v \rightarrow ^{ ( f ) \phi } v$
in
![]() $\Delta ( v )$
, for some
$\Delta ( v )$
, for some
![]() $f \in E( U_1 )$
, and no
$f \in E( U_1 )$
, and no
![]() $t$
-edge
$t$
-edge
![]() $v' \rightarrow ^t v$
. Any of the above graph properties holds for an inverse automaton over
$v' \rightarrow ^t v$
. Any of the above graph properties holds for an inverse automaton over
![]() $X \cup \{ t \}$
if it holds for its underlying graph.
$X \cup \{ t \}$
if it holds for its underlying graph.
Construction 3.3. [Reference Bennett and Jajcayová5, Construction 3.17] Let
![]() $\mathcal{D}$
be a
$\mathcal{D}$
be a
![]() $t$
-opuntoid automaton that is closed, relative to
$t$
-opuntoid automaton that is closed, relative to
![]() $\langle X \cup \{ t \} \mid R \rangle$
, and has a bud
$\langle X \cup \{ t \} \mid R \rangle$
, and has a bud
![]() $v_1$
. If
$v_1$
. If
![]() $v_1 \in V( \mathcal{D} )$
and there is a loop
$v_1 \in V( \mathcal{D} )$
and there is a loop
![]() $v_1 \rightarrow ^f v_1$
in
$v_1 \rightarrow ^f v_1$
in
![]() $\Delta ( v_1 )$
, for some
$\Delta ( v_1 )$
, for some
![]() $f \in E( U_1 )$
, and no
$f \in E( U_1 )$
, and no
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
, then we form the automaton
$v_1 \rightarrow ^t v_2$
, then we form the automaton
![]() $\mathcal{E}$
from
$\mathcal{E}$
from
![]() $\mathcal{D}$
by sewing on a
$\mathcal{D}$
by sewing on a
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
and then sewing the linear automaton of any word that defines
$v_1 \rightarrow ^t v_2$
and then sewing the linear automaton of any word that defines
![]() $( f ) \phi$
in
$( f ) \phi$
in
![]() $S^*$
at
$S^*$
at
![]() $v_2$
, for every
$v_2$
, for every
![]() $f \in E( U_1 )$
that labels a loop at
$f \in E( U_1 )$
that labels a loop at
![]() $v_1$
in
$v_1$
in
![]() $\Delta ( v_1 )$
. In Fig. 5, the dashed arrows represent the automata that are sewed and the dashed circle represents the new
$\Delta ( v_1 )$
. In Fig. 5, the dashed arrows represent the automata that are sewed and the dashed circle represents the new
![]() $\langle S \rangle$
-lobe created. Let
$\langle S \rangle$
-lobe created. Let
![]() $\mathcal{E}'$
denote the closed form of
$\mathcal{E}'$
denote the closed form of
![]() $\mathcal{E}$
, relative to
$\mathcal{E}$
, relative to
![]() $\langle S \cup \{ t \} \rangle$
. Let
$\langle S \cup \{ t \} \rangle$
. Let
![]() $v'_{\!\!1} \rightarrow ^t v'_{\!\!2}$
denote the image of
$v'_{\!\!1} \rightarrow ^t v'_{\!\!2}$
denote the image of
![]() $v_1 \rightarrow ^t v_2$
in
$v_1 \rightarrow ^t v_2$
in
![]() $\mathcal{E}$
. Then,
$\mathcal{E}$
. Then,
![]() $\mathcal{E}'$
is obtained from
$\mathcal{E}'$
is obtained from
![]() $\mathcal{E}$
by closing
$\mathcal{E}$
by closing
![]() $\Delta ( v'_{\!\!2} )$
, relative to
$\Delta ( v'_{\!\!2} )$
, relative to
![]() $\langle S \rangle$
. Let
$\langle S \rangle$
. Let
![]() $v''_{\!\!\!1} \rightarrow ^t v''_{\!\!\!2}$
denote the image of
$v''_{\!\!\!1} \rightarrow ^t v''_{\!\!\!2}$
denote the image of
![]() $v'_{\!\!1} \rightarrow ^t v'_{\!\!2}$
in
$v'_{\!\!1} \rightarrow ^t v'_{\!\!2}$
in
![]() $\mathcal{E}'$
. Then, let
$\mathcal{E}'$
. Then, let
![]() $\mathcal{D}'$
be the automaton obtained from
$\mathcal{D}'$
be the automaton obtained from
![]() $\mathcal{E}'$
by sewing on a
$\mathcal{E}'$
by sewing on a
![]() $t$
-edge from
$t$
-edge from
![]() $v_3$
to
$v_3$
to
![]() $v_4$
, for every related pair
$v_4$
, for every related pair
![]() $( v_3, v_4 )$
of
$( v_3, v_4 )$
of
![]() $v''_{\!\!\!1} \rightarrow ^t v''_{\!\!\!2}$
, other than
$v''_{\!\!\!1} \rightarrow ^t v''_{\!\!\!2}$
, other than
![]() $( v''_{\!\!\!1}, v''_{\!\!\!2} )$
.
$( v''_{\!\!\!1}, v''_{\!\!\!2} )$
.

Figure 5. Construction 3.3 illustrated.
We have an analogous construction if we have a vertex
![]() $v_2 \in V( \mathcal{D} )$
and there is a loop
$v_2 \in V( \mathcal{D} )$
and there is a loop
![]() $v_2 \rightarrow ^{ ( f ) \phi } v_2$
in
$v_2 \rightarrow ^{ ( f ) \phi } v_2$
in
![]() $\Delta ( v_2 )$
, for some
$\Delta ( v_2 )$
, for some
![]() $f \in E( U_1 )$
, and no
$f \in E( U_1 )$
, and no
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
.
$v_1 \rightarrow ^t v_2$
.
A
![]() $t$
-opuntoid graph
$t$
-opuntoid graph
![]() $\Gamma$
is complete if it has no buds. A complete
$\Gamma$
is complete if it has no buds. A complete
![]() $t$
-opuntoid graph is illustrated in Fig. 6, where the circles represent
$t$
-opuntoid graph is illustrated in Fig. 6, where the circles represent
![]() $\langle S \rangle$
-lobes and the arrows represent
$\langle S \rangle$
-lobes and the arrows represent
![]() $t$
-edges.
$t$
-edges.

Figure 6. A complete
![]() $t$
-opuntoid graph.
$t$
-opuntoid graph.
Lemma 3.4. [Reference Bennett and Jajcayová5, Lemmas 3.18, 3.19] Let
![]() $\mathcal{D}$
be a
$\mathcal{D}$
be a
![]() $t$
-opuntoid automaton, and let
$t$
-opuntoid automaton, and let
![]() $\mathcal{D}'$
be obtained from
$\mathcal{D}'$
be obtained from
![]() $\mathcal{D}$
by Construction 3.3. Then
$\mathcal{D}$
by Construction 3.3. Then
![]() $\mathcal{D}'$
is a
$\mathcal{D}'$
is a
![]() $t$
-opuntoid automaton and
$t$
-opuntoid automaton and
![]() $\mathcal{D}$
is a
$\mathcal{D}$
is a
![]() $t$
-subopuntoid subautomaton of
$t$
-subopuntoid subautomaton of
![]() $\mathcal{D}'$
. Further, if
$\mathcal{D}'$
. Further, if
![]() $\mathcal{D} \leadsto \mathcal{A}( S^*, w )$
then
$\mathcal{D} \leadsto \mathcal{A}( S^*, w )$
then
![]() $\mathcal{D}' \leadsto \mathcal{A}( S^*, w )$
. We have a directed system of all automata obtained from
$\mathcal{D}' \leadsto \mathcal{A}( S^*, w )$
. We have a directed system of all automata obtained from
![]() $\mathcal{D}$
by a finite number of applications of Construction 3.3. The direct limit
$\mathcal{D}$
by a finite number of applications of Construction 3.3. The direct limit
![]() $\mathcal{E}$
is a complete
$\mathcal{E}$
is a complete
![]() $t$
-opuntoid automaton. Thus, if
$t$
-opuntoid automaton. Thus, if
![]() $\mathcal{D} \leadsto \mathcal{A}( S^*, w )$
and we have a loop
$\mathcal{D} \leadsto \mathcal{A}( S^*, w )$
and we have a loop
![]() $v_1 \rightarrow ^{ e_1 } v_1$
for every
$v_1 \rightarrow ^{ e_1 } v_1$
for every
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
then
$v_1 \rightarrow ^t v_2$
then
![]() $\mathcal{E} \cong \mathcal{A}( S^*, w )$
.
$\mathcal{E} \cong \mathcal{A}( S^*, w )$
.
Algorithm 3.5. [Reference Bennett and Jajcayová5, Algorithm 3.20] For
![]() $w \in ( X \cup X^{-1} \cup \{ t, t^{-1} \} )^*$
, the Schützenberger automaton of
$w \in ( X \cup X^{-1} \cup \{ t, t^{-1} \} )^*$
, the Schützenberger automaton of
![]() $w$
, relative to
$w$
, relative to
![]() $\langle S^* \rangle$
, is constructed as follows:
$\langle S^* \rangle$
, is constructed as follows:
-
(i) Construct
 $\mathcal{A} = \mathcal{A}( S \cup \{ t \}, w )$
, using [Reference Jones, Margolis, Meakin and Stephen15]. We can assume
$\mathcal{A} = \mathcal{A}( S \cup \{ t \}, w )$
, using [Reference Jones, Margolis, Meakin and Stephen15]. We can assume
 $\mathcal{A}$
is
$\mathcal{A}$
is
 $t$
-cactoid and has the idempotent property.
$t$
-cactoid and has the idempotent property. -
(ii) Construct the direct limit
 $\mathcal{B}$
of the directed system of all automata obtained from
$\mathcal{B}$
of the directed system of all automata obtained from
 $\mathcal{A}$
by a finite number of applications of Construction 3.1. Then,
$\mathcal{A}$
by a finite number of applications of Construction 3.1. Then,
 $\mathcal{B}$
is
$\mathcal{B}$
is
 $t$
-cactoid, has the idempotent and equality propertie,s and has at most as many
$t$
-cactoid, has the idempotent and equality propertie,s and has at most as many
 $\langle S \rangle$
-lobes as
$\langle S \rangle$
-lobes as
 $\mathcal{A}$
.
$\mathcal{A}$
. -
(iii) If necessary, construct
 $\mathcal{B}'$
from
$\mathcal{B}'$
from
 $\mathcal{B}$
using Construction 3.2. Then ,
$\mathcal{B}$
using Construction 3.2. Then ,
 $\mathcal{B}'$
is
$\mathcal{B}'$
is
 $t$
-cactoid, has the idempotent and equality properties, and has fewer
$t$
-cactoid, has the idempotent and equality properties, and has fewer
 $\langle S \rangle$
-lobes than
$\langle S \rangle$
-lobes than
 $\mathcal{B}$
.
$\mathcal{B}$
. -
(iv) Steps (ii) and (iii) can be applied at most a finite number of times. The resulting automaton
 $\mathcal{C}$
is
$\mathcal{C}$
is
 $t$
-cactoid and has the idempotent, equality, and separation properties.
$t$
-cactoid and has the idempotent, equality, and separation properties. -
(v) The
 $t$
-saturated form
$t$
-saturated form
 $\mathcal{D}$
of
$\mathcal{D}$
of
 $\mathcal{C}$
is
$\mathcal{C}$
is
 $t$
-opuntoid and has finite
$t$
-opuntoid and has finite
 $\langle S \rangle$
-lobes.
$\langle S \rangle$
-lobes. -
(vi) Construct the direct limit
 $\mathcal{E}$
of the directed system of all automata obtained from
$\mathcal{E}$
of the directed system of all automata obtained from
 $\mathcal{D}$
by a finite number of applications of Construction 3.3. Then,
$\mathcal{D}$
by a finite number of applications of Construction 3.3. Then,
 $\mathcal{E}$
is a complete
$\mathcal{E}$
is a complete
 $t$
-opuntoid automaton and
$t$
-opuntoid automaton and
 $\mathcal{E} \cong \mathcal{A} ( S^*, w )$
.
$\mathcal{E} \cong \mathcal{A} ( S^*, w )$
.
Let
![]() $\Gamma$
be a
$\Gamma$
be a
![]() $t$
-opuntoid graph. Let
$t$
-opuntoid graph. Let
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
be adjacent
$\Delta _2$
be adjacent
![]() $\langle S \rangle$
-lobes of
$\langle S \rangle$
-lobes of
![]() $\Gamma$
. Then,
$\Gamma$
. Then,
![]() $\Delta _2$
feeds off
$\Delta _2$
feeds off
![]() $\Delta _1$
if there is a
$\Delta _1$
if there is a
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
of
$v_1 \rightarrow ^t v_2$
of
![]() $\Gamma$
from
$\Gamma$
from
![]() $\Delta _1$
to
$\Delta _1$
to
![]() $\Delta _2$
such that, for any loop
$\Delta _2$
such that, for any loop
![]() $v_2 \rightarrow ^y v_2$
in
$v_2 \rightarrow ^y v_2$
in
![]() $\Delta _2$
, there is a loop
$\Delta _2$
, there is a loop
![]() $v_2 \rightarrow ^g v_2$
in
$v_2 \rightarrow ^g v_2$
in
![]() $\Delta _2$
, for some
$\Delta _2$
, for some
![]() $g \in E( U_2 )$
with
$g \in E( U_2 )$
with
![]() $y \geq g$
in
$y \geq g$
in
![]() $S$
. We also say that
$S$
. We also say that
![]() $\Delta _2$
feeds off
$\Delta _2$
feeds off
![]() $\Delta _1$
if there is a
$\Delta _1$
if there is a
![]() $t$
-edge
$t$
-edge
![]() $v_2 \rightarrow ^t v_1$
of
$v_2 \rightarrow ^t v_1$
of
![]() $\Gamma$
from
$\Gamma$
from
![]() $\Delta _2$
to
$\Delta _2$
to
![]() $\Delta _1$
such that, for any loop
$\Delta _1$
such that, for any loop
![]() $v_2 \rightarrow ^y v_2$
in
$v_2 \rightarrow ^y v_2$
in
![]() $\Delta _2$
, there is a loop
$\Delta _2$
, there is a loop
![]() $v_2 \rightarrow ^f v_2$
in
$v_2 \rightarrow ^f v_2$
in
![]() $\Delta _2$
, for some
$\Delta _2$
, for some
![]() $f \in E( U_1 )$
with
$f \in E( U_1 )$
with
![]() $y \geq f$
in
$y \geq f$
in
![]() $S$
. For non-adjacent
$S$
. For non-adjacent
![]() $\langle S \rangle$
-lobes
$\langle S \rangle$
-lobes
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _n$
of
$\Delta _n$
of
![]() $\Gamma$
, we say
$\Gamma$
, we say
![]() $\Delta _n$
feeds off
$\Delta _n$
feeds off
![]() $\Delta _1$
if there is a sequence of
$\Delta _1$
if there is a sequence of
![]() $\langle S \rangle$
-lobes
$\langle S \rangle$
-lobes
![]() $\Delta _1, \Delta _2, \ldots, \Delta _n$
, where
$\Delta _1, \Delta _2, \ldots, \Delta _n$
, where
![]() $\Delta _{k+1}$
is adjacent to
$\Delta _{k+1}$
is adjacent to
![]() $\Delta _k$
and
$\Delta _k$
and
![]() $\Delta _{k+1}$
feeds off
$\Delta _{k+1}$
feeds off
![]() $\Delta _k$
, for
$\Delta _k$
, for
![]() $1 \leq k \leq n-1$
,
$1 \leq k \leq n-1$
,
Let
![]() $\Gamma '$
be a
$\Gamma '$
be a
![]() $t$
-subopuntoid subgraph of
$t$
-subopuntoid subgraph of
![]() $\Gamma$
. An
$\Gamma$
. An
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma$
that does not belong to
$\Gamma$
that does not belong to
![]() $\Gamma '$
is called external to
$\Gamma '$
is called external to
![]() $\Gamma '$
. An extremal
$\Gamma '$
. An extremal
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma '$
is called a parasite if it feeds off the unique
$\Gamma '$
is called a parasite if it feeds off the unique
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma '$
to which it is adjacent. The subgraph
$\Gamma '$
to which it is adjacent. The subgraph
![]() $\Gamma '$
is parasite-free if it has no parasites. The subgraph
$\Gamma '$
is parasite-free if it has no parasites. The subgraph
![]() $\Gamma '$
is a host of
$\Gamma '$
is a host of
![]() $\Gamma$
if it has finitely many
$\Gamma$
if it has finitely many
![]() $\langle S \rangle$
-lobes, is parasite-free, and every
$\langle S \rangle$
-lobes, is parasite-free, and every
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma$
that is external to
$\Gamma$
that is external to
![]() $\Gamma '$
feeds off some
$\Gamma '$
feeds off some
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma '$
.
$\Gamma '$
.
Theorem 3.6. [Reference Bennett and Jajcayová5, Theorem 3.26] Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be an HNN extension of an inverse semigroup
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be an HNN extension of an inverse semigroup
![]() $S$
, where
$S$
, where
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are inverse monoids that are lower bounded in
$U_2$
are inverse monoids that are lower bounded in
![]() $S$
. Then, the Schützenberger automata of
$S$
. Then, the Schützenberger automata of
![]() $S^*$
are complete
$S^*$
are complete
![]() $t$
-opuntoid automata with a host.
$t$
-opuntoid automata with a host.
Lemma 3.7. [Reference Bennett and Jajcayová5, Lemma 3.23] Let
![]() $\Gamma$
be a
$\Gamma$
be a
![]() $t$
-opuntoid graph. Then, a host of
$t$
-opuntoid graph. Then, a host of
![]() $\Gamma$
is a maximal parasite-free
$\Gamma$
is a maximal parasite-free
![]() $t$
-subopuntoid subgraph. If
$t$
-subopuntoid subgraph. If
![]() $\Gamma$
has more than one host, then every host is an
$\Gamma$
has more than one host, then every host is an
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma$
. The unique reduced
$\Gamma$
. The unique reduced
![]() $\langle S \rangle$
-lobe path between any two hosts, in the
$\langle S \rangle$
-lobe path between any two hosts, in the
![]() $\langle S \rangle$
-lobe tree of
$\langle S \rangle$
-lobe tree of
![]() $\Gamma$
, consists entirely of
$\Gamma$
, consists entirely of
![]() $\langle S \rangle$
-lobes that are hosts.
$\langle S \rangle$
-lobes that are hosts.
Thus, we can associate a number with a
![]() $t$
-opuntoid graph
$t$
-opuntoid graph
![]() $\Gamma$
that has a host, by defining
$\Gamma$
that has a host, by defining
![]() $n( \Gamma )$
to be the number of
$n( \Gamma )$
to be the number of
![]() $\langle S \rangle$
-lobes in any host. Either
$\langle S \rangle$
-lobes in any host. Either
![]() $\Gamma$
has one host, in which case
$\Gamma$
has one host, in which case
![]() $n( \Gamma ) \geq 1$
, or every host of
$n( \Gamma ) \geq 1$
, or every host of
![]() $\Gamma$
is an
$\Gamma$
is an
![]() $\langle S \rangle$
-lobe, in which case
$\langle S \rangle$
-lobe, in which case
![]() $n( \Gamma ) = 1$
.
$n( \Gamma ) = 1$
.
Lemma 3.8. [Reference Bennett and Jajcayová5, Lemma 3.24] Let
![]() $\mathcal{D}$
be a
$\mathcal{D}$
be a
![]() $t$
-opuntoid automaton with finitely many
$t$
-opuntoid automaton with finitely many
![]() $\langle S \rangle$
-lobes and a host
$\langle S \rangle$
-lobes and a host
![]() $\Sigma$
. If
$\Sigma$
. If
![]() $\mathcal{D}'$
is obtained from
$\mathcal{D}'$
is obtained from
![]() $\mathcal{D}$
by Construction 3.3, then
$\mathcal{D}$
by Construction 3.3, then
![]() $\Sigma$
is also a host of
$\Sigma$
is also a host of
![]() $\mathcal{D}'$
.
$\mathcal{D}'$
.
Lemma 3.9. [Reference Bennett and Jajcayová5, Corollary 3.29] Let
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Gamma '$
be complete
$\Gamma '$
be complete
![]() $t$
-opuntoid graphs that have hosts and let
$t$
-opuntoid graphs that have hosts and let
![]() $\Sigma$
be any host of
$\Sigma$
be any host of
![]() $\Gamma$
. Then, every isomorphism from
$\Gamma$
. Then, every isomorphism from
![]() $\Sigma$
onto some host of
$\Sigma$
onto some host of
![]() $\Gamma '$
extends (uniquely) to an isomorphism of
$\Gamma '$
extends (uniquely) to an isomorphism of
![]() $\Gamma$
onto
$\Gamma$
onto
![]() $\Gamma '$
.
$\Gamma '$
.
Lemma 3.10. [Reference Bennett and Jajcayová5, Lemma 3.31] If
![]() $\Gamma$
is a
$\Gamma$
is a
![]() $t$
-opuntoid graph with finitely many
$t$
-opuntoid graph with finitely many
![]() $\langle S \rangle$
-lobes, then the automorphism group of
$\langle S \rangle$
-lobes, then the automorphism group of
![]() $\Gamma$
is embedded into the automorphism group of some
$\Gamma$
is embedded into the automorphism group of some
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma$
.
$\Gamma$
.
Lemma 3.11. [Reference Bennett and Jajcayová5, Lemma 3.32] Let
![]() $\Gamma$
be a complete
$\Gamma$
be a complete
![]() $t$
-opuntoid graph that has a host. Let
$t$
-opuntoid graph that has a host. Let
![]() $\Gamma '$
be the subgraph that consists of the
$\Gamma '$
be the subgraph that consists of the
![]() $\langle S \rangle$
-lobes of every host of
$\langle S \rangle$
-lobes of every host of
![]() $\Gamma$
and the
$\Gamma$
and the
![]() $t$
-edges connecting them. Then,
$t$
-edges connecting them. Then,
![]() $\Gamma '$
is a
$\Gamma '$
is a
![]() $t$
-subopuntoid subgraph of
$t$
-subopuntoid subgraph of
![]() $\Gamma$
and the automorphism group of
$\Gamma$
and the automorphism group of
![]() $\Gamma$
is isomorphic to the automorphism group of
$\Gamma$
is isomorphic to the automorphism group of
![]() $ \Gamma '$
.
$ \Gamma '$
.
4. Lower bounded HNN extensions
In this section, let
![]() $U_1$
and
$U_1$
and
![]() $U_2$
denote inverse monoids of an inverse semigroup
$U_2$
denote inverse monoids of an inverse semigroup
![]() $S$
, with respective identities
$S$
, with respective identities
![]() $e_1$
and
$e_1$
and
![]() $e_2$
, let
$e_2$
, let
![]() $\phi \;:\; U_1 \rightarrow U_2$
be an isomorphism and let
$\phi \;:\; U_1 \rightarrow U_2$
be an isomorphism and let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension, as defined in [12]. That is, for each
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension, as defined in [12]. That is, for each
![]() $e \in E( S )$
and
$e \in E( S )$
and
![]() $i \in \{ 1, 2 \}$
, the set
$i \in \{ 1, 2 \}$
, the set
![]() $\{ u \in U_i \;:\; u \geq e \}$
is either empty or has a minimal element, denoted by
$\{ u \in U_i \;:\; u \geq e \}$
is either empty or has a minimal element, denoted by
![]() $f_i ( e )$
, and there does not exist an infinite sequence
$f_i ( e )$
, and there does not exist an infinite sequence
![]() $\{ u_k \}$
, where
$\{ u_k \}$
, where
![]() $u_k \in E( U_i )$
and
$u_k \in E( U_i )$
and
![]() $u_k > f_i ( e u_k ) > u_{ k+1 }$
, for all
$u_k > f_i ( e u_k ) > u_{ k+1 }$
, for all
![]() $k$
. The monoids
$k$
. The monoids
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are also lower bounded in
$U_2$
are also lower bounded in
![]() $S$
, as defined in Section 3, thus we can use the results of Section 3.
$S$
, as defined in Section 3, thus we can use the results of Section 3.
Theorem 4.1.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Then, the Schützenberger automata of
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Then, the Schützenberger automata of
![]() $S^*$
are, up to isomorphism, the complete
$S^*$
are, up to isomorphism, the complete
![]() $t$
-opuntoid automata that have a host, a loop
$t$
-opuntoid automata that have a host, a loop
![]() $v_1 \rightarrow ^{ e_1 } v_1$
for every
$v_1 \rightarrow ^{ e_1 } v_1$
for every
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
and
$v_1 \rightarrow ^t v_2$
and
![]() $\langle S \rangle$
-lobes isomorphic to Schützenberger graphs of
$\langle S \rangle$
-lobes isomorphic to Schützenberger graphs of
![]() $\langle S \rangle$
.
$\langle S \rangle$
.
Proof. The result is a restatement of Jajcayová [Reference Jajcayová14, Theorem 4.1] using the definitions of Section 3.
The Bass-Serre theory can be used to describe the maximal subgroups of
![]() $S^*$
, as follows; see Cohen [Reference Cohen7] and Dicks and Dunwoody [Reference Dicks and Dunwoody9, Chapters 1, 2, 3] for notation and definitions.
$S^*$
, as follows; see Cohen [Reference Cohen7] and Dicks and Dunwoody [Reference Dicks and Dunwoody9, Chapters 1, 2, 3] for notation and definitions.
Notation 4.2.
Let
![]() $\Gamma$
be a complete
$\Gamma$
be a complete
![]() $t$
-opuntoid graph that has a host, and let
$t$
-opuntoid graph that has a host, and let
![]() $\Gamma '$
denote the
$\Gamma '$
denote the
![]() $t$
-subopuntoid subgraph of
$t$
-subopuntoid subgraph of
![]() $\Gamma$
that consists of the
$\Gamma$
that consists of the
![]() $\langle S \rangle$
-lobes of every host and all
$\langle S \rangle$
-lobes of every host and all
![]() $t$
-edges connecting these hosts. Let
$t$
-edges connecting these hosts. Let
![]() $T( \Gamma ' )$
denote the
$T( \Gamma ' )$
denote the
![]() $\langle S \rangle$
-lobe tree of
$\langle S \rangle$
-lobe tree of
![]() $\Gamma '$
, and let
$\Gamma '$
, and let
![]() $G$
denote the automorphism group of
$G$
denote the automorphism group of
![]() $\Gamma '$
. For each
$\Gamma '$
. For each
![]() $\alpha \in G$
and
$\alpha \in G$
and
![]() $\langle S \rangle$
-lobe
$\langle S \rangle$
-lobe
![]() $\Delta$
of
$\Delta$
of
![]() $\Gamma '$
, we define the action of
$\Gamma '$
, we define the action of
![]() $\alpha$
on
$\alpha$
on
![]() $\Delta$
, written
$\Delta$
, written
![]() $\alpha \cdot \Delta$
, to be
$\alpha \cdot \Delta$
, to be
![]() $( \Delta ) \alpha$
, the image of
$( \Delta ) \alpha$
, the image of
![]() $\Delta$
under
$\Delta$
under
![]() $\alpha$
, which is also an
$\alpha$
, which is also an
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma '$
. We extend this action to an action of
$\Gamma '$
. We extend this action to an action of
![]() $T( \Gamma ' )$
by defining the action of
$T( \Gamma ' )$
by defining the action of
![]() $\alpha$
on the edge
$\alpha$
on the edge
![]() $( \Delta _1, \Delta _2 )$
to be equal to
$( \Delta _1, \Delta _2 )$
to be equal to
![]() $( ( \Delta _1 ) \alpha, ( \Delta _2 ) \alpha )$
.
$( ( \Delta _1 ) \alpha, ( \Delta _2 ) \alpha )$
.
The quotient graph
![]() $G \backslash T( \Gamma ' )$
is the graph of orbits of the action of
$G \backslash T( \Gamma ' )$
is the graph of orbits of the action of
![]() $G$
on
$G$
on
![]() $T( \Gamma ' )$
and is connected. There exist subsets
$T( \Gamma ' )$
and is connected. There exist subsets
![]() $T_0 \subseteq T \subseteq T( \Gamma ' )$
such that
$T_0 \subseteq T \subseteq T( \Gamma ' )$
such that
![]() $T_0$
is a subtree of
$T_0$
is a subtree of
![]() $T( \Gamma ' )$
,
$T( \Gamma ' )$
,
![]() $T_0$
and
$T_0$
and
![]() $T$
have the same vertices, the initial vertex of every edge of
$T$
have the same vertices, the initial vertex of every edge of
![]() $T$
is also a vertex of
$T$
is also a vertex of
![]() $T$
and
$T$
and
![]() $T$
, is a
$T$
, is a
![]() $G$
-transversal in
$G$
-transversal in
![]() $T( \Gamma ' )$
; that is,
$T( \Gamma ' )$
; that is,
![]() $T$
meets each
$T$
meets each
![]() $G$
-orbit exactly once, and thus, the map
$G$
-orbit exactly once, and thus, the map
![]() $T \rightarrow G \backslash T( \Gamma ' ) \;:\; y \rightarrow G \cdot y$
, defined for all edges and vertices
$T \rightarrow G \backslash T( \Gamma ' ) \;:\; y \rightarrow G \cdot y$
, defined for all edges and vertices
![]() $y$
, is bijective.
$y$
, is bijective.
We can make
![]() $T$
into a graph by specifying the initial vertex of each edge
$T$
into a graph by specifying the initial vertex of each edge
![]() $( \Delta _1,\Delta _2 )$
to be
$( \Delta _1,\Delta _2 )$
to be
![]() $\Delta _1$
and specifying the terminal vertex to be the unique vertex
$\Delta _1$
and specifying the terminal vertex to be the unique vertex
![]() $\Delta '_{\!\!2}$
of
$\Delta '_{\!\!2}$
of
![]() $T$
which lies in the same
$T$
which lies in the same
![]() $G$
-orbit as
$G$
-orbit as
![]() $\Delta _2$
. It then follows that the graph
$\Delta _2$
. It then follows that the graph
![]() $T$
is isomorphic to
$T$
is isomorphic to
![]() $G \backslash T( \Gamma ' )$
under the above map
$G \backslash T( \Gamma ' )$
under the above map
![]() $y \rightarrow G \cdot y$
, and
$y \rightarrow G \cdot y$
, and
![]() $T_0$
is a maximal subtree of
$T_0$
is a maximal subtree of
![]() $T$
, as well as a subtree of
$T$
, as well as a subtree of
![]() $T( \Gamma ' )$
.
$T( \Gamma ' )$
.
For any edge
![]() $y = ( \Delta _1, \Delta _2 )$
of
$y = ( \Delta _1, \Delta _2 )$
of
![]() $T$
, the
$T$
, the
![]() $\langle S \rangle$
-lobes
$\langle S \rangle$
-lobes
![]() $\Delta _2$
and
$\Delta _2$
and
![]() $\Delta '_{\!\!2}$
lie in the same
$\Delta '_{\!\!2}$
lie in the same
![]() $G$
-orbit, and thus, we can choose an element
$G$
-orbit, and thus, we can choose an element
![]() $\alpha _y \in G$
such that
$\alpha _y \in G$
such that
![]() $\alpha _y \cdot \Delta '_{\!\!2} = \Delta _2$
. If
$\alpha _y \cdot \Delta '_{\!\!2} = \Delta _2$
. If
![]() $y \in E( T_0 )$
, then
$y \in E( T_0 )$
, then
![]() $\Delta _2 \in V( T_0 ) = V( T )$
and so
$\Delta _2 \in V( T_0 ) = V( T )$
and so
![]() $\Delta '_{\!\!2} = \Delta _2$
, in which case we take
$\Delta '_{\!\!2} = \Delta _2$
, in which case we take
![]() $\alpha _y$
as the identity of
$\alpha _y$
as the identity of
![]() $G$
. Next, let
$G$
. Next, let
![]() $G( y )$
denote the stabilizer group of
$G( y )$
denote the stabilizer group of
![]() $y$
under the action of
$y$
under the action of
![]() $G$
; that is, the group
$G$
; that is, the group
![]() $G( y )$
is the subgroup of
$G( y )$
is the subgroup of
![]() $G$
consisting of all automorphisms of
$G$
consisting of all automorphisms of
![]() $\Gamma '$
which map
$\Gamma '$
which map
![]() $\Delta _1$
onto itself and
$\Delta _1$
onto itself and
![]() $\Delta _2$
onto itself. Similarly, for each vertex, we let
$\Delta _2$
onto itself. Similarly, for each vertex, we let
![]() $G( \Delta )$
denote the stabilizer group of
$G( \Delta )$
denote the stabilizer group of
![]() $\Delta$
under the action of
$\Delta$
under the action of
![]() $G$
. For any edge
$G$
. For any edge
![]() $y = ( \Delta _1, \Delta _2 )$
of
$y = ( \Delta _1, \Delta _2 )$
of
![]() $T$
, we have
$T$
, we have
![]() $G( y ) \subseteq G( \Delta _1 )$
and the map
$G( y ) \subseteq G( \Delta _1 )$
and the map
![]() $t_y \;:\; G( y ) \rightarrow G( \Delta '_{\!\!2} ) \;:\; \alpha \rightarrow \alpha _y \circ \alpha \circ \alpha ^{-1}_y$
defines a group monomorphism.
$t_y \;:\; G( y ) \rightarrow G( \Delta '_{\!\!2} ) \;:\; \alpha \rightarrow \alpha _y \circ \alpha \circ \alpha ^{-1}_y$
defines a group monomorphism.
We have a graph of groups
![]() $( G(\!-\!), T )$
. Since
$( G(\!-\!), T )$
. Since
![]() $T( \Gamma ' )$
is a tree, the fundamental group
$T( \Gamma ' )$
is a tree, the fundamental group
![]() $\Pi ( G(\!-\!), T, T_0 )$
of the graph of groups
$\Pi ( G(\!-\!), T, T_0 )$
of the graph of groups
![]() $( G(\!-\!), T )$
is then isomorphic to
$( G(\!-\!), T )$
is then isomorphic to
![]() $G$
. By Lemma 3.11, the automorphism group of
$G$
. By Lemma 3.11, the automorphism group of
![]() $\Gamma$
is isomorphic to
$\Gamma$
is isomorphic to
![]() $G$
. Hence, the automorphism group of
$G$
. Hence, the automorphism group of
![]() $\Gamma$
is isomorphic to
$\Gamma$
is isomorphic to
![]() $\Pi ( G(\!-\!), T, T_0 )$
. The group
$\Pi ( G(\!-\!), T, T_0 )$
. The group
![]() $\Pi ( G(\!-\!), T, T_0 )$
is generated by the disjoint union of
$\Pi ( G(\!-\!), T, T_0 )$
is generated by the disjoint union of
![]() $E( T )$
and the vertex groups of
$E( T )$
and the vertex groups of
![]() $( G(\!-\!), T )$
, subject to the relation
$( G(\!-\!), T )$
, subject to the relation
![]() $y^{-1} \cdot \alpha \cdot y = ( \alpha ) t_y$
, for all
$y^{-1} \cdot \alpha \cdot y = ( \alpha ) t_y$
, for all
![]() $y \in E( T )$
and all
$y \in E( T )$
and all
![]() $\alpha \in G( y )$
, and the relation
$\alpha \in G( y )$
, and the relation
![]() $y = 1$
, for all
$y = 1$
, for all
![]() $y \in E( T_0 )$
.
$y \in E( T_0 )$
.
Notation 4.3.
We define a graph of groups
![]() $( H(\!-\!), Y )$
for the HNN extension
$( H(\!-\!), Y )$
for the HNN extension
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
, as follows. The graph
$S^* = [ S;\; U_1, U_2;\; \phi ]$
, as follows. The graph
![]() $Y$
has vertices
$Y$
has vertices
![]() $V( Y )$
the
$V( Y )$
the
![]() $\mathcal{D}$
-classes of
$\mathcal{D}$
-classes of
![]() $S$
. The graph
$S$
. The graph
![]() $Y$
has edges
$Y$
has edges
![]() $E( Y )$
the set of all triples
$E( Y )$
the set of all triples
![]() $( D_1, D, D_2 )$
, where
$( D_1, D, D_2 )$
, where
![]() $D$
is a
$D$
is a
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $U_1$
,
$U_1$
,
![]() $D_1$
is the
$D_1$
is the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $S$
containing
$S$
containing
![]() $D$
, and
$D$
, and
![]() $D_2$
is the
$D_2$
is the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $S$
containing
$S$
containing
![]() $( D ) \phi$
.
$( D ) \phi$
.
We specify an
![]() $\mathcal{H}$
-class group within each
$\mathcal{H}$
-class group within each
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $S$
and specify an
$S$
and specify an
![]() $\mathcal{H}$
-class group within each
$\mathcal{H}$
-class group within each
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $U_1$
. Let
$U_1$
. Let
![]() $y = ( D_1, D, D_2 )$
be an edge of
$y = ( D_1, D, D_2 )$
be an edge of
![]() $Y$
and let
$Y$
and let
![]() $H_g$
,
$H_g$
,
![]() $H_f$
and
$H_f$
and
![]() $H_h$
be the specified
$H_h$
be the specified
![]() $\mathcal{H}$
-class groups of
$\mathcal{H}$
-class groups of
![]() $D_1$
,
$D_1$
,
![]() $D$
, and
$D$
, and
![]() $D_2$
, containing idempotents
$D_2$
, containing idempotents
![]() $g$
,
$g$
,
![]() $f$
, and
$f$
, and
![]() $h$
, respectively. Fix
$h$
, respectively. Fix
![]() $d_1 \in D_1$
such that
$d_1 \in D_1$
such that
![]() $f \mathcal{R} d_1 \mathcal{L} g$
in
$f \mathcal{R} d_1 \mathcal{L} g$
in
![]() $S$
and fix
$S$
and fix
![]() $d_2 \in D_2$
such that
$d_2 \in D_2$
such that
![]() $( f ) \phi \mathcal{R} d_2 \mathcal{L} h$
in
$( f ) \phi \mathcal{R} d_2 \mathcal{L} h$
in
![]() $S$
. The maps
$S$
. The maps
![]() $H_f \rightarrow H_g \;:\; s \rightarrow d^{-1}_1 s d_1$
and
$H_f \rightarrow H_g \;:\; s \rightarrow d^{-1}_1 s d_1$
and
![]() $H_{ ( f ) \phi } \rightarrow H_g \;:\; s \rightarrow d^{-1}_2 s d_2$
are group monomorphisms. Then,
$H_{ ( f ) \phi } \rightarrow H_g \;:\; s \rightarrow d^{-1}_2 s d_2$
are group monomorphisms. Then,
![]() $H( y ) = d_1^{-1} H_f d_1$
is a subgroup of
$H( y ) = d_1^{-1} H_f d_1$
is a subgroup of
![]() $H_g$
and the map
$H_g$
and the map
![]() $t_y \;:\; H( y ) \rightarrow H_h \;:\; d^{-1}_1 s d_1 \rightarrow d^{-1}_2 \cdot ( s ) \phi \cdot d_2$
is a group monomorphism.
$t_y \;:\; H( y ) \rightarrow H_h \;:\; d^{-1}_1 s d_1 \rightarrow d^{-1}_2 \cdot ( s ) \phi \cdot d_2$
is a group monomorphism.
The construction of the graph of groups
![]() $( H(\!-\!), Y )$
is completed by defining the vertex group
$( H(\!-\!), Y )$
is completed by defining the vertex group
![]() $H( D )$
, of each vertex
$H( D )$
, of each vertex
![]() $D$
, to be the specified
$D$
, to be the specified
![]() $\mathcal{H}$
-class group of
$\mathcal{H}$
-class group of
![]() $D$
and defining the edge group and monomorphism of each edge
$D$
and defining the edge group and monomorphism of each edge
![]() $y$
to be the group
$y$
to be the group
![]() $H( y )$
and the monomorphism
$H( y )$
and the monomorphism
![]() $t_y$
, respectively, as indicated above.
$t_y$
, respectively, as indicated above.
For
![]() $e \in E( S )$
, let
$e \in E( S )$
, let
![]() $Y_e$
denote the connected component of
$Y_e$
denote the connected component of
![]() $Y$
containing, as a vertex, the
$Y$
containing, as a vertex, the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $e$
in
$e$
in
![]() $T$
. If
$T$
. If
![]() $e \in E( U_1 )$
, then the
$e \in E( U_1 )$
, then the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $e$
in
$e$
in
![]() $S$
and the
$S$
and the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $( e ) \phi$
in
$( e ) \phi$
in
![]() $S$
are connected by an edge in
$S$
are connected by an edge in
![]() $Y$
and are thus in the same connected component. Let
$Y$
and are thus in the same connected component. Let
![]() $( H_e (\!-\!), Y_e )$
denote the restriction of
$( H_e (\!-\!), Y_e )$
denote the restriction of
![]() $( H (\!-\!), Y )$
to
$( H (\!-\!), Y )$
to
![]() $Y_e$
.
$Y_e$
.
The following result generalizes Yamamura [Reference Yamamura21, Theorem 5.2], on locally full HNN extensions, and overlaps with Ayyash [Reference Ayyash1, Theorem
![]() $5.4.1$
], on HNN extensions of finite inverse semigroups.
$5.4.1$
], on HNN extensions of finite inverse semigroups.
Theorem 4.4.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension and let
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension and let
![]() $e$
be an idempotent of
$e$
be an idempotent of
![]() $S$
. Then, the maximal subgroup of
$S$
. Then, the maximal subgroup of
![]() $S^*$
containing
$S^*$
containing
![]() $e$
is isomorphic to the fundamental group of the graph of groups
$e$
is isomorphic to the fundamental group of the graph of groups
![]() $( H_e(\!-\!), Y_e )$
.
$( H_e(\!-\!), Y_e )$
.
Proof. Let
![]() $\Gamma = S \Gamma ( S^*, e )$
. By Theorem 4.1, the graph
$\Gamma = S \Gamma ( S^*, e )$
. By Theorem 4.1, the graph
![]() $\Gamma$
is a complete
$\Gamma$
is a complete
![]() $t$
-opuntoid graph with a host such that the
$t$
-opuntoid graph with a host such that the
![]() $\langle S \rangle$
-lobes are isomorphic to Schützenberger graphs of
$\langle S \rangle$
-lobes are isomorphic to Schützenberger graphs of
![]() $\langle S \rangle$
. From Notation 4.2, the fundamental group
$\langle S \rangle$
. From Notation 4.2, the fundamental group
![]() $\Pi ( G(\!-\!), T, T_0 )$
of the graph of groups
$\Pi ( G(\!-\!), T, T_0 )$
of the graph of groups
![]() $( G(\!-\!), T )$
is isomorphic to the automorphism group of
$( G(\!-\!), T )$
is isomorphic to the automorphism group of
![]() $\Gamma$
and thus is also isomorphic to the maximal subgroup of
$\Gamma$
and thus is also isomorphic to the maximal subgroup of
![]() $S^*$
containing
$S^*$
containing
![]() $e$
. Hence, the theorem is completed by showing that the graphs of groups
$e$
. Hence, the theorem is completed by showing that the graphs of groups
![]() $( G(\!-\!), T )$
and
$( G(\!-\!), T )$
and
![]() $( H_e(\!-\!), Y_e )$
are conjugate isomorphic. We need to define a graph isomorphism between
$( H_e(\!-\!), Y_e )$
are conjugate isomorphic. We need to define a graph isomorphism between
![]() $T$
and
$T$
and
![]() $Y_e$
and define isomorphisms between the corresponding vertex and edge groups, such that the group isomorphisms commute with the corresponding edge monomorphisms.
$Y_e$
and define isomorphisms between the corresponding vertex and edge groups, such that the group isomorphisms commute with the corresponding edge monomorphisms.
From Algorithm 3.5, the Schützenberger graph
![]() $S \Gamma ( S, e )$
is embedded onto a host of
$S \Gamma ( S, e )$
is embedded onto a host of
![]() $\Gamma$
. Thus
$\Gamma$
. Thus
![]() $n ( \Gamma ) = 1$
, as defined in Section 3, and every host is an
$n ( \Gamma ) = 1$
, as defined in Section 3, and every host is an
![]() $\langle S \rangle$
-lobe, by Lemma 3.7. We define a graph map
$\langle S \rangle$
-lobe, by Lemma 3.7. We define a graph map
![]() $\psi \;:\; T \rightarrow Y$
as follows.
$\psi \;:\; T \rightarrow Y$
as follows.
Let
![]() $\Delta \in V( T )$
. If
$\Delta \in V( T )$
. If
![]() $v_1, v_2 \in V( \Delta )$
, then
$v_1, v_2 \in V( \Delta )$
, then
![]() $( v_i, \Delta, v_i ) \cong \mathcal{A}( S, e( v_i ) )$
, for
$( v_i, \Delta, v_i ) \cong \mathcal{A}( S, e( v_i ) )$
, for
![]() $i = 1, 2$
, and
$i = 1, 2$
, and
![]() $e( v_1 ) \mathcal{D} e( v_2 )$
in
$e( v_1 ) \mathcal{D} e( v_2 )$
in
![]() $S$
. Thus, we can define
$S$
. Thus, we can define
![]() $( \Delta ) \psi$
to be equal to the
$( \Delta ) \psi$
to be equal to the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $S$
containing
$S$
containing
![]() $e( v )$
, for any vertex
$e( v )$
, for any vertex
![]() $v$
of
$v$
of
![]() $\Delta$
.
$\Delta$
.
Let
![]() $( \Delta _1, \Delta _2 )$
be an edge of
$( \Delta _1, \Delta _2 )$
be an edge of
![]() $T$
. Then,
$T$
. Then,
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
are hosts of
$\Delta _2$
are hosts of
![]() $\Gamma$
and thus feed off each other, and there is a
$\Gamma$
and thus feed off each other, and there is a
![]() $t$
-edge from a vertex of
$t$
-edge from a vertex of
![]() $\Delta _1$
to a vertex of
$\Delta _1$
to a vertex of
![]() $\Delta _2$
. If
$\Delta _2$
. If
![]() $v_1 \rightarrow ^t v_2$
and
$v_1 \rightarrow ^t v_2$
and
![]() $v'_{\!\!1} \rightarrow ^t v'_{\!\!2}$
are
$v'_{\!\!1} \rightarrow ^t v'_{\!\!2}$
are
![]() $t$
-edges, where
$t$
-edges, where
![]() $v_1$
,
$v_1$
,
![]() $v'_{\!\!1}$
are vertices of
$v'_{\!\!1}$
are vertices of
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $v_2$
,
$v_2$
,
![]() $v'_{\!\!2}$
are vertices of
$v'_{\!\!2}$
are vertices of
![]() $\Delta _2$
, then we have
$\Delta _2$
, then we have
![]() $e( v_1 ), e( v'_{\!\!1} ) \in E( U_1 )$
,
$e( v_1 ), e( v'_{\!\!1} ) \in E( U_1 )$
,
![]() $e( v_2 ) = ( e( v_1 ) ) \phi$
,
$e( v_2 ) = ( e( v_1 ) ) \phi$
,
![]() $e( v'_{\!\!2} ) = ( e( v'_{\!\!1} ) ) \phi$
, with
$e( v'_{\!\!2} ) = ( e( v'_{\!\!1} ) ) \phi$
, with
![]() $e( v_1 ) \mathcal{D} e( v'_{\!\!1} )$
in
$e( v_1 ) \mathcal{D} e( v'_{\!\!1} )$
in
![]() $U_1$
and
$U_1$
and
![]() $e( v_2 ) \mathcal{D} e( v'_{\!\!2} )$
in
$e( v_2 ) \mathcal{D} e( v'_{\!\!2} )$
in
![]() $U_2$
. Thus, we can define
$U_2$
. Thus, we can define
![]() $( \Delta _1, \Delta _2 ) \psi$
to be the edge
$( \Delta _1, \Delta _2 ) \psi$
to be the edge
![]() $( D_1, D, D_2 )$
, where
$( D_1, D, D_2 )$
, where
![]() $D$
is the
$D$
is the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $U_1$
containing
$U_1$
containing
![]() $e( v_1 )$
,
$e( v_1 )$
,
![]() $D_1$
is the
$D_1$
is the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $S$
containing
$S$
containing
![]() $e( v_1 )$
, and
$e( v_1 )$
, and
![]() $D_2$
is the
$D_2$
is the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $S$
containing
$S$
containing
![]() $( e( v_1 ) ) \phi$
, for any
$( e( v_1 ) ) \phi$
, for any
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
, from a vertex
$v_1 \rightarrow ^t v_2$
, from a vertex
![]() $v_1$
of
$v_1$
of
![]() $\Delta _1$
to a vertex
$\Delta _1$
to a vertex
![]() $v_2$
to
$v_2$
to
![]() $\Delta _2$
.
$\Delta _2$
.
Let
![]() $\Gamma '$
be the
$\Gamma '$
be the
![]() $t$
-subopuntoid subgraph of
$t$
-subopuntoid subgraph of
![]() $\Gamma$
consisting of every host and let
$\Gamma$
consisting of every host and let
![]() $G = AUT( \Gamma ' )$
. As described in Notation 4.2, the initial vertex of the edge
$G = AUT( \Gamma ' )$
. As described in Notation 4.2, the initial vertex of the edge
![]() $( \Delta _1, \Delta _2 )$
is
$( \Delta _1, \Delta _2 )$
is
![]() $\Delta _1$
and the terminal vertex of the edge
$\Delta _1$
and the terminal vertex of the edge
![]() $( \Delta _1, \Delta _2 )$
is the unique vertex
$( \Delta _1, \Delta _2 )$
is the unique vertex
![]() $\Delta '_{\!\!2} \in V( T )$
that lies in the same
$\Delta '_{\!\!2} \in V( T )$
that lies in the same
![]() $G$
-orbit as
$G$
-orbit as
![]() $\Delta _2$
. Let
$\Delta _2$
. Let
![]() $v_1 \rightarrow ^t v_2$
be a
$v_1 \rightarrow ^t v_2$
be a
![]() $t$
-edge from a vertex
$t$
-edge from a vertex
![]() $v_1$
of
$v_1$
of
![]() $\Delta _1$
to a vertex
$\Delta _1$
to a vertex
![]() $v_2$
of
$v_2$
of
![]() $\Delta _2$
. Let
$\Delta _2$
. Let
![]() $e( v_1 ) \in D_1$
and
$e( v_1 ) \in D_1$
and
![]() $e( v_2 ) \in D_2$
. Then,
$e( v_2 ) \in D_2$
. Then,
![]() $( \Delta _1 ) \psi = D_1$
and
$( \Delta _1 ) \psi = D_1$
and
![]() $( \Delta '_{\!\!2} ) \psi = D_2$
, since
$( \Delta '_{\!\!2} ) \psi = D_2$
, since
![]() $\Delta '_{\!\!2} \cong \Delta _2$
. Thus, the map
$\Delta '_{\!\!2} \cong \Delta _2$
. Thus, the map
![]() $\psi \;:\; T \rightarrow Y$
defines a graph homomorphism.
$\psi \;:\; T \rightarrow Y$
defines a graph homomorphism.
We now show that
![]() $\psi$
defines a monomorphism. Suppose
$\psi$
defines a monomorphism. Suppose
![]() $\Delta$
and
$\Delta$
and
![]() $\Delta '$
are vertices of
$\Delta '$
are vertices of
![]() $T$
with
$T$
with
![]() $( \Delta ) \psi = ( \Delta ' ) \psi$
. Let
$( \Delta ) \psi = ( \Delta ' ) \psi$
. Let
![]() $v$
denote a vertex of
$v$
denote a vertex of
![]() $\Delta$
and let
$\Delta$
and let
![]() $v'$
denote a vertex of
$v'$
denote a vertex of
![]() $\Delta '$
. Then
$\Delta '$
. Then
![]() $( \Delta ) \psi = ( \Delta ' ) \psi$
implies that
$( \Delta ) \psi = ( \Delta ' ) \psi$
implies that
![]() $e( v ) \mathcal{D} e( v' )$
in
$e( v ) \mathcal{D} e( v' )$
in
![]() $S$
, in which case we have
$S$
, in which case we have
![]() $\Delta \cong \Delta '$
. Since
$\Delta \cong \Delta '$
. Since
![]() $\Delta$
and
$\Delta$
and
![]() $\Delta '$
are hosts, the isomorphism between them extends to an automorphism of
$\Delta '$
are hosts, the isomorphism between them extends to an automorphism of
![]() $\Gamma$
, by Lemma 3.9. Thus
$\Gamma$
, by Lemma 3.9. Thus
![]() $\Delta$
and
$\Delta$
and
![]() $\Delta '$
are in the same
$\Delta '$
are in the same
![]() $G$
-orbit and so
$G$
-orbit and so
![]() $\Delta = \Delta '$
, since
$\Delta = \Delta '$
, since
![]() $T$
is a transversal. We have shown that
$T$
is a transversal. We have shown that
![]() $\psi$
is one-one on vertices. Since
$\psi$
is one-one on vertices. Since
![]() $T$
is a tree, the map
$T$
is a tree, the map
![]() $\psi$
must also be one-one on the edges. Since
$\psi$
must also be one-one on the edges. Since
![]() $\Delta$
has a host that is isomorphic to
$\Delta$
has a host that is isomorphic to
![]() $S \Gamma ( S, e )$
, we have that
$S \Gamma ( S, e )$
, we have that
![]() $( T ) \psi$
is a connected subgraph of
$( T ) \psi$
is a connected subgraph of
![]() $Y_e$
.
$Y_e$
.
We now show that
![]() $( T ) \psi = Y_e$
. Let
$( T ) \psi = Y_e$
. Let
![]() $( D_1, D, D_2 )$
be an edge of
$( D_1, D, D_2 )$
be an edge of
![]() $Y_e$
, where
$Y_e$
, where
![]() $D_1 = ( \Delta _1 ) \psi$
, for some vertex
$D_1 = ( \Delta _1 ) \psi$
, for some vertex
![]() $\Delta _1$
of
$\Delta _1$
of
![]() $T$
. Let
$T$
. Let
![]() $f$
be an idempotent of
$f$
be an idempotent of
![]() $U_1$
that is in
$U_1$
that is in
![]() $D$
. There exists a vertex
$D$
. There exists a vertex
![]() $v_1$
of
$v_1$
of
![]() $\Delta _1$
such that
$\Delta _1$
such that
![]() $e( v_1 ) = f$
. Then, there must be a
$e( v_1 ) = f$
. Then, there must be a
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
, where
$v_1 \rightarrow ^t v_2$
, where
![]() $v_2$
is a vertex of an
$v_2$
is a vertex of an
![]() $\langle S \rangle$
-lobe
$\langle S \rangle$
-lobe
![]() $\Delta _2$
. Since
$\Delta _2$
. Since
![]() $\Delta _1$
is a host of
$\Delta _1$
is a host of
![]() $\Gamma$
and
$\Gamma$
and
![]() $e( v_2 ) = ( f ) \phi$
, it follows that
$e( v_2 ) = ( f ) \phi$
, it follows that
![]() $\Delta _2$
is also a host of
$\Delta _2$
is also a host of
![]() $\Gamma$
. Since
$\Gamma$
. Since
![]() $T$
meets each
$T$
meets each
![]() $G$
-orbit of
$G$
-orbit of
![]() $T( \Gamma ' )$
exactly once, there exists an edge
$T( \Gamma ' )$
exactly once, there exists an edge
![]() $( \Delta '_{\!\!1}, \Delta '_{\!\!2} )$
of
$( \Delta '_{\!\!1}, \Delta '_{\!\!2} )$
of
![]() $T$
that lies in the same
$T$
that lies in the same
![]() $G$
-orbit as
$G$
-orbit as
![]() $( \Delta _1, \Delta _2 )$
. Since
$( \Delta _1, \Delta _2 )$
. Since
![]() $\Delta _1 \in V( T )$
, we must have
$\Delta _1 \in V( T )$
, we must have
![]() $\Delta _1 = \Delta '_{\!\!1}$
. Then, there exists a
$\Delta _1 = \Delta '_{\!\!1}$
. Then, there exists a
![]() $t$
-edge
$t$
-edge
![]() $v'_{\!\!1} \rightarrow ^t v'_{\!\!2}$
from a vertex
$v'_{\!\!1} \rightarrow ^t v'_{\!\!2}$
from a vertex
![]() $v'_{\!\!1}$
of
$v'_{\!\!1}$
of
![]() $\Delta _1$
to a vertex
$\Delta _1$
to a vertex
![]() $v'_{\!\!2}$
of
$v'_{\!\!2}$
of
![]() $\Delta '_{\!\!2}$
, such that
$\Delta '_{\!\!2}$
, such that
![]() $e( v'_{\!\!1} ) = f$
and
$e( v'_{\!\!1} ) = f$
and
![]() $e( v'_{\!\!2} ) = ( f ) \phi$
. We then have
$e( v'_{\!\!2} ) = ( f ) \phi$
. We then have
![]() $( \Delta _1. \Delta '_{\!\!2} ) \psi = ( D_1, D, D_2 )$
. A similar proof shows that if
$( \Delta _1. \Delta '_{\!\!2} ) \psi = ( D_1, D, D_2 )$
. A similar proof shows that if
![]() $( D_1, D, D_2 )$
is an edge of
$( D_1, D, D_2 )$
is an edge of
![]() $Y_e$
, where
$Y_e$
, where
![]() $D_2 = ( \Delta _2 ) \psi$
, for some vertex
$D_2 = ( \Delta _2 ) \psi$
, for some vertex
![]() $\Delta _2$
of
$\Delta _2$
of
![]() $T$
, then
$T$
, then
![]() $( \Delta '_{\!\!1}. \Delta _2 ) \psi = ( D_1, D, D_2 )$
, for some edge
$( \Delta '_{\!\!1}. \Delta _2 ) \psi = ( D_1, D, D_2 )$
, for some edge
![]() $( \Delta '_{\!\!1}. \Delta _2 )$
of
$( \Delta '_{\!\!1}. \Delta _2 )$
of
![]() $T$
. It now follows that
$T$
. It now follows that
![]() $( T ) \psi$
is a maximal connected subgraph of
$( T ) \psi$
is a maximal connected subgraph of
![]() $Y_e$
. We have shown that
$Y_e$
. We have shown that
![]() $\psi \;:\; T \rightarrow Y$
defines a graph monomorphism onto
$\psi \;:\; T \rightarrow Y$
defines a graph monomorphism onto
![]() $Y_e$
.
$Y_e$
.
We now define the vertex group isomorphisms. Let
![]() $\Delta$
denote a vertex of
$\Delta$
denote a vertex of
![]() $T$
. Let
$T$
. Let
![]() $H( ( \Delta ) \psi ) = H_g$
, the
$H( ( \Delta ) \psi ) = H_g$
, the
![]() $\mathcal{H}$
-class group of
$\mathcal{H}$
-class group of
![]() $S$
with identity
$S$
with identity
![]() $g$
. If
$g$
. If
![]() $v$
is a vertex of
$v$
is a vertex of
![]() $\Delta$
then
$\Delta$
then
![]() $e( v ) \mathcal{D} g$
in
$e( v ) \mathcal{D} g$
in
![]() $S$
. Thus, we have an isomorphism
$S$
. Thus, we have an isomorphism
![]() $\pi \;:\; \Delta \rightarrow S \Gamma ( S, g )$
. The group
$\pi \;:\; \Delta \rightarrow S \Gamma ( S, g )$
. The group
![]() $G( \Delta )$
is the stabilizer group of
$G( \Delta )$
is the stabilizer group of
![]() $\Delta$
, under the action of
$\Delta$
, under the action of
![]() $G$
. Since
$G$
. Since
![]() $\Delta$
is a host of
$\Delta$
is a host of
![]() $\Gamma$
, any automorphism of
$\Gamma$
, any automorphism of
![]() $\Delta$
extends (uniquely) to an automorphism of
$\Delta$
extends (uniquely) to an automorphism of
![]() $\Gamma$
, by Lemma 3.9. Thus, we have an isomorphism
$\Gamma$
, by Lemma 3.9. Thus, we have an isomorphism
![]() $G( \Delta ) \rightarrow AUT ( \Delta )$
, under the mapping
$G( \Delta ) \rightarrow AUT ( \Delta )$
, under the mapping
![]() $\alpha \rightarrow \alpha _\Delta$
, where
$\alpha \rightarrow \alpha _\Delta$
, where
![]() $\alpha _\Delta$
denotes the restriction of
$\alpha _\Delta$
denotes the restriction of
![]() $\alpha$
to
$\alpha$
to
![]() $\Delta$
. We then have an isomorphism
$\Delta$
. We then have an isomorphism
![]() $AUT( \Delta ) \rightarrow AUT( S \Gamma ( S, g ) )$
, defined by
$AUT( \Delta ) \rightarrow AUT( S \Gamma ( S, g ) )$
, defined by
![]() $\alpha \rightarrow \pi ^{-1} \circ \alpha _\Delta \circ \pi$
. We have an isomorphism
$\alpha \rightarrow \pi ^{-1} \circ \alpha _\Delta \circ \pi$
. We have an isomorphism
![]() $AUT( S \Gamma ( S, g ) ) \rightarrow H_g$
, under the mapping
$AUT( S \Gamma ( S, g ) ) \rightarrow H_g$
, under the mapping
![]() $\beta \rightarrow ( g ) \beta$
; the set of vertices of
$\beta \rightarrow ( g ) \beta$
; the set of vertices of
![]() $S \Gamma ( S, g )$
is the
$S \Gamma ( S, g )$
is the
![]() $\mathcal{R}$
-class of
$\mathcal{R}$
-class of
![]() $S$
containing
$S$
containing
![]() $g$
. Hence we have an isomorphism
$g$
. Hence we have an isomorphism
![]() $\psi \;:\; G( \Delta ) \rightarrow H( ( \Delta ) \psi )$
, defined by
$\psi \;:\; G( \Delta ) \rightarrow H( ( \Delta ) \psi )$
, defined by
![]() $\alpha \rightarrow ( g ) \pi ^{-1} \circ \alpha _\Delta \circ \pi$
. The map
$\alpha \rightarrow ( g ) \pi ^{-1} \circ \alpha _\Delta \circ \pi$
. The map
![]() $\psi$
may be expressed by saying that
$\psi$
may be expressed by saying that
![]() $( \alpha ) \psi = s$
, where
$( \alpha ) \psi = s$
, where
![]() $s \in S$
such that
$s \in S$
such that
![]() $\mathcal{A}( S, s ) \cong ( v, \Delta, ( v ) \alpha )$
, for any vertex
$\mathcal{A}( S, s ) \cong ( v, \Delta, ( v ) \alpha )$
, for any vertex
![]() $v$
of
$v$
of
![]() $\Delta$
with
$\Delta$
with
![]() $e( v ) = g$
.
$e( v ) = g$
.
We now define the edge group isomorphisms. Let
![]() $y = ( \Delta _1, \Delta _2 )$
be an edge in
$y = ( \Delta _1, \Delta _2 )$
be an edge in
![]() $T$
and let
$T$
and let
![]() $( y ) \psi = ( D_1, D, D_2 )$
. Let
$( y ) \psi = ( D_1, D, D_2 )$
. Let
![]() $H_g$
and
$H_g$
and
![]() $H_f$
denote the specified
$H_f$
denote the specified
![]() $\mathcal{H}$
-class groups of
$\mathcal{H}$
-class groups of
![]() $D_1$
and
$D_1$
and
![]() $D$
, containing the identities
$D$
, containing the identities
![]() $g$
and
$g$
and
![]() $f$
, respectively. Thus,
$f$
, respectively. Thus,
![]() $H( D_1 ) = H_g$
and
$H( D_1 ) = H_g$
and
![]() $H( ( y ) \psi ) = d^{-1}_1 H_f d_1$
, where
$H( ( y ) \psi ) = d^{-1}_1 H_f d_1$
, where
![]() $d_1$
is the fixed element of
$d_1$
is the fixed element of
![]() $D_1$
such that
$D_1$
such that
![]() $f \mathcal{R} d_1 \mathcal{L} g$
in
$f \mathcal{R} d_1 \mathcal{L} g$
in
![]() $S$
. Let
$S$
. Let
![]() $v_1 \rightarrow ^t v_2$
be a
$v_1 \rightarrow ^t v_2$
be a
![]() $t$
-edge from a vertex
$t$
-edge from a vertex
![]() $v_1$
of
$v_1$
of
![]() $\Delta _1$
to a vertex
$\Delta _1$
to a vertex
![]() $v_2$
of
$v_2$
of
![]() $\Delta _2$
. Then,
$\Delta _2$
. Then,
![]() $e( v_1 ) \mathcal{R} a \mathcal{L} f$
, for some
$e( v_1 ) \mathcal{R} a \mathcal{L} f$
, for some
![]() $a \in U_1$
. Thus, we have a path
$a \in U_1$
. Thus, we have a path
![]() $v_1 \rightarrow ^a v_3$
, where
$v_1 \rightarrow ^a v_3$
, where
![]() $e( v_3) = f$
, and a path
$e( v_3) = f$
, and a path
![]() $v_3 \rightarrow ^{ d_1 } v_4$
, where
$v_3 \rightarrow ^{ d_1 } v_4$
, where
![]() $e( v_4 ) = g$
.
$e( v_4 ) = g$
.
Let
![]() $\alpha \in G( y )$
. Then,
$\alpha \in G( y )$
. Then,
![]() $\alpha$
stabilizes
$\alpha$
stabilizes
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
and so
$\Delta _2$
and so
![]() $( v_1 ) \alpha \rightarrow ^t ( v_2 ) \alpha$
is a
$( v_1 ) \alpha \rightarrow ^t ( v_2 ) \alpha$
is a
![]() $t$
-edge from
$t$
-edge from
![]() $\Delta _1$
to
$\Delta _1$
to
![]() $\Delta _2$
. Since
$\Delta _2$
. Since
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
are
$\Delta _2$
are
![]() $t$
-saturated, there is a path
$t$
-saturated, there is a path
![]() $v_1 \rightarrow ^b ( v_1 ) \alpha$
, for some
$v_1 \rightarrow ^b ( v_1 ) \alpha$
, for some
![]() $b \in U_1$
. Since, we have a path
$b \in U_1$
. Since, we have a path
![]() $v_1 \rightarrow ^{ a d_1 } v_4$
in
$v_1 \rightarrow ^{ a d_1 } v_4$
in
![]() $\Delta _1$
, we have a path
$\Delta _1$
, we have a path
![]() $( v_1 ) \alpha \rightarrow ^{ a d_1 } ( v_4 ) \alpha$
in
$( v_1 ) \alpha \rightarrow ^{ a d_1 } ( v_4 ) \alpha$
in
![]() $\Delta$
. Thus,
$\Delta$
. Thus,
![]() $( v_4, \Delta _1, ( v_4 ) \alpha ) \cong \mathcal{A}( S, s )$
, where
$( v_4, \Delta _1, ( v_4 ) \alpha ) \cong \mathcal{A}( S, s )$
, where
![]() $s = d^{-1}_1 ( f a^{-1}b a ) d_1$
and
$s = d^{-1}_1 ( f a^{-1}b a ) d_1$
and
![]() $f a^{-1}b a \in H_f$
. Hence,
$f a^{-1}b a \in H_f$
. Hence,
![]() $\psi \;:\; G( \Delta _1 ) \rightarrow H( ( \Delta _1 ) \psi )$
maps
$\psi \;:\; G( \Delta _1 ) \rightarrow H( ( \Delta _1 ) \psi )$
maps
![]() $G( y )$
into
$G( y )$
into
![]() $H( ( y ) \psi )$
.
$H( ( y ) \psi )$
.
Conversely, let
![]() $c \in H_f$
. Since
$c \in H_f$
. Since
![]() $\psi \;:\; G( \Delta _1 ) \rightarrow H( ( \Delta _1 ) \psi )$
is an isomorphism, there exists
$\psi \;:\; G( \Delta _1 ) \rightarrow H( ( \Delta _1 ) \psi )$
is an isomorphism, there exists
![]() $\alpha \in G( \Delta _1 )$
such that
$\alpha \in G( \Delta _1 )$
such that
![]() $( v_4, \Delta, ( v_4 ) \alpha ) \cong \mathcal{A}( S, d^{-1}_1 c d_1 )$
. Then we have
$( v_4, \Delta, ( v_4 ) \alpha ) \cong \mathcal{A}( S, d^{-1}_1 c d_1 )$
. Then we have
![]() $( v_3, \Delta _1, ( v_3 ) \alpha ) \cong \mathcal{A}( S, c )$
and
$( v_3, \Delta _1, ( v_3 ) \alpha ) \cong \mathcal{A}( S, c )$
and
![]() $( v_1, \Delta _1, ( v_1 ) \alpha ) \cong \mathcal{A}( S, a f c a^{-1} )$
. Thus the
$( v_1, \Delta _1, ( v_1 ) \alpha ) \cong \mathcal{A}( S, a f c a^{-1} )$
. Thus the
![]() $t$
-edge
$t$
-edge
![]() $( v_1 ) \alpha \rightarrow ^t ( v_2 ) \alpha$
must also be a
$( v_1 ) \alpha \rightarrow ^t ( v_2 ) \alpha$
must also be a
![]() $t$
-edge from
$t$
-edge from
![]() $\Delta _1$
to
$\Delta _1$
to
![]() $\Delta _2$
. This implies
$\Delta _2$
. This implies
![]() $\alpha \in G( y )$
. Thus the isomorphism
$\alpha \in G( y )$
. Thus the isomorphism
![]() $\psi \;:\; G( \Delta _1 ) \rightarrow H( ( \Delta _1 ) \psi )$
maps
$\psi \;:\; G( \Delta _1 ) \rightarrow H( ( \Delta _1 ) \psi )$
maps
![]() $G( y )$
onto
$G( y )$
onto
![]() $H( ( y ) \psi )$
.
$H( ( y ) \psi )$
.
Finally, we show that the isomorphisms between the vertex and edge groups of
![]() $( G(\!-\!), T )$
and
$( G(\!-\!), T )$
and
![]() $( H(\!-\!), Y_e )$
commute with the edge monomorphisms. Let
$( H(\!-\!), Y_e )$
commute with the edge monomorphisms. Let
![]() $y = ( \Delta _1, \Delta _2 )$
be an edge of
$y = ( \Delta _1, \Delta _2 )$
be an edge of
![]() $T$
, and let
$T$
, and let
![]() $( y ) \psi$
be equal to
$( y ) \psi$
be equal to
![]() $( D_1, D, D_2 )$
. Let
$( D_1, D, D_2 )$
. Let
![]() $H_g$
,
$H_g$
,
![]() $H_f$
and
$H_f$
and
![]() $H_h$
denote the specified
$H_h$
denote the specified
![]() $\mathcal{H}$
-class groups of
$\mathcal{H}$
-class groups of
![]() $D_1$
,
$D_1$
,
![]() $D$
and
$D$
and
![]() $D_2$
, containing idempotents
$D_2$
, containing idempotents
![]() $g$
,
$g$
,
![]() $f$
and
$f$
and
![]() $h$
, respectively. Let
$h$
, respectively. Let
![]() $d_1$
and
$d_1$
and
![]() $d_2$
be the fixed elements of
$d_2$
be the fixed elements of
![]() $D_1$
and
$D_1$
and
![]() $D_2$
, respectively, such that
$D_2$
, respectively, such that
![]() $f \mathcal{R} d_1 \mathcal{L} g$
and
$f \mathcal{R} d_1 \mathcal{L} g$
and
![]() $( f ) \phi \mathcal{R} d_2 \mathcal{L} h$
in
$( f ) \phi \mathcal{R} d_2 \mathcal{L} h$
in
![]() $S$
. The map
$S$
. The map
![]() $t_{ ( y ) \psi } \;:\; H( ( y ) \psi ) \rightarrow H_h$
defined by
$t_{ ( y ) \psi } \;:\; H( ( y ) \psi ) \rightarrow H_h$
defined by
![]() $d^{-1}_1 s d_1 \rightarrow d^{-1}_2 \cdot ( s ) \phi \cdot d_2$
, for
$d^{-1}_1 s d_1 \rightarrow d^{-1}_2 \cdot ( s ) \phi \cdot d_2$
, for
![]() $s \in H( ( y ) \psi )$
, is the edge monomorphism for
$s \in H( ( y ) \psi )$
, is the edge monomorphism for
![]() $( y ) \psi$
. Let
$( y ) \psi$
. Let
![]() $\Delta '_{\!\!2}$
be the unique vertex of
$\Delta '_{\!\!2}$
be the unique vertex of
![]() $T$
that belongs in the same
$T$
that belongs in the same
![]() $G$
-orbit as
$G$
-orbit as
![]() $\Delta _2$
, and let
$\Delta _2$
, and let
![]() $\alpha _y \in G$
such that
$\alpha _y \in G$
such that
![]() $\alpha _y \cdot \Delta '_{\!\!2} = \Delta _2$
. The edge monomorphism
$\alpha _y \cdot \Delta '_{\!\!2} = \Delta _2$
. The edge monomorphism
![]() $t_y \;:\; G( y ) \rightarrow G( \Delta '_{\!\!2} )$
for
$t_y \;:\; G( y ) \rightarrow G( \Delta '_{\!\!2} )$
for
![]() $y$
is given by
$y$
is given by
![]() $\alpha \rightarrow \alpha _y \circ \alpha \circ \alpha ^{-1}_y$
.
$\alpha \rightarrow \alpha _y \circ \alpha \circ \alpha ^{-1}_y$
.
The composition of the edge map
![]() $t_y$
with
$t_y$
with
![]() $\psi \;:\; G( \Delta '_{\!\!2} ) \rightarrow H( ( \Delta '_{\!\!2} )\psi )$
is the map
$\psi \;:\; G( \Delta '_{\!\!2} ) \rightarrow H( ( \Delta '_{\!\!2} )\psi )$
is the map
![]() $t_y \circ \psi \;:\; G( y ) \rightarrow H( ( \Delta '_{\!\!2} ) \psi ) \;:\; \alpha \rightarrow s$
, with
$t_y \circ \psi \;:\; G( y ) \rightarrow H( ( \Delta '_{\!\!2} ) \psi ) \;:\; \alpha \rightarrow s$
, with
![]() $\mathcal{A}( S, s ) \cong ( v, \Delta '_{\!\!2}, ( v ) \alpha _y \circ \alpha \circ \alpha ^{-1}_y )$
, for any vertex
$\mathcal{A}( S, s ) \cong ( v, \Delta '_{\!\!2}, ( v ) \alpha _y \circ \alpha \circ \alpha ^{-1}_y )$
, for any vertex
![]() $v$
of
$v$
of
![]() $\Delta '_{\!\!2}$
such that
$\Delta '_{\!\!2}$
such that
![]() $e( v ) = h$
. Since
$e( v ) = h$
. Since
![]() $\alpha _y$
maps
$\alpha _y$
maps
![]() $\Delta '_{\!\!2}$
isomorphically onto
$\Delta '_{\!\!2}$
isomorphically onto
![]() $\Delta _2$
, we can redefine this map by saying
$\Delta _2$
, we can redefine this map by saying
![]() $( \alpha ) t_y \circ \psi = s$
, where
$( \alpha ) t_y \circ \psi = s$
, where
![]() $s \in S$
such that
$s \in S$
such that
![]() $\mathcal{A}( S, s ) \cong ( v, \Delta _2, ( v ) \alpha )$
, for some vertex
$\mathcal{A}( S, s ) \cong ( v, \Delta _2, ( v ) \alpha )$
, for some vertex
![]() $v$
of
$v$
of
![]() $\Delta _2$
with
$\Delta _2$
with
![]() $e( v ) = h$
.
$e( v ) = h$
.
The composition of
![]() $\psi \;:\; G( y ) \rightarrow H( ( y ) \psi )$
with the edge map
$\psi \;:\; G( y ) \rightarrow H( ( y ) \psi )$
with the edge map
![]() $t_{ ( y ) \psi }$
is given by
$t_{ ( y ) \psi }$
is given by
![]() $\psi \circ t_{ ( y ) \psi } \;:\; G( y ) \rightarrow H( ( \Delta '_{\!\!2} ) \psi ) :$
$\psi \circ t_{ ( y ) \psi } \;:\; G( y ) \rightarrow H( ( \Delta '_{\!\!2} ) \psi ) :$
![]() $\alpha \rightarrow d^{-1}_2 \cdot ( r ) \phi \cdot d_2$
, where
$\alpha \rightarrow d^{-1}_2 \cdot ( r ) \phi \cdot d_2$
, where
![]() $r \in H_f$
such that
$r \in H_f$
such that
![]() $\mathcal{A}( S, r ) \cong ( v_1, \Delta _1, ( v_1) \alpha )$
, for some
$\mathcal{A}( S, r ) \cong ( v_1, \Delta _1, ( v_1) \alpha )$
, for some
![]() $t$
-edge
$t$
-edge
![]() $v_1 \rightarrow ^t v_2$
from a vertex
$v_1 \rightarrow ^t v_2$
from a vertex
![]() $v_1$
of
$v_1$
of
![]() $\Delta _1$
to a vertex
$\Delta _1$
to a vertex
![]() $v_2$
of
$v_2$
of
![]() $\Delta _2$
, with
$\Delta _2$
, with
![]() $e( v_1 ) = f$
.
$e( v_1 ) = f$
.
Since
![]() $e( v_2 ) = ( f ) \phi$
and
$e( v_2 ) = ( f ) \phi$
and
![]() $( f ) \phi \mathcal{R} d_2$
in
$( f ) \phi \mathcal{R} d_2$
in
![]() $S$
, there exists a vertex
$S$
, there exists a vertex
![]() $v'_{\!\!2}$
of
$v'_{\!\!2}$
of
![]() $\Delta _2$
such that
$\Delta _2$
such that
![]() $( v_2, \Delta _2, v'_{\!\!2} ) \cong \mathcal{A}( S, d_2 )$
. Since we have a path
$( v_2, \Delta _2, v'_{\!\!2} ) \cong \mathcal{A}( S, d_2 )$
. Since we have a path
![]() $v_1 \rightarrow ^r ( v_1 ) \alpha$
in
$v_1 \rightarrow ^r ( v_1 ) \alpha$
in
![]() $\Delta _1$
, we have a path
$\Delta _1$
, we have a path
![]() $v_2 \rightarrow ^{ ( r ) \phi } ( v_2 ) \alpha$
in
$v_2 \rightarrow ^{ ( r ) \phi } ( v_2 ) \alpha$
in
![]() $\Delta _2$
. Then,
$\Delta _2$
. Then,
![]() $( v_2, \Delta _2, ( v_2 ) \alpha ) \cong$
$( v_2, \Delta _2, ( v_2 ) \alpha ) \cong$
![]() $\mathcal{A}( S, ( r ) \phi )$
. Now
$\mathcal{A}( S, ( r ) \phi )$
. Now
![]() $( ( v_2 ) \alpha, \Delta _2, ( v'_{\!\!2} ) \alpha ) \cong$
$( ( v_2 ) \alpha, \Delta _2, ( v'_{\!\!2} ) \alpha ) \cong$
![]() $\mathcal{A}( S, d_2 )$
and so
$\mathcal{A}( S, d_2 )$
and so
![]() $( v'_{\!\!2}, \Delta _2, ( v'_{\!\!2} ) \alpha ) \cong$
$( v'_{\!\!2}, \Delta _2, ( v'_{\!\!2} ) \alpha ) \cong$
![]() $\mathcal{A}( S, d^{-1}_2 \cdot ( r ) \phi \cdot d_2 )$
. We have
$\mathcal{A}( S, d^{-1}_2 \cdot ( r ) \phi \cdot d_2 )$
. We have
![]() $e( v'_{\!\!2} ) = h$
and so
$e( v'_{\!\!2} ) = h$
and so
![]() $( \alpha ) t_y \circ \psi = d^{-1}_2 \cdot ( r ) \phi \cdot d_2 =$
$( \alpha ) t_y \circ \psi = d^{-1}_2 \cdot ( r ) \phi \cdot d_2 =$
![]() $\psi \circ t_{ ( y ) \psi }$
, as required, and the proof of the theorem is complete.
$\psi \circ t_{ ( y ) \psi }$
, as required, and the proof of the theorem is complete.
Notation 4.5.
We define an equivalence
![]() $\sim _i$
on
$\sim _i$
on
![]() $S$
by
$S$
by
![]() $s_1 \sim _i s_2$
if and only if
$s_1 \sim _i s_2$
if and only if
![]() $s_1 = s_2$
or
$s_1 = s_2$
or
![]() $s_1 \mathcal{R} s_2$
with
$s_1 \mathcal{R} s_2$
with
![]() $s_1 = s_2 u$
, for some
$s_1 = s_2 u$
, for some
![]() $u \in U_i$
, for
$u \in U_i$
, for
![]() $s_1, s_2 \in S$
, for
$s_1, s_2 \in S$
, for
![]() $i = 1, 2$
.
$i = 1, 2$
.
Theorem 4.6.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension, and let
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension, and let
![]() $e$
be an idempotent of
$e$
be an idempotent of
![]() $S^*$
that is not
$S^*$
that is not
![]() $\mathcal{D}$
-related to any element of
$\mathcal{D}$
-related to any element of
![]() $S$
. Then, the maximal subgroup of
$S$
. Then, the maximal subgroup of
![]() $S^*$
containing
$S^*$
containing
![]() $e$
is isomorphic to a subgroup
$e$
is isomorphic to a subgroup
![]() $H$
of
$H$
of
![]() $S$
, whose quotient
$S$
, whose quotient
![]() $H/ \sim _i$
is finite, for some
$H/ \sim _i$
is finite, for some
![]() $i \in \{ 1, 2 \}$
.
$i \in \{ 1, 2 \}$
.
Proof. Let
![]() $\Gamma = S \Gamma ( S^*, e )$
. Then, the maximal subgroup of
$\Gamma = S \Gamma ( S^*, e )$
. Then, the maximal subgroup of
![]() $S^*$
containing
$S^*$
containing
![]() $e$
is isomorphic to the automorphism group of
$e$
is isomorphic to the automorphism group of
![]() $\Gamma$
. If
$\Gamma$
. If
![]() $n ( \Gamma ) = 1$
, as defined in Section 3, then there exists an
$n ( \Gamma ) = 1$
, as defined in Section 3, then there exists an
![]() $\langle S \rangle$
-lobe
$\langle S \rangle$
-lobe
![]() $\Delta$
that is a host of
$\Delta$
that is a host of
![]() $\Gamma$
. Since
$\Gamma$
. Since
![]() $\Delta$
is isomorphic to a Schützenberger graph of
$\Delta$
is isomorphic to a Schützenberger graph of
![]() $S$
, we then have
$S$
, we then have
![]() $e \mathcal{D} g$
in
$e \mathcal{D} g$
in
![]() $S^*$
, for some
$S^*$
, for some
![]() $g \in E( S )$
, a contradiction. Thus,
$g \in E( S )$
, a contradiction. Thus,
![]() $n( \Gamma ) > 1$
and
$n( \Gamma ) > 1$
and
![]() $\Gamma$
has precisely one host
$\Gamma$
has precisely one host
![]() $\Sigma$
, consisting of at least two
$\Sigma$
, consisting of at least two
![]() $\langle S \rangle$
-lobes.
$\langle S \rangle$
-lobes.
The automorphism group of
![]() $\Gamma$
is isomorphic to the automorphism group of
$\Gamma$
is isomorphic to the automorphism group of
![]() $\Sigma$
, by Lemma 3.11. From Lemma 3.10, the automorphism group of
$\Sigma$
, by Lemma 3.11. From Lemma 3.10, the automorphism group of
![]() $\Sigma$
is embedded into the automorphism group of some
$\Sigma$
is embedded into the automorphism group of some
![]() $\langle S \rangle$
-lobe
$\langle S \rangle$
-lobe
![]() $\Delta$
of
$\Delta$
of
![]() $\Sigma$
, under the embedding
$\Sigma$
, under the embedding
![]() $\alpha \rightarrow \alpha _\Delta$
, where
$\alpha \rightarrow \alpha _\Delta$
, where
![]() $\alpha _\Delta$
denotes the restriction of
$\alpha _\Delta$
denotes the restriction of
![]() $\alpha$
to
$\alpha$
to
![]() $\Delta$
. Let
$\Delta$
. Let
![]() $v$
be a vertex of
$v$
be a vertex of
![]() $\Delta$
. We have
$\Delta$
. We have
![]() $\Delta \cong S \Gamma ( S, g )$
, where
$\Delta \cong S \Gamma ( S, g )$
, where
![]() $g = e( v )$
. Then, the map
$g = e( v )$
. Then, the map
![]() $\psi \;:\; AUT( \Gamma ) \rightarrow H_g$
defined by
$\psi \;:\; AUT( \Gamma ) \rightarrow H_g$
defined by
![]() $\alpha \rightarrow s$
, where
$\alpha \rightarrow s$
, where
![]() $( v, \Delta, ( v ) \alpha ) \cong \mathcal{A}( S, s )$
and
$( v, \Delta, ( v ) \alpha ) \cong \mathcal{A}( S, s )$
and
![]() $H_g$
is the
$H_g$
is the
![]() $\mathcal{H}$
-class of
$\mathcal{H}$
-class of
![]() $S$
containing
$S$
containing
![]() $g$
, defines a group monomorphism.
$g$
, defines a group monomorphism.
Let
![]() $H$
denote the image of
$H$
denote the image of
![]() $AUT ( \Gamma )$
under
$AUT ( \Gamma )$
under
![]() $\psi$
. Let
$\psi$
. Let
![]() $v_1 \rightarrow ^t v_2$
be a
$v_1 \rightarrow ^t v_2$
be a
![]() $t$
-edge of
$t$
-edge of
![]() $\Sigma$
, where one of the vertices
$\Sigma$
, where one of the vertices
![]() $v_1$
,
$v_1$
,
![]() $v_2$
belongs to
$v_2$
belongs to
![]() $\Delta$
. Suppose
$\Delta$
. Suppose
![]() $v_1 \in V( \Delta )$
. We can assume
$v_1 \in V( \Delta )$
. We can assume
![]() $v = v_1$
. Now let
$v = v_1$
. Now let
![]() $\alpha _1, \alpha _2 \in AUT( \Gamma )$
,
$\alpha _1, \alpha _2 \in AUT( \Gamma )$
,
![]() $( \alpha _1 ) \psi = s_1$
and
$( \alpha _1 ) \psi = s_1$
and
![]() $( \alpha _2 ) \psi = s_2$
. If
$( \alpha _2 ) \psi = s_2$
. If
![]() $( v_1 ) \alpha _1 \rightarrow ^t ( v_2 ) \alpha _1$
and
$( v_1 ) \alpha _1 \rightarrow ^t ( v_2 ) \alpha _1$
and
![]() $( v_1 ) \alpha _2 \rightarrow ( v_2 ) \alpha _2$
are
$( v_1 ) \alpha _2 \rightarrow ( v_2 ) \alpha _2$
are
![]() $t$
-edges from
$t$
-edges from
![]() $\Delta$
to an
$\Delta$
to an
![]() $\langle S \rangle$
-lobe
$\langle S \rangle$
-lobe
![]() $\Delta '$
of
$\Delta '$
of
![]() $\Sigma$
, then we have
$\Sigma$
, then we have
![]() $s_2 = s_1 u$
, for some
$s_2 = s_1 u$
, for some
![]() $u \in U_1$
, and so
$u \in U_1$
, and so
![]() $s_1 \sim _1 s_2$
. Thus, the number of
$s_1 \sim _1 s_2$
. Thus, the number of
![]() $\sim _1$
-classes in
$\sim _1$
-classes in
![]() $H$
is at most the number of
$H$
is at most the number of
![]() $\langle S \rangle$
-lobes in
$\langle S \rangle$
-lobes in
![]() $\Sigma$
that are adjacent to
$\Sigma$
that are adjacent to
![]() $\Delta$
. Since
$\Delta$
. Since
![]() $\Sigma$
has finitely many
$\Sigma$
has finitely many
![]() $\langle S \rangle$
-lobes, the group
$\langle S \rangle$
-lobes, the group
![]() $H$
has finitely many
$H$
has finitely many
![]() $\sim _1$
-classes. If
$\sim _1$
-classes. If
![]() $v_2 \in V( \Delta )$
, then a similar proof shows that the group
$v_2 \in V( \Delta )$
, then a similar proof shows that the group
![]() $H$
has finitely many
$H$
has finitely many
![]() $\sim _2$
-classes.
$\sim _2$
-classes.
Theorems 4.4 and 4.6 tell us that every maximal subgroup of
![]() $S^*$
is either isomorphic to the fundamental group of some graph of groups
$S^*$
is either isomorphic to the fundamental group of some graph of groups
![]() $( H_e (\!-\!), Y_e )$
, where the vertex and edge groups are subgroups of
$( H_e (\!-\!), Y_e )$
, where the vertex and edge groups are subgroups of
![]() $S$
, or is isomorphic to a subgroup of
$S$
, or is isomorphic to a subgroup of
![]() $S$
.
$S$
.
Corollary 4.7.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension.
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension.
-
(i) If
 $S$
is combinatorial then every maximal subgroup of
$S$
is combinatorial then every maximal subgroup of
 $S^*$
is a free group.
$S^*$
is a free group.
-
(ii)
 $S^*$
is combinatorial if and only if
$S^*$
is combinatorial if and only if
 $S$
is combinatorial and
$S$
is combinatorial and
 $Y$
is a forest.
$Y$
is a forest.
Proof. The results are immediate from Theorem 4.4.
Corollary 4.8.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Let
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Let
![]() $f \in E( U_1 )$
and
$f \in E( U_1 )$
and
![]() $H_f$
,
$H_f$
,
![]() $H_{ ( f )\phi }$
,
$H_{ ( f )\phi }$
,
![]() $G_f$
denote the maximal subgroups containing
$G_f$
denote the maximal subgroups containing
![]() $f$
,
$f$
,
![]() $( f )\phi$
,
$( f )\phi$
,
![]() $f$
in
$f$
in
![]() $S$
,
$S$
,
![]() $S$
,
$S$
,
![]() $U_1$
, respectively. Assuming
$U_1$
, respectively. Assuming
![]() $f \mathcal{D} g$
in
$f \mathcal{D} g$
in
![]() $S$
implies
$S$
implies
![]() $f \mathcal{D} g$
in
$f \mathcal{D} g$
in
![]() $U_1$
, for
$U_1$
, for
![]() $g \in E( U_1 )$
:
$g \in E( U_1 )$
:
-
(ii) If
 $( f ) \phi \mathcal{R} d \mathcal{L} f$
in
$( f ) \phi \mathcal{R} d \mathcal{L} f$
in
 $S$
, for
$S$
, for
 $d \in S$
, then the maximal subgroup of
$d \in S$
, then the maximal subgroup of
 $S^*$
containing
$S^*$
containing
 $f$
is isomorphic to the group HNN extension
$f$
is isomorphic to the group HNN extension
 $[ H_f;\; G_f, d^{-1} \cdot ( G_f ) \phi \cdot d ]$
.
$[ H_f;\; G_f, d^{-1} \cdot ( G_f ) \phi \cdot d ]$
. -
(iii) If
 $( f ) \phi {\mathcal{D}} f$
in
$( f ) \phi {\mathcal{D}} f$
in
 $S$
, then the maximal subgroup of
$S$
, then the maximal subgroup of
 $S^*$
containing
$S^*$
containing
 $f$
is isomorphic to the amalgamated free product of the group amalgam
$f$
is isomorphic to the amalgamated free product of the group amalgam
 $[ H_f, H_{ ( f )\phi };\; G_f ]$
.
$[ H_f, H_{ ( f )\phi };\; G_f ]$
.
Proof. Suppose
![]() $( f ) \phi \mathcal{R} d \mathcal{L} f$
in
$( f ) \phi \mathcal{R} d \mathcal{L} f$
in
![]() $S$
, for
$S$
, for
![]() $d \in S$
. Assuming
$d \in S$
. Assuming
![]() $f \mathcal{D} g$
in
$f \mathcal{D} g$
in
![]() $S$
implies
$S$
implies
![]() $f \mathcal{D} g$
in
$f \mathcal{D} g$
in
![]() $U_1$
, for
$U_1$
, for
![]() $g \in E( U_1 )$
, the component
$g \in E( U_1 )$
, the component
![]() $Y_f$
consists of one vertex
$Y_f$
consists of one vertex
![]() $D_1$
and one edge
$D_1$
and one edge
![]() $y = ( D_1, D, D_1 )$
. We may assume that the vertex group
$y = ( D_1, D, D_1 )$
. We may assume that the vertex group
![]() $H( y )$
is
$H( y )$
is
![]() $G_f$
and the vertex group
$G_f$
and the vertex group
![]() $H( D_1 )$
is
$H( D_1 )$
is
![]() $H_f$
. The group monomorphism
$H_f$
. The group monomorphism
![]() $t_y \;:\; H( y ) \rightarrow H( D_1 )$
is given by
$t_y \;:\; H( y ) \rightarrow H( D_1 )$
is given by
![]() $s \rightarrow d^{-1} \cdot ( s ) \phi \cdot d$
. By Theorem 4.4, the maximal subgroup of
$s \rightarrow d^{-1} \cdot ( s ) \phi \cdot d$
. By Theorem 4.4, the maximal subgroup of
![]() $S^*$
containing
$S^*$
containing
![]() $e$
is isomorphic to the HNN extension of groups
$e$
is isomorphic to the HNN extension of groups
![]() $[ H( D_1 );\; H( y ), ( H( y ) ) t_y;\; t_y ]$
$[ H( D_1 );\; H( y ), ( H( y ) ) t_y;\; t_y ]$
Suppose
![]() $( f ) \phi {\mathcal{D}} f$
in
$( f ) \phi {\mathcal{D}} f$
in
![]() $S$
. Assuming
$S$
. Assuming
![]() $f \mathcal{D} g$
in
$f \mathcal{D} g$
in
![]() $S$
implies
$S$
implies
![]() $f \mathcal{D} g$
in
$f \mathcal{D} g$
in
![]() $U_1$
, for
$U_1$
, for
![]() $g \in E( U_1 )$
, the component
$g \in E( U_1 )$
, the component
![]() $Y_f$
consists of two vertices
$Y_f$
consists of two vertices
![]() $D_1$
and
$D_1$
and
![]() $D_2$
connected by a single edge
$D_2$
connected by a single edge
![]() $y = ( D_1, D, D_2 )$
. We may assume that the vertex group
$y = ( D_1, D, D_2 )$
. We may assume that the vertex group
![]() $H( y )$
is
$H( y )$
is
![]() $G_f$
, the vertex group
$G_f$
, the vertex group
![]() $H( D_1 )$
is
$H( D_1 )$
is
![]() $H_f$
, and the vertex group
$H_f$
, and the vertex group
![]() $H( D_2 )$
is
$H( D_2 )$
is
![]() $H_{ ( f ) \phi }$
. The group monomorphism
$H_{ ( f ) \phi }$
. The group monomorphism
![]() $t_y \;:\; H( y ) \rightarrow H( D_2 )$
is given by
$t_y \;:\; H( y ) \rightarrow H( D_2 )$
is given by
![]() $s \rightarrow ( s ) \phi$
. Then, by Theorem 4.4, the maximal subgroup of
$s \rightarrow ( s ) \phi$
. Then, by Theorem 4.4, the maximal subgroup of
![]() $S^*$
containing
$S^*$
containing
![]() $e$
is isomorphic to the amalgamated free product of the group amalgam
$e$
is isomorphic to the amalgamated free product of the group amalgam
![]() $[ H( D_1 ), H ( D_2 );\; H( y ) \cong H( y ) t_y ]$
.
$[ H( D_1 ), H ( D_2 );\; H( y ) \cong H( y ) t_y ]$
.
Notation 4.9.
Similar to Ayyash and Cherubini [Reference Ayyash and Cherubini2], we define a binary relation
![]() $\prec _S$
on
$\prec _S$
on
![]() $E( U_1 ) \cup E( U_2 )$
. For
$E( U_1 ) \cup E( U_2 )$
. For
![]() $f, g \in E( U_1 ) \cup E( U_2 )$
, we write
$f, g \in E( U_1 ) \cup E( U_2 )$
, we write
![]() $f \prec _S g$
if
$f \prec _S g$
if
![]() $f \mathcal{D} h \leq g$
in
$f \mathcal{D} h \leq g$
in
![]() $S$
, for some
$S$
, for some
![]() $h \in E( S )$
. We then let
$h \in E( S )$
. We then let
![]() $\prec$
denote the transitive closure of
$\prec$
denote the transitive closure of
![]() $\prec _S$
and the set
$\prec _S$
and the set
![]() $\{ ( f, ( f ) \phi ), ( ( f ) \phi, f ) \;:\; f \in E( U_1 ) \}$
. As the next result shows, we are interested in when the intersection of
$\{ ( f, ( f ) \phi ), ( ( f ) \phi, f ) \;:\; f \in E( U_1 ) \}$
. As the next result shows, we are interested in when the intersection of
![]() $\prec$
and
$\prec$
and
![]() $\succ _S$
is contained in
$\succ _S$
is contained in
![]() $\prec _S$
.
$\prec _S$
.
An inverse semigroup is completely semisimple if two distinct idempotents in any
![]() $\mathcal{D}$
-class are not comparable, under the natural partial order. Equivalently, from [Reference Bennett3, Lemma 10], an inverse semigroup is completely semisimple if and only if the endomorphism monoid and the automorphism group coincide for every Schützenberger graph. We have the following result for lower bounded HNN extensions, which has been generalized in [Reference Bennett and Jajcayová5, Theorem 3.30].
$\mathcal{D}$
-class are not comparable, under the natural partial order. Equivalently, from [Reference Bennett3, Lemma 10], an inverse semigroup is completely semisimple if and only if the endomorphism monoid and the automorphism group coincide for every Schützenberger graph. We have the following result for lower bounded HNN extensions, which has been generalized in [Reference Bennett and Jajcayová5, Theorem 3.30].
Theorem 4.10 (Reference Ayyash and Cherubini2, Ayyash and Cherubini, Theorem 5.3). Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Then,
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Then,
![]() $S^*$
is completely semisimple if and only if
$S^*$
is completely semisimple if and only if
![]() $S$
is completely semisimple and
$S$
is completely semisimple and
![]() $\prec \cap \succ _S \subseteq \prec _S$
.
$\prec \cap \succ _S \subseteq \prec _S$
.
Corollary 4.11.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Suppose
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Suppose
![]() $S$
is completely semisimple and
$S$
is completely semisimple and
![]() $f \mathcal{D} ( f ) \phi$
, for all
$f \mathcal{D} ( f ) \phi$
, for all
![]() $f \in E( U_1 )$
. Then,
$f \in E( U_1 )$
. Then,
![]() $\prec \cap \succ _S \subseteq \prec _S$
and so
$\prec \cap \succ _S \subseteq \prec _S$
and so
![]() $S^*$
is completely semisimple.
$S^*$
is completely semisimple.
Proof. Let
![]() $f_1, g_1, f_2, g_2, \ldots f_n, g_n \in E( U_1 ) \cup E( U_2 )$
, for
$f_1, g_1, f_2, g_2, \ldots f_n, g_n \in E( U_1 ) \cup E( U_2 )$
, for
![]() $n \geq 1$
, where at least one of
$n \geq 1$
, where at least one of
![]() $f_k = g_k$
,
$f_k = g_k$
,
![]() $( f_k ) \phi = g_k$
and
$( f_k ) \phi = g_k$
and
![]() $( f_k ) \phi ^{-1} = g_k$
holds, for
$( f_k ) \phi ^{-1} = g_k$
holds, for
![]() $1 \leq k \leq n$
, and
$1 \leq k \leq n$
, and
![]() $g_k \prec _S f_{ k+1 }$
, for
$g_k \prec _S f_{ k+1 }$
, for
![]() $1 \leq k \leq n-1$
. Thus, we have
$1 \leq k \leq n-1$
. Thus, we have
![]() $f_1 \prec g_n$
. Assuming
$f_1 \prec g_n$
. Assuming
![]() $f \mathcal{D} ( f ) \phi$
, for all
$f \mathcal{D} ( f ) \phi$
, for all
![]() $f \in E( U_1 )$
, we have
$f \in E( U_1 )$
, we have
![]() $f_k \prec _S g_k$
, for
$f_k \prec _S g_k$
, for
![]() $1 \leq k \leq n$
. It then follows that
$1 \leq k \leq n$
. It then follows that
![]() $f_1 \prec _S g_n$
, as
$f_1 \prec _S g_n$
, as
![]() $\prec _S$
is transitive. Thus, we have
$\prec _S$
is transitive. Thus, we have
![]() $\prec = \prec _S$
. Hence
$\prec = \prec _S$
. Hence
![]() $S^*$
is completely semisimple, by Theorem 4.10.
$S^*$
is completely semisimple, by Theorem 4.10.
Corollary 4.12.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Suppose
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Suppose
![]() $S$
is completely semisimple and the following hold, for all
$S$
is completely semisimple and the following hold, for all
![]() $f, g \in E( U_1 )$
:
$f, g \in E( U_1 )$
:
-
(i) We do not have
 $f \prec _S ( g ) \phi$
in
$f \prec _S ( g ) \phi$
in
 $S$
and so
$S$
and so
 $E( U_1 ) \cap E( U_2 ) = \emptyset$
.
$E( U_1 ) \cap E( U_2 ) = \emptyset$
. -
(ii)
 $f \prec _S g$
implies
$f \prec _S g$
implies
 $f \mathcal{R} u \mathcal{L} u_1^{-1} u_1 \leq g$
, for some
$f \mathcal{R} u \mathcal{L} u_1^{-1} u_1 \leq g$
, for some
 $u \in U_1$
.
$u \in U_1$
. -
(iii)
 $( f ) \phi \prec _S ( g ) \phi$
implies
$( f ) \phi \prec _S ( g ) \phi$
implies
 $( f ) \phi \mathcal{R} ( u ) \phi \mathcal{L} ( u^{-1} u ) \phi \leq ( g ) \phi$
, for some
$( f ) \phi \mathcal{R} ( u ) \phi \mathcal{L} ( u^{-1} u ) \phi \leq ( g ) \phi$
, for some
 $u \in U_1$
.
$u \in U_1$
.
Then
![]() $\prec \cap \succ _S \subseteq \prec _S$
and so
$\prec \cap \succ _S \subseteq \prec _S$
and so
![]() $S^*$
is completely semisimple.
$S^*$
is completely semisimple.
Proof. Let
![]() $f_1, g_1, f_2, g_2, \ldots f_n, g_n \in E( U_1 ) \cup E( U_2 )$
, for
$f_1, g_1, f_2, g_2, \ldots f_n, g_n \in E( U_1 ) \cup E( U_2 )$
, for
![]() $n \geq 1$
, where at least one of
$n \geq 1$
, where at least one of
![]() $f_k = g_k$
,
$f_k = g_k$
,
![]() $( f_k ) \phi = g_k$
and
$( f_k ) \phi = g_k$
and
![]() $( f_k ) \phi ^{-1} = g_k$
holds, for
$( f_k ) \phi ^{-1} = g_k$
holds, for
![]() $1 \leq k \leq n$
, and
$1 \leq k \leq n$
, and
![]() $g_k \prec _S f_{ k+1 }$
, for
$g_k \prec _S f_{ k+1 }$
, for
![]() $1 \leq k \leq n-1$
. If
$1 \leq k \leq n-1$
. If
![]() $f_k = g_k$
, then
$f_k = g_k$
, then
![]() $g_{ k-1 } \prec _S f_k = g_k \prec _S f_{ k+1 }$
, and we can shorten the sequence. Thus we can assume
$g_{ k-1 } \prec _S f_k = g_k \prec _S f_{ k+1 }$
, and we can shorten the sequence. Thus we can assume
![]() $f_k \neq g_k$
.
$f_k \neq g_k$
.
Suppose
![]() $f_1 \in E( U_1 )$
and
$f_1 \in E( U_1 )$
and
![]() $( f_1 ) \phi = g_1 \in E( U_2 )$
. From condition (i) and
$( f_1 ) \phi = g_1 \in E( U_2 )$
. From condition (i) and
![]() $g_1 \prec _S f_2$
, we have
$g_1 \prec _S f_2$
, we have
![]() $f_2 \notin E( U_1 )$
and so
$f_2 \notin E( U_1 )$
and so
![]() $( f_2 ) \phi ^{-1} = g_2 \in E( U_1 )$
. From condition (iii) and
$( f_2 ) \phi ^{-1} = g_2 \in E( U_1 )$
. From condition (iii) and
![]() $g_1 \prec _S f_2$
, we have
$g_1 \prec _S f_2$
, we have
![]() $g_1 \mathcal{R} ( u_1 ) \phi \mathcal{L} ( u^{-1}_1 u_1 ) \phi \leq f_2$
, for some
$g_1 \mathcal{R} ( u_1 ) \phi \mathcal{L} ( u^{-1}_1 u_1 ) \phi \leq f_2$
, for some
![]() $u_1 \in U_1$
. Then applying
$u_1 \in U_1$
. Then applying
![]() $\phi ^{-1}$
, we have
$\phi ^{-1}$
, we have
![]() $f_1 \mathcal{R} u_1 \mathcal{L} u^{-1}_1 u_1 \leq g_2$
.
$f_1 \mathcal{R} u_1 \mathcal{L} u^{-1}_1 u_1 \leq g_2$
.
From condition (i) and
![]() $g_2 \prec _S f_3$
, we have
$g_2 \prec _S f_3$
, we have
![]() $f_3 \notin E( U_2 )$
and so
$f_3 \notin E( U_2 )$
and so
![]() $( f_3 ) \phi = g_3 \in E( U_ 2 )$
. From condition (ii) and
$( f_3 ) \phi = g_3 \in E( U_ 2 )$
. From condition (ii) and
![]() $g_2 \prec _S f_3$
, we have
$g_2 \prec _S f_3$
, we have
![]() $g_2 \mathcal{R} u_2 \mathcal{L} u^{-1}_2 u_2 \leq f_3$
, for some
$g_2 \mathcal{R} u_2 \mathcal{L} u^{-1}_2 u_2 \leq f_3$
, for some
![]() $u_2 \in U_1$
. Thus,
$u_2 \in U_1$
. Thus,
![]() $f_1 \mathcal{R} u_1u_2 \mathcal{L} u^{-1}_2 u^{-1}_1 u_1 u_2 \leq f_3$
, where
$f_1 \mathcal{R} u_1u_2 \mathcal{L} u^{-1}_2 u^{-1}_1 u_1 u_2 \leq f_3$
, where
![]() $u_1 u_2 \in U_1$
.
$u_1 u_2 \in U_1$
.
Continuing in this manner, we have
![]() $f_1 \mathcal{R} u \mathcal{L} u^{-1} u \leq f_{ 2k+1 }$
, for some
$f_1 \mathcal{R} u \mathcal{L} u^{-1} u \leq f_{ 2k+1 }$
, for some
![]() $u \in U_1$
, for
$u \in U_1$
, for
![]() $k \geq 1$
. Thus, if we also have
$k \geq 1$
. Thus, if we also have
![]() $f_1 \succ _S f_{ 2k+1 }$
then
$f_1 \succ _S f_{ 2k+1 }$
then
![]() $f_1 \mathcal{D} f_{ 2k+1 }$
in
$f_1 \mathcal{D} f_{ 2k+1 }$
in
![]() $U_1$
, since
$U_1$
, since
![]() $S$
is completely semisimple. Similarly, if
$S$
is completely semisimple. Similarly, if
![]() $f_1 \in E( U_2 )$
and
$f_1 \in E( U_2 )$
and
![]() $f_1 \succ _S f_{ 2k+1 }$
then
$f_1 \succ _S f_{ 2k+1 }$
then
![]() $f_1 \mathcal{D} f_{ 2k+1 }$
in
$f_1 \mathcal{D} f_{ 2k+1 }$
in
![]() $U_2$
. Hence,
$U_2$
. Hence,
![]() $\prec \cap \succ _S \subseteq \prec _S$
and so
$\prec \cap \succ _S \subseteq \prec _S$
and so
![]() $S^*$
is completely semisimple, by Theorem 4.10.
$S^*$
is completely semisimple, by Theorem 4.10.
We now establish a result that provides sufficient conditions for the HNN extension
![]() $S^*$
to have finite
$S^*$
to have finite
![]() $\mathcal{R}$
-classes. For
$\mathcal{R}$
-classes. For
![]() $S^*$
to have finite
$S^*$
to have finite
![]() $\mathcal{R}$
-classes it is necessary for
$\mathcal{R}$
-classes it is necessary for
![]() $S$
to have finite
$S$
to have finite
![]() $\mathcal{R}$
-classes. Since the bicyclic inverse semigroup has infinite
$\mathcal{R}$
-classes. Since the bicyclic inverse semigroup has infinite
![]() $\mathcal{R}$
-classes, an inverse semigroup with finite
$\mathcal{R}$
-classes, an inverse semigroup with finite
![]() $\mathcal{R}$
-classes cannot contain a copy of the bicyclic inverse semigroup and so must be completely semisimple.
$\mathcal{R}$
-classes cannot contain a copy of the bicyclic inverse semigroup and so must be completely semisimple.
Definition 4.13.
The relation
![]() $\prec$
is reflexive and transitive on
$\prec$
is reflexive and transitive on
![]() $E( U_1 ) \cup E( U_2 )$
. It follows that
$E( U_1 ) \cup E( U_2 )$
. It follows that
![]() $\prec \cap \succ$
defines an equivalence on
$\prec \cap \succ$
defines an equivalence on
![]() $E( U_1 ) \cup E( U_2 )$
. The
$E( U_1 ) \cup E( U_2 )$
. The
![]() $\prec \cap \succ$
equivalence classes are partially ordered by
$\prec \cap \succ$
equivalence classes are partially ordered by
![]() $[ f ] \leq [ g ]$
if and only if
$[ f ] \leq [ g ]$
if and only if
![]() $f \prec g$
, where
$f \prec g$
, where
![]() $[ f ]$
and
$[ f ]$
and
![]() $[ g ]$
denote the
$[ g ]$
denote the
![]() $\prec \cap \succ$
-classes of
$\prec \cap \succ$
-classes of
![]() $f, g \in E( U_1 )$
, respectively. We say that
$f, g \in E( U_1 )$
, respectively. We say that
![]() $E( U_1 ) \cup E( U_2 )$
is finite
$E( U_1 ) \cup E( U_2 )$
is finite
![]() $\prec \cap \succ$
-above if every strictly ascending chain of
$\prec \cap \succ$
-above if every strictly ascending chain of
![]() $\prec \cap \succ$
-classes is finite.
$\prec \cap \succ$
-classes is finite.
Lemma 4.14.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be any HNN extension where
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be any HNN extension where
![]() $S$
is completely semisimple and
$S$
is completely semisimple and
![]() $\prec \cap \succ _S \subseteq \prec _S$
. If
$\prec \cap \succ _S \subseteq \prec _S$
. If
![]() $f \prec \cap \succ g$
, where
$f \prec \cap \succ g$
, where
![]() $f, g \in E( U_1 ) \cup E( U_2 )$
, then
$f, g \in E( U_1 ) \cup E( U_2 )$
, then
![]() $f$
and
$f$
and
![]() $g$
are related by the equivalence on
$g$
are related by the equivalence on
![]() $E( U_1 ) \cup E( U_2 )$
generated by the
$E( U_1 ) \cup E( U_2 )$
generated by the
![]() $\mathcal{D}$
-relation on
$\mathcal{D}$
-relation on
![]() $S$
and the mapping
$S$
and the mapping
![]() $\phi$
.
$\phi$
.
Proof. For
![]() $f \prec \cap \succ g$
, where
$f \prec \cap \succ g$
, where
![]() $f, g \in E( U )$
, we have:
$f, g \in E( U )$
, we have:
-
(i) As
 $f \prec g$
, there exists
$f \prec g$
, there exists
 $f_1, g_1, f_2, g_2, \ldots f_n, g_n \in E( U_1 ) \cup E( U_2 )$
,
$f_1, g_1, f_2, g_2, \ldots f_n, g_n \in E( U_1 ) \cup E( U_2 )$
,
 $n \geq 1$
, where
$n \geq 1$
, where
 $f = f_1$
,
$f = f_1$
,
 $g = g_n$
, at least one of
$g = g_n$
, at least one of
 $f_k = g_k$
,
$f_k = g_k$
,
 $( f_k ) \phi = g_k$
and
$( f_k ) \phi = g_k$
and
 $( f_k ) \phi ^{-1} = g_k$
holds, for
$( f_k ) \phi ^{-1} = g_k$
holds, for
 $1 \leq k \leq n$
, and
$1 \leq k \leq n$
, and
 $g_k \prec _S f_{ k+1 }$
, for
$g_k \prec _S f_{ k+1 }$
, for
 $1 \leq k \leq n-1$
.
$1 \leq k \leq n-1$
. -
(ii) Since
 $f \succ g$
, there exists
$f \succ g$
, there exists
 $h_1, j_1, h_2, j_2, \ldots h_n, j_m \in E( U_1 ) \cup E( U_2 )$
,
$h_1, j_1, h_2, j_2, \ldots h_n, j_m \in E( U_1 ) \cup E( U_2 )$
,
 $m \geq 1$
, where
$m \geq 1$
, where
 $g = h_1$
,
$g = h_1$
,
 $f = j_m$
, at least one of
$f = j_m$
, at least one of
 $h_k = j_k$
,
$h_k = j_k$
,
 $( h_k ) \phi = j_k$
and
$( h_k ) \phi = j_k$
and
 $( h_k ) \phi ^{-1} = j_k$
holds, for
$( h_k ) \phi ^{-1} = j_k$
holds, for
 $1 \leq k \leq m$
, and
$1 \leq k \leq m$
, and
 $j_k \prec _S h_{ k+1 }$
, for
$j_k \prec _S h_{ k+1 }$
, for
 $1 \leq k \leq m-1$
.
$1 \leq k \leq m-1$
. -
(iii) Since
 $\prec \cap \succ _S \subseteq \prec _S$
and
$\prec \cap \succ _S \subseteq \prec _S$
and
 $g_k \prec _S f_{ k+1 } \prec g \prec f = f_1 \prec g_k$
, for
$g_k \prec _S f_{ k+1 } \prec g \prec f = f_1 \prec g_k$
, for
 $1 \leq k \leq n-1$
, we then have
$1 \leq k \leq n-1$
, we then have
 $g_k \succ _S f_{ k+1 }$
, for
$g_k \succ _S f_{ k+1 }$
, for
 $1 \leq k \leq n-1$
,
$1 \leq k \leq n-1$
, -
(iv) As
 $\prec \cap \succ _S \subseteq \prec _S$
and
$\prec \cap \succ _S \subseteq \prec _S$
and
 $j_k \prec _S h_{ k+1 } \prec f \prec g = h_1 \prec j_k$
, for
$j_k \prec _S h_{ k+1 } \prec f \prec g = h_1 \prec j_k$
, for
 $1 \leq k \leq m-1$
, we then have
$1 \leq k \leq m-1$
, we then have
 $j_k \succ _S h_{ k+1 }$
, for
$j_k \succ _S h_{ k+1 }$
, for
 $1 \leq k \leq m-1$
.
$1 \leq k \leq m-1$
. -
(v) Since
 $S$
is completely semisimple. the relation
$S$
is completely semisimple. the relation
 $\prec _S \cap \succ _S$
is the
$\prec _S \cap \succ _S$
is the
 $\mathcal{D}$
-relation on
$\mathcal{D}$
-relation on
 $S$
. Thus
$S$
. Thus
 $g_k \mathcal{D} f_{ k+1 }$
, for
$g_k \mathcal{D} f_{ k+1 }$
, for
 $1 \leq k \leq n-1$
, and
$1 \leq k \leq n-1$
, and
 $j_k \mathcal{D} h_{ k+1 }$
, for
$j_k \mathcal{D} h_{ k+1 }$
, for
 $1 \leq k \leq m-1$
.
$1 \leq k \leq m-1$
.
Hence
![]() $f$
and
$f$
and
![]() $g$
are related by the equivalence on
$g$
are related by the equivalence on
![]() $E( U_1 ) \cup E( U_2 )$
generated by the
$E( U_1 ) \cup E( U_2 )$
generated by the
![]() $\mathcal{D}$
-relation on
$\mathcal{D}$
-relation on
![]() $S$
and the mapping
$S$
and the mapping
![]() $\phi$
.
$\phi$
.
The fundamental group of a graph of groups whose underlying graph is a finite tree is obtained inductively by a process of repeating amalgamated free products of groups or HNN extensions of groups, one for each edge. The fundamental group is then referred to as a finite tree product of the vertex groups.
Lemma 4.15.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. If
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. If
![]() $S^*$
has finite
$S^*$
has finite
![]() $\mathcal{R}$
-classes, then every component of
$\mathcal{R}$
-classes, then every component of
![]() $Y$
is a finite tree and the resulting tree product is not proper.
$Y$
is a finite tree and the resulting tree product is not proper.
Proof. Suppose
![]() $S^*$
has finite
$S^*$
has finite
![]() $\mathcal{R}$
-classes. Let
$\mathcal{R}$
-classes. Let
![]() $e \in E( S )$
. Then, from Theorem 4.4, the fundamental group
$e \in E( S )$
. Then, from Theorem 4.4, the fundamental group
![]() $\Pi ( H_e(\!-\!), Y_e )$
is isomorphic to the
$\Pi ( H_e(\!-\!), Y_e )$
is isomorphic to the
![]() $\mathcal{H}$
-class of
$\mathcal{H}$
-class of
![]() $S^*$
containing
$S^*$
containing
![]() $e$
and so
$e$
and so
![]() $\Pi ( H_e(\!-\!), Y_e )$
finite. If
$\Pi ( H_e(\!-\!), Y_e )$
finite. If
![]() $Y_e$
is not a tree then
$Y_e$
is not a tree then
![]() $\Pi ( H_e(\!-\!), Y_e )$
is necessarily infinite, since it contains a free group. Thus
$\Pi ( H_e(\!-\!), Y_e )$
is necessarily infinite, since it contains a free group. Thus
![]() $Y_e$
is a tree.
$Y_e$
is a tree.
Suppose
![]() $Y_e$
is an infinite tree. From Theorem 4.4, the graph
$Y_e$
is an infinite tree. From Theorem 4.4, the graph
![]() $Y_e$
is isomorphic to the graph of orbits
$Y_e$
is isomorphic to the graph of orbits
![]() $AUT( \Gamma ' ) \backslash T( \Gamma ' )$
, where
$AUT( \Gamma ' ) \backslash T( \Gamma ' )$
, where
![]() $\Gamma '$
denotes the t-subopuntoid subgraph of
$\Gamma '$
denotes the t-subopuntoid subgraph of
![]() $\Gamma = S \Gamma ( S^*, e )$
that consists of all
$\Gamma = S \Gamma ( S^*, e )$
that consists of all
![]() $\langle S \rangle$
-lobes of
$\langle S \rangle$
-lobes of
![]() $\Gamma$
that are hosts and
$\Gamma$
that are hosts and
![]() $T( \Gamma ' )$
is the
$T( \Gamma ' )$
is the
![]() $\langle S \rangle$
-lobe tree of
$\langle S \rangle$
-lobe tree of
![]() $\Gamma '$
. Thus,
$\Gamma '$
. Thus,
![]() $AUT( \Gamma ' ) \backslash T( \Gamma ' )$
, and hence
$AUT( \Gamma ' ) \backslash T( \Gamma ' )$
, and hence
![]() $T( \Gamma ' )$
, has infinitely many vertices. This implies that
$T( \Gamma ' )$
, has infinitely many vertices. This implies that
![]() $\Gamma$
has infinitely many
$\Gamma$
has infinitely many
![]() $\langle S \rangle$
-lobes and we reach a contradiction, since
$\langle S \rangle$
-lobes and we reach a contradiction, since
![]() $\Gamma$
has as many vertices as the
$\Gamma$
has as many vertices as the
![]() $\mathcal{R}$
-class of
$\mathcal{R}$
-class of
![]() $S^*$
containing
$S^*$
containing
![]() $e$
. Hence,
$e$
. Hence,
![]() $Y_e$
is a finite tree. Any proper amalgamated free product of groups is necessarily infinite. Since
$Y_e$
is a finite tree. Any proper amalgamated free product of groups is necessarily infinite. Since
![]() $\Pi ( H_e(\!-\!), Y_e )$
is finite, it cannot be a proper tree product.
$\Pi ( H_e(\!-\!), Y_e )$
is finite, it cannot be a proper tree product.
In contrast with the situation for an HNN extension of a finite group, which is always infinite, an HNN extension of a finite inverse semigroup can have finite
![]() $\mathcal{R}$
-classes.
$\mathcal{R}$
-classes.
Theorem 4.16.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Suppose
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension. Suppose
![]() $S$
is completely semisimple, with finite
$S$
is completely semisimple, with finite
![]() $\mathcal{R}$
-classes,
$\mathcal{R}$
-classes,
![]() $\prec \cap \succ _S \subseteq \prec _S$
holds and
$\prec \cap \succ _S \subseteq \prec _S$
holds and
![]() $E( U_1 ) \cup E( U_2 )$
is finite
$E( U_1 ) \cup E( U_2 )$
is finite
![]() $\prec \cap \succ$
-above.
$\prec \cap \succ$
-above.
-
(i) If every component of
 $Y$
is a finite tree and has a tree product that is not proper, then
$Y$
is a finite tree and has a tree product that is not proper, then
 $S^*$
has finite
$S^*$
has finite
 $\mathcal{R}$
-classes.
$\mathcal{R}$
-classes.
-
(ii) If
 $e_1 = ( e_1 ) \phi$
belongs to a trivial
$e_1 = ( e_1 ) \phi$
belongs to a trivial
 $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
 $S$
and every component of
$S$
and every component of
 $Y$
, except for
$Y$
, except for
 $Y_{ e_1 }$
, is a finite tree and has a tree product that is not proper, then each Schützenberger graph of
$Y_{ e_1 }$
, is a finite tree and has a tree product that is not proper, then each Schützenberger graph of
 $\langle S^* \rangle$
has finitely many
$\langle S^* \rangle$
has finitely many
 $\langle S \rangle$
-lobes that have more than one vertex.
$\langle S \rangle$
-lobes that have more than one vertex.
Proof. Suppose every component of
![]() $Y$
is a finite tree and has a tree product that is not proper. Every such tree product is isomorphic to a maximal subgroup of
$Y$
is a finite tree and has a tree product that is not proper. Every such tree product is isomorphic to a maximal subgroup of
![]() $S$
and thus is finite, since
$S$
and thus is finite, since
![]() $S$
has finite
$S$
has finite
![]() $\mathcal{H}$
-classes. To prove that
$\mathcal{H}$
-classes. To prove that
![]() $S^*$
has finite
$S^*$
has finite
![]() $\mathcal{R}$
-classes, we show that every Schützenberger graph of
$\mathcal{R}$
-classes, we show that every Schützenberger graph of
![]() $\langle S^* \rangle$
has finitely many
$\langle S^* \rangle$
has finitely many
![]() $\langle S \rangle$
-lobes. We first show that every such graph has finitely many hosts.
$\langle S \rangle$
-lobes. We first show that every such graph has finitely many hosts.
Let
![]() $\Gamma$
be a Schützenberger graph of
$\Gamma$
be a Schützenberger graph of
![]() $\langle S^* \rangle$
. From Theorem 4.1, the graph
$\langle S^* \rangle$
. From Theorem 4.1, the graph
![]() $\Gamma$
is a complete
$\Gamma$
is a complete
![]() $t$
-opuntoid graph that has a host, where the
$t$
-opuntoid graph that has a host, where the
![]() $\langle S \rangle$
-lobes are isomorphic to Schützenberger graphs of
$\langle S \rangle$
-lobes are isomorphic to Schützenberger graphs of
![]() $\langle S \rangle$
. Let
$\langle S \rangle$
. Let
![]() $\Gamma '$
denote the
$\Gamma '$
denote the
![]() $t$
-subopuntoid subgraph of
$t$
-subopuntoid subgraph of
![]() $\Gamma$
that consists of the
$\Gamma$
that consists of the
![]() $\langle S \rangle$
-lobes of every host of
$\langle S \rangle$
-lobes of every host of
![]() $\Gamma$
and all
$\Gamma$
and all
![]() $t$
-edges connecting these hosts. If
$t$
-edges connecting these hosts. If
![]() $n( \Gamma ) >1$
then, by Lemma 3.7, the graph
$n( \Gamma ) >1$
then, by Lemma 3.7, the graph
![]() $\Gamma$
has precisely one host and so, since a host has finitely many
$\Gamma$
has precisely one host and so, since a host has finitely many
![]() $\langle S \rangle$
-lobes, the subgraph
$\langle S \rangle$
-lobes, the subgraph
![]() $\Gamma '$
has finitely many
$\Gamma '$
has finitely many
![]() $\langle S \rangle$
-lobes.
$\langle S \rangle$
-lobes.
If
![]() $n( \Gamma ) = 1$
, then the graph of orbits
$n( \Gamma ) = 1$
, then the graph of orbits
![]() $AUT( \Gamma ) \backslash T( \Gamma ' )$
is isomorphic to some connected component of
$AUT( \Gamma ) \backslash T( \Gamma ' )$
is isomorphic to some connected component of
![]() $Y$
, from the proof of Theorem 4.4, and is thus finite, by assumption. The tree product of this connected component is not proper, by assumption, and so
$Y$
, from the proof of Theorem 4.4, and is thus finite, by assumption. The tree product of this connected component is not proper, by assumption, and so
![]() $AUT( \Gamma )$
is isomorphic to a maximal subgroup of
$AUT( \Gamma )$
is isomorphic to a maximal subgroup of
![]() $S$
and is finite. Thus, the set of orbits of any vertex or edge of
$S$
and is finite. Thus, the set of orbits of any vertex or edge of
![]() $T( \Gamma ' )$
is also finite. It now follows that
$T( \Gamma ' )$
is also finite. It now follows that
![]() $T( \Gamma ' )$
has finitely many vertices and so
$T( \Gamma ' )$
has finitely many vertices and so
![]() $\Gamma '$
has finitely many
$\Gamma '$
has finitely many
![]() $\langle S \rangle$
-lobes. Hence
$\langle S \rangle$
-lobes. Hence
![]() $\Gamma$
has finitely many hosts.
$\Gamma$
has finitely many hosts.
We now choose an
![]() $\langle S \rangle$
-lobe
$\langle S \rangle$
-lobe
![]() $\Delta$
of
$\Delta$
of
![]() $\Gamma '$
and show that there is a bound on the length of any reduced
$\Gamma '$
and show that there is a bound on the length of any reduced
![]() $\langle S \rangle$
-lobe path in
$\langle S \rangle$
-lobe path in
![]() $\Gamma$
which starts in
$\Gamma$
which starts in
![]() $\Delta$
. Let
$\Delta$
. Let
![]() $\Delta = \Delta ^1, \Delta ^2, \ldots$
be a reduced
$\Delta = \Delta ^1, \Delta ^2, \ldots$
be a reduced
![]() $\langle S \rangle$
-lobe path in
$\langle S \rangle$
-lobe path in
![]() $\Gamma$
. Since
$\Gamma$
. Since
![]() $\Gamma '$
has finitely many
$\Gamma '$
has finitely many
![]() $\langle S \rangle$
-lobes, there is a least positive integer
$\langle S \rangle$
-lobes, there is a least positive integer
![]() $m > 1$
such that
$m > 1$
such that
![]() $\Delta ^m$
is external to
$\Delta ^m$
is external to
![]() $\Gamma '$
. Since either
$\Gamma '$
. Since either
![]() $\Gamma '$
or
$\Gamma '$
or
![]() $\Delta ^{m-1}$
is a host of
$\Delta ^{m-1}$
is a host of
![]() $\Gamma$
, we have
$\Gamma$
, we have
![]() $\Delta ^k \rightarrow \Delta ^{k+1}$
, for
$\Delta ^k \rightarrow \Delta ^{k+1}$
, for
![]() $k \geq m-1$
. The situation is illustrated in Fig. 7.
$k \geq m-1$
. The situation is illustrated in Fig. 7.

Figure 7. The
![]() $\langle S \rangle$
-lobes
$\langle S \rangle$
-lobes
![]() $\Delta ^{ m-1 }, \Delta ^m, \ldots, \Delta ^n$
of
$\Delta ^{ m-1 }, \Delta ^m, \ldots, \Delta ^n$
of
![]() $\Gamma$
.
$\Gamma$
.
Let
![]() $x_m \rightarrow ^t y_m$
be a
$x_m \rightarrow ^t y_m$
be a
![]() $t$
-edge from a vertex
$t$
-edge from a vertex
![]() $x_m$
of
$x_m$
of
![]() $\Delta ^{m-1}$
to a vertex
$\Delta ^{m-1}$
to a vertex
![]() $y_m$
of
$y_m$
of
![]() $\Delta ^m$
. The case when we have a
$\Delta ^m$
. The case when we have a
![]() $t$
-edge
$t$
-edge
![]() $y_m \rightarrow ^t x_m$
from a vertex
$y_m \rightarrow ^t x_m$
from a vertex
![]() $y_m$
of
$y_m$
of
![]() $\Delta ^m$
to a vertex
$\Delta ^m$
to a vertex
![]() $x_m$
of
$x_m$
of
![]() $\Delta ^{m-1}$
is similar. Since the
$\Delta ^{m-1}$
is similar. Since the
![]() $\langle S \rangle$
-lobes are isomorphic to Schützenberger graphs of
$\langle S \rangle$
-lobes are isomorphic to Schützenberger graphs of
![]() $\langle S \rangle$
, by Theorem 4.1, and
$\langle S \rangle$
, by Theorem 4.1, and
![]() $\Delta ^{ m-1} \rightarrow \Delta ^m$
, we have
$\Delta ^{ m-1} \rightarrow \Delta ^m$
, we have
![]() $( y_m, \Delta ^m, y_m ) \cong \mathcal{A} ( S, f_m )$
, for some
$( y_m, \Delta ^m, y_m ) \cong \mathcal{A} ( S, f_m )$
, for some
![]() $f_m \in E( U_2 )$
.
$f_m \in E( U_2 )$
.
Next, suppose we have
![]() $\Delta ^k \leftrightarrow \Delta ^{k+1}$
, for all
$\Delta ^k \leftrightarrow \Delta ^{k+1}$
, for all
![]() $k \geq m$
. For each
$k \geq m$
. For each
![]() $k \geq m$
, the reduced
$k \geq m$
, the reduced
![]() $\langle S \rangle$
-lobe path
$\langle S \rangle$
-lobe path
![]() $\Delta ^m, \Delta ^{m+1}, \ldots, \Delta ^k$
, including the
$\Delta ^m, \Delta ^{m+1}, \ldots, \Delta ^k$
, including the
![]() $t$
-edges connecting the
$t$
-edges connecting the
![]() $\langle S \rangle$
-lobes, forms a
$\langle S \rangle$
-lobes, forms a
![]() $t$
-opuntoid graph
$t$
-opuntoid graph
![]() $\Sigma _k$
, where each
$\Sigma _k$
, where each
![]() $\langle S \rangle$
-lobe is a host of
$\langle S \rangle$
-lobe is a host of
![]() $\Sigma _k$
. Since
$\Sigma _k$
. Since
![]() $\Delta ^k \leftrightarrow \Delta ^{k+1}$
, for all
$\Delta ^k \leftrightarrow \Delta ^{k+1}$
, for all
![]() $k \geq m$
, the graph
$k \geq m$
, the graph
![]() $\Sigma _k$
can be obtained from
$\Sigma _k$
can be obtained from
![]() $\Delta ^m$
by repeated applications of Construction 3.3.
$\Delta ^m$
by repeated applications of Construction 3.3.
Since
![]() $( y_m, \Delta ^m, y_m ) \cong \mathcal{A} ( S, f_m )$
, we have
$( y_m, \Delta ^m, y_m ) \cong \mathcal{A} ( S, f_m )$
, we have
![]() $( y_m, \Sigma _k, y_m ) \leadsto \mathcal{A} ( S^*, f_m )$
, by Lemma 3.4. Using Lemmas 3.4 and 3.8, it follows that
$( y_m, \Sigma _k, y_m ) \leadsto \mathcal{A} ( S^*, f_m )$
, by Lemma 3.4. Using Lemmas 3.4 and 3.8, it follows that
![]() $( y_m, \Sigma _k, y_m )$
is embedded onto a
$( y_m, \Sigma _k, y_m )$
is embedded onto a
![]() $t$
-subopuntoid subautomaton of
$t$
-subopuntoid subautomaton of
![]() $\mathcal{A} ( S^*, f_m )$
, where the image of each
$\mathcal{A} ( S^*, f_m )$
, where the image of each
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Sigma _k$
is also a host of
$\Sigma _k$
is also a host of
![]() $\mathcal{A} ( S^*, f_m )$
. Since
$\mathcal{A} ( S^*, f_m )$
. Since
![]() $S\Gamma ( S^*, f_m )$
has finitely many hosts, as proved above, the sequence of graphs
$S\Gamma ( S^*, f_m )$
has finitely many hosts, as proved above, the sequence of graphs
![]() $\Sigma _k$
is bounded. Thus there exists a least positive integer
$\Sigma _k$
is bounded. Thus there exists a least positive integer
![]() $n > m$
such that
$n > m$
such that
![]() $\Delta ^{ n-1 } \nleftarrow \Delta ^n$
.
$\Delta ^{ n-1 } \nleftarrow \Delta ^n$
.
Let
![]() $x_n \rightarrow ^t y_n$
be a
$x_n \rightarrow ^t y_n$
be a
![]() $t$
-edge from a vertex
$t$
-edge from a vertex
![]() $x_n$
of
$x_n$
of
![]() $\Delta ^{n-1}$
to a vertex
$\Delta ^{n-1}$
to a vertex
![]() $y_n$
of
$y_n$
of
![]() $\Delta ^n$
. The case when we have a
$\Delta ^n$
. The case when we have a
![]() $t$
-edge
$t$
-edge
![]() $y_n \rightarrow ^t x_n$
from a vertex
$y_n \rightarrow ^t x_n$
from a vertex
![]() $y_n$
of
$y_n$
of
![]() $\Delta ^n$
to a vertex
$\Delta ^n$
to a vertex
![]() $y_n$
of
$y_n$
of
![]() $\Delta ^{n-1}$
is similar. Since the
$\Delta ^{n-1}$
is similar. Since the
![]() $\langle S \rangle$
-lobes are isomorphic to Schützenberger graphs of
$\langle S \rangle$
-lobes are isomorphic to Schützenberger graphs of
![]() $\langle S \rangle$
, by Theorem 4.1, we have
$\langle S \rangle$
, by Theorem 4.1, we have
![]() $( y_n, \Delta ^n, y_n ) \cong \mathcal{A} ( S, f_n )$
, for some
$( y_n, \Delta ^n, y_n ) \cong \mathcal{A} ( S, f_n )$
, for some
![]() $f_n \in E( U_2 )$
. We show that
$f_n \in E( U_2 )$
. We show that
![]() $[ f_m ] < [ f_n ]$
. where
$[ f_m ] < [ f_n ]$
. where
![]() $[ f_k ]$
denotes the
$[ f_k ]$
denotes the
![]() $\prec \cap \succ$
-class of
$\prec \cap \succ$
-class of
![]() $f_k$
, for
$f_k$
, for
![]() $k = m, n$
.
$k = m, n$
.
Without loss of generality, we assume that we also have a
![]() $t$
-edge
$t$
-edge
![]() $x_k \rightarrow ^t y_k$
from a vertex
$x_k \rightarrow ^t y_k$
from a vertex
![]() $x_k$
of
$x_k$
of
![]() $\Delta ^{k-1}$
to a vertex
$\Delta ^{k-1}$
to a vertex
![]() $y_k$
of
$y_k$
of
![]() $\Delta ^k$
and let
$\Delta ^k$
and let
![]() $f_k \in E( U_2 )$
such that
$f_k \in E( U_2 )$
such that
![]() $( y_k, \Delta ^k, y_k ) \cong \mathcal{A} ( S, f_k )$
, for
$( y_k, \Delta ^k, y_k ) \cong \mathcal{A} ( S, f_k )$
, for
![]() $m+1 \leq k \leq n$
. Put
$m+1 \leq k \leq n$
. Put
![]() $g_k = ( f_k ) \phi ^{-1}$
, for
$g_k = ( f_k ) \phi ^{-1}$
, for
![]() $m \leq k \leq n$
. Since
$m \leq k \leq n$
. Since
![]() $\Delta ^k \leftrightarrow \Delta ^{ k+1 }$
, for
$\Delta ^k \leftrightarrow \Delta ^{ k+1 }$
, for
![]() $m \leq k \leq n-2$
, we have
$m \leq k \leq n-2$
, we have
![]() $( x_{ k+1 }, \Delta ^k, x_{ k+1 } ) \cong \mathcal{A} ( S, g_{ k+1 } )$
, for
$( x_{ k+1 }, \Delta ^k, x_{ k+1 } ) \cong \mathcal{A} ( S, g_{ k+1 } )$
, for
![]() $m \leq k \leq n-2$
. Since
$m \leq k \leq n-2$
. Since
![]() $\Delta ^{ n-1 } \nleftarrow \Delta ^n$
, we have
$\Delta ^{ n-1 } \nleftarrow \Delta ^n$
, we have
![]() $( x_n, \Delta ^{ n-1 }, x_n ) \cong \mathcal{A} ( S, g'_n )$
such that
$( x_n, \Delta ^{ n-1 }, x_n ) \cong \mathcal{A} ( S, g'_n )$
such that
![]() $g'_n < g_n$
in
$g'_n < g_n$
in
![]() $S$
, for some
$S$
, for some
![]() $g'_n \in E( S )$
. Now
$g'_n \in E( S )$
. Now
![]() $f_k \mathcal{D} g_{ k+1 }$
in
$f_k \mathcal{D} g_{ k+1 }$
in
![]() $S$
, for
$S$
, for
![]() $m \leq k \leq n-2$
, and
$m \leq k \leq n-2$
, and
![]() $f_{ n-1 } \mathcal{D} g'_n < g_n$
in
$f_{ n-1 } \mathcal{D} g'_n < g_n$
in
![]() $S$
.
$S$
.
Thus, the idempotents
![]() $f_m, g_{ m+1 }, \ldots, f_{ n-2 }, g_{ n-1 }, f_{ n-1 }$
are all
$f_m, g_{ m+1 }, \ldots, f_{ n-2 }, g_{ n-1 }, f_{ n-1 }$
are all
![]() $\prec \cap \succ$
-related and we also have
$\prec \cap \succ$
-related and we also have
![]() $f_{ n-1 } \prec _S g_n$
, and so
$f_{ n-1 } \prec _S g_n$
, and so
![]() $f_{ n-1 } \prec g_n$
, by the definitions of
$f_{ n-1 } \prec g_n$
, by the definitions of
![]() $\prec$
and
$\prec$
and
![]() $\prec _S$
. Suppose we have
$\prec _S$
. Suppose we have
![]() $f_{ n-1 } \succ g_n$
. Then
$f_{ n-1 } \succ g_n$
. Then
![]() $f_{ n-1 } \succ _S g_n$
, since it is assumed that
$f_{ n-1 } \succ _S g_n$
, since it is assumed that
![]() $\prec \cap \succ _S \subseteq \prec _S$
. As
$\prec \cap \succ _S \subseteq \prec _S$
. As
![]() $S$
is assumed completely semisimple, we then have
$S$
is assumed completely semisimple, we then have
![]() $f_{ n-1 } \mathcal{D} g'_n = g_n$
, a contradiction. Thus, we do not have
$f_{ n-1 } \mathcal{D} g'_n = g_n$
, a contradiction. Thus, we do not have
![]() $f_{ n-1 } \succ g_n$
and so
$f_{ n-1 } \succ g_n$
and so
![]() $[ f_m ] = [ f_{ n-1 } ] < [ g_n ] = [ f_n ]$
.
$[ f_m ] = [ f_{ n-1 } ] < [ g_n ] = [ f_n ]$
.
Similarly, there is a least positive integer
![]() $q > n$
with
$q > n$
with
![]() $\Delta ^{q-1} \nleftarrow \Delta ^q$
. Continuing in this manner, we obtain a strictly ascending sequence
$\Delta ^{q-1} \nleftarrow \Delta ^q$
. Continuing in this manner, we obtain a strictly ascending sequence
![]() $[ f_m ] < [ f_n ] < [ f_q ] \cdots$
. Since
$[ f_m ] < [ f_n ] < [ f_q ] \cdots$
. Since
![]() $S$
is finite
$S$
is finite
![]() $\prec \cap \succ$
-above, the above sequence must be finite and terminates in
$\prec \cap \succ$
-above, the above sequence must be finite and terminates in
![]() $[ e_1 ]$
. Thus, there is a bound on the length of any reduced
$[ e_1 ]$
. Thus, there is a bound on the length of any reduced
![]() $\langle S \rangle$
-lobe path in
$\langle S \rangle$
-lobe path in
![]() $\Gamma$
starting in
$\Gamma$
starting in
![]() $\Delta$
. Since
$\Delta$
. Since
![]() $S$
has finite
$S$
has finite
![]() $\mathcal{R}$
-classes, the number of
$\mathcal{R}$
-classes, the number of
![]() $\langle S \rangle$
-lobes in
$\langle S \rangle$
-lobes in
![]() $\Gamma$
that are adjacent to any given
$\Gamma$
that are adjacent to any given
![]() $\langle S \rangle$
-lobe is also finite. It now follows that
$\langle S \rangle$
-lobe is also finite. It now follows that
![]() $\Gamma$
has finitely many
$\Gamma$
has finitely many
![]() $\langle S \rangle$
-lobes and part (i) is proved.
$\langle S \rangle$
-lobes and part (i) is proved.
Assuming
![]() $e_1 = ( e_1 ) \phi$
belongs to a trivial
$e_1 = ( e_1 ) \phi$
belongs to a trivial
![]() $\mathcal{D}$
-class, the connected component
$\mathcal{D}$
-class, the connected component
![]() $Y_{ e_1 }$
of
$Y_{ e_1 }$
of
![]() $Y$
consists of one vertex and one loop, with all vertex and edge groups trivial. Every
$Y$
consists of one vertex and one loop, with all vertex and edge groups trivial. Every
![]() $\langle S \rangle$
-lobe of the Schützenberger graph
$\langle S \rangle$
-lobe of the Schützenberger graph
![]() $S \Gamma ( S^*, e_1 )$
has precisely one vertex. Using a proof similar to that in part (i), any Schützenberger graph
$S \Gamma ( S^*, e_1 )$
has precisely one vertex. Using a proof similar to that in part (i), any Schützenberger graph
![]() $\Gamma$
of
$\Gamma$
of
![]() $\langle S^* \rangle$
, other than
$\langle S^* \rangle$
, other than
![]() $S \Gamma ( S^*, e_1 )$
, has finitely many hosts. Then, since any
$S \Gamma ( S^*, e_1 )$
, has finitely many hosts. Then, since any
![]() $\langle S \rangle$
-lobe that feeds off a trivial
$\langle S \rangle$
-lobe that feeds off a trivial
![]() $\langle S \rangle$
-lobe must also be trivial, the proof that
$\langle S \rangle$
-lobe must also be trivial, the proof that
![]() $\Gamma$
has finitely many non-trivial
$\Gamma$
has finitely many non-trivial
![]() $\langle S \rangle$
-lobes is also similar to that in (i).
$\langle S \rangle$
-lobes is also similar to that in (i).
In Jajcayova [Reference Jajcayová13], it was shown that an HNN extension of a free inverse semigroup
![]() $S$
is lower bounded, and if
$S$
is lower bounded, and if
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are finitely generated, then the HNN extension has decidable word problem.
$U_2$
are finitely generated, then the HNN extension has decidable word problem.
Corollary 4.17.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be an HNN extension of a free inverse monoid and suppose the following hold, for all
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be an HNN extension of a free inverse monoid and suppose the following hold, for all
![]() $f, g \in E( U_1 )$
:
$f, g \in E( U_1 )$
:
-
(i) We do not have
 $f \prec _S ( g ) \phi$
in
$f \prec _S ( g ) \phi$
in
 $S$
and so
$S$
and so
 $E( U_1 ) \cap E( U_2 ) = \emptyset$
.
$E( U_1 ) \cap E( U_2 ) = \emptyset$
. -
(ii)
 $f \prec _S g$
implies
$f \prec _S g$
implies
 $f \mathcal{R} u \mathcal{L} u_1^{-1} u_1 \leq g$
, for some
$f \mathcal{R} u \mathcal{L} u_1^{-1} u_1 \leq g$
, for some
 $u \in U_1$
.
$u \in U_1$
. -
(iii)
 $( f ) \phi \prec _S ( g ) \phi$
implies
$( f ) \phi \prec _S ( g ) \phi$
implies
 $( f ) \phi \mathcal{R} ( u ) \phi \mathcal{L} ( u^{-1} u ) \phi \leq ( g ) \phi$
, for some
$( f ) \phi \mathcal{R} ( u ) \phi \mathcal{L} ( u^{-1} u ) \phi \leq ( g ) \phi$
, for some
 $u \in U_1$
.
$u \in U_1$
.
Then,
![]() $S^*$
is completely semisimple, combinatorial, and with finite
$S^*$
is completely semisimple, combinatorial, and with finite
![]() $\mathcal{R}$
-classes. If
$\mathcal{R}$
-classes. If
![]() $E( U_1 ) \cap E( U_2 ) = \{ 1 \}$
, the identity of
$E( U_1 ) \cap E( U_2 ) = \{ 1 \}$
, the identity of
![]() $S$
, and (i), (ii), and (iii) hold for
$S$
, and (i), (ii), and (iii) hold for
![]() $f, g \in E( U_1 ) \backslash \{ 1 \}$
, then
$f, g \in E( U_1 ) \backslash \{ 1 \}$
, then
![]() $S^*$
is completely semisimple, combinatorial, and there is a bound on the number of elements of
$S^*$
is completely semisimple, combinatorial, and there is a bound on the number of elements of
![]() $S$
needed to express the elements as a product, within each
$S$
needed to express the elements as a product, within each
![]() $\mathcal{R}$
-class of
$\mathcal{R}$
-class of
![]() $S^*$
.
$S^*$
.
Proof. We recall why the lower bounded properties hold. If
![]() $u \geq e$
, where
$u \geq e$
, where
![]() $u \in U_i$
and
$u \in U_i$
and
![]() $e \in E( S )$
, then we have
$e \in E( S )$
, then we have
![]() $u \in E( U_i )$
, for
$u \in E( U_i )$
, for
![]() $i = 1, 2$
, since
$i = 1, 2$
, since
![]() $S$
is free. For
$S$
is free. For
![]() $e \in E( S )$
, there are finitely many idempotents
$e \in E( S )$
, there are finitely many idempotents
![]() $f \in E( U_i )$
with
$f \in E( U_i )$
with
![]() $f \geq e$
, for
$f \geq e$
, for
![]() $i = 1, 2$
. Then, for
$i = 1, 2$
. Then, for
![]() $e \in E( S )$
, the set
$e \in E( S )$
, the set
![]() $\{ u \in U_i \;:\; u \geq e \}$
is either empty or has a least element
$\{ u \in U_i \;:\; u \geq e \}$
is either empty or has a least element
![]() $f_i ( e )$
, for
$f_i ( e )$
, for
![]() $i = 1, 2$
. Thus, the first condition of a lower bounded HNN extension is satisfied.
$i = 1, 2$
. Thus, the first condition of a lower bounded HNN extension is satisfied.
Let
![]() $e \in E( S )$
,
$e \in E( S )$
,
![]() $i \in \{ 1, 2 \}$
and
$i \in \{ 1, 2 \}$
and
![]() $\{ u_k \}$
be a sequence of idempotents in
$\{ u_k \}$
be a sequence of idempotents in
![]() $E( U_i )$
such that
$E( U_i )$
such that
![]() $u_k \geq f_i ( e u_k ) \geq u_{ k+1 }$
, for all
$u_k \geq f_i ( e u_k ) \geq u_{ k+1 }$
, for all
![]() $k$
. We have monomorphisms from
$k$
. We have monomorphisms from
![]() $\mathcal{A}( S, e )$
,
$\mathcal{A}( S, e )$
,
![]() $\mathcal{A}( S, u_k )$
and
$\mathcal{A}( S, u_k )$
and
![]() $\mathcal{A}( S, f( e u_k ) )$
into
$\mathcal{A}( S, f( e u_k ) )$
into
![]() $\mathcal{A}( S, e u_k )$
, for each
$\mathcal{A}( S, e u_k )$
, for each
![]() $k$
, which we regard as inclusions. Let
$k$
, which we regard as inclusions. Let
![]() $\Sigma _k = S \Gamma ( S, e ) \cap S \Gamma ( S, f( e u_k ) )$
. Suppose
$\Sigma _k = S \Gamma ( S, e ) \cap S \Gamma ( S, f( e u_k ) )$
. Suppose
![]() $\Sigma _k = \Sigma _{ k+1 }$
, for some
$\Sigma _k = \Sigma _{ k+1 }$
, for some
![]() $k$
. Now
$k$
. Now
![]() $u_k \geq f( u e_k ) \geq u_k \geq f( u e_{ k+1 } )$
. Then if
$u_k \geq f( u e_k ) \geq u_k \geq f( u e_{ k+1 } )$
. Then if
![]() $w \in E( U_I )$
and
$w \in E( U_I )$
and
![]() $w \geq e u_{ k+1 }$
in
$w \geq e u_{ k+1 }$
in
![]() $S$
, then we must have
$S$
, then we must have
![]() $w \geq u_{ k+1 }$
. Thus, we have
$w \geq u_{ k+1 }$
. Thus, we have
![]() $f( e u_{ k+1 } ) = u_{ k+1 }$
. Conversely, since
$f( e u_{ k+1 } ) = u_{ k+1 }$
. Conversely, since
![]() $S \Gamma ( S, e )$
is finite, we can have
$S \Gamma ( S, e )$
is finite, we can have
![]() $\Sigma _k \subsetneq \Sigma _{ k+1 }$
at most a finite number of times. Thus, the second condition of a lower bounded HNN extension is satisfied. Hence, the HNN extension
$\Sigma _k \subsetneq \Sigma _{ k+1 }$
at most a finite number of times. Thus, the second condition of a lower bounded HNN extension is satisfied. Hence, the HNN extension
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
is lower bounded.
$S^* = [ S;\; U_1, U_2;\; \phi ]$
is lower bounded.
Since
![]() $S$
is a free inverse semigroup, it is completely semisimple and has finite
$S$
is a free inverse semigroup, it is completely semisimple and has finite
![]() $\mathcal{R}$
-classes. From Corollary 4.12, we have
$\mathcal{R}$
-classes. From Corollary 4.12, we have
![]() $\prec \cap \succ _S \subseteq \prec _S$
and
$\prec \cap \succ _S \subseteq \prec _S$
and
![]() $S^*$
is completely semisimple. Further, the relation
$S^*$
is completely semisimple. Further, the relation
![]() $\prec \cap \succ$
is the
$\prec \cap \succ$
is the
![]() $\mathcal{D}$
-relation in
$\mathcal{D}$
-relation in
![]() $U_1$
on
$U_1$
on
![]() $E( U_1 )$
and the
$E( U_1 )$
and the
![]() $\mathcal{D}$
-relation in
$\mathcal{D}$
-relation in
![]() $U_2$
on
$U_2$
on
![]() $E( U_2 )$
. If
$E( U_2 )$
. If
![]() $f, g \in E( U_1 )$
and
$f, g \in E( U_1 )$
and
![]() $f \mathcal{R} u \mathcal{L} u^{-1}u < g$
, for some
$f \mathcal{R} u \mathcal{L} u^{-1}u < g$
, for some
![]() $u \in U_1$
, then
$u \in U_1$
, then
![]() $[ f ] < [ g ]$
, since
$[ f ] < [ g ]$
, since
![]() $S$
is completely semisimple. Since a free inverse monoid is finite
$S$
is completely semisimple. Since a free inverse monoid is finite
![]() $\mathcal{J}$
-above, we then have that
$\mathcal{J}$
-above, we then have that
![]() $E( U_1 ) \cup E( U_2 )$
is finite
$E( U_1 ) \cup E( U_2 )$
is finite
![]() $\prec \cap \succ$
-above.
$\prec \cap \succ$
-above.
Conditions (i), (ii), and (iii) imply that every component
![]() $Y_f$
of
$Y_f$
of
![]() $Y$
consists of two vertices, the
$Y$
consists of two vertices, the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $S$
containing
$S$
containing
![]() $f$
and the
$f$
and the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $S$
containing
$S$
containing
![]() $( f ) \phi$
, and one edge, the
$( f ) \phi$
, and one edge, the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $U_1$
containing
$U_1$
containing
![]() $f$
, for
$f$
, for
![]() $f \in E( U_1 )$
. Since a free inverse monoid is combinatorial, we now have that
$f \in E( U_1 )$
. Since a free inverse monoid is combinatorial, we now have that
![]() $S^*$
has finite
$S^*$
has finite
![]() $\mathcal{R}$
-classes, by Theorem 4.16 (i).
$\mathcal{R}$
-classes, by Theorem 4.16 (i).
If
![]() $E( U_1 ) \cap E( U_2 )$
consists of the identity of
$E( U_1 ) \cap E( U_2 )$
consists of the identity of
![]() $S$
, and (i), (ii), and (iii) hold for
$S$
, and (i), (ii), and (iii) hold for
![]() $f, g \in E( U_1 ) \backslash \{ 1 \}$
, then
$f, g \in E( U_1 ) \backslash \{ 1 \}$
, then
![]() $S^*$
is completely semisimple, combinatorial and has finite
$S^*$
is completely semisimple, combinatorial and has finite
![]() $\mathcal{R}$
-classes, by the above. Since
$\mathcal{R}$
-classes, by the above. Since
![]() $e_1 = 1 = e_2$
, each Schützenberger graph of
$e_1 = 1 = e_2$
, each Schützenberger graph of
![]() $\langle S^* \rangle$
has finitely many
$\langle S^* \rangle$
has finitely many
![]() $\langle S \rangle$
-lobes that have more than one vertex, from Theorem 4.16 (ii). Thus, if
$\langle S \rangle$
-lobes that have more than one vertex, from Theorem 4.16 (ii). Thus, if
![]() $r \in S^*$
then all the elements of the
$r \in S^*$
then all the elements of the
![]() $\mathcal{R}$
-class of
$\mathcal{R}$
-class of
![]() $S^*$
containing
$S^*$
containing
![]() $r$
can be expressed as a product involving fewer than
$r$
can be expressed as a product involving fewer than
![]() $N$
elements of
$N$
elements of
![]() $S$
, for some
$S$
, for some
![]() $N \geq 1$
.
$N \geq 1$
.
An inverse semigroup
![]() $S$
is residually finite if for every finite non-empty subset
$S$
is residually finite if for every finite non-empty subset
![]() $F \subseteq S$
there exists a homomorphism from
$F \subseteq S$
there exists a homomorphism from
![]() $S$
into some finite inverse semigroup
$S$
into some finite inverse semigroup
![]() $T$
which separates the elements of
$T$
which separates the elements of
![]() $F$
. Any inverse semigroup with finite
$F$
. Any inverse semigroup with finite
![]() $\mathcal{R}$
-classes is residually finite, from [Reference Jones, Margolis, Meakin and Stephen15, Lemma 5.3].
$\mathcal{R}$
-classes is residually finite, from [Reference Jones, Margolis, Meakin and Stephen15, Lemma 5.3].
Corollary 4.18.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be an HNN extension, where
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be an HNN extension, where
![]() $S$
is finite, combinatorial, and conditions (i), (ii), (iii) of Corollary 4.17 hold. Then,
$S$
is finite, combinatorial, and conditions (i), (ii), (iii) of Corollary 4.17 hold. Then,
![]() $S^*$
has finite
$S^*$
has finite
![]() $\mathcal{R}$
-classes and so is residually finite.
$\mathcal{R}$
-classes and so is residually finite.
Proof. Let
![]() $i \in \{ 1, 2 \}$
. Since
$i \in \{ 1, 2 \}$
. Since
![]() $U_i$
is finite, if
$U_i$
is finite, if
![]() $e \in E( S )$
then there exists a least idempotent
$e \in E( S )$
then there exists a least idempotent
![]() $f \in E( U_i )$
with
$f \in E( U_i )$
with
![]() $e \leq f$
. If
$e \leq f$
. If
![]() $u \in U_i$
with
$u \in U_i$
with
![]() $u \geq e$
. then
$u \geq e$
. then
![]() $f \mathcal{R} fu \mathcal{L} u^{-1} f u$
in
$f \mathcal{R} fu \mathcal{L} u^{-1} f u$
in
![]() $U_i$
and
$U_i$
and
![]() $u^{-1} f u \geq f$
, since
$u^{-1} f u \geq f$
, since
![]() $u^{-1} f u \in E( U_i )$
and
$u^{-1} f u \in E( U_i )$
and
![]() $u^{-1} f u \geq e$
. As
$u^{-1} f u \geq e$
. As
![]() $S$
is finite, and so completely semisimple, we must have
$S$
is finite, and so completely semisimple, we must have
![]() $u^{-1} f u = f$
. Then,
$u^{-1} f u = f$
. Then,
![]() $f u$
belongs to the maximal subgroup of
$f u$
belongs to the maximal subgroup of
![]() $U_1$
containing
$U_1$
containing
![]() $f$
, which is trivial. Hence
$f$
, which is trivial. Hence
![]() $f u = f$
and it follows that the HNN extension
$f u = f$
and it follows that the HNN extension
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
is lower bounded.
$S^* = [ S;\; U_1, U_2;\; \phi ]$
is lower bounded.
From Corollary 4.12, we have
![]() $\prec \cap \succ _S \subseteq \prec _S$
and
$\prec \cap \succ _S \subseteq \prec _S$
and
![]() $S^*$
is completely semisimple. As in the proof of Corollary 4.17, the relation
$S^*$
is completely semisimple. As in the proof of Corollary 4.17, the relation
![]() $\prec \cap \succ$
is the
$\prec \cap \succ$
is the
![]() $\mathcal{D}$
-relation in
$\mathcal{D}$
-relation in
![]() $U_1$
on
$U_1$
on
![]() $E( U_1 )$
and the
$E( U_1 )$
and the
![]() $\mathcal{D}$
-relation in
$\mathcal{D}$
-relation in
![]() $U_2$
on
$U_2$
on
![]() $E( U_2 )$
. If
$E( U_2 )$
. If
![]() $f, g \in E( U_1 )$
and
$f, g \in E( U_1 )$
and
![]() $f \mathcal{R} u \mathcal{L} u^{-1}u < g$
, for some
$f \mathcal{R} u \mathcal{L} u^{-1}u < g$
, for some
![]() $u \in U_1$
, then
$u \in U_1$
, then
![]() $[ f ] < [ g ]$
, since
$[ f ] < [ g ]$
, since
![]() $S$
is completely semisimple. Since
$S$
is completely semisimple. Since
![]() $S$
finite, we then have that
$S$
finite, we then have that
![]() $E( U_1 ) \cup E( U_2 )$
is finite
$E( U_1 ) \cup E( U_2 )$
is finite
![]() $\prec \cap \succ$
-above.
$\prec \cap \succ$
-above.
Conditions (i), (ii), and (iii) imply that every component
![]() $Y_f$
of
$Y_f$
of
![]() $Y$
consists of two vertices, the
$Y$
consists of two vertices, the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $S$
containing
$S$
containing
![]() $f$
and the
$f$
and the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $S$
containing
$S$
containing
![]() $( f ) \phi$
, and one edge, the
$( f ) \phi$
, and one edge, the
![]() $\mathcal{D}$
-class of
$\mathcal{D}$
-class of
![]() $U_1$
containing
$U_1$
containing
![]() $f$
, for
$f$
, for
![]() $f \in E( U_1 )$
. Since
$f \in E( U_1 )$
. Since
![]() $S$
is combinatorial, we now have that
$S$
is combinatorial, we now have that
![]() $S^*$
has finite
$S^*$
has finite
![]() $\mathcal{R}$
-classes, by Theorem 4.16 (i).
$\mathcal{R}$
-classes, by Theorem 4.16 (i).
An inverse semigroup
![]() $S$
is
$S$
is
![]() $E$
-unitary if
$E$
-unitary if
![]() $s \geq e$
implies
$s \geq e$
implies
![]() $s \in E( S )$
, for all
$s \in E( S )$
, for all
![]() $s \in S$
and
$s \in S$
and
![]() $e \in E( S )$
. From [Reference Stephen19, Theorem 3.8], we have that
$e \in E( S )$
. From [Reference Stephen19, Theorem 3.8], we have that
![]() $S$
is
$S$
is
![]() $E$
-unitary if and only if there exists a monomorphism from
$E$
-unitary if and only if there exists a monomorphism from
![]() $\mathcal{A}( S, s_1 )$
into
$\mathcal{A}( S, s_1 )$
into
![]() $\mathcal{A}( S, s_2 )$
, whenever
$\mathcal{A}( S, s_2 )$
, whenever
![]() $s_1 \geq s_2$
in
$s_1 \geq s_2$
in
![]() $S$
. Equivalently, the inverse semigroup
$S$
. Equivalently, the inverse semigroup
![]() $S$
is
$S$
is
![]() $E$
-unitary if and only if homomorphisms between Schützenberger graphs are monomorphic. For
$E$
-unitary if and only if homomorphisms between Schützenberger graphs are monomorphic. For
![]() $S^*$
to be
$S^*$
to be
![]() $E$
-unitary, the homomorphisms between Schützenberger graphs of
$E$
-unitary, the homomorphisms between Schützenberger graphs of
![]() $S^*$
must induce embeddings of the respective lobe trees.
$S^*$
must induce embeddings of the respective lobe trees.
Theorem 4.19.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension where
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension where
![]() $S$
is
$S$
is
![]() $E$
-unitary,
$E$
-unitary,
![]() $s u \in E( S )$
implies
$s u \in E( S )$
implies
![]() $s s^{-1} \sim _1 s$
, and
$s s^{-1} \sim _1 s$
, and
![]() $s \cdot ( u ) \phi \in E( S )$
implies
$s \cdot ( u ) \phi \in E( S )$
implies
![]() $s s^{-1} \sim _2 s$
, for all
$s s^{-1} \sim _2 s$
, for all
![]() $s \in S$
and
$s \in S$
and
![]() $u \in U_1$
. Then
$u \in U_1$
. Then
![]() $S^*$
is
$S^*$
is
![]() $E$
-unitary.
$E$
-unitary.
Proof. Let
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Gamma '$
be Schützenberger graphs of
$\Gamma '$
be Schützenberger graphs of
![]() $S^*$
and let
$S^*$
and let
![]() $\alpha \;:\; \Gamma \rightarrow \Gamma '$
be a homomorphism. Let
$\alpha \;:\; \Gamma \rightarrow \Gamma '$
be a homomorphism. Let
![]() $\beta$
denote the homomorphism
$\beta$
denote the homomorphism
![]() $T( \Gamma ) \rightarrow T( \Gamma ' )$
between the lobe trees induced by
$T( \Gamma ) \rightarrow T( \Gamma ' )$
between the lobe trees induced by
![]() $\alpha$
. We first show that
$\alpha$
. We first show that
![]() $\beta$
is an embedding.
$\beta$
is an embedding.
Let
![]() $\Delta ^1, \Delta ^2, \ldots, \Delta ^n$
be a reduced
$\Delta ^1, \Delta ^2, \ldots, \Delta ^n$
be a reduced
![]() $\langle S \rangle$
-lobe path in
$\langle S \rangle$
-lobe path in
![]() $\Gamma$
where
$\Gamma$
where
![]() $( \Delta ^1 ) \beta = ( \Delta ^n ) \beta$
. Then,
$( \Delta ^1 ) \beta = ( \Delta ^n ) \beta$
. Then,
![]() $( \Delta ^1 ) \beta, ( \Delta ^2 ) \beta, \ldots, ( \Delta ^n ) \beta$
denote the vertices of a loop in
$( \Delta ^1 ) \beta, ( \Delta ^2 ) \beta, \ldots, ( \Delta ^n ) \beta$
denote the vertices of a loop in
![]() $T( \Gamma ' )$
. Since
$T( \Gamma ' )$
. Since
![]() $T( \Gamma ' )$
is a tree, there exist some
$T( \Gamma ' )$
is a tree, there exist some
![]() $k \leq n-1$
such that
$k \leq n-1$
such that
![]() $( \Delta ^{k-1} ) \beta = ( \Delta ^{k+1} ) \beta$
. The
$( \Delta ^{k-1} ) \beta = ( \Delta ^{k+1} ) \beta$
. The
![]() $t$
-edges between
$t$
-edges between
![]() $( \Delta ^{ k-1 } ) \beta$
and
$( \Delta ^{ k-1 } ) \beta$
and
![]() $( \Delta ^k ) \beta$
all start in one
$( \Delta ^k ) \beta$
all start in one
![]() $\langle S \rangle$
-lobe and end in the other. Without loss of generality, assume all these
$\langle S \rangle$
-lobe and end in the other. Without loss of generality, assume all these
![]() $t$
-edges start in
$t$
-edges start in
![]() $( \Delta ^{ k-1 } ) \beta$
and end in
$( \Delta ^{ k-1 } ) \beta$
and end in
![]() $( \Delta ^k ) \beta$
. Then, there is a
$( \Delta ^k ) \beta$
. Then, there is a
![]() $t$
-edge
$t$
-edge
![]() $x_1 \rightarrow ^t y_1$
from a vertex
$x_1 \rightarrow ^t y_1$
from a vertex
![]() $x_1$
of
$x_1$
of
![]() $\Delta ^{k-1}$
to a vertex
$\Delta ^{k-1}$
to a vertex
![]() $y_1$
of
$y_1$
of
![]() $\Delta ^k$
and a
$\Delta ^k$
and a
![]() $t$
-edge
$t$
-edge
![]() $x_2 \rightarrow ^t y_2$
from a vertex
$x_2 \rightarrow ^t y_2$
from a vertex
![]() $x_2$
of
$x_2$
of
![]() $\Delta ^{k+1}$
to a vertex
$\Delta ^{k+1}$
to a vertex
![]() $y_2$
of
$y_2$
of
![]() $\Delta ^k$
. The situation is illustrated in Fig. 8.
$\Delta ^k$
. The situation is illustrated in Fig. 8.

Figure 8. The Schützenberger graphs
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Gamma '$
.
$\Gamma '$
.
Let
![]() $s \in S$
such that
$s \in S$
such that
![]() $( y_1, \Delta ^k, y_2 ) \cong \mathcal{A}( S, s )$
. Then, we have
$( y_1, \Delta ^k, y_2 ) \cong \mathcal{A}( S, s )$
. Then, we have
![]() $t$
-edges
$t$
-edges
![]() $( x_1 ) \alpha \rightarrow ^t ( y_1 ) \alpha$
and
$( x_1 ) \alpha \rightarrow ^t ( y_1 ) \alpha$
and
![]() $( x_2 ) \alpha \rightarrow ^t ( y_2 ) \alpha$
from
$( x_2 ) \alpha \rightarrow ^t ( y_2 ) \alpha$
from
![]() $( \Delta ^{k-1} ) \beta$
to
$( \Delta ^{k-1} ) \beta$
to
![]() $( \Delta ^k ) \beta$
in
$( \Delta ^k ) \beta$
in
![]() $\Gamma '$
. By the
$\Gamma '$
. By the
![]() $t$
-saturation property of
$t$
-saturation property of
![]() $t$
-opuntoid graphs, there exists a path
$t$
-opuntoid graphs, there exists a path
![]() $( y_2 ) \alpha \rightarrow ^{( u )\phi } ( y_1 ) \alpha$
in
$( y_2 ) \alpha \rightarrow ^{( u )\phi } ( y_1 ) \alpha$
in
![]() $( \Delta ^k ) \beta$
, for some
$( \Delta ^k ) \beta$
, for some
![]() $u \in U_1$
. Let
$u \in U_1$
. Let
![]() $r \in S$
such that
$r \in S$
such that
![]() $( ( y_1 ) \alpha, ( \Delta ^k ) \beta, ( y_2 ) \alpha ) \cong \mathcal{A}( S, r )$
. Then, we have
$( ( y_1 ) \alpha, ( \Delta ^k ) \beta, ( y_2 ) \alpha ) \cong \mathcal{A}( S, r )$
. Then, we have
![]() $s \geq r$
and
$s \geq r$
and
![]() $( u^{-1} ) \phi \geq r$
in
$( u^{-1} ) \phi \geq r$
in
![]() $S$
. Thus
$S$
. Thus
![]() $r r^{-1} \leq s \cdot ( u )\phi$
.
$r r^{-1} \leq s \cdot ( u )\phi$
.
Since
![]() $S$
is
$S$
is
![]() $E$
-unitary we that
$E$
-unitary we that
![]() $s \cdot ( u )\phi$
is idempotent. By the conditions of the statement of the theorem, we then have
$s \cdot ( u )\phi$
is idempotent. By the conditions of the statement of the theorem, we then have
![]() $ss^{-1} \sim _2 s$
. This implies that either
$ss^{-1} \sim _2 s$
. This implies that either
![]() $ss^{-1} = s$
or
$ss^{-1} = s$
or
![]() $ss^{-1} = s v$
, for some
$ss^{-1} = s v$
, for some
![]() $v \in U_2$
. The first case implies
$v \in U_2$
. The first case implies
![]() $y_1 = y_2$
and so
$y_1 = y_2$
and so
![]() $\Delta ^{k-1} = \Delta ^{ k+1 }$
, a contradiction since the original
$\Delta ^{k-1} = \Delta ^{ k+1 }$
, a contradiction since the original
![]() $\langle S \rangle$
-lobe path was reduced. The second case implies that there is a path
$\langle S \rangle$
-lobe path was reduced. The second case implies that there is a path
![]() $y_1 \rightarrow ^v y_2$
in
$y_1 \rightarrow ^v y_2$
in
![]() $\Delta ^k$
and so, by the
$\Delta ^k$
and so, by the
![]() $t$
-saturation property, we must have
$t$
-saturation property, we must have
![]() $\Delta ^{k-1} = \Delta ^{ k+1 }$
, again a contradiction.
$\Delta ^{k-1} = \Delta ^{ k+1 }$
, again a contradiction.
Hence,
![]() $\beta$
must be one-one on the vertices of
$\beta$
must be one-one on the vertices of
![]() $T( \Gamma )$
. Since
$T( \Gamma )$
. Since
![]() $T( \Gamma )$
is a tree, this implies that
$T( \Gamma )$
is a tree, this implies that
![]() $\beta$
is an embedding. Since
$\beta$
is an embedding. Since
![]() $S$
is
$S$
is
![]() $E$
-unitary, the homomorphisms between Schützenberger graphs of
$E$
-unitary, the homomorphisms between Schützenberger graphs of
![]() $\langle S \rangle$
are monomorphisms. Thus, each
$\langle S \rangle$
are monomorphisms. Thus, each
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma$
is embedded, under
$\Gamma$
is embedded, under
![]() $\alpha$
, into some
$\alpha$
, into some
![]() $\langle S \rangle$
-lobe of
$\langle S \rangle$
-lobe of
![]() $\Gamma '$
. It now follows that
$\Gamma '$
. It now follows that
![]() $\alpha$
must be monomorphic. Hence, the HNN extension
$\alpha$
must be monomorphic. Hence, the HNN extension
![]() $S^*$
is
$S^*$
is
![]() $E$
-unitary.
$E$
-unitary.
A subsemigroup
![]() $U$
of an inverse semigroup
$U$
of an inverse semigroup
![]() $S$
is a unitary subsemigroup if we have
$S$
is a unitary subsemigroup if we have
![]() $u s \in U$
implies
$u s \in U$
implies
![]() $s \in U$
, and
$s \in U$
, and
![]() $s u \in U$
implies
$s u \in U$
implies
![]() $s \in U$
, for all
$s \in U$
, for all
![]() $s \in S$
and
$s \in S$
and
![]() $u \in U$
. We note a few observations in the following corollary.
$u \in U$
. We note a few observations in the following corollary.
Corollary 4.20.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be an HNN extension where
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be an HNN extension where
![]() $S$
is an
$S$
is an
![]() $E$
-unitary inverse semigroup. If
$E$
-unitary inverse semigroup. If
![]() $S$
is a monoid and
$S$
is a monoid and
![]() $U_1$
,
$U_1$
,
![]() $U_2$
are subgroups of the groups of units of
$U_2$
are subgroups of the groups of units of
![]() $S$
then
$S$
then
![]() $S^*$
is
$S^*$
is
![]() $E$
-unitary. If
$E$
-unitary. If
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are semilattices satisfying the descending chain condition or are full unitary inverse subsemigroups of
$U_2$
are semilattices satisfying the descending chain condition or are full unitary inverse subsemigroups of
![]() $S$
then
$S$
then
![]() $S^*$
is
$S^*$
is
![]() $E$
-unitary.
$E$
-unitary.
Proof. Suppose
![]() $S$
is a monoid and
$S$
is a monoid and
![]() $U_1$
,
$U_1$
,
![]() $U_2$
are subgroups of the groups of units. If
$U_2$
are subgroups of the groups of units. If
![]() $u \geq e$
, for some
$u \geq e$
, for some
![]() $u \in U_1$
and
$u \in U_1$
and
![]() $e \in E( S )$
, then
$e \in E( S )$
, then
![]() $u = 1$
, the identity of the monoid, since
$u = 1$
, the identity of the monoid, since
![]() $S$
is
$S$
is
![]() $E$
-unitary. Similarly, if
$E$
-unitary. Similarly, if
![]() $( u ) \phi \geq e$
, for some
$( u ) \phi \geq e$
, for some
![]() $u \in U_1$
and
$u \in U_1$
and
![]() $e \in E( S )$
, then
$e \in E( S )$
, then
![]() $( u ) \phi = 1$
. It follows that
$( u ) \phi = 1$
. It follows that
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
is a lower bounded HNN extension. Suppose
$S^* = [ S;\; U_1, U_2;\; \phi ]$
is a lower bounded HNN extension. Suppose
![]() $s u \in E( S )$
, for some
$s u \in E( S )$
, for some
![]() $s \in S$
and
$s \in S$
and
![]() $u \in U_1$
. Then,
$u \in U_1$
. Then,
![]() $s u = s uu^{-1} s^{-1} = s s^{-1}$
, as
$s u = s uu^{-1} s^{-1} = s s^{-1}$
, as
![]() $u u^{-1} = 1$
, and so
$u u^{-1} = 1$
, and so
![]() $s s^{-1} \sim _1 s$
. Similarly, if
$s s^{-1} \sim _1 s$
. Similarly, if
![]() $s \cdot ( u ) \phi \in E( S )$
, for some
$s \cdot ( u ) \phi \in E( S )$
, for some
![]() $s \in S$
and
$s \in S$
and
![]() $u \in U_1$
, then
$u \in U_1$
, then
![]() $s s^{-1} \sim _2 s$
. Thus,
$s s^{-1} \sim _2 s$
. Thus,
![]() $S^*$
is
$S^*$
is
![]() $E$
-unitary, from Theorem 4.19.
$E$
-unitary, from Theorem 4.19.
Suppose
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are semilattices satisfying the descending chain condition. It is immediate that
$U_2$
are semilattices satisfying the descending chain condition. It is immediate that
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
is a lower bounded HNN extension. If
$S^* = [ S;\; U_1, U_2;\; \phi ]$
is a lower bounded HNN extension. If
![]() $s u \in E( S )$
, for some
$s u \in E( S )$
, for some
![]() $s \in S$
and
$s \in S$
and
![]() $u \in U_1$
, then
$u \in U_1$
, then
![]() $u \in U_1 = E( U_1 )$
implies
$u \in U_1 = E( U_1 )$
implies
![]() $s \in E( S )$
, since
$s \in E( S )$
, since
![]() $S$
is
$S$
is
![]() $E$
-unitary. Then
$E$
-unitary. Then
![]() $s s^{-1} = s$
implies
$s s^{-1} = s$
implies
![]() $s s^{-1} \sim _1 s$
. Similarly, if
$s s^{-1} \sim _1 s$
. Similarly, if
![]() $s \cdot ( u ) \phi \in E( S )$
, for some
$s \cdot ( u ) \phi \in E( S )$
, for some
![]() $s \in S$
and
$s \in S$
and
![]() $u \in U_1$
, then
$u \in U_1$
, then
![]() $s s^{-1} \sim _2 s$
. Thus
$s s^{-1} \sim _2 s$
. Thus
![]() $S^*$
is
$S^*$
is
![]() $E$
-unitary, from Theorem 4.19.
$E$
-unitary, from Theorem 4.19.
Suppose
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are full unitary inverse subsemigroups of
$U_2$
are full unitary inverse subsemigroups of
![]() $S$
. Since
$S$
. Since
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are full in
$U_2$
are full in
![]() $S$
, we have
$S$
, we have
![]() $E( U_1 ) = E( U_2 ) = E( S )$
, and it is then immediate that
$E( U_1 ) = E( U_2 ) = E( S )$
, and it is then immediate that
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
is a lower bounded HNN extension. If
$S^* = [ S;\; U_1, U_2;\; \phi ]$
is a lower bounded HNN extension. If
![]() $s u \in E( S ) = E( U_1 )$
, for some
$s u \in E( S ) = E( U_1 )$
, for some
![]() $s \in S$
and
$s \in S$
and
![]() $u \in U_1$
, then
$u \in U_1$
, then
![]() $s \in U_1$
, since
$s \in U_1$
, since
![]() $U_1$
is a unitary subsemigroup. Then,
$U_1$
is a unitary subsemigroup. Then,
![]() $s s^{-1} = s \cdot ( s^{-1} )$
, where
$s s^{-1} = s \cdot ( s^{-1} )$
, where
![]() $s^{-1} \in U_1$
, and so
$s^{-1} \in U_1$
, and so
![]() $s s^{-1} \sim _1 s$
. Similarly, if we have
$s s^{-1} \sim _1 s$
. Similarly, if we have
![]() $s \cdot ( u ) \phi \in E( S )$
, for some
$s \cdot ( u ) \phi \in E( S )$
, for some
![]() $s \in S$
and
$s \in S$
and
![]() $u \in U_1$
, then
$u \in U_1$
, then
![]() $s s^{-1} \sim _2 s$
. Hence,
$s s^{-1} \sim _2 s$
. Hence,
![]() $S^*$
is
$S^*$
is
![]() $E$
-unitary, from Theorem 4.19.
$E$
-unitary, from Theorem 4.19.
An inverse semigroup
![]() $S$
is
$S$
is
![]() $0$
-
$0$
-
![]() $E$
-unitary if
$E$
-unitary if
![]() $s \geq e$
implies
$s \geq e$
implies
![]() $s \in E( S )$
, for all
$s \in E( S )$
, for all
![]() $s \in S \backslash \{ 0 \}$
and
$s \in S \backslash \{ 0 \}$
and
![]() $e \in E( S ) \backslash \{ 0 \}$
. The inverse semigroup
$e \in E( S ) \backslash \{ 0 \}$
. The inverse semigroup
![]() $S$
is strongly
$S$
is strongly
![]() $0$
-
$0$
-
![]() $E$
-unitary if it admits an idempotent pure partial homomorphism to a group.
$E$
-unitary if it admits an idempotent pure partial homomorphism to a group.
Corollary 4.21.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension where
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be a lower bounded HNN extension where
![]() $S$
,
$S$
,
![]() $U_1$
, and
$U_1$
, and
![]() $U_2$
are
$U_2$
are
![]() $0$
-
$0$
-
![]() $E$
-unitary, sharing a common
$E$
-unitary, sharing a common
![]() $0$
. If
$0$
. If
![]() $s u \in E( S )$
implies
$s u \in E( S )$
implies
![]() $s s^{-1} \sim _1 s$
, and
$s s^{-1} \sim _1 s$
, and
![]() $s \cdot ( u ) \phi \in E( S )$
implies
$s \cdot ( u ) \phi \in E( S )$
implies
![]() $s s^{-1} \sim _2 s$
, for all
$s s^{-1} \sim _2 s$
, for all
![]() $s \in S \backslash \{ 0 \}$
and
$s \in S \backslash \{ 0 \}$
and
![]() $u \in U_1 \backslash \{ 0 \}$
, then
$u \in U_1 \backslash \{ 0 \}$
, then
![]() $S^*$
is
$S^*$
is
![]() $0$
-
$0$
-
![]() $E$
-unitary.
$E$
-unitary.
Proof. The proof is similar to that of Theorem 4.19.
The polycyclic monoid
![]() $P_n$
is the inverse monoid with zero that has the following presentation
$P_n$
is the inverse monoid with zero that has the following presentation
![]() $\langle a_1, a_2, \dots, a_n, 0, 1 \mid a_i^{-1} a_i = 1, a_i^{-1} a_j = 0, i \neq j \rangle$
, as an inverse monoid with zero. Non-zero elements can be written in the unique form
$\langle a_1, a_2, \dots, a_n, 0, 1 \mid a_i^{-1} a_i = 1, a_i^{-1} a_j = 0, i \neq j \rangle$
, as an inverse monoid with zero. Non-zero elements can be written in the unique form
![]() $xy^{-1}$
, where
$xy^{-1}$
, where
![]() $x, y$
are elements of
$x, y$
are elements of
![]() $A^*_n$
, the free monoid on
$A^*_n$
, the free monoid on
![]() $A_n = \{ a_1, \ldots, a_n \}$
. Multiplication is then defined by:
$A_n = \{ a_1, \ldots, a_n \}$
. Multiplication is then defined by:
 \begin{align*} x y^{-1} \cdot u v^{-1} = \begin{cases} x z v^{-1} & \text{if } u = yz \text{, for some word } z\\[5pt] x ( vz )^{-1} & \text{if } y = uz \text{, for some word } z\\[5pt] 0 & \text{otherwise} \end{cases} \end{align*}
\begin{align*} x y^{-1} \cdot u v^{-1} = \begin{cases} x z v^{-1} & \text{if } u = yz \text{, for some word } z\\[5pt] x ( vz )^{-1} & \text{if } y = uz \text{, for some word } z\\[5pt] 0 & \text{otherwise} \end{cases} \end{align*}
Idempotents are given by
![]() $xx^{ -1 }$
, where
$xx^{ -1 }$
, where
![]() $x \in A^*_n$
, and
$x \in A^*_n$
, and
![]() $x y^{-1} \mathcal{R} x x^{-1}$
. The monoid
$x y^{-1} \mathcal{R} x x^{-1}$
. The monoid
![]() $P_n$
is
$P_n$
is
![]() $0$
-
$0$
-
![]() $E$
-unitary,
$E$
-unitary,
![]() $0$
-bisimple, and combinatorial. For
$0$
-bisimple, and combinatorial. For
![]() $m \leq n$
, we have a natural embedding of
$m \leq n$
, we have a natural embedding of
![]() $P_m$
into
$P_m$
into
![]() $P_n$
, induced by the injection from
$P_n$
, induced by the injection from
![]() $A_m$
into
$A_m$
into
![]() $A_n$
. Polycyclic inverse monoids are used to construct
$A_n$
. Polycyclic inverse monoids are used to construct
![]() $C^*$
-algebras [Reference Cuntz8]. Nearly all the inverse semigroup studied in
$C^*$
-algebras [Reference Cuntz8]. Nearly all the inverse semigroup studied in
![]() $C^*$
-algebra theory are strongly
$C^*$
-algebra theory are strongly
![]() $0$
-
$0$
-
![]() $E$
-unitary [Reference Milan and Steinberg17, Section 5].
$E$
-unitary [Reference Milan and Steinberg17, Section 5].
Corollary 4.22.
Let
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
be an HNN extension where
$S^* = [ S;\; U_1, U_2;\; \phi ]$
be an HNN extension where
![]() $S = P_n$
,
$S = P_n$
,
![]() $U_1 = P_m$
, for
$U_1 = P_m$
, for
![]() $m \leq n$
, are the polycyclic inverse monoids and
$m \leq n$
, are the polycyclic inverse monoids and
![]() $\phi$
is induced by any injection from
$\phi$
is induced by any injection from
![]() $A_m$
into
$A_m$
into
![]() $A_b$
. Then,
$A_b$
. Then,
![]() $S^*$
is
$S^*$
is
![]() $0$
-
$0$
-
![]() $E$
-unitary with group of units isomorphic to a free group on a singleton and all other maximal subgroups are trivial.
$E$
-unitary with group of units isomorphic to a free group on a singleton and all other maximal subgroups are trivial.
Proof. Let
![]() $x x^{-1} \in E( S )$
. Since
$x x^{-1} \in E( S )$
. Since
![]() $S$
is
$S$
is
![]() $0$
-
$0$
-
![]() $E$
-unitary, if
$E$
-unitary, if
![]() $x x^{ -1 } \leq z y^{-1}$
, where
$x x^{ -1 } \leq z y^{-1}$
, where
![]() $z y^{-1} \in S$
, then
$z y^{-1} \in S$
, then
![]() $z y^{-1}$
is idempotent. If
$z y^{-1}$
is idempotent. If
![]() $x x^{ -1 } \leq y y^{ -1 }$
in
$x x^{ -1 } \leq y y^{ -1 }$
in
![]() $S$
then
$S$
then
![]() $x = y z$
, for some word
$x = y z$
, for some word
![]() $z$
. Thus, there are finitely many idempotents
$z$
. Thus, there are finitely many idempotents
![]() $y y^{ -1 }$
with
$y y^{ -1 }$
with
![]() $x x^{ -1 } \leq y y^{ -1 }$
. Hence, the set
$x x^{ -1 } \leq y y^{ -1 }$
. Hence, the set
![]() $\{ y y^{-1} \in U_i \;:\; y y^{-1} \geq x x^{-1} \}$
has a least element
$\{ y y^{-1} \in U_i \;:\; y y^{-1} \geq x x^{-1} \}$
has a least element
![]() $f_1 ( x x^{-1} )$
, possibly
$f_1 ( x x^{-1} )$
, possibly
![]() $1$
, for
$1$
, for
![]() $i = 1, 2$
. We have:
$i = 1, 2$
. We have:
 \begin{align*} x x^{-1} \cdot y y^{-1} = \begin{cases} x x^{-1} & \text{if } x = y z \text{, for some word } z\\[5pt] y y^{-1} & \text{if } y = x z \text{, for some word } z\\[5pt] 0 & \text{otherwise} \end{cases} \end{align*}
\begin{align*} x x^{-1} \cdot y y^{-1} = \begin{cases} x x^{-1} & \text{if } x = y z \text{, for some word } z\\[5pt] y y^{-1} & \text{if } y = x z \text{, for some word } z\\[5pt] 0 & \text{otherwise} \end{cases} \end{align*}
Let
![]() $y y^{-1} \in E( U_i )$
with
$y y^{-1} \in E( U_i )$
with
![]() $x x^{ -1 } \nleq y y^{ -1 }$
. Then either
$x x^{ -1 } \nleq y y^{ -1 }$
. Then either
![]() $x x^{-1} \cdot y y^{-1} = 0$
or we have
$x x^{-1} \cdot y y^{-1} = 0$
or we have
![]() $x x^{-1} \cdot y y^{ -1} = y y^{-1}$
. Assume
$x x^{-1} \cdot y y^{ -1} = y y^{-1}$
. Assume
![]() $x x^{-1} \geq y y^{-1}$
and so
$x x^{-1} \geq y y^{-1}$
and so
![]() $f_i ( x x^{-1} \cdot y y^{ -1} ) = y y^{-1}$
. If
$f_i ( x x^{-1} \cdot y y^{ -1} ) = y y^{-1}$
. If
![]() $y_1 y^{-1}_1 \in E( U_i )$
with
$y_1 y^{-1}_1 \in E( U_i )$
with
![]() $y y^{ -1} \geq y_1 y^{ -1 }_1$
then
$y y^{ -1} \geq y_1 y^{ -1 }_1$
then
![]() $f_i ( x x^{-1} \cdot y_1 y^{ -1}_1 )$
$f_i ( x x^{-1} \cdot y_1 y^{ -1}_1 )$
![]() $= f_i ( x x^{-1} \cdot y y^{ -1 } \cdot y_1 y^{ -1}_1 )$
$= f_i ( x x^{-1} \cdot y y^{ -1 } \cdot y_1 y^{ -1}_1 )$
![]() $= y y^{ -1 } \cdot y_1 y^{ -1}_1 = y_1 y^{-1}_1$
. It now follows that
$= y y^{ -1 } \cdot y_1 y^{ -1}_1 = y_1 y^{-1}_1$
. It now follows that
![]() $S^* = [ S;\; U_1, U_2;\; \phi ]$
is a lower bounded HNN extension.
$S^* = [ S;\; U_1, U_2;\; \phi ]$
is a lower bounded HNN extension.
Let
![]() $x y^{ -1 } \in S$
and
$x y^{ -1 } \in S$
and
![]() $u v^{ -1 } \in U_i$
such that
$u v^{ -1 } \in U_i$
such that
![]() $x y^{ -1 } \cdot u v^{ -1 }$
is idempotent, for
$x y^{ -1 } \cdot u v^{ -1 }$
is idempotent, for
![]() $i \in \{ 1, 2 \}$
. Suppose
$i \in \{ 1, 2 \}$
. Suppose
![]() $u = y z$
, for some word
$u = y z$
, for some word
![]() $z$
. Then,
$z$
. Then,
![]() $y \in U_i$
. Since
$y \in U_i$
. Since
![]() $x y^{ -1 } \cdot u v^{ -1 } = ( x z ) v^{ -1 }$
is idempotent, we have
$x y^{ -1 } \cdot u v^{ -1 } = ( x z ) v^{ -1 }$
is idempotent, we have
![]() $x z = v$
and so
$x z = v$
and so
![]() $x \in U_i$
. Thus
$x \in U_i$
. Thus
![]() $x y^{-1} \in U_i$
,
$x y^{-1} \in U_i$
,
![]() $x x^{ -1 } \cdot x y^{ -1} = x y^{ -1 }$
and so
$x x^{ -1 } \cdot x y^{ -1} = x y^{ -1 }$
and so
![]() $x x^{ -1 } \sim _i x y^{-1}$
. Suppose we have
$x x^{ -1 } \sim _i x y^{-1}$
. Suppose we have
![]() $y = u z$
, for some word
$y = u z$
, for some word
![]() $z$
. Then, since
$z$
. Then, since
![]() $x y^{ -1 } \cdot u v^{ -1 }$
$x y^{ -1 } \cdot u v^{ -1 }$
![]() $= x ( v z )^{ -1 }$
is idempotent, we have
$= x ( v z )^{ -1 }$
is idempotent, we have
![]() $x = v z$
. Thus we have
$x = v z$
. Thus we have
![]() $x x^{ -1 } \cdot v u^{-1}$
$x x^{ -1 } \cdot v u^{-1}$
![]() $= vz ( v z )^{ -1 } \cdot v u^{ -1 }$
$= vz ( v z )^{ -1 } \cdot v u^{ -1 }$
![]() $=vz ( u z )^{ -1 } = x y^{ -1 }$
and so
$=vz ( u z )^{ -1 } = x y^{ -1 }$
and so
![]() $x x^{ -1 } \sim _i x y^{-1}$
. It follows that
$x x^{ -1 } \sim _i x y^{-1}$
. It follows that
![]() $S^*$
is
$S^*$
is
![]() $0$
-
$0$
-
![]() $E$
-unitary, by Corollary 4.21.
$E$
-unitary, by Corollary 4.21.
Since
![]() $S$
is
$S$
is
![]() $0$
-bisimple, the component
$0$
-bisimple, the component
![]() $Y_1$
of the graph of groups
$Y_1$
of the graph of groups
![]() $Y$
, as defined in Notation 4.3, consists of one vertex and one edge, where
$Y$
, as defined in Notation 4.3, consists of one vertex and one edge, where
![]() $1$
is the identity of
$1$
is the identity of
![]() $S$
. Since
$S$
. Since
![]() $S$
is combinatorial, the fundamental group of the graph of groups
$S$
is combinatorial, the fundamental group of the graph of groups
![]() $( H_1 (\!-\!), Y_1 )$
is isomorphic to the free group on a singleton. The maximal subgroup of
$( H_1 (\!-\!), Y_1 )$
is isomorphic to the free group on a singleton. The maximal subgroup of
![]() $S^*$
containing
$S^*$
containing
![]() $1$
is isomorphic to the fundamental group of the graph of groups
$1$
is isomorphic to the fundamental group of the graph of groups
![]() $( H_1 (\!-\!), Y_1 )$
, by Theorem 4.4. All other maximal subgroups of
$( H_1 (\!-\!), Y_1 )$
, by Theorem 4.4. All other maximal subgroups of
![]() $S^*$
are trivial, by Theorem 4.6.
$S^*$
are trivial, by Theorem 4.6.
Acknowledgments
The second author wishes to thank J. C. Meakin for suggesting to study HNN extensions as part of her PhD., and for advice, support, and encouragement.
Funding statement
The second author was partially supported by grants APVV-19-0308 and VEGA 1/0437/23.
Competing interests
None.