No CrossRef data available.
Article contents
A Helfrich functional for compact surfaces in 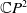 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$
Published online by Cambridge University Press: 04 October 2023
Abstract
Let 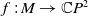 $f\;:\; M\rightarrow \mathbb{C}P^{2}$ be an isometric immersion of a compact surface in the complex projective plane
$f\;:\; M\rightarrow \mathbb{C}P^{2}$ be an isometric immersion of a compact surface in the complex projective plane 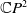 $\mathbb{C}P^{2}$. In this paper, we consider the Helfrich-type functional
$\mathbb{C}P^{2}$. In this paper, we consider the Helfrich-type functional 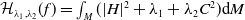 $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)=\int _{M}(|H|^{2}+\lambda _{1}+\lambda _{2} C^{2})\textrm{d} M$, where
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)=\int _{M}(|H|^{2}+\lambda _{1}+\lambda _{2} C^{2})\textrm{d} M$, where 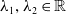 $\lambda _{1}, \lambda _{2}\in \mathbb{R}$ with
$\lambda _{1}, \lambda _{2}\in \mathbb{R}$ with 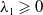 $\lambda _{1}\geqslant 0$,
$\lambda _{1}\geqslant 0$, 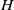 $H$ and
$H$ and 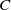 $C$ are respectively the mean curvature vector and the Kähler function of
$C$ are respectively the mean curvature vector and the Kähler function of 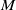 $M$ in
$M$ in 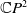 $\mathbb{C}P^{2}$. The critical surfaces of
$\mathbb{C}P^{2}$. The critical surfaces of 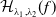 $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$ are called Helfrich surfaces. We compute the first variation of
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$ are called Helfrich surfaces. We compute the first variation of 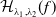 $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$ and classify the homogeneous Helfrich tori in
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$ and classify the homogeneous Helfrich tori in 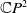 $\mathbb{C}P^{2}$. Moreover, we study the Helfrich energy of the homogeneous tori and show the lower bound of the Helfrich energy for such tori.
$\mathbb{C}P^{2}$. Moreover, we study the Helfrich energy of the homogeneous tori and show the lower bound of the Helfrich energy for such tori.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust


