Article contents
ON THE STRUCTURE OF GRAPHS WHICH ARE LOCALLY INDISTINGUISHABLE FROM A LATTICE
Published online by Cambridge University Press: 05 December 2016
Abstract
For each integer 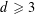 $d\geqslant 3$ , we obtain a characterization of all graphs in which the ball of radius
$d\geqslant 3$ , we obtain a characterization of all graphs in which the ball of radius 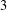 $3$ around each vertex is isomorphic to the ball of radius 3 in
$3$ around each vertex is isomorphic to the ball of radius 3 in 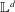 $\mathbb{L}^{d}$ , the graph of the
$\mathbb{L}^{d}$ , the graph of the 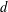 $d$ -dimensional integer lattice. The finite, connected graphs with this property have a highly rigid, ‘global’ algebraic structure; they can be viewed as quotient lattices of
$d$ -dimensional integer lattice. The finite, connected graphs with this property have a highly rigid, ‘global’ algebraic structure; they can be viewed as quotient lattices of 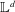 $\mathbb{L}^{d}$ in various compact
$\mathbb{L}^{d}$ in various compact 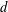 $d$ -dimensional orbifolds which arise from crystallographic groups. We give examples showing that ‘radius 3’ cannot be replaced by ‘radius 2’, and that ‘orbifold’ cannot be replaced by ‘manifold’. In the
$d$ -dimensional orbifolds which arise from crystallographic groups. We give examples showing that ‘radius 3’ cannot be replaced by ‘radius 2’, and that ‘orbifold’ cannot be replaced by ‘manifold’. In the 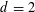 $d=2$ case, our methods yield new proofs of structure theorems of Thomassen [‘Tilings of the Torus and Klein bottle and vertex-transitive graphs on a fixed surface’, Trans. Amer. Math. Soc.323 (1991), 605–635] and of Márquez et al. [‘Locally grid graphs: classification and Tutte uniqueness’, Discrete Math.266 (2003), 327–352], and also yield short, ‘algebraic’ restatements of these theorems. Our proofs use a mixture of techniques and results from combinatorics, geometry and group theory.
$d=2$ case, our methods yield new proofs of structure theorems of Thomassen [‘Tilings of the Torus and Klein bottle and vertex-transitive graphs on a fixed surface’, Trans. Amer. Math. Soc.323 (1991), 605–635] and of Márquez et al. [‘Locally grid graphs: classification and Tutte uniqueness’, Discrete Math.266 (2003), 327–352], and also yield short, ‘algebraic’ restatements of these theorems. Our proofs use a mixture of techniques and results from combinatorics, geometry and group theory.
MSC classification
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2016
References
- 3
- Cited by


