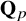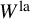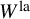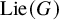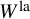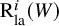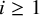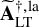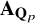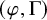1 Introduction
In p-adic Hodge theory and in the p-adic Langlands program, one often encounters a Banach space W with
![]() $\mathbf {Q}_p$
-coefficients endowed with an action of a p-adic Lie group G. It has proven useful to study the subrepresentation of G-locally analytic vectors
$\mathbf {Q}_p$
-coefficients endowed with an action of a p-adic Lie group G. It has proven useful to study the subrepresentation of G-locally analytic vectors
![]() $W^{\mathrm {la}} \subset W.$
One reason for this is that
$W^{\mathrm {la}} \subset W.$
One reason for this is that
![]() $W^{\mathrm {la}}$
has an action of the Lie algebra
$W^{\mathrm {la}}$
has an action of the Lie algebra
![]() $\mathrm {Lie}(G),$
which is often simpler to study than the action of G. Another reason for this usefulness is that
$\mathrm {Lie}(G),$
which is often simpler to study than the action of G. Another reason for this usefulness is that
![]() $W^{\mathrm {la}}$
sometimes behaves as a decompletion of W which is then closer to being of an algebraic or geometric nature.
$W^{\mathrm {la}}$
sometimes behaves as a decompletion of W which is then closer to being of an algebraic or geometric nature.
As a classical example we consider Sen theory. Let
![]() $\mathbf {Q}_p^{\mathrm {cyc}}$
denote the cyclotomic extension obtained by adding all p-power roots of unity to
$\mathbf {Q}_p^{\mathrm {cyc}}$
denote the cyclotomic extension obtained by adding all p-power roots of unity to
![]() $\mathbf {Q}_p$
, K be a finite extension of
$\mathbf {Q}_p$
, K be a finite extension of
![]() $\mathbf {Q}_p$
,
$\mathbf {Q}_p$
,
![]() $K^{\mathrm {cyc}} = K\mathbf {Q}_p^{\mathrm {cyc}}$
,
$K^{\mathrm {cyc}} = K\mathbf {Q}_p^{\mathrm {cyc}}$
,
![]() $H_K = \mathrm {Gal}(\overline {K}/K^{\mathrm {cyc}})$
and
$H_K = \mathrm {Gal}(\overline {K}/K^{\mathrm {cyc}})$
and
![]() $G = \mathrm {Gal}(K^{\mathrm {cyc}}/K)$
which is isomorphic to an open subgroup of
$G = \mathrm {Gal}(K^{\mathrm {cyc}}/K)$
which is isomorphic to an open subgroup of
![]() $\mathbf {Z}_p^\times $
. We also let
$\mathbf {Z}_p^\times $
. We also let
![]() $\mathbf {C}_p$
be the completion of
$\mathbf {C}_p$
be the completion of
![]() $\overline {\mathbf {Q}}_p$
. If X is a smooth proper variety over K, let
$\overline {\mathbf {Q}}_p$
. If X is a smooth proper variety over K, let
![]() $V = \mathrm {H}^{n}_{\text {\'et}}(X_{\overline {K}},\mathbf {Q}_p)$
. Then V is a representation of
$V = \mathrm {H}^{n}_{\text {\'et}}(X_{\overline {K}},\mathbf {Q}_p)$
. Then V is a representation of
![]() $\mathrm {Gal}(\overline {K}/K)$
, and we set
$\mathrm {Gal}(\overline {K}/K)$
, and we set
It can then be shown (see, e.g., Théorème 3.4 of [Reference Berger and ColmezBC16]) that
![]() $W^{\mathrm {la}}$
is a vector space over
$W^{\mathrm {la}}$
is a vector space over
![]() $K^{\mathrm {cyc}}$
to which W descends. Furthermore, the action of
$K^{\mathrm {cyc}}$
to which W descends. Furthermore, the action of
![]() $\mathrm {Lie}(G) \cong \mathbf {Z}_p$
gives a linear operator, called the Sen operator, which acts on
$\mathrm {Lie}(G) \cong \mathbf {Z}_p$
gives a linear operator, called the Sen operator, which acts on
![]() $W^{\mathrm {la}}$
. Its eigenvalues belong to
$W^{\mathrm {la}}$
. Its eigenvalues belong to
![]() $\mathbf {Z}$
and as a set are equal to the negatives of the Hodge numbers
$\mathbf {Z}$
and as a set are equal to the negatives of the Hodge numbers
![]() $\{h^{i,j}\}_{i+j=n}$
of X.
$\{h^{i,j}\}_{i+j=n}$
of X.
One issue with the classical definition of G-locally analytic vectors is that it is available only in the setting of
![]() $\mathbf {Q}_p$
-coefficients, while one would want to consider spaces W with
$\mathbf {Q}_p$
-coefficients, while one would want to consider spaces W with
![]() $\mathbf {Z}_p$
and
$\mathbf {Z}_p$
and
![]() $\mathbf {F}_p$
-coefficients as well. Nevertheless, it is clear that some phenomenon of this kind exists. For example, a Sen operator in a mixed characteristic was recently introduced in work of Bhatt-Lurie ([Reference Bhatt and LurieBL22]). It is unclear how to interpret it in terms of locally analytic vectors. In another direction, Berger and Rozensztajn introduce in ([Reference Berger and RozensztajnBR22], [Reference Berger and RozensztajnBR24]) the notion of super-Hölder vectors, which serve as an analogue of locally analytic vectors in characteristic p.
$\mathbf {F}_p$
-coefficients as well. Nevertheless, it is clear that some phenomenon of this kind exists. For example, a Sen operator in a mixed characteristic was recently introduced in work of Bhatt-Lurie ([Reference Bhatt and LurieBL22]). It is unclear how to interpret it in terms of locally analytic vectors. In another direction, Berger and Rozensztajn introduce in ([Reference Berger and RozensztajnBR22], [Reference Berger and RozensztajnBR24]) the notion of super-Hölder vectors, which serve as an analogue of locally analytic vectors in characteristic p.
In this article, we focus on the notion of locally analytic vectors for W with coefficients in a mixed characteristic setting, namely for
![]() $\mathbf {Z}_p$
-Tate algebras. This notion generalizes the classical notion and specializes to the super-Hölder vectors notion of Berger and Rozensztajn in the characteristic p setting. The basic idea is to use binomial expansions rather than Taylor series expansions to define analytic functions. This idea is well known to the experts, introduced, for example, in [Reference GulottaGul19], [Reference Johansson and NewtonJN19], and [Reference Berger and RozensztajnBR22]. One then defines a locally analytic vector to be an element w of W whose associated orbit map
$\mathbf {Z}_p$
-Tate algebras. This notion generalizes the classical notion and specializes to the super-Hölder vectors notion of Berger and Rozensztajn in the characteristic p setting. The basic idea is to use binomial expansions rather than Taylor series expansions to define analytic functions. This idea is well known to the experts, introduced, for example, in [Reference GulottaGul19], [Reference Johansson and NewtonJN19], and [Reference Berger and RozensztajnBR22]. One then defines a locally analytic vector to be an element w of W whose associated orbit map
![]() $\mathrm {orb}_{w}:G\rightarrow W$
is locally analytic.
$\mathrm {orb}_{w}:G\rightarrow W$
is locally analytic.
Why use binomial expansions instead of Taylor series expansions? First, we lose nothing by doing this: in characteristic 0, it is known by the Amice theorem [Reference AmiceAmi64] that locally analytic functions are the same as those with exponentially decreasing binomial expansions. Second, new analytic functions can be produced in mixed characteristic and characteristic p. This can be motivated by the example
![]() $R = \mathbf {F}_p((X))$
with the action of
$R = \mathbf {F}_p((X))$
with the action of
![]() $\mathbf {Z}_p$
given by
$\mathbf {Z}_p$
given by
![]() $a(X)=(1+X)^a$
(as considered in [Reference Berger and RozensztajnBR22]). We would like to consider such a function as analytic. Writing
$a(X)=(1+X)^a$
(as considered in [Reference Berger and RozensztajnBR22]). We would like to consider such a function as analytic. Writing
![]() $a\mapsto a(X) = \sum _{n \geq 0}\binom {a}{n}X^n$
, we see it has a binomial expansion in a with the coefficients
$a\mapsto a(X) = \sum _{n \geq 0}\binom {a}{n}X^n$
, we see it has a binomial expansion in a with the coefficients
![]() $X^n$
tending to
$X^n$
tending to
![]() $0$
exponentially in the topology of
$0$
exponentially in the topology of
![]() $\mathbf {F}_p((X)).$
On the other hand, it does not have a Taylor series expansion: indeed, in characteristic p, it is easy to see that Taylor series expansions only give rise to locally constant functions on
$\mathbf {F}_p((X)).$
On the other hand, it does not have a Taylor series expansion: indeed, in characteristic p, it is easy to see that Taylor series expansions only give rise to locally constant functions on
![]() $\mathbf {Z}_p^d,$
since they must factor through
$\mathbf {Z}_p^d,$
since they must factor through
![]() $\mathbf {F}_p^d.$
$\mathbf {F}_p^d.$
One nice feature of this new definition is that it allows to link locally analytic vectors in characteristic
![]() $0$
and characteristic p. A template for this situation is as follows: we are given a module A with coefficients in a
$0$
and characteristic p. A template for this situation is as follows: we are given a module A with coefficients in a
![]() $\mathbf {Z}_p$
-Tate algebra so that
$\mathbf {Z}_p$
-Tate algebra so that
![]() $\overline {A} = A/p$
is also a
$\overline {A} = A/p$
is also a
![]() $\mathbf {Z}_p$
-Tate algebra, together with an injection of
$\mathbf {Z}_p$
-Tate algebra, together with an injection of
![]() $A[1/p]$
into a
$A[1/p]$
into a
![]() $\mathbf {Q}_p$
-algebra B. If A and B are endowed with G-actions, we have maps
$\mathbf {Q}_p$
-algebra B. If A and B are endowed with G-actions, we have maps
![]() $A^{\mathrm {la}} \rightarrow B^{\mathrm {la}}$
and
$A^{\mathrm {la}} \rightarrow B^{\mathrm {la}}$
and
![]() $A^{\mathrm {la}} \rightarrow \overline {A}^{\mathrm {la}}$
. Now
$A^{\mathrm {la}} \rightarrow \overline {A}^{\mathrm {la}}$
. Now
![]() $B^{\mathrm {la}}$
is a
$B^{\mathrm {la}}$
is a
![]() $\mathbf {Q}_p$
-vector space and thus can be studied via p-adic analysis and the action of
$\mathbf {Q}_p$
-vector space and thus can be studied via p-adic analysis and the action of
![]() $\mathrm {Lie}(G).$
If the map
$\mathrm {Lie}(G).$
If the map
![]() $A^{\mathrm {la}} \rightarrow \overline {A}^{\mathrm {la}}$
is sufficiently well behaved (e.g., if it is surjective), one can use the inclusion of
$A^{\mathrm {la}} \rightarrow \overline {A}^{\mathrm {la}}$
is sufficiently well behaved (e.g., if it is surjective), one can use the inclusion of
![]() $A^{\mathrm {la}}\subset B^{\mathrm {la}}$
to study
$A^{\mathrm {la}}\subset B^{\mathrm {la}}$
to study
![]() $\overline {A}^{\mathrm {la}}$
and thus study the analytic vectors in a characteristic p object using p-adic analysis in characteristic
$\overline {A}^{\mathrm {la}}$
and thus study the analytic vectors in a characteristic p object using p-adic analysis in characteristic
![]() $0$
! A template example for this would be to take
$0$
! A template example for this would be to take
![]() $A=\mathbf {Z}_p[[X^{1/p^\infty }]]\langle p/X\rangle [1/X],$
the ring of functions of a preperfectoid pseudorigid disc,
$A=\mathbf {Z}_p[[X^{1/p^\infty }]]\langle p/X\rangle [1/X],$
the ring of functions of a preperfectoid pseudorigid disc,
![]() $\overline {A} = \mathbf {F}_p((X^{1/p^\infty }))$
and
$\overline {A} = \mathbf {F}_p((X^{1/p^\infty }))$
and
![]() $B=\mathbf {Z}_p[[X^{1/p^\infty }]]\langle p/X,X/p\rangle [1/X]=\mathbf {Z}_p[[X^{1/p^\infty }]]\langle p/X,X/p\rangle [1/p]$
the ring of functions on a preperfectoid annulus, with the action of
$B=\mathbf {Z}_p[[X^{1/p^\infty }]]\langle p/X,X/p\rangle [1/X]=\mathbf {Z}_p[[X^{1/p^\infty }]]\langle p/X,X/p\rangle [1/p]$
the ring of functions on a preperfectoid annulus, with the action of
![]() $\mathbf {Z}_p$
given by
$\mathbf {Z}_p$
given by
![]() $a(X)=(1+X)^a.$
The key point is that topology on B is both X-adic and p-adic, so it can be linked to A on the one hand, and studied via p-adic analysis of
$a(X)=(1+X)^a.$
The key point is that topology on B is both X-adic and p-adic, so it can be linked to A on the one hand, and studied via p-adic analysis of
![]() $B^{\mathrm {la}}$
on the other. A very similar example will be studied in our first application in §
$B^{\mathrm {la}}$
on the other. A very similar example will be studied in our first application in §
![]() $4.$
$4.$
The main goal of this paper is to analyze the extent to which
![]() $W\mapsto W^{\mathrm {la}}$
acts as a decompletion. We suppose W is a finite free module over a
$W\mapsto W^{\mathrm {la}}$
acts as a decompletion. We suppose W is a finite free module over a
![]() $\mathbf {Z}_p$
-Tate algebra R endowed with a semilinear action of a compact p-adic Lie group G. The main result of this article is the following.
$\mathbf {Z}_p$
-Tate algebra R endowed with a semilinear action of a compact p-adic Lie group G. The main result of this article is the following.
Theorem 1.1. Suppose that the ring R satisfies the Tate-Sen axioms (TS1)-(TS4) (see §
![]() $3.2$
).
$3.2$
).
Then:
-
1. The natural map
is an isomorphism. $$ \begin{align*}R \otimes_{R^{\mathrm{la}}} W^{\mathrm{la}} \rightarrow W\end{align*} $$
$$ \begin{align*}R \otimes_{R^{\mathrm{la}}} W^{\mathrm{la}} \rightarrow W\end{align*} $$
-
2. If moreover the Lie algebra
 $\mathrm {Lie}(G)$
is abelian, the derived locally analytic vectors
$\mathrm {Lie}(G)$
is abelian, the derived locally analytic vectors
 $\mathrm {R}_{\mathrm {la}}^i(W)$
of W are
$\mathrm {R}_{\mathrm {la}}^i(W)$
of W are
 $0$
for
$0$
for
 $i \geq 1$
.
$i \geq 1$
.
This theorem is a generalization of Theorem C of [Reference PoratPor24]. The basic idea of the proof is in essence to take a “fiber product” of the original method of [Reference PoratPor24] and the mixed characteristic results of [Reference PoratPor22b]. As Theorem C of [Reference PoratPor24] has been applied in several subsequent articles, we hope the current result will be useful in a similar way.
Note that the vanishing of
![]() $\mathrm {R}_{\mathrm {la}}^1(W)$
is precisely the type of behavior that will allow us to propagate information regarding locally analytic vectors along reductions. Indeed, if W lives over some mixed characteristic
$\mathrm {R}_{\mathrm {la}}^1(W)$
is precisely the type of behavior that will allow us to propagate information regarding locally analytic vectors along reductions. Indeed, if W lives over some mixed characteristic
![]() $\mathbf {Z}_p$
-Tate algebra such as
$\mathbf {Z}_p$
-Tate algebra such as
![]() $\mathbf {Z}_p[[X]]\langle p/X\rangle [1/X]$
, we also have the
$\mathbf {Z}_p[[X]]\langle p/X\rangle [1/X]$
, we also have the
![]() $\mathbf {F}_p$
-Banach space
$\mathbf {F}_p$
-Banach space
![]() $\overline {W}$
and an exact sequence
$\overline {W}$
and an exact sequence
After passing to locally analytic vectors, the vanishing of
![]() $\mathrm {R}_{\mathrm {la}}^1(W)$
implies that
$\mathrm {R}_{\mathrm {la}}^1(W)$
implies that
![]() $W^{\mathrm {la}}\rightarrow \overline {W}^{\mathrm {la}}$
is surjective.
$W^{\mathrm {la}}\rightarrow \overline {W}^{\mathrm {la}}$
is surjective.
We give three applications of our results. Our first result is a new proof of the main result of [Reference Berger and RozensztajnBR22]. There, Berger and Rozensztajn show that for the action of
![]() $G = \mathbf {Z}_p^\times $
on the X-adic completion of
$G = \mathbf {Z}_p^\times $
on the X-adic completion of
![]() $\cup _{n} \mathbf {F}_p((X^{1/p^n}))$
, taking G-locally analytic vectors undoes the X-adic completion. We show how to deduce this using characteristic 0 methods, as sketched above. Our second application is the introduction of an integral multivariable ring
$\cup _{n} \mathbf {F}_p((X^{1/p^n}))$
, taking G-locally analytic vectors undoes the X-adic completion. We show how to deduce this using characteristic 0 methods, as sketched above. Our second application is the introduction of an integral multivariable ring
![]() $\widetilde {\mathbf {A}}_{\mathrm {LT}}^{\dagger ,\mathrm {la}}$
in the Lubin-Tate setting, together with an appropriate overconvergence result for
$\widetilde {\mathbf {A}}_{\mathrm {LT}}^{\dagger ,\mathrm {la}}$
in the Lubin-Tate setting, together with an appropriate overconvergence result for
![]() $(\varphi ,\Gamma )$
-modules. Previously, such a ring was only available rationally with pro-analytic vectors (as in [Reference BergerBer16]). Our third and final result is a surprising description of the classical Cohen ring
$(\varphi ,\Gamma )$
-modules. Previously, such a ring was only available rationally with pro-analytic vectors (as in [Reference BergerBer16]). Our third and final result is a surprising description of the classical Cohen ring
![]() $\mathbf {{A}}_{\mathbf {Q}_p}$
appearing in the theory of
$\mathbf {{A}}_{\mathbf {Q}_p}$
appearing in the theory of
![]() $(\varphi ,\Gamma )$
-modules in terms of locally analytic vectors. We show how to endow the ring
$(\varphi ,\Gamma )$
-modules in terms of locally analytic vectors. We show how to endow the ring
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}$
of Witt vectors of
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}$
of Witt vectors of
![]() $\widehat {\mathbf {{\mathbf {Q}}}}_p^{\mathrm {cyc}}$
with the structure of a mixed-characteristic Fréchet space, and its ring of locally analytic vectors is
$\widehat {\mathbf {{\mathbf {Q}}}}_p^{\mathrm {cyc}}$
with the structure of a mixed-characteristic Fréchet space, and its ring of locally analytic vectors is
![]() $\varphi ^{-\infty }(\mathbf {{A}}_{\mathbf {Q}_p}).$
This reveals an analogy between
$\varphi ^{-\infty }(\mathbf {{A}}_{\mathbf {Q}_p}).$
This reveals an analogy between
![]() $\varphi ^{-\infty }(\mathbf {{A}}_{\mathbf {Q}_p})$
and the ring
$\varphi ^{-\infty }(\mathbf {{A}}_{\mathbf {Q}_p})$
and the ring
![]() $\cup _n \mathbf {Q}_p(\zeta _{p^n})[[t]]$
of locally analytic elements in
$\cup _n \mathbf {Q}_p(\zeta _{p^n})[[t]]$
of locally analytic elements in
![]() $\textbf {B}_{\mathrm {dR}}^+$
, and suggests a way to give a lift of the field of norms beyond the Lubin-Tate setting, a question studied by several authors and motivated by Iwasawa theory (see, for instance, [Reference BergerBer14], [Reference PoyetonPoy22]).
$\textbf {B}_{\mathrm {dR}}^+$
, and suggests a way to give a lift of the field of norms beyond the Lubin-Tate setting, a question studied by several authors and motivated by Iwasawa theory (see, for instance, [Reference BergerBer14], [Reference PoyetonPoy22]).
1.1 Structure of the article
In §
![]() $2$
we give the definitions and basic results regarding locally analytic vectors and functions in mixed characteristic. In §
$2$
we give the definitions and basic results regarding locally analytic vectors and functions in mixed characteristic. In §
![]() $3$
we prove the main result of the article. The reader may desire to skip this section if they are only interested in using the main result. Finally, in §
$3$
we prove the main result of the article. The reader may desire to skip this section if they are only interested in using the main result. Finally, in §
![]() $4$
we give three applications of our methods.
$4$
we give three applications of our methods.
1.2 Notations and conventions
1.2.1 Valuations
By a valuation on a ring R, we mean a map
![]() $\mathrm {val}_R:R \rightarrow (-\infty , \infty ] $
satisfying the following properties for
$\mathrm {val}_R:R \rightarrow (-\infty , \infty ] $
satisfying the following properties for
![]() $x, y \in R$
:
$x, y \in R$
:
-
(1)
 $\mathrm {val}_R(x) = \infty $
if and only if
$\mathrm {val}_R(x) = \infty $
if and only if
 $x = 0$
(i.e., R is separated);
$x = 0$
(i.e., R is separated); -
(2)
 $\mathrm {val}_R(xy) \geq \mathrm {val}_R(x) + \mathrm {val}_R(y)$
;
$\mathrm {val}_R(xy) \geq \mathrm {val}_R(x) + \mathrm {val}_R(y)$
; -
(3)
 $\mathrm {val}_R(x+y) \geq \min (\mathrm {val}_R(x), \mathrm {val}_R(y))$
.
$\mathrm {val}_R(x+y) \geq \min (\mathrm {val}_R(x), \mathrm {val}_R(y))$
.
This definition naturally extends to valuations on an R-module M. We set
![]() $M^+ := M^{\mathrm {val}_M \geq 0}.$
If
$M^+ := M^{\mathrm {val}_M \geq 0}.$
If
![]() $f:X\rightarrow M$
is a function, we set
$f:X\rightarrow M$
is a function, we set
![]() $\mathrm {val}_M^{\mathrm {op}}(f):=\inf _{x\in X}\mathrm {val}_M(f(x))$
for the operator valuation.
$\mathrm {val}_M^{\mathrm {op}}(f):=\inf _{x\in X}\mathrm {val}_M(f(x))$
for the operator valuation.
1.2.2
 $\mathbf {Z}_p$
-Tate algebras
$\mathbf {Z}_p$
-Tate algebras
A
![]() $\mathbf {Z}_p$
-Tate algebra is a Tate ring (see Definition 2.2.5 of [Reference Scholze and WeinsteinSW20]) which is a
$\mathbf {Z}_p$
-Tate algebra is a Tate ring (see Definition 2.2.5 of [Reference Scholze and WeinsteinSW20]) which is a
![]() $\mathbf {Z}_p$
-algebra, such that the map
$\mathbf {Z}_p$
-algebra, such that the map
![]() $\mathbf {Z}_p\rightarrow R$
is continuous. We can always endow such a ring with a valuation
$\mathbf {Z}_p\rightarrow R$
is continuous. We can always endow such a ring with a valuation
![]() $\mathrm {val}_R$
by taking some topologically nilpotent unit
$\mathrm {val}_R$
by taking some topologically nilpotent unit
![]() $\varpi \in R$
and letting
$\varpi \in R$
and letting
![]() $\mathrm {val}_R(x)=\inf _n\{\varpi ^nx\in R^+\}$
for some open subring
$\mathrm {val}_R(x)=\inf _n\{\varpi ^nx\in R^+\}$
for some open subring
![]() $R^+\subset R$
. However, it sometimes happens that there is a more natural valuation inducing the same topology which does not arise in this fashion, such as the X-adic valuation on
$R^+\subset R$
. However, it sometimes happens that there is a more natural valuation inducing the same topology which does not arise in this fashion, such as the X-adic valuation on
![]() $\mathbf {F}_p((X^{1/p^\infty }))$
. In any case, whenever R is a
$\mathbf {F}_p((X^{1/p^\infty }))$
. In any case, whenever R is a
![]() $\mathbf {Z}_p$
-Tate algebra endowed with a valuation
$\mathbf {Z}_p$
-Tate algebra endowed with a valuation
![]() $\mathrm {val}_R$
, we shall always assume:
$\mathrm {val}_R$
, we shall always assume:
-
(1) There is a topologically nilpotent unit
 $\varpi \in R$
such that for any R-module endowed with a valuation we have
$\varpi \in R$
such that for any R-module endowed with a valuation we have
 $\mathrm {val}_M(\varpi x)=\mathrm {val}_R(\varpi )+\mathrm {val}_M(x)$
for
$\mathrm {val}_M(\varpi x)=\mathrm {val}_R(\varpi )+\mathrm {val}_M(x)$
for
 $x\in M$
. In particular, we always have
$x\in M$
. In particular, we always have
 $\mathrm {val}_R(1) = 0$
, and
$\mathrm {val}_R(1) = 0$
, and -
(2) We have the inequalityFootnote 1
 $\mathrm {val}_R(p)> 0$
.
$\mathrm {val}_R(p)> 0$
.
1.2.3 Miscellaneous
Given
![]() $\underline {n} \in \mathbf {Z}^d$
we write
$\underline {n} \in \mathbf {Z}^d$
we write
![]() $|\underline {n}|_\infty =\max _{1 \leq i \leq d} |n_i|$
and
$|\underline {n}|_\infty =\max _{1 \leq i \leq d} |n_i|$
and
![]() $|\underline {n}|=\sum _{1\leq i \leq d}|n_i|$
. For a real number a we denote by
$|\underline {n}|=\sum _{1\leq i \leq d}|n_i|$
. For a real number a we denote by
![]() $\lfloor a \rfloor $
the largest integer which is smaller than or equal to a. Finally, for
$\lfloor a \rfloor $
the largest integer which is smaller than or equal to a. Finally, for
![]() ${\underline {x}} \in \mathbf {R}^d$
we let
${\underline {x}} \in \mathbf {R}^d$
we let
![]() $\lfloor \underline {x} \rfloor =\sum _{i=1}^d \lfloor x_i \rfloor .$
$\lfloor \underline {x} \rfloor =\sum _{i=1}^d \lfloor x_i \rfloor .$
2 Locally analytic functions and vectors in mixed characteristic
In this section we introduce the spaces of functions and analytic vectors that will appear in this article.
2.1 Locally analytic functions on
 $\mathbf {Z}_p^d$
$\mathbf {Z}_p^d$
Let R be a
![]() $\mathbf {Z}_p$
-Tate algebra with valuation
$\mathbf {Z}_p$
-Tate algebra with valuation
![]() $\mathrm {val}_R$
inducing its topology (recall our conventions regarding valuations in §
$\mathrm {val}_R$
inducing its topology (recall our conventions regarding valuations in §
![]() $1.2$
). Let M be an R-module endowed with a compatible valuation
$1.2$
). Let M be an R-module endowed with a compatible valuation
![]() $\mathrm {val}_M$
.
$\mathrm {val}_M$
.
In particular, when
![]() $M = R$
, we have the function from
$M = R$
, we have the function from
![]() $\mathbf {Z}_p^d$
to R given by
$\mathbf {Z}_p^d$
to R given by
 $$ \begin{align*}\underline{x}=(x_1,...,x_d) \mapsto \binom{\underline{x}}{\underline{n}} := \binom{x_1}{n_1}\cdot ... \cdot \binom{x_d}{n_d}.\end{align*} $$
$$ \begin{align*}\underline{x}=(x_1,...,x_d) \mapsto \binom{\underline{x}}{\underline{n}} := \binom{x_1}{n_1}\cdot ... \cdot \binom{x_d}{n_d}.\end{align*} $$
Given a function
![]() $f:\mathbf {Z}_p^d \rightarrow M$
and an element
$f:\mathbf {Z}_p^d \rightarrow M$
and an element
![]() $\underline {y} \in \mathbf {Z}_p^d$
, we write
$\underline {y} \in \mathbf {Z}_p^d$
, we write
![]() $\Delta _{\underline {y}}(f):\mathbf {Z}_p^d \rightarrow M$
for the function given by
$\Delta _{\underline {y}}(f):\mathbf {Z}_p^d \rightarrow M$
for the function given by
![]() $\Delta _{\underline {y}}(f)(\underline {x}) = f(\underline {x}+\underline {y})-f(\underline {x})$
. The operators
$\Delta _{\underline {y}}(f)(\underline {x}) = f(\underline {x}+\underline {y})-f(\underline {x})$
. The operators
![]() $\Delta _{\underline {y}}$
and
$\Delta _{\underline {y}}$
and
![]() $\Delta _{\underline {z}}$
are commuting for
$\Delta _{\underline {z}}$
are commuting for
![]() $\underline {y},\underline {z}\in \mathbf {Z}_p^d$
. We set
$\underline {y},\underline {z}\in \mathbf {Z}_p^d$
. We set
![]() $\Delta ^n_{\underline {y}}(f)$
for the n-th application of
$\Delta ^n_{\underline {y}}(f)$
for the n-th application of
![]() $\Delta _{\underline {y}}$
to f. Given a d-dimensional vector
$\Delta _{\underline {y}}$
to f. Given a d-dimensional vector
![]() $\underline {n}$
, we write
$\underline {n}$
, we write
![]() $\Delta ^{\underline {n}}=\Delta _{1}^{n_1}\circ ...\circ \Delta _{d}^{n_d}$
, where
$\Delta ^{\underline {n}}=\Delta _{1}^{n_1}\circ ...\circ \Delta _{d}^{n_d}$
, where
![]() $\Delta _{k} = \Delta _{1_k}$
for
$\Delta _{k} = \Delta _{1_k}$
for
![]() $1_k \in \mathbf {Z}_p^d$
being 1 on the k-th copy of
$1_k \in \mathbf {Z}_p^d$
being 1 on the k-th copy of
![]() $\mathbf {Z}_p$
and
$\mathbf {Z}_p$
and
![]() $0$
elsewhere. Setting
$0$
elsewhere. Setting
![]() $(-1)^{\underline {m}} = (-1)^{m_1+...+m_d}$
, it can be checked that
$(-1)^{\underline {m}} = (-1)^{m_1+...+m_d}$
, it can be checked that
 $$ \begin{align*}\Delta^{\underline{n}}(f)(\underline{x}) = \sum_{\underline{i}=\underline{0}}^{\underline{n}} (-1)^{\underline{n}+\underline{i}} \binom{\underline{n}}{\underline{i}} f(\underline{i}+\underline{x})\end{align*} $$
$$ \begin{align*}\Delta^{\underline{n}}(f)(\underline{x}) = \sum_{\underline{i}=\underline{0}}^{\underline{n}} (-1)^{\underline{n}+\underline{i}} \binom{\underline{n}}{\underline{i}} f(\underline{i}+\underline{x})\end{align*} $$
and that for
![]() $\underline {m} \leq \underline {n}$
one has
$\underline {m} \leq \underline {n}$
one has
![]() $\Delta ^{\underline {m}}(\binom {\underline {x}}{\underline {n}}) = \binom {\underline {x}}{\underline {n}-\underline {m}}.$
$\Delta ^{\underline {m}}(\binom {\underline {x}}{\underline {n}}) = \binom {\underline {x}}{\underline {n}-\underline {m}}.$
For this section it will also be important to introduce for
![]() $\underline {z} \in \mathbf {Z}_p^d$
the shift operator
$\underline {z} \in \mathbf {Z}_p^d$
the shift operator
![]() $\mathrm {sh}_{\underline {z}}$
given by
$\mathrm {sh}_{\underline {z}}$
given by
![]() $\mathrm {sh}_{\underline {z}}(f)(\underline {x}) = f(\underline {z}+\underline {x})$
. It commutes with the
$\mathrm {sh}_{\underline {z}}(f)(\underline {x}) = f(\underline {z}+\underline {x})$
. It commutes with the
![]() $\Delta _{\underline {y}}$
, and we have the identity
$\Delta _{\underline {y}}$
, and we have the identity
Recall §
![]() $1.2$
for the notation
$1.2$
for the notation
![]() $\mathrm {val}_M^{\mathrm {op}}.$
$\mathrm {val}_M^{\mathrm {op}}.$
Lemma 2.1. Let
![]() $\underline {y} \in \mathbf {Z}_p^d$
. Then for every
$\underline {y} \in \mathbf {Z}_p^d$
. Then for every
![]() $f:\mathbf {Z}_p^d \rightarrow M$
we have
$f:\mathbf {Z}_p^d \rightarrow M$
we have
Proof. Using continuity, we may restrict to the case
![]() $\underline {y} \in \mathbf {Z}^d_{\geq 0}$
. By writing
$\underline {y} \in \mathbf {Z}^d_{\geq 0}$
. By writing
![]() $\underline {y}$
as a sum of
$\underline {y}$
as a sum of
![]() $1_k$
’s and applying the identity (1) inductively, we may write
$1_k$
’s and applying the identity (1) inductively, we may write
for some
![]() $a_j \in \mathbf {Z}$
,
$a_j \in \mathbf {Z}$
,
![]() $\underline {z}_j \in \mathbf {Z}^d$
and
$\underline {z}_j \in \mathbf {Z}^d$
and
![]() $1 \leq i_j \leq d$
(the
$1 \leq i_j \leq d$
(the
![]() $i_j$
may repeat). Raising this to the n-th power, we obtain a writing of
$i_j$
may repeat). Raising this to the n-th power, we obtain a writing of
![]() $\Delta _{\underline {y}}$
as a
$\Delta _{\underline {y}}$
as a
![]() $\mathbf {Z}$
-linear combination up to shifts of
$\mathbf {Z}$
-linear combination up to shifts of
![]() $\Delta ^{\underline {m}}$
’s where for each
$\Delta ^{\underline {m}}$
’s where for each
![]() $\underline {m}$
we have
$\underline {m}$
we have
![]() $\sum {m_i}=n$
. For each such
$\sum {m_i}=n$
. For each such
![]() $\underline {m}$
, choose the maximal coordinate
$\underline {m}$
, choose the maximal coordinate
![]() $m_i$
. For every
$m_i$
. For every
![]() $g:\mathbf {Z}_p \rightarrow M$
one has
$g:\mathbf {Z}_p \rightarrow M$
one has
![]() $\mathrm {val}_M^{\mathrm {op}}(\Delta ^{\underline {m}}(g))\geq \mathrm {val}_M^{\mathrm {op}}(\Delta _i^{m_i}(g))$
; applying this observation to shifts of f and using that
$\mathrm {val}_M^{\mathrm {op}}(\Delta ^{\underline {m}}(g))\geq \mathrm {val}_M^{\mathrm {op}}(\Delta _i^{m_i}(g))$
; applying this observation to shifts of f and using that
![]() $m_i\geq \lceil n/d \rceil $
, this concludes the proof.
$m_i\geq \lceil n/d \rceil $
, this concludes the proof.
We write
![]() $\mathcal {C}^0(\mathbf {Z}_p^d,M)$
for the continuous functions from
$\mathcal {C}^0(\mathbf {Z}_p^d,M)$
for the continuous functions from
![]() $\mathbf {Z}_p$
to M. The following version of Mahler’s theorem shows each continuous function has an expansion in terms of the
$\mathbf {Z}_p$
to M. The following version of Mahler’s theorem shows each continuous function has an expansion in terms of the
![]() $\binom {\underline {x}}{\underline {n}}$
.
$\binom {\underline {x}}{\underline {n}}$
.
Theorem 2.2. The following are equivalent for a function
![]() $f:\mathbf {Z}_p^d \rightarrow M$
.
$f:\mathbf {Z}_p^d \rightarrow M$
.
-
1. We have
 $f \in \mathcal {C}^0(\mathbf {Z}_p^d,M).$
$f \in \mathcal {C}^0(\mathbf {Z}_p^d,M).$
-
2. The function f has an expansion of the form
 $f(\underline {x}) = \sum _{\underline {n}\in \mathbf {Z}_{\geq 0}^d} a_{\underline {n}}(f) \binom {\underline {x}}{\underline {n}}$
with
$f(\underline {x}) = \sum _{\underline {n}\in \mathbf {Z}_{\geq 0}^d} a_{\underline {n}}(f) \binom {\underline {x}}{\underline {n}}$
with
 $\mathrm {val}_M(a_{\underline {n}}(f)) \rightarrow \infty $
as
$\mathrm {val}_M(a_{\underline {n}}(f)) \rightarrow \infty $
as
 $|\underline {n}| \rightarrow \infty $
.
$|\underline {n}| \rightarrow \infty $
.
Furthermore, under these equivalent conditions we have
![]() $a_{\underline {n}} = \Delta ^{\underline {n}}(f)(\underline {0})$
and
$a_{\underline {n}} = \Delta ^{\underline {n}}(f)(\underline {0})$
and
![]() $\mathrm {val}_M^{\mathrm {op}}(f) = \inf _{\underline {n}\in \mathbf {Z}_{\geq 0}}\mathrm {val}_M(a_{\underline {n}}). $
$\mathrm {val}_M^{\mathrm {op}}(f) = \inf _{\underline {n}\in \mathbf {Z}_{\geq 0}}\mathrm {val}_M(a_{\underline {n}}). $
Proof. We follow the proof of Bojanic [Reference BojanicBoj74], see also Theorem 1.13 of [Reference Berger and RozensztajnBR22].
First, suppose f has an expansion of the form
![]() $f(\underline {x}) = \sum {a_{\underline {n}}}\binom {x}{\underline {n}}$
with
$f(\underline {x}) = \sum {a_{\underline {n}}}\binom {x}{\underline {n}}$
with
![]() $a_{\underline {n}} \rightarrow 0$
. Then f is continuous since it is the uniform limit of continuous functions. We now explain why do we have in this case the equality
$a_{\underline {n}} \rightarrow 0$
. Then f is continuous since it is the uniform limit of continuous functions. We now explain why do we have in this case the equality
Indeed, for each
![]() $\underline {n}$
, the element
$\underline {n}$
, the element
![]() $a_{\underline {n}}=\Delta ^{\underline {n}}(f)(\underline {0})$
is a sum of elements in
$a_{\underline {n}}=\Delta ^{\underline {n}}(f)(\underline {0})$
is a sum of elements in
![]() $\mathrm {Im}(f)$
, which shows
$\mathrm {Im}(f)$
, which shows
![]() $\inf _{\underline {x}}\mathrm {val}_M(f(\underline {x})) \leq \inf _{\underline {n}}\mathrm {val}_M(a_{\underline {n}}).$
The inequality in other direction is clear given the existence of the expansion.
$\inf _{\underline {x}}\mathrm {val}_M(f(\underline {x})) \leq \inf _{\underline {n}}\mathrm {val}_M(a_{\underline {n}}).$
The inequality in other direction is clear given the existence of the expansion.
Conversely, suppose f is continuous. We set
![]() $a_{\underline {n}} = \Delta ^{\underline {n}}(f)(0)$
. It suffices to show that
$a_{\underline {n}} = \Delta ^{\underline {n}}(f)(0)$
. It suffices to show that
![]() $a_{\underline {n}} \rightarrow 0$
; indeed, with that given, the function f and the one given by
$a_{\underline {n}} \rightarrow 0$
; indeed, with that given, the function f and the one given by
![]() $g(\underline {x}):=\sum _{\underline {n}}a_{\underline {n}}\binom {x}{\underline {n}}$
agree on
$g(\underline {x}):=\sum _{\underline {n}}a_{\underline {n}}\binom {x}{\underline {n}}$
agree on
![]() $\mathbf {Z}_{\geq 0}^d$
, hence are equal.
$\mathbf {Z}_{\geq 0}^d$
, hence are equal.
Since
![]() $\mathbf {Z}_p^d$
is compact, the function f is uniformly continuous. Fix
$\mathbf {Z}_p^d$
is compact, the function f is uniformly continuous. Fix
![]() $s \geq 0$
; then there exists
$s \geq 0$
; then there exists
![]() $t \geq 0$
such that if
$t \geq 0$
such that if
![]() $\mathrm {val}(\underline {x}-\underline {y}) \geq t$
then
$\mathrm {val}(\underline {x}-\underline {y}) \geq t$
then
![]() $\mathrm {val}_M(f(\underline {x})-f(\underline {y})) \geq s\mathrm {val}(p) + \mathrm {val}_{M}^{\mathrm {op}}(f)$
. The same statement, with the same t, holds for any
$\mathrm {val}_M(f(\underline {x})-f(\underline {y})) \geq s\mathrm {val}(p) + \mathrm {val}_{M}^{\mathrm {op}}(f)$
. The same statement, with the same t, holds for any
![]() $\Delta ^{\underline {n}}(f)$
. To conclude the proof, it suffices to show that if
$\Delta ^{\underline {n}}(f)$
. To conclude the proof, it suffices to show that if
![]() $|\underline {n}|_{\infty }$
is larger than
$|\underline {n}|_{\infty }$
is larger than
![]() $sp^t$
then
$sp^t$
then
![]() $\mathrm {val}(a_{\underline {n}})\geq s\mathrm {val}(p)+\mathrm {val}_M^{\mathrm {op}}(f)$
.
$\mathrm {val}(a_{\underline {n}})\geq s\mathrm {val}(p)+\mathrm {val}_M^{\mathrm {op}}(f)$
.
Now given a function g we have
for some element
![]() $y(\underline {x})$
with
$y(\underline {x})$
with
![]() $\mathrm {val}_M(y(\underline {x})) \geq \mathrm {val}_M^{\mathrm {op}}(g)$
. Taking g to be a function of the form
$\mathrm {val}_M(y(\underline {x})) \geq \mathrm {val}_M^{\mathrm {op}}(g)$
. Taking g to be a function of the form
![]() $\Delta ^{\underline {n}}(f)$
, we obtain
$\Delta ^{\underline {n}}(f)$
, we obtain
![]() $\mathrm {val}(g(\underline {x}+p^t1_i)-g(\underline {x})) \geq s\mathrm {val}(p) + \mathrm {val}_{M}^{\mathrm {op}}(f)$
and so for every
$\mathrm {val}(g(\underline {x}+p^t1_i)-g(\underline {x})) \geq s\mathrm {val}(p) + \mathrm {val}_{M}^{\mathrm {op}}(f)$
and so for every
![]() $\underline {n}$
and k we have the inequality
$\underline {n}$
and k we have the inequality
Now if
![]() $|\underline {n}|_{\infty }> sp^t$
then the k-th coordinate of
$|\underline {n}|_{\infty }> sp^t$
then the k-th coordinate of
![]() $\underline {n}$
is larger than
$\underline {n}$
is larger than
![]() $sp^t$
for some k. Applying (2) consecutively to
$sp^t$
for some k. Applying (2) consecutively to
shows
![]() $\mathrm {val}_{M}^{\mathrm {op}}(\Delta ^{\underline {n}}(f)),$
hence also
$\mathrm {val}_{M}^{\mathrm {op}}(\Delta ^{\underline {n}}(f)),$
hence also
![]() $a_{\underline {n}}(f)$
, has valuation at least
$a_{\underline {n}}(f)$
, has valuation at least
![]() $s\mathrm {val}(p) + \mathrm {val}_{M}^{\mathrm {op}}(f)$
. This finishes the proof.
$s\mathrm {val}(p) + \mathrm {val}_{M}^{\mathrm {op}}(f)$
. This finishes the proof.
We now give several definitions for analytic functions on
![]() $\mathbf {Z}_p^d$
and explain the relationships between them. See also [Reference Berger and RozensztajnBR22], [Reference Berger and RozensztajnBR24], §
$\mathbf {Z}_p^d$
and explain the relationships between them. See also [Reference Berger and RozensztajnBR22], [Reference Berger and RozensztajnBR24], §
![]() $3$
of [Reference GulottaGul19], and §
$3$
of [Reference GulottaGul19], and §
![]() $3.2$
of [Reference Johansson and NewtonJN19] for similar definitions.
$3.2$
of [Reference Johansson and NewtonJN19] for similar definitions.
Proposition 2.3. Let
![]() $\lambda , \mu \in \mathbf {R}$
. The following are equivalent for a function
$\lambda , \mu \in \mathbf {R}$
. The following are equivalent for a function
![]() $f:\mathbf {Z}_p^d \rightarrow M$
.
$f:\mathbf {Z}_p^d \rightarrow M$
.
-
1. The inequality
 $\mathrm {val}_M(a_{\underline {n}}(f)) \geq p^\lambda \cdot p^{\lfloor \log _p(|\underline {n}|_\infty ) \rfloor } + \mu $
holds for every
$\mathrm {val}_M(a_{\underline {n}}(f)) \geq p^\lambda \cdot p^{\lfloor \log _p(|\underline {n}|_\infty ) \rfloor } + \mu $
holds for every
 $\underline {n} \in \mathbf {Z}^d_{\geq 0}$
.
$\underline {n} \in \mathbf {Z}^d_{\geq 0}$
. -
2. The inequality
 $\mathrm {val}_M^{\mathrm {op}}(\Delta ^{n}_i(f)) \geq p^\lambda \cdot p^{\lfloor \log _p(n) \rfloor } + \mu $
holds for every
$\mathrm {val}_M^{\mathrm {op}}(\Delta ^{n}_i(f)) \geq p^\lambda \cdot p^{\lfloor \log _p(n) \rfloor } + \mu $
holds for every
 $1\leq i \leq d$
and
$1\leq i \leq d$
and
 $n \in \mathbf {Z}_{\geq 0}.$
$n \in \mathbf {Z}_{\geq 0}.$
Proof. To show 1 implies 2, we may assume
![]() $n=p^k$
. Write
$n=p^k$
. Write
![]() $f(\underline {x}) =\sum a_{\underline {n}} \binom {\underline {x}}{\underline {n}}$
(as we may according to 2.2), then
$f(\underline {x}) =\sum a_{\underline {n}} \binom {\underline {x}}{\underline {n}}$
(as we may according to 2.2), then
 $$ \begin{align*}\Delta_i^{p^k}(f)(\underline{x}) = \sum a_{\underline{n}} \Delta_i^{p^k}(\binom{\underline{x}}{\underline{n}}) = \sum_{\underline{n}:n_i\geq p^k} a_{\underline{n}}\binom{\underline{x}}{\underline{n}-1_ip^k},\end{align*} $$
$$ \begin{align*}\Delta_i^{p^k}(f)(\underline{x}) = \sum a_{\underline{n}} \Delta_i^{p^k}(\binom{\underline{x}}{\underline{n}}) = \sum_{\underline{n}:n_i\geq p^k} a_{\underline{n}}\binom{\underline{x}}{\underline{n}-1_ip^k},\end{align*} $$
for which each term has
![]() $\mathrm {val}\geq p^\lambda \cdot p^k + \mu $
by assumption.
$\mathrm {val}\geq p^\lambda \cdot p^k + \mu $
by assumption.
Conversely, choose i with
![]() $n_i = |\underline {n}|_\infty $
. Let
$n_i = |\underline {n}|_\infty $
. Let
![]() $\underline {n}'$
be
$\underline {n}'$
be
![]() $\underline {n}$
with the i-th coordinate removed. Then
$\underline {n}$
with the i-th coordinate removed. Then
As
![]() $\Delta ^{\underline {n}'}(f)$
is a
$\Delta ^{\underline {n}'}(f)$
is a
![]() $\mathbf {Z}$
-linear combination of shifts of f, we obtain that
$\mathbf {Z}$
-linear combination of shifts of f, we obtain that
![]() $a_{\underline {n}}(f)$
is a
$a_{\underline {n}}(f)$
is a
![]() $\mathbf {Z}$
-linear combination of
$\mathbf {Z}$
-linear combination of
![]() $\Delta _i^{n_i}(f)(t_j)$
for various
$\Delta _i^{n_i}(f)(t_j)$
for various
![]() $t_j$
. Each of these has valuation
$t_j$
. Each of these has valuation
![]() $\geq p^{\lfloor \log _p(n_i) \rfloor } + \mu =p^{\lfloor \log _p(|\underline {n}|_\infty ) \rfloor } + \mu ,$
as required.
$\geq p^{\lfloor \log _p(n_i) \rfloor } + \mu =p^{\lfloor \log _p(|\underline {n}|_\infty ) \rfloor } + \mu ,$
as required.
Definition 2.4.
-
1. Let
 $\mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)$
be the submodule of functions satisfying any of the equivalent conditions of Proposition 2.3. By condition 1 and Theorem 2.2, it is contained in
$\mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)$
be the submodule of functions satisfying any of the equivalent conditions of Proposition 2.3. By condition 1 and Theorem 2.2, it is contained in
 $\mathcal {C}^{0}(\mathbf {Z}_p^d,M)$
.
$\mathcal {C}^{0}(\mathbf {Z}_p^d,M)$
. -
2. Let
 $\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)\subset \mathcal {C}^0(\mathbf {Z}_p^d,M)$
be the submodule of functions f satisfying
$\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)\subset \mathcal {C}^0(\mathbf {Z}_p^d,M)$
be the submodule of functions f satisfying
 $\mathrm {val}_M(a_{\underline {n}}(f))-p^\lambda |\underline {n}|\rightarrow \infty $
. We endow it with the valuation (recall §
$\mathrm {val}_M(a_{\underline {n}}(f))-p^\lambda |\underline {n}|\rightarrow \infty $
. We endow it with the valuation (recall § $$ \begin{align*}\mathrm{val}_{\lambda}(f) := \inf_{\underline{n}}(a_{\underline{n}}(f)-\lfloor p^\lambda \underline{n} \rfloor)\end{align*} $$
$$ \begin{align*}\mathrm{val}_{\lambda}(f) := \inf_{\underline{n}}(a_{\underline{n}}(f)-\lfloor p^\lambda \underline{n} \rfloor)\end{align*} $$
 $1.2$
for the notation
$1.2$
for the notation
 $\lfloor p^\lambda \underline {n} \rfloor $
.)
$\lfloor p^\lambda \underline {n} \rfloor $
.)
Proposition 2.5. The modules
![]() $\mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)$
and
$\mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)$
and
![]() $\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
are stable under the shift operator
$\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
are stable under the shift operator
![]() $\mathrm {sh}_{\underline {z}}$
for any
$\mathrm {sh}_{\underline {z}}$
for any
![]() $\underline {z}\in \mathbf {Z}_p^d$
.
$\underline {z}\in \mathbf {Z}_p^d$
.
Furthermore, the action of
![]() $\mathbf {Z}_p^d$
on
$\mathbf {Z}_p^d$
on
![]() $\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
given by shifts is continuous and each element of
$\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
given by shifts is continuous and each element of
![]() $\mathbf {Z}_p^d$
acts as an isometry.
$\mathbf {Z}_p^d$
acts as an isometry.
Proof. For
![]() $\mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)$
the statement follows from Proposition 2.3. We now show the statement holds for
$\mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)$
the statement follows from Proposition 2.3. We now show the statement holds for
![]() $\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
. Suppose it were known for shifts by elements of
$\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
. Suppose it were known for shifts by elements of
![]() $\mathbf {Z}^d$
. Let
$\mathbf {Z}^d$
. Let
![]() $\underline {z} \in \mathbf {Z}_p^d$
and let
$\underline {z} \in \mathbf {Z}_p^d$
and let
![]() $f\in \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
. As f is uniformly continuous, we can find some m so that
$f\in \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
. As f is uniformly continuous, we can find some m so that
![]() $\mathrm {val}_M(f(\underline {x}+\underline {y})-f(\underline {x})> 1$
if
$\mathrm {val}_M(f(\underline {x}+\underline {y})-f(\underline {x})> 1$
if
![]() $\mathrm {val}(\underline {x}-\underline {y})> m$
. Choosing
$\mathrm {val}(\underline {x}-\underline {y})> m$
. Choosing
![]() $\underline {z}_0 \in \mathbf {Z}^d$
with
$\underline {z}_0 \in \mathbf {Z}^d$
with
![]() $\mathrm {val}(\underline {z}-\underline {z}_0)> m$
, we see that
$\mathrm {val}(\underline {z}-\underline {z}_0)> m$
, we see that
![]() $\mathrm {val}_M^{\mathrm {op}}(\mathrm {sh}_{\underline {z}}(f)-\mathrm {sh}_{\underline {z}_0}(f))> 1$
and
$\mathrm {val}_M^{\mathrm {op}}(\mathrm {sh}_{\underline {z}}(f)-\mathrm {sh}_{\underline {z}_0}(f))> 1$
and
![]() $\mathrm {sh}_{\underline {z}_0}(f) \in \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
which implies
$\mathrm {sh}_{\underline {z}_0}(f) \in \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
which implies
![]() $\mathrm {sh}_{\underline {z}}(f) \in \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
. This argument also shows the action of
$\mathrm {sh}_{\underline {z}}(f) \in \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
. This argument also shows the action of
![]() $\mathbf {Z}_p^d$
on
$\mathbf {Z}_p^d$
on
![]() $\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
is continuous (provided we show it exists). We thus reduce to the case where
$\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
is continuous (provided we show it exists). We thus reduce to the case where
![]() $\underline {z} \in \mathbf {Z}^d$
, which allows us to reduce further to the case
$\underline {z} \in \mathbf {Z}^d$
, which allows us to reduce further to the case
![]() $\underline {z}=1_i$
for
$\underline {z}=1_i$
for
![]() $1 \leq i \leq d$
. Finally, we have
$1 \leq i \leq d$
. Finally, we have
![]() $a_{\underline {n}}(\mathrm {sh}_{1_i}(f))=a_{\underline {n}}(f)+a_{\underline {n}+1_i}(f)$
which shows
$a_{\underline {n}}(\mathrm {sh}_{1_i}(f))=a_{\underline {n}}(f)+a_{\underline {n}+1_i}(f)$
which shows
![]() $\mathrm {sh}_{1_i}(f) \in \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
.
$\mathrm {sh}_{1_i}(f) \in \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
.
It remains to show each element of
![]() $\mathbf {Z}_p^d$
acts as an isometry on
$\mathbf {Z}_p^d$
acts as an isometry on
![]() $\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
. We may reduce again to showing that
$\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
. We may reduce again to showing that
![]() $\mathrm {sh}_{1_i}$
acts as an isometry. To show this, take
$\mathrm {sh}_{1_i}$
acts as an isometry. To show this, take
![]() $f \in \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
and let
$f \in \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
and let
![]() $\underline {n}_0$
be maximal with
$\underline {n}_0$
be maximal with
![]() $\mathrm {val}_\lambda (f) = \mathrm {val}_M(a_{\underline {n}_0}(f))-\lfloor p^\lambda \underline {n}_0 \rfloor )$
. Then
$\mathrm {val}_\lambda (f) = \mathrm {val}_M(a_{\underline {n}_0}(f))-\lfloor p^\lambda \underline {n}_0 \rfloor )$
. Then
![]() $\mathrm {val}_M(a_{\underline {n}_0+1_i}(f))> \mathrm {val}_M(a_{\underline {n}_0}(f))$
, and so the formula
$\mathrm {val}_M(a_{\underline {n}_0+1_i}(f))> \mathrm {val}_M(a_{\underline {n}_0}(f))$
, and so the formula
![]() $a_{\underline {n}}(\mathrm {sh}_{1_i}(f))=a_{\underline {n}}(f)+a_{\underline {n}+1_i}(f)$
shows
$a_{\underline {n}}(\mathrm {sh}_{1_i}(f))=a_{\underline {n}}(f)+a_{\underline {n}+1_i}(f)$
shows
![]() $\mathrm {val}_{\lambda }(\mathrm {sh}_{1_i}(f)) \leq \mathrm {val}_\lambda (f).$
Now by using the uniform continuity again, we know that for
$\mathrm {val}_{\lambda }(\mathrm {sh}_{1_i}(f)) \leq \mathrm {val}_\lambda (f).$
Now by using the uniform continuity again, we know that for
![]() $p^k$
for k sufficiently large we have
$p^k$
for k sufficiently large we have
![]() $\mathrm {val}_{\lambda }(\mathrm {sh}_{p^k 1_i}(f)) = \mathrm {val}_\lambda (f)$
. Hence the inequalities
$\mathrm {val}_{\lambda }(\mathrm {sh}_{p^k 1_i}(f)) = \mathrm {val}_\lambda (f)$
. Hence the inequalities
are all forced to be equalities, which shows
![]() $\mathrm {val}_{\lambda }(\mathrm {sh}_{1_i}(f)) = \mathrm {val}_\lambda (f),$
as required.
$\mathrm {val}_{\lambda }(\mathrm {sh}_{1_i}(f)) = \mathrm {val}_\lambda (f),$
as required.
Lemma 2.6. Let
![]() $\lambda \in \mathbf {R}$
and
$\lambda \in \mathbf {R}$
and
![]() $c> 0.$
Then there exist
$c> 0.$
Then there exist
![]() $l \geq 0$
such that for every
$l \geq 0$
such that for every
![]() $f \in \mathcal {C}^{\lambda \text {-an}}(\mathbf {Z}_p^d,M)$
and for every
$f \in \mathcal {C}^{\lambda \text {-an}}(\mathbf {Z}_p^d,M)$
and for every
![]() $1 \leq i \leq d$
we have
$1 \leq i \leq d$
we have
Proof. Let
![]() $l\geq 0$
be arbitrary. We have the Vandermonde identity
$l\geq 0$
be arbitrary. We have the Vandermonde identity
 $$ \begin{align*}\Delta_{p^l 1_i}(\binom{\underline{x}}{\underline{n}}) = \sum_{j=1}^{n_i}\binom{\underline{x}}{\underline{n}-j1_i}\binom{p^l}{j}.\end{align*} $$
$$ \begin{align*}\Delta_{p^l 1_i}(\binom{\underline{x}}{\underline{n}}) = \sum_{j=1}^{n_i}\binom{\underline{x}}{\underline{n}-j1_i}\binom{p^l}{j}.\end{align*} $$
Writing
![]() $f(\underline {x}) = \sum _{\underline {n}} a_{\underline {n}} \binom {\underline {x}}{\underline {n}},$
the identity above shows that
$f(\underline {x}) = \sum _{\underline {n}} a_{\underline {n}} \binom {\underline {x}}{\underline {n}},$
the identity above shows that
 $$ \begin{align*}\Delta_{p^l 1_i}(f) = \sum_{\underline{n}} (\sum_{j=1}^\infty a_{\underline{n} +j 1_i} \binom{p^l}{j}) \binom{\underline{x}}{\underline{n}},\end{align*} $$
$$ \begin{align*}\Delta_{p^l 1_i}(f) = \sum_{\underline{n}} (\sum_{j=1}^\infty a_{\underline{n} +j 1_i} \binom{p^l}{j}) \binom{\underline{x}}{\underline{n}},\end{align*} $$
and hence
 $$ \begin{align*}\Delta^{\underline{n}}(\Delta_{p^l 1_i}(f)(0)) = \sum_{j=1}^\infty a_{\underline{n}+j1_i} \binom{p^l}{j}.\end{align*} $$
$$ \begin{align*}\Delta^{\underline{n}}(\Delta_{p^l 1_i}(f)(0)) = \sum_{j=1}^\infty a_{\underline{n}+j1_i} \binom{p^l}{j}.\end{align*} $$
From this we get the lower bound
 $$ \begin{align*}\mathrm{val}_M(\Delta^{\underline{n}}(\Delta_{p^l 1_i}(f)(0))) \geq \inf_{j\geq 1}(\mathrm{val}(a_{\underline{n}+j1_i}) + \mathrm{val}(\binom{p^l}{j})).\end{align*} $$
$$ \begin{align*}\mathrm{val}_M(\Delta^{\underline{n}}(\Delta_{p^l 1_i}(f)(0))) \geq \inf_{j\geq 1}(\mathrm{val}(a_{\underline{n}+j1_i}) + \mathrm{val}(\binom{p^l}{j})).\end{align*} $$
On the other hand, by definition we have the inequality
 $$ \begin{align*}\mathrm{val}_M(a_{\underline{n}+j1_i}) \geq \sum_{i=1}^d\lfloor p^{\lambda}(n_i + j\delta_{ij})\rfloor + \mathrm{val}_{\lambda}(f).\end{align*} $$
$$ \begin{align*}\mathrm{val}_M(a_{\underline{n}+j1_i}) \geq \sum_{i=1}^d\lfloor p^{\lambda}(n_i + j\delta_{ij})\rfloor + \mathrm{val}_{\lambda}(f).\end{align*} $$
Putting this all together, we get
 $$ \begin{align*}\mathrm{val}_{\lambda}(\Delta_{p^l 1_i}(f)) &= \inf_{\underline{n}}(\mathrm{val}_M(\Delta^{\underline{n}}(\Delta_{p^l 1_i}(f)(0))) -\lfloor p^{\lambda} \underline{n} \rfloor)\\&\geq \mathrm{val}_{\lambda}(f)+ \inf_{j\geq 1}(p^\lambda j -1 + \mathrm{val}(\binom{p^l}{j})),\end{align*} $$
$$ \begin{align*}\mathrm{val}_{\lambda}(\Delta_{p^l 1_i}(f)) &= \inf_{\underline{n}}(\mathrm{val}_M(\Delta^{\underline{n}}(\Delta_{p^l 1_i}(f)(0))) -\lfloor p^{\lambda} \underline{n} \rfloor)\\&\geq \mathrm{val}_{\lambda}(f)+ \inf_{j\geq 1}(p^\lambda j -1 + \mathrm{val}(\binom{p^l}{j})),\end{align*} $$
and so any choice of l which satisfies
![]() $\inf _{j\geq 1}(p^\lambda j -1 + \mathrm {val}(\binom {p^l}{j}))> c$
works.
$\inf _{j\geq 1}(p^\lambda j -1 + \mathrm {val}(\binom {p^l}{j}))> c$
works.
Corollary 2.7. For every
![]() $\lambda $
and
$\lambda $
and
![]() $\lambda '$
there exists an
$\lambda '$
there exists an
![]() $l \geq 0$
such that restriction from
$l \geq 0$
such that restriction from
![]() $\mathbf {Z}_p^d$
to
$\mathbf {Z}_p^d$
to
![]() $p^l \mathbf {Z}_p^d$
maps
$p^l \mathbf {Z}_p^d$
maps
![]() $\mathcal {C}^{\lambda \text {-an}}(\mathbf {Z}_p^d,M)$
into
$\mathcal {C}^{\lambda \text {-an}}(\mathbf {Z}_p^d,M)$
into
![]() $\mathcal {C}^{\lambda '\text {-an}}(p^l \mathbf {Z}_p^d,M).$
$\mathcal {C}^{\lambda '\text {-an}}(p^l \mathbf {Z}_p^d,M).$
Proof. Choose any
![]() $c> p^{\lambda '} + 1$
and
$c> p^{\lambda '} + 1$
and
![]() $l\geq 0$
so that the previous lemma applies to c and
$l\geq 0$
so that the previous lemma applies to c and
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $f \in \mathcal {C}^{\lambda \text {-an}}(\mathbf {Z}_p^d,M)$
a function. We wish to show its restriction lies in
$f \in \mathcal {C}^{\lambda \text {-an}}(\mathbf {Z}_p^d,M)$
a function. We wish to show its restriction lies in
![]() $\mathcal {C}^{\lambda '\text {-an}}(p^l\mathbf {Z}_p^d,M)$
. We may assume f lies in
$\mathcal {C}^{\lambda '\text {-an}}(p^l\mathbf {Z}_p^d,M)$
. We may assume f lies in
![]() $\mathcal {C}^{\lambda \text {-an}}(\mathbf {Z}_p^d,M)^+.$
Let
$\mathcal {C}^{\lambda \text {-an}}(\mathbf {Z}_p^d,M)^+.$
Let
![]() $\Delta _{p^l}^{\underline {m}}$
denote the composition
$\Delta _{p^l}^{\underline {m}}$
denote the composition
![]() $\Delta ^{m_1}_{p^l 1_1} \circ ... \circ \Delta ^{m_d}_{p^l 1_d}.$
We need to show that
$\Delta ^{m_1}_{p^l 1_1} \circ ... \circ \Delta ^{m_d}_{p^l 1_d}.$
We need to show that
Applying the previous lemma successively to
![]() $f \in \mathcal {C}^{\lambda \text {-an}}(\mathbf {Z}_p^d,M)^+$
we get the inequality
$f \in \mathcal {C}^{\lambda \text {-an}}(\mathbf {Z}_p^d,M)^+$
we get the inequality
By the general inequality
![]() $\mathrm {val}_M(g(0)) \geq \mathrm {val}_\lambda (g)$
we deduce
$\mathrm {val}_M(g(0)) \geq \mathrm {val}_\lambda (g)$
we deduce
which gives the desired lower bound for the
![]() $\mathrm {val}_M(\Delta _{p^l}^{\underline {m}}(f)(0))$
.
$\mathrm {val}_M(\Delta _{p^l}^{\underline {m}}(f)(0))$
.
For
![]() $\lambda \leq \lambda '$
and
$\lambda \leq \lambda '$
and
![]() $\mu \leq \mu '$
we have natural maps
$\mu \leq \mu '$
we have natural maps
![]() $\mathcal {C}^{\lambda '\text {-}\mathrm {an}}(\mathbf {Z}_p^d,M) \rightarrow \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
and
$\mathcal {C}^{\lambda '\text {-}\mathrm {an}}(\mathbf {Z}_p^d,M) \rightarrow \mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)$
and
![]() $\mathcal {C}^{\mathrm {an}\text {-}\lambda ',\mu '}(\mathbf {Z}_p^d,M) \rightarrow \mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)$
. We will often consider filtered colimits along these maps. The following lemma shows it does not matter much which system we use.
$\mathcal {C}^{\mathrm {an}\text {-}\lambda ',\mu '}(\mathbf {Z}_p^d,M) \rightarrow \mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)$
. We will often consider filtered colimits along these maps. The following lemma shows it does not matter much which system we use.
Lemma 2.8. The systems
![]() $\{\mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)\}_{\lambda ,\mu }$
and
$\{\mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)\}_{\lambda ,\mu }$
and
![]() $\{\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)\}_\lambda $
are cofinal with respect to each other. Furthermore, up to cofinality the systems do not depend on the choice of basis of
$\{\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)\}_\lambda $
are cofinal with respect to each other. Furthermore, up to cofinality the systems do not depend on the choice of basis of
![]() $\mathbf {Z}_p^d$
.
$\mathbf {Z}_p^d$
.
Proof. The cofinality of
![]() $\{\mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)\}_{\lambda ,\mu }$
and
$\{\mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(\mathbf {Z}_p^d,M)\}_{\lambda ,\mu }$
and
![]() $\{\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)\}_\lambda $
follows from the inequality
$\{\mathcal {C}^{\lambda \text {-}\mathrm {an}}(\mathbf {Z}_p^d,M)\}_\lambda $
follows from the inequality
![]() $|\underline {n}|_\infty \leq |\underline {n}| \leq |\underline {n}|_\infty /d$
for
$|\underline {n}|_\infty \leq |\underline {n}| \leq |\underline {n}|_\infty /d$
for
![]() $\underline {n} \in \mathbf {Z}^d_{\geq 0}$
by condition 1 of Proposition 2.3. The cofinality with respect to a different basis follows from Lemma 2.1 and condition 2 of Proposition 2.3.
$\underline {n} \in \mathbf {Z}^d_{\geq 0}$
by condition 1 of Proposition 2.3. The cofinality with respect to a different basis follows from Lemma 2.1 and condition 2 of Proposition 2.3.
Definition 2.9. We let
![]() $\mathcal {C}^{\mathrm {la}}(\mathbf {Z}_p^d,M)$
be the colimit of any of these cofinal systems. Elements lying in this module are thought of as locally analytic functions of
$\mathcal {C}^{\mathrm {la}}(\mathbf {Z}_p^d,M)$
be the colimit of any of these cofinal systems. Elements lying in this module are thought of as locally analytic functions of
![]() $\mathbf {Z}_p^d$
which are valued in M.
$\mathbf {Z}_p^d$
which are valued in M.
2.2 Locally analytic vectors
Let M be as in the previous subsection and let G be a compact p-adic Lie group of dimension d which acts continuously on M by isometries. There exists an open uniform subgroup
![]() $G_0 \subset G$
by Corollary 4.3 of [Reference Dixon, Du Sautoy, Mann and SegalDDSMS03]. We can choose it to be normal. As
$G_0 \subset G$
by Corollary 4.3 of [Reference Dixon, Du Sautoy, Mann and SegalDDSMS03]. We can choose it to be normal. As
![]() $G_0$
is uniform, there exists an ordered basis
$G_0$
is uniform, there exists an ordered basis
![]() $g_1,...,g_d$
such that the coordinate map
$g_1,...,g_d$
such that the coordinate map
![]() $c:(x_1,...,x_d)\mapsto g_1^{x_1}\cdot ...\cdot g_d^{x_d}$
gives a homeomorphism of
$c:(x_1,...,x_d)\mapsto g_1^{x_1}\cdot ...\cdot g_d^{x_d}$
gives a homeomorphism of
![]() $\mathbf {Z}_p^d$
with
$\mathbf {Z}_p^d$
with
![]() $G_0$
. Set
$G_0$
. Set
![]() $G_i = G^{p^i} = \{g^{p^i}: g \in G_0\}$
. The
$G_i = G^{p^i} = \{g^{p^i}: g \in G_0\}$
. The
![]() $G_i$
are open normal subgroups of
$G_i$
are open normal subgroups of
![]() $G_0$
which correspond the
$G_0$
which correspond the
![]() $p^i \mathbf {Z}_p^d$
under c. We define
$p^i \mathbf {Z}_p^d$
under c. We define
![]() $\mathcal {C}^0(G_0,M), \mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(G_0,M), \mathcal {C}^{\lambda \text {-}\mathrm {an}}(G_0,M)$
and
$\mathcal {C}^0(G_0,M), \mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(G_0,M), \mathcal {C}^{\lambda \text {-}\mathrm {an}}(G_0,M)$
and
![]() $\mathcal {C}^{\mathrm {la}}(G_0,M)$
by pulling back along c the definitions of Definition 2.4. We are not claiming all of these are independent of the coordinate system chosen, but we shall see later the independence of the coordinate system for the most interesting objects considered here.
$\mathcal {C}^{\mathrm {la}}(G_0,M)$
by pulling back along c the definitions of Definition 2.4. We are not claiming all of these are independent of the coordinate system chosen, but we shall see later the independence of the coordinate system for the most interesting objects considered here.
If
![]() $g\in G_0$
there exists some maximal i so that
$g\in G_0$
there exists some maximal i so that
![]() $g^{p^{-i}} \in G_0$
; there then exists some basis of
$g^{p^{-i}} \in G_0$
; there then exists some basis of
![]() $G_0$
with
$G_0$
with
![]() $g^{p^{-i}}=g_1$
. For this basis, shifting in
$g^{p^{-i}}=g_1$
. For this basis, shifting in
![]() $G_0$
by g corresponds to shifting in
$G_0$
by g corresponds to shifting in
![]() $\mathbf {Z}_p^d$
by
$\mathbf {Z}_p^d$
by
![]() $c(g)$
. It then follows from Proposition 2.5 that
$c(g)$
. It then follows from Proposition 2.5 that
![]() $G_0$
acts on
$G_0$
acts on
![]() $\mathcal {C}^{\mathrm {la}}(G_0,M)$
by the formula
$\mathcal {C}^{\mathrm {la}}(G_0,M)$
by the formula
![]() $g(f)(x) = g(f(g^{-1}x))$
.
$g(f)(x) = g(f(g^{-1}x))$
.
Definition 2.10. We define locally analytic elements as follows.
-
1. SetFootnote 2
 $M^{G_0,\lambda \text {-}\mathrm {an}} = \mathcal {C}^{\lambda \text {-}\mathrm {an}}(G_0,M)^{G_0}$
and
$M^{G_0,\lambda \text {-}\mathrm {an}} = \mathcal {C}^{\lambda \text {-}\mathrm {an}}(G_0,M)^{G_0}$
and
 $M^{G_0,\mathrm {an}\text {-}\lambda ,\mu } = \mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(G_0,M)^{G_0}$
.
$M^{G_0,\mathrm {an}\text {-}\lambda ,\mu } = \mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(G_0,M)^{G_0}$
. -
2. Let
 $M^{G_0\text {-la}} := \mathcal {C}^{\mathrm {la}}(G_0,M)^{G_0}$
. We have
$M^{G_0\text {-la}} := \mathcal {C}^{\mathrm {la}}(G_0,M)^{G_0}$
. We have  $$ \begin{align*}M^{G_0\text{-la}} = \varinjlim_{\lambda}M^{G_0,\lambda\text{-}\mathrm{an}} = \varinjlim_{\lambda,\mu}M^{G_0,\mathrm{an}\text{-}\lambda,\mu}.\end{align*} $$
$$ \begin{align*}M^{G_0\text{-la}} = \varinjlim_{\lambda}M^{G_0,\lambda\text{-}\mathrm{an}} = \varinjlim_{\lambda,\mu}M^{G_0,\mathrm{an}\text{-}\lambda,\mu}.\end{align*} $$
There is a natural injective map
![]() $M^{G_0\text {-la}} \hookrightarrow M$
obtained by mapping
$M^{G_0\text {-la}} \hookrightarrow M$
obtained by mapping
![]() $f:G_0\rightarrow M$
to
$f:G_0\rightarrow M$
to
![]() $f(1)$
. Thus we will interchangeably regard
$f(1)$
. Thus we will interchangeably regard
![]() $M^{G_0\text {-la}}$
as the submodule of
$M^{G_0\text {-la}}$
as the submodule of
![]() $G_0$
-locally analytic elements in M. Under this injection,
$G_0$
-locally analytic elements in M. Under this injection,
![]() $M^{G_0\text {-la}}$
is actually stable under the entire G-action (not just the
$M^{G_0\text {-la}}$
is actually stable under the entire G-action (not just the
![]() $G_0$
-action). Indeed given
$G_0$
-action). Indeed given
![]() $m \in M^{G_0\text {-la}}$
,
$m \in M^{G_0\text {-la}}$
,
![]() $g\in G$
and
$g\in G$
and
![]() $g_0 \in G_0$
, we may write
$g_0 \in G_0$
, we may write
![]() $g_0g(m)=g(g^{-1}g_0g)(m)$
. Since
$g_0g(m)=g(g^{-1}g_0g)(m)$
. Since
![]() $G_0$
is normal,
$G_0$
is normal,
![]() $g_0 \mapsto g^{-1}g_0g$
is an automorphism of
$g_0 \mapsto g^{-1}g_0g$
is an automorphism of
![]() $G_0$
, hence of
$G_0$
, hence of
![]() $\mathbf {Z}_p^d$
if we choose for c the Lie algebra coordinates; this shows that
$\mathbf {Z}_p^d$
if we choose for c the Lie algebra coordinates; this shows that
![]() $g_0 \mapsto (g^{-1}g_0g)(m)$
is still an analytic function by Lemma 2.8. Hence the same holds for
$g_0 \mapsto (g^{-1}g_0g)(m)$
is still an analytic function by Lemma 2.8. Hence the same holds for
![]() $g_0 \mapsto g(g^{-1}g_0g)(m)$
as g acts on M as an isometry.
$g_0 \mapsto g(g^{-1}g_0g)(m)$
as g acts on M as an isometry.
Lemma 2.11. If
![]() $G_0' \subset G_0$
are uniform subgroups of G then
$G_0' \subset G_0$
are uniform subgroups of G then
![]() $M^{G_0\text {-}\mathrm {la}} \subset M^{G_0'\text {-}\mathrm {la}}.$
$M^{G_0\text {-}\mathrm {la}} \subset M^{G_0'\text {-}\mathrm {la}}.$
Proof. Let
![]() $f \in \mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(G_0,M)$
. By Lemma 2.1 and condition 2 of Proposition 2.3 we have that f restricts to
$f \in \mathcal {C}^{\mathrm {an}\text {-}\lambda ,\mu }(G_0,M)$
. By Lemma 2.1 and condition 2 of Proposition 2.3 we have that f restricts to
![]() $ \mathcal {C}^{\mathrm {an}\text {-}\lambda ',\mu '}(G_0',M)$
for some
$ \mathcal {C}^{\mathrm {an}\text {-}\lambda ',\mu '}(G_0',M)$
for some
![]() $\lambda ',\mu '$
, from which the lemma follows.
$\lambda ',\mu '$
, from which the lemma follows.
Definition 2.12. The locally analytic elements of M are given by
the colimit taken over uniform normal subgroups
![]() $G_0$
of G.
$G_0$
of G.
Remark 2.13. We have made the definition above to get a concept of locally analytic vectors independent of the choice of
![]() $G_0$
, which will suffice for this article. Of course, one already expects
$G_0$
, which will suffice for this article. Of course, one already expects
![]() $M^{G_0\text {-la}}$
to be independent of the choice of
$M^{G_0\text {-la}}$
to be independent of the choice of
![]() $G_0$
, as is known in the characteristic 0 theory. We plan to address this and other foundational issues in future work.
$G_0$
, as is known in the characteristic 0 theory. We plan to address this and other foundational issues in future work.
Example 2.14.
-
1. Suppose
 $R= \mathbf {Q}_p$
so that M is a
$R= \mathbf {Q}_p$
so that M is a
 $\mathbf {Q}_p$
-vector space with
$\mathbf {Q}_p$
-vector space with
 $\mathrm {val}_M$
making it a Banach space. In this case,
$\mathrm {val}_M$
making it a Banach space. In this case,
 $M^{\mathrm {la}}$
coincides with the usual locally analytic vectors (as defined, for example, in [Reference EmertonEme17]). This is a consequence of the Amice theorem (Chapitre 3 of [Reference AmiceAmi64], see also Théorème I.4.7 of [Reference ColmezCol10]).
$M^{\mathrm {la}}$
coincides with the usual locally analytic vectors (as defined, for example, in [Reference EmertonEme17]). This is a consequence of the Amice theorem (Chapitre 3 of [Reference AmiceAmi64], see also Théorème I.4.7 of [Reference ColmezCol10]).In this setting, the
 $G_0$
-action can be differentiated and one gets an action of the Lie algebra
$G_0$
-action can be differentiated and one gets an action of the Lie algebra
 $\mathrm {Lie}(G)$
, which is a key extra structure. Unfortunately, this action seems to be unavailable outside this special case. The reason is that when p is the topologically nilpotent unit, one can link functions of the form
$\mathrm {Lie}(G)$
, which is a key extra structure. Unfortunately, this action seems to be unavailable outside this special case. The reason is that when p is the topologically nilpotent unit, one can link functions of the form
 $\binom {x}{n}$
and
$\binom {x}{n}$
and
 $x^n$
by cancelling out the p-part of the denominator of
$x^n$
by cancelling out the p-part of the denominator of
 $\binom {x}{n}$
(see the proof of Théorème I.4.7 of [Reference ColmezCol10]). But it is unclear (at least to us) how to do something of this flavor more generally.
$\binom {x}{n}$
(see the proof of Théorème I.4.7 of [Reference ColmezCol10]). But it is unclear (at least to us) how to do something of this flavor more generally. -
2. Suppose M is an
 $\mathbf {F}_p$
-vector space. In this case, one checks using Proposition 2.3 that
$\mathbf {F}_p$
-vector space. In this case, one checks using Proposition 2.3 that
 $M^{\mathrm {la}}$
coincides with the super-Hölder vectors
$M^{\mathrm {la}}$
coincides with the super-Hölder vectors
 $M^{\mathrm {sh}} \subset M$
defined in [Reference Berger and RozensztajnBR24].
$M^{\mathrm {sh}} \subset M$
defined in [Reference Berger and RozensztajnBR24]. -
3. Suppose we have a perfectoid field
 $\widehat {K}_\infty $
in characteristic 0 with an action of
$\widehat {K}_\infty $
in characteristic 0 with an action of
 $\Gamma \cong \mathbf {Z}_p$
. Recall that we can form the tilt
$\Gamma \cong \mathbf {Z}_p$
. Recall that we can form the tilt
 $\widehat {K}_\infty ^{\flat }$
which is a perfectoid field in characteristic p, and there is a multiplicative map denoted
$\widehat {K}_\infty ^{\flat }$
which is a perfectoid field in characteristic p, and there is a multiplicative map denoted
 $\sharp $
from
$\sharp $
from
 $\widehat {K}_\infty ^{\flat }$
to
$\widehat {K}_\infty ^{\flat }$
to
 $\widehat {K}_\infty $
. For
$\widehat {K}_\infty $
. For
 $x \in \widehat {K}_\infty ^{\flat ,+}$
it is given by
$x \in \widehat {K}_\infty ^{\flat ,+}$
it is given by
 $x^\sharp = \lim _{n \rightarrow \infty } y_n^{p^n}$
where the
$x^\sharp = \lim _{n \rightarrow \infty } y_n^{p^n}$
where the
 $y_n$
are any lifts of
$y_n$
are any lifts of
 $x^{1/p^n}$
to
$x^{1/p^n}$
to
 $\widehat {K}_\infty ^+.$
$\widehat {K}_\infty ^+.$
Claim. Suppose that
![]() $x^\sharp $
is
$x^\sharp $
is
![]() $\Gamma $
-smooth. Then x is locally analytic.
$\Gamma $
-smooth. Then x is locally analytic.
Indeed, without loss of generality, we may assume
![]() $x^\sharp $
is fixed by
$x^\sharp $
is fixed by
![]() $\gamma $
and
$\gamma $
and
![]() $x\in \widehat {K}_\infty ^{\flat ,+}.$
The element
$x\in \widehat {K}_\infty ^{\flat ,+}.$
The element
![]() $\gamma ^p$
fixes
$\gamma ^p$
fixes
![]() $x^{1/p}$
, because the action on the p-th roots of x gives a homomorphism
$x^{1/p}$
, because the action on the p-th roots of x gives a homomorphism
![]() $\mathbf {Z}_p \rightarrow S_n$
with
$\mathbf {Z}_p \rightarrow S_n$
with
![]() $n \leq p$
, and any such homomorphism has to factor through
$n \leq p$
, and any such homomorphism has to factor through
![]() $\mathbf {Z}/p.$
Arguing similarly by induction, we see that
$\mathbf {Z}/p.$
Arguing similarly by induction, we see that
![]() $(x^{1/p^m})^\sharp $
is fixed by
$(x^{1/p^m})^\sharp $
is fixed by
![]() $\gamma ^{p^m}$
.
$\gamma ^{p^m}$
.
Hence, we get
which is
Hence
![]() $\mathrm {val}(\gamma ^{p^m}(x)-x) \geq p^m \mathrm {val}(p)$
which shows that x is locally analytic. This concludes the proof of the claim.
$\mathrm {val}(\gamma ^{p^m}(x)-x) \geq p^m \mathrm {val}(p)$
which shows that x is locally analytic. This concludes the proof of the claim.
For example, take the cyclotomic extension for
![]() $\widehat {K}_\infty $
with
$\widehat {K}_\infty $
with
![]() $\Gamma $
being the cyclotomic group. The tilt
$\Gamma $
being the cyclotomic group. The tilt
![]() $\widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
is isomorphic to the X-adic completion of
$\widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
is isomorphic to the X-adic completion of
![]() $\cup _n \mathbf {F}_p((X^{1/p^n}))$
. The element
$\cup _n \mathbf {F}_p((X^{1/p^n}))$
. The element
![]() $X \in \widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
has
$X \in \widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
has
![]() $X^\sharp = \zeta _p - 1 \in K_\infty $
, and so is locally analytic. This is of course also easy to check directly. Let us point out that the main theorem of [Reference Berger and RozensztajnBR22] gives the much stronger
$X^\sharp = \zeta _p - 1 \in K_\infty $
, and so is locally analytic. This is of course also easy to check directly. Let us point out that the main theorem of [Reference Berger and RozensztajnBR22] gives the much stronger
(
![]() $\widetilde {\mathbf {E}}^{\mathrm {sh}}$
in their notation) which shows that taking locally analytic vectors undoes the X-adic completion. In §
$\widetilde {\mathbf {E}}^{\mathrm {sh}}$
in their notation) which shows that taking locally analytic vectors undoes the X-adic completion. In §
![]() $4$
we shall show how to deduce this result from our main theorem.
$4$
we shall show how to deduce this result from our main theorem.
In Example 2.14.3 we had a field whose locally analytic vectors were also a field. This happens in general, as shown in the following.
Lemma 2.15.
-
(i) The abelian subgroup
 $R^{\mathrm {la}} \subset R$
is a subring.
$R^{\mathrm {la}} \subset R$
is a subring. -
(ii) Let
 $r \in R^\times \cap R^{\mathrm {la}}$
. Then
$r \in R^\times \cap R^{\mathrm {la}}$
. Then
 $r^{-1}\in R^{\mathrm {la}}.$
$r^{-1}\in R^{\mathrm {la}}.$
Proof. This is similar to argument of Lemma 2.5 of [Reference Berger and ColmezBC16] which we produce here for the convenience of the reader. We may assume
![]() $G=G_0$
is a uniform subgroup and identify it analytically with
$G=G_0$
is a uniform subgroup and identify it analytically with
![]() $\mathbf {Z}_p^d$
. Recall that locally analytic functions are those for which the valuation of
$\mathbf {Z}_p^d$
. Recall that locally analytic functions are those for which the valuation of
![]() $a_{\underline {n}}$
grows at least linearly with
$a_{\underline {n}}$
grows at least linearly with
![]() $|\underline {n}|.$
For (i), note that for
$|\underline {n}|.$
For (i), note that for
![]() $\underline {n},\underline {m}\in \mathbf {Z}^d_{\geq 0}$
we have
$\underline {n},\underline {m}\in \mathbf {Z}^d_{\geq 0}$
we have
 $$ \begin{align} \binom{\underline{x}}{\underline{n}}\cdot\binom{\underline{x}}{\underline{m}}=\sum_{\underline{k}\leq\underline{n}+\underline{m}}c_{\underline{k}}\binom{\underline{x}}{\underline{k}} \end{align} $$
$$ \begin{align} \binom{\underline{x}}{\underline{n}}\cdot\binom{\underline{x}}{\underline{m}}=\sum_{\underline{k}\leq\underline{n}+\underline{m}}c_{\underline{k}}\binom{\underline{x}}{\underline{k}} \end{align} $$
for some
![]() $c_{\underline {k}} \in \mathbf {Z}.$
This proves
$c_{\underline {k}} \in \mathbf {Z}.$
This proves
![]() $R^{\mathrm {la}}$
is a ring. For (ii), write
$R^{\mathrm {la}}$
is a ring. For (ii), write
![]() $\mathrm {orb}_r(\underline {x})= r+\sum _{\underline {n} \neq 0}a_{\underline {n}}\binom {\underline {x}}{\underline {n}}$
. We have the identity
$\mathrm {orb}_r(\underline {x})= r+\sum _{\underline {n} \neq 0}a_{\underline {n}}\binom {\underline {x}}{\underline {n}}$
. We have the identity
 $$ \begin{align*}\mathrm{orb}_{1/r}(\underline{x})=\frac{1}{r}\sum_{j \geq 0}(-1)^j(\sum_{\underline{n}\neq 0}a_{\underline{n}}\binom{\underline{x}}{\underline{n}}/r)^j,\end{align*} $$
$$ \begin{align*}\mathrm{orb}_{1/r}(\underline{x})=\frac{1}{r}\sum_{j \geq 0}(-1)^j(\sum_{\underline{n}\neq 0}a_{\underline{n}}\binom{\underline{x}}{\underline{n}}/r)^j,\end{align*} $$
which is still locally analytic.
Proposition 2.16. Suppose that M is free of rank d over R, and suppose
![]() $m_1,...,m_d$
is an R-basis of M with
$m_1,...,m_d$
is an R-basis of M with
![]() $g \mapsto \mathrm {Mat}(g)$
locally analytic in each coordinate. Then
$g \mapsto \mathrm {Mat}(g)$
locally analytic in each coordinate. Then
![]() $M^{\mathrm {la}} = \oplus _i R^{\mathrm {la}} \cdot m_i.$
$M^{\mathrm {la}} = \oplus _i R^{\mathrm {la}} \cdot m_i.$
Proof. Again, we reproduce the argument of 2.3 of [Reference Berger and ColmezBC16] for the convenience of the reader. Let
![]() $a_{ij}(g)$
be the coordinates of
$a_{ij}(g)$
be the coordinates of
![]() $g\mapsto \mathrm {Mat}(g)$
. Then
$g\mapsto \mathrm {Mat}(g)$
. Then
![]() $g(m_i)=\sum _{j}a_{ij}(g)m_j,$
so each
$g(m_i)=\sum _{j}a_{ij}(g)m_j,$
so each
![]() $m_i$
is locally analytic. This proves the inclusion
$m_i$
is locally analytic. This proves the inclusion
![]() $\oplus _i R^{\mathrm {la}} \cdot m_i \subset M^{\mathrm {la}}$
. Conversely, let
$\oplus _i R^{\mathrm {la}} \cdot m_i \subset M^{\mathrm {la}}$
. Conversely, let
![]() $m \in M^{\mathrm {la}}$
. Write
$m \in M^{\mathrm {la}}$
. Write
![]() $m=\sum _i r_i m_i$
with
$m=\sum _i r_i m_i$
with
![]() $r_i \in R.$
By assumption, we may write
$r_i \in R.$
By assumption, we may write
![]() $g(m) = \sum _i f_i(g)m_i$
with each
$g(m) = \sum _i f_i(g)m_i$
with each
![]() $f_i$
locally analytic. Applying g to
$f_i$
locally analytic. Applying g to
![]() $m = \sum _i r_i m_i$
, we get the identity
$m = \sum _i r_i m_i$
, we get the identity
![]() $g(r_i) = \sum _{j}b_{ij}(g)f_j(g),$
where
$g(r_i) = \sum _{j}b_{ij}(g)f_j(g),$
where
![]() $b_{ij}(g)$
are the coordinates of
$b_{ij}(g)$
are the coordinates of
![]() $\mathrm {Mat}(g)^{-t}$
. These are polynomials in the
$\mathrm {Mat}(g)^{-t}$
. These are polynomials in the
![]() $a_{ij}(g)$
multiplied by
$a_{ij}(g)$
multiplied by
![]() $\det (g)$
, hence are locally analytic by the previous lemma.
$\det (g)$
, hence are locally analytic by the previous lemma.
2.3 Higher locally analytic elements
It will be useful for us to define a derived functor for
![]() $M \mapsto M^{\mathrm {la}}$
. As
$M \mapsto M^{\mathrm {la}}$
. As
![]() $M^{\mathrm {la}} = \varinjlim _{G_0}\mathcal {C}^{\mathrm {la}}(G_0,M)^{G_0}$
, we may extend this definition to
$M^{\mathrm {la}} = \varinjlim _{G_0}\mathcal {C}^{\mathrm {la}}(G_0,M)^{G_0}$
, we may extend this definition to
![]() $i\geq 0$
by setting
$i\geq 0$
by setting
Here we are considering continuous cocycles, taking the inductive topology on
![]() $\mathcal {C}^{\mathrm {la}}(G_0,M)$
induced from that of its submodules
$\mathcal {C}^{\mathrm {la}}(G_0,M)$
induced from that of its submodules
![]() $\mathcal {C}^{\lambda \text {-}\mathrm {an}}(G_0,M).$
$\mathcal {C}^{\lambda \text {-}\mathrm {an}}(G_0,M).$
We shall call these groups the higher locally analytic elements of M. If
is a short exact sequence of submodules in the appropriate category then we claim that we have a long exact sequence
This requires some explanation. Using the open mapping theorem in this setting (Theorem 2.2.8 of [Reference Kedlaya and LiuKL11]) we conclude that all the mappings are strict. From here the argument for exactness is the same as Lemma 2.2.2 of [Reference PanPan22].
3 Decompletion
In this section we shall prove decompletion results for G-modules M as in §
![]() $2$
under more assumptions. Subsection §
$2$
under more assumptions. Subsection §
![]() $3.1$
will state the results while the rest of the subsections will be devoted to their proof.
$3.1$
will state the results while the rest of the subsections will be devoted to their proof.
3.1 Statement of the results
The setup is as follows. Let
![]() $(\widetilde {\Lambda }, \widetilde {\Lambda }^+)$
be a pair of topological rings with
$(\widetilde {\Lambda }, \widetilde {\Lambda }^+)$
be a pair of topological rings with
![]() $\widetilde {\Lambda }^+ \subset \widetilde {\Lambda }$
and
$\widetilde {\Lambda }^+ \subset \widetilde {\Lambda }$
and
![]() $\varpi $
an element of
$\varpi $
an element of
![]() $\widetilde {\Lambda }^+$
. We assume
$\widetilde {\Lambda }^+$
. We assume
![]() $\widetilde {\Lambda }$
is a Tate algebra over
$\widetilde {\Lambda }$
is a Tate algebra over
![]() $\mathbf {Z}_p$
with
$\mathbf {Z}_p$
with
![]() $\widetilde {\Lambda }^+$
a ring of definition, and
$\widetilde {\Lambda }^+$
a ring of definition, and
![]() $\varpi $
a topologically nilpotent unit. We assume
$\varpi $
a topologically nilpotent unit. We assume
![]() $\widetilde {\Lambda }^+$
is
$\widetilde {\Lambda }^+$
is
![]() $\varpi $
-adically complete, and endow
$\varpi $
-adically complete, and endow
![]() $\widetilde {\Lambda }$
with a valuation
$\widetilde {\Lambda }$
with a valuation
![]() $\mathrm {val}_{\widetilde {\Lambda }}$
making it so that
$\mathrm {val}_{\widetilde {\Lambda }}$
making it so that
![]() $\widetilde {\Lambda }^+=\widetilde {\Lambda }^{\mathrm {val}\geq 0}$
and
$\widetilde {\Lambda }^+=\widetilde {\Lambda }^{\mathrm {val}\geq 0}$
and
![]() $\mathrm {val}_{\widetilde {\Lambda }}(\varpi x) = \mathrm {val}_{\widetilde {\Lambda }}(\varpi )+ \mathrm {val}_{\widetilde {\Lambda }}(x)$
. Finally, we assume that we are given a compact p-adic Lie group G acting on
$\mathrm {val}_{\widetilde {\Lambda }}(\varpi x) = \mathrm {val}_{\widetilde {\Lambda }}(\varpi )+ \mathrm {val}_{\widetilde {\Lambda }}(x)$
. Finally, we assume that we are given a compact p-adic Lie group G acting on
![]() $\widetilde {\Lambda }$
by isometries. We let M be a finite free module over
$\widetilde {\Lambda }$
by isometries. We let M be a finite free module over
![]() $\widetilde {\Lambda }$
, endowed with a
$\widetilde {\Lambda }$
, endowed with a
![]() $\varpi $
-adic topology and a semilinear G-action. We may choose a G-stable
$\varpi $
-adic topology and a semilinear G-action. We may choose a G-stable
![]() $\widetilde {\Lambda }^+$
-lattice
$\widetilde {\Lambda }^+$
-lattice
![]() $M^+ \subset M$
so that the topology on M is induced from the
$M^+ \subset M$
so that the topology on M is induced from the
![]() $\varpi $
-adic valuation
$\varpi $
-adic valuation
![]() $\mathrm {val}_M$
making
$\mathrm {val}_M$
making
![]() $M^+$
the open unit ball (this valuation is implicitly needed to make sense of
$M^+$
the open unit ball (this valuation is implicitly needed to make sense of
![]() $\mathrm {R}^i_{\mathrm {la}}(M)$
in what follows).
$\mathrm {R}^i_{\mathrm {la}}(M)$
in what follows).
The main result of this section is the following result which generalizes Theorem C of [Reference PoratPor24].
Theorem 3.1. Suppose that the pair
![]() $(\widetilde {\Lambda }, \widetilde {\Lambda }^+)$
satisfies the Tate-Sen axioms (TS1)-(TS4) (see §
$(\widetilde {\Lambda }, \widetilde {\Lambda }^+)$
satisfies the Tate-Sen axioms (TS1)-(TS4) (see §
![]() $3.2$
). Then
$3.2$
). Then
-
1. The natural map
is an isomorphism. $$ \begin{align*}\widetilde{\Lambda} \otimes_{\widetilde{\Lambda}^{\mathrm{la}}} M^{\mathrm{la}} \rightarrow M\end{align*} $$
$$ \begin{align*}\widetilde{\Lambda} \otimes_{\widetilde{\Lambda}^{\mathrm{la}}} M^{\mathrm{la}} \rightarrow M\end{align*} $$
-
2. If moreover the Lie algebra
 $\mathrm {Lie}(G)$
is abelian, we have
$\mathrm {Lie}(G)$
is abelian, we have
 $\mathrm {R}_{\mathrm {la}}^i(M) = 0$
for
$\mathrm {R}_{\mathrm {la}}^i(M) = 0$
for
 $i \geq 1$
.
$i \geq 1$
.
Corollary 3.2. Let M be as above, and assume further that
![]() $G\cong \mathbf {Z}_p$
. Then there exist natural isomorphisms
$G\cong \mathbf {Z}_p$
. Then there exist natural isomorphisms
for
![]() $ i\geq 0$
.
$ i\geq 0$
.
Proof. As
![]() $\Gamma \cong \mathbf {Z}_p$
we know that
$\Gamma \cong \mathbf {Z}_p$
we know that
![]() $\mathrm {H}^{i}(G,M) = \mathrm {H}^{i}(G,M^{\mathrm {la}}) = 0$
for
$\mathrm {H}^{i}(G,M) = \mathrm {H}^{i}(G,M^{\mathrm {la}}) = 0$
for
![]() $i \geq 2$
(see V, 2.2.3.3 of [Reference LazardLaz65]), while the equality for
$i \geq 2$
(see V, 2.2.3.3 of [Reference LazardLaz65]), while the equality for
![]() $i=0$
is obvious. So the only nontrivial case is
$i=0$
is obvious. So the only nontrivial case is
![]() $i=1$
. Choosing
$i=1$
. Choosing
![]() $\gamma $
for a generator of G, we have an exact sequence
$\gamma $
for a generator of G, we have an exact sequence
Taking locally analytic vectors (regarding
![]() $\mathrm {H}^{0}(G,M)$
and
$\mathrm {H}^{0}(G,M)$
and
![]() $\mathrm {H}^{1}(G,M)$
as having a trivial G-action) we obtain an exact sequence
$\mathrm {H}^{1}(G,M)$
as having a trivial G-action) we obtain an exact sequence
First, we claim
![]() $\mathrm {R}_{\mathrm {la}}^1(M/\mathrm {H}^{0}(G,M))=0$
. This is because there is an exact sequence
$\mathrm {R}_{\mathrm {la}}^1(M/\mathrm {H}^{0}(G,M))=0$
. This is because there is an exact sequence
and both of its outer terms vanish (the
![]() $\mathrm {R}_{\mathrm {la}}^1$
term because of the theorem, the
$\mathrm {R}_{\mathrm {la}}^1$
term because of the theorem, the
![]() $\mathrm {R}_{\mathrm {la}}^2$
term because
$\mathrm {R}_{\mathrm {la}}^2$
term because
![]() $\Gamma \cong \mathbf {Z}_p$
).
$\Gamma \cong \mathbf {Z}_p$
).
On the other hand, we claim that
![]() $(M/\mathrm {H}^{0}(G,M))^{\mathrm {la}} = M^{\mathrm {la}}/\mathrm {H}^{0}(G,M).$
This reduces to showing
$(M/\mathrm {H}^{0}(G,M))^{\mathrm {la}} = M^{\mathrm {la}}/\mathrm {H}^{0}(G,M).$
This reduces to showing
![]() $\mathrm {R}^1_{\mathrm {la}}(\mathrm {H}^{0}(G,M)) = 0$
; for this vanishing we need to show that
$\mathrm {R}^1_{\mathrm {la}}(\mathrm {H}^{0}(G,M)) = 0$
; for this vanishing we need to show that
![]() $\gamma -1$
acts surjectively on
$\gamma -1$
acts surjectively on
![]() $\mathcal {C}^{\mathrm {la}}(\Gamma ,\mathrm {H}^{0}(G,M))$
. Now if
$\mathcal {C}^{\mathrm {la}}(\Gamma ,\mathrm {H}^{0}(G,M))$
. Now if
![]() $\sum _n a_n \binom {x}{n} \in \mathcal {C}^{\mathrm {la}}(\Gamma ,\mathrm {H}^{0}(G,M))$
with the coordinate x corresponding to
$\sum _n a_n \binom {x}{n} \in \mathcal {C}^{\mathrm {la}}(\Gamma ,\mathrm {H}^{0}(G,M))$
with the coordinate x corresponding to
![]() $\gamma $
, then
$\gamma $
, then
![]() $(\gamma -1)(\sum _n a_n \binom {x}{n}) = \sum _n a_n \binom {x}{n-1}$
, from which the surjectivity is clearly seen.
$(\gamma -1)(\sum _n a_n \binom {x}{n}) = \sum _n a_n \binom {x}{n-1}$
, from which the surjectivity is clearly seen.
Putting the two claims together, we obtain an exact sequence
which shows
![]() $\mathrm {H}^{0}(G,M)$
is the cokernel of
$\mathrm {H}^{0}(G,M)$
is the cokernel of
![]() $M^{\mathrm {la}}\xrightarrow {\gamma -1} M^{\mathrm {la}}$
, that is to say naturally isomorphic to
$M^{\mathrm {la}}\xrightarrow {\gamma -1} M^{\mathrm {la}}$
, that is to say naturally isomorphic to
![]() $\mathrm {H}^{1}(G,M^{\mathrm {la}})$
, as required.
$\mathrm {H}^{1}(G,M^{\mathrm {la}})$
, as required.
We end this subsection with a few natural conjectures.
Conjecture 3.3. The statement of Theorem 3.1 holds for any compact p-adic Lie group G (with no assumption on
![]() $\mathrm {Lie}(G)$
).
$\mathrm {Lie}(G)$
).
The following is an analogy of Theorem 1.5 of [Reference Jacinto and CamargoRJRC22].
Conjecture 3.4. There exists a spectral sequence
Finally, we have a conjecture regarding cohomology which follows from the previous two conjectures.
Conjecture 3.5. Suppose
![]() $\widetilde {\Lambda }$
satisfies the Tate-Sen axioms (TS1)-(TS4) (see §
$\widetilde {\Lambda }$
satisfies the Tate-Sen axioms (TS1)-(TS4) (see §
![]() $3.2$
below), and that G is a compact p-adic Lie group. Then there exist natural isomorphisms
$3.2$
below), and that G is a compact p-adic Lie group. Then there exist natural isomorphisms
for
![]() $ i\geq 0$
.
$ i\geq 0$
.
3.2 The Tate-Sen method
In this section we recall the Tate-Sen method introduced in [Reference Berger and ColmezBC08] as well as some extensions of it introduced in [Reference PoratPor22b] and [Reference PoratPor24].
Let
![]() $\widetilde {\Lambda }$
and G be as in §
$\widetilde {\Lambda }$
and G be as in §
![]() $3.1$
. We let
$3.1$
. We let
![]() $G_0$
be an open and normal uniform subgroup of G (such a subgroup always exists by Corollary 4.3 of [Reference Dixon, Du Sautoy, Mann and SegalDDSMS03]). We suppose
$G_0$
be an open and normal uniform subgroup of G (such a subgroup always exists by Corollary 4.3 of [Reference Dixon, Du Sautoy, Mann and SegalDDSMS03]). We suppose
![]() $G_0$
is endowed with a continuous character
$G_0$
is endowed with a continuous character
![]() $\chi : G_0 \rightarrow \mathbf {Z}_p^\times $
with open image and let
$\chi : G_0 \rightarrow \mathbf {Z}_p^\times $
with open image and let
![]() $H_0 = \ker \chi $
. If
$H_0 = \ker \chi $
. If
![]() $g \in G_0$
, let
$g \in G_0$
, let
![]() $n(g) = \mathrm {val}_p(\chi (g)-1) \in \mathbf {Z}$
. For
$n(g) = \mathrm {val}_p(\chi (g)-1) \in \mathbf {Z}$
. For
![]() $G_0'$
an open subgroup of
$G_0'$
an open subgroup of
![]() $G_0$
, set
$G_0$
, set
![]() $H' = G_0' \cap H_0$
. Let
$H' = G_0' \cap H_0$
. Let
![]() $G_{H'}$
be the normalizer of
$G_{H'}$
be the normalizer of
![]() $H'$
in
$H'$
in
![]() $G_0$
. Note
$G_0$
. Note
![]() $G_{H'}$
is open in
$G_{H'}$
is open in
![]() $G_0$
since
$G_0$
since
![]() $G^{\prime }0 \subset G_{H'}$
. Finally let
$G^{\prime }0 \subset G_{H'}$
. Finally let
![]() $\widetilde {\Gamma }_{H'} = G_{H'}/H'$
and write
$\widetilde {\Gamma }_{H'} = G_{H'}/H'$
and write
![]() $C_{H'}$
for the center of
$C_{H'}$
for the center of
![]() $\widetilde {\Gamma }_{H'}$
. By Lemma 3.1.1 of [Reference Berger and ColmezBC08] the group
$\widetilde {\Gamma }_{H'}$
. By Lemma 3.1.1 of [Reference Berger and ColmezBC08] the group
![]() $C_{H'}$
is open in
$C_{H'}$
is open in
![]() $\widetilde {\Gamma }_{H'}$
. Let
$\widetilde {\Gamma }_{H'}$
. Let
![]() $n_1(H')$
be the smallest positive integer such that
$n_1(H')$
be the smallest positive integer such that
![]() $\chi (C_{H'})$
contains
$\chi (C_{H'})$
contains
![]() $1+p^n\mathbf {Z}_p$
.
$1+p^n\mathbf {Z}_p$
.
The Tate-Sen axioms are the following:
(TS1) There exists
![]() $c_1> 0$
such that for each pair
$c_1> 0$
such that for each pair
![]() $H_1 \subset H_2$
of open subgroups of
$H_1 \subset H_2$
of open subgroups of
![]() $H_0$
there exists
$H_0$
there exists
![]() $\alpha \in \widetilde {\Lambda }^{H_1}$
such that
$\alpha \in \widetilde {\Lambda }^{H_1}$
such that
![]() $\mathrm {val}(\alpha )> -c_1$
and
$\mathrm {val}(\alpha )> -c_1$
and
![]() $\sum _{\tau \in H_2/H_1} \tau (\alpha ) = 1$
.
$\sum _{\tau \in H_2/H_1} \tau (\alpha ) = 1$
.
(TS2) There exists
![]() $c_2> 0$
and for each open subgroup H of
$c_2> 0$
and for each open subgroup H of
![]() $H_0$
an integer
$H_0$
an integer
![]() $n(H)$
, as well as an increasing sequence
$n(H)$
, as well as an increasing sequence
![]() $(\Lambda _{H,n})_ {n\geq n(H)}$
of closed subalgebras of
$(\Lambda _{H,n})_ {n\geq n(H)}$
of closed subalgebras of
![]() $\widetilde {\Lambda }^{H}$
, each containing
$\widetilde {\Lambda }^{H}$
, each containing
![]() $\varpi ^{\pm 1}$
, and
$\varpi ^{\pm 1}$
, and
![]() $\Lambda _{H,n}$
-linear maps
$\Lambda _{H,n}$
-linear maps
![]() $R_{H,n} : \widetilde {\Lambda }^{H} \rightarrow \Lambda _{H,n}$
such that
$R_{H,n} : \widetilde {\Lambda }^{H} \rightarrow \Lambda _{H,n}$
such that
-
(1) If
 $H_1 \subset H_2$
then
$H_1 \subset H_2$
then
 $\Lambda _{H_2,n} \subset \Lambda _{H_1,n}$
and
$\Lambda _{H_2,n} \subset \Lambda _{H_1,n}$
and
 $R_{H_1,n}|_{\widetilde {\Lambda }^{H_2}} = R_{H_2,n}$
.
$R_{H_1,n}|_{\widetilde {\Lambda }^{H_2}} = R_{H_2,n}$
. -
(2)
 $R_{H,n}(x) = x$
if
$R_{H,n}(x) = x$
if
 $x \in \Lambda _{H,n}$
.
$x \in \Lambda _{H,n}$
. -
(3)
 $g(\Lambda _{H,n}) = \Lambda _{gHg^{-1},n}$
and
$g(\Lambda _{H,n}) = \Lambda _{gHg^{-1},n}$
and
 $g(R_{H,n}(x)) = R_{gHg^{-1}}(gx)$
if
$g(R_{H,n}(x)) = R_{gHg^{-1}}(gx)$
if
 $g \in G_0$
.
$g \in G_0$
. -
(4) If
 $n \geq n(H)$
and if
$n \geq n(H)$
and if
 $x \in \widetilde {\Lambda }^{H}$
then
$x \in \widetilde {\Lambda }^{H}$
then
 $\mathrm {val}(R_{H,n}(x)) \geq \mathrm {val}(x) - c_2$
.
$\mathrm {val}(R_{H,n}(x)) \geq \mathrm {val}(x) - c_2$
. -
(5) If
 $x \in \widetilde {\Lambda }^{H}$
then
$x \in \widetilde {\Lambda }^{H}$
then
 $\lim _{n\rightarrow \infty }(R_{H,n}(x)).$
$\lim _{n\rightarrow \infty }(R_{H,n}(x)).$
(TS3) There exists
![]() $c_3> 0$
and, for each open subgroup
$c_3> 0$
and, for each open subgroup
![]() $G'$
of
$G'$
of
![]() $G_0$
an integer
$G_0$
an integer
![]() $n(G') \geq n_1(H')$
where
$n(G') \geq n_1(H')$
where
![]() $H' = G' \cap H_0$
, such that if
$H' = G' \cap H_0$
, such that if
![]() $n(\gamma ) \leq n \leq n(G')$
for
$n(\gamma ) \leq n \leq n(G')$
for
![]() $\gamma \in \widetilde {\Gamma }_{H'}$
then
$\gamma \in \widetilde {\Gamma }_{H'}$
then
![]() $\gamma -1$
is invertible on
$\gamma -1$
is invertible on
![]() $X_{H',n} = (1 - R_{H',n})(\widetilde {\Lambda }^{H'})$
and
$X_{H',n} = (1 - R_{H',n})(\widetilde {\Lambda }^{H'})$
and
![]() $\mathrm {val}((\gamma - 1)^{-1}(x)) \geq \mathrm {val}(x)-c_3.$
$\mathrm {val}((\gamma - 1)^{-1}(x)) \geq \mathrm {val}(x)-c_3.$
(TS4) For any sufficiently small open
![]() $G' \subset G_0$
and
$G' \subset G_0$
and
![]() $n \geq n(G')$
, there exists a positive real number
$n \geq n(G')$
, there exists a positive real number
![]() $t = t(G', n)> 0$
such that if
$t = t(G', n)> 0$
such that if
![]() $\gamma \in G'$
and
$\gamma \in G'$
and
![]() $x \in \Lambda _{H',n}$
then
$x \in \Lambda _{H',n}$
then
![]() $\mathrm {val}((\gamma - 1)(x)) \geq \mathrm {val}(x) + t$
.
$\mathrm {val}((\gamma - 1)(x)) \geq \mathrm {val}(x) + t$
.
Note that with the exception of (TS4), this is exactly the setting of §
![]() $4.1$
of [Reference PoratPor22b], except that we do not assume
$4.1$
of [Reference PoratPor22b], except that we do not assume
![]() $\chi $
is defined on the entire group. Also, we have slightly switched notation: our
$\chi $
is defined on the entire group. Also, we have slightly switched notation: our
![]() $H',G'$
are denoted there by
$H',G'$
are denoted there by
![]() $H,G$
. We apologize for the possible confusion. We now recall some definitions and results from §
$H,G$
. We apologize for the possible confusion. We now recall some definitions and results from §
![]() $4.4$
of loc. cit. which are in turn a small variant of the content appearing in §
$4.4$
of loc. cit. which are in turn a small variant of the content appearing in §
![]() $3$
of [Reference Berger and ColmezBC08].
$3$
of [Reference Berger and ColmezBC08].
We have the following two additive tensor categories, where
![]() $G'$
is an open subgroup of
$G'$
is an open subgroup of
![]() $G_0$
:
$G_0$
:
-
(1)
 $\mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G')$
, the category of finite free
$\mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G')$
, the category of finite free
 $\widetilde {\Lambda }^+$
-semilinear representations of
$\widetilde {\Lambda }^+$
-semilinear representations of
 $G_0$
such that for some basis
$G_0$
such that for some basis
 $\mathrm {val}(\mathrm {Mat}(\gamma )-1)> c_1+2c_2+2c_3$
for
$\mathrm {val}(\mathrm {Mat}(\gamma )-1)> c_1+2c_2+2c_3$
for
 $\gamma \in G'$
.
$\gamma \in G'$
. -
(2)
 $\mathrm {Mod}^{G_0}_{\Lambda _{H',n}^+}(G')$
, the category of finite free
$\mathrm {Mod}^{G_0}_{\Lambda _{H',n}^+}(G')$
, the category of finite free
 $\Lambda _{H',n}^+$
-semilinear representations of
$\Lambda _{H',n}^+$
-semilinear representations of
 $G_0$
that are fixed by
$G_0$
that are fixed by
 $H' = G'\cap H_0$
and which have a
$H' = G'\cap H_0$
and which have a
 $c_3$
-fixed basis for the
$c_3$
-fixed basis for the
 $G'$
action, that is, for some basis
$G'$
action, that is, for some basis
 $\mathrm {val}(\mathrm {Mat}(\gamma )-I)>c_3$
for
$\mathrm {val}(\mathrm {Mat}(\gamma )-I)>c_3$
for
 $\gamma \in G'.$
$\gamma \in G'.$
Definition 3.6. Let
![]() $M^+ \in \mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G')$
. We let
$M^+ \in \mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G')$
. We let
![]() $D_{H',n}^+(M^+)$
be the union of all finitely generated
$D_{H',n}^+(M^+)$
be the union of all finitely generated
![]() $\Lambda ^+_{H',n}$
-submodules of
$\Lambda ^+_{H',n}$
-submodules of
![]() $M^+$
which are stable by
$M^+$
which are stable by
![]() $G_0$
, fixed by
$G_0$
, fixed by
![]() $H'$
and which are generated by a
$H'$
and which are generated by a
![]() $c_3$
-fixed set of generators. We let
$c_3$
-fixed set of generators. We let
![]() $D_{H',n}(M) = D_{H',n}^+(M^+)[1/\varpi ]$
.
$D_{H',n}(M) = D_{H',n}^+(M^+)[1/\varpi ]$
.
The following is Proposition 4.9 of [Reference PoratPor22b]. It uses only the axioms (TS1)-(TS3).
Proposition 3.7. Let
![]() $n \geq n(G').$
The association
$n \geq n(G').$
The association
![]() $M^+\mapsto D_{H',n}^+(M^+)$
gives an equivalence of categories from
$M^+\mapsto D_{H',n}^+(M^+)$
gives an equivalence of categories from
![]() $\mathrm {Mod}^{G_0}_{\Lambda _{H',n}^+}(G')$
to
$\mathrm {Mod}^{G_0}_{\Lambda _{H',n}^+}(G')$
to
![]() $\mathrm {Mod}^{G_0}_{\Lambda _{H',n}^+}(G')$
. The inverse functor is given by
$\mathrm {Mod}^{G_0}_{\Lambda _{H',n}^+}(G')$
. The inverse functor is given by
![]() $D^+\mapsto \widetilde {\Lambda }^+\otimes _{\Lambda _{H',n}^+}D^+.$
$D^+\mapsto \widetilde {\Lambda }^+\otimes _{\Lambda _{H',n}^+}D^+.$
A few words on this proposition are in order. This kind of Tate-Sen decompletion result has a long history going back to Tate’s paper on p-divisible groups (see §
![]() $3$
of [Reference TateTat67] for the first ancestor of these ideas). Roughly speaking, this equivalence should be viewed as a form of descent from representations where the action of
$3$
of [Reference TateTat67] for the first ancestor of these ideas). Roughly speaking, this equivalence should be viewed as a form of descent from representations where the action of
![]() $\gamma -1$
is sufficiently contracting to analytic representations. It has also been understood to have connection with p-adic Simpson theory, see, for example, Theorem 3.4 of [Reference WangWan23]. We should note that when p is topologically nilpotent in
$\gamma -1$
is sufficiently contracting to analytic representations. It has also been understood to have connection with p-adic Simpson theory, see, for example, Theorem 3.4 of [Reference WangWan23]. We should note that when p is topologically nilpotent in
![]() $\widetilde {\Lambda }$
, that is, in characteristic zero, it appears implicitly in §
$\widetilde {\Lambda }$
, that is, in characteristic zero, it appears implicitly in §
![]() $3$
of [Reference Berger and ColmezBC08], see also §
$3$
of [Reference Berger and ColmezBC08], see also §
![]() $5$
C of [Reference PoratPor24] where it was spelled out. In [Reference PoratPor22b] it was generalized to allow for
$5$
C of [Reference PoratPor24] where it was spelled out. In [Reference PoratPor22b] it was generalized to allow for
![]() $\mathbf {Z}_p$
-Tate algebra coefficients.
$\mathbf {Z}_p$
-Tate algebra coefficients.
Lemma 3.8. Let
![]() $N^+, M^+ \in \mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G')$
. Then
$N^+, M^+ \in \mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G')$
. Then
![]() $N^+ \otimes _{\widetilde {\Lambda }^+} M^+$
lies in
$N^+ \otimes _{\widetilde {\Lambda }^+} M^+$
lies in
![]() $\mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G')$
and
$\mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G')$
and
![]() $D^+_{H',n}(M^+) \otimes _{\Lambda ^+_{H',n}} D^+_{H',n}(M^+) = D^+_{H',n}(M^+ \otimes _{\widetilde {\Lambda }^+} N^+)$
.
$D^+_{H',n}(M^+) \otimes _{\Lambda ^+_{H',n}} D^+_{H',n}(M^+) = D^+_{H',n}(M^+ \otimes _{\widetilde {\Lambda }^+} N^+)$
.
Proof. Suppose
![]() $\{e_i\}_{1\leq i \leq n}$
and
$\{e_i\}_{1\leq i \leq n}$
and
![]() $\{f_j\}_{1\leq j \leq m}$
are respective bases of
$\{f_j\}_{1\leq j \leq m}$
are respective bases of
![]() $N^+$
and
$N^+$
and
![]() $M^+$
such that
$M^+$
such that
![]() $\mathrm {val}(\mathrm {Mat}_{\{e_i\}}(\gamma )-1),\mathrm {val}(\mathrm {Mat}_{\{f_j\}}(\gamma )-1)> c_1+2c_2+2c_3$
for
$\mathrm {val}(\mathrm {Mat}_{\{e_i\}}(\gamma )-1),\mathrm {val}(\mathrm {Mat}_{\{f_j\}}(\gamma )-1)> c_1+2c_2+2c_3$
for
![]() $\gamma \in G'.$
Using the identity
$\gamma \in G'.$
Using the identity
we see that
![]() $\{e_i \otimes f_j\}_{1\leq i \leq n, 1\leq j \leq m}$
is a basis of
$\{e_i \otimes f_j\}_{1\leq i \leq n, 1\leq j \leq m}$
is a basis of
![]() $N^+ \otimes _{\widetilde {\Lambda }^+} M^+$
with
$N^+ \otimes _{\widetilde {\Lambda }^+} M^+$
with
Hence,
![]() $N^+ \otimes _{\widetilde {\Lambda }^+} M^+$
lies in
$N^+ \otimes _{\widetilde {\Lambda }^+} M^+$
lies in
![]() $\mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G')$
. Next, we show that
$\mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G')$
. Next, we show that
Both the left- and right-hand side are objects of
![]() $\mathrm {Mod}^{G_0}_{\Lambda _{H',n}^+}(G')$
, so by virtue of Proposition 3.7 it is enough to show they are equal after tensoring with
$\mathrm {Mod}^{G_0}_{\Lambda _{H',n}^+}(G')$
, so by virtue of Proposition 3.7 it is enough to show they are equal after tensoring with
![]() $\widetilde {\Lambda }^+$
. To show this, we compute
$\widetilde {\Lambda }^+$
. To show this, we compute
 $$ \begin{align*} \widetilde{\Lambda}^+\otimes_{\Lambda^+_{H',n}}(D^+_{H',n}(M^+) \otimes_{\Lambda^+_{H',n}} D^+_{H',n}(M^+)) &= M^+ \otimes_{\Lambda^+_{H',n}} D^+_{H',n}(M^+) \\ &=M^+ \otimes_{\widetilde{\Lambda}^+}(\widetilde{\Lambda}^+\otimes_{\Lambda^+_{H',n}} D^+_{H',n}(M^+))\\ &= M^+ \otimes_{\widetilde{\Lambda}^+}N^+\\ &= \widetilde{\Lambda}^+\otimes_{\Lambda^+_{H',n}}D^+_{H',n}(M^+ \otimes_{\widetilde{\Lambda}^+} N^+). \end{align*} $$
$$ \begin{align*} \widetilde{\Lambda}^+\otimes_{\Lambda^+_{H',n}}(D^+_{H',n}(M^+) \otimes_{\Lambda^+_{H',n}} D^+_{H',n}(M^+)) &= M^+ \otimes_{\Lambda^+_{H',n}} D^+_{H',n}(M^+) \\ &=M^+ \otimes_{\widetilde{\Lambda}^+}(\widetilde{\Lambda}^+\otimes_{\Lambda^+_{H',n}} D^+_{H',n}(M^+))\\ &= M^+ \otimes_{\widetilde{\Lambda}^+}N^+\\ &= \widetilde{\Lambda}^+\otimes_{\Lambda^+_{H',n}}D^+_{H',n}(M^+ \otimes_{\widetilde{\Lambda}^+} N^+). \end{align*} $$
This completes the proof.
We have the following result which allows us to control the action of
![]() $\gamma -1$
on
$\gamma -1$
on
![]() $D_{H',n}(M)$
.
$D_{H',n}(M)$
.
Proposition 3.9. If (TS4) holds then there exists some element
![]() $s = s(G',n)> 0$
, independent of M, so that for
$s = s(G',n)> 0$
, independent of M, so that for
![]() $\gamma \in G'$
and
$\gamma \in G'$
and
![]() $x \in D_{H',n}(M)$
we have
$x \in D_{H',n}(M)$
we have
![]() $\mathrm {val}((\gamma -1)(x)) \geq \mathrm {val}(x) + s$
.
$\mathrm {val}((\gamma -1)(x)) \geq \mathrm {val}(x) + s$
.
Proof. We know that
![]() $D_{H',n}^+(M)^+$
has a basis of
$D_{H',n}^+(M)^+$
has a basis of
![]() $c_3$
-fixed elements. Using the identity
$c_3$
-fixed elements. Using the identity
we see that
![]() $(\gamma -1)(D_{H',n}^+(M)^+) \subset \varpi ^{s}D_{H',n}^+(M)^+$
for
$(\gamma -1)(D_{H',n}^+(M)^+) \subset \varpi ^{s}D_{H',n}^+(M)^+$
for
![]() $s = \mathrm {min}(c_3,t)$
where
$s = \mathrm {min}(c_3,t)$
where
![]() $t = t(G',n)$
is as in (TS4). If
$t = t(G',n)$
is as in (TS4). If
![]() $x \in \varpi ^n\cdot D_{H',n}^+(M)^+$
then writing
$x \in \varpi ^n\cdot D_{H',n}^+(M)^+$
then writing
![]() $x = \varpi ^n y$
and using the same identity as before we conclude that
$x = \varpi ^n y$
and using the same identity as before we conclude that
![]() $(\gamma -1)(x) \in \varpi ^{n+s}\cdot D_{H',n}^+(M)^+.$
This concludes the proof.
$(\gamma -1)(x) \in \varpi ^{n+s}\cdot D_{H',n}^+(M)^+.$
This concludes the proof.
Corollary 3.10. If (TS4) holds then
![]() $D_{H',n}(M) \subset M^{G'\text {-la}}.$
$D_{H',n}(M) \subset M^{G'\text {-la}}.$
Proof. Use the expansion
![]() $\gamma ^{x}(m)=\sum _{n\geq 0}(\gamma -1)^{n}(m)\binom {x}{n}$
for
$\gamma ^{x}(m)=\sum _{n\geq 0}(\gamma -1)^{n}(m)\binom {x}{n}$
for
![]() $x\in \mathbf {Z}_p$
.
$x\in \mathbf {Z}_p$
.
We are now in a position to prove the first part of our main theorem.
Proof of part 1 of Theorem 3.1.
For
![]() $G'$
small enough and n large enough the descent to
$G'$
small enough and n large enough the descent to
![]() $D_{H',n}$
applies (this can always be achieved because of continuity). We need to show that the natural map
$D_{H',n}$
applies (this can always be achieved because of continuity). We need to show that the natural map
is an isomorphism. We shall that show this map is an isomorphism for
![]() $G'$
small enough when
$G'$
small enough when
![]() $M^{\mathrm {la}}$
is replaced with
$M^{\mathrm {la}}$
is replaced with
![]() $M^{G'\text {-la}}$
, which suffices (the transition maps along different
$M^{G'\text {-la}}$
, which suffices (the transition maps along different
![]() $G'$
’s are then forced to be isomorphisms). By Corollary 3.10 we have
$G'$
’s are then forced to be isomorphisms). By Corollary 3.10 we have
![]() $D_{H',n} \subset M^{G'\text {-la}}$
and we know M descends to
$D_{H',n} \subset M^{G'\text {-la}}$
and we know M descends to
![]() $D_{H',n}$
, so the
$D_{H',n}$
, so the
![]() $\Lambda _{H',n}$
-basis of
$\Lambda _{H',n}$
-basis of
![]() $D_{H',n}$
gives a
$D_{H',n}$
gives a
![]() $\widetilde {\Lambda }$
-basis of M consisting of
$\widetilde {\Lambda }$
-basis of M consisting of
![]() $G'$
-locally analytic elements. By Proposition 2.16 we have
$G'$
-locally analytic elements. By Proposition 2.16 we have
![]() $M^{G' \text {-la}} = \widetilde {\Lambda }^{G'\text {-la}} \otimes _{\Lambda _{H',n}} D_{H',n}$
and so the natural isomorphism
$M^{G' \text {-la}} = \widetilde {\Lambda }^{G'\text {-la}} \otimes _{\Lambda _{H',n}} D_{H',n}$
and so the natural isomorphism
![]() $\widetilde {\Lambda } \otimes _{\Lambda _{H',n}} D_{H',n} \xrightarrow {\cong } M$
is identified with the map
$\widetilde {\Lambda } \otimes _{\Lambda _{H',n}} D_{H',n} \xrightarrow {\cong } M$
is identified with the map
![]() $\widetilde {\Lambda } \otimes _{{\Lambda }^{G'\text {-la}}} M^{G'\text {-la}} \rightarrow M$
, which concludes the proof.
$\widetilde {\Lambda } \otimes _{{\Lambda }^{G'\text {-la}}} M^{G'\text {-la}} \rightarrow M$
, which concludes the proof.
3.3 Descending analytic functions
From now on we suppose (TS1)-(TS4) hold and that
![]() $\mathrm {Lie}(G)$
is abelian. It follows that
$\mathrm {Lie}(G)$
is abelian. It follows that
![]() $G_0$
is abelian also. By Proposition 2.5 we have that
$G_0$
is abelian also. By Proposition 2.5 we have that
![]() $\mathcal {C}^{\lambda \text {-an}}(G_0,M)$
is a
$\mathcal {C}^{\lambda \text {-an}}(G_0,M)$
is a
![]() $G_0$
-module for every
$G_0$
-module for every
![]() $\lambda \in \mathbf {R}$
. Recall (Definition 2.4) that
$\lambda \in \mathbf {R}$
. Recall (Definition 2.4) that
![]() $\mathcal {C}^{\lambda \text {-an}}(G_0,M)$
is endowed with the valuation
$\mathcal {C}^{\lambda \text {-an}}(G_0,M)$
is endowed with the valuation
We set
with its induced valuation. We now note a few properties of the
![]() $\widetilde {\Lambda }$
-modules
$\widetilde {\Lambda }$
-modules
![]() $M_{\underline {n},\lambda }$
. First, each
$M_{\underline {n},\lambda }$
. First, each
![]() $M_{\underline {n},\lambda }$
is preserved under the
$M_{\underline {n},\lambda }$
is preserved under the
![]() $G_0$
-action because
$G_0$
-action because
![]() $\Delta ^{\underline {n}}$
is
$\Delta ^{\underline {n}}$
is
![]() $G_0$
-equivariant, and so is actually a
$G_0$
-equivariant, and so is actually a
![]() $G_0$
-semilinear submodule of
$G_0$
-semilinear submodule of
![]() $\mathcal {C}^{\lambda \text {-an}}(G_0,M)$
. We have
$\mathcal {C}^{\lambda \text {-an}}(G_0,M)$
. We have
![]() $M_{\underline {n},\lambda } \subset M_{\underline {n'},\lambda }$
when
$M_{\underline {n},\lambda } \subset M_{\underline {n'},\lambda }$
when
![]() $\underline {n} \leq \underline {n'}$
. The limit
$\underline {n} \leq \underline {n'}$
. The limit
![]() $\varinjlim _{\underline {n}}{M_{\underline {n},\lambda }} \subset \mathcal {C}^{\lambda \text {-an}}(G_0,M)$
, indexed over
$\varinjlim _{\underline {n}}{M_{\underline {n},\lambda }} \subset \mathcal {C}^{\lambda \text {-an}}(G_0,M)$
, indexed over
![]() $\underline {n} \in \mathbf {Z}_{\geq 0}^d$
, is dense in
$\underline {n} \in \mathbf {Z}_{\geq 0}^d$
, is dense in
![]() $\mathcal {C}^{\lambda \text {-an}}(G_0,M)$
. Let
$\mathcal {C}^{\lambda \text {-an}}(G_0,M)$
. Let
![]() $m_1, ..., m_{\mathrm {rank}(M)}$
be a
$m_1, ..., m_{\mathrm {rank}(M)}$
be a
![]() $\widetilde {\Lambda }^+$
basis of
$\widetilde {\Lambda }^+$
basis of
![]() $M^+$
, which we choose once and for all. One sees that
$M^+$
, which we choose once and for all. One sees that
![]() $M_{\underline {n},\lambda }$
is finite free over
$M_{\underline {n},\lambda }$
is finite free over
![]() $\widetilde {\Lambda }$
with a basis given by the functions
$\widetilde {\Lambda }$
with a basis given by the functions
![]() $\underline {x}\mapsto m_i\varpi ^{ \lfloor p^{\lambda }\underline {k}\rfloor }\binom {\underline {x}}{\underline {k}}$
for
$\underline {x}\mapsto m_i\varpi ^{ \lfloor p^{\lambda }\underline {k}\rfloor }\binom {\underline {x}}{\underline {k}}$
for
![]() $\underline {k}\leq \underline {n}$
and
$\underline {k}\leq \underline {n}$
and
![]() $1\leq i \leq \mathrm {rank}(M)$
. Finally we note this implies
$1\leq i \leq \mathrm {rank}(M)$
. Finally we note this implies
![]() $M_{\underline {n},\lambda }\cdot M_{\underline {n'},\lambda } \subset M_{\underline {n}+\underline {n'},\lambda }$
when
$M_{\underline {n},\lambda }\cdot M_{\underline {n'},\lambda } \subset M_{\underline {n}+\underline {n'},\lambda }$
when
![]() $M=\widetilde {\Lambda }$
.
$M=\widetilde {\Lambda }$
.
Definition 3.11.
-
1. A subgroup
 $G_0$
is called c-small if
$G_0$
is called c-small if
 $\mathrm {val}(g-1)(\varpi )> c$
and if
$\mathrm {val}(g-1)(\varpi )> c$
and if
 $\mathrm {val}(g-1)(m_i) \geq c$
for each basis element
$\mathrm {val}(g-1)(m_i) \geq c$
for each basis element
 $m_i$
.
$m_i$
. -
2. An element
 $\lambda \in \mathbf {R}$
is called c-small if
$\lambda \in \mathbf {R}$
is called c-small if
 $\lambda> \log _p(c+1).$
$\lambda> \log _p(c+1).$
-
3. We say a pair
 $(G_0,\lambda )$
is c-small if both
$(G_0,\lambda )$
is c-small if both
 $G_0$
and
$G_0$
and
 $\lambda $
are c-small.
$\lambda $
are c-small.
Warning 3.12. The functoriality of c-smallness does not coincide with that of
![]() $(G_0, \lambda ) \mapsto \mathcal {C}^{\lambda \text {-an}}(G_0,M)$
. Namely, if the pair
$(G_0, \lambda ) \mapsto \mathcal {C}^{\lambda \text {-an}}(G_0,M)$
. Namely, if the pair
![]() $(G_0, \lambda )$
maps to the pair
$(G_0, \lambda )$
maps to the pair
![]() $(G_0', \lambda ')$
in the direct limit defining the
$(G_0', \lambda ')$
in the direct limit defining the
![]() $\mathrm {R}^{i}_{\mathrm {la}}$
then it is not true in general that
$\mathrm {R}^{i}_{\mathrm {la}}$
then it is not true in general that
![]() $(G_0', \lambda ')$
is still c-small. This is because
$(G_0', \lambda ')$
is still c-small. This is because
![]() $(G_0, \lambda )$
maps to
$(G_0, \lambda )$
maps to
![]() $(G_0', \lambda ')$
when
$(G_0', \lambda ')$
when
![]() $G_0' \subset G_0$
and
$G_0' \subset G_0$
and
![]() $\lambda ' \leq \lambda $
, but the c-smallness of
$\lambda ' \leq \lambda $
, but the c-smallness of
![]() $(G_0', \lambda ')$
is only guaranteed when
$(G_0', \lambda ')$
is only guaranteed when
![]() $\lambda ' \geq \lambda $
.
$\lambda ' \geq \lambda $
.
Lemma 3.13. Let
![]() $c> 0$
,
$c> 0$
,
![]() $\lambda \in \mathbf {R}$
and
$\lambda \in \mathbf {R}$
and
![]() $G_0$
a subgroup.
$G_0$
a subgroup.
-
1. If
 $G_0$
is c-small then there exists some
$G_0$
is c-small then there exists some
 $l \geq 0$
depending on
$l \geq 0$
depending on
 $\lambda $
and c such that for every
$\lambda $
and c such that for every
 $g \in G_l$
and for every
$g \in G_l$
and for every
 $\underline {n}$
one has
$\underline {n}$
one has
 $\mathrm {val}(\mathrm {Mat}(g)-I) \geq c$
for
$\mathrm {val}(\mathrm {Mat}(g)-I) \geq c$
for
 $M_{\underline {n},\lambda }$
(taking the
$M_{\underline {n},\lambda }$
(taking the
 $\widetilde {\Lambda }$
-basis described above).
$\widetilde {\Lambda }$
-basis described above). -
2. If
 $(G_0, \lambda )$
is c-small, one can take
$(G_0, \lambda )$
is c-small, one can take
 $l=0$
in 1.
$l=0$
in 1.
Proof. Each basis element of each
![]() $M_{\underline {n},\lambda }$
is of the form
$M_{\underline {n},\lambda }$
is of the form
![]() $m_i\varpi ^{\lfloor p^{\lambda }\underline {k} \rfloor }\binom {\underline {x}}{\underline {k}}$
for some
$m_i\varpi ^{\lfloor p^{\lambda }\underline {k} \rfloor }\binom {\underline {x}}{\underline {k}}$
for some
![]() $m_i$
for
$m_i$
for
![]() $1 \leq i \leq \mathrm {rank}(M)$
and
$1 \leq i \leq \mathrm {rank}(M)$
and
![]() $\underline {k} \leq {\underline {n}}.$
Using the identity
$\underline {k} \leq {\underline {n}}.$
Using the identity
one reduces to showing each of the valuations of
![]() $(g-1)(m_i)$
,
$(g-1)(m_i)$
,
![]() $(g-1)(\varpi ^{\lfloor p^{\lambda }\underline {k} \rfloor })$
and
$(g-1)(\varpi ^{\lfloor p^{\lambda }\underline {k} \rfloor })$
and
![]() $(g-1)(\binom {\underline {x}}{\underline {k}})$
are
$(g-1)(\binom {\underline {x}}{\underline {k}})$
are
![]() $> c$
.
$> c$
.
First, the valuation of the
![]() $(g-1)(m_i)$
is
$(g-1)(m_i)$
is
![]() $> c$
by the c-smallness of
$> c$
by the c-smallness of
![]() $G_0$
. Second, the valuation of the term
$G_0$
. Second, the valuation of the term
![]() $(g-1)(\varpi ^{\lfloor p^{\lambda }\underline {k} \rfloor })$
is
$(g-1)(\varpi ^{\lfloor p^{\lambda }\underline {k} \rfloor })$
is
![]() $\geq \mathrm {val}((g-1)(\varpi ))> c$
by virtue of the identity
$\geq \mathrm {val}((g-1)(\varpi ))> c$
by virtue of the identity
![]() $(g-1)(\varpi ^n) = (g-1)(\varpi ^{n-1})g(\varpi )+(g-1)(\varpi )\varpi .$
$(g-1)(\varpi ^n) = (g-1)(\varpi ^{n-1})g(\varpi )+(g-1)(\varpi )\varpi .$
Finally, we need to estimate
![]() $(g-1)(\binom {\underline {x}}{\underline {k}})$
. First, by using the identity
$(g-1)(\binom {\underline {x}}{\underline {k}})$
. First, by using the identity
we may reduce to the case where g is a basis element, and hence its action is given by
![]() $\mathrm {sh}_{p^l1_i}$
for some
$\mathrm {sh}_{p^l1_i}$
for some
![]() $1 \leq i \leq d$
. We then have the Vandermonde identity
$1 \leq i \leq d$
. We then have the Vandermonde identity
 $$ \begin{align*}(\mathrm{sh}_{p^l 1_i}-1)(\binom{\underline{x}}{\underline{k}}) = \sum_{j=1}^{k_i}\binom{\underline{x}}{\underline{k}-j1_i}\binom{p^l}{j}.\end{align*} $$
$$ \begin{align*}(\mathrm{sh}_{p^l 1_i}-1)(\binom{\underline{x}}{\underline{k}}) = \sum_{j=1}^{k_i}\binom{\underline{x}}{\underline{k}-j1_i}\binom{p^l}{j}.\end{align*} $$
We have
![]() $\mathrm {val}_{ \lambda }(\binom {\underline {x}}{\underline {k}}) = -\lfloor p^\lambda \underline {k} \rfloor $
and
$\mathrm {val}_{ \lambda }(\binom {\underline {x}}{\underline {k}}) = -\lfloor p^\lambda \underline {k} \rfloor $
and
![]() $\mathrm {val}_{ \lambda }(\binom {\underline {x}}{\underline {k}-j1_i} = -\lfloor p^\lambda (\underline {k}-j1_i) \rfloor $
, so it suffices to show
$\mathrm {val}_{ \lambda }(\binom {\underline {x}}{\underline {k}-j1_i} = -\lfloor p^\lambda (\underline {k}-j1_i) \rfloor $
, so it suffices to show
 $$ \begin{align*}-\lfloor p^\lambda(\underline{k}-j1_i) \rfloor + \mathrm{val}(\binom{p^l}{j})> -\lfloor p^\lambda\underline{k} \rfloor+c\end{align*} $$
$$ \begin{align*}-\lfloor p^\lambda(\underline{k}-j1_i) \rfloor + \mathrm{val}(\binom{p^l}{j})> -\lfloor p^\lambda\underline{k} \rfloor+c\end{align*} $$
for every
![]() $j \leq k_i$
. This inequality follows in turn from the simpler inequality
$j \leq k_i$
. This inequality follows in turn from the simpler inequality
 $$ \begin{align*}\lfloor p^\lambda j \rfloor + \mathrm{val}(\binom{p^l}{j})> c.\end{align*} $$
$$ \begin{align*}\lfloor p^\lambda j \rfloor + \mathrm{val}(\binom{p^l}{j})> c.\end{align*} $$
If
![]() $(G_0,\lambda )$
is c-small then
$(G_0,\lambda )$
is c-small then
![]() $p^\lambda> c + 1$
and the inequality holds for all
$p^\lambda> c + 1$
and the inequality holds for all
![]() $j \geq 1$
and
$j \geq 1$
and
![]() $l=0$
. Otherwise, it is clear one can choose l large enough so that the inequality holds for all
$l=0$
. Otherwise, it is clear one can choose l large enough so that the inequality holds for all
![]() $j \geq 1$
.
$j \geq 1$
.
Now choose any
![]() $c> c_1 + 2c_2 + 2c_3$
, and suppose
$c> c_1 + 2c_2 + 2c_3$
, and suppose
![]() $(G_0,\lambda )$
is c-small. From the lemma, each
$(G_0,\lambda )$
is c-small. From the lemma, each
![]() $M_{\underline {i},\lambda }^+$
lies in the category
$M_{\underline {i},\lambda }^+$
lies in the category
![]() $\mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G_0)$
. By the Tate-Sen method we have
$\mathrm {Mod}^{G_0}_{\widetilde {\Lambda }^+}(G_0)$
. By the Tate-Sen method we have
![]() $\Lambda _{H_0,n}^+$
-modules
$\Lambda _{H_0,n}^+$
-modules
![]() $D_{H_0,n}^+(M_{\underline {i},\lambda }^+)$
lying in
$D_{H_0,n}^+(M_{\underline {i},\lambda }^+)$
lying in
![]() $\mathrm {Mod}^{G_0}_{\Lambda _{H_0,n}^+}(G_0)$
for
$\mathrm {Mod}^{G_0}_{\Lambda _{H_0,n}^+}(G_0)$
for
![]() $n \geq n_0(M,\lambda )$
. The
$n \geq n_0(M,\lambda )$
. The
![]() $D_{H_0,n}^+(M_{\underline {i},\lambda }^+)$
form a direct system, and we set
$D_{H_0,n}^+(M_{\underline {i},\lambda }^+)$
form a direct system, and we set
and
![]() $D^{\lambda }_{H_0,n}(M) = D^{\lambda ,+}_{H_0,n}(M^+)[1/\varpi ].$
$D^{\lambda }_{H_0,n}(M) = D^{\lambda ,+}_{H_0,n}(M^+)[1/\varpi ].$
The natural isomorphisms
glue to an isomorphism
exhibiting
![]() $\mathcal {C}^{\lambda \text {-an}}(G_0,M)^+$
as a descent of
$\mathcal {C}^{\lambda \text {-an}}(G_0,M)^+$
as a descent of
![]() $D^{\lambda ,+}_{H_0,n}(M^+)$
.
$D^{\lambda ,+}_{H_0,n}(M^+)$
.
If we only assume that
![]() $G_0$
is c-small (but no assumptions on
$G_0$
is c-small (but no assumptions on
![]() $\lambda $
) then we still get a descent, but now each
$\lambda $
) then we still get a descent, but now each
![]() $M_{\underline {i},\lambda }^+$
only lies in
$M_{\underline {i},\lambda }^+$
only lies in
![]() $\mathrm {Mod}^{G_l}_{\widetilde {\Lambda }^+}(G_0)$
for some
$\mathrm {Mod}^{G_l}_{\widetilde {\Lambda }^+}(G_0)$
for some
![]() $l \geq 0$
. In this case, we only get a descent to a module
$l \geq 0$
. In this case, we only get a descent to a module
![]() $D_{H_l,n}^+(M_{\underline {i},\lambda }^+)$
lying in
$D_{H_l,n}^+(M_{\underline {i},\lambda }^+)$
lying in
![]() $\mathrm {Mod}^{G_l}_{\Lambda _{H_l,n}^+}(G_0)$
and an isomorphism
$\mathrm {Mod}^{G_l}_{\Lambda _{H_l,n}^+}(G_0)$
and an isomorphism
In the c-small case the module
![]() $D^{\lambda ,+}_{H_0,n}(M)$
admits an alternative description.
$D^{\lambda ,+}_{H_0,n}(M)$
admits an alternative description.
Proposition 3.14. Let
![]() $(G_0,\lambda )$
be a c-small pair and suppose we have chosen coordinates of
$(G_0,\lambda )$
be a c-small pair and suppose we have chosen coordinates of
![]() $G_0$
such that
$G_0$
such that
![]() $G_0 \cong \Gamma _0 \times H_0$
with
$G_0 \cong \Gamma _0 \times H_0$
with
![]() $\Gamma _0$
corresponding to the 1st coordinate and
$\Gamma _0$
corresponding to the 1st coordinate and
![]() $H_0$
corresponds to the other coordinates.
$H_0$
corresponds to the other coordinates.
Then there is a natural isomorphism
Proof. Given
![]() $\underline {k} \in \mathbf {Z}^d_{\geq 0}$
let
$\underline {k} \in \mathbf {Z}^d_{\geq 0}$
let
![]() ${\underline {k}}_{\Gamma _0}$
denote the first coordinate of
${\underline {k}}_{\Gamma _0}$
denote the first coordinate of
![]() $\underline {k}$
(corresponding to
$\underline {k}$
(corresponding to
![]() $\Gamma _0$
) and let
$\Gamma _0$
) and let
![]() ${\underline {k}}_{H_0}$
denote
${\underline {k}}_{H_0}$
denote
![]() $\underline {k}$
without the first coordinate (corresponding to
$\underline {k}$
without the first coordinate (corresponding to
![]() $H_0$
). The description of the
$H_0$
). The description of the
![]() $\widetilde {\Lambda }^+$
-basis of
$\widetilde {\Lambda }^+$
-basis of
![]() $M^+_{\underline {k},\lambda }$
shows that there is an isomorphism
$M^+_{\underline {k},\lambda }$
shows that there is an isomorphism
which can be rewritten as
Now one observes that
![]() $\mathcal {C}^{\lambda \text {-an}}( \Gamma _0,\widetilde {\Lambda }^+)^{\Delta ^{\underline {k}_{\Gamma _0}}=0}$
has a basis given by
$\mathcal {C}^{\lambda \text {-an}}( \Gamma _0,\widetilde {\Lambda }^+)^{\Delta ^{\underline {k}_{\Gamma _0}}=0}$
has a basis given by
![]() $\varpi ^{\lfloor p^\lambda m \rfloor }\binom {x}{m}$
for
$\varpi ^{\lfloor p^\lambda m \rfloor }\binom {x}{m}$
for
![]() $0 \leq m < \underline {k}_{\Gamma _0}.$
It is c-fixed for the
$0 \leq m < \underline {k}_{\Gamma _0}.$
It is c-fixed for the
![]() $\Gamma _0$
-action because
$\Gamma _0$
-action because
![]() $(G_0,\lambda )$
is c-small (this is the same argument appearing in Lemma 3.13). Hence by Proposition 4.10 of [Reference PoratPor22b] there is a natural isomorphism
$(G_0,\lambda )$
is c-small (this is the same argument appearing in Lemma 3.13). Hence by Proposition 4.10 of [Reference PoratPor22b] there is a natural isomorphism
We then conclude by applying Lemma 3.8, taking the limit over
![]() $\underline {k}$
and taking the completion.
$\underline {k}$
and taking the completion.
3.4 Cohomology of c-small pairs
Choose any
![]() $c> c_1 + 2c_2 + 2c_3$
and fix a c-small pair
$c> c_1 + 2c_2 + 2c_3$
and fix a c-small pair
![]() $(G_0,\lambda ).$
In this subsection we shall simplify the
$(G_0,\lambda ).$
In this subsection we shall simplify the
![]() $G_0$
-cohomology of
$G_0$
-cohomology of
![]() $\mathcal {C}^{\lambda \text {-an}}(G_0,M)$
.
$\mathcal {C}^{\lambda \text {-an}}(G_0,M)$
.
For every
![]() $\lambda $
and
$\lambda $
and
![]() $n\geq n_0(M,\lambda )$
we have modules
$n\geq n_0(M,\lambda )$
we have modules
![]() $D^{\lambda ,+}_{H_0,n}(M^+)$
defined as in (4). In what follows, whenever we compute inside a cohomology group depending on
$D^{\lambda ,+}_{H_0,n}(M^+)$
defined as in (4). In what follows, whenever we compute inside a cohomology group depending on
![]() $\lambda $
and involving n, we are going to implicitly assume
$\lambda $
and involving n, we are going to implicitly assume
![]() $n \geq n_0(M,\lambda )$
so that
$n \geq n_0(M,\lambda )$
so that
![]() $D^{\lambda ,+}_{H_0,n}(M^+)$
is defined. We set
$D^{\lambda ,+}_{H_0,n}(M^+)$
is defined. We set
![]() $\Gamma _0 = G_0/H_0$
, which is isomorphic to
$\Gamma _0 = G_0/H_0$
, which is isomorphic to
![]() $\mathbf {Z}_p$
(for sufficiently small
$\mathbf {Z}_p$
(for sufficiently small
![]() $G_0$
).
$G_0$
).
Proposition 3.15. For
![]() $i \geq 0$
we have natural isomorphisms
$i \geq 0$
we have natural isomorphisms
Proof. Inverting
![]() $\varpi $
in the isomorphism (5), we have natural isomorphisms
$\varpi $
in the isomorphism (5), we have natural isomorphisms
By Proposition 5.8 of [Reference PoratPor24], the cohomology
![]() $\mathrm {H}^i(H_0,\mathcal {C}^{\lambda \text {-an}}(G_0,M))$
is zero for
$\mathrm {H}^i(H_0,\mathcal {C}^{\lambda \text {-an}}(G_0,M))$
is zero for
![]() $i \ge 1$
. Note that in that setting one assumes that the valuation is p-adic, but the same proof works for a
$i \ge 1$
. Note that in that setting one assumes that the valuation is p-adic, but the same proof works for a
![]() $\varpi $
-adic valuation defined by an arbitrary topologically nilpotent unit
$\varpi $
-adic valuation defined by an arbitrary topologically nilpotent unit
![]() $\varpi $
. We conclude the proof by applying the Hochschild-Serre spectral sequence (see [Reference KedlayaKed16, Lemma 3.3] for a version which applies in our setting).
$\varpi $
. We conclude the proof by applying the Hochschild-Serre spectral sequence (see [Reference KedlayaKed16, Lemma 3.3] for a version which applies in our setting).
Recall that we have maps
![]() $R_{H_0,n}: \widetilde {\Lambda }^{H_0} \rightarrow \Lambda _{H_0,n}$
which are projections. Setting
$R_{H_0,n}: \widetilde {\Lambda }^{H_0} \rightarrow \Lambda _{H_0,n}$
which are projections. Setting
![]() $X_{H_0,n} = \ker R_{H_0,n}$
, we obtain a decomposition
$X_{H_0,n} = \ker R_{H_0,n}$
, we obtain a decomposition
![]() $\widetilde {\Lambda }^{H_0} \cong X_{H_0,n} \oplus \Lambda _{H_0,n}$
. This allows us to write a
$\widetilde {\Lambda }^{H_0} \cong X_{H_0,n} \oplus \Lambda _{H_0,n}$
. This allows us to write a
![]() $\Gamma _0$
-equivariant decomposition
$\Gamma _0$
-equivariant decomposition
and hence for
![]() $i \geq 1$
$i \geq 1$
In particular, for
![]() $i \geq 2$
the cohomology is zero because
$i \geq 2$
the cohomology is zero because
![]() $\Gamma _0 \cong \mathbf {Z}_p.$
$\Gamma _0 \cong \mathbf {Z}_p.$
Proposition 3.16. We have
![]() $\mathrm {H}^1(\Gamma _0,X_{H_0,n}\otimes _{\Lambda _{H_0,n}} D^{\lambda }_{H_0,n}) = 0.$
$\mathrm {H}^1(\Gamma _0,X_{H_0,n}\otimes _{\Lambda _{H_0,n}} D^{\lambda }_{H_0,n}) = 0.$
Proof. In the above decomposition of the
![]() $\Gamma _0$
-cohomology of
$\Gamma _0$
-cohomology of
the left-hand side does not depend on n. Hence, the same holds for the right-hand side. Therefore, it suffices to show that
Write
![]() $\gamma $
for a generator of
$\gamma $
for a generator of
![]() $\Gamma _0$
. It suffices to show that every
$\Gamma _0$
. It suffices to show that every
is in the image of
![]() $\gamma -1$
for some
$\gamma -1$
for some
![]() $X_{H_0,n'} \otimes _{\Lambda _{H_0,n'}} D_{H_0,n'}^{\lambda }(M)$
, with
$X_{H_0,n'} \otimes _{\Lambda _{H_0,n'}} D_{H_0,n'}^{\lambda }(M)$
, with
![]() $n'$
depending only on n.
$n'$
depending only on n.
By Proposition 3.9, we know that there exists some
![]() $s> 0$
such that
$s> 0$
such that
For some power
![]() $\gamma '$
of
$\gamma '$
of
![]() $\gamma $
we therefore have
$\gamma $
we therefore have
Take
![]() $n' \geq n$
so that
$n' \geq n$
so that
![]() $n(\gamma ') \leq n'$
. For such
$n(\gamma ') \leq n'$
. For such
![]() $n'$
, we know that
$n'$
, we know that
![]() $\mathrm {val}{(\gamma '-1)(x)}\geq \mathrm {val}(x)-c_2$
for
$\mathrm {val}{(\gamma '-1)(x)}\geq \mathrm {val}(x)-c_2$
for
![]() $x \in X_{H_0,n'}$
.
$x \in X_{H_0,n'}$
.
Let
![]() $\alpha $
be such that
$\alpha $
be such that
![]() $(\gamma ^{\prime -1}-1)(\alpha ) = a$
. Consider the series
$(\gamma ^{\prime -1}-1)(\alpha ) = a$
. Consider the series
 $$ \begin{align*}y = \sum_{i=0}^\infty (\gamma^{\prime-1}-1)^{-i}(\alpha) \otimes (\gamma'-1)^{i}(b).\end{align*} $$
$$ \begin{align*}y = \sum_{i=0}^\infty (\gamma^{\prime-1}-1)^{-i}(\alpha) \otimes (\gamma'-1)^{i}(b).\end{align*} $$
The series converges because
![]() $\mathrm {val}(\gamma ^{\prime -1}-1)^{-1}(x) \geq \mathrm {val}(x) -c_3$
while
$\mathrm {val}(\gamma ^{\prime -1}-1)^{-1}(x) \geq \mathrm {val}(x) -c_3$
while
![]() $\mathrm {val}((\gamma '-1)(x))\geq \mathrm {val}(x) +2c_3$
by our choice of
$\mathrm {val}((\gamma '-1)(x))\geq \mathrm {val}(x) +2c_3$
by our choice of
![]() $n'$
. A direct computation shows that
$n'$
. A direct computation shows that
![]() $(\gamma '-1)(y) = a \otimes b$
. As
$(\gamma '-1)(y) = a \otimes b$
. As
![]() $\gamma '-1$
is divisible by
$\gamma '-1$
is divisible by
![]() $\gamma -1$
, this proves
$\gamma -1$
, this proves
![]() $a \otimes b$
is in the image of
$a \otimes b$
is in the image of
![]() $\gamma -1$
, as required.
$\gamma -1$
, as required.
Putting this all together, we get
Theorem 3.17. Let
![]() $c> c_1 + 2c_2+ 2c_3$
and let
$c> c_1 + 2c_2+ 2c_3$
and let
![]() $(G_0,\lambda )$
be a c-small pair. Then
$(G_0,\lambda )$
be a c-small pair. Then
![]() $\mathrm {H}^i(G_0,\mathcal {C}^{\lambda \text {-an}}(G_0,M)) = 0$
for
$\mathrm {H}^i(G_0,\mathcal {C}^{\lambda \text {-an}}(G_0,M)) = 0$
for
![]() $i \geq 2$
, and
$i \geq 2$
, and
3.5 Vanishing of higher locally analytic vectors
Recall that
In this subsection we shall complete the proof of Theorem 3.1 by showing that
![]() $\mathrm {R}^i_{\mathrm {la}}(M) = 0$
for
$\mathrm {R}^i_{\mathrm {la}}(M) = 0$
for
![]() $i\geq 1$
.
$i\geq 1$
.
Proof. As always, we fix some
![]() $c> c_1 +2c_2 + 2c_3$
. We claim that c-small pairs
$c> c_1 +2c_2 + 2c_3$
. We claim that c-small pairs
![]() $(G_0,\lambda )$
are cofinal in the above direct limit. This is a consequence of Corollary 2.7 together with the observation that if
$(G_0,\lambda )$
are cofinal in the above direct limit. This is a consequence of Corollary 2.7 together with the observation that if
![]() $G_0$
is c-small, so is
$G_0$
is c-small, so is
![]() $G_l$
. In particular, we have seen that
$G_l$
. In particular, we have seen that
![]() $\mathrm {H}^i(G_0,\mathcal {C}^{\lambda \text {-an}}(G_0,M) = 0$
for
$\mathrm {H}^i(G_0,\mathcal {C}^{\lambda \text {-an}}(G_0,M) = 0$
for
![]() $i\geq 2$
and c-small pairs
$i\geq 2$
and c-small pairs
![]() $(G_0,\lambda )$
, so it automatically follows that
$(G_0,\lambda )$
, so it automatically follows that
![]() $\mathrm {R}^i_{\mathrm {la}}(M) = 0$
for
$\mathrm {R}^i_{\mathrm {la}}(M) = 0$
for
![]() $i \geq 2$
. The nontrivial part is showing the vanishing of
$i \geq 2$
. The nontrivial part is showing the vanishing of
![]() $\mathrm {R}^1_{\mathrm {la}}(M).$
Using the cofinality of c-small pairs, this is a consequence of the following proposition.
$\mathrm {R}^1_{\mathrm {la}}(M).$
Using the cofinality of c-small pairs, this is a consequence of the following proposition.
Proposition 3.18. Let
![]() $(G_0,\lambda )$
be a c-small pair and let
$(G_0,\lambda )$
be a c-small pair and let
![]() $f\in \mathrm {H}^1(G_0,\mathcal {C}^{\lambda \text {-an}}(G_0,M))$
. Then there exist some
$f\in \mathrm {H}^1(G_0,\mathcal {C}^{\lambda \text {-an}}(G_0,M))$
. Then there exist some
![]() $l \geq 0$
and some
$l \geq 0$
and some
![]() $\lambda ' \leq \lambda $
so that f is mapped to
$\lambda ' \leq \lambda $
so that f is mapped to
![]() $0$
in
$0$
in
![]() $\mathrm {H}^1(G_l,\mathcal {C}^{\lambda ' \text {-an}}(G_l,M)).$
$\mathrm {H}^1(G_l,\mathcal {C}^{\lambda ' \text {-an}}(G_l,M)).$
Proof. Recall that in 3.17 we have shown an isomorphism for
![]() $n \geq n(M,\lambda )$
$n \geq n(M,\lambda )$
and so
![]() $f \in \mathrm {H}^1(\Gamma _0,D_{H_0,n}(M)).$
Using
$f \in \mathrm {H}^1(\Gamma _0,D_{H_0,n}(M)).$
Using
![]() $\mathrm {H}^1(\Gamma _0,D_{H_0,n}(M)) \cong D_{H_0,n}(M)/(\gamma -1),$
we may think of f as an element of
$\mathrm {H}^1(\Gamma _0,D_{H_0,n}(M)) \cong D_{H_0,n}(M)/(\gamma -1),$
we may think of f as an element of
![]() $D_{H_0,n}(M)$
. Let
$D_{H_0,n}(M)$
. Let
![]() $s = s(G_0,n)$
be the constant appearing in Proposition 3.9, and choose
$s = s(G_0,n)$
be the constant appearing in Proposition 3.9, and choose
![]() $\lambda '$
small enough that
$\lambda '$
small enough that
![]() $p^{\lambda '} < s$
. Choose
$p^{\lambda '} < s$
. Choose
![]() $l \geq 0$
large enough so that 1 of Lemma 3.13 applies. We are going to show that f is mapped to
$l \geq 0$
large enough so that 1 of Lemma 3.13 applies. We are going to show that f is mapped to
![]() $0$
in
$0$
in
![]() $\mathrm {H}^1(G_l,\mathcal {C}^{\lambda ' \text {-an}}(G_l,M)).$
$\mathrm {H}^1(G_l,\mathcal {C}^{\lambda ' \text {-an}}(G_l,M)).$
By Proposition 3.14 we may write f as function (in the variable of
![]() $\Gamma _0$
)
$\Gamma _0$
)
 $$ \begin{align*}f(x) = \sum_{n \geq 0}{m_n}\binom{x}{n}\end{align*} $$
$$ \begin{align*}f(x) = \sum_{n \geq 0}{m_n}\binom{x}{n}\end{align*} $$
where
![]() $m_n \in D^{\lambda }_{H_0,n}(\mathcal {C}^{\lambda \text {-an}}(H_0,M))$
and
$m_n \in D^{\lambda }_{H_0,n}(\mathcal {C}^{\lambda \text {-an}}(H_0,M))$
and
![]() $\mathrm {val}_\lambda (m_n) - \lfloor p^\lambda n \rfloor \rightarrow \infty .$
$\mathrm {val}_\lambda (m_n) - \lfloor p^\lambda n \rfloor \rightarrow \infty .$
Consider now the function given by
 $$ \begin{align*}F(x) = \sum_{k \geq 0} (-1)^k \sum_{n \geq 0} (\gamma-1)^k(\gamma^{-k}(m_n))\binom{x}{n+k+1}.\end{align*} $$
$$ \begin{align*}F(x) = \sum_{k \geq 0} (-1)^k \sum_{n \geq 0} (\gamma-1)^k(\gamma^{-k}(m_n))\binom{x}{n+k+1}.\end{align*} $$
Recalling that
![]() $\gamma $
acts on
$\gamma $
acts on
![]() $\binom {x}{n+k+1}$
by shifts, one easily checks that
$\binom {x}{n+k+1}$
by shifts, one easily checks that
![]() $(\gamma -1)(F) = f.$
The problem is that this sum is not guaranteed to converge in
$(\gamma -1)(F) = f.$
The problem is that this sum is not guaranteed to converge in
![]() $D^{\lambda }_{H_0,n}(M)$
. Indeed, what we have is
$D^{\lambda }_{H_0,n}(M)$
. Indeed, what we have is
and
 $$ \begin{align*}\mathrm{val}_\lambda(\binom{x}{n+k+1}) = -\lfloor p^\lambda (n+k+1)\rfloor\end{align*} $$
$$ \begin{align*}\mathrm{val}_\lambda(\binom{x}{n+k+1}) = -\lfloor p^\lambda (n+k+1)\rfloor\end{align*} $$
so we get the estimate
 $$ \begin{align*}\mathrm{val}_\lambda((\gamma-1)^k(\gamma^{-k}(m_n))\binom{x}{n+k+1}) \geq k(s-p^\lambda) + (\mathrm{val}_{\lambda}(m_n) - \lfloor p^\lambda n \rfloor) + O(1).\end{align*} $$
$$ \begin{align*}\mathrm{val}_\lambda((\gamma-1)^k(\gamma^{-k}(m_n))\binom{x}{n+k+1}) \geq k(s-p^\lambda) + (\mathrm{val}_{\lambda}(m_n) - \lfloor p^\lambda n \rfloor) + O(1).\end{align*} $$
This estimate would be good enough (i.e., tend to
![]() $\infty $
as
$\infty $
as
![]() $k, n \rightarrow \infty $
) if we had
$k, n \rightarrow \infty $
) if we had
![]() $s> p^\lambda .$
Unfortunately, there is no reason why this would be the case.
$s> p^\lambda .$
Unfortunately, there is no reason why this would be the case.
There is a trick which fixes this problem: the estimate is good enough when
![]() $\lambda $
is replaced with
$\lambda $
is replaced with
![]() $\lambda ',$
because
$\lambda ',$
because
![]() $s> p^{\lambda '}$
. In other words, by the same estimate we see that under the natural map
$s> p^{\lambda '}$
. In other words, by the same estimate we see that under the natural map
the sum does converge (using
![]() $\mathrm {val}_{\lambda '} \geq \mathrm {val}_{\lambda }$
). This means that the image of f in
$\mathrm {val}_{\lambda '} \geq \mathrm {val}_{\lambda }$
). This means that the image of f in
![]() $D^{\lambda '}_{H_l,n}(M)$
lies in the image of
$D^{\lambda '}_{H_l,n}(M)$
lies in the image of
![]() $\gamma -1$
. Thus, decomposing as in 3.15 and the subsequent paragraph to get an isomorphism of
$\gamma -1$
. Thus, decomposing as in 3.15 and the subsequent paragraph to get an isomorphism of
![]() $\mathrm {H}^1(G_0,\mathcal {C}^{\lambda ' \text {-an}}(G_0,M))$
with
$\mathrm {H}^1(G_0,\mathcal {C}^{\lambda ' \text {-an}}(G_0,M))$
with
we obtain that under the natural map
the element f lands in
By the inflation restriction sequence, this is the same as
![]() $\mathrm {H}^1(H_0/H_l,D^{\lambda '}_{H_l,n}(M)^{\Gamma _0})$
. Thus composing with the restriction map to
$\mathrm {H}^1(H_0/H_l,D^{\lambda '}_{H_l,n}(M)^{\Gamma _0})$
. Thus composing with the restriction map to
![]() $\mathrm {H}^1(G_l,\mathcal {C}^{\lambda ' \text {-an}}(G_0,M))$
(and hence also with the further composition to
$\mathrm {H}^1(G_l,\mathcal {C}^{\lambda ' \text {-an}}(G_0,M))$
(and hence also with the further composition to
![]() $\mathrm {H}^1(G_l,\mathcal {C}^{\lambda ' \text {-an}}(G_l,M))$
) we see that f is mapped to zero, as required!
$\mathrm {H}^1(G_l,\mathcal {C}^{\lambda ' \text {-an}}(G_l,M))$
) we see that f is mapped to zero, as required!
Remark 3.19. The proof shows that vanishing of
![]() $\mathrm {R}^{i}_{\mathrm {la}}(M)$
for
$\mathrm {R}^{i}_{\mathrm {la}}(M)$
for
![]() $i\geq 1$
is true in the strong sense, namely, for each pair
$i\geq 1$
is true in the strong sense, namely, for each pair
![]() $(G_0, \lambda )$
in the direct limit
$(G_0, \lambda )$
in the direct limit
there exists some other pair
![]() $(G_0',\lambda ')$
so that the entire map
$(G_0',\lambda ')$
so that the entire map
is zero.
4 Applications
In this section we shall give three applications of our methods. For this we shall need to introduce a few objects which are standard in p-adic Hodge theory. For more details, we refer the reader to [Reference ColmezCol08] or §
![]() $2.1$
of [Reference PoratPor22b]. Let
$2.1$
of [Reference PoratPor22b]. Let
![]() $\mathbf {C}_p$
be the completion of the algebraic closure of
$\mathbf {C}_p$
be the completion of the algebraic closure of
![]() $\mathbf {Q}_p$
. Let
$\mathbf {Q}_p$
. Let
![]() $\mathbf {C}_p^\flat $
be its tilt with ring of integers
$\mathbf {C}_p^\flat $
be its tilt with ring of integers
![]() $\mathbf {C}_p^{\flat ,+}$
. Let
$\mathbf {C}_p^{\flat ,+}$
. Let
![]() $\mathrm {A}_{\inf }$
be the Witt vectors of
$\mathrm {A}_{\inf }$
be the Witt vectors of
![]() $\mathbf {C}_p^{\flat ,+}$
. Let
$\mathbf {C}_p^{\flat ,+}$
. Let
![]() $\varepsilon = (\zeta _p,\zeta _p^2,...)$
be a sequence of compatible p-power roots of unity and let
$\varepsilon = (\zeta _p,\zeta _p^2,...)$
be a sequence of compatible p-power roots of unity and let
![]() $\varpi = \varepsilon - 1 \in \mathbf {C}^{\flat ,+}$
so that
$\varpi = \varepsilon - 1 \in \mathbf {C}^{\flat ,+}$
so that
![]() $[\varpi ] \in \mathrm {A}_{\mathrm {inf}}$
. The ring
$[\varpi ] \in \mathrm {A}_{\mathrm {inf}}$
. The ring
![]() $\widetilde {\mathbf {A}}^{(0,r],\circ }$
is defined to be the p-adic completion of
$\widetilde {\mathbf {A}}^{(0,r],\circ }$
is defined to be the p-adic completion of
![]() $\mathrm {A}_{\mathrm {inf}}\langle p/[\varpi ]^{1/r}\rangle $
. The completion is p-adic, but we take the
$\mathrm {A}_{\mathrm {inf}}\langle p/[\varpi ]^{1/r}\rangle $
. The completion is p-adic, but we take the
![]() $[\varpi ]$
-adic topology. We define
$[\varpi ]$
-adic topology. We define
![]() $\widetilde {\mathbf {A}}^{(0,r]}$
as
$\widetilde {\mathbf {A}}^{(0,r]}$
as
![]() $\widetilde {\mathbf {A}}^{(0,r],\circ }[1/[\varpi ]]$
with the
$\widetilde {\mathbf {A}}^{(0,r],\circ }[1/[\varpi ]]$
with the
![]() $[\varpi ]$
-adic topology. We define also the ring
$[\varpi ]$
-adic topology. We define also the ring
![]() $\widetilde {\mathbf {A}}^{[s,r]}:=\mathrm {A}_{\mathrm {inf}}\langle [\varpi ]^{1/s}/p, p/[\varpi ]^{1/r}\rangle ,$
with the completion and topology being p-adic or
$\widetilde {\mathbf {A}}^{[s,r]}:=\mathrm {A}_{\mathrm {inf}}\langle [\varpi ]^{1/s}/p, p/[\varpi ]^{1/r}\rangle ,$
with the completion and topology being p-adic or
![]() $[\varpi ]$
-adic (they are the same) and
$[\varpi ]$
-adic (they are the same) and
![]() $\widetilde {\mathbf {B}}^{[s,r]}:=\widetilde {\mathbf {A}}^{[s,r]}[1/p] = \widetilde {\mathbf {A}}^{[s,r]}[1/[\varpi ]].$
Each ring R just introduced has a continuous action of
$\widetilde {\mathbf {B}}^{[s,r]}:=\widetilde {\mathbf {A}}^{[s,r]}[1/p] = \widetilde {\mathbf {A}}^{[s,r]}[1/[\varpi ]].$
Each ring R just introduced has a continuous action of
![]() $\mathrm {Gal}(\overline {\mathbf {Q}}_p/\mathbf {Q}_p)$
. Let K be a finite extension of
$\mathrm {Gal}(\overline {\mathbf {Q}}_p/\mathbf {Q}_p)$
. Let K be a finite extension of
![]() $\mathbf {Q}_p$
. Let
$\mathbf {Q}_p$
. Let
![]() $\mathbf {Q}_p^{\mathrm {cyc}} = \mathbf {Q}_p(\zeta _{p^\infty }), K^{\mathrm {cyc}} = K\mathbf {Q}_p^{\mathrm {cyc}}$
and
$\mathbf {Q}_p^{\mathrm {cyc}} = \mathbf {Q}_p(\zeta _{p^\infty }), K^{\mathrm {cyc}} = K\mathbf {Q}_p^{\mathrm {cyc}}$
and
![]() $H_K = \mathrm {Gal}(\overline {\mathbf {Q}}_p/K^{\mathrm {cyc}})$
. We set
$H_K = \mathrm {Gal}(\overline {\mathbf {Q}}_p/K^{\mathrm {cyc}})$
. We set
![]() $R_{K} := R^{H_K}$
so that
$R_{K} := R^{H_K}$
so that
![]() $R_{K}$
has an action of
$R_{K}$
has an action of
![]() $\mathrm {Gal}(\overline {\mathbf {Q}}_p/K)/H_K \cong \mathrm {Gal}(K^{\mathrm {cyc}}/K)$
. This latter group we call
$\mathrm {Gal}(\overline {\mathbf {Q}}_p/K)/H_K \cong \mathrm {Gal}(K^{\mathrm {cyc}}/K)$
. This latter group we call
![]() $\Gamma _K$
and it is isomorphic to an open subgroup of
$\Gamma _K$
and it is isomorphic to an open subgroup of
![]() $\mathbf {Z}_p^\times $
via the cyclotomic character. With this notation we have
$\mathbf {Z}_p^\times $
via the cyclotomic character. With this notation we have
![]() $\widetilde {\mathbf {E}}_{K} := \widetilde {\mathbf {A}}^{(0,r]}_{K}/p$
(it does not depend on r). This field was mentioned in Example 2.14.3 when
$\widetilde {\mathbf {E}}_{K} := \widetilde {\mathbf {A}}^{(0,r]}_{K}/p$
(it does not depend on r). This field was mentioned in Example 2.14.3 when
![]() $K=\mathbf {Q}_p$
. The field
$K=\mathbf {Q}_p$
. The field
![]() $\widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
can be equivalently defined as the X-adic completion of
$\widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
can be equivalently defined as the X-adic completion of
![]() $\cup _n \mathbf {F}_p((X^{1/p^n}))$
. The action of
$\cup _n \mathbf {F}_p((X^{1/p^n}))$
. The action of
![]() $\Gamma _{\mathbf {Q}_p} = \mathbf {Z}_p^\times $
is given as follows: an element a acts on
$\Gamma _{\mathbf {Q}_p} = \mathbf {Z}_p^\times $
is given as follows: an element a acts on
![]() $f(X) \in \widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
by the formula
$f(X) \in \widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
by the formula
![]() $(a\cdot f)(X) = f((1+X)^a -1).$
We also have “deperfected” rings defined as follows. We let
$(a\cdot f)(X) = f((1+X)^a -1).$
We also have “deperfected” rings defined as follows. We let
![]() $\mathbf {A}_{\mathbf {Q}_p}$
be the p-adic completion of
$\mathbf {A}_{\mathbf {Q}_p}$
be the p-adic completion of
![]() $\mathbf {Z}_p[[T]][1/T]$
. It is naturally embedded into
$\mathbf {Z}_p[[T]][1/T]$
. It is naturally embedded into
![]() $\widetilde {\mathbf {A}} = W(\mathbf {C}_p^\flat )$
by mapping T to the element
$\widetilde {\mathbf {A}} = W(\mathbf {C}_p^\flat )$
by mapping T to the element
![]() $[\varepsilon ]-1 \in \mathrm {A}_{\inf }$
which lifts
$[\varepsilon ]-1 \in \mathrm {A}_{\inf }$
which lifts
![]() $\varpi $
. We have
$\varpi $
. We have
![]() $\mathbf {A}_{\mathbf {Q}_p}/p \cong \mathbf {F}_p((X)) \subset \widetilde {\mathbf {E}}_{\mathbf {Q}_p}.$
To each K one can associate the field of norms
$\mathbf {A}_{\mathbf {Q}_p}/p \cong \mathbf {F}_p((X)) \subset \widetilde {\mathbf {E}}_{\mathbf {Q}_p}.$
To each K one can associate the field of norms
![]() $\mathbf {E}_K \subset \widetilde {\mathbf {E}}_K$
so that
$\mathbf {E}_K \subset \widetilde {\mathbf {E}}_K$
so that
![]() $\mathbf {E}_{\mathbf {Q}_p} = \mathbf {F}_p((X)),$
and there is a standard way to define rings
$\mathbf {E}_{\mathbf {Q}_p} = \mathbf {F}_p((X)),$
and there is a standard way to define rings
![]() $\mathbf {A}_{K}$
containing
$\mathbf {A}_{K}$
containing
![]() $\mathbf {A}_{\mathbf {Q}_p}$
so that
$\mathbf {A}_{\mathbf {Q}_p}$
so that
![]() $\mathbf {A}_{K}/p \cong \mathbf {E}_K$
(see §
$\mathbf {A}_{K}/p \cong \mathbf {E}_K$
(see §
![]() $6$
of [Reference ColmezCol08]). The ring
$6$
of [Reference ColmezCol08]). The ring
![]() $\widetilde {\mathbf {A}}^{(0,r],\circ }$
embeds into
$\widetilde {\mathbf {A}}^{(0,r],\circ }$
embeds into
![]() $\widetilde {\mathbf {A}}$
and one sets
$\widetilde {\mathbf {A}}$
and one sets
![]() $\mathbf {A}^{(0,r],\circ }_{K} = \mathbf {A}^{(0,r],\circ } \cap \mathbf {A}_{K}$
. We then let
$\mathbf {A}^{(0,r],\circ }_{K} = \mathbf {A}^{(0,r],\circ } \cap \mathbf {A}_{K}$
. We then let
![]() $\mathbf {A}^{(0,r]}_{K} = \mathbf {A}^{(0,r],\circ }_{K}[1/T]$
. We let
$\mathbf {A}^{(0,r]}_{K} = \mathbf {A}^{(0,r],\circ }_{K}[1/T]$
. We let
![]() $\mathbf {A}^{[s,r]}_{\mathbf {Q}_p}$
be the completion of the image of
$\mathbf {A}^{[s,r]}_{\mathbf {Q}_p}$
be the completion of the image of
![]() $\mathbf {A}^{(0,r]}_{K}$
in
$\mathbf {A}^{(0,r]}_{K}$
in
![]() $\widetilde {\mathbf {A}}^{(0,r]}_{K}$
. Finally, we set
$\widetilde {\mathbf {A}}^{(0,r]}_{K}$
. Finally, we set
![]() $\mathbf {B}^{(0,r]}_{K} = \mathbf {A}^{(0,r]}_{K}[1/p]$
and
$\mathbf {B}^{(0,r]}_{K} = \mathbf {A}^{(0,r]}_{K}[1/p]$
and
![]() $\mathbf {B}^{[s,r]}_{K} = \mathbf {A}^{[s,r]}_{K}[1/p]$
. In addition to the
$\mathbf {B}^{[s,r]}_{K} = \mathbf {A}^{[s,r]}_{K}[1/p]$
. In addition to the
![]() $\Gamma _K$
-action above, these rings are endowed with a
$\Gamma _K$
-action above, these rings are endowed with a
![]() $\Gamma _K$
-equivariant Frobenius operator
$\Gamma _K$
-equivariant Frobenius operator
![]() $\varphi $
which maps rings defined via an interval I to rings on the interval
$\varphi $
which maps rings defined via an interval I to rings on the interval
![]() $p^{-1}I$
. We let also
$p^{-1}I$
. We let also
![]() $K^{\mathrm {LT}}$
denote a Lubin-Tate extension of K,
$K^{\mathrm {LT}}$
denote a Lubin-Tate extension of K,
![]() $H_{\mathrm {LT}} = \mathrm {Gal}(\overline {\mathbf {Q}}_p/K^{\mathrm {LT}})$
and
$H_{\mathrm {LT}} = \mathrm {Gal}(\overline {\mathbf {Q}}_p/K^{\mathrm {LT}})$
and
![]() $\Gamma _{\mathrm {LT}} = \mathrm {Gal}(\overline {\mathbf {Q}}_p/K)/H_{\mathrm {LT}}.$
$\Gamma _{\mathrm {LT}} = \mathrm {Gal}(\overline {\mathbf {Q}}_p/K)/H_{\mathrm {LT}}.$
Proposition 4.1. The Tate-Sen axioms (TS1)-(TS4) of §
![]() $3.2$
are satisfied in the following cases:
$3.2$
are satisfied in the following cases:
-
1. When
 $\widetilde {\Lambda } = \widetilde {\mathbf {A}}^{(0,r]}_{\mathbf {Q}_p}$
,
$\widetilde {\Lambda } = \widetilde {\mathbf {A}}^{(0,r]}_{\mathbf {Q}_p}$
,
 $\widetilde {\Lambda }^+ = \widetilde {\mathbf {A}}^{(0,r],\circ }_{\mathbf {Q}_p}$
and
$\widetilde {\Lambda }^+ = \widetilde {\mathbf {A}}^{(0,r],\circ }_{\mathbf {Q}_p}$
and
 $\Lambda _{n} = \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{\mathbf {Q}_p})$
for
$\Lambda _{n} = \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{\mathbf {Q}_p})$
for
 $1/r \in \mathbf {Z}[1/p]_{\geq 0}$
with
$1/r \in \mathbf {Z}[1/p]_{\geq 0}$
with
 $r < 1$
(we omit subscripts H in
$r < 1$
(we omit subscripts H in
 $\Lambda _{H,n}$
because
$\Lambda _{H,n}$
because
 $H_0 = 1$
in this case).
$H_0 = 1$
in this case). -
2. When
 $\widetilde {\Lambda } = \widetilde {\mathbf {A}}^{(0,r],H_{{LT}}}$
,
$\widetilde {\Lambda } = \widetilde {\mathbf {A}}^{(0,r],H_{{LT}}}$
,
 $\widetilde {\Lambda }^+ = \widetilde {\mathbf {A}}^{(0,r],\circ }\cap \widetilde {\Lambda }$
and
$\widetilde {\Lambda }^+ = \widetilde {\mathbf {A}}^{(0,r],\circ }\cap \widetilde {\Lambda }$
and
 $\Lambda _{H_L,n} = \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{L})$
for
$\Lambda _{H_L,n} = \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{L})$
for
 $1/r \in \mathbf {Z}[1/p]_{\geq 0}$
with
$1/r \in \mathbf {Z}[1/p]_{\geq 0}$
with
 $r < 1$
.
$r < 1$
.
Proof. Case 1: the axioms (TS1)-(TS3) are verified in §
![]() $5.1$
of [Reference PoratPor22b]. It suffices to show that for any
$5.1$
of [Reference PoratPor22b]. It suffices to show that for any
![]() $a\in 1+p\mathbf {Z}_p \subset \Gamma _{\mathbf {Q}_p}$
and
$a\in 1+p\mathbf {Z}_p \subset \Gamma _{\mathbf {Q}_p}$
and
![]() $k\in \mathbf {Z}$
we have
$k\in \mathbf {Z}$
we have
for some positive constant c. Indeed, one computes (using the formula
![]() $a(T)=(1+T)^a-1)$
) that
$a(T)=(1+T)^a-1)$
) that
 $$ \begin{align*}(a-1)(\varphi^{-n}(T^k)) = \varphi^{-n}(T^k)\cdot\varphi^{-n}((a+\sum_{m \geq 1}\binom{a}{m+1}T)^k-1).\end{align*} $$
$$ \begin{align*}(a-1)(\varphi^{-n}(T^k)) = \varphi^{-n}(T^k)\cdot\varphi^{-n}((a+\sum_{m \geq 1}\binom{a}{m+1}T)^k-1).\end{align*} $$
As
![]() $a \equiv _p 1$
it follows that
$a \equiv _p 1$
it follows that
 $$ \begin{align*}\mathrm{val}(\varphi^{-n}((a+\sum_{m \geq 1}\binom{a}{m+1}T)^k-1)) \geq \min(\mathrm{val}(p),\mathrm{val}(\varphi^{-n}(T)))> 0\end{align*} $$
$$ \begin{align*}\mathrm{val}(\varphi^{-n}((a+\sum_{m \geq 1}\binom{a}{m+1}T)^k-1)) \geq \min(\mathrm{val}(p),\mathrm{val}(\varphi^{-n}(T)))> 0\end{align*} $$
as required.
Case 2: Again (TS2) and (TS3) are checked in [Reference PoratPor22b]. (TS1) is shown in Lemma 10.1 of [Reference ColmezCol08]. For (TS4), we argue as follows. The ring
![]() $\Lambda _{H_L,n}$
is endowed with the action of some finite index subgroup of
$\Lambda _{H_L,n}$
is endowed with the action of some finite index subgroup of
![]() $\Gamma _{\mathbf {Q}_p}.$
It is finite free over
$\Gamma _{\mathbf {Q}_p}.$
It is finite free over
![]() $\Lambda _{n}$
so one may choose a
$\Lambda _{n}$
so one may choose a
![]() $\Lambda _{n}$
-basis
$\Lambda _{n}$
-basis
![]() $e_1,...,e_d.$
By possibly choosing an even smaller subgroup
$e_1,...,e_d.$
By possibly choosing an even smaller subgroup
![]() $\Gamma '$
of
$\Gamma '$
of
![]() $\Gamma _{\mathbf {Q}_p}$
one can arrange that
$\Gamma _{\mathbf {Q}_p}$
one can arrange that
![]() $\Gamma ' \subset 1 +p\mathbf {Z}_p$
and that the action of
$\Gamma ' \subset 1 +p\mathbf {Z}_p$
and that the action of
![]() $\gamma '-1$
of a generator
$\gamma '-1$
of a generator
![]() $\gamma '$
of
$\gamma '$
of
![]() $\Gamma '$
has
$\Gamma '$
has
![]() $\mathrm {val}((\gamma '-1)(e_i)> c$
for some constant c. Now if
$\mathrm {val}((\gamma '-1)(e_i)> c$
for some constant c. Now if
![]() $\gamma $
is a generator
$\gamma $
is a generator
![]() $1+p\mathbf {Z}_p$
then we already know
$1+p\mathbf {Z}_p$
then we already know
![]() $\mathrm {val}^{\mathrm {op}}_{\Lambda _n}(\gamma -1) \geq c'$
for some
$\mathrm {val}^{\mathrm {op}}_{\Lambda _n}(\gamma -1) \geq c'$
for some
![]() $c'> 0$
. Since
$c'> 0$
. Since
![]() $\gamma -1$
divides
$\gamma -1$
divides
![]() $\gamma '-1$
we see (TS4) holds with
$\gamma '-1$
we see (TS4) holds with
![]() $t = \min (c,c').$
$t = \min (c,c').$
4.1 Computation of locally analytic elements in
 $\widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
$\widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
Recall the main result of [Reference Berger and RozensztajnBR22]:
Theorem 4.2. We have
![]() $\widetilde {\mathbf {E}}^{\mathrm {la}}_{\mathbf {Q}_p} = \cup _n \mathbf {F}_p((X^{1/p^n})).$
$\widetilde {\mathbf {E}}^{\mathrm {la}}_{\mathbf {Q}_p} = \cup _n \mathbf {F}_p((X^{1/p^n})).$
We shall now explain how to derive this result by reducing rather formally to a previously known result of Berger in characteristic 0 which is proven with aid of p-adic analysis. Though as a whole the proof of [Reference Berger and RozensztajnBR22] is simpler than ours, the method we present here illustrates our hope of using this new technique of linking analytic vectors in characteristic 0 and characteristic p in other contexts as well.
Lemma 4.3. We have
![]() $\widetilde {\mathbf {A}}^{(0,r]}_{\mathbf {Q}_p} \cap \varphi ^{-n}(\mathbf {B}^{[p^{-n}s,p^{-n}r]}_{\mathbf {Q}_p}) = \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{\mathbf {Q}_p})$
.
$\widetilde {\mathbf {A}}^{(0,r]}_{\mathbf {Q}_p} \cap \varphi ^{-n}(\mathbf {B}^{[p^{-n}s,p^{-n}r]}_{\mathbf {Q}_p}) = \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{\mathbf {Q}_p})$
.
Proof. The inclusion of the right-hand side in the left-hand side is clear. Conversely, suppose x lies on the right-hand side. By applying
![]() $\varphi ^n$
, we may reduce to the case
$\varphi ^n$
, we may reduce to the case
![]() $n = 0$
. So we have
$n = 0$
. So we have
![]() $x \in \widetilde {\mathbf {A}}^{(0,r]}_{\mathbf {Q}_p} \cap \mathbf {B}^{[s,r]}_{\mathbf {Q}_p},$
whence x lies in the larger ring
$x \in \widetilde {\mathbf {A}}^{(0,r]}_{\mathbf {Q}_p} \cap \mathbf {B}^{[s,r]}_{\mathbf {Q}_p},$
whence x lies in the larger ring
![]() $\widetilde {\mathbf {B}}^{(0,r]}_{\mathbf {Q}_p} \cap \mathbf {B}^{[s,r]}_{\mathbf {Q}_p} = \mathbf {B}^{(0,r]}_{\mathbf {Q}_p}.$
Thus we reduce to showing
$\widetilde {\mathbf {B}}^{(0,r]}_{\mathbf {Q}_p} \cap \mathbf {B}^{[s,r]}_{\mathbf {Q}_p} = \mathbf {B}^{(0,r]}_{\mathbf {Q}_p}.$
Thus we reduce to showing
![]() $\mathbf {B}^{(0,r]}_{\mathbf {Q}_p}/\mathbf {A}^{(0,r]}_{\mathbf {Q}_p} \rightarrow \widetilde {\mathbf {B}}^{(0,r]}_{\mathbf {Q}_p}/\widetilde {\mathbf {A}}^{(0,r]}_{\mathbf {Q}_p}$
is injective. This reduces further to showing
$\mathbf {B}^{(0,r]}_{\mathbf {Q}_p}/\mathbf {A}^{(0,r]}_{\mathbf {Q}_p} \rightarrow \widetilde {\mathbf {B}}^{(0,r]}_{\mathbf {Q}_p}/\widetilde {\mathbf {A}}^{(0,r]}_{\mathbf {Q}_p}$
is injective. This reduces further to showing
![]() $\widetilde {\mathbf {A}}^{(0,r]}/\mathbf {A}^{(0,r]}_{\mathbf {Q}_p}$
is p-torsionfree. In fact it suffices to show
$\widetilde {\mathbf {A}}^{(0,r]}/\mathbf {A}^{(0,r]}_{\mathbf {Q}_p}$
is p-torsionfree. In fact it suffices to show
![]() $\widetilde {\mathbf {A}}^{(0,r],\circ }/\mathbf {A}^{(0,r],\circ }_{\mathbf {Q}_p}$
is p-torsionfree, because
$\widetilde {\mathbf {A}}^{(0,r],\circ }/\mathbf {A}^{(0,r],\circ }_{\mathbf {Q}_p}$
is p-torsionfree, because
![]() $\widetilde {\mathbf {A}}^{(0,r]}/\mathbf {A}^{(0,r]}_{\mathbf {Q}_p}$
is its
$\widetilde {\mathbf {A}}^{(0,r]}/\mathbf {A}^{(0,r]}_{\mathbf {Q}_p}$
is its
![]() $[\varpi ]$
-adic localization.
$[\varpi ]$
-adic localization.
Next, recall that
![]() $\mathbf {A}^{(0,r],\circ }_{\mathbf {Q}_p} = \widetilde {\mathbf {A}}^{(0,r],\circ }\cap \widetilde {\mathbf {A}}_{\mathbf {Q}_p}$
, so
$\mathbf {A}^{(0,r],\circ }_{\mathbf {Q}_p} = \widetilde {\mathbf {A}}^{(0,r],\circ }\cap \widetilde {\mathbf {A}}_{\mathbf {Q}_p}$
, so
![]() $\widetilde {\mathbf {A}}^{(0,r]}/\mathbf {A}^{(0,r]}_{\mathbf {Q}_p}$
injects into
$\widetilde {\mathbf {A}}^{(0,r]}/\mathbf {A}^{(0,r]}_{\mathbf {Q}_p}$
injects into
![]() $\widetilde {\mathbf {A}}/\mathbf {A}_{\mathbf {Q}_p}$
. This will be p-torsionfree provided that
$\widetilde {\mathbf {A}}/\mathbf {A}_{\mathbf {Q}_p}$
. This will be p-torsionfree provided that
![]() $\mathbf {A}_{\mathbf {Q}_p}\otimes {\mathbf {F}_p} \rightarrow \widetilde {\mathbf {A}} \otimes {\mathbf {F}_p}$
is injective. But this is easy: it is simply the map
$\mathbf {A}_{\mathbf {Q}_p}\otimes {\mathbf {F}_p} \rightarrow \widetilde {\mathbf {A}} \otimes {\mathbf {F}_p}$
is injective. But this is easy: it is simply the map
![]() $\mathbf {F}_p((X)) \rightarrow \mathbf {C}^\flat _p$
.
$\mathbf {F}_p((X)) \rightarrow \mathbf {C}^\flat _p$
.
Recall Theorem 4.4 of [Reference BergerBer16].
Theorem 4.4. We have
![]() $\widetilde {\mathbf {B}}^{[s,r],\mathrm {la}}_{\mathbf {Q}_p} = \cup _n \varphi ^{-n}(\mathbf {B}^{[p^{-n}s,p^{-n}r]}_{\mathbf {Q}_p}).$
$\widetilde {\mathbf {B}}^{[s,r],\mathrm {la}}_{\mathbf {Q}_p} = \cup _n \varphi ^{-n}(\mathbf {B}^{[p^{-n}s,p^{-n}r]}_{\mathbf {Q}_p}).$
We have the following corollary which is the mixed characteristic version of Theorem 4.2 and Theorem 4.4.
Corollary 4.5. We have
![]() $\widetilde {\mathbf {A}}^{(0,r],\mathrm {la}}_{\mathbf {Q}_p} = \cup _n \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{\mathbf {Q}_p}).$
$\widetilde {\mathbf {A}}^{(0,r],\mathrm {la}}_{\mathbf {Q}_p} = \cup _n \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{\mathbf {Q}_p}).$
Proof. Indeed, choosing some arbitrary s, we have
So by Lemma 4.3, the ring
![]() $ \widetilde {\mathbf {A}}^{(0,r],\mathrm {la}}_{\mathbf {Q}_p}$
is contained in
$ \widetilde {\mathbf {A}}^{(0,r],\mathrm {la}}_{\mathbf {Q}_p}$
is contained in
![]() $\cup _n \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{\mathbf {Q}_p})$
. Conversely, any element in
$\cup _n \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{\mathbf {Q}_p})$
. Conversely, any element in
![]() $\cup _n \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{\mathbf {Q}_p})$
is locally analytic by Corollary 3.10.
$\cup _n \varphi ^{-n}(\mathbf {A}^{(0,p^{-n}r]}_{\mathbf {Q}_p})$
is locally analytic by Corollary 3.10.
From this we can deduce a new proof of Theorem 4.2, which after this setup becomes a one liner. Take some
![]() $0 < r < 1$
with
$0 < r < 1$
with
![]() $1/r \in \mathbf {Z}[1/p]$
and consider the short exact sequence
$1/r \in \mathbf {Z}[1/p]$
and consider the short exact sequence
By Theorem 3.1 and Proposition 4.1 we have
![]() $\mathrm {R}^1_{\mathrm {la}}(\widetilde {\mathbf {A}}^{(0,r],\mathrm {la}}) = 0,$
so
$\mathrm {R}^1_{\mathrm {la}}(\widetilde {\mathbf {A}}^{(0,r],\mathrm {la}}) = 0,$
so
![]() $\widetilde {\mathbf {E}}_{\mathbf {Q}_p}^{\mathrm {la}} = \widetilde {\mathbf {A}}^{(0,r],\mathrm {la}}/p.$
Passing to locally analytic vectors, we get
$\widetilde {\mathbf {E}}_{\mathbf {Q}_p}^{\mathrm {la}} = \widetilde {\mathbf {A}}^{(0,r],\mathrm {la}}/p.$
Passing to locally analytic vectors, we get
4.2 Descent of Lubin-Tate
 $(\varphi ,\Gamma )$
-modules to locally analytic vectors
$(\varphi ,\Gamma )$
-modules to locally analytic vectors
Recall that according to Lubin-Tate theory the Lubin-Tate character gives an isomorphism
![]() $\Gamma _{\mathrm {LT}} \xrightarrow {\cong } \mathcal {O}_{K}^\times .$
The norm of the Lubin-Tate character is an unramified twist of the cyclotomic character, which shows that
$\Gamma _{\mathrm {LT}} \xrightarrow {\cong } \mathcal {O}_{K}^\times .$
The norm of the Lubin-Tate character is an unramified twist of the cyclotomic character, which shows that
![]() $K_{\mathrm {LT}}$
contains a twist
$K_{\mathrm {LT}}$
contains a twist
![]() $K^{\mathrm {cyc},\eta }$
of the cyclotomic extension
$K^{\mathrm {cyc},\eta }$
of the cyclotomic extension
![]() $K^{\mathrm {cyc}}$
by an unramified character
$K^{\mathrm {cyc}}$
by an unramified character
![]() $\eta $
.
$\eta $
.
In the theory p-adic Galois representations and the p-adic Langlands program
![]() $(\varphi ,\Gamma )$
-modules have played a central role. In particular, the overconvergence theorem of Cherbonnier-Colmez ([Reference Cherbonnier and ColmezCC98]) has been a crucial component in providing a link between the Banach and the analytic sides of the Galois side for
$(\varphi ,\Gamma )$
-modules have played a central role. In particular, the overconvergence theorem of Cherbonnier-Colmez ([Reference Cherbonnier and ColmezCC98]) has been a crucial component in providing a link between the Banach and the analytic sides of the Galois side for
![]() $\mathrm {GL}_2(\mathbf {Q}_p).$
When
$\mathrm {GL}_2(\mathbf {Q}_p).$
When
![]() $\mathbf {Q}_p$
is replaced with a finite extension K, the situation with overconvergence is more complicated, as we shall now explain.
$\mathbf {Q}_p$
is replaced with a finite extension K, the situation with overconvergence is more complicated, as we shall now explain.
In this context one considers a big Robba ring
![]() $\widetilde {\mathbf {B}}_{\mathrm {rig},\mathrm {LT}}^\dagger $
and a “deperfected” Robba ring
$\widetilde {\mathbf {B}}_{\mathrm {rig},\mathrm {LT}}^\dagger $
and a “deperfected” Robba ring
![]() $\mathbf {B}_{\mathrm {rig},\mathrm {LT}}^\dagger $
which is a ring of power series in one variable converging in an annulus (see [Reference BergerBer16], where these rings are denoted
$\mathbf {B}_{\mathrm {rig},\mathrm {LT}}^\dagger $
which is a ring of power series in one variable converging in an annulus (see [Reference BergerBer16], where these rings are denoted
![]() $\widetilde {\mathbf {B}}_{\mathrm {rig},K}^\dagger $
and
$\widetilde {\mathbf {B}}_{\mathrm {rig},K}^\dagger $
and
![]() ${\mathbf {B}}_{\mathrm {rig},K}^\dagger $
, respectively). Both of these rings are endowed with a Frobenius operator
${\mathbf {B}}_{\mathrm {rig},K}^\dagger $
, respectively). Both of these rings are endowed with a Frobenius operator
![]() $\varphi $
and an action of
$\varphi $
and an action of
![]() $\Gamma _{\mathrm {LT}}.$
By the main result of Fourquaux-Xie ([Reference Fourquaux and XieFX14]) it is known that when
$\Gamma _{\mathrm {LT}}.$
By the main result of Fourquaux-Xie ([Reference Fourquaux and XieFX14]) it is known that when
![]() $K \neq \mathbf {Q}_p$
there exist
$K \neq \mathbf {Q}_p$
there exist
![]() $(\varphi ,\Gamma _{\mathrm {LT}})$
-modules over
$(\varphi ,\Gamma _{\mathrm {LT}})$
-modules over
![]() $\widetilde {\mathbf {B}}_{\mathrm {rig},\mathrm {LT}}^\dagger $
which are not overconvergent, that is, do not descend to
$\widetilde {\mathbf {B}}_{\mathrm {rig},\mathrm {LT}}^\dagger $
which are not overconvergent, that is, do not descend to
![]() $\mathbf {B}_{\mathrm {rig},\mathrm {LT}}^\dagger $
. The main theorem of [Reference BergerBer16] gives a sufficient condition for this to happen, namely, K-analyticity. However, in §
$\mathbf {B}_{\mathrm {rig},\mathrm {LT}}^\dagger $
. The main theorem of [Reference BergerBer16] gives a sufficient condition for this to happen, namely, K-analyticity. However, in §
![]() $8$
of [Reference BergerBer16] it is also shown that an arbitrary
$8$
of [Reference BergerBer16] it is also shown that an arbitrary
![]() $(\varphi ,\Gamma _{\mathrm {LT}})$
-module over
$(\varphi ,\Gamma _{\mathrm {LT}})$
-module over
![]() $\widetilde {\mathbf {B}}_{\mathrm {rig},\mathrm {LT}}^\dagger $
descends to the multivariable ring
$\widetilde {\mathbf {B}}_{\mathrm {rig},\mathrm {LT}}^\dagger $
descends to the multivariable ring
![]() $\widetilde {\mathbf {B}}_{\mathrm {rig},\mathrm {LT}}^{\dagger ,\mathrm {pa}}$
of pro-analytic vectors.
$\widetilde {\mathbf {B}}_{\mathrm {rig},\mathrm {LT}}^{\dagger ,\mathrm {pa}}$
of pro-analytic vectors.
The ring
![]() $\widetilde {\mathbf {B}}_{\mathrm {rig},K}^{\dagger ,\mathrm {pa}}$
is a
$\widetilde {\mathbf {B}}_{\mathrm {rig},K}^{\dagger ,\mathrm {pa}}$
is a
![]() $\mathbf {Q}_p$
-algebra and as such it is a characteristic 0 object. On the other hand, when
$\mathbf {Q}_p$
-algebra and as such it is a characteristic 0 object. On the other hand, when
![]() $K= \mathbf {Q}_p$
, Cherbonnier-Colmez shows there is a descent to an integral ring
$K= \mathbf {Q}_p$
, Cherbonnier-Colmez shows there is a descent to an integral ring
![]() $\mathbf {A}_{\mathbf {Q}_p}^\dagger $
where p is not invertible. We will now give an integral version of this descent when
$\mathbf {A}_{\mathbf {Q}_p}^\dagger $
where p is not invertible. We will now give an integral version of this descent when
![]() $K \neq \mathbf {Q}_p.$
$K \neq \mathbf {Q}_p.$
Let
![]() $\widetilde {\mathbf {A}}_{\mathrm {LT}} = \widetilde {\mathbf {A}}^{H_{\mathrm {LT}}}$
and
$\widetilde {\mathbf {A}}_{\mathrm {LT}} = \widetilde {\mathbf {A}}^{H_{\mathrm {LT}}}$
and
![]() $\widetilde {\mathbf {A}}^{\dagger }_{\mathrm {LT}} = \varinjlim _{r} \mathbf {A}^{(0,r]}_{\mathrm {LT}}$
where
$\widetilde {\mathbf {A}}^{\dagger }_{\mathrm {LT}} = \varinjlim _{r} \mathbf {A}^{(0,r]}_{\mathrm {LT}}$
where
![]() $\mathbf {A}^{(0,r]}_{\mathrm {LT}} := \mathbf {A}^{(0,r],H_{\mathrm {LT}}}.$
The idea is that the ring
$\mathbf {A}^{(0,r]}_{\mathrm {LT}} := \mathbf {A}^{(0,r],H_{\mathrm {LT}}}.$
The idea is that the ring
![]() $\widetilde {\mathbf {A}}^{\dagger ,\mathrm {la}}_{\mathrm {LT}}$
is an appropriate integral analogue of
$\widetilde {\mathbf {A}}^{\dagger ,\mathrm {la}}_{\mathrm {LT}}$
is an appropriate integral analogue of
![]() $\widetilde {\mathbf {B}}_{\mathrm {rig},K}^{\dagger ,\mathrm {pa}}$
.
$\widetilde {\mathbf {B}}_{\mathrm {rig},K}^{\dagger ,\mathrm {pa}}$
.
Theorem 4.7. Every
![]() $(\varphi ,\Gamma )$
-module over
$(\varphi ,\Gamma )$
-module over
![]() $\widetilde {\mathbf {A}}^{\dagger }_{\mathrm {LT}}$
descends uniquely to a
$\widetilde {\mathbf {A}}^{\dagger }_{\mathrm {LT}}$
descends uniquely to a
![]() $(\varphi ,\Gamma )$
-module over
$(\varphi ,\Gamma )$
-module over
![]() $\widetilde {\mathbf {A}}^{\dagger ,\mathrm {la}}_{\mathrm {LT}}.$
$\widetilde {\mathbf {A}}^{\dagger ,\mathrm {la}}_{\mathrm {LT}}.$
Proof. When
![]() $K^{\mathrm {cyc}} \subset K^{\mathrm {LT}}$
this follows from part 2 of Proposition 4.1 and part 1 of Theorem 3.1. In general, one can descend along an unramified twist (see §
$K^{\mathrm {cyc}} \subset K^{\mathrm {LT}}$
this follows from part 2 of Proposition 4.1 and part 1 of Theorem 3.1. In general, one can descend along an unramified twist (see §
![]() $8$
[Reference BergerBer16] for a similar argument).
$8$
[Reference BergerBer16] for a similar argument).
Remark 4.8. Corollary 4.5 shows that when
![]() $K = \mathbf {Q}_p$
we recover the usual integral descent of Cherbonnier-Colmez.
$K = \mathbf {Q}_p$
we recover the usual integral descent of Cherbonnier-Colmez.
4.3 Pro-analytic and locally analytic vectors in
 $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}$
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}$
In this subsection we work out an analogy between
![]() $\mathrm {B}_{\mathrm {dR},\mathbf {Q}_p}^{+}$
of
$\mathrm {B}_{\mathrm {dR},\mathbf {Q}_p}^{+}$
of
![]() $H_{\mathbf {Q}_p}$
fixed-points of
$H_{\mathbf {Q}_p}$
fixed-points of
![]() $\mathrm {B}_{\mathrm {dR}}^+$
and the ring
$\mathrm {B}_{\mathrm {dR}}^+$
and the ring
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}.$
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}.$
Let
![]() $\{M_n\}_n$
be an inverse system of finite free modules over corresponding
$\{M_n\}_n$
be an inverse system of finite free modules over corresponding
![]() $\mathbf {Z}_p$
-Tate algebras
$\mathbf {Z}_p$
-Tate algebras
![]() $\{R_n\}_n$
endowed with the action of a compact p-adic Lie group G. For the inverse limit
$\{R_n\}_n$
endowed with the action of a compact p-adic Lie group G. For the inverse limit
![]() $M = \varprojlim _n M_n$
we define the pro-analytic vectors
$M = \varprojlim _n M_n$
we define the pro-analytic vectors
and the locally analytic vectors
Clearly there is a natural map
![]() $M^{\mathrm {la}} \rightarrow M^{\mathrm {pa}}$
. Furthermore, it can be shown that when
$M^{\mathrm {la}} \rightarrow M^{\mathrm {pa}}$
. Furthermore, it can be shown that when
![]() $R = \varprojlim _n R_n$
itself is a
$R = \varprojlim _n R_n$
itself is a
![]() $\mathbf {Z}_p$
-Tate algebra then
$\mathbf {Z}_p$
-Tate algebra then
![]() $M^{\mathrm {pa}} = M^{\mathrm {la}}$
and that the new definition of locally analytic vectors agrees with the old one of §
$M^{\mathrm {pa}} = M^{\mathrm {la}}$
and that the new definition of locally analytic vectors agrees with the old one of §
![]() $2.$
For example, when the
$2.$
For example, when the
![]() $M_n$
are G-Banach spaces, the module M is a G-Fréchet space and we recover the definitions appearing in [Reference Berger and ColmezBC16] and [Reference BergerBer16].
$M_n$
are G-Banach spaces, the module M is a G-Fréchet space and we recover the definitions appearing in [Reference Berger and ColmezBC16] and [Reference BergerBer16].
The ring
![]() $\mathrm {B}_{\mathrm {dR},{\mathbf {Q}_p}}^{+}$
has the structure of a
$\mathrm {B}_{\mathrm {dR},{\mathbf {Q}_p}}^{+}$
has the structure of a
![]() $\Gamma _{\mathbf {Q}_p}$
-Fréchet space. Indeed, letting t denote Fontaine’s element, one has
$\Gamma _{\mathbf {Q}_p}$
-Fréchet space. Indeed, letting t denote Fontaine’s element, one has
It turns out there is a very nice description of the pro-analytic and locally analytic elements in
![]() $\mathrm {B}_{\mathrm {dR},\mathbf {Q}_p}^{+}$
(Proposition 2.6 of [Reference PoratPor22a]).
$\mathrm {B}_{\mathrm {dR},\mathbf {Q}_p}^{+}$
(Proposition 2.6 of [Reference PoratPor22a]).
Theorem 4.9. We have
![]() $\mathrm {B}_{\mathrm {dR},\mathbf {Q}_p}^{+,\mathrm {la}} = \cup _n\mathbf {Q}_p(\zeta _{p^n})[[t]]$
and
$\mathrm {B}_{\mathrm {dR},\mathbf {Q}_p}^{+,\mathrm {la}} = \cup _n\mathbf {Q}_p(\zeta _{p^n})[[t]]$
and
![]() $\mathrm {B}_{\mathrm {dR},\mathbf {Q}_p}^{+,\mathrm {pa}} = \mathbf {Q}_p^{\mathrm {cyc}}[[t]]$
.
$\mathrm {B}_{\mathrm {dR},\mathbf {Q}_p}^{+,\mathrm {pa}} = \mathbf {Q}_p^{\mathrm {cyc}}[[t]]$
.
In a direct analogy with this we can consider the ring
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}$
as the inverse limit
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}$
as the inverse limit
with each
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}/p^n$
being a
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}/p^n$
being a
![]() $\mathbf {Z}_p$
-Tate algebra (with topologically nilpotent unit T). For example, we have
$\mathbf {Z}_p$
-Tate algebra (with topologically nilpotent unit T). For example, we have
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}/p^n = \widetilde {\mathbf {E}}_{\mathbf {Q}_p}.$
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}/p^n = \widetilde {\mathbf {E}}_{\mathbf {Q}_p}.$
The third application of our main theorem is then the following result.
Theorem 4.10. We have
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {la}} = \varphi ^{-\infty }(\mathbf {{A}}_{\mathbf {Q}_p})$
and
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {la}} = \varphi ^{-\infty }(\mathbf {{A}}_{\mathbf {Q}_p})$
and
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {pa}} = \varprojlim _{n} \varphi ^{-\infty }(\mathbf {{A}_{{\mathbf {Q}_p}}})/p^n.$
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {pa}} = \varprojlim _{n} \varphi ^{-\infty }(\mathbf {{A}_{{\mathbf {Q}_p}}})/p^n.$
Remark 4.11. The ring
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {pa}}$
can also be thought of as the subring of elements in
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {pa}}$
can also be thought of as the subring of elements in
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}$
that for every
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}$
that for every
![]() $n\geq 1$
are congruent to an element of
$n\geq 1$
are congruent to an element of
![]() $\varphi ^{-\infty }(\mathbf {{A}_{{\mathbf {Q}_p}}})$
modulo
$\varphi ^{-\infty }(\mathbf {{A}_{{\mathbf {Q}_p}}})$
modulo
![]() $p^n$
. This shows that the containment
$p^n$
. This shows that the containment
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {la}} \subset \widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {pa}}$
is strict. For example, the power series
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {la}} \subset \widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {pa}}$
is strict. For example, the power series
![]() $\sum _{n \geq 0} p^n \varphi ^{-n}(1+T)$
belongs to
$\sum _{n \geq 0} p^n \varphi ^{-n}(1+T)$
belongs to
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {pa}}$
but not to
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {pa}}$
but not to
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {la}}$
.
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {la}}$
.
Remark 4.12. It has been desirable to have a theory of
![]() $(\varphi ,\Gamma )$
modules when
$(\varphi ,\Gamma )$
modules when
![]() $\Gamma = \mathrm {Gal}(\overline {K}/K)/H$
is not Lubin-Tate. However, in such cases it seems difficult to find a suitable lift of the field of norms, that is, a replacement for the ring
$\Gamma = \mathrm {Gal}(\overline {K}/K)/H$
is not Lubin-Tate. However, in such cases it seems difficult to find a suitable lift of the field of norms, that is, a replacement for the ring
![]() $\mathbf {{A}}_K$
. A lift that is a power series ring inside
$\mathbf {{A}}_K$
. A lift that is a power series ring inside
![]() $\widetilde {\mathbf {A}}^{H}$
is known not to exist under certain assumptions ([Reference BergerBer14], [Reference PoyetonPoy22]). When
$\widetilde {\mathbf {A}}^{H}$
is known not to exist under certain assumptions ([Reference BergerBer14], [Reference PoyetonPoy22]). When
![]() $\Gamma $
is abelian, Theorem 4.10 suggests to consider
$\Gamma $
is abelian, Theorem 4.10 suggests to consider
![]() $\widetilde {\mathbf {A}}^{H,\mathrm {la}}$
or
$\widetilde {\mathbf {A}}^{H,\mathrm {la}}$
or
![]() $\widetilde {\mathbf {A}}^{H,\mathrm {pa}}$
as a suitable lift instead. Unpublished computations of ours suggest that in general
$\widetilde {\mathbf {A}}^{H,\mathrm {pa}}$
as a suitable lift instead. Unpublished computations of ours suggest that in general
![]() $\widetilde {\mathbf {A}}^{H,\mathrm {pa}}$
surjects onto
$\widetilde {\mathbf {A}}^{H,\mathrm {pa}}$
surjects onto
![]() $\widetilde {\mathbf {E}}^{H,\mathrm {la}}$
and so gives a valid lift.
$\widetilde {\mathbf {E}}^{H,\mathrm {la}}$
and so gives a valid lift.
We now proceed to proving Theorem 4.10. The description of
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {pa}}$
follows directly from the following lemma.
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {pa}}$
follows directly from the following lemma.
Lemma 4.13. Let
![]() $0 < r < 1$
. We have
$0 < r < 1$
. We have
Proof. We have
by devissage to the case
![]() $n=1$
(where both are equal to
$n=1$
(where both are equal to
![]() $\widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
). By Theorem 3.1 we have
$\widetilde {\mathbf {E}}_{\mathbf {Q}_p}$
). By Theorem 3.1 we have
![]() $\mathrm {R}^1_{\mathrm {la}}(p^{n-1}\widetilde {\mathbf {{A}}}^{(0,r]}_{\mathbf {Q}_p}/p^n) = 0$
. Hence by devissage we deduce
$\mathrm {R}^1_{\mathrm {la}}(p^{n-1}\widetilde {\mathbf {{A}}}^{(0,r]}_{\mathbf {Q}_p}/p^n) = 0$
. Hence by devissage we deduce
(the case
![]() $n=1$
being Theorem 4.2). Finally, we need to explain why
$n=1$
being Theorem 4.2). Finally, we need to explain why
but this is once again true by devissage.
We now turn to studying
![]() $\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {la}}.$
$\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{\mathrm {la}}.$
Lemma 4.14.
-
1. Given
 $\Gamma \subset \Gamma _{\mathbf {Q}_p}$
open,
$\Gamma \subset \Gamma _{\mathbf {Q}_p}$
open,
 $\lambda \in \mathbf {R}$
and
$\lambda \in \mathbf {R}$
and
 $r < 1$
there exists an
$r < 1$
there exists an
 $m \geq 0$
such that
$m \geq 0$
such that  $$ \begin{align*}(\widetilde{\mathbf{{A}}}_{\mathbf{Q}_p}^{(0,r]})^{\Gamma,\lambda\text{-an}} \subset \varphi^{-m}(\mathbf{{A}}_{\mathbf{Q}_p}^{(0,rp^{-m}]}).\end{align*} $$
$$ \begin{align*}(\widetilde{\mathbf{{A}}}_{\mathbf{Q}_p}^{(0,r]})^{\Gamma,\lambda\text{-an}} \subset \varphi^{-m}(\mathbf{{A}}_{\mathbf{Q}_p}^{(0,rp^{-m}]}).\end{align*} $$
-
2. Given
 $m \geq 0$
and
$m \geq 0$
and
 $r < 1$
there exists
$r < 1$
there exists
 $\Gamma \subset \Gamma _{\mathbf {Q}_p}$
open and
$\Gamma \subset \Gamma _{\mathbf {Q}_p}$
open and
 $\lambda \in \mathbf {R}$
such that
$\lambda \in \mathbf {R}$
such that  $$ \begin{align*}\varphi^{-m}(\mathbf{{A}}_{\mathbf{Q}_p}^{(0,rp^{-m}]})\subset (\widetilde{\mathbf{{A}}}_{\mathbf{Q}_p}^{(0,r]})^{\Gamma,\lambda\text{-an}}.\end{align*} $$
$$ \begin{align*}\varphi^{-m}(\mathbf{{A}}_{\mathbf{Q}_p}^{(0,rp^{-m}]})\subset (\widetilde{\mathbf{{A}}}_{\mathbf{Q}_p}^{(0,r]})^{\Gamma,\lambda\text{-an}}.\end{align*} $$
Proof. Part 1 follows from Theorem 4.4 of [Reference BergerBer16] and Lemma 4.3. Part 2 follows from Corollary 3.10.
Proposition 4.15.
-
1. For
 $\Gamma \subset \Gamma _{\mathbf {Q}_p}$
open and
$\Gamma \subset \Gamma _{\mathbf {Q}_p}$
open and
 $\lambda \in \mathbf {R}$
there exists some
$\lambda \in \mathbf {R}$
there exists some
 $m \geq 0$
so that for all
$m \geq 0$
so that for all
 $n \geq 1$
there is an inclusion
$n \geq 1$
there is an inclusion  $$ \begin{align*}(\widetilde{\mathbf{{A}}}_{\mathbf{Q}_p}^{(0,r]}/p^n)^{\Gamma,\lambda \text{-an}} \subset \varphi^{-m}(\mathbf{{A}}_{\mathbf{Q}_p}^{(0,rp^{-m}]})/p^n.\end{align*} $$
$$ \begin{align*}(\widetilde{\mathbf{{A}}}_{\mathbf{Q}_p}^{(0,r]}/p^n)^{\Gamma,\lambda \text{-an}} \subset \varphi^{-m}(\mathbf{{A}}_{\mathbf{Q}_p}^{(0,rp^{-m}]})/p^n.\end{align*} $$
-
2. Given
 $m \geq 0$
there exists
$m \geq 0$
there exists
 $\Gamma \subset \Gamma _{\mathbf {Q}_p}$
open and
$\Gamma \subset \Gamma _{\mathbf {Q}_p}$
open and
 $\lambda \in \mathbf {R}$
so that for all
$\lambda \in \mathbf {R}$
so that for all
 $n \geq 0$
there is an inclusion
$n \geq 0$
there is an inclusion  $$ \begin{align*}\varphi^{-m}(\mathbf{{A}}_{\mathbf{Q}_p}^{(0,rp^{-m}]})/p^n \subset (\widetilde{\mathbf{{A}}}_{\mathbf{Q}_p}^{(0,r]}/p^n)^{\Gamma,\lambda \text{-an}}.\end{align*} $$
$$ \begin{align*}\varphi^{-m}(\mathbf{{A}}_{\mathbf{Q}_p}^{(0,rp^{-m}]})/p^n \subset (\widetilde{\mathbf{{A}}}_{\mathbf{Q}_p}^{(0,r]}/p^n)^{\Gamma,\lambda \text{-an}}.\end{align*} $$
Proof. We start by proving part 2. There is a surjection
Hence by part 2 of the previous lemma and functoriality, there exists some pair
![]() $\Gamma , \lambda $
, independent of n, such that every element of
$\Gamma , \lambda $
, independent of n, such that every element of
![]() $\varphi ^{-m}(\mathbf {{A}}_{\mathbf {Q}_p}^{(0,rp^{-m}]})/p^n$
lies in
$\varphi ^{-m}(\mathbf {{A}}_{\mathbf {Q}_p}^{(0,rp^{-m}]})/p^n$
lies in
![]() $(\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{(0,r]}/p^n)^{\Gamma ,\lambda \text {-an}}$
. The proof of part 1 is similar but we need another trick, because we do not know that
$(\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{(0,r]}/p^n)^{\Gamma ,\lambda \text {-an}}$
. The proof of part 1 is similar but we need another trick, because we do not know that
![]() $(\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{(0,r]})^{\Gamma ,\lambda \text {-an}}$
surjects onto
$(\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{(0,r]})^{\Gamma ,\lambda \text {-an}}$
surjects onto
![]() $(\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{(0,r]}/p^n)^{\Gamma ,\lambda \text {-an}}$
. Rather, we note that by Remark 3.19, the entirety of
$(\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{(0,r]}/p^n)^{\Gamma ,\lambda \text {-an}}$
. Rather, we note that by Remark 3.19, the entirety of
![]() $\mathrm {R}^1_{\Gamma ,\lambda }(\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{(0,r]})$
maps to zero in some
$\mathrm {R}^1_{\Gamma ,\lambda }(\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{(0,r]})$
maps to zero in some
![]() $\mathrm {R}^1_{\Gamma ',\lambda '}(\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{(0,r]})$
. This implies that given a pair
$\mathrm {R}^1_{\Gamma ',\lambda '}(\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{(0,r]})$
. This implies that given a pair
![]() $(\Gamma ,\lambda )$
there exists some other pair
$(\Gamma ,\lambda )$
there exists some other pair
![]() $(\Gamma ',\lambda ')$
so that for all
$(\Gamma ',\lambda ')$
so that for all
![]() $n\geq 1$
we have that elements of
$n\geq 1$
we have that elements of
![]() $(\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{(0,r]}/p^n)^{\Gamma ,\lambda \text {-an}}$
lift to
$(\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{(0,r]}/p^n)^{\Gamma ,\lambda \text {-an}}$
lift to
![]() $(\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{(0,r]})^{\Gamma ',\lambda ' \text {-an}}$
. We can now argue as before by applying part 1 of the previous lemma (for the pair
$(\widetilde {\mathbf {A}}_{\mathbf {Q}_p}^{(0,r]})^{\Gamma ',\lambda ' \text {-an}}$
. We can now argue as before by applying part 1 of the previous lemma (for the pair
![]() $\Gamma ',\lambda '$
).
$\Gamma ',\lambda '$
).
Corollary 4.16. We have
![]() $\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{\mathrm {la}} = \varphi ^{-\infty }(\mathbf {{A}}_{\mathbf {Q}_p}).$
$\widetilde {\mathbf {{A}}}_{\mathbf {Q}_p}^{\mathrm {la}} = \varphi ^{-\infty }(\mathbf {{A}}_{\mathbf {Q}_p}).$
Proof. The proposition shows that the direct systems
and
are cofinal. So the corresponding direct limits ranging over
![]() $\Gamma ,\lambda $
and over m are naturally isomorphic. These give
$\Gamma ,\lambda $
and over m are naturally isomorphic. These give
![]() $\mathbf {{A}}_{\mathbf {Q}_p}^{\mathrm {la}}$
and
$\mathbf {{A}}_{\mathbf {Q}_p}^{\mathrm {la}}$
and
![]() $\varphi ^{-\infty }(\mathbf {{A}}_{\mathbf {Q}_p})$
, respectively, and hence we establish the desired equality.
$\varphi ^{-\infty }(\mathbf {{A}}_{\mathbf {Q}_p})$
, respectively, and hence we establish the desired equality.
Acknowledgments
I would like to thank Chengyang Bao, Laurent Berger, Hui Gao, Léo Poyeton, and the anonymous referee for their helpful comments. This work was supported by the European Research Council (ERC 101078157).