Article contents
INVARIANT MEASURES CONCENTRATED ON COUNTABLE STRUCTURES
Published online by Cambridge University Press: 28 June 2016
Abstract
Let  $L$ be a countable language. We say that a countable infinite
$L$ be a countable language. We say that a countable infinite 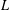 $L$ -structure
$L$ -structure 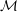 ${\mathcal{M}}$ admits an invariant measure when there is a probability measure on the space of
${\mathcal{M}}$ admits an invariant measure when there is a probability measure on the space of 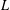 $L$ -structures with the same underlying set as
$L$ -structures with the same underlying set as 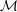 ${\mathcal{M}}$ that is invariant under permutations of that set, and that assigns measure one to the isomorphism class of
${\mathcal{M}}$ that is invariant under permutations of that set, and that assigns measure one to the isomorphism class of 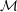 ${\mathcal{M}}$ . We show that
${\mathcal{M}}$ . We show that 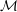 ${\mathcal{M}}$ admits an invariant measure if and only if it has trivial definable closure, that is, the pointwise stabilizer in
${\mathcal{M}}$ admits an invariant measure if and only if it has trivial definable closure, that is, the pointwise stabilizer in  $\text{Aut}({\mathcal{M}})$ of an arbitrary finite tuple of
$\text{Aut}({\mathcal{M}})$ of an arbitrary finite tuple of  ${\mathcal{M}}$ fixes no additional points. When
${\mathcal{M}}$ fixes no additional points. When 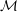 ${\mathcal{M}}$ is a Fraïssé limit in a relational language, this amounts to requiring that the age of
${\mathcal{M}}$ is a Fraïssé limit in a relational language, this amounts to requiring that the age of  ${\mathcal{M}}$ have strong amalgamation. Our results give rise to new instances of structures that admit invariant measures and structures that do not.
${\mathcal{M}}$ have strong amalgamation. Our results give rise to new instances of structures that admit invariant measures and structures that do not.
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2016
References
- 11
- Cited by


