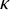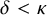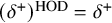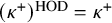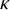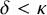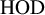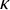1 Introduction
In 1963, Cohen established that Cantor’s continuum problem cannot be solved from the accepted ZFC axioms of set theory [Reference CohenCoh63]. This is the problem of determining which among Cantor’s transfinite cardinal numbers
is the cardinality of the continuum
![]() $\mathbb R$
. More precisely, what Cohen showed is that the axioms cannot rule out that
$\mathbb R$
. More precisely, what Cohen showed is that the axioms cannot rule out that
![]() $|\mathbb R| = \aleph _2$
, while Gödel [Reference GödelGöd39] had already shown that the possibility
$|\mathbb R| = \aleph _2$
, while Gödel [Reference GödelGöd39] had already shown that the possibility
![]() $|\mathbb R| = \aleph _1$
could not be ruled out.
$|\mathbb R| = \aleph _1$
could not be ruled out.
Of course, Cantor himself ruled out that
![]() $|\mathbb R|$
is
$|\mathbb R|$
is
![]() $\aleph _0$
by proving that the real numbers form an uncountable set. Later, König [Reference KönigKön05] showed that
$\aleph _0$
by proving that the real numbers form an uncountable set. Later, König [Reference KönigKön05] showed that
![]() $|\mathbb R|$
is not equal to
$|\mathbb R|$
is not equal to
![]() $\aleph _\omega $
,
$\aleph _\omega $
,
![]() $\aleph _{\omega +\omega }$
, or, more generally,
$\aleph _{\omega +\omega }$
, or, more generally,
![]() $\aleph _\alpha $
for any limit ordinal
$\aleph _\alpha $
for any limit ordinal
![]() $\alpha $
of countable cofinality. Soon after Cohen’s theorem, Solovay showed that there are no restrictions on the cardinality of the continuum besides those established by Cantor and König. For example, it is consistent with the ZFC axioms that
$\alpha $
of countable cofinality. Soon after Cohen’s theorem, Solovay showed that there are no restrictions on the cardinality of the continuum besides those established by Cantor and König. For example, it is consistent with the ZFC axioms that
![]() $|\mathbb R| = \aleph _{19}$
or
$|\mathbb R| = \aleph _{19}$
or
![]() $|\mathbb R| = \aleph _{\omega \cdot \omega +1}$
or
$|\mathbb R| = \aleph _{\omega \cdot \omega +1}$
or
![]() $|\mathbb R| = \aleph _{\omega _5}$
.
$|\mathbb R| = \aleph _{\omega _5}$
.
The cardinality of the continuum is denoted by
![]() $2^{\aleph _0}$
, recognizing that
$2^{\aleph _0}$
, recognizing that
![]() $\mathbb R$
is equinumerous with the set of functions from
$\mathbb R$
is equinumerous with the set of functions from
![]() $\mathbb N$
into a set of size
$\mathbb N$
into a set of size
![]() $2$
. For each cardinal number
$2$
. For each cardinal number
![]() $\kappa $
,
$\kappa $
,
![]() $2^\kappa $
denotes the cardinality of the set of functions from a set of size
$2^\kappa $
denotes the cardinality of the set of functions from a set of size
![]() $\kappa $
to a set of size
$\kappa $
to a set of size
![]() $2$
. The function
$2$
. The function
![]() $\kappa \mapsto 2^\kappa $
is known as the continuum function.
$\kappa \mapsto 2^\kappa $
is known as the continuum function.
After Solovay’s result classifying all possible values of
![]() $2^{\aleph _0}$
, set theorists took up the problem of classifying the possibilities for the continuum function itself. Obviously, we have
$2^{\aleph _0}$
, set theorists took up the problem of classifying the possibilities for the continuum function itself. Obviously, we have
![]() $2^\kappa \leq 2^\lambda $
whenever
$2^\kappa \leq 2^\lambda $
whenever
![]() $\kappa \leq \lambda $
. Also,
$\kappa \leq \lambda $
. Also,
![]() $2^\kappa> \kappa $
by Cantor’s theorem, and furthermore
$2^\kappa> \kappa $
by Cantor’s theorem, and furthermore
![]() $\operatorname {\mathrm {cf}}(2^\kappa )> \kappa $
by König’s theorem.
$\operatorname {\mathrm {cf}}(2^\kappa )> \kappa $
by König’s theorem.
Are there any other restrictions on the continuum function, or is the situation analogous to Solovay’s theorem for
![]() $2^{\aleph _0}$
, where no further constraints are possible? In 1966, Easton [Reference EastonEas70] showed the latter for regular cardinals – that is, those cardinals
$2^{\aleph _0}$
, where no further constraints are possible? In 1966, Easton [Reference EastonEas70] showed the latter for regular cardinals – that is, those cardinals
![]() $\kappa $
that are not the limit of fewer than
$\kappa $
that are not the limit of fewer than
![]() $\kappa $
smaller cardinals. That is, Easton showed that no restrictions on the behavior of the continuum function on regular cardinals can be established in ZFC except the ones mentioned in the previous paragraphs.
$\kappa $
smaller cardinals. That is, Easton showed that no restrictions on the behavior of the continuum function on regular cardinals can be established in ZFC except the ones mentioned in the previous paragraphs.
Following Easton’s theorem, the outstanding open problem in set theory was to generalize the result to all cardinals, showing without restriction that the continuum function obeys no laws other than those discovered by Cantor and König. This paper is inspired by a theorem of Silver [Reference SilverSil75], which shows such a generalization of Easton’s theorem is not possible: in fact, there are intricate and subtle restrictions on the behavior of the continuum function at singular (i.e., non-regular) cardinals. To this day, the problem of completely classifying the possible behavior of the continuum function at singular cardinals remains open, though the theory of singular cardinal arithmetic has since blossomed into one of the deepest subjects in set theory.
Silver’s theorem reveals that the value of
![]() $2^{\aleph _{\omega _1}}$
is tied to the values of
$2^{\aleph _{\omega _1}}$
is tied to the values of
![]() $2^{\aleph _\alpha }$
for ordinals
$2^{\aleph _\alpha }$
for ordinals
![]() $\alpha < \omega _1$
. More precisely, if
$\alpha < \omega _1$
. More precisely, if
![]() $2^{\aleph _\alpha } = \aleph _{\alpha +1}$
for all limit ordinals
$2^{\aleph _\alpha } = \aleph _{\alpha +1}$
for all limit ordinals
![]() $\alpha < \omega _1$
, then
$\alpha < \omega _1$
, then
![]() $2^{\aleph _{\omega _1}} = \aleph _{\omega _1+1}$
. He showed moreover that if
$2^{\aleph _{\omega _1}} = \aleph _{\omega _1+1}$
. He showed moreover that if
![]() $\kappa $
is a singular cardinal of uncountable cofinality and
$\kappa $
is a singular cardinal of uncountable cofinality and
![]() $2^\lambda = \lambda ^+$
for a stationary set of
$2^\lambda = \lambda ^+$
for a stationary set of
![]() $\lambda < \kappa $
, then
$\lambda < \kappa $
, then
![]() $2^\kappa = \kappa ^+$
.
$2^\kappa = \kappa ^+$
.
Silver’s theorem can be construed as a compactness property of the continuum function. Compactness describes a general pattern in set theory: the properties of a structure are determined by its small substructures. The most familiar compactness phenomena involve infinite structures and their finite substructures: for example, the Compactness Theorem in first-order logic states that the satisfiability of a first-order theory is determined by the satisfiability of its finite fragments. Compactness properties of larger regular cardinals often turn out to be related to large cardinal properties – for instance, the tree property and stationary reflection. However, singular cardinals have been found to have compactness properties that are provable in ZFC – for instance, Shelah’s singular compactness theorem in algebra, which led to his solution of Whitehead’s problem [Reference ShelahShe74].
This paper establishes analogs of Silver’s theorem in the context of set-theoretic definability. Gödel [Reference GödelGöd46] introduced the concept of ordinal definability in an attempt to formalize the intuitive concept of mathematical definability. A set is ordinal definable if it is definable over the universe of sets using finitely many ordinal numbers as parameters.
The behavior of ordinal definability is highly sensitive to the structure of the universe of sets, and for this reason, it is subject to the same independence phenomena that hinder our understanding of the continuum function. The main results of this paper show for the first time that ordinal definability at singular cardinals of uncountable cofinality exhibits patterns of compactness parallel to those that Silver identified for the continuum function.
Our theorems concern two invariants of ordinal definability, which play the role of the continuum function in our analogs of Silver’s theorem. First, we define the ordinal definable cofinality of an ordinal
![]() $\alpha $
, denoted by
$\alpha $
, denoted by
![]() $\operatorname {\mathrm {cf}}^{\operatorname {\mathrm {OD}}}(\alpha )$
, as the least ordinal
$\operatorname {\mathrm {cf}}^{\operatorname {\mathrm {OD}}}(\alpha )$
, as the least ordinal
![]() $\delta $
such that there is an ordinal definable cofinal function from
$\delta $
such that there is an ordinal definable cofinal function from
![]() $\delta $
to
$\delta $
to
![]() $\alpha $
. Second, we define the ordinal definable successor of
$\alpha $
. Second, we define the ordinal definable successor of
![]() $\alpha $
, denoted by
$\alpha $
, denoted by
![]() $\alpha ^{+\operatorname {\mathrm {OD}}}$
, as the supremum of all ordinals
$\alpha ^{+\operatorname {\mathrm {OD}}}$
, as the supremum of all ordinals
![]() $\gamma $
for which there is an ordinal definable surjection from
$\gamma $
for which there is an ordinal definable surjection from
![]() $\alpha $
to
$\alpha $
to
![]() $\gamma $
.Footnote
1
With this notation in hand, we can state our compactness theorems for ordinal definability.
$\gamma $
.Footnote
1
With this notation in hand, we can state our compactness theorems for ordinal definability.
Theorem. Suppose that
![]() $\kappa $
is a singular cardinal with uncountable cofinality and that
$\kappa $
is a singular cardinal with uncountable cofinality and that
![]() $\{\delta <\kappa \mathrel {|} {\operatorname {\mathrm {cf}}^{\operatorname {\mathrm {OD}}}(\delta ) <\delta }\}$
is stationary. Then
$\{\delta <\kappa \mathrel {|} {\operatorname {\mathrm {cf}}^{\operatorname {\mathrm {OD}}}(\delta ) <\delta }\}$
is stationary. Then
![]() $\operatorname {\mathrm {cf}}^{\operatorname {\mathrm {OD}}}(\kappa )<\kappa $
.
$\operatorname {\mathrm {cf}}^{\operatorname {\mathrm {OD}}}(\kappa )<\kappa $
.
Our theorem on the ordinal definable successor function is significantly harder to prove, and moreover, we do not know how to prove it for arbitrary singular cardinals.
Theorem. Suppose that
![]() $\kappa $
is a singular strong limit cardinal of uncountable cofinality and
$\kappa $
is a singular strong limit cardinal of uncountable cofinality and
![]() $\{\delta <\kappa \mathrel {|} \delta ^{+\operatorname {\mathrm {OD}}}=\delta ^+\}$
is stationary. Then
$\{\delta <\kappa \mathrel {|} \delta ^{+\operatorname {\mathrm {OD}}}=\delta ^+\}$
is stationary. Then
![]() $\kappa ^{+\operatorname {\mathrm {OD}}}=\kappa ^+$
.
$\kappa ^{+\operatorname {\mathrm {OD}}}=\kappa ^+$
.
The theorems above are proved by combining the technique of generic ultrapowers (see §2.1) with variants of Vopenka’s theorem that every set belongs to a forcing extension of HOD. In addition, in §3.1, we employ set-theoretic forcing to show that the hypothesis employed may not be relaxed. Thus, our results are provably optimal.
Finally, we show that the first of our compactness theorems does not extend to arbitrary
![]() $\omega $
-club amenable models (see p.13). This contrasts with the main results of [Reference GoldbergGol23] where the first author showed that most known results about HOD – for example, the
$\omega $
-club amenable models (see p.13). This contrasts with the main results of [Reference GoldbergGol23] where the first author showed that most known results about HOD – for example, the
![]() $\operatorname {\mathrm {HOD}}$
dichotomy theorem – can actually be proved for an arbitrary inner model that is
$\operatorname {\mathrm {HOD}}$
dichotomy theorem – can actually be proved for an arbitrary inner model that is
![]() $\omega $
-club amenable.
$\omega $
-club amenable.
Theorem. Assume that every set T belongs to an inner model with a measurable cardinal of Mitchell order 2 above
![]() $\operatorname {\mathrm {rank}}(T)$
. Then for every cardinal
$\operatorname {\mathrm {rank}}(T)$
. Then for every cardinal
![]() $\lambda $
, there is an
$\lambda $
, there is an
![]() $\omega $
-club amenable inner model M that is correct about cardinals and cofinalities below
$\omega $
-club amenable inner model M that is correct about cardinals and cofinalities below
![]() $\lambda $
while
$\lambda $
while
![]() $(\lambda ^+)^M < \lambda ^+$
.
$(\lambda ^+)^M < \lambda ^+$
.
The notation of this paper is standard in set theory. In §2, we provide the reader with some preliminaries regarding
![]() $\operatorname {\mathrm {HOD}}$
and the theory of generic ultrapowers. §3 is devoted to prove the above theorems and discuss their optimality. Finally, in §4, we leave some related open questions.
$\operatorname {\mathrm {HOD}}$
and the theory of generic ultrapowers. §3 is devoted to prove the above theorems and discuss their optimality. Finally, in §4, we leave some related open questions.
2 Preliminaries and notation
This section collects some set-theoretic tools employed through the paper. The material here is standard and is included just for the benefit of our readers. We also introduce some relevant terminology.
2.1 Generic ultrapowers
Fix a set X. A set
![]() $\mathcal {I}\subseteq \mathcal {P}(X)$
is called an ideal if
$\mathcal {I}\subseteq \mathcal {P}(X)$
is called an ideal if
![]() $\emptyset \in \mathcal {I}$
,
$\emptyset \in \mathcal {I}$
,
![]() $X\notin \mathcal {I}$
and
$X\notin \mathcal {I}$
and
![]() $\mathcal {I}$
is closed under subsets and finite unions. Dually, a set
$\mathcal {I}$
is closed under subsets and finite unions. Dually, a set
![]() $\mathcal {F}\subseteq \mathcal {P}(X)$
is a filter if
$\mathcal {F}\subseteq \mathcal {P}(X)$
is a filter if
![]() $\emptyset \notin \mathcal {F}$
,
$\emptyset \notin \mathcal {F}$
,
![]() $X\in \mathcal {F}$
and
$X\in \mathcal {F}$
and
![]() $\mathcal {F}$
is closed under supersets and finite intersections. A filter
$\mathcal {F}$
is closed under supersets and finite intersections. A filter
![]() $\mathcal {U}$
is called an ultrafilter if it satisfies the following additional property: given
$\mathcal {U}$
is called an ultrafilter if it satisfies the following additional property: given
![]() $A\in \mathcal {P}(X)$
, either
$A\in \mathcal {P}(X)$
, either
![]() $A\in \mathcal {U}$
or
$A\in \mathcal {U}$
or
![]() $X\setminus A\in \mathcal {U}$
; equivalently,
$X\setminus A\in \mathcal {U}$
; equivalently,
![]() $\mathcal {U}$
is a
$\mathcal {U}$
is a
![]() $\subseteq $
-maximal filter.
$\subseteq $
-maximal filter.
Given an ideal
![]() $\mathcal {I}\subseteq \mathcal {P}(X)$
, its dual filter
$\mathcal {I}\subseteq \mathcal {P}(X)$
, its dual filter
![]() $\mathcal {I}^*$
is defined as
$\mathcal {I}^*$
is defined as
![]() $\{X\setminus A\mathrel {|} A\in \mathcal {I}\}$
. A set
$\{X\setminus A\mathrel {|} A\in \mathcal {I}\}$
. A set
![]() $A\in \mathcal {P}(X)$
has
$A\in \mathcal {P}(X)$
has
![]() $\mathcal {I}$
-positive measure if
$\mathcal {I}$
-positive measure if
![]() $A\notin I$
, and
$A\notin I$
, and
![]() $\mathcal {I}^+$
denotes the collection of all sets with
$\mathcal {I}^+$
denotes the collection of all sets with
![]() $\mathcal {I}$
-positive measure. Note that
$\mathcal {I}$
-positive measure. Note that
![]() $\mathcal {I}^*$
is a filter,
$\mathcal {I}^*$
is a filter,
![]() $\mathcal {I}^*\subseteq \mathcal {I}^+$
and
$\mathcal {I}^*\subseteq \mathcal {I}^+$
and
![]() $A\in \mathcal {I}^+$
if and only if
$A\in \mathcal {I}^+$
if and only if
![]() $A\cap B\neq \emptyset $
for all
$A\cap B\neq \emptyset $
for all
![]() $B\in \mathcal {I}^*.$
These concepts have natural parallels in the setting of filters
$B\in \mathcal {I}^*.$
These concepts have natural parallels in the setting of filters
![]() $\mathcal {F}\subseteq \mathcal {P}(X)$
as well [Reference JechJec03, §7].
$\mathcal {F}\subseteq \mathcal {P}(X)$
as well [Reference JechJec03, §7].
Given an ideal
![]() $\mathcal {I}\subseteq \mathcal {P}(X)$
, define an equivalence relation
$\mathcal {I}\subseteq \mathcal {P}(X)$
, define an equivalence relation
![]() $\sim _{\mathcal {I}}$
on
$\sim _{\mathcal {I}}$
on
![]() $P(X)$
as follows:
$P(X)$
as follows:
This yields a quotient
![]() $\mathcal {P}(X)/\mathcal {I}$
, which, endowed with the order
$\mathcal {P}(X)/\mathcal {I}$
, which, endowed with the order
gives rise to a Boolean algebra. After removing the zero element from
![]() $\mathcal {P}(\kappa )/\mathcal {I}$
, the partial ordering
$\mathcal {P}(\kappa )/\mathcal {I}$
, the partial ordering
![]() $\leq $
becomes a separative order.
$\leq $
becomes a separative order.
There is another presentation of the poset
![]() $(\mathcal {P}(X)/\mathcal {I}\setminus \{[\emptyset ]\},\leq )$
as
$(\mathcal {P}(X)/\mathcal {I}\setminus \{[\emptyset ]\},\leq )$
as
![]() $\mathbb {P}:=(\mathcal {I}^+,\subset )$
. The two posets are forcing equivalent in the sense that they give rise to the same generic extensions. Indeed, the former poset is the separative quotient of the latter. A V-generic filter
$\mathbb {P}:=(\mathcal {I}^+,\subset )$
. The two posets are forcing equivalent in the sense that they give rise to the same generic extensions. Indeed, the former poset is the separative quotient of the latter. A V-generic filter
![]() $G\subseteq \mathbb {P}$
yields a V-ultrafilter on X extending the dual filter
$G\subseteq \mathbb {P}$
yields a V-ultrafilter on X extending the dual filter
![]() $\mathcal {I}^*$
. If
$\mathcal {I}^*$
. If
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $\kappa $
-complete, then G is also V-
$\kappa $
-complete, then G is also V-
![]() $\kappa $
-complete.Footnote
2
For details concerning these facts, see [Reference JechJec03, §22].
$\kappa $
-complete.Footnote
2
For details concerning these facts, see [Reference JechJec03, §22].
Suppose that
![]() $\mathcal {I}\subseteq \mathcal {P}(\kappa )$
is an ideal containing all singletons and that it is
$\mathcal {I}\subseteq \mathcal {P}(\kappa )$
is an ideal containing all singletons and that it is
![]() $\kappa $
-complete (i.e.,
$\kappa $
-complete (i.e.,
![]() $\bigcup _{\alpha <\lambda }A_\alpha \in \mathcal {I}$
provided
$\bigcup _{\alpha <\lambda }A_\alpha \in \mathcal {I}$
provided
![]() $\langle A_\alpha \mathrel {|} \alpha <\lambda \rangle \subseteq \mathcal {I}$
with
$\langle A_\alpha \mathrel {|} \alpha <\lambda \rangle \subseteq \mathcal {I}$
with
![]() $\lambda <\kappa $
).
$\lambda <\kappa $
).
Let
![]() $G\subseteq \mathbb {P}$
be a V-generic filter. Working in
$G\subseteq \mathbb {P}$
be a V-generic filter. Working in
![]() $V[G]$
, we can define the generic ultrapower of V by G. Namely, in
$V[G]$
, we can define the generic ultrapower of V by G. Namely, in
![]() $V[G]$
, one defines the structure
$V[G]$
, one defines the structure
where for each two functions
![]() $f, g\colon X\rightarrow V$
(in V)
$f, g\colon X\rightarrow V$
(in V)
and
Here and in the future, we will denote by
![]() $[f]_G$
the
$[f]_G$
the
![]() $=_G$
equivalence class of f, omitting the subscript when there is no chance of confusion.
$=_G$
equivalence class of f, omitting the subscript when there is no chance of confusion.
It turns out that
![]() $\operatorname {\mathrm {Ult}}(V,G)$
is a model of ZFC, yet not necessarily well-founded, even if G is V-
$\operatorname {\mathrm {Ult}}(V,G)$
is a model of ZFC, yet not necessarily well-founded, even if G is V-
![]() $\kappa $
-complete for an uncountable cardinal
$\kappa $
-complete for an uncountable cardinal
![]() $\kappa $
. As usual, an appropriate version of Łoś’s theorem holds. Namely,
$\kappa $
. As usual, an appropriate version of Łoś’s theorem holds. Namely,
where
![]() $\varphi (v_1,\dots , v_{n})$
is a first-order formula in the language
$\varphi (v_1,\dots , v_{n})$
is a first-order formula in the language
![]() $\{=, \in \}$
.
$\{=, \in \}$
.
This ensures that the map
![]() $j_G\colon \langle V,\in \rangle \rightarrow \operatorname {\mathrm {Ult}}(V,G)$
given by
$j_G\colon \langle V,\in \rangle \rightarrow \operatorname {\mathrm {Ult}}(V,G)$
given by
![]() $a\mapsto [c_a]_G$
is an elementary embedding, where
$a\mapsto [c_a]_G$
is an elementary embedding, where
![]() $c_a\colon X\rightarrow V$
is the constant function with value a.
$c_a\colon X\rightarrow V$
is the constant function with value a.
The combinatorial properties of the ideal
![]() $\mathcal {I}$
(in V) are related to the properties of the embedding
$\mathcal {I}$
(in V) are related to the properties of the embedding
![]() $j_G : V\to \operatorname {\mathrm {Ult}}(V,G)$
in the generic extension
$j_G : V\to \operatorname {\mathrm {Ult}}(V,G)$
in the generic extension
![]() $V[G]$
. For example,
$V[G]$
. For example,
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $\kappa $
-complete if and only if the maximal condition
$\kappa $
-complete if and only if the maximal condition
![]() $[X]$
forces that the critical point of
$[X]$
forces that the critical point of
![]() $j_G$
is at least
$j_G$
is at least
![]() $\kappa $
.
$\kappa $
.
The generic ultrapower construction will play a prominent role in the forthcoming §3. We refer the reader to [Reference JechJec03, §22] or Foreman’s excellent handbook chapter [Reference ForemanFor09] for any notion not considered in this account.
Remark 2.1. Let
![]() $\mathcal {F}\subseteq \mathcal {P}(X)$
be a filter and
$\mathcal {F}\subseteq \mathcal {P}(X)$
be a filter and
![]() $\mathcal {I}:=\{X\setminus F\mathrel {|} F\in \mathcal {F}\}$
be its dual ideal. Since the
$\mathcal {I}:=\{X\setminus F\mathrel {|} F\in \mathcal {F}\}$
be its dual ideal. Since the
![]() $\mathcal {F}$
-positive sets are exactly the
$\mathcal {F}$
-positive sets are exactly the
![]() $\mathcal {I}$
-positive sets, all the previous comments remain valid starting with a filter
$\mathcal {I}$
-positive sets, all the previous comments remain valid starting with a filter
![]() $\mathcal {F}$
and taking
$\mathcal {F}$
and taking
![]() $\mathbb {P}:=(\mathcal {F}^+,\subseteq )$
. This will be the approach we take through §3. We decided to phrase the discussion here in the language of ideals just because this is the approach pursued in reference texts, such as [Reference JechJec03, Reference ForemanFor09].
$\mathbb {P}:=(\mathcal {F}^+,\subseteq )$
. This will be the approach we take through §3. We decided to phrase the discussion here in the language of ideals just because this is the approach pursued in reference texts, such as [Reference JechJec03, Reference ForemanFor09].
Definition 2.2. Given a filter
![]() $\mathcal {F}\subseteq \mathcal {P}(X)$
and functions
$\mathcal {F}\subseteq \mathcal {P}(X)$
and functions
![]() $f,g\colon X\rightarrow V$
, denote
$f,g\colon X\rightarrow V$
, denote
Similarly, if
![]() $\mathcal {I}\subseteq \mathcal {P}(X)$
is an ideal,
$\mathcal {I}\subseteq \mathcal {P}(X)$
is an ideal,
2.2 Ordinal definability and forcing
A set X is called ordinal definable if it is definable by a formula of the language of set theory using ordinals as parameters. More formally, there is
![]() $\varphi (x,\vec {y})$
and
$\varphi (x,\vec {y})$
and
![]() $\langle \alpha _*,\alpha _0,\dots \alpha _n\rangle \in \operatorname {\mathrm {Ord}}^{<\omega }$
such that
$\langle \alpha _*,\alpha _0,\dots \alpha _n\rangle \in \operatorname {\mathrm {Ord}}^{<\omega }$
such that
The class of ordinal definable sets is denoted by
![]() $\operatorname {\mathrm {OD}}$
. Since
$\operatorname {\mathrm {OD}}$
. Since
![]() $\operatorname {\mathrm {OD}}$
need not be transitive, one looks at a special subclass of
$\operatorname {\mathrm {OD}}$
need not be transitive, one looks at a special subclass of
![]() $\operatorname {\mathrm {OD}}$
– the Hereditarily ordinal definable sets,
$\operatorname {\mathrm {OD}}$
– the Hereditarily ordinal definable sets,
![]() $\operatorname {\mathrm {HOD}}$
. A set X is Hereditarily Ordinal Definable (or, simply, in
$\operatorname {\mathrm {HOD}}$
. A set X is Hereditarily Ordinal Definable (or, simply, in
![]() $\operatorname {\mathrm {HOD}}$
) if
$\operatorname {\mathrm {HOD}}$
) if
![]() $X\in \operatorname {\mathrm {OD}}$
and the transitive closure of
$X\in \operatorname {\mathrm {OD}}$
and the transitive closure of
![]() $\{X\}$
is contained in
$\{X\}$
is contained in
![]() $\operatorname {\mathrm {OD}}$
. It turns that
$\operatorname {\mathrm {OD}}$
. It turns that
![]() $\operatorname {\mathrm {HOD}}$
is an inner model; namely, it is a transitive class containing the ordinals and satisfying all the ZFC axioms.
$\operatorname {\mathrm {HOD}}$
is an inner model; namely, it is a transitive class containing the ordinals and satisfying all the ZFC axioms.
At many places in this paper, we shall be preoccupied with the following issue. Suppose that
![]() $\mathbb {P}\in \operatorname {\mathrm {OD}}$
is a forcing poset and
$\mathbb {P}\in \operatorname {\mathrm {OD}}$
is a forcing poset and
![]() $G\subseteq \mathbb {P}$
is V-generic – how does
$G\subseteq \mathbb {P}$
is V-generic – how does
![]() $\operatorname {\mathrm {HOD}}^{V[G]}$
compare to
$\operatorname {\mathrm {HOD}}^{V[G]}$
compare to
![]() $\operatorname {\mathrm {HOD}}^V$
? Here,
$\operatorname {\mathrm {HOD}}^V$
? Here,
![]() $\operatorname {\mathrm {HOD}}^V$
(resp.
$\operatorname {\mathrm {HOD}}^V$
(resp.
![]() $\operatorname {\mathrm {HOD}}^{V[G]}$
) stands for the class
$\operatorname {\mathrm {HOD}}^{V[G]}$
) stands for the class
![]() $\operatorname {\mathrm {HOD}}$
as computed in V (resp. in
$\operatorname {\mathrm {HOD}}$
as computed in V (resp. in
![]() $V[G]$
). In special circumstances, we have
$V[G]$
). In special circumstances, we have
![]() $\operatorname {\mathrm {HOD}}^{V[G]}\subseteq \operatorname {\mathrm {HOD}}$
– for example, if
$\operatorname {\mathrm {HOD}}^{V[G]}\subseteq \operatorname {\mathrm {HOD}}$
– for example, if
![]() $\mathbb {P}$
is cone/weakly homogeneous:
$\mathbb {P}$
is cone/weakly homogeneous:
Definition 2.3. A poset
![]() $\mathbb {P}$
is weakly homogeneous if for for all
$\mathbb {P}$
is weakly homogeneous if for for all
![]() $p,q\in \mathbb {P}$
, there is an automorphism
$p,q\in \mathbb {P}$
, there is an automorphism
![]() $\varphi \colon \mathbb {P}\rightarrow \mathbb {P}$
making
$\varphi \colon \mathbb {P}\rightarrow \mathbb {P}$
making
![]() $\varphi (p)$
and q compatible.
$\varphi (p)$
and q compatible.
Similarly,
![]() $\mathbb {P}$
is cone-homogeneous if for all
$\mathbb {P}$
is cone-homogeneous if for all
![]() $p,q\in \mathbb {P}$
, there are
$p,q\in \mathbb {P}$
, there are
![]() $p^*\leq p$
and
$p^*\leq p$
and
![]() $q^*\leq q$
together with an isomorphism
$q^*\leq q$
together with an isomorphism
![]() $\varphi \colon \mathbb {P}/p^*\rightarrow \mathbb {P}/q^*$
.
$\varphi \colon \mathbb {P}/p^*\rightarrow \mathbb {P}/q^*$
.
We used
![]() $\mathbb {P}/p$
to denote the subposet of
$\mathbb {P}/p$
to denote the subposet of
![]() $\mathbb {P}$
with universe
$\mathbb {P}$
with universe
![]() $\{q\in \mathbb {P}\mathrel {|} q\leq p\}$
. It is clear that every weakly homogeneous forcing is cone-homogeneous.
$\{q\in \mathbb {P}\mathrel {|} q\leq p\}$
. It is clear that every weakly homogeneous forcing is cone-homogeneous.
Lemma 2.4 (Folklore).
If
![]() $\mathbb {P}\in \operatorname {\mathrm {OD}}$
is a cone-homogeneous forcing poset, then
$\mathbb {P}\in \operatorname {\mathrm {OD}}$
is a cone-homogeneous forcing poset, then
![]() $\operatorname {\mathrm {HOD}}^{V[G]}\subseteq \operatorname {\mathrm {HOD}}^V$
for all V-generic
$\operatorname {\mathrm {HOD}}^{V[G]}\subseteq \operatorname {\mathrm {HOD}}^V$
for all V-generic
![]() $G\subseteq \mathbb {P}$
.
$G\subseteq \mathbb {P}$
.
Sometimes we will need to assume (see, for example, §3.1) that
![]() $\operatorname {\mathrm {HOD}}$
encompasses large cardinals which exist in V. This can be done by forcing
$\operatorname {\mathrm {HOD}}$
encompasses large cardinals which exist in V. This can be done by forcing
![]() $"V=\operatorname {\mathrm {HOD}}$
” with McAloon iteration coding V into the continuum function. The said iteration preserves large cardinals (see [Reference Fuchs, Hamkins and ReitzFHR15, Reference Bagaria and PovedaBP23]) and produces a model V such that
$"V=\operatorname {\mathrm {HOD}}$
” with McAloon iteration coding V into the continuum function. The said iteration preserves large cardinals (see [Reference Fuchs, Hamkins and ReitzFHR15, Reference Bagaria and PovedaBP23]) and produces a model V such that
![]() $V\subseteq \operatorname {\mathrm {HOD}}^{V^{\mathbb {Q}}}$
for any set-sized forcing
$V\subseteq \operatorname {\mathrm {HOD}}^{V^{\mathbb {Q}}}$
for any set-sized forcing
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
3 Two compactness theorems for HOD
In this section, we prove our compactness theorems for
![]() $\operatorname {\mathrm {HOD}}$
(Theorems 3.4 and 3.5). Our results are very much in the spirit of Silver’s classical theorem that the generalized continuum hypothesis cannot first fail at a singular cardinal of uncountable cofinality [Reference SilverSil75]. The overall idea is to extract some information about ordinal definability from Silver’s argument, which heavily uses the technique of generic ultrapowers from §2.1.
$\operatorname {\mathrm {HOD}}$
(Theorems 3.4 and 3.5). Our results are very much in the spirit of Silver’s classical theorem that the generalized continuum hypothesis cannot first fail at a singular cardinal of uncountable cofinality [Reference SilverSil75]. The overall idea is to extract some information about ordinal definability from Silver’s argument, which heavily uses the technique of generic ultrapowers from §2.1.
Let us begin with the following key result:
Theorem 3.1 (Casey–Goldberg).
For any strong limit cardinal
![]() $\lambda $
,
$\lambda $
,
Proof. Let ![]() and let
and let ![]() . Let us assume that
. Let us assume that
![]() $\omega < \delta < \lambda ^+$
.
$\omega < \delta < \lambda ^+$
.
We must show that
![]() $\delta = \operatorname {\mathrm {cf}}(\lambda )$
. Let
$\delta = \operatorname {\mathrm {cf}}(\lambda )$
. Let
![]() $\mathscr {F}$
denote the restriction of the closed unbounded filter on
$\mathscr {F}$
denote the restriction of the closed unbounded filter on
![]() $\kappa $
to
$\kappa $
to
![]() $\text {HOD}$
; that is,
$\text {HOD}$
; that is, ![]() . Since
. Since
![]() $\mathrm {Cub}_\kappa $
is ordinal definable it is easy to check that
$\mathrm {Cub}_\kappa $
is ordinal definable it is easy to check that
![]() $\mathscr {F}\in \text {HOD}$
and that it is a filter in
$\mathscr {F}\in \text {HOD}$
and that it is a filter in
![]() $\operatorname {\mathrm {HOD}}$
. We will denote by
$\operatorname {\mathrm {HOD}}$
. We will denote by
![]() $\mathscr {F}^{+}$
the
$\mathscr {F}^{+}$
the
![]() $\mathscr {F}$
-positive sets, as computed in
$\mathscr {F}$
-positive sets, as computed in
![]() $\operatorname {\mathrm {HOD}}$
– namely, the collection of all
$\operatorname {\mathrm {HOD}}$
– namely, the collection of all
![]() $A\in \mathcal {P}(\kappa )^{\operatorname {\mathrm {HOD}}}$
intersecting all members of
$A\in \mathcal {P}(\kappa )^{\operatorname {\mathrm {HOD}}}$
intersecting all members of
![]() $\mathscr {F}$
.
$\mathscr {F}$
.
Claim 3.1.1. In
![]() $\operatorname {\mathrm {HOD}}$
,
$\operatorname {\mathrm {HOD}}$
,
![]() $\mathscr {F}$
is weakly normal in the sense that if
$\mathscr {F}$
is weakly normal in the sense that if
![]() $S\in \mathscr {F}^+$
and
$S\in \mathscr {F}^+$
and
![]() $f\colon S\to \kappa $
is a regressive function in
$f\colon S\to \kappa $
is a regressive function in
![]() $\operatorname {\mathrm {HOD}}$
, there is
$\operatorname {\mathrm {HOD}}$
, there is
![]() $\beta < \kappa $
such that
$\beta < \kappa $
such that
Footnote
3
Moreover, if
![]() $\gamma \in \operatorname {\mathrm {Ord}}$
,
$\gamma \in \operatorname {\mathrm {Ord}}$
,
![]() $\operatorname {\mathrm {cf}}^V(\gamma ) \neq \delta $
,
$\operatorname {\mathrm {cf}}^V(\gamma ) \neq \delta $
,
![]() $S\in \mathscr {F}^{+}$
, and
$S\in \mathscr {F}^{+}$
, and
![]() $f\colon S\to \gamma $
is any function in
$f\colon S\to \gamma $
is any function in
![]() $\operatorname {\mathrm {HOD}}$
, then there is some
$\operatorname {\mathrm {HOD}}$
, then there is some
![]() $\beta < \gamma $
such that
$\beta < \gamma $
such that
Finally,
![]() $ (\mathscr {F}^{+},\subset )$
is forcing equivalent in
$ (\mathscr {F}^{+},\subset )$
is forcing equivalent in
![]() $\operatorname {\mathrm {HOD}}$
to a poset of size less than
$\operatorname {\mathrm {HOD}}$
to a poset of size less than
![]() $(2^\delta )^{+V}$
.
$(2^\delta )^{+V}$
.
Proof of claim.
The bounding properties of
![]() $\mathscr {F}$
in
$\mathscr {F}$
in
![]() $\text {HOD}$
follow from the corresponding properties of
$\text {HOD}$
follow from the corresponding properties of
![]() $\text {Cub}_\kappa $
in V. That is, if
$\text {Cub}_\kappa $
in V. That is, if
![]() $S\in \mathscr {F}^+$
and
$S\in \mathscr {F}^+$
and
![]() $f : S\to \kappa $
is a regressive function in V, then f is bounded on a stationary set, and if
$f : S\to \kappa $
is a regressive function in V, then f is bounded on a stationary set, and if
![]() $\gamma $
is an ordinal whose cofinality is not
$\gamma $
is an ordinal whose cofinality is not
![]() $\delta $
and
$\delta $
and
![]() $f : S\to \gamma $
is any function in V, then f is bounded on a stationary set. We leave these as exercises with the following hints. First, by restricting to a club in
$f : S\to \gamma $
is any function in V, then f is bounded on a stationary set. We leave these as exercises with the following hints. First, by restricting to a club in
![]() $\kappa $
of ordertype
$\kappa $
of ordertype
![]() $\delta $
, one can reduce to the more familiar case that
$\delta $
, one can reduce to the more familiar case that
![]() $\kappa = \delta $
. Second, to prove the statement about functions into
$\kappa = \delta $
. Second, to prove the statement about functions into
![]() $\gamma $
, one can split into cases based on whether the cofinality of
$\gamma $
, one can split into cases based on whether the cofinality of
![]() $\gamma $
is less than
$\gamma $
is less than
![]() $\delta $
or greater than
$\delta $
or greater than
![]() $\delta $
; in the former case, one appeals to the
$\delta $
; in the former case, one appeals to the
![]() $\delta $
-completeness of the club filter, and in the latter case, one uses that functions from
$\delta $
-completeness of the club filter, and in the latter case, one uses that functions from
![]() $\delta $
to
$\delta $
to
![]() $\gamma $
are bounded everywhere.
$\gamma $
are bounded everywhere.
Finally,
![]() $(\mathscr {F}^+,\subset )$
is equivalent in
$(\mathscr {F}^+,\subset )$
is equivalent in
![]() $\text {HOD}$
to a forcing of size less than
$\text {HOD}$
to a forcing of size less than
![]() $(2^\delta )^{+V}$
because its separative quotient
$(2^\delta )^{+V}$
because its separative quotient
![]() $\mathbb Q$
has cardinality less than
$\mathbb Q$
has cardinality less than
![]() $(2^\delta )^{+V}$
: note that the underlying set of
$(2^\delta )^{+V}$
: note that the underlying set of
![]() $\mathbb Q$
is precisely the set of equivalence classes of
$\mathbb Q$
is precisely the set of equivalence classes of
![]() $\mathscr {F}^+$
modulo the non-stationary ideal on
$\mathscr {F}^+$
modulo the non-stationary ideal on
![]() $\kappa $
(in V). In
$\kappa $
(in V). In
![]() $\text {HOD}$
, choose a set
$\text {HOD}$
, choose a set
![]() $\mathscr {T}\subseteq \mathscr {F}^+$
such that for each
$\mathscr {T}\subseteq \mathscr {F}^+$
such that for each
![]() $S\in \mathscr {F}^+$
, there is exactly one
$S\in \mathscr {F}^+$
, there is exactly one
![]() $S'\in \mathscr {T}$
such that
$S'\in \mathscr {T}$
such that
![]() $S\mathrel {\triangle } S'$
is non-stationary (in V). Then
$S\mathrel {\triangle } S'$
is non-stationary (in V). Then
![]() $|\mathscr {T}|^{\text {HOD}} = |\mathbb Q|^{\text {HOD}}$
, and
$|\mathscr {T}|^{\text {HOD}} = |\mathbb Q|^{\text {HOD}}$
, and
![]() $V\models "|\mathscr {T}| \leq 2^\delta $
”. To see this last inequality, fix a closed unbounded set
$V\models "|\mathscr {T}| \leq 2^\delta $
”. To see this last inequality, fix a closed unbounded set
![]() $C\subseteq \kappa $
of ordertype
$C\subseteq \kappa $
of ordertype
![]() $\delta $
. Then
$\delta $
. Then
![]() $\langle S\cap C \mathrel {|} S\in \mathscr {T}\rangle $
is a sequence of distinct subsets of C from which we deduce that
$\langle S\cap C \mathrel {|} S\in \mathscr {T}\rangle $
is a sequence of distinct subsets of C from which we deduce that
![]() $V\models |\mathscr T| \leq |\mathcal {P}(C)| = 2^\delta $
.
$V\models |\mathscr T| \leq |\mathcal {P}(C)| = 2^\delta $
.
By forcing over
![]() $\text {HOD}$
with
$\text {HOD}$
with
![]() $(\mathscr {F}^+,\subset )$
, we extend
$(\mathscr {F}^+,\subset )$
, we extend
![]() $\mathscr {F}$
to a
$\mathscr {F}$
to a
![]() $\operatorname {\mathrm {HOD}}$
-weakly normal
$\operatorname {\mathrm {HOD}}$
-weakly normal
![]() $\text {HOD}$
-ultrafilter G on
$\text {HOD}$
-ultrafilter G on
![]() $\kappa $
with the property that if
$\kappa $
with the property that if
![]() $\gamma $
is an ordinal with
$\gamma $
is an ordinal with
![]() $\operatorname {\mathrm {cf}}^V(\gamma )\neq \delta $
then every
$\operatorname {\mathrm {cf}}^V(\gamma )\neq \delta $
then every
![]() $f\colon \kappa \to \gamma $
in
$f\colon \kappa \to \gamma $
in
![]() $\operatorname {\mathrm {HOD}}$
is bounded on a set in G. (This is by the moreover part of the claim together with a density argument.) In particular, the generic ultrapower map
$\operatorname {\mathrm {HOD}}$
is bounded on a set in G. (This is by the moreover part of the claim together with a density argument.) In particular, the generic ultrapower map
![]() $i\colon \operatorname {\mathrm {HOD}}\rightarrow N:=\operatorname {\mathrm {Ult}}(\operatorname {\mathrm {HOD}}, G)$
is continuous at ordinals
$i\colon \operatorname {\mathrm {HOD}}\rightarrow N:=\operatorname {\mathrm {Ult}}(\operatorname {\mathrm {HOD}}, G)$
is continuous at ordinals
![]() $\gamma $
of V-cofinality distinct from
$\gamma $
of V-cofinality distinct from
![]() $\delta $
. Note that N may not be well-founded, so N-ordinals may fail to be ordinals.
$\delta $
. Note that N may not be well-founded, so N-ordinals may fail to be ordinals.
Since G is
![]() $\operatorname {\mathrm {HOD}}$
-weakly normal (because so is
$\operatorname {\mathrm {HOD}}$
-weakly normal (because so is
![]() $\mathscr {F}$
), it follows that
$\mathscr {F}$
), it follows that
(Since N may not be well-founded, these objects are not really ordinals, but elements of
![]() $\text {Ord}^N$
, and the order relation, which we will simply denote by
$\text {Ord}^N$
, and the order relation, which we will simply denote by
![]() $<$
, is the canonical order of the ordinals as computed in N. If
$<$
, is the canonical order of the ordinals as computed in N. If
![]() $A\subseteq \text {Ord}^N$
, we write
$A\subseteq \text {Ord}^N$
, we write
![]() $\sup (A)$
for the least upper bound of A in this order, if it exists. Note that this least upper bound exists whenever A belongs to N, and may or may not exist otherwise. In this particular case,
$\sup (A)$
for the least upper bound of A in this order, if it exists. Note that this least upper bound exists whenever A belongs to N, and may or may not exist otherwise. In this particular case,
![]() $\sup i[\kappa ]$
exists and is equal to
$\sup i[\kappa ]$
exists and is equal to
![]() $[\text {id}]_G$
by weak normality, even though
$[\text {id}]_G$
by weak normality, even though
![]() $i[\kappa ]$
may not belong to N.)
$i[\kappa ]$
may not belong to N.)
Assume towards a contradiction that
By this assumption and our previous comments,
![]() $i(\lambda ) = \sup i[\lambda ]$
(i.e., i is continuous at
$i(\lambda ) = \sup i[\lambda ]$
(i.e., i is continuous at
![]() $\lambda $
) as every
$\lambda $
) as every
![]() $f\colon \kappa \to \lambda $
is bounded on a set in G.
$f\colon \kappa \to \lambda $
is bounded on a set in G.
Since
![]() $\kappa =\lambda ^{+\operatorname {\mathrm {HOD}}}$
,
$\kappa =\lambda ^{+\operatorname {\mathrm {HOD}}}$
,
![]() $\{\xi <\kappa \mathrel {|} \operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\xi )\leq \lambda \}\in G$
, and so
$\{\xi <\kappa \mathrel {|} \operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\xi )\leq \lambda \}\in G$
, and so
![]() $\operatorname {\mathrm {cf}}(\sup i[\kappa ]) \leq \sup i[\lambda ]$
. Let us next argue that this inequality is strict.
$\operatorname {\mathrm {cf}}(\sup i[\kappa ]) \leq \sup i[\lambda ]$
. Let us next argue that this inequality is strict.
Note that
![]() $\text {HOD}[G]\models "\operatorname {\mathrm {cf}}(\sup i[\kappa ]) = \kappa $
”: Indeed,
$\text {HOD}[G]\models "\operatorname {\mathrm {cf}}(\sup i[\kappa ]) = \kappa $
”: Indeed,
![]() $\kappa $
remains regular in
$\kappa $
remains regular in
![]() $\text {HOD}[G]$
because G comes from a forcing equivalent to another of cardinality less than
$\text {HOD}[G]$
because G comes from a forcing equivalent to another of cardinality less than
![]() $(2^\delta )^{+V}<\lambda $
.
$(2^\delta )^{+V}<\lambda $
.
Because
![]() $\operatorname {\mathrm {HOD}}[G]\models "\operatorname {\mathrm {cf}}(\sup i[\lambda ])=\operatorname {\mathrm {cf}}(\lambda )\leq \lambda <\kappa $
”, it follows that
$\operatorname {\mathrm {HOD}}[G]\models "\operatorname {\mathrm {cf}}(\sup i[\lambda ])=\operatorname {\mathrm {cf}}(\lambda )\leq \lambda <\kappa $
”, it follows that
Therefore, N satisfies the same; namely,
In particular, we must have
Let
![]() $C\in N$
be such that
$C\in N$
be such that
Recall that i is continuous at ordinals whose V-cofinality is not equal to
![]() $\delta $
. In particular, i is continuous at ordinals whose
$\delta $
. In particular, i is continuous at ordinals whose
![]() $V[G]$
-cofinality
$V[G]$
-cofinality
![]() $\gamma $
lies between
$\gamma $
lies between
![]() $(2^\delta )^+$
and
$(2^\delta )^+$
and
![]() $\lambda $
: by preservation of regular cardinals, such an ordinal has the same cofinality in V. Thus, for any such
$\lambda $
: by preservation of regular cardinals, such an ordinal has the same cofinality in V. Thus, for any such
![]() $\gamma $
, a familiar argument shows that
$\gamma $
, a familiar argument shows that
![]() $i[\kappa ]\cap C$
is
$i[\kappa ]\cap C$
is
![]() $\gamma $
-closed cofinal in
$\gamma $
-closed cofinal in
![]() $\sup i[\kappa ]$
. Hence,
$\sup i[\kappa ]$
. Hence,
![]() $i^{-1}[C]$
is cofinal in
$i^{-1}[C]$
is cofinal in
![]() $\kappa $
.
$\kappa $
.
Let ![]() , and note that there is some
, and note that there is some
![]() $A\in \operatorname {\mathrm {HOD}}$
unbounded in
$A\in \operatorname {\mathrm {HOD}}$
unbounded in
![]() $\kappa $
contained in B because G is generic for a partial order which in
$\kappa $
contained in B because G is generic for a partial order which in
![]() $\operatorname {\mathrm {HOD}}$
has size less than
$\operatorname {\mathrm {HOD}}$
has size less than
![]() $(2^\delta )^{+V} <\lambda < \kappa $
. Since
$(2^\delta )^{+V} <\lambda < \kappa $
. Since
![]() $i[A]\subseteq C$
, letting
$i[A]\subseteq C$
, letting
![]() $f\colon A\to \kappa $
be the transitive collapse,
$f\colon A\to \kappa $
be the transitive collapse,
![]() $i[\kappa ]\subseteq \bar {C}$
where
$i[\kappa ]\subseteq \bar {C}$
where
![]() $\bar {C} := i(f)[C]$
.
$\bar {C} := i(f)[C]$
.
Note that
Fix a
![]() $V[G]$
-regular cardinal
$V[G]$
-regular cardinal
![]() $\gamma \in (\delta ,\lambda )$
such that
$\gamma \in (\delta ,\lambda )$
such that
Then
![]() $i[\gamma ]\subseteq \bar C\cap i(\gamma )$
, and so
$i[\gamma ]\subseteq \bar C\cap i(\gamma )$
, and so
In particular, i is discontinuous at
![]() $\gamma $
. However, i must be continuous at
$\gamma $
. However, i must be continuous at
![]() $\gamma $
because
$\gamma $
because
![]() $\operatorname {\mathrm {cf}}(\gamma )\neq \delta $
. This yields a contradiction showing that our original assumption that
$\operatorname {\mathrm {cf}}(\gamma )\neq \delta $
. This yields a contradiction showing that our original assumption that
![]() $\operatorname {\mathrm {cf}}(\lambda )\neq \delta $
was false.
$\operatorname {\mathrm {cf}}(\lambda )\neq \delta $
was false.
The proof of Theorem 3.4 requires another technical result.
Definition 3.2. Let
![]() $V\subseteq W$
be two transitive models of
$V\subseteq W$
be two transitive models of
![]() $\mathrm {ZFC}$
and
$\mathrm {ZFC}$
and
![]() $\kappa \in V$
be such that
$\kappa \in V$
be such that
![]() $V\models `\kappa $
is a regular cardinal’. We say that the pair
$V\models `\kappa $
is a regular cardinal’. We say that the pair
![]() $(V,W)$
has the
$(V,W)$
has the
![]() $\kappa $
-uniform cover property if for every function
$\kappa $
-uniform cover property if for every function
![]() $f\in W$
with
$f\in W$
with
![]() $\operatorname {\mathrm {dom}}(f)\in V$
and
$\operatorname {\mathrm {dom}}(f)\in V$
and
![]() $\operatorname {\mathrm {ran}}(f)\subseteq V$
, there is yet another function
$\operatorname {\mathrm {ran}}(f)\subseteq V$
, there is yet another function
![]() $F\in V$
with
$F\in V$
with
![]() $\operatorname {\mathrm {dom}}(F)=\operatorname {\mathrm {dom}}(f)$
, and for all
$\operatorname {\mathrm {dom}}(F)=\operatorname {\mathrm {dom}}(f)$
, and for all
![]() $i\in \operatorname {\mathrm {dom}}(f)$
,
$i\in \operatorname {\mathrm {dom}}(f)$
,
![]() $f(i)\in F(i)$
and
$f(i)\in F(i)$
and
![]() $V\models |F(i)|<\kappa $
.
$V\models |F(i)|<\kappa $
.
If
![]() $\mathbb {P}\in V$
is a
$\mathbb {P}\in V$
is a
![]() $\kappa $
-cc forcing poset and
$\kappa $
-cc forcing poset and
![]() $G\subseteq \mathbb {P}$
is a generic filter, then standard arguments show that
$G\subseteq \mathbb {P}$
is a generic filter, then standard arguments show that
![]() $(V, V[G])$
has the
$(V, V[G])$
has the
![]() $\kappa $
-uniform cover property. Conversely, a remarkable theorem by Bukovský [Reference BukovskỳBuk73] says that if
$\kappa $
-uniform cover property. Conversely, a remarkable theorem by Bukovský [Reference BukovskỳBuk73] says that if
![]() $(V,W)$
has the
$(V,W)$
has the
![]() $\kappa $
-uniform cover property, then there is a poset
$\kappa $
-uniform cover property, then there is a poset
![]() $\mathbb {P}\in V$
that has the
$\mathbb {P}\in V$
that has the
![]() $\kappa $
-cc in V,
$\kappa $
-cc in V,
![]() $W\models "|\mathbb {P}|\leq 2^\kappa "$
and W is a generic extension of V by
$W\models "|\mathbb {P}|\leq 2^\kappa "$
and W is a generic extension of V by
![]() $\mathbb {P}$
(see [Reference SchindlerSch20, Theorem 3.11])
$\mathbb {P}$
(see [Reference SchindlerSch20, Theorem 3.11])
Lemma 3.3. Suppose
![]() $\mathbb P\in \operatorname {\mathrm {OD}}$
is a
$\mathbb P\in \operatorname {\mathrm {OD}}$
is a
![]() $\kappa $
-cc forcing and
$\kappa $
-cc forcing and
![]() $G\subseteq \mathbb P$
is a V-generic. Let N be the class of sets that are hereditarily definable in the structure
$G\subseteq \mathbb P$
is a V-generic. Let N be the class of sets that are hereditarily definable in the structure
![]() $\langle V[G],V,G,{\in }\rangle $
from ordinal parameters. Then the pair
$\langle V[G],V,G,{\in }\rangle $
from ordinal parameters. Then the pair
![]() $(\operatorname {\mathrm {HOD}}, N)$
has the
$(\operatorname {\mathrm {HOD}}, N)$
has the
![]() $\kappa $
-uniform cover property.
$\kappa $
-uniform cover property.
In particular, N is a forcing extension of
![]() $\operatorname {\mathrm {HOD}}$
by a forcing
$\operatorname {\mathrm {HOD}}$
by a forcing
![]() $\mathbb {Q}\in \operatorname {\mathrm {HOD}}$
such that
$\mathbb {Q}\in \operatorname {\mathrm {HOD}}$
such that
![]() $\operatorname {\mathrm {HOD}}\models "\mathbb {Q}$
is
$\operatorname {\mathrm {HOD}}\models "\mathbb {Q}$
is
![]() $\kappa $
-cc” and
$\kappa $
-cc” and
![]() $N\models "|\mathbb {Q}|\leq 2^\kappa "$
.
$N\models "|\mathbb {Q}|\leq 2^\kappa "$
.
Proof. Clearly,
![]() $\operatorname {\mathrm {HOD}}\subseteq N$
. We verify that
$\operatorname {\mathrm {HOD}}\subseteq N$
. We verify that
![]() $(\text {HOD}, N)$
has the
$(\text {HOD}, N)$
has the
![]() $\kappa $
-uniform cover property. Fix an ordinal
$\kappa $
-uniform cover property. Fix an ordinal
![]() $\lambda $
and a function
$\lambda $
and a function
![]() $f : \lambda \to \lambda $
that is definable in the structure
$f : \lambda \to \lambda $
that is definable in the structure
![]() $\langle V[G],V,G,{\in }\rangle $
from ordinal parameters. Let
$\langle V[G],V,G,{\in }\rangle $
from ordinal parameters. Let
![]() $\varphi (x_0,x_1,x_2)$
be a formula in the language of
$\varphi (x_0,x_1,x_2)$
be a formula in the language of
![]() $\langle V[G],V,G,{\in }\rangle $
such that for some ordinal
$\langle V[G],V,G,{\in }\rangle $
such that for some ordinal
![]() $\beta $
,
$\beta $
,
![]() $f(\xi ) = \zeta $
if and only if
$f(\xi ) = \zeta $
if and only if
![]() $\langle V[G],V,G,{\in }\rangle $
satisfies
$\langle V[G],V,G,{\in }\rangle $
satisfies
![]() $\varphi (\xi ,\zeta , \beta )$
. Then let
$\varphi (\xi ,\zeta , \beta )$
. Then let
Note that F is ordinal definable (because so is
![]() $\mathbb {P}$
) and that
$\mathbb {P}$
) and that
![]() $f(\xi )\in F(\xi )$
. Since
$f(\xi )\in F(\xi )$
. Since
![]() $\mathbb P$
is
$\mathbb P$
is
![]() $\kappa $
-cc, it also follows that
$\kappa $
-cc, it also follows that
![]() $\operatorname {\mathrm {HOD}}\models |F(\xi )| < \kappa $
.
$\operatorname {\mathrm {HOD}}\models |F(\xi )| < \kappa $
.
We are now in a position to prove our first main result:
Theorem 3.4. If
![]() $\kappa $
is a strong limit singular cardinal of uncountable cofinality and
$\kappa $
is a strong limit singular cardinal of uncountable cofinality and
![]() $\{\delta <\kappa \mathrel {|} (\delta ^+)^{\mathrm {HOD}}=\delta ^+\}$
is stationary, then
$\{\delta <\kappa \mathrel {|} (\delta ^+)^{\mathrm {HOD}}=\delta ^+\}$
is stationary, then
![]() $(\kappa ^+)^{\mathrm {HOD}}=\kappa ^+.$
$(\kappa ^+)^{\mathrm {HOD}}=\kappa ^+.$
Proof. The first attempt at a proof, on which the correct proof will elaborate, proceeds as follows. Let
![]() $\iota = \operatorname {\mathrm {cf}}(\kappa )$
and fix
$\iota = \operatorname {\mathrm {cf}}(\kappa )$
and fix
![]() $f\colon \iota \rightarrow \kappa $
an increasing continuous cofinal function. Let
$f\colon \iota \rightarrow \kappa $
an increasing continuous cofinal function. Let
![]() $\mathcal {F}$
be the club filter on
$\mathcal {F}$
be the club filter on
![]() $\iota $
. Then, by assumption,
$\iota $
. Then, by assumption,
By forcing with
![]() $\mathcal {F}^+$
below S, one produces a generic filter
$\mathcal {F}^+$
below S, one produces a generic filter
![]() $G\subseteq \mathcal {F}^+$
extending the filter
$G\subseteq \mathcal {F}^+$
extending the filter
![]() $\mathcal {F}$
, which is V-
$\mathcal {F}$
, which is V-
![]() $\iota $
-complete and V-normal. In particular,
$\iota $
-complete and V-normal. In particular,
Then we take the generic ultrapower
![]() $j_G : V\to M_G$
, using only functions
$j_G : V\to M_G$
, using only functions
![]() $f\colon \iota \rightarrow V$
in the ground model V (see §2.1). By V-normality of G,
$f\colon \iota \rightarrow V$
in the ground model V (see §2.1). By V-normality of G,
The ultrapower
![]() $M_G$
has its own version of
$M_G$
has its own version of
![]() $\kappa $
, the unique ordinal
$\kappa $
, the unique ordinal
![]() $\kappa _*$
of
$\kappa _*$
of
![]() $M_G$
that is ‘
$M_G$
that is ‘
![]() $\kappa $
-like’ in the sense that each of its predecessors has cardinality less than
$\kappa $
-like’ in the sense that each of its predecessors has cardinality less than
![]() $\kappa $
, whereas the set of predecessors of
$\kappa $
, whereas the set of predecessors of
![]() $\kappa _*$
has cardinality exactly
$\kappa _*$
has cardinality exactly
![]() $\kappa $
. Indeed,
$\kappa $
. Indeed,
![]() $\kappa _* = j_G(f)(\iota )$
, where as above
$\kappa _* = j_G(f)(\iota )$
, where as above
![]() $f\colon \iota \rightarrow \kappa $
is any cofinal continuous function in V. Note that if
$f\colon \iota \rightarrow \kappa $
is any cofinal continuous function in V. Note that if
![]() $M_G$
is well-founded, then
$M_G$
is well-founded, then
![]() $\kappa _* = \kappa $
, but we must deal with the possibility that
$\kappa _* = \kappa $
, but we must deal with the possibility that
![]() $M_G$
is ill-founded.
$M_G$
is ill-founded.
Let us begin with an easy (yet useful) observation.
Claim 3.4.1. In
![]() $V[G]$
,
$V[G]$
,
![]() $|(\kappa _*^+)^{M_G}| \geq \kappa ^+$
.
$|(\kappa _*^+)^{M_G}| \geq \kappa ^+$
.
Proof of claim.
In V, fix a sequence of functions
![]() $\langle h_\alpha \rangle _{\alpha < \kappa ^+}\subseteq \prod _{\xi < \iota } f(\xi )^+$
that is increasing in the order of domination modulo the bounded ideal on
$\langle h_\alpha \rangle _{\alpha < \kappa ^+}\subseteq \prod _{\xi < \iota } f(\xi )^+$
that is increasing in the order of domination modulo the bounded ideal on
![]() $\iota $
; namely, for each
$\iota $
; namely, for each
![]() $\alpha <\beta < \kappa ^+$
,
$\alpha <\beta < \kappa ^+$
,
![]() $\{\xi <\iota \mathrel {|} h_\alpha (\xi )\geq h_\beta (\xi )\}$
is bounded in
$\{\xi <\iota \mathrel {|} h_\alpha (\xi )\geq h_\beta (\xi )\}$
is bounded in
![]() $\iota $
. Such a sequence exists because this reduced product is
$\iota $
. Such a sequence exists because this reduced product is
![]() $\kappa ^+$
-directed. Note that in
$\kappa ^+$
-directed. Note that in
![]() $V[G]$
,
$V[G]$
,
![]() $\langle j_G(h_\alpha )(\iota )\rangle _{\alpha < \kappa ^+}$
is an increasing sequence of length
$\langle j_G(h_\alpha )(\iota )\rangle _{\alpha < \kappa ^+}$
is an increasing sequence of length
![]() $\kappa ^+$
consisting of predecessors of
$\kappa ^+$
consisting of predecessors of
![]() $(\kappa _*^+)^{M_G}$
. Thus,
$(\kappa _*^+)^{M_G}$
. Thus,
![]() $|(\kappa _*^+)^{M_G}|\geq \kappa ^{+V}$
. But
$|(\kappa _*^+)^{M_G}|\geq \kappa ^{+V}$
. But
![]() $\kappa ^{+V} = \kappa ^{+V[G]}$
since G is added by
$\kappa ^{+V} = \kappa ^{+V[G]}$
since G is added by
![]() $(\mathcal {F}^+,\subseteq )$
, which is a forcing of size
$(\mathcal {F}^+,\subseteq )$
, which is a forcing of size
![]() $2^\iota <\kappa $
.
$2^\iota <\kappa $
.
Let ![]() . By
. By
![]() $(\dagger )$
and
$(\dagger )$
and
![]() $(\dagger \dagger )$
above,
$(\dagger \dagger )$
above,
![]() $(\kappa _*^+)^H = (\kappa _*^+)^{M_G}$
.
$(\kappa _*^+)^H = (\kappa _*^+)^{M_G}$
.
Let N denote the inner model of
![]() $V[G]$
consisting of all sets hereditarily ordinal definable in the structure
$V[G]$
consisting of all sets hereditarily ordinal definable in the structure
![]() $\langle V[G],V,G,{\in }\rangle $
. The model N is a
$\langle V[G],V,G,{\in }\rangle $
. The model N is a
![]() $\kappa $
-cc forcing extension of
$\kappa $
-cc forcing extension of
![]() $\text {HOD}$
by Lemma 3.3, and so
$\text {HOD}$
by Lemma 3.3, and so
![]() $(\kappa ^+)^{\text {HOD}} = (\kappa ^+)^{N}$
.Footnote
4
If the structure H were a subclass of N, then we could finally conclude that
$(\kappa ^+)^{\text {HOD}} = (\kappa ^+)^{N}$
.Footnote
4
If the structure H were a subclass of N, then we could finally conclude that
The intuition that H should be a subclass of N comes from our experience with well-founded ultrapowers. The structure
![]() $M_G$
is definable over the structure
$M_G$
is definable over the structure
![]() $\langle V[G],V,G,{\in }\rangle $
, and so if
$\langle V[G],V,G,{\in }\rangle $
, and so if
![]() $M_G$
were well-founded, then any element of H, being ordinal definable in
$M_G$
were well-founded, then any element of H, being ordinal definable in
![]() $M_G$
, would be ordinal definable in
$M_G$
, would be ordinal definable in
![]() $\langle V[G],V,G,{\in }\rangle $
; this would yield
$\langle V[G],V,G,{\in }\rangle $
; this would yield
![]() $H\subseteq N$
. If H is ill-founded, however, then ordinals of
$H\subseteq N$
. If H is ill-founded, however, then ordinals of
![]() $M_G$
are not really ordinals, so it is not clear that ordinal definable elements of
$M_G$
are not really ordinals, so it is not clear that ordinal definable elements of
![]() $M_G$
are ordinal definable in
$M_G$
are ordinal definable in
![]() $\langle V[G],V,G,{\in }\rangle $
. To handle the possibility that H is not well-founded, we take a different approach.
$\langle V[G],V,G,{\in }\rangle $
. To handle the possibility that H is not well-founded, we take a different approach.
Instead, we consider the V-ultrafilter
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\kappa $
given by
$\kappa $
given by ![]() , where
, where
and the ultrapower
of
![]() $\text {HOD}$
by
$\text {HOD}$
by
![]() $\mathcal {U}\cap \text {HOD}$
, using only functions in
$\mathcal {U}\cap \text {HOD}$
, using only functions in
![]() $\text {HOD}$
.
$\text {HOD}$
.
An important observation is that
![]() $\mathcal {U}$
is ordinal definable in the structure
$\mathcal {U}$
is ordinal definable in the structure
![]() $\langle V[G],V,G,{\in }\rangle $
. This is because
$\langle V[G],V,G,{\in }\rangle $
. This is because
![]() $f^{\prime }_*(G) =\mathcal {U}$
for any increasing continuous cofinal map
$f^{\prime }_*(G) =\mathcal {U}$
for any increasing continuous cofinal map
![]() $f' : \iota \to \kappa $
. Therefore,
$f' : \iota \to \kappa $
. Therefore,
![]() $H_0\subseteq N$
: The point is that the structure
$H_0\subseteq N$
: The point is that the structure
![]() $H_0$
has for its universe the class of ordinal definable functions from
$H_0$
has for its universe the class of ordinal definable functions from
![]() $\kappa $
into
$\kappa $
into
![]() $\text {HOD}$
, which is a subclass of
$\text {HOD}$
, which is a subclass of
![]() $\text {HOD}$
and hence of N; the (possibly non-standard) membership and equality predicates of
$\text {HOD}$
and hence of N; the (possibly non-standard) membership and equality predicates of
![]() $H_0$
are ordinal definable over
$H_0$
are ordinal definable over
![]() $\langle V[G],V,G,{\in }\rangle $
as they are definable from
$\langle V[G],V,G,{\in }\rangle $
as they are definable from
![]() $\mathcal {U}\cap \operatorname {\mathrm {HOD}}$
, which belongs to N.
$\mathcal {U}\cap \operatorname {\mathrm {HOD}}$
, which belongs to N.
Let ![]() . Then
. Then
![]() $\kappa _0$
is the unique
$\kappa _0$
is the unique
![]() $\kappa $
-like ordinal of
$\kappa $
-like ordinal of
![]() $H_0$
, in the same sense that
$H_0$
, in the same sense that
![]() $\kappa _*$
is the unique
$\kappa _*$
is the unique
![]() $\kappa $
-like ordinal of
$\kappa $
-like ordinal of
![]() $M_G$
. In fact, there is an embedding
$M_G$
. In fact, there is an embedding
![]() $k : H_0\to H$
defined by
$k : H_0\to H$
defined by
such that
![]() $k\circ j_{\mathcal U} = j_G\mathbin \upharpoonright \operatorname {\mathrm {HOD}}$
, which one can easily check is well-defined and elementary. This embedding restricts to an injective map from
$k\circ j_{\mathcal U} = j_G\mathbin \upharpoonright \operatorname {\mathrm {HOD}}$
, which one can easily check is well-defined and elementary. This embedding restricts to an injective map from
![]() $\kappa _0$
to
$\kappa _0$
to
![]() $\kappa _*$
, so that the
$\kappa _*$
, so that the
![]() $\kappa $
-likeness of
$\kappa $
-likeness of
![]() $\kappa _0$
follows from that of
$\kappa _0$
follows from that of
![]() $\kappa _*$
.
$\kappa _*$
.
The argument from above shows that
![]() $|(\kappa _0^+)^{H_0}| = |(\kappa ^+)^{\text {HOD}}|$
in N. We also obtain the following:
$|(\kappa _0^+)^{H_0}| = |(\kappa ^+)^{\text {HOD}}|$
in N. We also obtain the following:
Claim 3.4.2.
![]() $N\models \kappa ^{+}=|(\kappa _0^{+})^{H_0}|.$
$N\models \kappa ^{+}=|(\kappa _0^{+})^{H_0}|.$
Proof of claim.
By Lemma 3.3,
![]() $(\kappa ^+)^N=(\kappa ^+)^{\operatorname {\mathrm {HOD}}}$
. Thus, as
$(\kappa ^+)^N=(\kappa ^+)^{\operatorname {\mathrm {HOD}}}$
. Thus, as
![]() $H_0,\operatorname {\mathrm {HOD}}\subseteq N$
and
$H_0,\operatorname {\mathrm {HOD}}\subseteq N$
and
![]() $|(\kappa _0^+)^{H_0}| = |(\kappa ^+)^{\text {HOD}}|$
in N,
$|(\kappa _0^+)^{H_0}| = |(\kappa ^+)^{\text {HOD}}|$
in N,
![]() $N\models |(\kappa _0^+)^{H_0}| = |(\kappa ^+)^{\text {HOD}}|=\kappa ^+$
.
$N\models |(\kappa _0^+)^{H_0}| = |(\kappa ^+)^{\text {HOD}}|=\kappa ^+$
.
Next, we work towards showing that the previous claim is incompatible with
![]() $"(\kappa ^+)^{\text {HOD}} < \kappa ^+"$
. This will yield the desired contradiction and as a result will lead to the proof of the theorem.
$"(\kappa ^+)^{\text {HOD}} < \kappa ^+"$
. This will yield the desired contradiction and as a result will lead to the proof of the theorem.
Let us begin with an auxiliary claim:
Claim 3.4.3. There is a
![]() $<_{\mathcal {U}}$
-increasing sequence
$<_{\mathcal {U}}$
-increasing sequence
![]() $\langle g_\alpha \mathrel {|} \alpha < (\kappa ^+)^{\operatorname {\mathrm {HOD}}}\rangle \subseteq \prod _{\delta < \kappa } (\delta ^+)^V$
in
$\langle g_\alpha \mathrel {|} \alpha < (\kappa ^+)^{\operatorname {\mathrm {HOD}}}\rangle \subseteq \prod _{\delta < \kappa } (\delta ^+)^V$
in
![]() $\operatorname {\mathrm {HOD}}$
, such that letting
$\operatorname {\mathrm {HOD}}$
, such that letting ![]() ,
,
![]() $\langle \gamma _\alpha \mathrel {|} {\alpha < (\kappa ^+)^{\operatorname {\mathrm {HOD}}}}\rangle $
is an increasing cofinal sequence in
$\langle \gamma _\alpha \mathrel {|} {\alpha < (\kappa ^+)^{\operatorname {\mathrm {HOD}}}}\rangle $
is an increasing cofinal sequence in
![]() $(\kappa _0^+)^{H_0}$
.
$(\kappa _0^+)^{H_0}$
.
Proof of claim.
We note first that there is such a sequence in N. This is simply because N satisfies that
![]() $|(\kappa _0^+)^{H_0}| = (\kappa ^+)^{\text {HOD}} = \kappa ^+$
, and moreover by the proof of this fact, N satisfies that
$|(\kappa _0^+)^{H_0}| = (\kappa ^+)^{\text {HOD}} = \kappa ^+$
, and moreover by the proof of this fact, N satisfies that
![]() $\operatorname {\mathrm {cf}}((\kappa _0^+)^{H_0}) = \kappa ^+$
, so in N, one can choose representatives for an increasing cofinal sequence in
$\operatorname {\mathrm {cf}}((\kappa _0^+)^{H_0}) = \kappa ^+$
, so in N, one can choose representatives for an increasing cofinal sequence in
![]() $(\kappa _0^+)^{H_0}$
, which is simply a
$(\kappa _0^+)^{H_0}$
, which is simply a
![]() ${<}_{\mathcal U}$
-increasing sequence
${<}_{\mathcal U}$
-increasing sequence
![]() $\langle g_\alpha \mathrel {|} \alpha < (\kappa ^+)^{\operatorname {\mathrm {HOD}}}\rangle \subseteq \prod _{\delta < \kappa } (\delta ^+)^V$
such that letting
$\langle g_\alpha \mathrel {|} \alpha < (\kappa ^+)^{\operatorname {\mathrm {HOD}}}\rangle \subseteq \prod _{\delta < \kappa } (\delta ^+)^V$
such that letting ![]() ,
,
![]() $\langle \gamma _\alpha \mathrel {|} {\alpha < (\kappa ^+)^{\operatorname {\mathrm {HOD}}}}\rangle $
is cofinal in
$\langle \gamma _\alpha \mathrel {|} {\alpha < (\kappa ^+)^{\operatorname {\mathrm {HOD}}}}\rangle $
is cofinal in
![]() $(\kappa _0^+)^{H_0}$
.
$(\kappa _0^+)^{H_0}$
.
Now we pull the sequence down to
![]() $\operatorname {\mathrm {HOD}}$
. Let
$\operatorname {\mathrm {HOD}}$
. Let
![]() $\mathbb {P}:=(\mathcal {F}^+,\subseteq )$
denote our poset. Since
$\mathbb {P}:=(\mathcal {F}^+,\subseteq )$
denote our poset. Since
![]() $\kappa $
is a strong limit cardinal (in V) and
$\kappa $
is a strong limit cardinal (in V) and
![]() $|\mathbb {P}|^V<\kappa $
, there is some V-regular
$|\mathbb {P}|^V<\kappa $
, there is some V-regular
![]() $\gamma <\kappa $
such that
$\gamma <\kappa $
such that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\gamma $
-cc. By Lemma 3.3, the pair
$\gamma $
-cc. By Lemma 3.3, the pair
![]() $(\operatorname {\mathrm {HOD}},N)$
has the
$(\operatorname {\mathrm {HOD}},N)$
has the
![]() $\gamma $
-uniform cover property, so there is
$\gamma $
-uniform cover property, so there is
![]() $\mathbb {Q}\in \operatorname {\mathrm {HOD}}$
with
$\mathbb {Q}\in \operatorname {\mathrm {HOD}}$
with
![]() $N\models "|\mathbb {Q}|=2^\gamma "$
and
$N\models "|\mathbb {Q}|=2^\gamma "$
and
![]() $N = \operatorname {\mathrm {HOD}}[F]$
where F is a
$N = \operatorname {\mathrm {HOD}}[F]$
where F is a
![]() $\operatorname {\mathrm {HOD}}$
-generic filter for
$\operatorname {\mathrm {HOD}}$
-generic filter for
![]() $\mathbb {Q}$
. Note that
$\mathbb {Q}$
. Note that
because
![]() $\kappa $
remains a strong limit cardinal in
$\kappa $
remains a strong limit cardinal in
![]() $V[G]$
.
$V[G]$
.
Let
![]() $\langle \dot {g}_\alpha \mathrel {|} \alpha < (\kappa ^+)^{\text {HOD}}\rangle \in \text {HOD}$
be a sequence of
$\langle \dot {g}_\alpha \mathrel {|} \alpha < (\kappa ^+)^{\text {HOD}}\rangle \in \text {HOD}$
be a sequence of
![]() $\mathbb Q$
-names for functions in
$\mathbb Q$
-names for functions in
![]() $\text {HOD}$
such that
$\text {HOD}$
such that
![]() $(\dot {g}_\alpha )_F = g_\alpha $
. Since
$(\dot {g}_\alpha )_F = g_\alpha $
. Since
![]() $|\mathbb Q| < \kappa $
, there is a condition
$|\mathbb Q| < \kappa $
, there is a condition
![]() $p\in F$
deciding the value of
$p\in F$
deciding the value of
![]() $\dot {g}_\alpha $
for unboundedly many
$\dot {g}_\alpha $
for unboundedly many
![]() $\alpha < \kappa ^{+\text {HOD}}$
; that is, for an unbounded set
$\alpha < \kappa ^{+\text {HOD}}$
; that is, for an unbounded set
![]() $S\subseteq (\kappa ^+)^{\text {HOD}}$
in
$S\subseteq (\kappa ^+)^{\text {HOD}}$
in
![]() $\operatorname {\mathrm {HOD}}$
, for each
$\operatorname {\mathrm {HOD}}$
, for each
![]() $\alpha \in S$
,
$\alpha \in S$
,
![]() $p\Vdash _{\mathbb P}\dot {g}_\alpha = \check {g}_\alpha $
. Now
$p\Vdash _{\mathbb P}\dot {g}_\alpha = \check {g}_\alpha $
. Now
![]() $\langle g_\alpha \mathrel {|} \alpha \in S\rangle \in \operatorname {\mathrm {HOD}}$
is as desired.Footnote
5
$\langle g_\alpha \mathrel {|} \alpha \in S\rangle \in \operatorname {\mathrm {HOD}}$
is as desired.Footnote
5
Assume towards a contradiction that
![]() $(\kappa ^+)^{\text {HOD}} < \kappa ^+$
. We would like to derive a uniform
$(\kappa ^+)^{\text {HOD}} < \kappa ^+$
. We would like to derive a uniform
![]() $H_0$
-ultrafilter
$H_0$
-ultrafilter
![]() $\mathcal D$
on
$\mathcal D$
on
![]() $\kappa _0^{+H_0}$
from the factor embedding
$\kappa _0^{+H_0}$
from the factor embedding
![]() $k : H_0\to H$
. The next claim allows us to ensure that
$k : H_0\to H$
. The next claim allows us to ensure that
![]() $\mathcal D$
will be ordinal definable in the structure
$\mathcal D$
will be ordinal definable in the structure
![]() $\langle V[G],V,G,{\in }\rangle $
:
$\langle V[G],V,G,{\in }\rangle $
:
Claim 3.4.4.
![]() $k[\kappa _0^{+H_0}]$
has a least upper bound
$k[\kappa _0^{+H_0}]$
has a least upper bound
![]() $\nu <(\kappa _*^+)^{H}$
in H.
$\nu <(\kappa _*^+)^{H}$
in H.
Proof of claim.
By Theorem 3.1,
![]() $\operatorname {\mathrm {cf}}(\kappa ^{+\text {HOD}}) \leq \iota $
. Let
$\operatorname {\mathrm {cf}}(\kappa ^{+\text {HOD}}) \leq \iota $
. Let ![]() and
and
![]() $A\subseteq \kappa ^{+\text {HOD}}$
be a cofinal set of ordertype
$A\subseteq \kappa ^{+\text {HOD}}$
be a cofinal set of ordertype
![]() $\rho $
. Then
$\rho $
. Then
![]() $\langle \gamma _\alpha \rangle _{\alpha \in A}$
is cofinal in
$\langle \gamma _\alpha \rangle _{\alpha \in A}$
is cofinal in
![]() $(\kappa _0^+)^{H_0}$
, and hence,
$(\kappa _0^+)^{H_0}$
, and hence,
![]() $\langle k(\gamma _\alpha )\rangle _{\alpha \in A}$
is cofinal in
$\langle k(\gamma _\alpha )\rangle _{\alpha \in A}$
is cofinal in
![]() $k[\kappa _0^{+H_0}]$
. But
$k[\kappa _0^{+H_0}]$
. But
![]() $\langle k(\gamma _\alpha )\rangle _{\alpha \in A}\in M_G$
: Letting
$\langle k(\gamma _\alpha )\rangle _{\alpha \in A}\in M_G$
: Letting
![]() $\langle g^*_\alpha \rangle _{\alpha < j_G(\kappa ^{+\text {HOD}})} = j_G(\langle g_\alpha \rangle _{\alpha < \kappa ^{+\text {HOD}}})$
,
$\langle g^*_\alpha \rangle _{\alpha < j_G(\kappa ^{+\text {HOD}})} = j_G(\langle g_\alpha \rangle _{\alpha < \kappa ^{+\text {HOD}}})$
,
with
![]() $j_G[A]\in M_G$
. (As
$j_G[A]\in M_G$
. (As
![]() $\operatorname {\mathrm {crit}}(j_G)=\iota $
,
$\operatorname {\mathrm {crit}}(j_G)=\iota $
,
![]() $A\in V$
, and
$A\in V$
, and
![]() $|A| \leq \iota $
.) Since
$|A| \leq \iota $
.) Since
![]() $\langle k(\gamma _\alpha )\rangle _{\alpha \in A}$
is a set of ordinals in
$\langle k(\gamma _\alpha )\rangle _{\alpha \in A}$
is a set of ordinals in
![]() $M_G$
, it has a least upper bound
$M_G$
, it has a least upper bound
![]() $\nu $
, and since
$\nu $
, and since
![]() $\langle k(\gamma _\alpha )\rangle _{\alpha \in A}$
is cofinal in
$\langle k(\gamma _\alpha )\rangle _{\alpha \in A}$
is cofinal in
![]() $k[\kappa _0^{+H_0}]$
,
$k[\kappa _0^{+H_0}]$
,
![]() $\nu $
is the least upper bound of
$\nu $
is the least upper bound of
![]() $k[\kappa _0^{+H_0}]$
.
$k[\kappa _0^{+H_0}]$
.
Note that
![]() $\nu <(\kappa _*^+)^{H}$
: First, by our comments after Claim 3.4.1,
$\nu <(\kappa _*^+)^{H}$
: First, by our comments after Claim 3.4.1,
![]() $(\kappa _*^+)^{H}=(\kappa ^+_*)^{M_G}$
, so
$(\kappa _*^+)^{H}=(\kappa ^+_*)^{M_G}$
, so
![]() $(\kappa _*^+)^H$
is regular in
$(\kappa _*^+)^H$
is regular in
![]() $M_G$
. Second, the previous argument shows that
$M_G$
. Second, the previous argument shows that
![]() $\operatorname {\mathrm {cf}}^{M_G}(\nu )\leq \iota $
, which is less than
$\operatorname {\mathrm {cf}}^{M_G}(\nu )\leq \iota $
, which is less than
![]() $\kappa $
. Therefore,
$\kappa $
. Therefore,
![]() $\nu <(\kappa _*^+)^{H}$
.
$\nu <(\kappa _*^+)^{H}$
.
Let
![]() $\mathcal {D}$
be the
$\mathcal {D}$
be the
![]() $H_0$
-ultrafilter on
$H_0$
-ultrafilter on
![]() $(\kappa _0^+)^{H_0}$
derived from k using
$(\kappa _0^+)^{H_0}$
derived from k using
![]() $\nu $
; namely,
$\nu $
; namely,
Let ![]() , again using only functions in
, again using only functions in
![]() $H_0$
. Let
$H_0$
. Let
![]() $i : H_0\to H_1$
be the ultrapower embedding, and let
$i : H_0\to H_1$
be the ultrapower embedding, and let ![]() . Then,
. Then,
Note that
![]() $\mathcal {D}$
is ordinal definable in the structure
$\mathcal {D}$
is ordinal definable in the structure
![]() $\langle V[G],V,G,{\in }\rangle $
, and hence,
$\langle V[G],V,G,{\in }\rangle $
, and hence,
![]() $H_1\subseteq N$
, by the same argument as for
$H_1\subseteq N$
, by the same argument as for
![]() $H_0$
. Since the ultrapower embedding
$H_0$
. Since the ultrapower embedding
![]() $i : H_0\to H_1$
is definable over
$i : H_0\to H_1$
is definable over
![]() $\langle V[G],V,G,{\in }\rangle $
from ordinal parameters,
$\langle V[G],V,G,{\in }\rangle $
from ordinal parameters,
The next claim yields the desired contradiction with Claim 3.4.2:
Claim 3.4.5.
![]() $N\models |(\kappa _0^+)^{H_0}|\leq \kappa .$
$N\models |(\kappa _0^+)^{H_0}|\leq \kappa .$
Proof of claim.
Since
![]() $i[\kappa _0^{+H_0}]\subseteq \bar \nu $
, it follows that
$i[\kappa _0^{+H_0}]\subseteq \bar \nu $
, it follows that
![]() $|\kappa _0^{+H_0}|^N \leq |\bar \nu |^N$
. Also,
$|\kappa _0^{+H_0}|^N \leq |\bar \nu |^N$
. Also,
![]() $\bar \nu < i(\kappa _0^{+H_0}) = i(\kappa _0)^{+H_1}$
. Since
$\bar \nu < i(\kappa _0^{+H_0}) = i(\kappa _0)^{+H_1}$
. Since
![]() $H_1\subseteq N$
, we have the following inequalities:
$H_1\subseteq N$
, we have the following inequalities:
The latter equality being true in that
![]() $i(\kappa _0)$
is
$i(\kappa _0)$
is
![]() $\kappa $
-like, as it embeds into
$\kappa $
-like, as it embeds into
![]() $\kappa _*$
.
$\kappa _*$
.
Since we get a contradiction, our initial assumption that
![]() $"(\kappa ^+)^{\text {HOD}} < \kappa ^+$
” was false, and this proves the theorem.
$"(\kappa ^+)^{\text {HOD}} < \kappa ^+$
” was false, and this proves the theorem.
Let us now prove our second compactness theorem. This uses a slightly different technique (due to Casey–Goldberg) to prove the theorem for an arbitrary singular cardinal of uncountable cofinality; a direct adaptation of the argument from Theorem 3.4 would only prove the result for strong limit cardinals.
Theorem 3.5. If
![]() $\kappa $
is a singular cardinal of uncountable cofinality and
$\kappa $
is a singular cardinal of uncountable cofinality and
![]() $\{\delta < \kappa \mathrel {|} \operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\delta ) < \delta \}$
is stationary in
$\{\delta < \kappa \mathrel {|} \operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\delta ) < \delta \}$
is stationary in
![]() $\kappa $
, then
$\kappa $
, then
![]() $\operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\kappa ) < \kappa $
.
$\operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\kappa ) < \kappa $
.
Proof. Assume towards a contradiction that
![]() $\kappa $
is a regular cardinal in
$\kappa $
is a regular cardinal in
![]() $\operatorname {\mathrm {HOD}}$
. For the rest of the proof,
$\operatorname {\mathrm {HOD}}$
. For the rest of the proof,
![]() $\mathcal {F}$
denotes the closed unbounded filter on
$\mathcal {F}$
denotes the closed unbounded filter on
![]() $\kappa $
.
$\kappa $
.
We claim that in
![]() $\operatorname {\mathrm {HOD}}$
, the filter
$\operatorname {\mathrm {HOD}}$
, the filter
![]() $\bar {\mathcal {F}} = \mathcal {F}\cap \operatorname {\mathrm {HOD}}$
is weakly normal in the sense that every regressive function
$\bar {\mathcal {F}} = \mathcal {F}\cap \operatorname {\mathrm {HOD}}$
is weakly normal in the sense that every regressive function
![]() $f : A\to \kappa $
in
$f : A\to \kappa $
in
![]() $\operatorname {\mathrm {HOD}}$
defined on a set
$\operatorname {\mathrm {HOD}}$
defined on a set
![]() $A\in \bar {\mathcal {F}}$
admits some
$A\in \bar {\mathcal {F}}$
admits some
![]() $\gamma < \kappa $
such that
$\gamma < \kappa $
such that
![]() $\{\alpha \in A \mathrel {|} f(\alpha ) < \gamma \}\in \bar {\mathcal {F}}$
.Footnote
6
Fix
$\{\alpha \in A \mathrel {|} f(\alpha ) < \gamma \}\in \bar {\mathcal {F}}$
.Footnote
6
Fix
![]() $f\in \operatorname {\mathrm {HOD}}$
, and assume towards a contradiction that no such
$f\in \operatorname {\mathrm {HOD}}$
, and assume towards a contradiction that no such
![]() $\gamma $
exists.
$\gamma $
exists.
By Fodor’s Lemma, it is not hard to see that any regressive function defined on a stationary subset of
![]() $\kappa $
is bounded on a stationary set. (This is the argument used in Claim 3.1.1.) Therefore, let
$\kappa $
is bounded on a stationary set. (This is the argument used in Claim 3.1.1.) Therefore, let
![]() $\gamma _0$
be least such that the function
$\gamma _0$
be least such that the function
![]() $f : A\to \kappa $
is bounded by
$f : A\to \kappa $
is bounded by
![]() $\gamma _0$
on a stationary subset of A. By our assumption, the set
$\gamma _0$
on a stationary subset of A. By our assumption, the set
![]() $A_1$
of ordinals
$A_1$
of ordinals
![]() $\alpha \in A$
such that
$\alpha \in A$
such that
![]() $f(\alpha ) \geq \gamma _0$
is stationary as well. Let
$f(\alpha ) \geq \gamma _0$
is stationary as well. Let
![]() $\gamma _1$
be least such that
$\gamma _1$
be least such that
![]() $f\mathbin \upharpoonright A_1$
is bounded below
$f\mathbin \upharpoonright A_1$
is bounded below
![]() $\gamma _1$
on a stationary set. Continuing this way, we can produce a continuous sequence
$\gamma _1$
on a stationary set. Continuing this way, we can produce a continuous sequence
![]() $\langle \gamma _i\mathrel {|} {i < \kappa }\rangle $
such that for all
$\langle \gamma _i\mathrel {|} {i < \kappa }\rangle $
such that for all
![]() $i < \delta $
,
$i < \delta $
,
is stationary. We use our assumption that
![]() $\kappa $
is regular in
$\kappa $
is regular in
![]() $\operatorname {\mathrm {HOD}}$
to ensure that the process can be continued at limit ordinals
$\operatorname {\mathrm {HOD}}$
to ensure that the process can be continued at limit ordinals
![]() $i < \kappa $
. (Note that the entire construction is internal to
$i < \kappa $
. (Note that the entire construction is internal to
![]() $\operatorname {\mathrm {HOD}}$
.) But since
$\operatorname {\mathrm {HOD}}$
.) But since
![]() $\operatorname {\mathrm {cf}}(\kappa ) < \kappa $
, there cannot be
$\operatorname {\mathrm {cf}}(\kappa ) < \kappa $
, there cannot be
![]() $\kappa $
-many disjoint stationary subsets of
$\kappa $
-many disjoint stationary subsets of
![]() $\kappa $
.
$\kappa $
.
A similar argument shows that if
![]() $\gamma < \kappa $
is regular in
$\gamma < \kappa $
is regular in
![]() $\operatorname {\mathrm {HOD}}$
, greater than
$\operatorname {\mathrm {HOD}}$
, greater than
![]() $\operatorname {\mathrm {cf}}(\kappa )$
, and of a different V-cofinality from
$\operatorname {\mathrm {cf}}(\kappa )$
, and of a different V-cofinality from
![]() $\kappa $
, then
$\kappa $
, then
![]() $\bar {\mathcal {F}}$
is
$\bar {\mathcal {F}}$
is
![]() $\gamma $
-indecomposable in
$\gamma $
-indecomposable in
![]() $\operatorname {\mathrm {HOD}}$
in the following sense: Working in
$\operatorname {\mathrm {HOD}}$
in the following sense: Working in
![]() $\operatorname {\mathrm {HOD}}$
, any function
$\operatorname {\mathrm {HOD}}$
, any function
![]() $f\colon B\rightarrow \gamma $
with
$f\colon B\rightarrow \gamma $
with
![]() $B\in \bar {\mathcal {F}}$
is bounded below
$B\in \bar {\mathcal {F}}$
is bounded below
![]() $\gamma $
on a set in
$\gamma $
on a set in
![]() $\bar {\mathcal {F}}$
.
$\bar {\mathcal {F}}$
.
Until further notice, let us work in
![]() $\operatorname {\mathrm {HOD}}$
and denote
$\operatorname {\mathrm {HOD}}$
and denote
Since
![]() $S\in \bar {\mathcal {F}}^+$
, there is an ultrafilter U extending
$S\in \bar {\mathcal {F}}^+$
, there is an ultrafilter U extending
Since
![]() $\bar {\mathcal {F}}$
is weakly normal, U is weakly normal, and since
$\bar {\mathcal {F}}$
is weakly normal, U is weakly normal, and since
![]() $S\in U$
, U concentrates on singular cardinals. Therefore, by [Reference KetonenKet72, Theorem 1.3], U is
$S\in U$
, U concentrates on singular cardinals. Therefore, by [Reference KetonenKet72, Theorem 1.3], U is
![]() $(\nu ,\kappa )$
-regular for some
$(\nu ,\kappa )$
-regular for some
![]() $\nu < \kappa $
.Footnote
7
$\nu < \kappa $
.Footnote
7
Claim 3.5.1.
U is
![]() $\gamma $
-decomposable for every regular cardinal in
$\gamma $
-decomposable for every regular cardinal in
![]() $(\nu ,\kappa )$
.
$(\nu ,\kappa )$
.
Proof of claim.
Let
![]() $\langle A_\alpha \rangle _{\alpha <\kappa }$
be a witness for
$\langle A_\alpha \rangle _{\alpha <\kappa }$
be a witness for
![]() $"U$
is
$"U$
is
![]() $(\nu ,\kappa )$
-regular”. Namely, this is a collection of U-measure one sets such that
$(\nu ,\kappa )$
-regular”. Namely, this is a collection of U-measure one sets such that
![]() $\bigcap _{\alpha \in I} A_\alpha =\emptyset $
for all
$\bigcap _{\alpha \in I} A_\alpha =\emptyset $
for all
![]() $I\subseteq \kappa $
with
$I\subseteq \kappa $
with
![]() $|I|=\nu $
. Let
$|I|=\nu $
. Let
![]() $\gamma \in (\nu ,\kappa )$
be regular, and define a function
$\gamma \in (\nu ,\kappa )$
be regular, and define a function
![]() $f\colon \kappa \rightarrow \gamma $
as
$f\colon \kappa \rightarrow \gamma $
as
![]() $f(\alpha ):=\sup \{\beta <\gamma \mathrel {|} \alpha \in A_\beta \}.$
The fact that
$f(\alpha ):=\sup \{\beta <\gamma \mathrel {|} \alpha \in A_\beta \}.$
The fact that
![]() $\langle A_\alpha \rangle _{\alpha <\kappa }$
witnesses
$\langle A_\alpha \rangle _{\alpha <\kappa }$
witnesses
![]() $(\nu ,\kappa )$
-regularity ensures that f is well-defined. Note that f cannot be bounded below
$(\nu ,\kappa )$
-regularity ensures that f is well-defined. Note that f cannot be bounded below
![]() $\gamma $
on a set in U: Otherwise,
$\gamma $
on a set in U: Otherwise,
![]() $A:=\{\alpha <\kappa \mathrel {|} f(\alpha )<\beta \}\in U$
, for some
$A:=\{\alpha <\kappa \mathrel {|} f(\alpha )<\beta \}\in U$
, for some
![]() $\beta <\gamma $
, but by definition,
$\beta <\gamma $
, but by definition,
![]() $A\cap A_\beta =\emptyset $
. Therefore, U is
$A\cap A_\beta =\emptyset $
. Therefore, U is
![]() $\gamma $
-decomposable.
$\gamma $
-decomposable.
Now we return to V. Since
![]() $\bar {\mathcal {F}}$
is
$\bar {\mathcal {F}}$
is
![]() $\gamma $
-indecomposable in
$\gamma $
-indecomposable in
![]() $\operatorname {\mathrm {HOD}}$
for all ordinals
$\operatorname {\mathrm {HOD}}$
for all ordinals
![]() $\gamma $
that are regular in
$\gamma $
that are regular in
![]() $\operatorname {\mathrm {HOD}}$
, greater than
$\operatorname {\mathrm {HOD}}$
, greater than
![]() $\operatorname {\mathrm {cf}}(\kappa )$
, and of different V-cofinality from
$\operatorname {\mathrm {cf}}(\kappa )$
, and of different V-cofinality from
![]() $\kappa $
, U is
$\kappa $
, U is
![]() $\gamma $
-indecomposable for such ordinals.
$\gamma $
-indecomposable for such ordinals.
It follows that for all ordinals
![]() $\gamma \in (\max \{\nu ,\operatorname {\mathrm {cf}}(\kappa )\},\kappa )$
, if
$\gamma \in (\max \{\nu ,\operatorname {\mathrm {cf}}(\kappa )\},\kappa )$
, if
![]() $\gamma $
is regular in
$\gamma $
is regular in
![]() $\operatorname {\mathrm {HOD}}$
, then
$\operatorname {\mathrm {HOD}}$
, then
![]() $\operatorname {\mathrm {cf}}(\gamma ) = \operatorname {\mathrm {cf}}(\kappa )$
; otherwise, the previous paragraph implies U is
$\operatorname {\mathrm {cf}}(\gamma ) = \operatorname {\mathrm {cf}}(\kappa )$
; otherwise, the previous paragraph implies U is
![]() $\gamma $
-indecomposable while the paragraph preceding it implies U is
$\gamma $
-indecomposable while the paragraph preceding it implies U is
![]() $\gamma $
-decomposable. But
$\gamma $
-decomposable. But
![]() $\kappa $
is a limit of V-regular cardinals, and these are certainly regular in
$\kappa $
is a limit of V-regular cardinals, and these are certainly regular in
![]() $\operatorname {\mathrm {HOD}}$
and do not have the same cofinality as
$\operatorname {\mathrm {HOD}}$
and do not have the same cofinality as
![]() $\kappa $
. This is a contradiction.
$\kappa $
. This is a contradiction.
3.1 Optimality
In this section, we discuss the optimality of Theorems 3.4 and 3.5. Some of our arguments require rather technical Prikry-type forcings. Instead of elaborating on their precise definitions (which are fairly long), we give appropriate references. Let us begin with Theorem 3.4. The next shows that the cofinality assumption is necessary in Theorem 3.4:
Proposition 3.6. Assume that
![]() $\kappa $
is a
$\kappa $
is a
![]() $\kappa ^+$
-supercompact cardinal. Then, there is a generic extension where
$\kappa ^+$
-supercompact cardinal. Then, there is a generic extension where
-
1.
 $\kappa $
is a strong limit cardinal with
$\kappa $
is a strong limit cardinal with
 $\operatorname {\mathrm {cf}}(\kappa )=\omega $
,
$\operatorname {\mathrm {cf}}(\kappa )=\omega $
, -
2.
 $\delta ^{+\operatorname {\mathrm {HOD}}}=\delta ^+$
for all
$\delta ^{+\operatorname {\mathrm {HOD}}}=\delta ^+$
for all
 $\delta <\kappa $
,
$\delta <\kappa $
, -
3. and
 $(\kappa ^{+\mathrm {HOD}})<\kappa ^+.$
$(\kappa ^{+\mathrm {HOD}})<\kappa ^+.$
Proof. By forcing with McAloon iteration, we may assume that
![]() $"V=\operatorname {\mathrm {HOD}}$
” holds (see p.5). Let
$"V=\operatorname {\mathrm {HOD}}$
” holds (see p.5). Let
![]() $\mathcal {U}$
be a
$\mathcal {U}$
be a
![]() $\kappa $
-complete, normal and fine ultrafilter over
$\kappa $
-complete, normal and fine ultrafilter over
![]() $\mathcal {P}_\kappa (\kappa ^+)$
. Let us force with the Supercompact Prikry forcing with respect to
$\mathcal {P}_\kappa (\kappa ^+)$
. Let us force with the Supercompact Prikry forcing with respect to
![]() $\mathcal {U}$
([Reference GitikGit10, §1]). This forcing is easily shown to be cone-homogeneous so that
$\mathcal {U}$
([Reference GitikGit10, §1]). This forcing is easily shown to be cone-homogeneous so that
![]() $\operatorname {\mathrm {HOD}}^{V[G]}= V$
holds for all V-generic
$\operatorname {\mathrm {HOD}}^{V[G]}= V$
holds for all V-generic
![]() $G\subseteq \mathbb {P}$
. This forcing does not introduce bounded subsets of
$G\subseteq \mathbb {P}$
. This forcing does not introduce bounded subsets of
![]() $\kappa $
so, in
$\kappa $
so, in
![]() $V[G]$
,
$V[G]$
,
![]() $V[G]_\kappa =V_\kappa $
. Also,
$V[G]_\kappa =V_\kappa $
. Also,
![]() $\kappa $
becomes a strong limit cardinal with
$\kappa $
becomes a strong limit cardinal with
![]() $\operatorname {\mathrm {cf}}(\kappa )=\omega $
. This gives (1) and (2) above. Finally, in
$\operatorname {\mathrm {cf}}(\kappa )=\omega $
. This gives (1) and (2) above. Finally, in
![]() $V[G]$
,
$V[G]$
,
![]() $(\kappa ^+)^V$
is collapsed to
$(\kappa ^+)^V$
is collapsed to
![]() $\kappa $
, and hence,
$\kappa $
, and hence,
![]() $(\kappa ^+)^{\operatorname {\mathrm {HOD}}^{V[G]}}=(\kappa ^+)^{V}<\kappa ^{+}.$
$(\kappa ^+)^{\operatorname {\mathrm {HOD}}^{V[G]}}=(\kappa ^+)^{V}<\kappa ^{+}.$
The hypothesis
![]() $`\{\delta <\kappa \mathrel {|} \delta ^{+\operatorname {\mathrm {HOD}}}=\delta ^+\}$
is stationary’ is also necessary:
$`\{\delta <\kappa \mathrel {|} \delta ^{+\operatorname {\mathrm {HOD}}}=\delta ^+\}$
is stationary’ is also necessary:
Theorem 3.7. Suppose that
![]() $\kappa $
is a
$\kappa $
is a
![]() $\kappa ^{+2}$
-supercompact cardinal such that
$\kappa ^{+2}$
-supercompact cardinal such that
![]() $2^{\kappa ^{+n}}=\kappa ^{n+1}$
for
$2^{\kappa ^{+n}}=\kappa ^{n+1}$
for
![]() $n<\omega $
. Then, for each regular uncountable cardinal
$n<\omega $
. Then, for each regular uncountable cardinal
![]() $\mu <\kappa $
, there is a generic extension where
$\mu <\kappa $
, there is a generic extension where
-
1.
 $\kappa $
is a strong limit cardinal with cofinality
$\kappa $
is a strong limit cardinal with cofinality
 $\mu $
.
$\mu $
. -
2.
 $\kappa ^{+\operatorname {\mathrm {HOD}}}<\kappa ^+$
.
$\kappa ^{+\operatorname {\mathrm {HOD}}}<\kappa ^+$
. -
3. There is a club
 $C\subseteq \kappa $
with
$C\subseteq \kappa $
with
 $\operatorname {\mathrm {otp}}(C)=\mu $
such that
$\operatorname {\mathrm {otp}}(C)=\mu $
such that  $$ \begin{align*}\delta^{+\operatorname{\mathrm{HOD}}}=\delta^+\text{ for all cardinals }\delta<\kappa\text{ not in }\operatorname{\mathrm{acc}}(C).\end{align*} $$
$$ \begin{align*}\delta^{+\operatorname{\mathrm{HOD}}}=\delta^+\text{ for all cardinals }\delta<\kappa\text{ not in }\operatorname{\mathrm{acc}}(C).\end{align*} $$
Proof. By preliminarily forcing with McAloon’s iteration, we may assume that
![]() $V\subseteq \operatorname {\mathrm {HOD}}^{V^{\mathbb {Q}}}$
for any set-sized forcing
$V\subseteq \operatorname {\mathrm {HOD}}^{V^{\mathbb {Q}}}$
for any set-sized forcing
![]() $\mathbb {Q}$
. If this iteration is started at a sufficiently large regular cardinal, our hypothesis on
$\mathbb {Q}$
. If this iteration is started at a sufficiently large regular cardinal, our hypothesis on
![]() $\kappa $
are maintained.
$\kappa $
are maintained.
Suppose that
![]() $j\colon V\rightarrow M$
is a
$j\colon V\rightarrow M$
is a
![]() $\kappa ^{+2}$
-supercompact embedding. Let
$\kappa ^{+2}$
-supercompact embedding. Let
![]() $\mu <\kappa $
be a regular cardinal and let u be the
$\mu <\kappa $
be a regular cardinal and let u be the
![]() $(\kappa ,\kappa ^+)$
-measure sequence of length
$(\kappa ,\kappa ^+)$
-measure sequence of length
![]() $\mu $
derived from j. Namely,
$\mu $
derived from j. Namely,
![]() $u=\langle u_\alpha \mathrel {|} \alpha <\mu \rangle $
, where
$u=\langle u_\alpha \mathrel {|} \alpha <\mu \rangle $
, where ![]() and
and ![]() for
for
![]() $\alpha>0$
. Notice that M contains every
$\alpha>0$
. Notice that M contains every
![]() $(\kappa ,\kappa ^+)$
-measure sequence of length less than
$(\kappa ,\kappa ^+)$
-measure sequence of length less than
![]() $\mu $
so u above indeed exists. In addition, by the argument in [Reference Cummings, Friedman and GolshaniCFG15, Lemma 3.2], u belongs to
$\mu $
so u above indeed exists. In addition, by the argument in [Reference Cummings, Friedman and GolshaniCFG15, Lemma 3.2], u belongs to
![]() $\mathcal {U}^{\sup }_\infty $
.Footnote
8
$\mathcal {U}^{\sup }_\infty $
.Footnote
8
Let
![]() $\mathbb {R}^{\sup }_u$
be the supercompact Radin forcing defined from u [Reference Cummings, Friedman and GolshaniCFG15]. Let
$\mathbb {R}^{\sup }_u$
be the supercompact Radin forcing defined from u [Reference Cummings, Friedman and GolshaniCFG15]. Let
![]() $G\subseteq \mathbb {R}^{\sup }_u$
a V-generic filter. Combining [Reference Cummings, Friedman and GolshaniCFG15, Corollary 4.2] with our forcing preparation,
$G\subseteq \mathbb {R}^{\sup }_u$
a V-generic filter. Combining [Reference Cummings, Friedman and GolshaniCFG15, Corollary 4.2] with our forcing preparation,
where
![]() $G^{\phi }$
is a V-generic for a plain Radin forcing
$G^{\phi }$
is a V-generic for a plain Radin forcing
![]() $\mathbb {R}_u$
– hence, for a cardinal-preserving poset. In particular, the following inequalities hold:
$\mathbb {R}_u$
– hence, for a cardinal-preserving poset. In particular, the following inequalities hold:
The above yields item (2) of the theorem.
Let
![]() $\langle w_\alpha \mathrel {|} \alpha <\mu \rangle $
be an injective enumeration of
$\langle w_\alpha \mathrel {|} \alpha <\mu \rangle $
be an injective enumeration of
![]() $\{w\mathrel {|} w \text {appears in} p\in G\}$
. Denote
$\{w\mathrel {|} w \text {appears in} p\in G\}$
. Denote ![]() and
and ![]() . The increasing enumeration of
. The increasing enumeration of
![]() $\{\kappa _{w_\alpha }\mathrel {|} \alpha <\mu \}$
yields a club
$\{\kappa _{w_\alpha }\mathrel {|} \alpha <\mu \}$
yields a club
![]() $C\subseteq \kappa $
of order-type
$C\subseteq \kappa $
of order-type
![]() $\mu $
and by forcing below an appropriate condition
$\mu $
and by forcing below an appropriate condition
![]() $\mu $
remains regular in
$\mu $
remains regular in
![]() $V[G]$
. In addition, standard arguments show that
$V[G]$
. In addition, standard arguments show that
![]() $\kappa $
remains a strong limit in
$\kappa $
remains a strong limit in
![]() $V[G]$
(see [Reference Cummings, Friedman and GolshaniCFG15, Lemma 3.10(6)]). These two observations combined yield item (1) of the theorem. Finally, [Reference Cummings, Friedman and GolshaniCFG15, Lemma 3.10(8)] shows that the only V-cardinals
$V[G]$
(see [Reference Cummings, Friedman and GolshaniCFG15, Lemma 3.10(6)]). These two observations combined yield item (1) of the theorem. Finally, [Reference Cummings, Friedman and GolshaniCFG15, Lemma 3.10(8)] shows that the only V-cardinals
![]() ${\leq }\kappa $
that survive after passing to
${\leq }\kappa $
that survive after passing to
![]() $V[G]$
are those outside
$V[G]$
are those outside
Thus, for every
![]() $V[G]$
-cardinal
$V[G]$
-cardinal
![]() $\delta \notin \operatorname {\mathrm {acc}}(C)$
, we have that
$\delta \notin \operatorname {\mathrm {acc}}(C)$
, we have that
![]() $(\delta ^+)^V$
does not belong to the above union and thus
$(\delta ^+)^V$
does not belong to the above union and thus
![]() $(\delta ^+)^V=(\delta ^+)^{V[G]}$
. By our previous observations, this yields
$(\delta ^+)^V=(\delta ^+)^{V[G]}$
. By our previous observations, this yields
![]() $(\delta ^+)^{\operatorname {\mathrm {HOD}}^{V[G]}}=(\delta ^+)^V=(\delta ^+)^{V[G]},$
as claimed.
$(\delta ^+)^{\operatorname {\mathrm {HOD}}^{V[G]}}=(\delta ^+)^V=(\delta ^+)^{V[G]},$
as claimed.
Remark 3.8. The exact consistency strength of the configuration described above is unclear to us. Since the configuration violates the weak covering theorem for K [Reference Jensen and SteelJS13, Reference Mitchell, Schimmerling and SteelMSS97], one obtains the lower bound of a Woodin cardinal, but presumably one can obtain a stronger lower bound.
The following theorem shows that the assumptions of Theorem 3.5 are provably optimal. Starting with appropriate large cardinal assumptions, it is consistent for
![]() $\{\delta <\kappa \mathrel {|} \operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\delta )<\delta \}$
to be non-stationary and
$\{\delta <\kappa \mathrel {|} \operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\delta )<\delta \}$
to be non-stationary and
![]() $\kappa $
to be inaccessible in
$\kappa $
to be inaccessible in
![]() $\text {HOD}$
. This is a special case of a recent theorem of the authors [Reference Goldberg, Osinski and PovedaGOP24, Theorem 4.6] which utilizes the Supercompact Radin forcing of Theorem 3.7. We state the theorem without proof:
$\text {HOD}$
. This is a special case of a recent theorem of the authors [Reference Goldberg, Osinski and PovedaGOP24, Theorem 4.6] which utilizes the Supercompact Radin forcing of Theorem 3.7. We state the theorem without proof:
Theorem 3.9. Suppose that
![]() $\delta $
is a supercompact cardinal and the
$\delta $
is a supercompact cardinal and the
![]() $\mathrm {GCH}$
holds. Then, there is a generic extension where
$\mathrm {GCH}$
holds. Then, there is a generic extension where
![]() $\delta $
remains supercompact and there is a club
$\delta $
remains supercompact and there is a club
![]() $D\subseteq \delta $
consisting of cardinals
$D\subseteq \delta $
consisting of cardinals
![]() $\kappa $
for which
$\kappa $
for which
In particular, every
![]() $\lambda \in E^\kappa _{\omega _1}\cap \operatorname {\mathrm {acc}}(D)$
is a singular of uncountable cofinality for which
$\lambda \in E^\kappa _{\omega _1}\cap \operatorname {\mathrm {acc}}(D)$
is a singular of uncountable cofinality for which
![]() $\{\theta <\lambda \mathrel {|} \operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\theta )=\theta \}$
contains a club and
$\{\theta <\lambda \mathrel {|} \operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\theta )=\theta \}$
contains a club and
![]() $\operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\lambda )=\lambda $
.
$\operatorname {\mathrm {cf}}^{\operatorname {\mathrm {HOD}}}(\lambda )=\lambda $
.
To obtain the above configuration, it would be natural to utilize Ben-Neria-Unger’s method from [Reference Ben-Neria and UngerBNU17, Theorem 1.3]. However, an apparent drawback of this alternative approach is that it does not seem amenable to preserving large cardinals at the level of strong compactness. This limitation is primarily caused by the club-shooting poset used after the nonstationary support iteration of Prikry-type forcings. It turns out that the preservation of supercompacts becomes interesting in light of the HOD dichotomy theorem proved in [Reference GoldbergGol23].
3.2 On
 $\omega $
-club amenability
$\omega $
-club amenability
The first author showed that many of the known results on HOD – for example, the
![]() $\operatorname {\mathrm {HOD}}$
dichotomy theorem – can actually proved for an arbitrary inner model that is
$\operatorname {\mathrm {HOD}}$
dichotomy theorem – can actually proved for an arbitrary inner model that is
![]() $\omega $
-club amenable [Reference GoldbergGol23].
$\omega $
-club amenable [Reference GoldbergGol23].
A set
![]() $C\subseteq \delta $
is an
$C\subseteq \delta $
is an
![]() $\omega $
-club in
$\omega $
-club in
![]() $\delta $
(for
$\delta $
(for
![]() $\operatorname {\mathrm {cf}}(\delta )\geq \omega _1$
) if it is unbounded (in
$\operatorname {\mathrm {cf}}(\delta )\geq \omega _1$
) if it is unbounded (in
![]() $\delta $
) and whenever S is a countable subset of C,
$\delta $
) and whenever S is a countable subset of C,
![]() $\sup (S)\in C$
. The
$\sup (S)\in C$
. The
![]() $\omega $
-club filter on
$\omega $
-club filter on
![]() $\delta $
, denoted by
$\delta $
, denoted by
![]() $\mathscr {C}_\delta $
, is the collection of all subsets of
$\mathscr {C}_\delta $
, is the collection of all subsets of
![]() $\delta $
that contain an
$\delta $
that contain an
![]() $\omega $
-club.
$\omega $
-club.
Definition 3.10. An inner model M is
![]() $\omega $
-club amenable if
$\omega $
-club amenable if
![]() $\mathscr {C}_\delta \cap M \in M$
for all ordinals
$\mathscr {C}_\delta \cap M \in M$
for all ordinals
![]() $\delta $
with uncountable cofinality.
$\delta $
with uncountable cofinality.
Not much is known about the size of HOD that does not already hold of any
![]() $\omega $
-club amenable model, so it is natural to seek properties that are more specific to
$\omega $
-club amenable model, so it is natural to seek properties that are more specific to
![]() $\operatorname {\mathrm {HOD}}$
. In this section, we show that Theorem 3.4 does not generalize to an arbitrary
$\operatorname {\mathrm {HOD}}$
. In this section, we show that Theorem 3.4 does not generalize to an arbitrary
![]() $\omega $
-club amenable model.
$\omega $
-club amenable model.
Let
![]() $\vec {\mathscr C}$
denote the proper class
$\vec {\mathscr C}$
denote the proper class
![]() $\{(\delta ,S) \mathrel {|} \operatorname {\mathrm {cf}}(\delta ) \geq \omega _1,S\in \mathscr C_\delta \}$
. If one builds the constructible universe relative to the sequence
$\{(\delta ,S) \mathrel {|} \operatorname {\mathrm {cf}}(\delta ) \geq \omega _1,S\in \mathscr C_\delta \}$
. If one builds the constructible universe relative to the sequence
![]() $\vec {\mathscr C}$
, then one obtains an
$\vec {\mathscr C}$
, then one obtains an
![]() $\omega $
-club amenable model. More generally,
$\omega $
-club amenable model. More generally,
Lemma 3.11. For any class A,
![]() $M = L[A,\vec {\mathscr {C}}]$
is
$M = L[A,\vec {\mathscr {C}}]$
is
![]() $\omega $
-club amenable.
$\omega $
-club amenable.
To construct
![]() $\omega $
-club amenable models that do not satisfy the conclusion of Theorem 3.4, we need a mild large cardinal hypothesis. Namely, we will assume that for all sets X, X-sword exists. Let us now define this hypothesis precisely.
$\omega $
-club amenable models that do not satisfy the conclusion of Theorem 3.4, we need a mild large cardinal hypothesis. Namely, we will assume that for all sets X, X-sword exists. Let us now define this hypothesis precisely.
If X is a set of rank
![]() $\lambda $
, we say that X-sword exists if there is a coarse X-sword mouse, which is an iterable transitive structure
$\lambda $
, we say that X-sword exists if there is a coarse X-sword mouse, which is an iterable transitive structure
![]() $(M, \vec {U},U,W)$
with the following properties:
$(M, \vec {U},U,W)$
with the following properties:
-
• M is an transitive model of
 $\mathrm {ZFC}^-$
with largest cardinal
$\mathrm {ZFC}^-$
with largest cardinal
 $\kappa $
.
$\kappa $
. -
•
 $X\cap M\in M$
and
$X\cap M\in M$
and
 $\vec {U}\in M$
.
$\vec {U}\in M$
. -
•
 $M\vDash \vec {U}$
is a coherent sequence of normal ultrafilters of length
$M\vDash \vec {U}$
is a coherent sequence of normal ultrafilters of length
 $\kappa $
.
$\kappa $
. -
•
 $o^{\vec {U}}(\delta ) = 0$
whenever
$o^{\vec {U}}(\delta ) = 0$
whenever
 $\delta \leq \lambda $
$\delta \leq \lambda $
-
•
 $o^{\vec {U}}(\delta )\leq 1$
whenever
$o^{\vec {U}}(\delta )\leq 1$
whenever
 $\lambda < \delta < \kappa $
.
$\lambda < \delta < \kappa $
. -
• W is a weakly amenable M-normal M-ultrafilter on
 $\kappa $
$\kappa $
-
•
 $j_W^M(\vec {U}) \mathbin \upharpoonright \kappa +1 = \vec {U}^{\frown } U$
.
$j_W^M(\vec {U}) \mathbin \upharpoonright \kappa +1 = \vec {U}^{\frown } U$
.
The notation for coherent sequences comes from Mitchell’s handbook article [Reference MitchellMit09]. Things are a bit simpler here since all measures on
![]() $\vec {U}$
have order 0. One may therefore think of
$\vec {U}$
have order 0. One may therefore think of
![]() $\vec {U}$
as a partial function with
$\vec {U}$
as a partial function with
![]() $o^{\vec {U}}(\alpha ) = 0$
if
$o^{\vec {U}}(\alpha ) = 0$
if
![]() $\vec {U}$
is not defined on
$\vec {U}$
is not defined on
![]() $\alpha $
, and
$\alpha $
, and
![]() $o^{\vec {U}}(\alpha ) = 1$
if it is.
$o^{\vec {U}}(\alpha ) = 1$
if it is.
We emphasize that the notion of a coarse X-sword mouse is defined for an arbitrary set X, not necessarily a set of ordinals, and this will be relevant below.
The hypothesis that X-sword exists for every set X follows from the existence of a proper class of measurable cardinals of Mitchell order 2. To see this, assume W is a measure on
![]() $\kappa $
of order
$\kappa $
of order
![]() $1$
and
$1$
and
![]() $\vec {U}$
is a sequence of measures of order 0 defined on all measurable cardinals between
$\vec {U}$
is a sequence of measures of order 0 defined on all measurable cardinals between
![]() $\gamma $
and
$\gamma $
and
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $U = [\alpha \mapsto U_\alpha ]_W$
. Then
$U = [\alpha \mapsto U_\alpha ]_W$
. Then
![]() $(H_{\kappa ^+},\vec {U}, U,W)$
is a coarse X-sword mouse for every
$(H_{\kappa ^+},\vec {U}, U,W)$
is a coarse X-sword mouse for every
![]() $X\in V_\gamma $
.
$X\in V_\gamma $
.
In terms of consistency strength, the hypothesis that X-sword exists for every set X is a bit weaker than the existence of a single measurable cardinal of Mitchell order 2: it is not hard to show that it holds in
![]() $V_\kappa $
if
$V_\kappa $
if
![]() $\kappa $
is a measurable cardinal of Mitchell order 2.
$\kappa $
is a measurable cardinal of Mitchell order 2.
Suppose
![]() $\mathcal M = (M,\vec {U},U,W)$
is a coarse X-sword mouse and
$\mathcal M = (M,\vec {U},U,W)$
is a coarse X-sword mouse and
![]() $\mathcal H$
is transitive with a
$\mathcal H$
is transitive with a
![]() $\Sigma _1$
-elementary
$\Sigma _1$
-elementary
![]() $\pi :\mathcal H\to \mathcal M$
such that
$\pi :\mathcal H\to \mathcal M$
such that
![]() $X\cap M\in \operatorname {\mathrm {ran}}(\pi )$
. Then
$X\cap M\in \operatorname {\mathrm {ran}}(\pi )$
. Then
![]() $\mathcal H$
is a coarse
$\mathcal H$
is a coarse
![]() $\pi ^{-1}(X\cap M)$
-sword mouse. Similarly, if
$\pi ^{-1}(X\cap M)$
-sword mouse. Similarly, if
![]() $\mathcal M$
is a coarse X-sword mouse and there is a cofinal
$\mathcal M$
is a coarse X-sword mouse and there is a cofinal
![]() $\Sigma _0$
-elementary
$\Sigma _0$
-elementary
![]() $\pi : \mathcal M\to \mathcal N$
, then
$\pi : \mathcal M\to \mathcal N$
, then
![]() $\mathcal N$
is a coarse
$\mathcal N$
is a coarse
![]() $\pi (X\cap M)$
-sword mouse if it is iterable. These facts are straightforward, except that the statement that a structure M satisfies
$\pi (X\cap M)$
-sword mouse if it is iterable. These facts are straightforward, except that the statement that a structure M satisfies
![]() $\text {ZFC}^-$
may seem too complicated to be preserved under such weak forms of elementarity. This is not really an issue, however, since the fact that M satisfies
$\text {ZFC}^-$
may seem too complicated to be preserved under such weak forms of elementarity. This is not really an issue, however, since the fact that M satisfies
![]() $\text {ZFC}^-$
follows from the fact that M satisfies
$\text {ZFC}^-$
follows from the fact that M satisfies
![]() $\Sigma _0$
-Separation and the Well-Ordering Theorem combined with the weak amenability of
$\Sigma _0$
-Separation and the Well-Ordering Theorem combined with the weak amenability of
![]() $W,$
which yields that
$W,$
which yields that
![]() $M = H(\kappa ^+)^{\text {Ult}_0(M,W)}$
, which is a model of
$M = H(\kappa ^+)^{\text {Ult}_0(M,W)}$
, which is a model of
![]() $\text {ZFC}^-$
.
$\text {ZFC}^-$
.
The following lemmas, suggested by one of the anonymous referees, vastly simplify the proof of Lemma 3.14 below.
Lemma 3.12. Suppose X is a set and
![]() $\mathcal M = (M,\vec {U},U,W)$
is a coarse X-sword mouse such that
$\mathcal M = (M,\vec {U},U,W)$
is a coarse X-sword mouse such that
![]() $o(M)$
is as small as possible. Then
$o(M)$
is as small as possible. Then
![]() $\operatorname {\mathrm {cf}}(o(M)) = \omega $
.
$\operatorname {\mathrm {cf}}(o(M)) = \omega $
.
Proof. Let
![]() $\theta> \lambda $
be a sufficiently large regular cardinal, and let H be a countable transitive set admitting an elementary embedding
$\theta> \lambda $
be a sufficiently large regular cardinal, and let H be a countable transitive set admitting an elementary embedding
![]() $\pi : H\to H(\theta )$
with
$\pi : H\to H(\theta )$
with
![]() $\{X,\mathcal M\}\subseteq \operatorname {\mathrm {ran}}(\pi )$
. Let
$\{X,\mathcal M\}\subseteq \operatorname {\mathrm {ran}}(\pi )$
. Let
![]() $\bar X = \pi ^{-1}(X)$
and
$\bar X = \pi ^{-1}(X)$
and
![]() $\bar {\mathcal M} = \pi ^{-1}(\mathcal M)$
, and note that
$\bar {\mathcal M} = \pi ^{-1}(\mathcal M)$
, and note that
![]() $\bar {\mathcal M}$
is countable and
$\bar {\mathcal M}$
is countable and
![]() $\pi $
restricts to an elementary embedding
$\pi $
restricts to an elementary embedding
![]() $i : \bar {\mathcal M}\to \mathcal M$
. We claim
$i : \bar {\mathcal M}\to \mathcal M$
. We claim
![]() $i[o(\bar M)]$
is cofinal in
$i[o(\bar M)]$
is cofinal in
![]() $o(M)$
, which will establish the lemma. Suppose not, and let
$o(M)$
, which will establish the lemma. Suppose not, and let
![]() $N\subseteq M$
be the transitive closure of
$N\subseteq M$
be the transitive closure of
![]() $i[\bar M]$
. Then
$i[\bar M]$
. Then
![]() $o(N) < o(M)$
. To get a contradiction, it suffices to show that
$o(N) < o(M)$
. To get a contradiction, it suffices to show that
![]() $\mathcal N = (N,\vec {U},U\cap N,W\cap N)$
is a coarse X-sword mouse. Everything except iterability follows from the fact that
$\mathcal N = (N,\vec {U},U\cap N,W\cap N)$
is a coarse X-sword mouse. Everything except iterability follows from the fact that
![]() $i : \bar {\mathcal M}\to \mathcal N$
is a cofinal
$i : \bar {\mathcal M}\to \mathcal N$
is a cofinal
![]() $\Sigma _0$
-elementary embedding. The iterability of
$\Sigma _0$
-elementary embedding. The iterability of
![]() $\mathcal N$
follows from that of
$\mathcal N$
follows from that of
![]() $\mathcal M$
since any iterate of
$\mathcal M$
since any iterate of
![]() $\mathcal N$
admits a
$\mathcal N$
admits a
![]() $\Sigma _0$
-elementary embedding into an iterate of
$\Sigma _0$
-elementary embedding into an iterate of
![]() $\mathcal M$
.
$\mathcal M$
.
Lemma 3.13. Suppose X is a set and
![]() $\mathcal M = (M,\vec {U},U,W)$
is a coarse X-sword mouse with largest cardinal
$\mathcal M = (M,\vec {U},U,W)$
is a coarse X-sword mouse with largest cardinal
![]() $\kappa $
. Assume the following hold:
$\kappa $
. Assume the following hold:
-
•
 $M = \mathrm {Hull}_{\Sigma _1}^{\mathcal M}(\alpha \cup \{p\})$
for some
$M = \mathrm {Hull}_{\Sigma _1}^{\mathcal M}(\alpha \cup \{p\})$
for some
 $p\in M$
and
$p\in M$
and
 $\alpha \geq \operatorname {\mathrm {rank}}(X)$
.
$\alpha \geq \operatorname {\mathrm {rank}}(X)$
. -
•
 $M = \bigcup _{\xi < o(M)} M_\xi $
, where
$M = \bigcup _{\xi < o(M)} M_\xi $
, where
 $\langle M_\xi \rangle _{\xi < o(M)}$
is an increasing sequence of transitive sets in M that contain
$\langle M_\xi \rangle _{\xi < o(M)}$
is an increasing sequence of transitive sets in M that contain
 $V_\kappa ^M$
.
$V_\kappa ^M$
.
Then every ordinal
![]() $\delta> \alpha $
that is regular in M satisfies
$\delta> \alpha $
that is regular in M satisfies
![]() $\operatorname {\mathrm {cf}}(\delta ) = \operatorname {\mathrm {cf}}(o(M))$
.
$\operatorname {\mathrm {cf}}(\delta ) = \operatorname {\mathrm {cf}}(o(M))$
.
Proof. For
![]() $\xi < o(M)$
, let
$\xi < o(M)$
, let
![]() $\mathcal M_\xi = (M_\xi ,\vec {U},U\cap M_\xi ,W\cap M_\xi )$
and let
$\mathcal M_\xi = (M_\xi ,\vec {U},U\cap M_\xi ,W\cap M_\xi )$
and let
![]() $H_\xi = \text {Hull}^{\mathcal M_\xi }_{\Sigma _1}(\alpha \cup \{p\})$
. Note that for all
$H_\xi = \text {Hull}^{\mathcal M_\xi }_{\Sigma _1}(\alpha \cup \{p\})$
. Note that for all
![]() $\xi < o(M)$
,
$\xi < o(M)$
,
![]() $H_\xi \in M$
and
$H_\xi \in M$
and
![]() $M\vDash |H_\xi | \leq \alpha $
; also for
$M\vDash |H_\xi | \leq \alpha $
; also for
![]() $\xi \leq \xi '< o(M)$
,
$\xi \leq \xi '< o(M)$
,
![]() $H_\xi \subseteq H_{\xi '}$
. Moreover, for any
$H_\xi \subseteq H_{\xi '}$
. Moreover, for any
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (x)$
and any
$\varphi (x)$
and any
![]() $a\in M$
,
$a\in M$
,
![]() $\mathcal M\vDash \varphi (a)$
if and only if
$\mathcal M\vDash \varphi (a)$
if and only if
![]() $\mathcal M_\xi \vDash \varphi (a)$
for all sufficiently large
$\mathcal M_\xi \vDash \varphi (a)$
for all sufficiently large
![]() $\xi $
if and only if
$\xi $
if and only if
![]() $\mathcal M_\xi \vDash \varphi (a)$
for some
$\mathcal M_\xi \vDash \varphi (a)$
for some
![]() $\xi $
. It follows that
$\xi $
. It follows that
 $$\begin{align*}M = \text{Hull}^{\mathcal M}_{\Sigma_1}(\alpha\cup \{p\}) = \bigcup_{\xi < o(M)}H_\xi.\end{align*}$$
$$\begin{align*}M = \text{Hull}^{\mathcal M}_{\Sigma_1}(\alpha\cup \{p\}) = \bigcup_{\xi < o(M)}H_\xi.\end{align*}$$
Now suppose
![]() $\delta> \alpha $
is regular in M. For
$\delta> \alpha $
is regular in M. For
![]() $\xi < o(M)$
, let
$\xi < o(M)$
, let
![]() $\beta _\xi = \sup (\delta \cap H_\xi )$
. Then
$\beta _\xi = \sup (\delta \cap H_\xi )$
. Then
![]() $\beta _\xi < \delta $
since
$\beta _\xi < \delta $
since
![]() $\delta $
is regular in M and
$\delta $
is regular in M and
![]() $M\vDash |H_\xi | \leq \alpha < \delta $
. Since
$M\vDash |H_\xi | \leq \alpha < \delta $
. Since
![]() $\langle \beta _\xi \rangle _{\xi < o(M)}$
is weakly increasing and cofinal in
$\langle \beta _\xi \rangle _{\xi < o(M)}$
is weakly increasing and cofinal in
![]() $\delta $
, it follows that
$\delta $
, it follows that
![]() $\operatorname {\mathrm {cf}}(\delta ) = \operatorname {\mathrm {cf}}(o(M))$
.
$\operatorname {\mathrm {cf}}(\delta ) = \operatorname {\mathrm {cf}}(o(M))$
.
Lemma 3.14. Assume that for all sets X, X-sword exists. Then for any cardinal
![]() $\lambda $
and any set
$\lambda $
and any set
![]() $A\subseteq \lambda $
,
$A\subseteq \lambda $
,
![]() $L[A,\vec {\mathscr {C}}]$
does not correctly compute
$L[A,\vec {\mathscr {C}}]$
does not correctly compute
![]() $\lambda ^+$
.
$\lambda ^+$
.
Proof. Fix a set
![]() $A\subseteq \lambda $
. Using a pairing function on
$A\subseteq \lambda $
. Using a pairing function on
![]() $\lambda $
, it is not hard to construct a family X of subsets of
$\lambda $
, it is not hard to construct a family X of subsets of
![]() $\lambda $
such that for any class E,
$\lambda $
such that for any class E,
![]() $L[X, E] = L[A,\mathscr {C}\mathbin \upharpoonright (\lambda +1),E]$
. In particular,
$L[X, E] = L[A,\mathscr {C}\mathbin \upharpoonright (\lambda +1),E]$
. In particular,
where
![]() $(\lambda ,\infty ) = \{\xi \in \operatorname {\mathrm {Ord}} : \xi> \lambda \}$
.
$(\lambda ,\infty ) = \{\xi \in \operatorname {\mathrm {Ord}} : \xi> \lambda \}$
.
Let
![]() $\mathcal M = (M,\vec {U},U,W)$
be a coarse X-sword mouse such that
$\mathcal M = (M,\vec {U},U,W)$
be a coarse X-sword mouse such that
![]() $o(M)$
is as small as possible. Note that letting
$o(M)$
is as small as possible. Note that letting
![]() $\bar M = L_{o(M)}[X,\vec {U},U, W]$
, the structure
$\bar M = L_{o(M)}[X,\vec {U},U, W]$
, the structure
![]() $\bar {\mathcal M} = (\bar M, \vec {U}\cap \bar M, U\cap \bar M, W\cap \bar M)$
is also a coarse X-sword mouse, and so we may assume
$\bar {\mathcal M} = (\bar M, \vec {U}\cap \bar M, U\cap \bar M, W\cap \bar M)$
is also a coarse X-sword mouse, and so we may assume
![]() $\mathcal M = \bar {\mathcal M}$
. This guarantees that
$\mathcal M = \bar {\mathcal M}$
. This guarantees that
![]() $M = \bigcup _{\xi < o(M)} M_\xi $
, where
$M = \bigcup _{\xi < o(M)} M_\xi $
, where
![]() $\langle M_\xi \rangle _{\xi < o(M)}$
is an increasing sequence of transitive sets in M that contain
$\langle M_\xi \rangle _{\xi < o(M)}$
is an increasing sequence of transitive sets in M that contain
![]() $V_\kappa ^M$
: take
$V_\kappa ^M$
: take
![]() $M_\xi = L_{\gamma +\xi }[X,\vec {U},U,W]$
where
$M_\xi = L_{\gamma +\xi }[X,\vec {U},U,W]$
where
![]() $\gamma < o(M)$
is least such that
$\gamma < o(M)$
is least such that
![]() $V_\kappa ^M \subseteq L_\gamma [X,\vec {U},U,W]$
. Similarly, we may assume that
$V_\kappa ^M \subseteq L_\gamma [X,\vec {U},U,W]$
. Similarly, we may assume that
since the transitive collapse of
![]() $\mathrm {Hull}_{\Sigma _1}^{\mathcal M}(\lambda \cup \{X\cap M\})$
is again a coarse X-sword mouse. Thus, we may ensure that
$\mathrm {Hull}_{\Sigma _1}^{\mathcal M}(\lambda \cup \{X\cap M\})$
is again a coarse X-sword mouse. Thus, we may ensure that
![]() $\mathcal M$
satisfies the hypotheses of Lemmas 3.12 and 3.13. In particular, every M-regular cardinal
$\mathcal M$
satisfies the hypotheses of Lemmas 3.12 and 3.13. In particular, every M-regular cardinal
![]() $\delta> \lambda $
has countable cofinality in
$\delta> \lambda $
has countable cofinality in
![]() $V.$
$V.$
We claim that
![]() $L[A,\vec {\mathscr {C}}]$
is contained in a proper initial segment N of a proper class iterate of
$L[A,\vec {\mathscr {C}}]$
is contained in a proper initial segment N of a proper class iterate of
![]() $\mathcal M$
. Granting this, we have
$\mathcal M$
. Granting this, we have
![]() $\lambda ^{+L[A,\vec {\mathscr {C}}]} \leq \lambda ^{+N} = \lambda ^{+M} < \lambda ^+$
. (The final inequality comes from the fact that
$\lambda ^{+L[A,\vec {\mathscr {C}}]} \leq \lambda ^{+N} = \lambda ^{+M} < \lambda ^+$
. (The final inequality comes from the fact that
![]() $\lambda ^{+M}$
has countable cofinality in V.) Thus, our claim suffices to finish the proof.
$\lambda ^{+M}$
has countable cofinality in V.) Thus, our claim suffices to finish the proof.
The idea is to iterate
![]() $\mathcal M$
to a model
$\mathcal M$
to a model
![]() $\mathcal N$
with the following property. For each ordinal
$\mathcal N$
with the following property. For each ordinal
![]() $\delta> \lambda $
,
$\delta> \lambda $
,
![]() $o^{\mathcal N}(\delta )> 0$
if and only if
$o^{\mathcal N}(\delta )> 0$
if and only if
![]() $\delta $
is regular in
$\delta $
is regular in
![]() $\mathcal N$
and has uncountable cofinality in V; moreover, in this case, the unique measure on
$\mathcal N$
and has uncountable cofinality in V; moreover, in this case, the unique measure on
![]() $\delta $
on the sequence of
$\delta $
on the sequence of
![]() $\mathcal N$
is equal to
$\mathcal N$
is equal to
![]() $\mathscr C_\delta \cap \mathcal N$
.
$\mathscr C_\delta \cap \mathcal N$
.
The iteration is defined by selecting at each stage the first total measure on the sequence of the current iterate that lies on an ordinal of countable cofinality. More formally, we define an iterated ultrapower
of
![]() $\mathcal M$
by setting
$\mathcal M$
by setting
![]() $U_\alpha $
equal to the first measure on the sequence
$U_\alpha $
equal to the first measure on the sequence
![]() $\vec {U}^{\mathcal M_\alpha \frown } U^{\mathcal M_\alpha }$
that lies on an ordinal
$\vec {U}^{\mathcal M_\alpha \frown } U^{\mathcal M_\alpha }$
that lies on an ordinal
![]() $\kappa _\alpha $
of countable cofinality in V; if there is no such measure, set
$\kappa _\alpha $
of countable cofinality in V; if there is no such measure, set
![]() $U_\alpha $
equal to the top measure
$U_\alpha $
equal to the top measure
![]() $W^{\mathcal M_\alpha }$
. For
$W^{\mathcal M_\alpha }$
. For
![]() $\alpha \leq \beta \in \text {Ord}$
, let
$\alpha \leq \beta \in \text {Ord}$
, let
denote the iterated ultrapower embedding.
For any ordinal
![]() $\xi $
, the structure
$\xi $
, the structure
![]() $M_\alpha \cap V_\xi $
is eventually constant, and therefore, we can define an inner model N of ZFC such that for all ordinals
$M_\alpha \cap V_\xi $
is eventually constant, and therefore, we can define an inner model N of ZFC such that for all ordinals
![]() $\xi $
,
$\xi $
,
![]() $N\cap V_\xi $
is equal to the eventual value of
$N\cap V_\xi $
is equal to the eventual value of
![]() $M_\alpha \cap V_\xi $
. Similarly, we can define a sequence of N-ultrafilters
$M_\alpha \cap V_\xi $
. Similarly, we can define a sequence of N-ultrafilters
![]() $\vec {U}^{\mathcal N} : \operatorname {\mathrm {Ord}} \to N$
by setting
$\vec {U}^{\mathcal N} : \operatorname {\mathrm {Ord}} \to N$
by setting
![]() $\vec {U}^{\mathcal N}(\delta )$
equal to the eventual value of
$\vec {U}^{\mathcal N}(\delta )$
equal to the eventual value of
![]() $U^{\mathcal M_\alpha }(\delta )$
. We let
$U^{\mathcal M_\alpha }(\delta )$
. We let
![]() $\mathcal N = (N,\vec {U}^{\mathcal N})$
.
$\mathcal N = (N,\vec {U}^{\mathcal N})$
.
By the definition of the iteration, it is clear that if for some ordinal
![]() $\delta $
,
$\delta $
,
![]() $o^{\mathcal N}(\delta )> 0$
, then
$o^{\mathcal N}(\delta )> 0$
, then
![]() $\delta $
has uncountable cofinality.
$\delta $
has uncountable cofinality.
We claim that conversely, if
![]() $\delta> \lambda $
is a regular cardinal of N that has uncountable cofinality in V, then
$\delta> \lambda $
is a regular cardinal of N that has uncountable cofinality in V, then
![]() $o^{\mathcal N}(\delta ) = 1$
and
$o^{\mathcal N}(\delta ) = 1$
and
![]() $\vec {U}^{\mathcal N}(\delta ) = \mathscr {C}_\delta \cap N$
. Since the models
$\vec {U}^{\mathcal N}(\delta ) = \mathscr {C}_\delta \cap N$
. Since the models
![]() $\mathcal M_\alpha $
converge to
$\mathcal M_\alpha $
converge to
![]() $\mathcal N$
, to prove the claim, it suffices to show, by induction on
$\mathcal N$
, to prove the claim, it suffices to show, by induction on
![]() $\alpha \in \operatorname {\mathrm {Ord}}$
, that if
$\alpha \in \operatorname {\mathrm {Ord}}$
, that if
![]() $\delta> \lambda $
is a regular cardinal of
$\delta> \lambda $
is a regular cardinal of
![]() $M_\alpha $
that has uncountable cofinality in V, then either
$M_\alpha $
that has uncountable cofinality in V, then either
![]() $o^{\vec {U}^{\mathcal M_\alpha }}(\delta ) = 1$
and
$o^{\vec {U}^{\mathcal M_\alpha }}(\delta ) = 1$
and
![]() $\vec {U}^{\mathcal M_\alpha }(\delta ) = \mathscr {C}_\delta \cap M_\alpha $
or
$\vec {U}^{\mathcal M_\alpha }(\delta ) = \mathscr {C}_\delta \cap M_\alpha $
or
![]() $\delta $
is the largest cardinal of
$\delta $
is the largest cardinal of
![]() $\mathcal M_\alpha $
and
$\mathcal M_\alpha $
and
![]() $U^{\mathcal M_\alpha } = \mathscr {C}_\delta \cap M_\alpha $
.
$U^{\mathcal M_\alpha } = \mathscr {C}_\delta \cap M_\alpha $
.
For the case that
![]() $\alpha = 0$
, note that our choice of
$\alpha = 0$
, note that our choice of
![]() $\mathcal M_0 = \mathcal M$
, we have
$\mathcal M_0 = \mathcal M$
, we have
![]() $\mathcal M = \text {Hull}^{\mathcal M}_{\Sigma _1}(\lambda \cup \{X\cap M\})$
, and so by the referee’s Lemmas 3.12 and 3.13, if
$\mathcal M = \text {Hull}^{\mathcal M}_{\Sigma _1}(\lambda \cup \{X\cap M\})$
, and so by the referee’s Lemmas 3.12 and 3.13, if
![]() $\delta> \lambda $
is a regular cardinal of M, then
$\delta> \lambda $
is a regular cardinal of M, then
![]() $\delta $
has countable cofinality in V. Thus, the base case holds vacuously.
$\delta $
has countable cofinality in V. Thus, the base case holds vacuously.
Now assume the induction hypothesis holds for
![]() $\mathcal M_\alpha $
, and we claim it is true for
$\mathcal M_\alpha $
, and we claim it is true for
![]() $\mathcal M_{\alpha +1}$
. Suppose therefore that
$\mathcal M_{\alpha +1}$
. Suppose therefore that
![]() $\delta> \lambda $
is a regular cardinal of
$\delta> \lambda $
is a regular cardinal of
![]() $M_{\alpha +1}$
. Note that
$M_{\alpha +1}$
. Note that
![]() $\mathcal M_\alpha | \kappa _\alpha = \mathcal M_{\alpha +1} |\kappa _\alpha $
, so for ordinals
$\mathcal M_\alpha | \kappa _\alpha = \mathcal M_{\alpha +1} |\kappa _\alpha $
, so for ordinals
![]() $\delta $
in the open interval
$\delta $
in the open interval
![]() $(\lambda ,\kappa _\alpha )$
, the induction hypothesis for
$(\lambda ,\kappa _\alpha )$
, the induction hypothesis for
![]() $\mathcal M_\alpha $
easily implies the induction hypothesis for
$\mathcal M_\alpha $
easily implies the induction hypothesis for
![]() $\mathcal M_{\alpha +1}$
. A slightly more complicated variation of this argument establishes the induction hypothesis for
$\mathcal M_{\alpha +1}$
. A slightly more complicated variation of this argument establishes the induction hypothesis for
![]() $\mathcal M_{\alpha +1}$
in the case that
$\mathcal M_{\alpha +1}$
in the case that
![]() $\delta = \kappa _\alpha $
: by the definition of the iteration, either
$\delta = \kappa _\alpha $
: by the definition of the iteration, either
![]() $\kappa _\alpha $
has countable cofinality, in which case we have nothing to show, or else
$\kappa _\alpha $
has countable cofinality, in which case we have nothing to show, or else
![]() $U_\alpha = W^{\mathcal {M}_\alpha }$
, in which case the fact that
$U_\alpha = W^{\mathcal {M}_\alpha }$
, in which case the fact that
![]() $U^{\mathcal M_\alpha } = \vec {U}^{\mathcal M_{\alpha +1}}(\kappa _\alpha )$
implies the induction hypothesis holds for
$U^{\mathcal M_\alpha } = \vec {U}^{\mathcal M_{\alpha +1}}(\kappa _\alpha )$
implies the induction hypothesis holds for
![]() $\mathcal M_{\alpha +1}$
with respect to
$\mathcal M_{\alpha +1}$
with respect to
![]() $\delta = \kappa _\alpha $
.
$\delta = \kappa _\alpha $
.
To finish the successor case, we show that if
![]() $\delta> \kappa _\alpha $
is regular in
$\delta> \kappa _\alpha $
is regular in
![]() $M_{\alpha +1}$
, then
$M_{\alpha +1}$
, then
![]() $\operatorname {\mathrm {cf}}(\delta ) = \omega $
, so the induction hypothesis holds vacuously in the interval
$\operatorname {\mathrm {cf}}(\delta ) = \omega $
, so the induction hypothesis holds vacuously in the interval
![]() $(\kappa _\alpha ,o(M_{\alpha +1}))$
. Since
$(\kappa _\alpha ,o(M_{\alpha +1}))$
. Since
![]() $M_{\alpha +1}$
is generated by the critical points of the iteration along with the range of
$M_{\alpha +1}$
is generated by the critical points of the iteration along with the range of
![]() $j_{0\alpha +1}$
,
$j_{0\alpha +1}$
,
![]() $\mathcal M_{\alpha +1} = \text {Hull} ^{\mathcal {M}_{\alpha +1}}_{\Sigma _1}((\kappa _{\alpha }+1)\cup \{X\cap M\})$
. Since there is a cofinal embedding from M to
$\mathcal M_{\alpha +1} = \text {Hull} ^{\mathcal {M}_{\alpha +1}}_{\Sigma _1}((\kappa _{\alpha }+1)\cup \{X\cap M\})$
. Since there is a cofinal embedding from M to
![]() $M_{\alpha +1}$
, Lemma 3.12 implies that
$M_{\alpha +1}$
, Lemma 3.12 implies that
![]() $\operatorname {\mathrm {cf}}(o(M_{\alpha +1})) = \omega $
. Therefore, we can apply Lemma 3.13 to obtain that
$\operatorname {\mathrm {cf}}(o(M_{\alpha +1})) = \omega $
. Therefore, we can apply Lemma 3.13 to obtain that
![]() $\operatorname {\mathrm {cf}}(\delta ) = \omega $
, as desired.
$\operatorname {\mathrm {cf}}(\delta ) = \omega $
, as desired.
Finally, we consider the limit case. Suppose
![]() $\alpha $
is a limit ordinal and
$\alpha $
is a limit ordinal and
![]() $\delta> \lambda $
is a regular cardinal of
$\delta> \lambda $
is a regular cardinal of
![]() $M_\alpha $
. Let
$M_\alpha $
. Let
![]() $\gamma = \sup _{\beta < \alpha }\kappa _\beta $
. As in the previous case, if
$\gamma = \sup _{\beta < \alpha }\kappa _\beta $
. As in the previous case, if
![]() $\delta < \gamma $
, the desired conclusion is immediate from the induction hypothesis. Moreover, since
$\delta < \gamma $
, the desired conclusion is immediate from the induction hypothesis. Moreover, since
![]() $\mathcal M_\alpha = \text {Hull}^{\mathcal M_\alpha }_{\Sigma _1}(\gamma \cup \{X\cap M\})$
, if
$\mathcal M_\alpha = \text {Hull}^{\mathcal M_\alpha }_{\Sigma _1}(\gamma \cup \{X\cap M\})$
, if
![]() $\delta> \gamma $
, then by Lemma 3.13,
$\delta> \gamma $
, then by Lemma 3.13,
![]() $\operatorname {\mathrm {cf}}(\delta ) = \omega $
, and there is nothing to prove.
$\operatorname {\mathrm {cf}}(\delta ) = \omega $
, and there is nothing to prove.
It therefore suffices to consider the case that
![]() $\delta = \gamma $
.
$\delta = \gamma $
.
For each
![]() $\beta < \alpha $
, let
$\beta < \alpha $
, let
![]() $\delta _\beta = j_{\beta \alpha }^{-1}[\delta ]$
. Note that
$\delta _\beta = j_{\beta \alpha }^{-1}[\delta ]$
. Note that
![]() $\delta _\beta \geq \kappa _\beta $
for all
$\delta _\beta \geq \kappa _\beta $
for all
![]() $\beta < \alpha $
. Moreover, for sufficiently large
$\beta < \alpha $
. Moreover, for sufficiently large
![]() $\beta < \alpha $
,
$\beta < \alpha $
,
![]() $j_{\beta \alpha }(\delta _\beta ) = \delta $
, and therefore for any
$j_{\beta \alpha }(\delta _\beta ) = \delta $
, and therefore for any
![]() $\beta ' \geq \beta $
with
$\beta ' \geq \beta $
with
![]() $\beta ' < \alpha $
,
$\beta ' < \alpha $
,
![]() $j_{\beta \beta '}(\delta _\beta ) = \delta _{\beta '}$
.
$j_{\beta \beta '}(\delta _\beta ) = \delta _{\beta '}$
.
Assume first that for sufficiently large
![]() $\beta < \alpha $
,
$\beta < \alpha $
,
![]() $\delta _\beta \neq \kappa _\beta $
. Then in fact
$\delta _\beta \neq \kappa _\beta $
. Then in fact
![]() $\delta _\beta> \kappa _\beta $
, and so by Lemma 3.13,
$\delta _\beta> \kappa _\beta $
, and so by Lemma 3.13,
![]() $\operatorname {\mathrm {cf}}(\delta _\beta ) = \omega $
. Moreover, it follows that for sufficiently large
$\operatorname {\mathrm {cf}}(\delta _\beta ) = \omega $
. Moreover, it follows that for sufficiently large
![]() $\beta < \alpha $
,
$\beta < \alpha $
,
![]() $j_{\beta \alpha }$
is continuous at
$j_{\beta \alpha }$
is continuous at
![]() $\delta _\beta $
and
$\delta _\beta $
and
![]() $j_{\beta \alpha }(\delta _\beta ) = \delta $
, so
$j_{\beta \alpha }(\delta _\beta ) = \delta $
, so
![]() $\delta $
has countable cofinality as well, and we are done.
$\delta $
has countable cofinality as well, and we are done.
To finish the induction, assume instead that
![]() $\kappa _\beta = \delta _\beta $
for cofinally many
$\kappa _\beta = \delta _\beta $
for cofinally many
![]() $\beta < \alpha $
. In this case, the set
$\beta < \alpha $
. In this case, the set
![]() $C = \{\kappa _\beta : \beta < \alpha \text { and }j_{\beta \alpha }(\kappa _\beta ) = \delta \}$
is unbounded in
$C = \{\kappa _\beta : \beta < \alpha \text { and }j_{\beta \alpha }(\kappa _\beta ) = \delta \}$
is unbounded in
![]() $\delta $
. Moreover, it is
$\delta $
. Moreover, it is
![]() $\omega $
-closed in
$\omega $
-closed in
![]() $\delta $
, since if
$\delta $
, since if
![]() $\langle \beta _n\rangle _{n < \omega }$
is an increasing sequence of ordinals with
$\langle \beta _n\rangle _{n < \omega }$
is an increasing sequence of ordinals with
![]() $\kappa _{\beta _n} \in C$
and
$\kappa _{\beta _n} \in C$
and
![]() $\beta $
is their supremum, then we claim
$\beta $
is their supremum, then we claim
![]() $\kappa _\beta = \sup _{n < \omega } \kappa _{\beta _n}$
. Clearly,
$\kappa _\beta = \sup _{n < \omega } \kappa _{\beta _n}$
. Clearly,
![]() $\kappa _\beta \geq \sup _{n < \omega } \kappa _{\beta _n}$
, and the reverse inequality follows from the choice of
$\kappa _\beta \geq \sup _{n < \omega } \kappa _{\beta _n}$
, and the reverse inequality follows from the choice of
![]() $\kappa _\beta $
in our construction of the iterated ultrapower, noting that
$\kappa _\beta $
in our construction of the iterated ultrapower, noting that
![]() $\sup _{n < \omega }\kappa _{\beta _n}$
has countable cofinality and carries a measure on the
$\sup _{n < \omega }\kappa _{\beta _n}$
has countable cofinality and carries a measure on the
![]() $\mathcal M_\beta $
-sequence. The latter fact uses that
$\mathcal M_\beta $
-sequence. The latter fact uses that
![]() $\sup _{n < \omega } \kappa _{\beta _n} = j_{\beta _0\beta }(\kappa _{\beta _0})$
.
$\sup _{n < \omega } \kappa _{\beta _n} = j_{\beta _0\beta }(\kappa _{\beta _0})$
.
Similarly,
![]() $o^{\mathcal M_\alpha }(\delta ) \geq 1$
. Let
$o^{\mathcal M_\alpha }(\delta ) \geq 1$
. Let
![]() $Z = \vec {U}^{\mathcal M_\alpha }(\delta )$
if
$Z = \vec {U}^{\mathcal M_\alpha }(\delta )$
if
![]() $\delta $
is less than the largest cardinal of
$\delta $
is less than the largest cardinal of
![]() $\mathcal M_\alpha $
, and let
$\mathcal M_\alpha $
, and let
![]() $Z = U^{\mathcal M_\alpha }$
otherwise. The standard argument (going back to Kunen) shows that for any
$Z = U^{\mathcal M_\alpha }$
otherwise. The standard argument (going back to Kunen) shows that for any
![]() $A\in P(\delta )\cap M_\alpha $
,
$A\in P(\delta )\cap M_\alpha $
,
![]() $A\in Z$
if and only if
$A\in Z$
if and only if
![]() $C\setminus \eta \subseteq A$
for some
$C\setminus \eta \subseteq A$
for some
![]() $\eta < \delta $
. Therefore, if
$\eta < \delta $
. Therefore, if
![]() $\delta $
has uncountable cofinality, then
$\delta $
has uncountable cofinality, then
![]() $Z = \mathscr {C}_\delta \cap \mathcal M_\alpha $
.
$Z = \mathscr {C}_\delta \cap \mathcal M_\alpha $
.
This completes our transfinite induction and establishes that if
![]() $\delta> \lambda $
is a regular cardinal of N that has uncountable cofinality in V, then
$\delta> \lambda $
is a regular cardinal of N that has uncountable cofinality in V, then
![]() $o^{\mathcal N}(\delta ) = 1$
and
$o^{\mathcal N}(\delta ) = 1$
and
![]() $\vec {U}^{\mathcal N}(\delta ) = \mathscr {C}_\delta \cap N$
.
$\vec {U}^{\mathcal N}(\delta ) = \mathscr {C}_\delta \cap N$
.
From this, it follows that
![]() $L[A,\vec {\mathscr {C}}]$
is a definable inner model of
$L[A,\vec {\mathscr {C}}]$
is a definable inner model of
![]() $\mathcal N$
, since in fact
$\mathcal N$
, since in fact
![]() $L[A,\vec {\mathscr {C}}] = L[X,\vec {\mathscr {C}}\mathbin \upharpoonright (\lambda ,\infty )]$
is definable over
$L[A,\vec {\mathscr {C}}] = L[X,\vec {\mathscr {C}}\mathbin \upharpoonright (\lambda ,\infty )]$
is definable over
![]() $\mathcal N$
using the parameter
$\mathcal N$
using the parameter
![]() $X\cap N$
and the sequence
$X\cap N$
and the sequence
![]() $\vec {U}^{\mathcal N}$
. As explained above, it follows that
$\vec {U}^{\mathcal N}$
. As explained above, it follows that
![]() $\lambda ^{+L[A,\vec {\mathscr C}]} < \lambda ^+,$
which completes the proof.
$\lambda ^{+L[A,\vec {\mathscr C}]} < \lambda ^+,$
which completes the proof.
Putting everything together, we arrive at the following corollary:
Corollary 3.15. Suppose that for every set X, X-sword exists. Then for every cardinal
![]() $\lambda $
, there is an
$\lambda $
, there is an
![]() $\omega $
-club amenable inner model M that is correct about cardinals and cofinalities
$\omega $
-club amenable inner model M that is correct about cardinals and cofinalities
![]() $\leq \lambda $
while
$\leq \lambda $
while
![]() $(\lambda ^+)^M < \lambda ^+$
.
$(\lambda ^+)^M < \lambda ^+$
.
Proof. Fix a sequence
![]() $\langle a_\alpha \rangle _{\alpha \leq \lambda }$
such that for every limit ordinal
$\langle a_\alpha \rangle _{\alpha \leq \lambda }$
such that for every limit ordinal
![]() $\alpha \leq \lambda $
,
$\alpha \leq \lambda $
,
![]() $a_\alpha $
is a cofinal subset of
$a_\alpha $
is a cofinal subset of
![]() $\alpha $
ordertype
$\alpha $
ordertype
![]() $\operatorname {\mathrm {cf}}(\alpha )$
. This sequence can be coded by a set
$\operatorname {\mathrm {cf}}(\alpha )$
. This sequence can be coded by a set
![]() $A\subseteq \lambda $
, and by Lemma 3.14, the inner model
$A\subseteq \lambda $
, and by Lemma 3.14, the inner model
![]() $M = L[A,\vec {\mathscr {C}}]$
is an
$M = L[A,\vec {\mathscr {C}}]$
is an
![]() $\omega $
-club amenable model such that
$\omega $
-club amenable model such that
![]() $\lambda ^{+M} < \lambda ^+$
.
$\lambda ^{+M} < \lambda ^+$
.
4 Open questions and remarks
The following is a configuration not handled by our arguments:
Question 1. Suppose that
![]() $\kappa $
is a strong limit singular cardinal of uncountable cofinality and that
$\kappa $
is a strong limit singular cardinal of uncountable cofinality and that
![]() $\{\delta <\kappa \mathrel {|} (\delta ^{++})^{\operatorname {\mathrm {HOD}}}\geq \delta ^+\}$
is stationary. Is it true that
$\{\delta <\kappa \mathrel {|} (\delta ^{++})^{\operatorname {\mathrm {HOD}}}\geq \delta ^+\}$
is stationary. Is it true that
![]() $(\kappa ^{++})^{\operatorname {\mathrm {HOD}}}\geq \kappa ^+$
?
$(\kappa ^{++})^{\operatorname {\mathrm {HOD}}}\geq \kappa ^+$
?
We do not know either if other
![]() $\operatorname {\mathrm {HOD}}$
-related properties behave in a compact-like way. For instance, the following is open.
$\operatorname {\mathrm {HOD}}$
-related properties behave in a compact-like way. For instance, the following is open.
Question 2. Suppose that
![]() $\kappa $
is a singular strong limit cardinal with uncountable cofinality and that
$\kappa $
is a singular strong limit cardinal with uncountable cofinality and that
![]() $\{\delta <\kappa \mathrel {|} \delta ^+\;\text {is not}\ \omega \text {-strongly measurable in} \operatorname {\mathrm {HOD}}\}$
is stationary. Is it true that
$\{\delta <\kappa \mathrel {|} \delta ^+\;\text {is not}\ \omega \text {-strongly measurable in} \operatorname {\mathrm {HOD}}\}$
is stationary. Is it true that
![]() $\kappa ^+$
is not
$\kappa ^+$
is not
![]() $\omega $
-strongly measurable in
$\omega $
-strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
?
$\operatorname {\mathrm {HOD}}$
?
There is another intriguing question connecting Woodin’s HOD Conjecture with Theorem 3.4. Assuming the existence of strong enough large cardinals, in [Reference PovedaPov23, Theorem 3.1] it was proved that a cardinal
![]() $\kappa $
can be
$\kappa $
can be
![]() ${<}\lambda $
-extendible for a singular a strong limit cardinal
${<}\lambda $
-extendible for a singular a strong limit cardinal
![]() $\lambda $
with
$\lambda $
with
![]() $\operatorname {\mathrm {cf}}(\lambda )=\omega $
and
$\operatorname {\mathrm {cf}}(\lambda )=\omega $
and
![]() $(\lambda ^+)^{\operatorname {\mathrm {HOD}}_x}<\lambda ^+$
for all subsets
$(\lambda ^+)^{\operatorname {\mathrm {HOD}}_x}<\lambda ^+$
for all subsets
![]() $x\subseteq \lambda $
. In simple terms, the HOD Conjecture can fail locally.Footnote
9
$x\subseteq \lambda $
. In simple terms, the HOD Conjecture can fail locally.Footnote
9
A natural speculation is whether this failure can take place at a strong limit singular of uncountable cofinality.
Question 3. Is the following configuration consistent with ZFC?
-
1.
 $\kappa $
is
$\kappa $
is
 ${<}\lambda $
-extendible.
${<}\lambda $
-extendible. -
2.
 $\lambda $
strong limit with
$\lambda $
strong limit with
 $\operatorname {\mathrm {cf}}(\lambda )\geq \omega _1.$
$\operatorname {\mathrm {cf}}(\lambda )\geq \omega _1.$
-
3.
 $(\lambda ^+)^{\mathrm {HOD}}<\lambda ^+$
$(\lambda ^+)^{\mathrm {HOD}}<\lambda ^+$
Granting the HOD Conjecture, Theorem 3.4 suggests that the answer to Question 3 is negative. For suppose Clause (3) above holds. Then, by Theorem 3.4, the set
![]() $\{\delta <\lambda \mathrel {|} (\delta ^+)^{\mathrm {HOD}}<\delta ^+\}$
contains a club. In particular, the degree of extendibility of
$\{\delta <\lambda \mathrel {|} (\delta ^+)^{\mathrm {HOD}}<\delta ^+\}$
contains a club. In particular, the degree of extendibility of
![]() $\kappa $
overlaps a singular cardinal
$\kappa $
overlaps a singular cardinal
![]() $\delta <\lambda $
witnessing
$\delta <\lambda $
witnessing
![]() $(\delta ^+)^{\operatorname {\mathrm {HOD}}}<\delta ^+$
. This is on the verge of refuting the HOD Conjecture. Note, however, that it does not outright preclude it, the reason being that
$(\delta ^+)^{\operatorname {\mathrm {HOD}}}<\delta ^+$
. This is on the verge of refuting the HOD Conjecture. Note, however, that it does not outright preclude it, the reason being that
![]() $V_\lambda $
may not satisfy
$V_\lambda $
may not satisfy
![]() $\mathrm {ZF}$
. A negative answer would point out yet another difference between singular cardinals of countable and uncountable cofinality.
$\mathrm {ZF}$
. A negative answer would point out yet another difference between singular cardinals of countable and uncountable cofinality.
Acknowledgements
We thank the referees for their detailed comments and corrections to previous drafts of this paper.
Competing interest
The authors have no competing interests to declare.
Funding statement
Goldberg was supported in part by NSF Grant No. 2401789. Poveda was supported by the Department of Mathematics and the Center of Mathematical Sciences and Applications at Harvard University.