Article contents
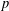 $p$-ADIC
$p$-ADIC 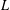 $L$-FUNCTIONS FOR UNITARY GROUPS
$L$-FUNCTIONS FOR UNITARY GROUPS
Published online by Cambridge University Press: 06 May 2020
Abstract
This paper completes the construction of 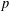 $p$-adic
$p$-adic 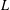 $L$-functions for unitary groups. More precisely, in Harris, Li and Skinner [‘
$L$-functions for unitary groups. More precisely, in Harris, Li and Skinner [‘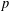 $p$-adic
$p$-adic 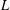 $L$-functions for unitary Shimura varieties. I. Construction of the Eisenstein measure’, Doc. Math.Extra Vol. (2006), 393–464 (electronic)], three of the authors proposed an approach to constructing such
$L$-functions for unitary Shimura varieties. I. Construction of the Eisenstein measure’, Doc. Math.Extra Vol. (2006), 393–464 (electronic)], three of the authors proposed an approach to constructing such 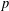 $p$-adic
$p$-adic 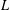 $L$-functions (Part I). Building on more recent results, including the first named author’s construction of Eisenstein measures and
$L$-functions (Part I). Building on more recent results, including the first named author’s construction of Eisenstein measures and 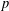 $p$-adic differential operators [Eischen, ‘A
$p$-adic differential operators [Eischen, ‘A 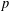 $p$-adic Eisenstein measure for unitary groups’, J. Reine Angew. Math.699 (2015), 111–142; ‘
$p$-adic Eisenstein measure for unitary groups’, J. Reine Angew. Math.699 (2015), 111–142; ‘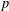 $p$-adic differential operators on automorphic forms on unitary groups’, Ann. Inst. Fourier (Grenoble)62(1) (2012), 177–243], Part II of the present paper provides the calculations of local
$p$-adic differential operators on automorphic forms on unitary groups’, Ann. Inst. Fourier (Grenoble)62(1) (2012), 177–243], Part II of the present paper provides the calculations of local 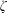 $\unicode[STIX]{x1D701}$-integrals occurring in the Euler product (including at
$\unicode[STIX]{x1D701}$-integrals occurring in the Euler product (including at  $p$). Part III of the present paper develops the formalism needed to pair Eisenstein measures with Hida families in the setting of the doubling method.
$p$). Part III of the present paper develops the formalism needed to pair Eisenstein measures with Hida families in the setting of the doubling method.
MSC classification
Information
- Type
- Number Theory
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2020
References
- 13
- Cited by


