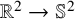1. Introduction
1.1. Setting of the problem
Consider the harmonic map heat flow (HMHF) for maps
![]() $u: \mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
– that is, the gradient flow of the Dirichlet energy
$u: \mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
– that is, the gradient flow of the Dirichlet energy
for the
![]() $L^2$
inner product. The initial value problem for the HMHF is given by
$L^2$
inner product. The initial value problem for the HMHF is given by
 $$ \begin{align} \partial_t u &= \Delta u + u \left\lvert{\nabla u}\right\rvert^2 \nonumber\\ u(0, x) &= u_0(x). \end{align} $$
$$ \begin{align} \partial_t u &= \Delta u + u \left\lvert{\nabla u}\right\rvert^2 \nonumber\\ u(0, x) &= u_0(x). \end{align} $$
We consider initial data in the energy class
The HMHF was proved to be well-posed in
![]() $\mathcal {E}$
by Struwe [Reference Struwe28], and we can associate to each initial data
$\mathcal {E}$
by Struwe [Reference Struwe28], and we can associate to each initial data
![]() $u_0 \in \mathcal {E}$
a maximal time of existence
$u_0 \in \mathcal {E}$
a maximal time of existence
![]() $T_+= T_+(u_0) \in (0, \infty ]$
and unique solution
$T_+= T_+(u_0) \in (0, \infty ]$
and unique solution
![]() $u(t) \in \mathcal {E}$
, which is regular for
$u(t) \in \mathcal {E}$
, which is regular for
![]() $t \in (0, T_+)$
. The maximal time
$t \in (0, T_+)$
. The maximal time
![]() $T_+$
is characterized as the first time at which energy concentrates at a point in space; see Lemma 2.7. Of fundamental importance is the energy identity
$T_+$
is characterized as the first time at which energy concentrates at a point in space; see Lemma 2.7. Of fundamental importance is the energy identity
 $$ \begin{align} E(u(t_2)) + \int_{t_1}^{t_2} \| \mathcal T(u(t)) \|_{L^2(\mathbb{R}^2)}^2\, \mathrm{d} t = E(u(t_1)), \end{align} $$
$$ \begin{align} E(u(t_2)) + \int_{t_1}^{t_2} \| \mathcal T(u(t)) \|_{L^2(\mathbb{R}^2)}^2\, \mathrm{d} t = E(u(t_1)), \end{align} $$
which holds for any
![]() $0 \le t_1 < t_2 < T_+$
(see [Reference Struwe28, Lemma 3.4]), and where
$0 \le t_1 < t_2 < T_+$
(see [Reference Struwe28, Lemma 3.4]), and where
![]() $\mathcal T(u):= \Delta u + u \left \lvert {\nabla u}\right \rvert ^2 $
, which is called the tension of u.
$\mathcal T(u):= \Delta u + u \left \lvert {\nabla u}\right \rvert ^2 $
, which is called the tension of u.
The HMHF for maps between Riemannian manifolds was introduced by Eells and Sampson [Reference Eells and Sampson12]. Though we do not do this here, when studying the HMHF for maps
![]() $\mathbb {R}^2 \to \mathbb {S}^2$
, it is natural to further restrict the class of initial data by intersecting the space
$\mathbb {R}^2 \to \mathbb {S}^2$
, it is natural to further restrict the class of initial data by intersecting the space
![]() $\mathcal E$
with the set of continuous maps
$\mathcal E$
with the set of continuous maps
![]() $u_ 0$
that tend to a fixed vector on
$u_ 0$
that tend to a fixed vector on
![]() $\mathbb {S}^2$
at
$\mathbb {S}^2$
at
![]() $\infty $
(i.e., such that there exists
$\infty $
(i.e., such that there exists
![]() $u_\infty \in \mathbb {S}^2$
so that
$u_\infty \in \mathbb {S}^2$
so that
![]() $ \lim _{x \to \infty } |u_0(x) - u_\infty | = 0$
). By assigning to the point at
$ \lim _{x \to \infty } |u_0(x) - u_\infty | = 0$
). By assigning to the point at
![]() $\infty $
the vector
$\infty $
the vector
![]() $u_\infty $
,
$u_\infty $
,
![]() $u_0$
induces a continuous map
$u_0$
induces a continuous map
![]() $\widetilde u_0: \mathbb {S}^2 \to \mathbb {S}^2$
, and we can define the topological degree of
$\widetilde u_0: \mathbb {S}^2 \to \mathbb {S}^2$
, and we can define the topological degree of
![]() $u_0$
to be the degree of
$u_0$
to be the degree of
![]() $\widetilde u_0$
. One can show that this condition is preserved by the flow – that is, the solution
$\widetilde u_0$
. One can show that this condition is preserved by the flow – that is, the solution
![]() $u(t, x)$
satisfies
$u(t, x)$
satisfies
![]() $ \lim _{x \to \infty } |u(t, x) - u_\infty | = 0$
for all
$ \lim _{x \to \infty } |u(t, x) - u_\infty | = 0$
for all
![]() $0\le t< T_+$
. Under this restriction, the solution
$0\le t< T_+$
. Under this restriction, the solution
![]() $u(t, x)$
gives a continuous deformation of the initial data
$u(t, x)$
gives a continuous deformation of the initial data
![]() $u_0(x)$
within its homotopy class, which was one of the motivations mentioned in [Reference Eells and Sampson12].
$u_0(x)$
within its homotopy class, which was one of the motivations mentioned in [Reference Eells and Sampson12].
Harmonic maps
![]() $\omega :\mathbb {R}^2\to \mathbb S^2 \subset \mathbb {R}^3$
have vanishing tension and give stationary solutions to (1.2). They are formal critical points of the energy (1.1) and satisfy the PDE
$\omega :\mathbb {R}^2\to \mathbb S^2 \subset \mathbb {R}^3$
have vanishing tension and give stationary solutions to (1.2). They are formal critical points of the energy (1.1) and satisfy the PDE
It is a well-known general property of harmonic maps in two dimensions that they are conformal (up to change of orientation) and minimize the energy in their homotopy class; [Reference Eells and Lemaire10, Reference Eells and Wood11, Reference Lemaire19]. The energy of a harmonic map
![]() $\omega $
is given by
$\omega $
is given by
![]() $E(\omega ) = 4 \pi | \deg (\omega )|$
. Weak solutions – that is,
$E(\omega ) = 4 \pi | \deg (\omega )|$
. Weak solutions – that is,
![]() $\omega \in \mathcal {E}$
for which (1.5) holds in the weak sense – are smooth by a result of Hélein [Reference Hélein and Eells15]; see Theorem 2.1 in Section 2.1.
$\omega \in \mathcal {E}$
for which (1.5) holds in the weak sense – are smooth by a result of Hélein [Reference Hélein and Eells15]; see Theorem 2.1 in Section 2.1.
An influential series of works by Struwe [Reference Struwe28], Qing [Reference Qing23], Ding-Tian [Reference Ding and Tian9], Wang [Reference Wang37], Qing-Tian [Reference Qing and Tian24], Lin-Wang [Reference Lin and Wang20] and Topping [Reference Topping31] showed that solutions
![]() $u(t)$
to (1.2) admit a bubble decomposition along a well-chosen sequence of times
$u(t)$
to (1.2) admit a bubble decomposition along a well-chosen sequence of times
![]() $t_n \to T_+$
; see also the book by Lin-Wang [Reference Lin and Wang21]. In these works, the bubbling time sequence
$t_n \to T_+$
; see also the book by Lin-Wang [Reference Lin and Wang21]. In these works, the bubbling time sequence
![]() $t_n \to T_+$
and corresponding sequence of maps
$t_n \to T_+$
and corresponding sequence of maps
![]() $u(t_n)$
become a Palais-Smale sequence after rescaling. Indeed, in the case when
$u(t_n)$
become a Palais-Smale sequence after rescaling. Indeed, in the case when
![]() $T_+ = \infty $
, it follows from (1.4) that
$T_+ = \infty $
, it follows from (1.4) that
so there exists a sequence
![]() $t_n \to \infty $
so that
$t_n \to \infty $
so that
By similar logic, in the case of finite time blow-up (
![]() $T_+ < \infty $
), there is a sequence
$T_+ < \infty $
), there is a sequence
![]() $t_n \to T_+$
so that
$t_n \to T_+$
so that
In other words, after the rescaling
![]() $u_n(x) := u(t_n, \sqrt {t_n}x)$
(or
$u_n(x) := u(t_n, \sqrt {t_n}x)$
(or
![]() $u_n(x) = u(t_n, \sqrt {T_+-t_n} x)$
), the
$u_n(x) = u(t_n, \sqrt {T_+-t_n} x)$
), the
![]() $u_n$
are Palais-Smale sequences for the energy functional because
$u_n$
are Palais-Smale sequences for the energy functional because
![]() $\sup _nE(u_n) < \infty $
and
$\sup _nE(u_n) < \infty $
and
in
![]() $L^2$
. Elliptic bubbling analysis (see, for example, [Reference Brezis and Coron2, Reference Qing23, Reference Struwe28]) is then used to extract bubbles up to the scale
$L^2$
. Elliptic bubbling analysis (see, for example, [Reference Brezis and Coron2, Reference Qing23, Reference Struwe28]) is then used to extract bubbles up to the scale
![]() $\sqrt {t_n}$
(or
$\sqrt {t_n}$
(or
![]() $\sqrt {T_+- t_n}$
in the case
$\sqrt {T_+- t_n}$
in the case
![]() $T_+ <\infty $
). The main result of this paper (see Theorem 1.1 below) is distinct from this classical literature in that we show bubbling occurs along every time sequence (after passing to a suitable subsequence) without the aid of a Palais-Smale sequence in the sense described above. However, the works [Reference Lin and Wang21, Reference Qing and Tian24] show
$T_+ <\infty $
). The main result of this paper (see Theorem 1.1 below) is distinct from this classical literature in that we show bubbling occurs along every time sequence (after passing to a suitable subsequence) without the aid of a Palais-Smale sequence in the sense described above. However, the works [Reference Lin and Wang21, Reference Qing and Tian24] show
![]() $L^\infty $
convergence, including in the neck regions between the bubbles, whereas here we control only the energy in the neck regions; we do not address the question of
$L^\infty $
convergence, including in the neck regions between the bubbles, whereas here we control only the energy in the neck regions; we do not address the question of
![]() $L^\infty $
convergence on the neck regions.
$L^\infty $
convergence on the neck regions.
1.2. Statement of the results
The goal of this paper is to give asymptotic descriptions of solutions
![]() $u(t)$
to (1.2) with initial data
$u(t)$
to (1.2) with initial data
![]() $u_0 \in \mathcal {E}$
. Our first main result is that every sequence of times tending to the maximal time admits a subsequence
$u_0 \in \mathcal {E}$
. Our first main result is that every sequence of times tending to the maximal time admits a subsequence
![]() $t_n \to T_+$
along which
$t_n \to T_+$
along which
![]() $u(t_n)$
admits a decomposition into a finite superposition of rescaled and translated harmonic maps.
$u(t_n)$
admits a decomposition into a finite superposition of rescaled and translated harmonic maps.
We use the notation
![]() $D(y, \rho ) \subset \mathbb {R}^2$
to denote the open disc of radius
$D(y, \rho ) \subset \mathbb {R}^2$
to denote the open disc of radius
![]() $\rho>0$
centered at the point
$\rho>0$
centered at the point
![]() $y \in \mathbb {R}^2$
.
$y \in \mathbb {R}^2$
.
Theorem 1.1 (Bubble decomposition along any time sequence).
Let
![]() $u(t)$
be the unique solution to (1.2) associated to initial data
$u(t)$
be the unique solution to (1.2) associated to initial data
![]() $u_0 \in \mathcal {E}$
. Let
$u_0 \in \mathcal {E}$
. Let
![]() $T_+ = T_+(u_0) \in (0, \infty ]$
denote the maximal time of existence.
$T_+ = T_+(u_0) \in (0, \infty ]$
denote the maximal time of existence.
(Finite time blow-up) Suppose
![]() $T_+ < \infty $
. There exist a finite energy map
$T_+ < \infty $
. There exist a finite energy map
![]() $u^*: \mathbb {R}^2 \to \mathbb {S}^2$
, an integer
$u^*: \mathbb {R}^2 \to \mathbb {S}^2$
, an integer
![]() $L \ge 1$
and points
$L \ge 1$
and points
![]() $\{x^\ell \}_{\ell =1}^L \subset \mathbb {R}^2$
with the following properties.
$\{x^\ell \}_{\ell =1}^L \subset \mathbb {R}^2$
with the following properties.
Let
![]() $t_n \to T_+$
be any time sequence. After passing to a subsequence, which we still denote by
$t_n \to T_+$
be any time sequence. After passing to a subsequence, which we still denote by
![]() $t_n$
, we can associate to each
$t_n$
, we can associate to each
![]() $\ell \in \{1, \dots , L\}$
an integer
$\ell \in \{1, \dots , L\}$
an integer
![]() $M^{(\ell )}$
, sequences
$M^{(\ell )}$
, sequences
![]() $a_{ j, n}^{(\ell )} \in \mathbb {R}^2$
and
$a_{ j, n}^{(\ell )} \in \mathbb {R}^2$
and
![]() $\lambda _{ j, n}^{(\ell )} \in (0, \infty )$
for each
$\lambda _{ j, n}^{(\ell )} \in (0, \infty )$
for each
![]() $j \in \{1, \dots , M^{(\ell )}\}$
, with
$j \in \{1, \dots , M^{(\ell )}\}$
, with
![]() $a_{ j, n}^{(\ell )} \to x^{\ell }$
,
$a_{ j, n}^{(\ell )} \to x^{\ell }$
,
![]() $\frac {\lambda _{ j, n}^{(\ell )}}{\sqrt {T_+- t_n}} \to 0$
as
$\frac {\lambda _{ j, n}^{(\ell )}}{\sqrt {T_+- t_n}} \to 0$
as
![]() $n \to \infty $
, and nontrivial harmonic maps
$n \to \infty $
, and nontrivial harmonic maps
![]() $\omega _{1}^{(\ell )}, \dots , \omega _{M^{(\ell )}}^{(\ell )}$
so that
$\omega _{1}^{(\ell )}, \dots , \omega _{M^{(\ell )}}^{(\ell )}$
so that
 $$ \begin{align} \lim_{n \to \infty} \bigg( \frac{\lambda_{ j, n}^{(\ell)}}{\lambda_{ k, n}^{(\ell)}} + \frac{\lambda_{k, n}^{(\ell)}}{\lambda_{ j, n}^{(\ell)}} + \frac{ | a_{j, n}^{(\ell)} - a_{k, n}^{(\ell)}|}{ \lambda_{ j, n}^{(\ell)}}\bigg) = \infty \quad \textrm{for all}\,\, j \neq k , \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \bigg( \frac{\lambda_{ j, n}^{(\ell)}}{\lambda_{ k, n}^{(\ell)}} + \frac{\lambda_{k, n}^{(\ell)}}{\lambda_{ j, n}^{(\ell)}} + \frac{ | a_{j, n}^{(\ell)} - a_{k, n}^{(\ell)}|}{ \lambda_{ j, n}^{(\ell)}}\bigg) = \infty \quad \textrm{for all}\,\, j \neq k , \end{align} $$
and
 $$ \begin{align} \lim_{n \to \infty} E \bigg( u(t_n) - u^* - \sum_{\ell = 1}^{L} \sum_{j =1}^{M^{(\ell)}} \Big( \omega_{j}^{(\ell)} \Big( \frac{ \cdot - a_{ j, n}^{(\ell)}}{\lambda_{ j, n}^{(\ell)}} \Big) - \omega_{j}^{(\ell)}(\infty) \Big) \bigg) = 0, \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E \bigg( u(t_n) - u^* - \sum_{\ell = 1}^{L} \sum_{j =1}^{M^{(\ell)}} \Big( \omega_{j}^{(\ell)} \Big( \frac{ \cdot - a_{ j, n}^{(\ell)}}{\lambda_{ j, n}^{(\ell)}} \Big) - \omega_{j}^{(\ell)}(\infty) \Big) \bigg) = 0, \end{align} $$
where
![]() $\omega _{j}^{(\ell )}(\infty ) := \lim _{\left \lvert {x}\right \rvert \to \infty } \omega _{j}^{(\ell )} (x) \in \mathbb {S}^2$
.
$\omega _{j}^{(\ell )}(\infty ) := \lim _{\left \lvert {x}\right \rvert \to \infty } \omega _{j}^{(\ell )} (x) \in \mathbb {S}^2$
.
Moreover, there exists a sequence
![]() $r_n \to \infty $
with the following property. Fix any
$r_n \to \infty $
with the following property. Fix any
![]() $\ell \in \{1, \dots , L\}$
. For each
$\ell \in \{1, \dots , L\}$
. For each
![]() $j \in \{1, \dots , M^{(\ell )}\}$
, there exists
$j \in \{1, \dots , M^{(\ell )}\}$
, there exists
![]() $0 \le K_j^{(\ell )}< M^{(\ell )}$
many discs
$0 \le K_j^{(\ell )}< M^{(\ell )}$
many discs
![]() $D(x_{j, k, n}, \mu _{j,k, n}) \subset D(a_{j, n}^{(\ell )}, r_n \lambda _{j, n}^{(\ell )})$
such that for each
$D(x_{j, k, n}, \mu _{j,k, n}) \subset D(a_{j, n}^{(\ell )}, r_n \lambda _{j, n}^{(\ell )})$
such that for each
![]() $k \in \{1, \dots , K_j^{(\ell )}\}$
,
$k \in \{1, \dots , K_j^{(\ell )}\}$
,
 $$ \begin{align} \lim_{n \to \infty} \Big( \frac{\mu_{j,k, n}}{\lambda_{j, n}^{(\ell)}} + \frac{\mu_{j, k, n}}{ \operatorname{dist}(x_{j, k, n}, \partial D( a_{j, n}^{(\ell)}, r_n \lambda_{j, n}^{(\ell)}))}\Big) = 0, \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \Big( \frac{\mu_{j,k, n}}{\lambda_{j, n}^{(\ell)}} + \frac{\mu_{j, k, n}}{ \operatorname{dist}(x_{j, k, n}, \partial D( a_{j, n}^{(\ell)}, r_n \lambda_{j, n}^{(\ell)}))}\Big) = 0, \end{align} $$
and so that
 $$ \begin{align} \lim_{n \to \infty} \Big\| u(t_n) - \omega_{j}^{(\ell)} \Big( \frac{ \cdot - a_{ j, n}^{(\ell)}}{\lambda_{ j, n}^{(\ell)}} \Big) \Big\|_{L^\infty( D^*_{j, n})} = 0, \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \Big\| u(t_n) - \omega_{j}^{(\ell)} \Big( \frac{ \cdot - a_{ j, n}^{(\ell)}}{\lambda_{ j, n}^{(\ell)}} \Big) \Big\|_{L^\infty( D^*_{j, n})} = 0, \end{align} $$
where
![]() $D^*_{j, n} = D(a_{j, n}^{(\ell )}, r_n \lambda _{j, n}^{(\ell )}) \setminus \bigcup _{k =1}^{K_j^{(\ell )}} D(x_{j, k, n}, \mu _{j,k, n})$
.
$D^*_{j, n} = D(a_{j, n}^{(\ell )}, r_n \lambda _{j, n}^{(\ell )}) \setminus \bigcup _{k =1}^{K_j^{(\ell )}} D(x_{j, k, n}, \mu _{j,k, n})$
.
Finally, there exist constants
![]() $\omega _\infty ^{(1)}, \dots , \omega _{\infty }^{(L)} \in \mathbb {S}^2$
and sequences
$\omega _\infty ^{(1)}, \dots , \omega _{\infty }^{(L)} \in \mathbb {S}^2$
and sequences
![]() $\xi _n, \nu _n \to 0$
so that for each
$\xi _n, \nu _n \to 0$
so that for each
![]() $\ell \in \{1, \dots , L\}$
,
$\ell \in \{1, \dots , L\}$
,
 $$ \begin{align} \lim_{n \to \infty}\Big( \| u( t_n) - \omega^{(\ell)}_{\infty} \|_{L^{\infty}( D( x^{\ell}, \nu_n) \setminus D( x^{\ell}, \xi_n))} + \frac{\xi_n}{\sqrt{T_+-t_n}} + \frac{\sqrt{T_+-t_n}}{\nu_n} \Big) = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty}\Big( \| u( t_n) - \omega^{(\ell)}_{\infty} \|_{L^{\infty}( D( x^{\ell}, \nu_n) \setminus D( x^{\ell}, \xi_n))} + \frac{\xi_n}{\sqrt{T_+-t_n}} + \frac{\sqrt{T_+-t_n}}{\nu_n} \Big) = 0. \end{align} $$
(Global solution) Suppose
![]() $T_+= \infty $
. Let
$T_+= \infty $
. Let
![]() $t_n \to \infty $
be any time sequence. After passing to a subsequence, which we still denote by
$t_n \to \infty $
be any time sequence. After passing to a subsequence, which we still denote by
![]() $t_n$
, we can find an integer
$t_n$
, we can find an integer
![]() $M \ge 0$
, sequences
$M \ge 0$
, sequences
![]() $a_{j, n} \in \mathbb {R}^2$
and
$a_{j, n} \in \mathbb {R}^2$
and
![]() $\lambda _{ j, n} \in (0, \infty )$
for each
$\lambda _{ j, n} \in (0, \infty )$
for each
![]() $j \in \{1, \dots , M\}$
, with
$j \in \{1, \dots , M\}$
, with
![]() $ \lim _{n \to \infty } \frac {|a_{j, n}| + \lambda _{ j, n}}{\sqrt {t_n}} = 0$
, and nontrivial harmonic maps
$ \lim _{n \to \infty } \frac {|a_{j, n}| + \lambda _{ j, n}}{\sqrt {t_n}} = 0$
, and nontrivial harmonic maps
![]() $\omega _1, \dots , \omega _{M}$
, so that
$\omega _1, \dots , \omega _{M}$
, so that
 $$ \begin{align} \lim_{n \to \infty} \bigg( \frac{\lambda_{j, n}}{\lambda_{k, n}} + \frac{\lambda_{k, n}}{\lambda_{j, n}} + \frac{ | a_{ j, n} - a_{k, n}|}{ \lambda_{j, n}} \bigg) = \infty \quad \textrm{for all} \, \, j \neq k, \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \bigg( \frac{\lambda_{j, n}}{\lambda_{k, n}} + \frac{\lambda_{k, n}}{\lambda_{j, n}} + \frac{ | a_{ j, n} - a_{k, n}|}{ \lambda_{j, n}} \bigg) = \infty \quad \textrm{for all} \, \, j \neq k, \end{align} $$
and
 $$ \begin{align} \lim_{n \to \infty} E \bigg( u(t_n) - \omega_\infty - \sum_{j =1}^{M} \Big(\omega_{j} \Big( \frac{ \cdot - a_{ j, n}}{\lambda_{ j, n}} \Big) - \omega_{j}(\infty)\Big) \bigg) = 0, \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E \bigg( u(t_n) - \omega_\infty - \sum_{j =1}^{M} \Big(\omega_{j} \Big( \frac{ \cdot - a_{ j, n}}{\lambda_{ j, n}} \Big) - \omega_{j}(\infty)\Big) \bigg) = 0, \end{align} $$
where
![]() $\omega _{j}(\infty ) := \lim _{\left \lvert {x}\right \rvert \to \infty } \omega _{j} (x) \in \mathbb {S}^2$
.
$\omega _{j}(\infty ) := \lim _{\left \lvert {x}\right \rvert \to \infty } \omega _{j} (x) \in \mathbb {S}^2$
.
Moreover, there exists a sequence
![]() $r_n \to \infty $
with the following property. For each
$r_n \to \infty $
with the following property. For each
![]() $j \in \{1, \dots , M\}$
, there exists
$j \in \{1, \dots , M\}$
, there exists
![]() $0 \le K_j< M$
many discs
$0 \le K_j< M$
many discs
![]() $D(x_{j, k, n}, \mu _{j,k, n}) \subset D(a_{j, n}, r_n \lambda _{j, n})$
such that for each
$D(x_{j, k, n}, \mu _{j,k, n}) \subset D(a_{j, n}, r_n \lambda _{j, n})$
such that for each
![]() $k \in \{1, \dots , K_j\}$
,
$k \in \{1, \dots , K_j\}$
,
and so that
 $$ \begin{align} \lim_{n \to \infty} \Big\| u(t_n) - \omega_{j}^{(\ell)} \Big( \frac{ \cdot - a_{ j, n}^{(\ell)}}{\lambda_{ j, n}^{(\ell)}} \Big) \Big\|_{L^\infty( D^*_{j, n})} = 0, \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \Big\| u(t_n) - \omega_{j}^{(\ell)} \Big( \frac{ \cdot - a_{ j, n}^{(\ell)}}{\lambda_{ j, n}^{(\ell)}} \Big) \Big\|_{L^\infty( D^*_{j, n})} = 0, \end{align} $$
where
![]() $D^*_{j, n} = D(a_{j, n}, r_n \lambda _{j, n}) \setminus \bigcup _{k =1}^{K_j} D(x_{j, k, n}, \mu _{j,k, n})$
.
$D^*_{j, n} = D(a_{j, n}, r_n \lambda _{j, n}) \setminus \bigcup _{k =1}^{K_j} D(x_{j, k, n}, \mu _{j,k, n})$
.
Finally, there exists a constant
![]() $\omega _\infty \in \mathbb {S}^2$
and sequences
$\omega _\infty \in \mathbb {S}^2$
and sequences
![]() $\xi _n, \nu _n \in (0, \infty )$
so that
$\xi _n, \nu _n \in (0, \infty )$
so that
 $$ \begin{align} \lim_{n \to \infty}\Big( \| u( t_n) - \omega_{\infty} \|_{L^{\infty}( D( x^{\ell}, \nu_n) \setminus D( x^{\ell}, \xi_n))} + \frac{\xi_n}{\sqrt{t_n}} + \frac{\sqrt{t_n}}{\nu_n} \Big) = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty}\Big( \| u( t_n) - \omega_{\infty} \|_{L^{\infty}( D( x^{\ell}, \nu_n) \setminus D( x^{\ell}, \xi_n))} + \frac{\xi_n}{\sqrt{t_n}} + \frac{\sqrt{t_n}}{\nu_n} \Big) = 0. \end{align} $$
Remark 1.2. One can also study the two-dimensional HMHF for more general domains and targets – that is, for maps
![]() $u: \mathcal M \to \mathcal N$
, where
$u: \mathcal M \to \mathcal N$
, where
![]() $\mathcal M$
is a
$\mathcal M$
is a
![]() $2$
-dimensional closed, orientable Riemannian manifold (or
$2$
-dimensional closed, orientable Riemannian manifold (or
![]() $\mathbb {R}^2$
) and
$\mathbb {R}^2$
) and
![]() $\mathcal N$
is a closed n-dimensional sub-manifold of
$\mathcal N$
is a closed n-dimensional sub-manifold of
![]() $\mathbb {R}^N$
for some N – as in this, case the bubbling theory of [Reference Ding and Tian9, Reference Lin and Wang20, Reference Qing23, Reference Qing and Tian24, Reference Struwe28] is understood. But we do not pursue this here. Moreover, the choice of
$\mathbb {R}^N$
for some N – as in this, case the bubbling theory of [Reference Ding and Tian9, Reference Lin and Wang20, Reference Qing23, Reference Qing and Tian24, Reference Struwe28] is understood. But we do not pursue this here. Moreover, the choice of
![]() $\mathbb {R}^2$
as the domain is for convenience, as we could have instead considered maps
$\mathbb {R}^2$
as the domain is for convenience, as we could have instead considered maps
![]() $u: \mathbb {S}^2 \to \mathbb {S}^2$
.
$u: \mathbb {S}^2 \to \mathbb {S}^2$
.
We deduce Theorem 1.1 as a consequence of a more refined result, where we show that every smooth solution
![]() $ u(t)$
converges, continuously in time, to the family of multi-bubble configurations, locally about any point in space. To state this result, we first define a notion of scale and center of a nontrivial harmonic map.
$ u(t)$
converges, continuously in time, to the family of multi-bubble configurations, locally about any point in space. To state this result, we first define a notion of scale and center of a nontrivial harmonic map.
Definition 1.3 (Scale of a harmonic map).
To each non-constant harmonic map
![]() $\omega : \mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
and each
$\omega : \mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
and each
![]() $\gamma _0 \in (0, 2\pi )$
, we associate a scale
$\gamma _0 \in (0, 2\pi )$
, we associate a scale
![]() $\lambda ( \omega; \gamma _0)$
defined by
$\lambda ( \omega; \gamma _0)$
defined by
Definition 1.4 (Center of a harmonic map).
Given the scale of a harmonic map
![]() $\omega $
as above, we define the associated center of
$\omega $
as above, we define the associated center of
![]() $\omega $
by fixing a choice of
$\omega $
by fixing a choice of
![]() $a = a(\omega; \gamma _0) \in \mathbb {R}^2$
so that
$a = a(\omega; \gamma _0) \in \mathbb {R}^2$
so that
We prove in Lemma 2.3 that these notions are well-defined and transform naturally under the rescaling and translation of a harmonic map. Indeed, the scale
![]() $\lambda ( \omega; \gamma _0)$
is a uniquely defined, strictly positive number. Regarding a choice of center, equality occurs in (1.17). However,
$\lambda ( \omega; \gamma _0)$
is a uniquely defined, strictly positive number. Regarding a choice of center, equality occurs in (1.17). However,
![]() $a(\omega; \gamma _0)$
is defined only up to a distance of
$a(\omega; \gamma _0)$
is defined only up to a distance of
![]() $2\lambda ( \omega; \gamma _0)$
. Given a harmonic map
$2\lambda ( \omega; \gamma _0)$
. Given a harmonic map
![]() $\omega (x)$
, translating by
$\omega (x)$
, translating by
![]() $b \in \mathbb {R}^2$
and rescaling by
$b \in \mathbb {R}^2$
and rescaling by
![]() $\mu \in (0, \infty )$
, we obtain
$\mu \in (0, \infty )$
, we obtain
![]() $ \omega _{b, \mu }(x) := \omega \big ( \frac {x - b}{\mu })$
. Then
$ \omega _{b, \mu }(x) := \omega \big ( \frac {x - b}{\mu })$
. Then
![]() $\lambda (\omega _{b, \mu }) = \lambda (\omega )\mu $
and
$\lambda (\omega _{b, \mu }) = \lambda (\omega )\mu $
and
![]() $|a(\omega _{b, \mu })- a(\omega )\mu -b| \le 2\lambda (\omega )\mu $
.
$|a(\omega _{b, \mu })- a(\omega )\mu -b| \le 2\lambda (\omega )\mu $
.
Definition 1.5 (Multi-bubble configuration).
Let
![]() $M \in \{0,1, 2, \dots \}$
. We define an M-bubble configuration to be a superposition
$M \in \{0,1, 2, \dots \}$
. We define an M-bubble configuration to be a superposition
 $$ \begin{align} \mathcal Q( \omega, \omega_1, \dots, \omega_M; x) = \omega+ \sum_{j=1}^M ( \omega_j(x) - \omega_j(\infty)), \end{align} $$
$$ \begin{align} \mathcal Q( \omega, \omega_1, \dots, \omega_M; x) = \omega+ \sum_{j=1}^M ( \omega_j(x) - \omega_j(\infty)), \end{align} $$
where
![]() $\omega \in \mathbb {S}^2$
is a constant, and each
$\omega \in \mathbb {S}^2$
is a constant, and each
![]() $\omega _j: \mathbb {R}^2 \to \mathbb {S}^2$
is a smooth non-constant harmonic map, and
$\omega _j: \mathbb {R}^2 \to \mathbb {S}^2$
is a smooth non-constant harmonic map, and
![]() $\omega _j(\infty ):= \lim _{\left \lvert {x}\right \rvert \to \infty } \omega _j(x)$
. We include constant maps as
$\omega _j(\infty ):= \lim _{\left \lvert {x}\right \rvert \to \infty } \omega _j(x)$
. We include constant maps as
![]() $M=0$
.
$M=0$
.
We will occasionally use boldface notation,
![]() $\boldsymbol {\omega }: = (\omega , \omega _1, \dots , \omega _M)$
, for finite sequences of harmonic maps with
$\boldsymbol {\omega }: = (\omega , \omega _1, \dots , \omega _M)$
, for finite sequences of harmonic maps with
![]() $\omega \in \mathbb {S}^2$
a constant harmonic map and
$\omega \in \mathbb {S}^2$
a constant harmonic map and
![]() $\omega _{1}, \dots , \omega _{M}$
non-constant, and we reserve the arrow notation for vectors (finite sequences) in other contexts. With this notation, we will often express multi-bubbles as
$\omega _{1}, \dots , \omega _{M}$
non-constant, and we reserve the arrow notation for vectors (finite sequences) in other contexts. With this notation, we will often express multi-bubbles as
![]() $ \mathcal Q( \boldsymbol {\omega }):=\mathcal Q( \omega , \omega _1, \dots , \omega _M)$
. We reserve the character
$ \mathcal Q( \boldsymbol {\omega }):=\mathcal Q( \omega , \omega _1, \dots , \omega _M)$
. We reserve the character
![]() $\mathfrak {h}$
to denote an infinite sequence of non-constant harmonic maps (i.e.,
$\mathfrak {h}$
to denote an infinite sequence of non-constant harmonic maps (i.e.,
![]() $\mathfrak {h}:= \{ \omega _{n}\}_{n =1}^\infty $
, where each
$\mathfrak {h}:= \{ \omega _{n}\}_{n =1}^\infty $
, where each
![]() $\omega _n$
is a harmonic map).
$\omega _n$
is a harmonic map).
Definition 1.6 (Localized distance to a multi-bubble configuration).
Let
![]() $\xi , \rho , \nu \in (0, \infty )$
, with
$\xi , \rho , \nu \in (0, \infty )$
, with
![]() $\xi \le \rho \le \nu $
,
$\xi \le \rho \le \nu $
,
![]() $y \in \mathbb {R}^2$
,
$y \in \mathbb {R}^2$
,
![]() $u: D( y, \nu ) \to \mathbb {S}^2$
and
$u: D( y, \nu ) \to \mathbb {S}^2$
and
![]() $\gamma _0 \in (0, 2\pi )$
as in Definition 1.3. Let
$\gamma _0 \in (0, 2\pi )$
as in Definition 1.3. Let
![]() $M \in \{0, 1, 2, \dots \}$
,
$M \in \{0, 1, 2, \dots \}$
,
![]() $\omega \in \mathbb {S}^2$
a constant, and let
$\omega \in \mathbb {S}^2$
a constant, and let
![]() $\omega _1, \dots , \omega _M$
be non-constant harmonic maps with centers
$\omega _1, \dots , \omega _M$
be non-constant harmonic maps with centers
![]() $a(\omega _j)\in D( y, \xi )$
for each
$a(\omega _j)\in D( y, \xi )$
for each
![]() $j \in \{1, \dots , M\}$
and scales
$j \in \{1, \dots , M\}$
and scales
![]() $\lambda (\omega _{j}) \in (0, \infty )$
. Let
$\lambda (\omega _{j}) \in (0, \infty )$
. Let
![]() $\mathcal Q( \boldsymbol {\omega })$
be the associated multi-bubble configuration. Let
$\mathcal Q( \boldsymbol {\omega })$
be the associated multi-bubble configuration. Let
![]() $ \vec \nu = (\nu , \nu _1, \dots , \nu _M) \in (0, \infty )^{M+1}$
be such that
$ \vec \nu = (\nu , \nu _1, \dots , \nu _M) \in (0, \infty )^{M+1}$
be such that
![]() $D(a(\omega _j), \nu _j) \subset D(y, \xi )$
for each
$D(a(\omega _j), \nu _j) \subset D(y, \xi )$
for each
![]() $j \in \{1, \dots , M\}$
. Let
$j \in \{1, \dots , M\}$
. Let
![]() $\vec \xi = (\xi , \xi _1, \dots ,\xi _M) \in (0, \infty )^{M+1}$
be such that
$\vec \xi = (\xi , \xi _1, \dots ,\xi _M) \in (0, \infty )^{M+1}$
be such that
![]() $\xi _j < \lambda (\omega _j)$
for each
$\xi _j < \lambda (\omega _j)$
for each
![]() $j \in \{1, \dots , M\}$
. Denote by
$j \in \{1, \dots , M\}$
. Denote by
![]() $\mathcal I_j:= \{ k \neq j \mid D(a(\omega _k), \xi _j) \subset D(a(\omega _j), \nu _j)\}$
, and let
$\mathcal I_j:= \{ k \neq j \mid D(a(\omega _k), \xi _j) \subset D(a(\omega _j), \nu _j)\}$
, and let
 $$ \begin{align} D_{j}^*:=D( a(\omega_j), \nu_j) \setminus \bigcup_{k\in \mathcal I_j }D(a(\omega_k), \xi_j). \end{align} $$
$$ \begin{align} D_{j}^*:=D( a(\omega_j), \nu_j) \setminus \bigcup_{k\in \mathcal I_j }D(a(\omega_k), \xi_j). \end{align} $$
Define
 $$ \begin{align} \mathbf{d}_{\gamma_0}( u, \mathcal Q( \boldsymbol{\omega}); D(y, \rho); \vec \nu, \vec \xi) &:= E\big( u - \mathcal Q( \boldsymbol{\omega}); D(y, \rho)\big) + \sum_j \| u - \omega_j \|_{L^\infty( D_j^*)} \nonumber\\[-3pt] & \quad + \| u - \omega \|_{L^{\infty}(D( y, \nu) \setminus D(y, \xi))} + E(u; D( y, \nu) \setminus D(y, \xi))+ \frac{\xi}{\rho} + \frac{\rho}{\nu} \nonumber\\ & \quad + \sum_{j \neq k} \bigg( \frac{\lambda(\omega_j)}{\lambda(\omega_k)} + \frac{\lambda(\omega_k)}{\lambda(\omega_j)} + \frac{| a(\omega_j) - a(\omega_k)|}{\lambda(\omega_j)} \bigg)^{-1} \nonumber\\ & \quad + \sum_j \Big(\frac{\lambda(\omega_j)}{ \operatorname{dist}( a(\omega_j), \partial D(y, \xi))} + \frac{\lambda(\omega_j)}{\nu_j} + \frac{\xi_j}{\lambda(\omega_j)}\Big) \nonumber\\ & \quad + \sum_j \sum_{k \in\mathcal I_j }\frac{\xi_j}{\operatorname{dist}(a(\omega_k), \partial D( a(\omega_j), \nu_j))}. \end{align} $$
$$ \begin{align} \mathbf{d}_{\gamma_0}( u, \mathcal Q( \boldsymbol{\omega}); D(y, \rho); \vec \nu, \vec \xi) &:= E\big( u - \mathcal Q( \boldsymbol{\omega}); D(y, \rho)\big) + \sum_j \| u - \omega_j \|_{L^\infty( D_j^*)} \nonumber\\[-3pt] & \quad + \| u - \omega \|_{L^{\infty}(D( y, \nu) \setminus D(y, \xi))} + E(u; D( y, \nu) \setminus D(y, \xi))+ \frac{\xi}{\rho} + \frac{\rho}{\nu} \nonumber\\ & \quad + \sum_{j \neq k} \bigg( \frac{\lambda(\omega_j)}{\lambda(\omega_k)} + \frac{\lambda(\omega_k)}{\lambda(\omega_j)} + \frac{| a(\omega_j) - a(\omega_k)|}{\lambda(\omega_j)} \bigg)^{-1} \nonumber\\ & \quad + \sum_j \Big(\frac{\lambda(\omega_j)}{ \operatorname{dist}( a(\omega_j), \partial D(y, \xi))} + \frac{\lambda(\omega_j)}{\nu_j} + \frac{\xi_j}{\lambda(\omega_j)}\Big) \nonumber\\ & \quad + \sum_j \sum_{k \in\mathcal I_j }\frac{\xi_j}{\operatorname{dist}(a(\omega_k), \partial D( a(\omega_j), \nu_j))}. \end{align} $$
We define a localized distance function to the family of all multi-bubble configurations as follows.
Definition 1.7 (Localized multi-bubble proximity function).
Let
![]() $y \in \mathbb {R}^2$
,
$y \in \mathbb {R}^2$
,
![]() $\rho \in (0, \infty )$
,
$\rho \in (0, \infty )$
,
![]() $u: D( y, \rho ) \to \mathbb {S}^2$
, and let
$u: D( y, \rho ) \to \mathbb {S}^2$
, and let
![]() $\gamma _0 \in (0,2 \pi )$
as in Definition 1.3. We define
$\gamma _0 \in (0,2 \pi )$
as in Definition 1.3. We define
where the infimum above is taken over all possible M-bubble configurations
![]() $\mathcal Q(\boldsymbol {\omega })$
and over all admissible
$\mathcal Q(\boldsymbol {\omega })$
and over all admissible
![]() $\vec \nu = (\nu , \nu _1, \dots , \nu _M)\in (0, \infty )^{M+1}, \vec \xi = (\xi , \xi _1, \dots , \xi _M) \in (0, \infty )^{M+1}$
in the sense of Definition 1.6. Since
$\vec \nu = (\nu , \nu _1, \dots , \nu _M)\in (0, \infty )^{M+1}, \vec \xi = (\xi , \xi _1, \dots , \xi _M) \in (0, \infty )^{M+1}$
in the sense of Definition 1.6. Since
![]() $\gamma _0$
will eventually be fixed, we will often suppress the dependence of
$\gamma _0$
will eventually be fixed, we will often suppress the dependence of
![]() $\mathbf {d}_{\gamma _0}$
and
$\mathbf {d}_{\gamma _0}$
and
![]() $\boldsymbol {\delta }_{\gamma _0}$
on
$\boldsymbol {\delta }_{\gamma _0}$
on
![]() $\gamma _0$
and just write
$\gamma _0$
and just write
![]() $\mathbf {d}, \boldsymbol {\delta }$
.
$\mathbf {d}, \boldsymbol {\delta }$
.
We prove the following theorem.
Theorem 1.8 (Convergence to multi-bubbles in continuous time).
Let
![]() $u(t)$
be the unique solution to (1.2) associated to initial data
$u(t)$
be the unique solution to (1.2) associated to initial data
![]() $u_0 \in \mathcal {E}$
. Let
$u_0 \in \mathcal {E}$
. Let
![]() $T_+ = T_+(u_0) \in (0, \infty ]$
denote the maximal time of existence. There exists
$T_+ = T_+(u_0) \in (0, \infty ]$
denote the maximal time of existence. There exists
![]() $\gamma _0 = \gamma _0(E( u_0))>0$
as in Definition 1.3 sufficiently small so that the following conclusions hold.
$\gamma _0 = \gamma _0(E( u_0))>0$
as in Definition 1.3 sufficiently small so that the following conclusions hold.
(Finite time blow-up) Suppose
![]() $T_+< \infty $
. For every
$T_+< \infty $
. For every
![]() $y \in \mathbb {R}^2$
,
$y \in \mathbb {R}^2$
,
Moreover, let
![]() $t_n \to T_+$
be any sequence and let
$t_n \to T_+$
be any sequence and let
![]() $D(y_n, \rho _n)$
be any sequence of discs such that
$D(y_n, \rho _n)$
be any sequence of discs such that
![]() $D(y_n, R_n \rho _n) \subset D(y, \sqrt {T_+-t})$
for some sequence
$D(y_n, R_n \rho _n) \subset D(y, \sqrt {T_+-t})$
for some sequence
![]() $R_n \to \infty $
. Suppose
$R_n \to \infty $
. Suppose
![]() $\alpha _n, \beta _n$
are sequences with
$\alpha _n, \beta _n$
are sequences with
![]() $\alpha _n \to 0$
,
$\alpha _n \to 0$
,
![]() $\beta _n \to \infty $
,
$\beta _n \to \infty $
,
![]() $\lim _{n \to \infty } \beta _n R_n^{-1} = 0$
, and
$\lim _{n \to \infty } \beta _n R_n^{-1} = 0$
, and
Then,
(Global solution) Suppose
![]() $T_+ = \infty $
. For every
$T_+ = \infty $
. For every
![]() $y \in \mathbb {R}^2$
,
$y \in \mathbb {R}^2$
,
Moreover, let
![]() $t_n \to \infty $
be any sequence and let
$t_n \to \infty $
be any sequence and let
![]() $D(y_n, \nu _n)$
any sequence of discs such that
$D(y_n, \nu _n)$
any sequence of discs such that
![]() $D(y_n, R_n \nu _n) \subset D(y, \sqrt {t_n})$
for some sequence
$D(y_n, R_n \nu _n) \subset D(y, \sqrt {t_n})$
for some sequence
![]() $R_n \to \infty $
. Suppose
$R_n \to \infty $
. Suppose
![]() $\alpha _n, \beta _n$
are sequences with
$\alpha _n, \beta _n$
are sequences with
![]() $\alpha _n \to 0$
,
$\alpha _n \to 0$
,
![]() $\beta _n \to \infty $
,
$\beta _n \to \infty $
,
![]() $\lim _{n \to \infty } \beta _n R_n^{-1} = 0$
and
$\lim _{n \to \infty } \beta _n R_n^{-1} = 0$
and
Then,
Remark 1.9. Theorem 1.8 can be viewed as partial progress toward the following questions, which arise naturally from the classical sequential bubbling results [Reference Ding and Tian9, Reference Lin and Wang20, Reference Qing23, Reference Qing and Tian24, Reference Struwe28, Reference Topping31, Reference Wang37]:
-
• Can the harmonic maps (bubbles) appearing in Theorem 1.1 be taken independently of the time sequence? For example, Theorem 1.8 does not fix even the number of bubbles in the decomposition, but rather proves convergence in continuous time to the entire family of multi-bubble configurations.
-
• In particular, can the decomposition in Theorem 1.1 be taken in continuous time – that is, does
 $u(t)$
converge in the energy space to
$u(t)$
converge in the energy space to
 $u^*$
plus a superposition of a fixed collection of harmonic maps that are continuously modulated by a finite number of parameters independently of the degree (for example, via the underlying symmetries such as scaling, spatial translations, and rotations)?
$u^*$
plus a superposition of a fixed collection of harmonic maps that are continuously modulated by a finite number of parameters independently of the degree (for example, via the underlying symmetries such as scaling, spatial translations, and rotations)?
Topping [Reference Topping30, Reference Topping33] made important progress on these and related questions in the case of a global-in-time solution (
![]() $T_+ = \infty $
), showing the uniqueness of the locations of the bubbling points and that
$T_+ = \infty $
), showing the uniqueness of the locations of the bubbling points and that
![]() $u(t)$
converges weakly to a unique harmonic map as
$u(t)$
converges weakly to a unique harmonic map as
![]() $t \to \infty $
, all under restrictions on the configurations of bubbles appearing in the sequential decomposition. His assumption, roughly, is that all of the concentrating bubbles have the same orientation. Here, we do not make any assumptions on the orientations of the bubbles, but our results in the global-in-time case are of a different nature, and we do not recover Topping’s conclusions.
$t \to \infty $
, all under restrictions on the configurations of bubbles appearing in the sequential decomposition. His assumption, roughly, is that all of the concentrating bubbles have the same orientation. Here, we do not make any assumptions on the orientations of the bubbles, but our results in the global-in-time case are of a different nature, and we do not recover Topping’s conclusions.
Topping answered the questions above in the negative for the HMHF for maps from
![]() $\mathbb {S}^2$
into certain target manifolds; see [Reference Topping31].
$\mathbb {S}^2$
into certain target manifolds; see [Reference Topping31].
The first two authors answered the questions above in the affirmative in the case that the target is
![]() $\mathbb {S}^2$
and the initial data for (1.2) is k-equivariant; see [Reference Jendrej and Lawrie16].
$\mathbb {S}^2$
and the initial data for (1.2) is k-equivariant; see [Reference Jendrej and Lawrie16].
Remark 1.10. One can view Theorem 1.8 as a statement about the nonexistence of bubble collisions (asymptotically in time) that destroy multi-bubble structure. Here a bubble collision on a disc
![]() $D(y, \rho )$
is defined via the growth of the function
$D(y, \rho )$
is defined via the growth of the function
![]() $\boldsymbol {\delta }(u(t); D(y, \rho ))$
(i.e.,
$\boldsymbol {\delta }(u(t); D(y, \rho ))$
(i.e.,
![]() $u(t)$
starts close to, but then moves away from the family of multi-bubble configurations on some time interval). Roughly speaking, Theorem 1.8 reduces the questions in Remark 1.9 to an analysis of the dynamics of solutions close to the manifold of multi-bubble configurations. Note that [Reference Bernand-Mantel, Muratov and Simon1, Reference Deng, Sun and Wei8, Reference Topping36] suggest proximity to multi-bubbles cannot be achieved exclusively from energy considerations.
$u(t)$
starts close to, but then moves away from the family of multi-bubble configurations on some time interval). Roughly speaking, Theorem 1.8 reduces the questions in Remark 1.9 to an analysis of the dynamics of solutions close to the manifold of multi-bubble configurations. Note that [Reference Bernand-Mantel, Muratov and Simon1, Reference Deng, Sun and Wei8, Reference Topping36] suggest proximity to multi-bubbles cannot be achieved exclusively from energy considerations.
Remark 1.11. There are solutions to the HMHF that develop a bubbling singularity in finite time, the first being the examples of Coron and Ghidaglia [Reference Coron and Ghidaglia4] (in dimensions
![]() $\ge 3$
) and Chang, Ding and Ye [Reference Chang, Yue Ding and Ye3] in two dimensions. Guan, Gustafson and Tsai [Reference Guan, Gustafson and Tsai13] and Gustafson, Nakanishi and Tsai [Reference Gustafson, Nakanishi and Tsai14] showed that k-equivariant harmonic maps are asymptotically stable for perturbations within their equivariance classes when
$\ge 3$
) and Chang, Ding and Ye [Reference Chang, Yue Ding and Ye3] in two dimensions. Guan, Gustafson and Tsai [Reference Guan, Gustafson and Tsai13] and Gustafson, Nakanishi and Tsai [Reference Gustafson, Nakanishi and Tsai14] showed that k-equivariant harmonic maps are asymptotically stable for perturbations within their equivariance classes when
![]() $k \ge 3$
, and thus, there is no finite time blow-up for energies close to the harmonic map in that setting. For
$k \ge 3$
, and thus, there is no finite time blow-up for energies close to the harmonic map in that setting. For
![]() $k=2$
, [Reference Gustafson, Nakanishi and Tsai14] gave examples of solutions exhibiting infinite time blow-up and eternal oscillations, and recently, Wei, Zhang and Zhou [Reference Wei, Zhang and Zhou38] constructed such examples in the case
$k=2$
, [Reference Gustafson, Nakanishi and Tsai14] gave examples of solutions exhibiting infinite time blow-up and eternal oscillations, and recently, Wei, Zhang and Zhou [Reference Wei, Zhang and Zhou38] constructed such examples in the case
![]() $k=1$
. When
$k=1$
. When
![]() $k=1$
, the ground state harmonic map is unstable, as Topping [Reference Topping32] proved that there are solutions blowing up in finite time with any initial energy that is slightly above the ground state. Raphaël and Schweyer constructed a stable equivariant blow-up regime for
$k=1$
, the ground state harmonic map is unstable, as Topping [Reference Topping32] proved that there are solutions blowing up in finite time with any initial energy that is slightly above the ground state. Raphaël and Schweyer constructed a stable equivariant blow-up regime for
![]() $k=1$
in [Reference Raphaël and Schweyer25] and then equivariant blow-up solutions with different rates in [Reference Raphaël and Schweyer26]. Davila, Del Pino and Wei [Reference Dávila, del Pino and Wei6] constructed examples of solutions simultaneously concentrating a single copy of the ground state harmonic map at distinct points in space. See also the work of Topping on reverse bubbling [Reference Topping35] and on the existence of bubble towers [Reference Topping34], and the recent work of Del Pino, Musso and Wei [Reference del Pino, Musso and Wei7] for a construction of bubble towers with an arbitrary number of bubbles in the case of the critical semi-linear heat equation.
$k=1$
in [Reference Raphaël and Schweyer25] and then equivariant blow-up solutions with different rates in [Reference Raphaël and Schweyer26]. Davila, Del Pino and Wei [Reference Dávila, del Pino and Wei6] constructed examples of solutions simultaneously concentrating a single copy of the ground state harmonic map at distinct points in space. See also the work of Topping on reverse bubbling [Reference Topping35] and on the existence of bubble towers [Reference Topping34], and the recent work of Del Pino, Musso and Wei [Reference del Pino, Musso and Wei7] for a construction of bubble towers with an arbitrary number of bubbles in the case of the critical semi-linear heat equation.
1.3. Summary of the proof
We give an informal description of the proof of Theorem 1.8 and then we discuss how to deduce Theorem 1.1 from it.
To fix ideas, we consider a solution blowing up at a finite time
![]() $T_+< \infty $
. Theorem 1.8 is proved by contradicting the finiteness of the integral
$T_+< \infty $
. Theorem 1.8 is proved by contradicting the finiteness of the integral
 $$ \begin{align} \int_0^{T_+} \| \mathcal T( u(t)) \|_{L^2}^2 \, \mathrm{d} t < \infty \end{align} $$
$$ \begin{align} \int_0^{T_+} \| \mathcal T( u(t)) \|_{L^2}^2 \, \mathrm{d} t < \infty \end{align} $$
via a collision analysis in the event that the theorem fails. The collision analysis hinges on the notion of a minimal collision energy and the corresponding collision (time) intervals that accompany it. These are defined as follows (see Section 3.1). We let K be the smallest integer so that there exist time sequences
![]() $\sigma _n, \tau _n \to T_+$
, a sequence of discs
$\sigma _n, \tau _n \to T_+$
, a sequence of discs
![]() $D(y_n, \rho _n) \subset \mathbb {R}^2$
, a number
$D(y_n, \rho _n) \subset \mathbb {R}^2$
, a number
![]() $\eta>0$
and a sequence
$\eta>0$
and a sequence
![]() $\epsilon _n \to 0$
so that
$\epsilon _n \to 0$
so that
![]() $\boldsymbol {\delta }(u(\sigma _n); D( y_n, \rho _n)) \le \epsilon _n$
,
$\boldsymbol {\delta }(u(\sigma _n); D( y_n, \rho _n)) \le \epsilon _n$
,
![]() $\boldsymbol {\delta }( u(\tau _n); D(y_n, \rho _n)) \ge \eta $
, and
$\boldsymbol {\delta }( u(\tau _n); D(y_n, \rho _n)) \ge \eta $
, and
![]() $E( u( \sigma _n); D( y_n, \rho _n)) \to 4 K \pi $
as
$E( u( \sigma _n); D( y_n, \rho _n)) \to 4 K \pi $
as
![]() $n\to \infty $
. To ensure that K is well-defined and
$n\to \infty $
. To ensure that K is well-defined and
![]() $\ge 1$
in the event that theorem fails (see Lemma 3.3), we also require that
$\ge 1$
in the event that theorem fails (see Lemma 3.3), we also require that
![]() $|[\sigma _n, \tau _n]| \le \epsilon _n \rho _n^2$
. We emphasize that the quantization of the energy of harmonic maps
$|[\sigma _n, \tau _n]| \le \epsilon _n \rho _n^2$
. We emphasize that the quantization of the energy of harmonic maps
![]() $\mathbb {R}^2 \to \mathbb {S}^2$
is used to define K as above. Roughly speaking, the intervals
$\mathbb {R}^2 \to \mathbb {S}^2$
is used to define K as above. Roughly speaking, the intervals
![]() $I_n :=[\sigma _n, \tau _n]$
have the property that u is close to a multi-bubble configuration on the left endpoint
$I_n :=[\sigma _n, \tau _n]$
have the property that u is close to a multi-bubble configuration on the left endpoint
![]() $t = \sigma _n$
(which we call bubbling times) and far from every multi-bubble at the right endpoint
$t = \sigma _n$
(which we call bubbling times) and far from every multi-bubble at the right endpoint
![]() $t = \tau _n$
(which we call ejection times).
$t = \tau _n$
(which we call ejection times).
The minimality of K is used crucially to relate the lengths of the collision intervals
![]() $|I_n|$
to the largest scale of the bubbles involved in the collision (i.e., those bubbles that concentrate within the discs
$|I_n|$
to the largest scale of the bubbles involved in the collision (i.e., those bubbles that concentrate within the discs
![]() $D(y_n, \rho _n)$
). We call this largest scale
$D(y_n, \rho _n)$
). We call this largest scale
![]() $\lambda _{\max , n}$
, and the key Lemma 3.4 shows (roughly) that every sequence of collision intervals
$\lambda _{\max , n}$
, and the key Lemma 3.4 shows (roughly) that every sequence of collision intervals
![]() $I_n$
has subintervals
$I_n$
has subintervals
![]() $J_n$
of length at least
$J_n$
of length at least
on which
![]() $u(t)$
bounded away from the multi-bubble family (i.e,.
$u(t)$
bounded away from the multi-bubble family (i.e,.
![]() $\boldsymbol {\delta }( u(t); D(y_n, \rho _n)) \ge \epsilon>0$
for all
$\boldsymbol {\delta }( u(t); D(y_n, \rho _n)) \ge \epsilon>0$
for all
![]() $t \in J_n$
, for some
$t \in J_n$
, for some
![]() $\epsilon>0$
). The intuition behind this is the following. Suppose there were a sequence of intervals
$\epsilon>0$
). The intuition behind this is the following. Suppose there were a sequence of intervals
![]() $J_n = [s_n, t_n] \subset I_n$
for which the
$J_n = [s_n, t_n] \subset I_n$
for which the
![]() $s_n$
’s are bubbling times and the
$s_n$
’s are bubbling times and the
![]() $t_n$
’s are ejection times, but
$t_n$
’s are ejection times, but
![]() $|J_n| \ll \lambda _{\max , n}^2$
. This leads to a contradiction of the minimality of K because the time-interval
$|J_n| \ll \lambda _{\max , n}^2$
. This leads to a contradiction of the minimality of K because the time-interval
![]() $J_n$
is too short relative to the scales of the largest bubbles (
$J_n$
is too short relative to the scales of the largest bubbles (
![]() $\lambda _{\max , n}$
) for them to become involved in a collision; thus, collisions are captured on smaller discs
$\lambda _{\max , n}$
) for them to become involved in a collision; thus, collisions are captured on smaller discs
![]() $D(\widetilde y_n, \widetilde \rho _n) \subset D(y_n, \rho _n)$
with
$D(\widetilde y_n, \widetilde \rho _n) \subset D(y_n, \rho _n)$
with
![]() $\widetilde \rho _n \ll \lambda _{\max , n}$
, and these carry strictly less energy than
$\widetilde \rho _n \ll \lambda _{\max , n}$
, and these carry strictly less energy than
![]() $4 \pi K$
; see the proof of Lemma 3.4.
$4 \pi K$
; see the proof of Lemma 3.4.
The fact that
![]() $u(t)$
is at least distance
$u(t)$
is at least distance
![]() $\epsilon>0$
away from the multi-bubble family on
$\epsilon>0$
away from the multi-bubble family on
![]() $J_n$
can be combined with the classical localized elliptic bubbling lemma described in Section 1.1 (the Compactness Lemma 2.15) to show that on the interval
$J_n$
can be combined with the classical localized elliptic bubbling lemma described in Section 1.1 (the Compactness Lemma 2.15) to show that on the interval
![]() $J_n$
, the tension satisfies
$J_n$
, the tension satisfies
The main point here is that the Compactness Lemma 2.15 says that
![]() $u(t)$
bubbles at scale
$u(t)$
bubbles at scale
![]() $\lambda _{\max , n}$
along any sequence of times
$\lambda _{\max , n}$
along any sequence of times
![]() $\widetilde s_n$
for which
$\widetilde s_n$
for which
![]() $\lim _{n \to \infty } \lambda _{\max , n}^2\| \mathcal T(u(\widetilde s_n)) \|_{L^2}^2 = 0$
, which is impossible. At this point, we have contradicted (1.28) since the previous two displayed equations combine to give
$\lim _{n \to \infty } \lambda _{\max , n}^2\| \mathcal T(u(\widetilde s_n)) \|_{L^2}^2 = 0$
, which is impossible. At this point, we have contradicted (1.28) since the previous two displayed equations combine to give
 $$ \begin{align} \sum_n \int_{J_n} \| \mathcal T( u(t)) \|_{L^2}^2 \, \mathrm{d} t \gtrsim \sum_n \left\lvert{J_n}\right\rvert \lambda_{\max, n}^{-2} \gtrsim \sum_n 1 = \infty. \end{align} $$
$$ \begin{align} \sum_n \int_{J_n} \| \mathcal T( u(t)) \|_{L^2}^2 \, \mathrm{d} t \gtrsim \sum_n \left\lvert{J_n}\right\rvert \lambda_{\max, n}^{-2} \gtrsim \sum_n 1 = \infty. \end{align} $$
The idea of a (minimal) collision energy and associated collision time intervals are related to analogous concepts in the first two authors’ work on the soliton resolution conjecture for nonlinear waves and on continuous bubbling for the k-equivariant HMHF; see [Reference Jendrej and Lawrie16, Reference Jendrej and Lawrie17, Reference Jendrej and Lawrie18]. Unlike in these earlier works, we do not use modulation analysis in this paper.
Theorem 1.8 and the Compactness Lemma 2.15 are the main ingredients in the proof of Theorem 1.1. Again, focusing on the finite time blow-up case, it is well-known (see Lemma 2.13) that energy does not concentrate at or outside the self-similar scale
![]() $\sqrt {T_+-t}$
, so it suffices to examine the behavior of
$\sqrt {T_+-t}$
, so it suffices to examine the behavior of
![]() $u(t)$
restricted to discs
$u(t)$
restricted to discs
![]() $D( y, \sqrt {T_+-t})$
, for
$D( y, \sqrt {T_+-t})$
, for
![]() $y \in \mathbb {R}^2$
a point where energy concentrates. Let
$y \in \mathbb {R}^2$
a point where energy concentrates. Let
![]() $t_n \to T_+$
be any time sequence. By Theorem 1.8, and after passing to a subsequence, there exists an integer
$t_n \to T_+$
be any time sequence. By Theorem 1.8, and after passing to a subsequence, there exists an integer
![]() $ \widetilde M \ge 1$
and a sequence of M-bubble configurations
$ \widetilde M \ge 1$
and a sequence of M-bubble configurations
![]() $\boldsymbol {\Omega }_{n} = (\Omega _n, \Omega _{1, n}, \dots , \Omega _{\widetilde M, n})$
and sequences
$\boldsymbol {\Omega }_{n} = (\Omega _n, \Omega _{1, n}, \dots , \Omega _{\widetilde M, n})$
and sequences
![]() $\vec \xi _n, \vec \nu _n$
as in Definition 1.6 so that
$\vec \xi _n, \vec \nu _n$
as in Definition 1.6 so that
However, the decomposition in Theorem 1.1 involves a fixed collection of finitely many harmonic maps,
![]() $\omega _1, \dots , \omega _M$
(i.e., a collection independent of n). To find such a collection from the
$\omega _1, \dots , \omega _M$
(i.e., a collection independent of n). To find such a collection from the
![]() $\Omega _{j, n}$
we apply the Compactness Lemma 2.15 to each
$\Omega _{j, n}$
we apply the Compactness Lemma 2.15 to each
![]() $\Omega _{j, n}$
, obtaining a fixed collection of bubbles
$\Omega _{j, n}$
, obtaining a fixed collection of bubbles
![]() $\{\omega _{j, k}\}_{k =1}^{L_j}$
for each
$\{\omega _{j, k}\}_{k =1}^{L_j}$
for each
![]() $j \in \{1, \dots , \widetilde M\}$
. A delicate point is that the scales and centers
$j \in \{1, \dots , \widetilde M\}$
. A delicate point is that the scales and centers
![]() $(b_{j, k, n}, \mu _{j, k, n})$
associated to the harmonic maps
$(b_{j, k, n}, \mu _{j, k, n})$
associated to the harmonic maps
![]() $\omega _{j, k}$
given by the Compactness Lemma 2.15 may not satisfy (1.6) for distinct j. But this potential pitfall is remedied by the refined information in Theorem 1.8, which says
$\omega _{j, k}$
given by the Compactness Lemma 2.15 may not satisfy (1.6) for distinct j. But this potential pitfall is remedied by the refined information in Theorem 1.8, which says
![]() $u(t)$
approaches the multi-bubble family at every smaller scale
$u(t)$
approaches the multi-bubble family at every smaller scale
![]() $\rho _n \le \sqrt {T_+-t_n}$
(excluding of course the precise scales of the bubbles themselves).
$\rho _n \le \sqrt {T_+-t_n}$
(excluding of course the precise scales of the bubbles themselves).
In Section 2, we give background information on harmonic maps and the harmonic map heat flow. Much of Section 2 is classical, except perhaps the notions of scale and center of harmonic maps and Lemma 2.12, which involves the propagation of localized
![]() $L^\infty $
estimates for solutions to (1.2), which we did not find a reference for in the literature. Section 3 contains the proofs of the main theorems.
$L^\infty $
estimates for solutions to (1.2), which we did not find a reference for in the literature. Section 3 contains the proofs of the main theorems.
1.4. Notational conventions
Constants are denoted
![]() $C, C_0, C_1, c, c_0, c_1$
. We write
$C, C_0, C_1, c, c_0, c_1$
. We write
![]() $A \lesssim B$
if
$A \lesssim B$
if
![]() $A \leq CB$
and
$A \leq CB$
and
![]() $A \gtrsim B$
if
$A \gtrsim B$
if
![]() $A \geq cB$
. Given sequences
$A \geq cB$
. Given sequences
![]() $A_n, B_n$
, we write
$A_n, B_n$
, we write
![]() $A_n \ll B_n$
if
$A_n \ll B_n$
if
![]() $\lim _{n\to \infty } A_n / B_n = 0$
.
$\lim _{n\to \infty } A_n / B_n = 0$
.
For any sets
![]() $X, Y, Z$
, we identify
$X, Y, Z$
, we identify
![]() $Z^{X\times Y}$
with
$Z^{X\times Y}$
with
![]() $(Z^Y)^X$
, which means that if
$(Z^Y)^X$
, which means that if
![]() $\phi : X\times Y \to Z$
is a function, then for any
$\phi : X\times Y \to Z$
is a function, then for any
![]() $x \in X$
, we can view
$x \in X$
, we can view
![]() $\phi (x)$
as a function
$\phi (x)$
as a function
![]() $Y \to Z$
given by
$Y \to Z$
given by
![]() $(\phi (x))(y) := \phi (x, y)$
.
$(\phi (x))(y) := \phi (x, y)$
.
2. Preliminaries
2.1. Properties of harmonic maps
We use a few well-known features of finite energy harmonic maps
![]() $\omega : \mathbb {R}^2 \to \mathbb {S}^2$
– namely, their smoothness, the invariance of harmonicity and the energy under conformal transformations of the domain, and the fact that the energy is quantized.
$\omega : \mathbb {R}^2 \to \mathbb {S}^2$
– namely, their smoothness, the invariance of harmonicity and the energy under conformal transformations of the domain, and the fact that the energy is quantized.
Theorem 2.1. [Reference Hélein and Eells15, Theorem 4.1.1][Reference Eells and Sampson12, pg. 126, Proposition][Reference Sacks and Uhlenbeck27, Theorem 3.6] [Reference Lemaire19, Section 8, the Remarque on pg. 65]
Let
![]() $\omega :\mathbb {R}^2\to \mathbb S^2$
be a weak non-constant solution to (1.5) of finite energy. Then
$\omega :\mathbb {R}^2\to \mathbb S^2$
be a weak non-constant solution to (1.5) of finite energy. Then
![]() $\omega $
is smooth and extends as a smooth harmonic map from the sphere to itself of nonzero degree, which minimizes the energy (1.1) in its degree class with
$\omega $
is smooth and extends as a smooth harmonic map from the sphere to itself of nonzero degree, which minimizes the energy (1.1) in its degree class with
![]() $E(\omega )=4\pi |\deg (\omega )|$
.
$E(\omega )=4\pi |\deg (\omega )|$
.
Remark 2.2. The regularity statement above is due to Hélein and holds in the more general setting of weak harmonic maps
![]() $\omega \in H^1(\mathcal M, \mathcal N)$
, where
$\omega \in H^1(\mathcal M, \mathcal N)$
, where
![]() $\mathcal M$
is a closed, two-dimensional, orientable Riemannian manifold and
$\mathcal M$
is a closed, two-dimensional, orientable Riemannian manifold and
![]() $\mathcal N$
is a smooth compact Riemannian manifold. The extension of a smooth, finite energy harmonic map
$\mathcal N$
is a smooth compact Riemannian manifold. The extension of a smooth, finite energy harmonic map
![]() $\omega : \mathbb {R}^2 \to \mathbb {S}^2$
to a smooth, finite energy harmonic map
$\omega : \mathbb {R}^2 \to \mathbb {S}^2$
to a smooth, finite energy harmonic map
![]() $\widetilde \omega : \mathbb {S}^2 \to \mathbb {S}^2$
is a consequence of the conformal equivalence between
$\widetilde \omega : \mathbb {S}^2 \to \mathbb {S}^2$
is a consequence of the conformal equivalence between
![]() $\mathbb {R}^2$
and
$\mathbb {R}^2$
and
![]() $\mathbb {S}^2\setminus \{p_0\}$
via the stereographic projection map and the Removable Singularity Theorem of Sacks-Uhlenbeck [Reference Sacks and Uhlenbeck27]. Here we also use the fact, due to Eells and Sampson [Reference Eells and Sampson12], that in the case of orientable two-dimensional Riemannian manifolds
$\mathbb {S}^2\setminus \{p_0\}$
via the stereographic projection map and the Removable Singularity Theorem of Sacks-Uhlenbeck [Reference Sacks and Uhlenbeck27]. Here we also use the fact, due to Eells and Sampson [Reference Eells and Sampson12], that in the case of orientable two-dimensional Riemannian manifolds
![]() $\mathcal M, \mathcal N$
, if
$\mathcal M, \mathcal N$
, if
![]() $\omega : \mathcal M \to \mathcal N$
is smooth and
$\omega : \mathcal M \to \mathcal N$
is smooth and
![]() $\phi : \mathcal M \to \mathcal M$
is a conformal diffeomorphism, then
$\phi : \mathcal M \to \mathcal M$
is a conformal diffeomorphism, then
![]() $\omega \circ \phi $
is harmonic if and only if
$\omega \circ \phi $
is harmonic if and only if
![]() $\omega $
is, and moreover,
$\omega $
is, and moreover,
![]() $E( \omega ) = E(\omega \circ \phi )$
. The relationship between the topological degree and the energy (energy quantization) generalizes to harmonic maps between closed, two-dimensional, orientable, Riemannian manifolds
$E( \omega ) = E(\omega \circ \phi )$
. The relationship between the topological degree and the energy (energy quantization) generalizes to harmonic maps between closed, two-dimensional, orientable, Riemannian manifolds
![]() $\omega : \mathcal M \to \mathcal N$
, where we have
$\omega : \mathcal M \to \mathcal N$
, where we have
![]() $E( \omega ) = \mathrm {Area}(\mathcal N)|\deg (\omega )|$
; see, for example, Lemaire [Reference Lemaire19, Section 8, the Remarque on pg. 65].
$E( \omega ) = \mathrm {Area}(\mathcal N)|\deg (\omega )|$
; see, for example, Lemaire [Reference Lemaire19, Section 8, the Remarque on pg. 65].
2.1.1. The scale and center of a harmonic map
Given a non-constant harmonic map
![]() $\omega :\mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
, recall the notion of scale
$\omega :\mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
, recall the notion of scale
![]() $\lambda ( \omega; \gamma _0)$
and center
$\lambda ( \omega; \gamma _0)$
and center
![]() $a(\omega; \gamma _0)$
from Definition 1.3 and Defintion 1.4.
$a(\omega; \gamma _0)$
from Definition 1.3 and Defintion 1.4.
Lemma 2.3 (Center and scale).
Let
![]() $\gamma _0 \in (0, 2\pi )$
and let
$\gamma _0 \in (0, 2\pi )$
and let
![]() $\omega : \mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
be a non-constant harmonic map. Then
$\omega : \mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
be a non-constant harmonic map. Then
![]() $\lambda (\omega ) = \lambda (\omega , \gamma _0)$
as in Definition 1.3 is uniquely defined and strictly positive. Moreover, there exists
$\lambda (\omega ) = \lambda (\omega , \gamma _0)$
as in Definition 1.3 is uniquely defined and strictly positive. Moreover, there exists
![]() $a(\omega ) = a(\omega , \gamma _0)$
as in Definition 1.4. For all
$a(\omega ) = a(\omega , \gamma _0)$
as in Definition 1.4. For all
![]() $b \in \mathbb {R}^2$
and
$b \in \mathbb {R}^2$
and
![]() $\mu \in (0, \infty )$
,
$\mu \in (0, \infty )$
,
Proof. Since
![]() $E(\omega ;D(0,R))\to E(\omega )$
as
$E(\omega ;D(0,R))\to E(\omega )$
as
![]() $R\to \infty $
, it follows that the scale
$R\to \infty $
, it follows that the scale
![]() $\lambda (\omega )$
is well-defined. If
$\lambda (\omega )$
is well-defined. If
![]() $\lambda ( \omega )=0$
, then there exists
$\lambda ( \omega )=0$
, then there exists
![]() $a_n\in \mathbb {R}^2$
so that
$a_n\in \mathbb {R}^2$
so that
If
![]() $n\ne m$
, the
$n\ne m$
, the
![]() $D(a_n, 1/n)\cap D(a_m, 1/m)\ne \emptyset $
. Indeed, otherwise,
$D(a_n, 1/n)\cap D(a_m, 1/m)\ne \emptyset $
. Indeed, otherwise,
whence
![]() $E(\omega )\le 2\gamma _0< 4\pi $
, which contradicts that
$E(\omega )\le 2\gamma _0< 4\pi $
, which contradicts that
![]() $\omega $
is not constant. Therefore,
$\omega $
is not constant. Therefore,
![]() $\{a_n\}_{n=1}^\infty $
is a Cauchy sequence in
$\{a_n\}_{n=1}^\infty $
is a Cauchy sequence in
![]() $\mathbb {R}^2$
, and
$\mathbb {R}^2$
, and
![]() $a_n\to a_\infty $
. Passing to the limit in (2.2) gives a contradiction.
$a_n\to a_\infty $
. Passing to the limit in (2.2) gives a contradiction.
To see that a center
![]() $a(\omega )$
can be chosen, take
$a(\omega )$
can be chosen, take
![]() $\lambda _n\to \lambda (\omega )$
and
$\lambda _n\to \lambda (\omega )$
and
![]() $a_n\in \mathbb {R}^2$
such that
$a_n\in \mathbb {R}^2$
such that
As before, we conclude that no two disks
![]() $\{D( a_n, \lambda _n)\}_{n=1}^\infty $
can be disjoint. Thus,
$\{D( a_n, \lambda _n)\}_{n=1}^\infty $
can be disjoint. Thus,
![]() $a_n\in \mathbb {R}^2$
lie in a compact set, and we may assume that
$a_n\in \mathbb {R}^2$
lie in a compact set, and we may assume that
![]() $a_n\to a_\infty $
as
$a_n\to a_\infty $
as
![]() $n\to \infty $
, which is a desired center. We note that
$n\to \infty $
, which is a desired center. We note that
![]() $\lambda ( \omega )$
is uniquely defined, but
$\lambda ( \omega )$
is uniquely defined, but
![]() $a(\omega )$
is defined only up to a distance of
$a(\omega )$
is defined only up to a distance of
![]() $2\lambda ( \omega )$
. The properties (2.1) are immediate from the definitions.
$2\lambda ( \omega )$
. The properties (2.1) are immediate from the definitions.
Lemma 2.4 (Decay of harmonic maps).
There exists
![]() $\gamma _0 \in (0, 2 \pi )$
with the following property. For any
$\gamma _0 \in (0, 2 \pi )$
with the following property. For any
![]() $0<\gamma \le \gamma _0$
and any harmonic map
$0<\gamma \le \gamma _0$
and any harmonic map
![]() $\omega : \mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
, the exterior energy decays at the following rate:
$\omega : \mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
, the exterior energy decays at the following rate:
for all
![]() $R \ge 2$
.
$R \ge 2$
.
We use the following
![]() $\epsilon $
-compactness result of Ding and Tian [Reference Ding and Tian9] in the proof of Lemma 2.4.
$\epsilon $
-compactness result of Ding and Tian [Reference Ding and Tian9] in the proof of Lemma 2.4.
Lemma 2.5 (
 $\epsilon $
-compactness).
$\epsilon $
-compactness).
[Reference Ding and Tian9, Lemma 2.1] Let
![]() $y \in \mathbb {R}^2$
and let
$y \in \mathbb {R}^2$
and let
![]() $u:D(y, 1) \to \mathbb {S}^2 \subset \mathbb {R}^3$
belong to the class
$u:D(y, 1) \to \mathbb {S}^2 \subset \mathbb {R}^3$
belong to the class
![]() $W^{2, 2}(D(y, 1); \mathbb {S}^2)$
. Then there exists
$W^{2, 2}(D(y, 1); \mathbb {S}^2)$
. Then there exists
![]() $\epsilon _0>0, C>0$
such that if
$\epsilon _0>0, C>0$
such that if
![]() $E(u; D(y, 1)) < \epsilon _0$
, then
$E(u; D(y, 1)) < \epsilon _0$
, then
where
![]() $u_{\operatorname {avg}}$
denotes the mean of u over the disc
$u_{\operatorname {avg}}$
denotes the mean of u over the disc
![]() $D(y, 1)$
. In particular,
$D(y, 1)$
. In particular,
Proof of Lemma 2.4.
With loss of generality,
![]() $a(\omega; \gamma )=0$
and
$a(\omega; \gamma )=0$
and
![]() $\lambda (\omega; \gamma )=1$
. Consider the harmonic map
$\lambda (\omega; \gamma )=1$
. Consider the harmonic map
![]() $\tilde \omega (z)=\omega (1/z)$
for which
$\tilde \omega (z)=\omega (1/z)$
for which
![]() $0$
is a removable singularity (see [Reference Sacks and Uhlenbeck27]) and
$0$
is a removable singularity (see [Reference Sacks and Uhlenbeck27]) and
![]() $E(\tilde \omega ;D(0;1))\le \gamma $
. Applying Lemma 2.5, we conclude that
$E(\tilde \omega ;D(0;1))\le \gamma $
. Applying Lemma 2.5, we conclude that
whence
![]() $\tilde \omega \in W^{1,p}(D(0,1/2))$
for any
$\tilde \omega \in W^{1,p}(D(0,1/2))$
for any
![]() $2<p<\infty $
. From the equation
$2<p<\infty $
. From the equation
![]() $\Delta \tilde \omega +\tilde \omega |\nabla \tilde \omega |^2=0$
, it follows that
$\Delta \tilde \omega +\tilde \omega |\nabla \tilde \omega |^2=0$
, it follows that
![]() $D^2 \tilde \omega \in L^p(D(0,1/2))$
for any
$D^2 \tilde \omega \in L^p(D(0,1/2))$
for any
![]() $2<p<\infty $
. In particular, there exists an absolute constant
$2<p<\infty $
. In particular, there exists an absolute constant
![]() $\gamma _0>0$
such that
$\gamma _0>0$
such that
![]() $0< \gamma \le \gamma _0$
ensures that
$0< \gamma \le \gamma _0$
ensures that
whence
![]() $E(\omega ,\mathbb {R}^2\setminus D(0,1/r))=E(\tilde \omega ,D(0,r))\le \pi r^2$
for all
$E(\omega ,\mathbb {R}^2\setminus D(0,1/r))=E(\tilde \omega ,D(0,r))\le \pi r^2$
for all
![]() $r\le \frac 12$
.
$r\le \frac 12$
.
Lemma 2.6 (Energy of multi-bubbles).
Let
![]() $y_n \in \mathbb {R}^2$
,
$y_n \in \mathbb {R}^2$
,
![]() $\rho _n>0$
be sequences, and
$\rho _n>0$
be sequences, and
![]() $M \in \mathbb {N}$
. Let
$M \in \mathbb {N}$
. Let
![]() $\omega _\infty \in \mathbb {S}^2$
be a constant, let
$\omega _\infty \in \mathbb {S}^2$
be a constant, let
![]() $\omega _{1}, \dots , \omega _{M}$
be nontrivial harmonic maps, and let
$\omega _{1}, \dots , \omega _{M}$
be nontrivial harmonic maps, and let
![]() $b_{n, j} \in D( y_n, \rho _n)$
and
$b_{n, j} \in D( y_n, \rho _n)$
and
![]() $\mu _{n ,j} \in (0, \infty )$
for
$\mu _{n ,j} \in (0, \infty )$
for
![]() $j \in \{1, \dots , M\}$
be sequences so that
$j \in \{1, \dots , M\}$
be sequences so that
 $$ \begin{align} \lim_{n \to \infty} \Bigg[\sum_{j \neq k} \bigg( \frac{\mu_{n, j}}{\mu_{n, k} } + \frac{\mu_{n, k}}{\mu_{n, j}} + \frac{| b_{n, j} - b_{n, k}|}{\mu_{n, j}} \bigg)^{-1} + \sum_{j=1}^{M} \frac{\mu_{n, j}}{ \operatorname{dist}(b_{n, j}, \partial D(y_n, \rho_n))} \Bigg] = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \Bigg[\sum_{j \neq k} \bigg( \frac{\mu_{n, j}}{\mu_{n, k} } + \frac{\mu_{n, k}}{\mu_{n, j}} + \frac{| b_{n, j} - b_{n, k}|}{\mu_{n, j}} \bigg)^{-1} + \sum_{j=1}^{M} \frac{\mu_{n, j}}{ \operatorname{dist}(b_{n, j}, \partial D(y_n, \rho_n))} \Bigg] = 0. \end{align} $$
Then
 $$ \begin{align} \lim_{n \to \infty} E\Big( \mathcal Q\big(\omega_{\infty}, \omega_{1} \big( \frac{\cdot - b_{n, 1}}{\mu_{n, 1}}\big), \dots, \omega_{M}\big( \frac{\cdot - b_{n, M}}{\mu_{n, M}}\big)\big); D( y_n, \rho_n)\Big) = \sum_{j =1}^M E( \omega_j). \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( \mathcal Q\big(\omega_{\infty}, \omega_{1} \big( \frac{\cdot - b_{n, 1}}{\mu_{n, 1}}\big), \dots, \omega_{M}\big( \frac{\cdot - b_{n, M}}{\mu_{n, M}}\big)\big); D( y_n, \rho_n)\Big) = \sum_{j =1}^M E( \omega_j). \end{align} $$
Proof of Lemma 2.6.
To simplify notation within the proof, we use the shorthand
![]() $\omega _{n, j} = \omega _j\big ( \frac {\cdot - b_{n, j}}{\mu _{n, j}} \big )$
. Expanding the energy, we obtain
$\omega _{n, j} = \omega _j\big ( \frac {\cdot - b_{n, j}}{\mu _{n, j}} \big )$
. Expanding the energy, we obtain
 $$ \begin{align*} E( \mathcal Q(\omega_{n, 1}, \dots, \omega_{n, M}); D( y_n, \rho_n)) = \sum_{j=1}^M E(\omega_{n, j}; D( y_n, \rho_n)) + \frac12\sum_{j\ne k } \int_{D(y_n,\rho_n)} \nabla \omega_{n, j}\nabla \omega_{n, k}. \end{align*} $$
$$ \begin{align*} E( \mathcal Q(\omega_{n, 1}, \dots, \omega_{n, M}); D( y_n, \rho_n)) = \sum_{j=1}^M E(\omega_{n, j}; D( y_n, \rho_n)) + \frac12\sum_{j\ne k } \int_{D(y_n,\rho_n)} \nabla \omega_{n, j}\nabla \omega_{n, k}. \end{align*} $$
By the separation condition (2.6) with respect to
![]() $\partial D(y_n,\rho _n)$
and Lemma 2.4,
$\partial D(y_n,\rho _n)$
and Lemma 2.4,
as
![]() $n\to \infty $
. However, if
$n\to \infty $
. However, if
![]() $j\ne k$
, then
$j\ne k$
, then
 $$ \begin{align} \Big| \int_{D(y_n,\rho_n)} \nabla \omega_{n, j}\nabla \omega_{n, k} \Big| \le \int |\nabla \omega_{n, j}| |\nabla \omega_{n, k}| = o_n(1) \end{align} $$
$$ \begin{align} \Big| \int_{D(y_n,\rho_n)} \nabla \omega_{n, j}\nabla \omega_{n, k} \Big| \le \int |\nabla \omega_{n, j}| |\nabla \omega_{n, k}| = o_n(1) \end{align} $$
by the first term of (2.6).
2.2. Properties of the harmonic map heat flow
2.2.1. Well-posedness
The starting point for our analysis of the HMHF is the classical result of Struwe [Reference Struwe28], which says that the initial value problem is well-posed for data in the energy space and solutions are regular up to their maximal time.
Following Struwe, we introduce the space,
 $$ \begin{align} \mathcal V_{\tau}^T:= \Big\{& u: [\tau, T] \times \mathbb{R}^2 \to \mathbb{S}^2 \subset \mathbb{R}^3 \mid \, u\, \, \textrm{is measurable, and } \nonumber\\ &\quad \sup_{t \in [\tau, T]} E( u(t)) + \int_{\tau}^T \|\partial_t u(t)\|_{L^2}^2 + \| \nabla^2 u(t)\|_{L^2}^2 \, \mathrm{d} t < \infty \Big\}. \end{align} $$
$$ \begin{align} \mathcal V_{\tau}^T:= \Big\{& u: [\tau, T] \times \mathbb{R}^2 \to \mathbb{S}^2 \subset \mathbb{R}^3 \mid \, u\, \, \textrm{is measurable, and } \nonumber\\ &\quad \sup_{t \in [\tau, T]} E( u(t)) + \int_{\tau}^T \|\partial_t u(t)\|_{L^2}^2 + \| \nabla^2 u(t)\|_{L^2}^2 \, \mathrm{d} t < \infty \Big\}. \end{align} $$
We use the shorthand
![]() $\mathcal V^T = \mathcal V_0^T$
.
$\mathcal V^T = \mathcal V_0^T$
.
Theorem 2.7 (Local well-posedness).
[Reference Struwe28, Theorem 4.1] Let
![]() $u_0 \in \mathcal {E}$
. Then there exists a maximal time of existence
$u_0 \in \mathcal {E}$
. Then there exists a maximal time of existence
![]() $T_+= T_+(u_0)$
and a unique solution
$T_+= T_+(u_0)$
and a unique solution
![]() $u \in \bigcap _{T < T_+} \mathcal V^T$
to (1.2) with
$u \in \bigcap _{T < T_+} \mathcal V^T$
to (1.2) with
![]() $u(0)= u_0$
. The solution
$u(0)= u_0$
. The solution
![]() $u(t)$
is regular (e.g.,
$u(t)$
is regular (e.g.,
![]() $C^2$
) on the open interval
$C^2$
) on the open interval
![]() $(0, T_+)$
.
$(0, T_+)$
.
A finite maximal time
![]() $T_+< \infty $
is characterized by the existence of an integer
$T_+< \infty $
is characterized by the existence of an integer
![]() $L \ge 1$
, a number
$L \ge 1$
, a number
![]() $\epsilon _0>0$
and points
$\epsilon _0>0$
and points
![]() $\{x_{\ell }\}_{\ell =1}^L \subset \mathbb {R}^2$
such that
$\{x_{\ell }\}_{\ell =1}^L \subset \mathbb {R}^2$
such that
The
![]() $\{x_{\ell }\}_{\ell =1}^L$
are called bubbling points, and there are at most finitely many. There exists a finite energy mapping
$\{x_{\ell }\}_{\ell =1}^L$
are called bubbling points, and there are at most finitely many. There exists a finite energy mapping
![]() $u^*: \mathbb {R}^2 \to \mathbb {S}^2$
, called the body map, such that
$u^*: \mathbb {R}^2 \to \mathbb {S}^2$
, called the body map, such that
![]() $u(t) \rightharpoonup u^*$
as
$u(t) \rightharpoonup u^*$
as
![]() $t \to T_+$
weakly in
$t \to T_+$
weakly in
![]() $H^1( \mathbb {R}^2; \mathbb {S}^2)$
and strongly in
$H^1( \mathbb {R}^2; \mathbb {S}^2)$
and strongly in
![]() $H^1_{\mathrm {loc}}( \mathbb {R}^2 \setminus \{x_{\ell }\}_{\ell =1}^L; \mathbb {S}^2)$
.
$H^1_{\mathrm {loc}}( \mathbb {R}^2 \setminus \{x_{\ell }\}_{\ell =1}^L; \mathbb {S}^2)$
.
The energy
![]() $E(u(t))$
is continuous and nonincreasing as a function of
$E(u(t))$
is continuous and nonincreasing as a function of
![]() $t \in [0, T_+)$
, and for any
$t \in [0, T_+)$
, and for any
![]() $t_1 \le t_2 \in [0, T_+)$
, there holds
$t_1 \le t_2 \in [0, T_+)$
, there holds
 $$ \begin{align} E(u(t_2)) + \int_{t_1}^{t_2} \| \mathcal T(u(t)) \|_{L^2}^2\, \mathrm{d} t = E(u(t_1)). \end{align} $$
$$ \begin{align} E(u(t_2)) + \int_{t_1}^{t_2} \| \mathcal T(u(t)) \|_{L^2}^2\, \mathrm{d} t = E(u(t_1)). \end{align} $$
In particular, there exists
![]() $E_+:= \lim _{t \to T_+} E( u(t))$
, and
$E_+:= \lim _{t \to T_+} E( u(t))$
, and
 $$ \begin{align} \int_0^{T_+}\| \mathcal T(u(t)) \|_{L^2}^2\, \mathrm{d} t < \infty. \end{align} $$
$$ \begin{align} \int_0^{T_+}\| \mathcal T(u(t)) \|_{L^2}^2\, \mathrm{d} t < \infty. \end{align} $$
Remark 2.8. Lemma 2.7 is proved by Struwe for the HMHF in the case of maps from a closed Riemannian surface
![]() $\mathcal M$
to a compact Riemannian manifold
$\mathcal M$
to a compact Riemannian manifold
![]() $\mathcal N$
; see [Reference Struwe28, Theorem 4.1]. The same arguments hold for
$\mathcal N$
; see [Reference Struwe28, Theorem 4.1]. The same arguments hold for
![]() $\mathcal M= \mathbb {R}^2$
.
$\mathcal M= \mathbb {R}^2$
.
Lemma 2.9 (Localized energy inequality).
There exists a constant
![]() $C>0$
with the following property. Let
$C>0$
with the following property. Let
![]() $u(t)$
be a solution to (1.2) with initial data
$u(t)$
be a solution to (1.2) with initial data
![]() $u_0$
as in Lemma 2.7, on its maximal interval
$u_0$
as in Lemma 2.7, on its maximal interval
![]() $I_{\max } = [0, T_+)$
. Let
$I_{\max } = [0, T_+)$
. Let
![]() $0 < t_1 < t_2 < T_+$
. Let
$0 < t_1 < t_2 < T_+$
. Let
![]() $R>0$
,
$R>0$
,
![]() $\phi \in C^{\infty }_0(\mathbb {R}^2)$
satisfy
$\phi \in C^{\infty }_0(\mathbb {R}^2)$
satisfy
![]() $0 \le \phi (x) \le 1$
and
$0 \le \phi (x) \le 1$
and
![]() $\left \lvert {\nabla \phi }\right \rvert \le R^{-1}$
. Then
$\left \lvert {\nabla \phi }\right \rvert \le R^{-1}$
. Then
and
Proof of Lemma 2.9.
Take the dot product of the equation (1.2) with
![]() $\partial _t u \phi ^2$
and integrate by parts to obtain the identity
$\partial _t u \phi ^2$
and integrate by parts to obtain the identity
 $$ \begin{align} \| \partial_t u(t) \phi \|_{L^2}^2 + \frac{1}{2} \frac{\mathrm{d}}{\mathrm{d} t} \| \nabla u(t) \phi \|_{L^2}^2 = - \sum_{j =1}^2 \int_{\mathbb{R}^2} \partial_j u(t, x) \cdot \partial_t u(t, x) \partial_j \phi(x) \phi(x) \, \mathrm{d} x. \end{align} $$
$$ \begin{align} \| \partial_t u(t) \phi \|_{L^2}^2 + \frac{1}{2} \frac{\mathrm{d}}{\mathrm{d} t} \| \nabla u(t) \phi \|_{L^2}^2 = - \sum_{j =1}^2 \int_{\mathbb{R}^2} \partial_j u(t, x) \cdot \partial_t u(t, x) \partial_j \phi(x) \phi(x) \, \mathrm{d} x. \end{align} $$
Integrating the above from
![]() $t_1$
to
$t_1$
to
![]() $t_2$
we obtain the identity
$t_2$
we obtain the identity
 $$ \begin{align} \int_{t_1}^{t_2} \| \partial_t u(t) \phi \|_{L^2}^2 \, \mathrm{d} t + \frac{1}{2} \| \nabla u(t_2) \phi \|_{L^2}^2 &= \frac{1}{2} \| \nabla u(t_1) \phi \|_{L^2}^2 \nonumber\\ &\quad - \int_{t_1}^{t_2}\sum_{j =1}^2 \int_{\mathbb{R}^2} \partial_j u(t, x) \cdot \partial_t u(t, x) \partial_j \phi(x) \phi(x) \, \mathrm{d} x, \mathrm{d} t. \end{align} $$
$$ \begin{align} \int_{t_1}^{t_2} \| \partial_t u(t) \phi \|_{L^2}^2 \, \mathrm{d} t + \frac{1}{2} \| \nabla u(t_2) \phi \|_{L^2}^2 &= \frac{1}{2} \| \nabla u(t_1) \phi \|_{L^2}^2 \nonumber\\ &\quad - \int_{t_1}^{t_2}\sum_{j =1}^2 \int_{\mathbb{R}^2} \partial_j u(t, x) \cdot \partial_t u(t, x) \partial_j \phi(x) \phi(x) \, \mathrm{d} x, \mathrm{d} t. \end{align} $$
The right-hand side above is bounded by
 $$ \begin{align} \int_{t_1}^{t_2} \Big| \sum_{j =1}^2 \int_{\mathbb{R}^2} \partial_j u(t, x) \cdot \partial_t u(t, x) \partial_j \phi(x) \phi(x) \, \mathrm{d} x \, \mathrm{d} t \Big| \lesssim \int_{t_1}^{t_2}\frac{ \sqrt{E( u_0)}}{R} \| \partial_t u(t) \phi \|_{L^2}\, \mathrm{d} t. \end{align} $$
$$ \begin{align} \int_{t_1}^{t_2} \Big| \sum_{j =1}^2 \int_{\mathbb{R}^2} \partial_j u(t, x) \cdot \partial_t u(t, x) \partial_j \phi(x) \phi(x) \, \mathrm{d} x \, \mathrm{d} t \Big| \lesssim \int_{t_1}^{t_2}\frac{ \sqrt{E( u_0)}}{R} \| \partial_t u(t) \phi \|_{L^2}\, \mathrm{d} t. \end{align} $$
The lemma readily follows after an application of Cauchy Schwarz, where we note that in obtaining (2.14), we also make use of the energy identity (2.11).
Lemma 2.10. Let
![]() $u_n(t)$
be a sequence of HMHFs with initial data
$u_n(t)$
be a sequence of HMHFs with initial data
![]() $u_{n, 0} \in \mathcal {E}$
defined on time intervals
$u_{n, 0} \in \mathcal {E}$
defined on time intervals
![]() $I_n :=[0, \tau _n]$
for a sequence
$I_n :=[0, \tau _n]$
for a sequence
![]() $\tau _n>0$
with
$\tau _n>0$
with
![]() $\lim _{ n \to \infty } \tau _n = 0$
, and satisfying
$\lim _{ n \to \infty } \tau _n = 0$
, and satisfying
![]() $\limsup _{n \to \infty }E( u_{n, 0}) < \infty $
. Let
$\limsup _{n \to \infty }E( u_{n, 0}) < \infty $
. Let
![]() $\omega $
be a harmonic map and let
$\omega $
be a harmonic map and let
![]() $R_n>0$
be a sequence such that
$R_n>0$
be a sequence such that
![]() $\lim _{n \to \infty } \tau _n R_n^{-2} =0$
. Suppose that
$\lim _{n \to \infty } \tau _n R_n^{-2} =0$
. Suppose that
Then
Next, let
![]() $\epsilon _n>0$
be a sequence with
$\epsilon _n>0$
be a sequence with
![]() $ \epsilon _n < R_n$
for all n and such that
$ \epsilon _n < R_n$
for all n and such that
![]() $\lim _{n \to \infty } \tau _n\epsilon _n^{-2} = 0$
. Let
$\lim _{n \to \infty } \tau _n\epsilon _n^{-2} = 0$
. Let
![]() $L \ge 1$
be an integer and let
$L \ge 1$
be an integer and let
![]() $\{x_\ell \}_{\ell =1}^L \subset \mathbb {R}^2$
be such that the discs
$\{x_\ell \}_{\ell =1}^L \subset \mathbb {R}^2$
be such that the discs
![]() $D(x_\ell , \epsilon _n)$
are disjoint and satisfy
$D(x_\ell , \epsilon _n)$
are disjoint and satisfy
![]() $D(x_{\ell }, \epsilon _n) \subset D(0, R_n)$
for each n and each
$D(x_{\ell }, \epsilon _n) \subset D(0, R_n)$
for each n and each
![]() $\ell \in \{1, \dots , L\}$
. Moreover,
$\ell \in \{1, \dots , L\}$
. Moreover,
![]() $|x_\ell -x_m|\ge 100\epsilon _n$
if
$|x_\ell -x_m|\ge 100\epsilon _n$
if
![]() $\ell \ne m$
. Suppose that
$\ell \ne m$
. Suppose that
 $$ \begin{align} \lim_{n \to \infty} E\Big(u_{n, 0} - \omega; D(0, 2R_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell} , 2^{-1}\epsilon_n)\Big) = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big(u_{n, 0} - \omega; D(0, 2R_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell} , 2^{-1}\epsilon_n)\Big) = 0. \end{align} $$
Then
 $$ \begin{align} \lim_{n \to \infty} E\Big(u_{n}(\tau_n) - \omega; D(0, R_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell}, \epsilon_n)\Big) = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big(u_{n}(\tau_n) - \omega; D(0, R_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell}, \epsilon_n)\Big) = 0. \end{align} $$
Proof of Lemma 2.10.
The proof is very similar to the Proof of Lemma 2.9. We prove the estimate (2.21), as the proof of (2.19) is analogous. Set
![]() $v_n(t):= u_n(t) - \omega $
. Then
$v_n(t):= u_n(t) - \omega $
. Then
Let
![]() $\phi _n \in C^\infty _0( \mathbb {R}^2)$
and take the dot product of the above with
$\phi _n \in C^\infty _0( \mathbb {R}^2)$
and take the dot product of the above with
![]() $\partial _t v_n \phi _n^2$
. Recalling that
$\partial _t v_n \phi _n^2$
. Recalling that
![]() $\partial _tv_n = \partial _t u_n \perp u_n$
, integrating by parts, and integrating in time from
$\partial _tv_n = \partial _t u_n \perp u_n$
, integrating by parts, and integrating in time from
![]() $0$
to
$0$
to
![]() $\tau _n$
, we obtain the inequality
$\tau _n$
, we obtain the inequality
 $$ \begin{align} \frac{1}{2} \| \nabla v_n(\tau_n) \phi_n \|_{L^2}^2 &+ \int_0^{\tau_n} \| \partial_t v_n (t) \phi_n \|_{L^2}^2 \, \mathrm{d} t \le \frac{1}{2} \| \nabla u_{n, 0} \phi_n \|_{L^2}^2 \nonumber\\ &+ \int_0^{\tau_n} \int_{\mathbb{R}^2} | \nabla v_n(t)| | \partial_t v_n(t) | |\nabla \phi_n| \phi_n\, \mathrm{d} x \, \mathrm{d} t + \int_{0}^{\tau_n} \int_{\mathbb{R}^2} | \nabla \omega|^2 | \partial_t v_n| \phi_n^2 \, \mathrm{d} x \, \mathrm{d} t. \end{align} $$
$$ \begin{align} \frac{1}{2} \| \nabla v_n(\tau_n) \phi_n \|_{L^2}^2 &+ \int_0^{\tau_n} \| \partial_t v_n (t) \phi_n \|_{L^2}^2 \, \mathrm{d} t \le \frac{1}{2} \| \nabla u_{n, 0} \phi_n \|_{L^2}^2 \nonumber\\ &+ \int_0^{\tau_n} \int_{\mathbb{R}^2} | \nabla v_n(t)| | \partial_t v_n(t) | |\nabla \phi_n| \phi_n\, \mathrm{d} x \, \mathrm{d} t + \int_{0}^{\tau_n} \int_{\mathbb{R}^2} | \nabla \omega|^2 | \partial_t v_n| \phi_n^2 \, \mathrm{d} x \, \mathrm{d} t. \end{align} $$
Now, let
![]() $\phi _n$
be cutoffs supported in the region
$\phi _n$
be cutoffs supported in the region
![]() $D(0, 2R_n) \setminus \bigcup _{\ell =1}^L D(x_{\ell } , 2^{-1}\epsilon _n))$
and
$D(0, 2R_n) \setminus \bigcup _{\ell =1}^L D(x_{\ell } , 2^{-1}\epsilon _n))$
and
![]() $= 1$
in the region
$= 1$
in the region
![]() $D(0, R_n) \setminus \bigcup _{\ell =1}^L D(x_{\ell } , \epsilon _n))$
, satisfying the bound
$D(0, R_n) \setminus \bigcup _{\ell =1}^L D(x_{\ell } , \epsilon _n))$
, satisfying the bound
![]() $| \nabla \phi _n| \lesssim \epsilon _n^{-1}$
. The first term of the last line above satisfies
$| \nabla \phi _n| \lesssim \epsilon _n^{-1}$
. The first term of the last line above satisfies
 $$ \begin{align} \int_0^{\tau_n} \int_{\mathbb{R}^2} | \nabla v_n(t)| | \partial_t v_n(t) | |\nabla \phi_n| \phi_n\, \mathrm{d} x \, \mathrm{d} t \lesssim ( E( u_{n, 0}) + E( \omega)) \frac{ \tau_n}{\epsilon_n^2} + \frac{1}{2} \int_0^{\tau_n} \| \partial_t v_n (t) \phi_n \|_{L^2}^2 \, \mathrm{d} t, \end{align} $$
$$ \begin{align} \int_0^{\tau_n} \int_{\mathbb{R}^2} | \nabla v_n(t)| | \partial_t v_n(t) | |\nabla \phi_n| \phi_n\, \mathrm{d} x \, \mathrm{d} t \lesssim ( E( u_{n, 0}) + E( \omega)) \frac{ \tau_n}{\epsilon_n^2} + \frac{1}{2} \int_0^{\tau_n} \| \partial_t v_n (t) \phi_n \|_{L^2}^2 \, \mathrm{d} t, \end{align} $$
and the second term on the right above can be absorbed into the left-hand side of (2.23). Similarly,
and the second term on the right above can be absorbed into the left-hand side of (2.23). The limit (2.21) readily follows.
2.2.2. Local
 $L^\infty $
estimates for the heat flow
$L^\infty $
estimates for the heat flow
We use the notation
![]() $e^{t \Delta }$
to denote the heat propagator in
$e^{t \Delta }$
to denote the heat propagator in
![]() $\mathbb {R}^2$
– that is,
$\mathbb {R}^2$
– that is,
where here
![]() $v: \mathbb {R}^2 \to \mathbb {R}^3$
. We also recall Duhamel’s formula,
$v: \mathbb {R}^2 \to \mathbb {R}^3$
. We also recall Duhamel’s formula,
 $$ \begin{align} v(t) = e^{t \Delta} v(0) + \int_0^t e^{(t-s) \Delta} ( \partial_s v(s) - \Delta v(s)) \, \mathrm{d} s. \end{align} $$
$$ \begin{align} v(t) = e^{t \Delta} v(0) + \int_0^t e^{(t-s) \Delta} ( \partial_s v(s) - \Delta v(s)) \, \mathrm{d} s. \end{align} $$
Lemma 2.11 (Parabolic Strichartz estimates). [Reference Tao29, Lemma 2.5]
There exists a constant
![]() $C_0>0$
with the following property. Let
$C_0>0$
with the following property. Let
![]() $v_0 \in L^2(\mathbb {R}^2; \mathbb {R}^3)$
. Let
$v_0 \in L^2(\mathbb {R}^2; \mathbb {R}^3)$
. Let
![]() $T>0$
,
$T>0$
,
![]() $I:= [0, T]$
and let
$I:= [0, T]$
and let
![]() $F \in L^1([0, T]; L^2(\mathbb {R}^2; \mathbb {R}^3))$
. Let
$F \in L^1([0, T]; L^2(\mathbb {R}^2; \mathbb {R}^3))$
. Let
![]() $v(t)$
denote the unique solution to the linear heat equation
$v(t)$
denote the unique solution to the linear heat equation
 $$ \begin{align} \partial_t v - \Delta v &= F \nonumber\\ v(0) &= v_0. \end{align} $$
$$ \begin{align} \partial_t v - \Delta v &= F \nonumber\\ v(0) &= v_0. \end{align} $$
Then
Proof. Setting
![]() $(Tf)(t):=e^{t\Delta }f$
for
$(Tf)(t):=e^{t\Delta }f$
for
![]() $t\ge 0$
, one has
$t\ge 0$
, one has
![]() $T^* F=\int _0^\infty e^{s\Delta } F(s)\, ds$
. Starting from the two-dimension estimate
$T^* F=\int _0^\infty e^{s\Delta } F(s)\, ds$
. Starting from the two-dimension estimate
![]() $\|(Tf)(t)\|_\infty \lesssim t^{-1} \|f\|_1$
, we have
$\|(Tf)(t)\|_\infty \lesssim t^{-1} \|f\|_1$
, we have
whence
The right-hand side is
![]() $L^2_t((0,\infty ))$
bounded and we conclude that
$L^2_t((0,\infty ))$
bounded and we conclude that
Thus,
![]() $\langle TT^*F,F\rangle =\|T^*F\|_2^2\lesssim \|F\|_{L^2((0,\infty ),L^1(\mathbb {R}^2))}^2$
, and by duality, we obtain the
$\langle TT^*F,F\rangle =\|T^*F\|_2^2\lesssim \|F\|_{L^2((0,\infty ),L^1(\mathbb {R}^2))}^2$
, and by duality, we obtain the
![]() $F=0$
case of (2.29), viz.
$F=0$
case of (2.29), viz.
![]() $\|Tv_0\|_{L^2((0,\infty ),L^\infty (\mathbb {R}^2))}\lesssim \|v_0\|_2$
. However, if
$\|Tv_0\|_{L^2((0,\infty ),L^\infty (\mathbb {R}^2))}\lesssim \|v_0\|_2$
. However, if
![]() $v_0=0$
, then
$v_0=0$
, then
 $$\begin{align*}v(t) = \int_0^t e^{(t-s)\Delta} F(s)\, ds = \int_0^\infty \chi_{[s\le t]}\, e^{(t-s)\Delta} F(s)\, ds, \end{align*}$$
$$\begin{align*}v(t) = \int_0^t e^{(t-s)\Delta} F(s)\, ds = \int_0^\infty \chi_{[s\le t]}\, e^{(t-s)\Delta} F(s)\, ds, \end{align*}$$
whence
as claimed.
Lemma 2.12. Let
![]() $u_n(t)$
be a sequence of solutions to (1.2) with initial data
$u_n(t)$
be a sequence of solutions to (1.2) with initial data
![]() $u_{n, 0} \in \mathcal {E} \cap C^0( \mathbb {R}^2; \mathbb {R}^3)$
and
$u_{n, 0} \in \mathcal {E} \cap C^0( \mathbb {R}^2; \mathbb {R}^3)$
and
![]() $\limsup _{n \to \infty } E( u_{n, 0}) < \infty $
, defined on time intervals
$\limsup _{n \to \infty } E( u_{n, 0}) < \infty $
, defined on time intervals
![]() $I_n :=[0, \tau _n]$
for a sequence
$I_n :=[0, \tau _n]$
for a sequence
![]() $\tau _n>0$
with
$\tau _n>0$
with
![]() $\lim _{n \to \infty } \tau _n = 0$
. Let
$\lim _{n \to \infty } \tau _n = 0$
. Let
![]() $\omega $
be a harmonic map (possibly constant) and let
$\omega $
be a harmonic map (possibly constant) and let
![]() $R_n>0$
be a sequence so that
$R_n>0$
be a sequence so that
![]() $\lim _{n \to \infty } \tau _n R_n^{-2} = 0$
. Suppose that
$\lim _{n \to \infty } \tau _n R_n^{-2} = 0$
. Suppose that
Then
Next, let
![]() $\epsilon _n>0$
be a sequence with
$\epsilon _n>0$
be a sequence with
![]() $\epsilon _n < R_n$
for all n and such that
$\epsilon _n < R_n$
for all n and such that
![]() $\lim _{n \to \infty } \tau _n\epsilon _n^{-2} = 0$
. Let
$\lim _{n \to \infty } \tau _n\epsilon _n^{-2} = 0$
. Let
![]() $L \ge 1$
be an integer and let
$L \ge 1$
be an integer and let
![]() $\{x_\ell \}_{\ell =1}^L \subset \mathbb {R}^2$
be such that the discs
$\{x_\ell \}_{\ell =1}^L \subset \mathbb {R}^2$
be such that the discs
![]() $D(x_\ell , \epsilon _n)$
are disjoint and satisfy
$D(x_\ell , \epsilon _n)$
are disjoint and satisfy
![]() $D(x_{\ell }, \epsilon _n) \subset D(0, R_n)$
for each n and each
$D(x_{\ell }, \epsilon _n) \subset D(0, R_n)$
for each n and each
![]() $\ell \in \{1, \dots , L\}$
. Moreover,
$\ell \in \{1, \dots , L\}$
. Moreover,
![]() $|x_\ell -x_m|\ge 100\epsilon _n$
if
$|x_\ell -x_m|\ge 100\epsilon _n$
if
![]() $\ell \ne m$
. Suppose that
$\ell \ne m$
. Suppose that
 $$ \begin{align} \lim_{n \to \infty} \Big( \| u_{n, 0} - \omega \|_{L^\infty(D(0, 4R_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell} , 4^{-1}\epsilon_n))}+E\Big(u_{n, 0} - \omega; D(0, 4R_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell} , 4^{-1}\epsilon_n)\Big) \Big) = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \Big( \| u_{n, 0} - \omega \|_{L^\infty(D(0, 4R_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell} , 4^{-1}\epsilon_n))}+E\Big(u_{n, 0} - \omega; D(0, 4R_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell} , 4^{-1}\epsilon_n)\Big) \Big) = 0. \end{align} $$
Then
Proof. We begin with a solution
![]() $u_n(t)$
of the heat flow satisfying
$u_n(t)$
of the heat flow satisfying
We pick
![]() $\phi _1$
to be the ground state of the Dirichlet Laplacian on the disk
$\phi _1$
to be the ground state of the Dirichlet Laplacian on the disk
![]() $D(0,3R_n/2)$
and set
$D(0,3R_n/2)$
and set
![]() $v(t)=(u(t)-\omega )\phi _1$
, dropping the index n for simplicity. We normalize
$v(t)=(u(t)-\omega )\phi _1$
, dropping the index n for simplicity. We normalize
![]() $\phi _1(0)=1$
, which means that
$\phi _1(0)=1$
, which means that
![]() $\|\phi _1\|_\infty =1$
. Then
$\|\phi _1\|_\infty =1$
. Then
![]() $-\Delta \phi _1=\lambda _1^2\phi _1$
,
$-\Delta \phi _1=\lambda _1^2\phi _1$
,
![]() $\lambda _1^2\simeq R_n^{-2}$
and
$\lambda _1^2\simeq R_n^{-2}$
and
Since
![]() $\phi _1$
is not globally smooth, we cannot solve this heat equation on the plane but rather need to use the heat flow on the region
$\phi _1$
is not globally smooth, we cannot solve this heat equation on the plane but rather need to use the heat flow on the region
![]() $\Omega =\overline {D(0,3R_n/2)}$
with Dirichlet boundary conditions. By the Beurling-Deny theorem (see Davies [Reference Davies5, Theorem 1.3.5]), the heat flow is a contraction on
$\Omega =\overline {D(0,3R_n/2)}$
with Dirichlet boundary conditions. By the Beurling-Deny theorem (see Davies [Reference Davies5, Theorem 1.3.5]), the heat flow is a contraction on
![]() $L^\infty (\Omega )$
, and we conclude that
$L^\infty (\Omega )$
, and we conclude that
 $$ \begin{align} \max_{0\le t\le T}\|v(t)\|_\infty \le \|v(0)\|_\infty &+ \int_I \| (|\nabla u(s)|^2 u(s) - |\nabla\omega|^2\omega)\phi_1\|_\infty \, \mathrm{d} s \nonumber\\& + 2\int_I \| \nabla (u(s) -\omega) \nabla \phi_1\|_\infty \, \mathrm{d} s + \lambda_1^2 |I| \|v\|_{L^\infty(I\times\mathbb{R}^2) } \end{align} $$
$$ \begin{align} \max_{0\le t\le T}\|v(t)\|_\infty \le \|v(0)\|_\infty &+ \int_I \| (|\nabla u(s)|^2 u(s) - |\nabla\omega|^2\omega)\phi_1\|_\infty \, \mathrm{d} s \nonumber\\& + 2\int_I \| \nabla (u(s) -\omega) \nabla \phi_1\|_\infty \, \mathrm{d} s + \lambda_1^2 |I| \|v\|_{L^\infty(I\times\mathbb{R}^2) } \end{align} $$
with
![]() $[0,\tau _n]=I$
. If
$[0,\tau _n]=I$
. If
![]() $\lambda _1^2 |I|\le \frac 12 $
, then the final term gets absorbed to the left-hand side. Next,
$\lambda _1^2 |I|\le \frac 12 $
, then the final term gets absorbed to the left-hand side. Next,
 $$ \begin{align} \| (|\nabla u(s)|^2 u(s) - |\nabla\omega|^2\omega)\phi_1\|_\infty & \le 2(\| \phi_2 \nabla (u(s)-\omega)\|_\infty^2 +\|\phi_2 \nabla \omega\|_\infty^2)\|v(s)\|_\infty \nonumber\\ &+ \|\omega\|_\infty \|\phi_2\nabla(u-\omega)\|_\infty(\|\phi_2\nabla (u-\omega)\|_\infty + 2\|\phi_2\nabla \omega\|_2), \end{align} $$
$$ \begin{align} \| (|\nabla u(s)|^2 u(s) - |\nabla\omega|^2\omega)\phi_1\|_\infty & \le 2(\| \phi_2 \nabla (u(s)-\omega)\|_\infty^2 +\|\phi_2 \nabla \omega\|_\infty^2)\|v(s)\|_\infty \nonumber\\ &+ \|\omega\|_\infty \|\phi_2\nabla(u-\omega)\|_\infty(\|\phi_2\nabla (u-\omega)\|_\infty + 2\|\phi_2\nabla \omega\|_2), \end{align} $$
where
![]() $\phi _2$
is a smooth cutoff to
$\phi _2$
is a smooth cutoff to
![]() $D(0,2R_n)$
with
$D(0,2R_n)$
with
![]() $\phi _1\phi _2=\phi _1$
. We further bound
$\phi _1\phi _2=\phi _1$
. We further bound
using that
![]() $\|\nabla \phi _1\|_\infty \lesssim R_n^{-1}$
, which follows by scaling. Define
$\|\nabla \phi _1\|_\infty \lesssim R_n^{-1}$
, which follows by scaling. Define
![]() $w(s):= \phi _2\nabla (u(s) -\omega ) $
and let
$w(s):= \phi _2\nabla (u(s) -\omega ) $
and let
![]() $X:=L^\infty (I; L^\infty (\mathbb {R}^2))$
,
$X:=L^\infty (I; L^\infty (\mathbb {R}^2))$
,
![]() $Y:=L^2(I; L^\infty (\mathbb {R}^2; \mathbb {R}^3))$
. Then (2.35) implies that
$Y:=L^2(I; L^\infty (\mathbb {R}^2; \mathbb {R}^3))$
. Then (2.35) implies that
which in turn simplifies to
To bound w, we use the PDE
 $$ \begin{align} \partial_t w -\Delta w &= \phi_2 \nabla (u|\nabla u|^2) - 2\sum_{j=1}^2 \nabla \partial_j (u-\omega) \partial_j \phi_2 \nonumber\\ & \quad - \nabla(u-\omega)\Delta \phi_2 - \phi_2 \nabla(\omega |\nabla \omega|^2) =: G. \end{align} $$
$$ \begin{align} \partial_t w -\Delta w &= \phi_2 \nabla (u|\nabla u|^2) - 2\sum_{j=1}^2 \nabla \partial_j (u-\omega) \partial_j \phi_2 \nonumber\\ & \quad - \nabla(u-\omega)\Delta \phi_2 - \phi_2 \nabla(\omega |\nabla \omega|^2) =: G. \end{align} $$
By (2.29), and with
![]() $Z:=L^1(I; L^2(\mathbb {R}^2; \mathbb {R}^3)$
,
$Z:=L^1(I; L^2(\mathbb {R}^2; \mathbb {R}^3)$
,
To bound G, we estimate with a smooth cutoff
![]() $\phi _3$
to
$\phi _3$
to
![]() $D(0,3R_n)$
so that
$D(0,3R_n)$
so that
![]() $\phi _2\phi _3=\phi _2$
,
$\phi _2\phi _3=\phi _2$
,
 $$ \begin{align} \| \phi_2 \nabla (u|\nabla u|^2) \|_2 &\lesssim \| \phi_2\nabla u\|_\infty \| \phi_3 \nabla u \|_4^2 + \|\phi_2\nabla u\|_\infty \|\phi_3 D^2u \|_2 \nonumber\\ \| \nabla \partial_j (u-\omega) \partial_j \phi_2 \|_2 &\lesssim R_n^{-1}\| \phi_3 D^2 (u-\omega) \|_2 \\ \|\Delta \phi_2 \nabla(u-\omega)\|_2 &\lesssim R_n^{-2}\|\phi_3 \nabla(u-\omega)\|_2\nonumber \end{align} $$
$$ \begin{align} \| \phi_2 \nabla (u|\nabla u|^2) \|_2 &\lesssim \| \phi_2\nabla u\|_\infty \| \phi_3 \nabla u \|_4^2 + \|\phi_2\nabla u\|_\infty \|\phi_3 D^2u \|_2 \nonumber\\ \| \nabla \partial_j (u-\omega) \partial_j \phi_2 \|_2 &\lesssim R_n^{-1}\| \phi_3 D^2 (u-\omega) \|_2 \\ \|\Delta \phi_2 \nabla(u-\omega)\|_2 &\lesssim R_n^{-2}\|\phi_3 \nabla(u-\omega)\|_2\nonumber \end{align} $$
as well as
![]() $\| \phi _2 \nabla (\omega |\nabla \omega |^2)\|_2 \lesssim 1$
. Furthermore,
$\| \phi _2 \nabla (\omega |\nabla \omega |^2)\|_2 \lesssim 1$
. Furthermore,
 $$ \begin{align} \| \phi_2\nabla u\|_\infty &\lesssim \| w\|_\infty +1 \nonumber\\ \| \phi_3 \nabla u \|_4 &\lesssim \| \phi_3 \nabla (u-\omega) \|_4 + 1\\ \|\phi_3 D^2u \|_2 &\lesssim \|\phi_3 D^2 (u-\omega) \|_2 +1\nonumber \end{align} $$
$$ \begin{align} \| \phi_2\nabla u\|_\infty &\lesssim \| w\|_\infty +1 \nonumber\\ \| \phi_3 \nabla u \|_4 &\lesssim \| \phi_3 \nabla (u-\omega) \|_4 + 1\\ \|\phi_3 D^2u \|_2 &\lesssim \|\phi_3 D^2 (u-\omega) \|_2 +1\nonumber \end{align} $$
uniformly in
![]() $R_n$
. By (2.39) therefore,
$R_n$
. By (2.39) therefore,
To perform energy estimates on
![]() $u-\omega $
, we apply the methods of Struwe [Reference Struwe28] to the PDE
$u-\omega $
, we apply the methods of Struwe [Reference Struwe28] to the PDE
Integrating by parts against
![]() $\phi _3^2 \partial _t(u-\omega )$
implies that (with
$\phi _3^2 \partial _t(u-\omega )$
implies that (with
![]() $T=\tau _n$
)
$T=\tau _n$
)
 $$ \begin{align} & \int_0^T \int_{\mathbb{R}^2} |\partial_t(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_0^T\int_{\mathbb{R}^2} \nabla(u(t)-\omega) \cdot \nabla[\partial_t (u-\omega)\phi_3^2]\, \mathrm{d} x \mathrm{d} t \nonumber\\& \quad = \int_0^T \int_{\mathbb{R}^2} (u-\omega)|\nabla\omega|^2 \cdot\partial_t (u-\omega)\phi_3^2\, \mathrm{d} x \mathrm{d} t + \int_0^T \int_{\mathbb{R}^2} u\cdot \partial_t (u-\omega)\phi_3^2(|\nabla u(t)|^2-|\nabla \omega|^2) \, \mathrm{d} x \mathrm{d} t , \end{align} $$
$$ \begin{align} & \int_0^T \int_{\mathbb{R}^2} |\partial_t(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_0^T\int_{\mathbb{R}^2} \nabla(u(t)-\omega) \cdot \nabla[\partial_t (u-\omega)\phi_3^2]\, \mathrm{d} x \mathrm{d} t \nonumber\\& \quad = \int_0^T \int_{\mathbb{R}^2} (u-\omega)|\nabla\omega|^2 \cdot\partial_t (u-\omega)\phi_3^2\, \mathrm{d} x \mathrm{d} t + \int_0^T \int_{\mathbb{R}^2} u\cdot \partial_t (u-\omega)\phi_3^2(|\nabla u(t)|^2-|\nabla \omega|^2) \, \mathrm{d} x \mathrm{d} t , \end{align} $$
which implies
 $$ \begin{align} & \int_0^T \int_{\mathbb{R}^2} |\partial_t(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_{\mathbb{R}^2} |\nabla(u(T)-\omega)|^2\phi_3^2\, \mathrm{d} x \nonumber\\& \quad \lesssim o(1) + \int_0^T \int_{\mathbb{R}^2} ||\nabla u(t)|^2-|\nabla \omega|^2|^2\,\phi_3^2\, \mathrm{d} x \mathrm{d} t+ \int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)-\omega)|^2 |\nabla\phi_3|^2\, \mathrm{d} x \mathrm{d} t \\& \quad \lesssim o(1) + \int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)- \omega)|^4 \,\phi_3^2\, \mathrm{d} x \mathrm{d} t. \nonumber \end{align} $$
$$ \begin{align} & \int_0^T \int_{\mathbb{R}^2} |\partial_t(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_{\mathbb{R}^2} |\nabla(u(T)-\omega)|^2\phi_3^2\, \mathrm{d} x \nonumber\\& \quad \lesssim o(1) + \int_0^T \int_{\mathbb{R}^2} ||\nabla u(t)|^2-|\nabla \omega|^2|^2\,\phi_3^2\, \mathrm{d} x \mathrm{d} t+ \int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)-\omega)|^2 |\nabla\phi_3|^2\, \mathrm{d} x \mathrm{d} t \\& \quad \lesssim o(1) + \int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)- \omega)|^4 \,\phi_3^2\, \mathrm{d} x \mathrm{d} t. \nonumber \end{align} $$
The final term on the second line of (2.45) is dominated by
![]() $TR_n^{-2} (E(u(0))+E(\omega ))$
and so can be absorbed in the
$TR_n^{-2} (E(u(0))+E(\omega ))$
and so can be absorbed in the
![]() $O(\tau _nR_n^{-2})$
. Multiplying (2.43) by
$O(\tau _nR_n^{-2})$
. Multiplying (2.43) by
![]() $-\phi _3^2\Delta (u-\omega )$
and integrating by parts yields
$-\phi _3^2\Delta (u-\omega )$
and integrating by parts yields
 $$ \begin{align} & \sum_{j=1}^2 \int_0^T \int_{\mathbb{R}^2} \partial_t |\partial_j(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_0^T\int_{\mathbb{R}^2} |\Delta(u(t)-\omega)|^2 \phi_3^2\, \mathrm{d} x \mathrm{d} t \nonumber\\& \quad = \sum_{j=1}^2 \int_0^T \!\!\!\!\int_{\mathbb{R}^2}\! \partial_j[(u-\omega)|\nabla\omega|^2\phi_3^2] \cdot\partial_j (u-\omega)\, dxdt - 2\sum_{j=1}^2\int_0^T \!\!\!\!\int_{\mathbb{R}^2}\! \partial_t (u-\omega) \phi_3 \partial_j \phi_3 \cdot\partial_j (u-\omega) \, \mathrm{d} x \mathrm{d} t \nonumber \\& \qquad - \int_0^T \int_{\mathbb{R}^2} \Delta (u-\omega) \cdot [\phi_3^2(|\nabla u(t)|^2-|\nabla \omega|^2)u] \, \mathrm{d} x \mathrm{d} t, \end{align} $$
$$ \begin{align} & \sum_{j=1}^2 \int_0^T \int_{\mathbb{R}^2} \partial_t |\partial_j(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_0^T\int_{\mathbb{R}^2} |\Delta(u(t)-\omega)|^2 \phi_3^2\, \mathrm{d} x \mathrm{d} t \nonumber\\& \quad = \sum_{j=1}^2 \int_0^T \!\!\!\!\int_{\mathbb{R}^2}\! \partial_j[(u-\omega)|\nabla\omega|^2\phi_3^2] \cdot\partial_j (u-\omega)\, dxdt - 2\sum_{j=1}^2\int_0^T \!\!\!\!\int_{\mathbb{R}^2}\! \partial_t (u-\omega) \phi_3 \partial_j \phi_3 \cdot\partial_j (u-\omega) \, \mathrm{d} x \mathrm{d} t \nonumber \\& \qquad - \int_0^T \int_{\mathbb{R}^2} \Delta (u-\omega) \cdot [\phi_3^2(|\nabla u(t)|^2-|\nabla \omega|^2)u] \, \mathrm{d} x \mathrm{d} t, \end{align} $$
which implies
 $$ \begin{align} & -\frac12 \int_0^T \int_{\mathbb{R}^2} |\partial_t(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_{\mathbb{R}^2} |\nabla(u(T)-\omega)|^2\phi_3^2\, dx + \frac12\int_0^T\int_{\mathbb{R}^2} |\Delta(u(t)-\omega)|^2 \phi_3^2\, \mathrm{d} x \mathrm{d} t \nonumber\\& \quad \lesssim o(1)+ \int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)- \omega)|^4 \,\phi_3^2\, \mathrm{d} x \mathrm{d} t. \end{align} $$
$$ \begin{align} & -\frac12 \int_0^T \int_{\mathbb{R}^2} |\partial_t(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_{\mathbb{R}^2} |\nabla(u(T)-\omega)|^2\phi_3^2\, dx + \frac12\int_0^T\int_{\mathbb{R}^2} |\Delta(u(t)-\omega)|^2 \phi_3^2\, \mathrm{d} x \mathrm{d} t \nonumber\\& \quad \lesssim o(1)+ \int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)- \omega)|^4 \,\phi_3^2\, \mathrm{d} x \mathrm{d} t. \end{align} $$
Adding this to (2.45), we obtain
 $$ \begin{align} & \int_0^T \int_{\mathbb{R}^2} |\partial_t(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_{\mathbb{R}^2} |\nabla(u(T)-\omega)|^2\phi_3^2\, dx + \int_0^T\int_{\mathbb{R}^2} |D^2(u(t)-\omega)|^2 \phi_3^2\, \mathrm{d} x \mathrm{d} t \nonumber\\& \quad \lesssim o(1) + \int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)- \omega)|^4 \,\phi_3^2\, \mathrm{d} x \mathrm{d} t. \end{align} $$
$$ \begin{align} & \int_0^T \int_{\mathbb{R}^2} |\partial_t(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_{\mathbb{R}^2} |\nabla(u(T)-\omega)|^2\phi_3^2\, dx + \int_0^T\int_{\mathbb{R}^2} |D^2(u(t)-\omega)|^2 \phi_3^2\, \mathrm{d} x \mathrm{d} t \nonumber\\& \quad \lesssim o(1) + \int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)- \omega)|^4 \,\phi_3^2\, \mathrm{d} x \mathrm{d} t. \end{align} $$
For the third term on the left-hand side, we used another integration by parts to bound
 $$\begin{align*}\int_0^T\int_{\mathbb{R}^2} |D^2(u(t)-\omega)|^2 \phi_3^2\, dx dt \lesssim \int_0^T\int_{\mathbb{R}^2} |\Delta(u(t)-\omega)|^2 \phi_3^2\, \mathrm{d} x \mathrm{d} t +\tau_n R_n^{-2}. \end{align*}$$
$$\begin{align*}\int_0^T\int_{\mathbb{R}^2} |D^2(u(t)-\omega)|^2 \phi_3^2\, dx dt \lesssim \int_0^T\int_{\mathbb{R}^2} |\Delta(u(t)-\omega)|^2 \phi_3^2\, \mathrm{d} x \mathrm{d} t +\tau_n R_n^{-2}. \end{align*}$$
By [Reference Struwe28, Lemma 3.2],
 $$ \begin{align} \int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)- \omega)|^4 \,\phi_3^2\, dxdt &\lesssim \sup_{0\le t\le T} \int_{D(0,3R_n)} |\nabla (u(t,x)-\omega(x))|^2\, \mathrm{d} x \nonumber\\ &\qquad \Big(\int_0^T\int_{\mathbb{R}^2} |D^2(u(t)-\omega)|^2 \phi_3^2\, dx dt + \tau_n R_n^{-2}\Big). \end{align} $$
$$ \begin{align} \int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)- \omega)|^4 \,\phi_3^2\, dxdt &\lesssim \sup_{0\le t\le T} \int_{D(0,3R_n)} |\nabla (u(t,x)-\omega(x))|^2\, \mathrm{d} x \nonumber\\ &\qquad \Big(\int_0^T\int_{\mathbb{R}^2} |D^2(u(t)-\omega)|^2 \phi_3^2\, dx dt + \tau_n R_n^{-2}\Big). \end{align} $$
By Lemma 2.10, the local energy on
![]() $D(0,3)$
is small. Hence, we conclude from (2.48) and the bound (2.49) that
$D(0,3)$
is small. Hence, we conclude from (2.48) and the bound (2.49) that
 $$ \begin{align} & \int_0^T \int_{\mathbb{R}^2} |\partial_t(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_{\mathbb{R}^2} |\nabla(u(T)-\omega)|^2\phi_3^2\, dx + \int_0^T\int_{\mathbb{R}^2} |D^2(u(t)-\omega)|^2 \phi_3^2\, \mathrm{d} x \mathrm{d} t \nonumber\\& \quad +\int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)- \omega)|^4 \,\phi_3^2\, \mathrm{d} x \mathrm{d} t \lesssim o(1). \end{align} $$
$$ \begin{align} & \int_0^T \int_{\mathbb{R}^2} |\partial_t(u-\omega)|^2 \phi_3^2 \, \mathrm{d} x \mathrm{d} t+ \int_{\mathbb{R}^2} |\nabla(u(T)-\omega)|^2\phi_3^2\, dx + \int_0^T\int_{\mathbb{R}^2} |D^2(u(t)-\omega)|^2 \phi_3^2\, \mathrm{d} x \mathrm{d} t \nonumber\\& \quad +\int_0^T \int_{\mathbb{R}^2} |\nabla (u(t)- \omega)|^4 \,\phi_3^2\, \mathrm{d} x \mathrm{d} t \lesssim o(1). \end{align} $$
Inserting this bound into (2.42) yields
![]() $\|w\|_Y=o(1)$
, whence from (2.37), finally
$\|w\|_Y=o(1)$
, whence from (2.37), finally
![]() $\|v\|_X=o(1)$
. This finishes the proof for disks.
$\|v\|_X=o(1)$
. This finishes the proof for disks.
For the punctured disks, we would like to proceed in the same fashion. As a first step, it appears that we would need to obtain bounds on the suitably normalized ground state eigenfunction
![]() $\phi _1$
of the Dirichlet Laplacian on the punctured disk
$\phi _1$
of the Dirichlet Laplacian on the punctured disk
 $$ \begin{align*}D^*(0,4R_n)=D(0,4R_n)\setminus \bigcup_{\ell=1}^L D(x_\ell,\epsilon_n/4),\end{align*} $$
$$ \begin{align*}D^*(0,4R_n)=D(0,4R_n)\setminus \bigcup_{\ell=1}^L D(x_\ell,\epsilon_n/4),\end{align*} $$
where
![]() $x_\ell $
are as stated in the lemma. This turns out to be misguided as we will now see, in addition to being delicate in terms of obtaining the needed bounds on
$x_\ell $
are as stated in the lemma. This turns out to be misguided as we will now see, in addition to being delicate in terms of obtaining the needed bounds on
![]() $\phi _1$
uniformly in the choice of holes. In fact, it suffices to select
$\phi _1$
uniformly in the choice of holes. In fact, it suffices to select
![]() $\phi _1$
smooth on
$\phi _1$
smooth on
![]() $\Omega =\overline {D^*(0,4R_n)}$
, vanishing on
$\Omega =\overline {D^*(0,4R_n)}$
, vanishing on
![]() $\partial \Omega $
so that
$\partial \Omega $
so that
![]() $-\Delta \phi _1 = V\phi _1$
with
$-\Delta \phi _1 = V\phi _1$
with
![]() $\|V\|_{L^\infty (\Omega )}\lesssim \epsilon _n^{-2}$
uniformly in all parameters. By rescaling, it will also suffice to set
$\|V\|_{L^\infty (\Omega )}\lesssim \epsilon _n^{-2}$
uniformly in all parameters. By rescaling, it will also suffice to set
![]() $R_n=1$
.
$R_n=1$
.
We define, with
![]() $r=|x|$
and
$r=|x|$
and
![]() $r_\ell =|x-x_\ell |$
,
$r_\ell =|x-x_\ell |$
,
 $$ \begin{align} \phi_1(x):= \chi_0(r) \prod_{\ell=1}^L \chi_\ell(r_\ell) \end{align} $$
$$ \begin{align} \phi_1(x):= \chi_0(r) \prod_{\ell=1}^L \chi_\ell(r_\ell) \end{align} $$
with smooth functions
![]() $\chi _j>0$
on the interior of
$\chi _j>0$
on the interior of
![]() $\Omega $
,
$\Omega $
,
![]() $0\le j\le L$
that we now specify. First,
$0\le j\le L$
that we now specify. First,
![]() $\chi _0(r)=1$
for
$\chi _0(r)=1$
for
![]() $r\le 2$
, and on the annulus
$r\le 2$
, and on the annulus
![]() $3\le r\le 4$
,
$3\le r\le 4$
,
![]() $\chi _0(r)$
agrees with the
$\chi _0(r)$
agrees with the
![]() $L^\infty $
-normalized Dirichlet ground state of the disk
$L^\infty $
-normalized Dirichlet ground state of the disk
![]() $D(0,4)$
. To define
$D(0,4)$
. To define
![]() $\chi _\ell $
, consider all radial Dirchlet eigenfunctions,
$\chi _\ell $
, consider all radial Dirchlet eigenfunctions,
![]() $\{\psi _n\}_{n=1}^\infty $
on the annulus
$\{\psi _n\}_{n=1}^\infty $
on the annulus
![]() $D(0,1)\setminus D(0,\gamma )$
. Then
$D(0,1)\setminus D(0,\gamma )$
. Then
![]() $\psi _n(r)=a_nJ_0(\mu _n r)+b_nY_0(\mu _n r)$
, where
$\psi _n(r)=a_nJ_0(\mu _n r)+b_nY_0(\mu _n r)$
, where
![]() $\mu _n^2$
is the eigenvalue for
$\mu _n^2$
is the eigenvalue for
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $a_n,b_n\in \mathbb {R}$
. Since
$a_n,b_n\in \mathbb {R}$
. Since
![]() $a_n^2+b_n^2>0$
, and
$a_n^2+b_n^2>0$
, and
![]() $\psi _n(\gamma )=\psi _n(1)=0$
, the spectrum is characterized by the conditions
$\psi _n(\gamma )=\psi _n(1)=0$
, the spectrum is characterized by the conditions
Note that the ratio
![]() $R(x):=Y_0(x)/J_0(x)$
is strictly increasing on the interval
$R(x):=Y_0(x)/J_0(x)$
is strictly increasing on the interval
![]() $(0,\rho _1)$
where
$(0,\rho _1)$
where
![]() $\rho _1>0$
is the smallest positive zero of
$\rho _1>0$
is the smallest positive zero of
![]() $J_0$
, as well as on any subsequent interval
$J_0$
, as well as on any subsequent interval
![]() $(\rho _j,\rho _{j+1})$
,
$(\rho _j,\rho _{j+1})$
,
![]() $j\ge 1$
. This follows from the fact that the Wronskian
$j\ge 1$
. This follows from the fact that the Wronskian
![]() $Y_0'(x)J_0(x)-Y_0(x)J_0'(x)=2/(\pi x)>0$
. The first crossing of the graphs, which determines the smallest energy
$Y_0'(x)J_0(x)-Y_0(x)J_0'(x)=2/(\pi x)>0$
. The first crossing of the graphs, which determines the smallest energy
![]() $\mu _1>0$
, is determined by
$\mu _1>0$
, is determined by
![]() $R(x)=R(\gamma x)$
. The expansion
$R(x)=R(\gamma x)$
. The expansion
![]() $R(x)=\frac {2}{\pi }\log x+O(1)$
for
$R(x)=\frac {2}{\pi }\log x+O(1)$
for
![]() $x\to 0+$
shows that
$x\to 0+$
shows that
![]() $R(x)>R(x\gamma )$
for all
$R(x)>R(x\gamma )$
for all
![]() $0<x<\rho _1$
, and the first crossing occurs at
$0<x<\rho _1$
, and the first crossing occurs at
![]() $x\in (\rho _1,\rho _2)$
and so the ground state energy
$x\in (\rho _1,\rho _2)$
and so the ground state energy
![]() $\mu _1\in (\rho _1,\rho _2)$
. Similarly, we find the other energies
$\mu _1\in (\rho _1,\rho _2)$
. Similarly, we find the other energies
![]() $\mu _j\in (\rho _j,\rho _{j+1})$
, for
$\mu _j\in (\rho _j,\rho _{j+1})$
, for
![]() $j\ge 1$
. We select an eigenfunction
$j\ge 1$
. We select an eigenfunction
![]() $\psi _k$
with
$\psi _k$
with
![]() $\mu _k\simeq \gamma ^{-1}$
. This is possible due to the zeros of
$\mu _k\simeq \gamma ^{-1}$
. This is possible due to the zeros of
![]() $J_0(x)$
forming, to leading order, an arithmetic progression.
$J_0(x)$
forming, to leading order, an arithmetic progression.
We can now define
![]() $\chi _\ell $
in (2.51) by centering this
$\chi _\ell $
in (2.51) by centering this
![]() $\psi _k$
for
$\psi _k$
for
![]() $\gamma =\epsilon _\ell $
at
$\gamma =\epsilon _\ell $
at
![]() $x_\ell $
and gluing it smoothly with the constant
$x_\ell $
and gluing it smoothly with the constant
![]() $1$
at a distance
$1$
at a distance
![]() $\simeq \epsilon _\ell $
away from the
$\simeq \epsilon _\ell $
away from the
![]() $x_\ell $
hole. The resulting function
$x_\ell $
hole. The resulting function
![]() $\chi _\ell>0$
will then satisfy
$\chi _\ell>0$
will then satisfy
![]() $\chi _\ell (x)\ge \frac 12$
provided
$\chi _\ell (x)\ge \frac 12$
provided
![]() $|x-x_\ell |\gtrsim \epsilon _\ell $
.
$|x-x_\ell |\gtrsim \epsilon _\ell $
.
The associated cutoff function
![]() $\phi _1$
satisfies
$\phi _1$
satisfies
 $$ \begin{align} \phi_1(x) \ge c_0 \|\phi_1\|_\infty \text{ for all } x\in D(0,3R_n)\setminus \bigcup_{\ell=1}^L D(x_\ell,\epsilon_n/2) \end{align} $$
$$ \begin{align} \phi_1(x) \ge c_0 \|\phi_1\|_\infty \text{ for all } x\in D(0,3R_n)\setminus \bigcup_{\ell=1}^L D(x_\ell,\epsilon_n/2) \end{align} $$
with some absolute constant
![]() $c_0>0$
, independently of
$c_0>0$
, independently of
![]() $R_n, \epsilon _n$
and the choice of the centers
$R_n, \epsilon _n$
and the choice of the centers
![]() $x_\ell $
as above. It is clear from the preceding that the ground state would have energy
$x_\ell $
as above. It is clear from the preceding that the ground state would have energy
![]() $\simeq 1$
and does not satisfy (2.52). Furthermore,
$\simeq 1$
and does not satisfy (2.52). Furthermore,
![]() $\|\nabla \phi _1\|_\infty \lesssim \epsilon _n^{-1}\| \phi _1\|_\infty $
and most importantly,
$\|\nabla \phi _1\|_\infty \lesssim \epsilon _n^{-1}\| \phi _1\|_\infty $
and most importantly,
 $$\begin{align*}\|\phi_1^{-1}\Delta\phi_1\|_\infty \le \sum_{\ell=0}^L \| \chi_\ell^{-1}\Delta \chi_\ell\|_\infty \lesssim \epsilon_n^{-2}, \end{align*}$$
$$\begin{align*}\|\phi_1^{-1}\Delta\phi_1\|_\infty \le \sum_{\ell=0}^L \| \chi_\ell^{-1}\Delta \chi_\ell\|_\infty \lesssim \epsilon_n^{-2}, \end{align*}$$
as desired. Because of our assumption
![]() $\tau _n \epsilon _n^{-2}\to 0$
as
$\tau _n \epsilon _n^{-2}\to 0$
as
![]() $n\to \infty $
, the proof above applies. In the final step, we use (2.21) to control the
$n\to \infty $
, the proof above applies. In the final step, we use (2.21) to control the
![]() $L^4$
-norm as before, with one modification: we apply [Reference Struwe28, Lemma 3.2] locally on
$L^4$
-norm as before, with one modification: we apply [Reference Struwe28, Lemma 3.2] locally on
![]() $\epsilon _n$
-disks and then cover the punctured disk
$\epsilon _n$
-disks and then cover the punctured disk
![]() $D^*(0,4R_n)$
with
$D^*(0,4R_n)$
with
![]() $\epsilon _n$
-disks followed by a summation over the disks in the cover. Cf. [Reference Struwe28, Lemma 3.1, 3.3].
$\epsilon _n$
-disks followed by a summation over the disks in the cover. Cf. [Reference Struwe28, Lemma 3.1, 3.3].
2.2.3. Concentration properties of the heat flow
Here we record the fact that the harmonic map heat flow cannot concentrate energy at the self-similar scale. The case of finite time blow-up was treated by Topping in [Reference Topping31], and the global in time case follows quickly from a local energy inequality as in Lemma 2.9.
Lemma 2.13 (No self-similar concentration in the blow-up case).
[Reference Topping31, Proof of Theorem 1.6, page 288] Let
![]() $u(t)$
be the solution to (1.2) with maximal time of existence
$u(t)$
be the solution to (1.2) with maximal time of existence
![]() $T_+< \infty $
and initial data
$T_+< \infty $
and initial data
![]() $u_0 \in \mathcal {E}$
. Let
$u_0 \in \mathcal {E}$
. Let
![]() $x_0 \in \mathbb {R}^2$
denote a bubbling point in the sense of Lemma 2.7 and suppose that
$x_0 \in \mathbb {R}^2$
denote a bubbling point in the sense of Lemma 2.7 and suppose that
![]() $r>0$
is sufficiently small so that
$r>0$
is sufficiently small so that
![]() $D(x_0, r)$
does not contain any other bubbling point. Then
$D(x_0, r)$
does not contain any other bubbling point. Then
for any
![]() $\alpha>0$
, where
$\alpha>0$
, where
![]() $u^*$
is as in Lemma 2.7. In particular, there exist
$u^*$
is as in Lemma 2.7. In particular, there exist
![]() $T_0 < T_+$
and functions
$T_0 < T_+$
and functions
![]() $\nu , \xi : [T_0, T_+) \to (0, \infty )$
such that
$\nu , \xi : [T_0, T_+) \to (0, \infty )$
such that
![]() $\lim _{t \to T_+} (\nu (t) + \xi (t)) = 0$
and
$\lim _{t \to T_+} (\nu (t) + \xi (t)) = 0$
and
 $$ \begin{align} \lim_{ t \to T_+}\Big( \frac{\xi(t)}{\sqrt{T_+-t}} + \frac{\sqrt{T_+- t}}{\nu(t)} \Big) = 0, \end{align} $$
$$ \begin{align} \lim_{ t \to T_+}\Big( \frac{\xi(t)}{\sqrt{T_+-t}} + \frac{\sqrt{T_+- t}}{\nu(t)} \Big) = 0, \end{align} $$
and so that
Lemma 2.14 (No self-similar concentration in the global case).
Let
![]() $u(t)$
be the solution to (1.2) with initial data
$u(t)$
be the solution to (1.2) with initial data
![]() $u_0 \in \mathcal {E}$
. Suppose that
$u_0 \in \mathcal {E}$
. Suppose that
![]() $T_+ = \infty $
. Let
$T_+ = \infty $
. Let
![]() $y \in \mathbb {R}^2$
. Then
$y \in \mathbb {R}^2$
. Then
for any
![]() $\alpha>0$
. In particular, there exist
$\alpha>0$
. In particular, there exist
![]() $T_0 < \infty $
and a function
$T_0 < \infty $
and a function
![]() $ \xi : [T_0, \infty ) \to (0, \infty )$
such that
$ \xi : [T_0, \infty ) \to (0, \infty )$
such that
 $$ \begin{align} \lim_{ t \to T_+} \frac{\xi(t)}{\sqrt{t}} = 0, \end{align} $$
$$ \begin{align} \lim_{ t \to T_+} \frac{\xi(t)}{\sqrt{t}} = 0, \end{align} $$
and so that
Proof. Fix
![]() $y \in \mathbb {R}^2$
and
$y \in \mathbb {R}^2$
and
![]() $\alpha>0$
. Let
$\alpha>0$
. Let
![]() $\epsilon>0$
and, using (2.12), choose
$\epsilon>0$
and, using (2.12), choose
![]() $T_0>0$
so that
$T_0>0$
so that
 $$ \begin{align} \frac{4 \sqrt{E( u(0))}}{ \alpha} \Big( \int_{T_0}^\infty \| \partial_t u(t) \|_{L^2}^2 \, \mathrm{d} t \Big)^{\frac{1}{2}} \le \frac{\epsilon}{2}. \end{align} $$
$$ \begin{align} \frac{4 \sqrt{E( u(0))}}{ \alpha} \Big( \int_{T_0}^\infty \| \partial_t u(t) \|_{L^2}^2 \, \mathrm{d} t \Big)^{\frac{1}{2}} \le \frac{\epsilon}{2}. \end{align} $$
Next, let
![]() $T_1 \ge T_0$
be sufficiently large so that
$T_1 \ge T_0$
be sufficiently large so that
for all
![]() $T \ge T_1$
. Fixing any such T, we set
$T \ge T_1$
. Fixing any such T, we set
where
![]() $\chi (r)$
is a smooth function on
$\chi (r)$
is a smooth function on
![]() $(0, \infty )$
such that
$(0, \infty )$
such that
![]() $\chi (r) = 1$
for
$\chi (r) = 1$
for
![]() $r \le 1$
,
$r \le 1$
,
![]() $\chi (r) = 0$
if
$\chi (r) = 0$
if
![]() $r \ge 4$
, and
$r \ge 4$
, and
![]() $\left \lvert {\chi '(r)}\right \rvert \le 1$
for all
$\left \lvert {\chi '(r)}\right \rvert \le 1$
for all
![]() $r \in (0, \infty )$
. We now use the identity (2.16) on the time interval
$r \in (0, \infty )$
. We now use the identity (2.16) on the time interval
![]() $[T_0, T$
] and with the function
$[T_0, T$
] and with the function
![]() $\phi = \phi _T$
to obtain the inequality
$\phi = \phi _T$
to obtain the inequality
 $$ \begin{align} \frac{1}{2} \| \nabla u(T) \phi_T \|_{L^2}^2 & \le \frac{1}{2} \| \nabla u(T_0) \phi_T\|_{L^2}^2 + \int_{T_0}^T \left\lvert{\nabla u(t) }\right\rvert \left\lvert{ \partial_t u(t) }\right\rvert \left\lvert{ \nabla \phi_T}\right\rvert \phi_T\, \mathrm{d} t \nonumber\\ &\le E( u(T_0); \mathbb{R}^2 \setminus D(y, \frac{\alpha\sqrt{T}}{4})) + \frac{4 \sqrt{E( u(0))}}{ \alpha} \Big( \int_{T_0}^\infty \| \partial_t u(t) \|_{L^2}^2 \, \mathrm{d} t \Big)^{\frac{1}{2}} \le \epsilon, \end{align} $$
$$ \begin{align} \frac{1}{2} \| \nabla u(T) \phi_T \|_{L^2}^2 & \le \frac{1}{2} \| \nabla u(T_0) \phi_T\|_{L^2}^2 + \int_{T_0}^T \left\lvert{\nabla u(t) }\right\rvert \left\lvert{ \partial_t u(t) }\right\rvert \left\lvert{ \nabla \phi_T}\right\rvert \phi_T\, \mathrm{d} t \nonumber\\ &\le E( u(T_0); \mathbb{R}^2 \setminus D(y, \frac{\alpha\sqrt{T}}{4})) + \frac{4 \sqrt{E( u(0))}}{ \alpha} \Big( \int_{T_0}^\infty \| \partial_t u(t) \|_{L^2}^2 \, \mathrm{d} t \Big)^{\frac{1}{2}} \le \epsilon, \end{align} $$
which holds for all
![]() $T \ge T_1$
, completing the proof.
$T \ge T_1$
, completing the proof.
2.3. Localized sequential bubbling
The following localized sequential bubbling lemma proved in a series of works by Struwe [Reference Struwe28], Qing [Reference Qing23], Ding-Tian [Reference Ding and Tian9], Wang [Reference Wang37], Qing-Tian [Reference Qing and Tian24] and Lin-Wang [Reference Lin and Wang20]. We state as a lemma below a summary of these works, which can be found, for example, in Topping’s paper [Reference Topping30, Theorem 1.1].
Theorem 2.15 (Compactness Lemma). [Reference Qing23, Theorem 1.2], [Reference Topping30, Theorem 1.1]
Let
![]() $u_n: \mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
be a sequence of
$u_n: \mathbb {R}^2 \to \mathbb {S}^2 \subset \mathbb {R}^3$
be a sequence of
![]() $C^2$
maps such that
$C^2$
maps such that
![]() $\limsup _{n \to \infty } E( u_n) < \infty $
. Let
$\limsup _{n \to \infty } E( u_n) < \infty $
. Let
![]() $\rho _n \in (0, \infty )$
be a sequence and suppose that
$\rho _n \in (0, \infty )$
be a sequence and suppose that
Then, for every sequence
![]() $y_n \in \mathbb {R}^2$
, there exists a sequence
$y_n \in \mathbb {R}^2$
, there exists a sequence
![]() $R_n \to \infty $
a fixed integer
$R_n \to \infty $
a fixed integer
![]() $M \ge 0$
, a constant
$M \ge 0$
, a constant
![]() $C>0$
, a harmonic map
$C>0$
, a harmonic map
![]() $\omega _0$
(possibly constant), non-constant harmonic maps
$\omega _0$
(possibly constant), non-constant harmonic maps
![]() $\omega _1, \dots , \omega _M$
, and sequences of vectors
$\omega _1, \dots , \omega _M$
, and sequences of vectors
![]() $ b_{ 1, n}, \dots , b_{ M, n} \in D( y_n, C \rho _n)$
and scales
$ b_{ 1, n}, \dots , b_{ M, n} \in D( y_n, C \rho _n)$
and scales
![]() $\mu _{ 1, n}, \dots , \mu _{ M, n} \in (0, \infty )$
so that
$\mu _{ 1, n}, \dots , \mu _{ M, n} \in (0, \infty )$
so that
![]() $\max _j\mu _{j,n}/\rho _n\to 0$
as
$\max _j\mu _{j,n}/\rho _n\to 0$
as
![]() $n\to \infty $
and
$n\to \infty $
and
 $$ \begin{align} \lim_{n \to \infty} &\Bigg[ E\Big( u_n - \omega_0\big( \frac{\cdot - y_n}{ \rho_n}\big)- \sum_{j=1}^M \big( \omega_{j} \big( \frac{\cdot - b_{ j, n}}{\mu_{ j, n}} \big) - \omega_{j}(\infty) \big); D( y_n, R_n \rho_n)\Big) \nonumber\\ &\quad + \Big\|u_n - \omega_0\big( \frac{\cdot - y_n}{ \rho_n}\big) - \sum_{j=1}^M \big( \omega_{j} \big( \frac{\cdot - b_{ j, n}}{\mu_{ j, n}} \big) - \omega_{j}(\infty) \big) \Big\|_{L^\infty( D( y_n, R_n \rho_n))} \\ &\quad + \sum_{j\neq k} \Big( \frac{\mu_{j, n}}{\mu_{k, n}} + \frac{\mu_{ k, n}}{\mu_{ j, n}} + \frac{|b_{ k, n} - b_{ j, n}|^2}{\mu_{ j, n} \mu_{ k, n}} \Big)^{-1} + \sum_{j=1}^M \frac{ \mu_{ j, n}}{\operatorname{dist}( b_{ j, n} , \partial D( y_n, C\rho_n))} \Bigg] = 0. \nonumber \end{align} $$
$$ \begin{align} \lim_{n \to \infty} &\Bigg[ E\Big( u_n - \omega_0\big( \frac{\cdot - y_n}{ \rho_n}\big)- \sum_{j=1}^M \big( \omega_{j} \big( \frac{\cdot - b_{ j, n}}{\mu_{ j, n}} \big) - \omega_{j}(\infty) \big); D( y_n, R_n \rho_n)\Big) \nonumber\\ &\quad + \Big\|u_n - \omega_0\big( \frac{\cdot - y_n}{ \rho_n}\big) - \sum_{j=1}^M \big( \omega_{j} \big( \frac{\cdot - b_{ j, n}}{\mu_{ j, n}} \big) - \omega_{j}(\infty) \big) \Big\|_{L^\infty( D( y_n, R_n \rho_n))} \\ &\quad + \sum_{j\neq k} \Big( \frac{\mu_{j, n}}{\mu_{k, n}} + \frac{\mu_{ k, n}}{\mu_{ j, n}} + \frac{|b_{ k, n} - b_{ j, n}|^2}{\mu_{ j, n} \mu_{ k, n}} \Big)^{-1} + \sum_{j=1}^M \frac{ \mu_{ j, n}}{\operatorname{dist}( b_{ j, n} , \partial D( y_n, C\rho_n))} \Bigg] = 0. \nonumber \end{align} $$
In particular,
![]() $\lim _{n \to \infty } \boldsymbol {\delta }( u_n; D( y_n, \widetilde R_n \rho _n)) = 0$
for any sequence
$\lim _{n \to \infty } \boldsymbol {\delta }( u_n; D( y_n, \widetilde R_n \rho _n)) = 0$
for any sequence
![]() $1 \ll \widetilde R_n \ll R_n$
. There exist
$1 \ll \widetilde R_n \ll R_n$
. There exist
![]() $L\le M$
points
$L\le M$
points
![]() $x_{1}, \dots , x_{L} \in D(0, C)$
so that
$x_{1}, \dots , x_{L} \in D(0, C)$
so that
 $$ \begin{align} u_n(y_n + \rho_n \cdot) &\rightharpoonup \omega_0 \, \, \textrm{weakly in} \, \, H^{1}(D(0, C); \mathbb{S}^2) \nonumber\\ u_n(y_n + \rho_n \cdot) &\to \omega_0 \, \, \textrm{strongly in} \, \, W^{2, 2}_{\mathrm{loc}}(D(0, C)\setminus \{x_{1}, \dots, x_{L}\}; \mathbb{S}^2). \end{align} $$
$$ \begin{align} u_n(y_n + \rho_n \cdot) &\rightharpoonup \omega_0 \, \, \textrm{weakly in} \, \, H^{1}(D(0, C); \mathbb{S}^2) \nonumber\\ u_n(y_n + \rho_n \cdot) &\to \omega_0 \, \, \textrm{strongly in} \, \, W^{2, 2}_{\mathrm{loc}}(D(0, C)\setminus \{x_{1}, \dots, x_{L}\}; \mathbb{S}^2). \end{align} $$
For each
![]() $j \in \{1, \dots , M\}$
, there exist a finite set of points
$j \in \{1, \dots , M\}$
, there exist a finite set of points
![]() $S_j$
, possibly empty and with
$S_j$
, possibly empty and with
![]() $\# S_j \le M-1$
, such that
$\# S_j \le M-1$
, such that
Finally, there exists an integer
![]() $K \ge 0$
so that
$K \ge 0$
so that
Remark 2.16. Theorem 2.15 can be combined with Lemmas 2.13, 2.14 and the bound (2.12) to prove a sequential decomposition as in Theorem 1.1 along the well-chosen sequence of times described in Section 1.1; see, for example, [Reference Topping31, Section 2]. We note that the second statement (2.64) gives
![]() $L^\infty $
convergence on the whole disc
$L^\infty $
convergence on the whole disc
![]() $D( y_n, R_n \rho _n)$
rather than just at the scales of the bubbles, which is all that is required for
$D( y_n, R_n \rho _n)$
rather than just at the scales of the bubbles, which is all that is required for
![]() $\boldsymbol {\delta }( u_n; D(y_n, \widetilde R_n \rho _n))$
to tend to zero for
$\boldsymbol {\delta }( u_n; D(y_n, \widetilde R_n \rho _n))$
to tend to zero for
![]() $1 \ll \widetilde R_n \ll R_n$
; see Definition 1.6.
$1 \ll \widetilde R_n \ll R_n$
; see Definition 1.6.
Remark 2.17. Parker [Reference Parker22] proved an earlier version of Theorem 2.15 in the case when the sequence
![]() $u_n$
consists of harmonic maps (i.e.,
$u_n$
consists of harmonic maps (i.e.,
![]() $\mathcal T(u_n) = 0$
for each n). We use this restricted version of Theorem 2.15 (for sequences consisting only of harmonic maps) at several instances in the next section.
$\mathcal T(u_n) = 0$
for each n). We use this restricted version of Theorem 2.15 (for sequences consisting only of harmonic maps) at several instances in the next section.
3. Proofs of the main results
3.1. The minimal collision energy
For the remainder of the paper, we fix a solution
![]() $u(t)$
of (1.2), defined on the time interval
$u(t)$
of (1.2), defined on the time interval
![]() $I_+=[0, T_+)$
, where
$I_+=[0, T_+)$
, where
![]() $T_+<\infty $
in the finite time blow-up case and
$T_+<\infty $
in the finite time blow-up case and
![]() $T_+= \infty $
in the global case. We fix
$T_+= \infty $
in the global case. We fix
![]() $\gamma _0>0$
such that
$\gamma _0>0$
such that
![]() $\gamma _0 \le \min \{\frac {1}{100}, \frac {1}{100E( u_0)}\}$
and sufficiently small so that Lemma 2.4 holds. From now on, we omit the subscript
$\gamma _0 \le \min \{\frac {1}{100}, \frac {1}{100E( u_0)}\}$
and sufficiently small so that Lemma 2.4 holds. From now on, we omit the subscript
![]() $\gamma _0$
from
$\gamma _0$
from
![]() $\mathbf {d}_{\gamma _0}$
, and
$\mathbf {d}_{\gamma _0}$
, and
![]() $\boldsymbol {\delta }_{\gamma _0}$
and for a harmonic map,
$\boldsymbol {\delta }_{\gamma _0}$
and for a harmonic map,
![]() $\omega $
we write
$\omega $
we write
![]() $\lambda (\omega ) = \lambda (\omega; \gamma _0)$
and
$\lambda (\omega ) = \lambda (\omega; \gamma _0)$
and
![]() $a(\omega ) = a(\omega; \gamma _0)$
for the scale and center.
$a(\omega ) = a(\omega; \gamma _0)$
for the scale and center.
Our strategy is to study collisions of bubbles, which we define as follows.
Definition 3.1 (The minimal collision energy).
Let K be the smallest natural number with the following properties. There exist sequences
![]() $y_n \in \mathbb {R}^2$
,
$y_n \in \mathbb {R}^2$
,
![]() $\rho _n, \epsilon _n \in (0, \infty )$
,
$\rho _n, \epsilon _n \in (0, \infty )$
,
![]() $\sigma _n, \tau _n \in (0, T_+)$
and
$\sigma _n, \tau _n \in (0, T_+)$
and
![]() $\eta>0$
, with
$\eta>0$
, with
![]() $\epsilon _n \to 0$
,
$\epsilon _n \to 0$
,
![]() $0 < \sigma _n < \tau _n<T_+$
,
$0 < \sigma _n < \tau _n<T_+$
,
![]() $\sigma _n, \tau _n \to T_+$
, so that
$\sigma _n, \tau _n \to T_+$
, so that
-
1.
 $\boldsymbol {\delta }( u( \sigma _n); D(y_n, \rho _n)) \le \epsilon _n; $
$\boldsymbol {\delta }( u( \sigma _n); D(y_n, \rho _n)) \le \epsilon _n; $
-
2.
 $\boldsymbol {\delta }( u( \tau _n); D(y_n, \rho _n)) \ge \eta $
;
$\boldsymbol {\delta }( u( \tau _n); D(y_n, \rho _n)) \ge \eta $
; -
3. the interval
 $I_n:= [\sigma _n, \tau _n]$
satisfies
$I_n:= [\sigma _n, \tau _n]$
satisfies
 $| I_n | \le \epsilon _n \rho _n^2$
;
$| I_n | \le \epsilon _n \rho _n^2$
; -
4.
 $E( u(\sigma _n); D( y_n, \rho _n)) \to 4 K \pi $
as
$E( u(\sigma _n); D( y_n, \rho _n)) \to 4 K \pi $
as
 $ n \to \infty $
;
$ n \to \infty $
;
We call
![]() $[\sigma _n, \tau _n]$
a sequence of collision intervals associated to K and the parameters
$[\sigma _n, \tau _n]$
a sequence of collision intervals associated to K and the parameters
![]() $y_n, \rho _n, \epsilon _n$
and
$y_n, \rho _n, \epsilon _n$
and
![]() $\eta $
, and we write
$\eta $
, and we write
![]() $[\sigma _n, \tau _n] \in \mathcal C_K(y_n, \rho _n, \epsilon _n, \eta )$
.
$[\sigma _n, \tau _n] \in \mathcal C_K(y_n, \rho _n, \epsilon _n, \eta )$
.
Remark 3.2. By Definition 1.6 and Property (1) in Definition 3.1, we can associate to each sequence of collision intervals
![]() $[\sigma _n, \tau _n] \in \mathcal C_K(y_n, \rho _n, \epsilon _n, \eta )$
sequences
$[\sigma _n, \tau _n] \in \mathcal C_K(y_n, \rho _n, \epsilon _n, \eta )$
sequences
![]() $\xi _n, \nu _n \in (0, \infty )$
with
$\xi _n, \nu _n \in (0, \infty )$
with
![]() $\lim _{n \to \infty }( \frac { \xi _n}{\rho _n} + \frac {\rho _n}{\nu _n}) = 0$
, and a sequence of constants
$\lim _{n \to \infty }( \frac { \xi _n}{\rho _n} + \frac {\rho _n}{\nu _n}) = 0$
, and a sequence of constants
![]() $\omega _n \in \mathbb {S}^2$
so that
$\omega _n \in \mathbb {S}^2$
so that
Using Property (3) in Definition 3.1, we can always ensure (by enlarging the excised discs above) that
Then, by Lemma 2.9 and Lemma 2.12, the limits above can be propagated throughout the whole collision interval
![]() $I_n$
yielding
$I_n$
yielding
Moreover, the above holds after enlarging
![]() $\xi _n$
or shrinking
$\xi _n$
or shrinking
![]() $\nu _n$
(i.e, for any
$\nu _n$
(i.e, for any
![]() $\widetilde \xi _n, \widetilde \nu _n$
with
$\widetilde \xi _n, \widetilde \nu _n$
with
![]() $\xi _n \ll \widetilde \xi _n \ll \rho _n \ll \widetilde \nu _n \ll \nu _n$
).
$\xi _n \ll \widetilde \xi _n \ll \rho _n \ll \widetilde \nu _n \ll \nu _n$
).
Lemma 3.3 (Existence of
 $K \ge 1$
).
$K \ge 1$
).
If Theorem 1.8 is false, then K is well-defined and
![]() $K \ge 1$
.
$K \ge 1$
.
Proof of Lemma 3.3.
Assume Theorem 1.8 is false (in either the case
![]() $T_+< \infty $
or
$T_+< \infty $
or
![]() $T_+ = \infty $
). Then we can find
$T_+ = \infty $
). Then we can find
![]() $\eta>0$
, sequences
$\eta>0$
, sequences
![]() $\tau _n \to T_+$
,
$\tau _n \to T_+$
,
![]() $y_n \in \mathbb {R}^2$
,
$y_n \in \mathbb {R}^2$
,
![]() $0< \rho _n <\infty $
with
$0< \rho _n <\infty $
with
![]() $\rho _n \le \sqrt {T_+ - t_n}$
in the case
$\rho _n \le \sqrt {T_+ - t_n}$
in the case
![]() $T_+< \infty $
and
$T_+< \infty $
and
![]() $\rho _n \le \sqrt {t_n}$
in the case
$\rho _n \le \sqrt {t_n}$
in the case
![]() $T_+ = \infty $
so that
$T_+ = \infty $
so that
and sequences
![]() $\alpha _n \to 0$
and
$\alpha _n \to 0$
and
![]() $\beta _n \to \infty $
so that
$\beta _n \to \infty $
so that
In case
![]() $\rho _n \simeq \sqrt {T_+- \tau _n}$
or
$\rho _n \simeq \sqrt {T_+- \tau _n}$
or
![]() $\rho _n \simeq \sqrt {t_n}$
, the existence of
$\rho _n \simeq \sqrt {t_n}$
, the existence of
![]() $\alpha _n, \beta _n$
as above is guaranteed by Lemma 2.13 or Lemma 2.14.
$\alpha _n, \beta _n$
as above is guaranteed by Lemma 2.13 or Lemma 2.14.
We claim that there exists a sequence of times
![]() $\sigma _n < \tau _n$
,
$\sigma _n < \tau _n$
,
![]() $\sigma _n \to T_+$
, such that
$\sigma _n \to T_+$
, such that
If not, we could find numbers
![]() $c, c_0>0$
and a subsequence of the
$c, c_0>0$
and a subsequence of the
![]() $\tau _n$
so that
$\tau _n$
so that
But then
 $$ \begin{align} \int_0^{T_+} \| \mathcal T(u(t)) \|_{L^2}^2 \, \mathrm{d} t \ge \sum_n \int_{\tau_{n}- c \rho_n^2}^{\tau_{n}} \| \mathcal T(u(t)) \|_{L^2}^2 \, \mathrm{d} t \ge c_0 \sum_n \int_{\tau_{n}- c \rho_n^2}^{\tau_{n}} \rho_n^{-2} \, \mathrm{d} t = \infty, \end{align} $$
$$ \begin{align} \int_0^{T_+} \| \mathcal T(u(t)) \|_{L^2}^2 \, \mathrm{d} t \ge \sum_n \int_{\tau_{n}- c \rho_n^2}^{\tau_{n}} \| \mathcal T(u(t)) \|_{L^2}^2 \, \mathrm{d} t \ge c_0 \sum_n \int_{\tau_{n}- c \rho_n^2}^{\tau_{n}} \rho_n^{-2} \, \mathrm{d} t = \infty, \end{align} $$
and the above contradicts (2.12).
Using (2.14) from Lemma 2.9 and the fact that
![]() $|E( u(\sigma _n)) - E( u(\tau _n))| \to 0$
since
$|E( u(\sigma _n)) - E( u(\tau _n))| \to 0$
since
![]() $\sigma _n, \tau _n \to T_+$
(see Lemma 2.7), we see that (3.5) can be used to ensure that
$\sigma _n, \tau _n \to T_+$
(see Lemma 2.7), we see that (3.5) can be used to ensure that
Given the sequence
![]() $\sigma _n$
in (3.6), we can apply the Compactness Lemma 2.15 to
$\sigma _n$
in (3.6), we can apply the Compactness Lemma 2.15 to
![]() $u(\sigma _n)$
and conclude that after passing to a subsequence (which we still denote by
$u(\sigma _n)$
and conclude that after passing to a subsequence (which we still denote by
![]() $\sigma _n$
), we see that a bubble decomposition as in (2.64) holds for some sequence
$\sigma _n$
), we see that a bubble decomposition as in (2.64) holds for some sequence
![]() $R_n \to \infty $
. Because of (3.9), we see that the harmonic map
$R_n \to \infty $
. Because of (3.9), we see that the harmonic map
![]() $\omega _0$
in (2.64) must be constant (i.e.,
$\omega _0$
in (2.64) must be constant (i.e.,
![]() $\omega _0(x) = \omega \in \mathbb {S}^2$
), and we can conclude that
$\omega _0(x) = \omega \in \mathbb {S}^2$
), and we can conclude that
By Lemma 2.6, we can find an integer
![]() $K \ge 0$
so that
$K \ge 0$
so that
We have shown that Properties (1)–(4) hold for the intervals
![]() $[\sigma _n,\tau _n]$
. This proves that K is well-defined and
$[\sigma _n,\tau _n]$
. This proves that K is well-defined and
![]() $\ge 0$
.
$\ge 0$
.
We claim that
![]() $K \ge 1$
. Suppose
$K \ge 1$
. Suppose
![]() $K=0$
and
$K=0$
and
![]() $y_n, \rho _n, \epsilon _n, \sigma _n, \tau _n$
are as in Definition (3.1). But then, we can find
$y_n, \rho _n, \epsilon _n, \sigma _n, \tau _n$
are as in Definition (3.1). But then, we can find
![]() $\xi _n, \nu _n$
and
$\xi _n, \nu _n$
and
![]() $\omega \in \mathbb {S}^2$
as in (3.3) in Remark 3.2. By Lemma 2.9, we have
$\omega \in \mathbb {S}^2$
as in (3.3) in Remark 3.2. By Lemma 2.9, we have
and by (3.3) in Remark 3.2, we have
which makes it impossible for
![]() $(2)$
in Definition 3.1 to be satisfied. This proves that
$(2)$
in Definition 3.1 to be satisfied. This proves that
![]() $K \ge 1$
.
$K \ge 1$
.
3.2. Lengths of collision intervals
We assume that Theorem 1.8 is false. Let
![]() $K\ge 1$
be as in Lemma 3.3 and let
$K\ge 1$
be as in Lemma 3.3 and let
![]() $y_n \in \mathbb {R}^2$
,
$y_n \in \mathbb {R}^2$
,
![]() $\rho _n \in (0, \infty )$
,
$\rho _n \in (0, \infty )$
,
![]() $\epsilon _n \to 0$
,
$\epsilon _n \to 0$
,
![]() $0 < \sigma _n < \tau _n<T_+$
with
$0 < \sigma _n < \tau _n<T_+$
with
![]() $\sigma _n, \tau _n \to T_+$
, and
$\sigma _n, \tau _n \to T_+$
, and
![]() $\eta>0$
be a choice of parameters given by Definition 3.1 (i.e.,
$\eta>0$
be a choice of parameters given by Definition 3.1 (i.e.,
![]() $[\sigma _n, \tau _n] \in \mathcal C_K(y_n, \rho _n, \epsilon _n, \eta )$
).
$[\sigma _n, \tau _n] \in \mathcal C_K(y_n, \rho _n, \epsilon _n, \eta )$
).
Lemma 3.4 (Length of a collision interval).
There exists
![]() $\eta _0>0$
sufficiently small so that for each
$\eta _0>0$
sufficiently small so that for each
![]() $\eta \in (0, \eta _0]$
, there exists
$\eta \in (0, \eta _0]$
, there exists
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $c_0>0$
with the following properties. Let
$c_0>0$
with the following properties. Let
![]() $[\sigma , \tau ] \subset [\sigma _n, \tau _n]$
be any subinterval such that
$[\sigma , \tau ] \subset [\sigma _n, \tau _n]$
be any subinterval such that
and let
![]() $\omega \in \mathbb {S}^2$
and
$\omega \in \mathbb {S}^2$
and
![]() $ \omega _1, \dots , \omega _M$
be any collection of non-constant harmonic maps, and
$ \omega _1, \dots , \omega _M$
be any collection of non-constant harmonic maps, and
![]() $\vec \nu = (\nu , \nu _{1}, \dots , \nu _{M}), \vec \xi = (\xi , \xi _{1}, \dots , \xi _{M}) \in (0, \infty )^{M+1}$
any admissible vectors in the sense of Definition 1.6 such that
$\vec \nu = (\nu , \nu _{1}, \dots , \nu _{M}), \vec \xi = (\xi , \xi _{1}, \dots , \xi _{M}) \in (0, \infty )^{M+1}$
any admissible vectors in the sense of Definition 1.6 such that
Then
Corollary 3.5. Let
![]() $\eta _0>0$
be as in Lemma 3.4,
$\eta _0>0$
be as in Lemma 3.4,
![]() $\eta \in (0, \eta _0]$
, and
$\eta \in (0, \eta _0]$
, and
![]() $[\sigma _n, \tau _n] \in \mathcal C_K(y_n, \rho _n, \epsilon _n, \eta )$
. Then there exist
$[\sigma _n, \tau _n] \in \mathcal C_K(y_n, \rho _n, \epsilon _n, \eta )$
. Then there exist
![]() $\epsilon \in (0, \eta )$
,
$\epsilon \in (0, \eta )$
,
![]() $c_0>0\ n_0 \in \mathbb {N}$
and
$c_0>0\ n_0 \in \mathbb {N}$
and
![]() $s_n \in (\sigma _n, \tau _n)$
such that for all
$s_n \in (\sigma _n, \tau _n)$
such that for all
![]() $n \ge n_0$
, the following conclusions hold. First,
$n \ge n_0$
, the following conclusions hold. First,
Moreover, for each
![]() $n \ge n_0$
, let
$n \ge n_0$
, let
![]() $M_n \in \mathbb {N}$
, and
$M_n \in \mathbb {N}$
, and
![]() $\mathcal Q(\boldsymbol {\omega }_n)$
be any sequence of
$\mathcal Q(\boldsymbol {\omega }_n)$
be any sequence of
![]() $M_n$
-bubble configurations, and let
$M_n$
-bubble configurations, and let
![]() $\vec \nu _n = (\nu _{n}, \nu _{1, n}, \dots , \nu _{M, n}), \vec \xi _n = (\xi _{n}, \xi _{1, n}, \dots , \xi _{M, n}) \in (0, \infty )^{M+1}$
be any admissible sequences in the sense of Definition 1.6 such that
$\vec \nu _n = (\nu _{n}, \nu _{1, n}, \dots , \nu _{M, n}), \vec \xi _n = (\xi _{n}, \xi _{1, n}, \dots , \xi _{M, n}) \in (0, \infty )^{M+1}$
be any admissible sequences in the sense of Definition 1.6 such that
for each n, and define
Then
![]() $s_n + c_0 \lambda _{\max }(s_n)^2 \le \tau _n$
, and
$s_n + c_0 \lambda _{\max }(s_n)^2 \le \tau _n$
, and
We make the following definitions.
Definition 3.6. We say that two triples
![]() $(\omega _j, a_{ j, n}, \lambda _{j, n})$
and
$(\omega _j, a_{ j, n}, \lambda _{j, n})$
and
![]() $(\omega _{j'}, a_{ j', n}, \lambda _{j', n})$
where
$(\omega _{j'}, a_{ j', n}, \lambda _{j', n})$
where
![]() $\omega _j, \omega _{j'}$
are nontrivial harmonic maps,
$\omega _j, \omega _{j'}$
are nontrivial harmonic maps,
![]() $a_{ j, n}, a_{ j', n} \in \mathbb {R}^2$
are sequences of vectors in
$a_{ j, n}, a_{ j', n} \in \mathbb {R}^2$
are sequences of vectors in
![]() $\mathbb {R}^2$
, and
$\mathbb {R}^2$
, and
![]() $\lambda _{ j, n}, \lambda _{ j', n} \in (0, \infty )$
are sequences of scales, are asymptotically orthogonal if
$\lambda _{ j, n}, \lambda _{ j', n} \in (0, \infty )$
are sequences of scales, are asymptotically orthogonal if
 $$ \begin{align} \lim_{n \to \infty} \Big( \frac{\lambda_{ j, n}}{\lambda_{ j', n}} + \frac{\lambda_{ j', n}}{\lambda_{ j, n}} + \frac{\left\lvert{ a_{ j, n} - a_{ j', n}}\right\rvert^2}{\lambda_{ j, n} \lambda_{ j', n}} \Big) = \infty. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \Big( \frac{\lambda_{ j, n}}{\lambda_{ j', n}} + \frac{\lambda_{ j', n}}{\lambda_{ j, n}} + \frac{\left\lvert{ a_{ j, n} - a_{ j', n}}\right\rvert^2}{\lambda_{ j, n} \lambda_{ j', n}} \Big) = \infty. \end{align} $$
Definition 3.7. We say that a sequence of nontrivial harmonic maps
![]() $ \mathfrak {h} = \{\omega _{n}\}_{n =1}^\infty $
is a descendant sequence of an ancestor sequence of harmonic maps
$ \mathfrak {h} = \{\omega _{n}\}_{n =1}^\infty $
is a descendant sequence of an ancestor sequence of harmonic maps
![]() $\mathfrak {H} = \{\Omega _{n}\}_{n =1}^\infty $
if
$\mathfrak {H} = \{\Omega _{n}\}_{n =1}^\infty $
if
![]() $\frac {\lambda (\Omega _{n})}{\lambda (\omega _{n})} \to \infty $
, and there exists a constant
$\frac {\lambda (\Omega _{n})}{\lambda (\omega _{n})} \to \infty $
, and there exists a constant
![]() $C>0$
so that the discs
$C>0$
so that the discs
![]() $D( a(\omega _{n}), \lambda (\omega _{n})) \subset D(a(\Omega _{n}), C \lambda (\Omega _{ n}))$
for all sufficiently large n. We denote this relation by
$D( a(\omega _{n}), \lambda (\omega _{n})) \subset D(a(\Omega _{n}), C \lambda (\Omega _{ n}))$
for all sufficiently large n. We denote this relation by
![]() $\{\omega _n\}\prec \{\Omega _n\}$
, and
$\{\omega _n\}\prec \{\Omega _n\}$
, and
![]() $\{\omega _n\}\preceq \{\Omega _n\}$
allows for equality. Given a natural number M, a collection of sequences of harmonic maps
$\{\omega _n\}\preceq \{\Omega _n\}$
allows for equality. Given a natural number M, a collection of sequences of harmonic maps
![]() $(\mathfrak {h}_1, \dots , \mathfrak {h}_M) = ( \{\omega _{1, n}\}_{n =1}^\infty , \dots , \{\omega _{1, n}\}_{n =1}^\infty )$
with asymptotically orthogonal centers and scales are partially ordered by
$(\mathfrak {h}_1, \dots , \mathfrak {h}_M) = ( \{\omega _{1, n}\}_{n =1}^\infty , \dots , \{\omega _{1, n}\}_{n =1}^\infty )$
with asymptotically orthogonal centers and scales are partially ordered by
![]() $\preceq $
. The roots are defined to be the maximal elements relative to this partial order. In other words, a sequence of harmonic maps
$\preceq $
. The roots are defined to be the maximal elements relative to this partial order. In other words, a sequence of harmonic maps
![]() $\mathfrak {h}_j$
is a root if it is not a descendant sequence of any ancestor sequence
$\mathfrak {h}_j$
is a root if it is not a descendant sequence of any ancestor sequence
![]() $\mathfrak {h}_{j'}$
for any
$\mathfrak {h}_{j'}$
for any
![]() $j' \in \{1, \dots , M\}$
. We denote by
$j' \in \{1, \dots , M\}$
. We denote by
Finally, to each root
![]() $\mathfrak {h}_{j}$
, we can associate a bubble tree
$\mathfrak {h}_{j}$
, we can associate a bubble tree
![]() $\mathcal T(j):= \{ \mathfrak {h}_{j'} \mid \mathfrak {h}_{j'} \preceq \mathfrak {h}_j\}$
.
$\mathcal T(j):= \{ \mathfrak {h}_{j'} \mid \mathfrak {h}_{j'} \preceq \mathfrak {h}_j\}$
.
Proof of Lemma 3.4.
If the Lemma were false, we could find intervals
![]() $[s_n, t_n] \subset [\sigma _n, \tau _n]$
so that
$[s_n, t_n] \subset [\sigma _n, \tau _n]$
so that
integers
![]() $M_n \ge 0$
, sequences of
$M_n \ge 0$
, sequences of
![]() $M_n$
-bubble configurations
$M_n$
-bubble configurations
![]() $\mathcal Q(\boldsymbol {\omega }_n)$
, and sequences of vectors
$\mathcal Q(\boldsymbol {\omega }_n)$
, and sequences of vectors
![]() $\vec \nu _n = (\nu _n, \nu _{1, n}, \dots , \nu _{M_n, n}) \in (0, \infty )^{M_n+1}, \vec \xi _n = (\xi _n, \xi _{1, n}, \dots , \xi _{M_n, n}) \in (0, \infty )^{M_n+1}$
such that
$\vec \nu _n = (\nu _n, \nu _{1, n}, \dots , \nu _{M_n, n}) \in (0, \infty )^{M_n+1}, \vec \xi _n = (\xi _n, \xi _{1, n}, \dots , \xi _{M_n, n}) \in (0, \infty )^{M_n+1}$
such that
and so that for
![]() $\lambda _{\max , n}:= \max _{j =1, \dots , M_n} \lambda ( \omega _{j, n})$
, we have
$\lambda _{\max , n}:= \max _{j =1, \dots , M_n} \lambda ( \omega _{j, n})$
, we have
 $$ \begin{align} \lim_{n \to \infty} \frac{(t_n - s_n)^{\frac{1}{2}}}{\lambda_{\max, n}} = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \frac{(t_n - s_n)^{\frac{1}{2}}}{\lambda_{\max, n}} = 0. \end{align} $$
Passing to a subsequence, we may assume that
![]() $M_n = M$
is a fixed integer and
$M_n = M$
is a fixed integer and
![]() $\omega _{ n} = \omega \in \mathbb {S}^2$
is a fixed constant.
$\omega _{ n} = \omega \in \mathbb {S}^2$
is a fixed constant.
Consider the sequences of harmonic maps,
![]() $\mathfrak {h}_j = \{\omega _{j, n}\}_{n =1}^\infty $
, for
$\mathfrak {h}_j = \{\omega _{j, n}\}_{n =1}^\infty $
, for
![]() $j = 1, \dots , M$
, together with sequences of centers
$j = 1, \dots , M$
, together with sequences of centers
![]() $a(\omega _{j, n})$
and scales
$a(\omega _{j, n})$
and scales
![]() $\lambda (\omega _{j, n})$
, and the partial order
$\lambda (\omega _{j, n})$
, and the partial order
![]() $\prec $
on
$\prec $
on
![]() $( \mathfrak {h}_1, \dots , \mathfrak {h}_M)$
as in Definition 3.7. Using the language of Definition 3.7, we observe that, after passing to a subsequence in n, there exists a sequence
$( \mathfrak {h}_1, \dots , \mathfrak {h}_M)$
as in Definition 3.7. Using the language of Definition 3.7, we observe that, after passing to a subsequence in n, there exists a sequence
![]() $\widetilde R_n \to \infty $
so that for any root sequences
$\widetilde R_n \to \infty $
so that for any root sequences
![]() $\mathfrak {h}_j = \{\omega _{j, n}\}_{n =1}^\infty $
,
$\mathfrak {h}_j = \{\omega _{j, n}\}_{n =1}^\infty $
,
![]() $\mathfrak {h}_{j'} = \{\omega _{j, n}\}_{n =1}^\infty $
with
$\mathfrak {h}_{j'} = \{\omega _{j, n}\}_{n =1}^\infty $
with
![]() $j, j' \in \mathcal {R}$
, the discs
$j, j' \in \mathcal {R}$
, the discs
![]() $D( a(\omega _{j, n}), 4R_n\lambda (\omega _{j, n}))$
and
$D( a(\omega _{j, n}), 4R_n\lambda (\omega _{j, n}))$
and
![]() $D( a(\omega _{j', n}), 4R_n\lambda (\omega _{j', n}))$
are disjoint for each n for any sequence
$D( a(\omega _{j', n}), 4R_n\lambda (\omega _{j', n}))$
are disjoint for each n for any sequence
![]() $R_n \le \widetilde R_n$
. By Lemma 2.4,
$R_n \le \widetilde R_n$
. By Lemma 2.4,
for each
![]() $j \in \mathcal R$
and for any sequence
$j \in \mathcal R$
and for any sequence
![]() $R_n \to \infty $
, and hence, by (3.24),
$R_n \to \infty $
, and hence, by (3.24),
 $$ \begin{align} \lim_{n \to \infty} E( u(s_n); D( y_n, \rho_n) \setminus \bigcup_{ j \in \mathcal R} D( a( \omega_{j, n}), 4^{-1}R_n \lambda(\omega_{j, n}))) = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E( u(s_n); D( y_n, \rho_n) \setminus \bigcup_{ j \in \mathcal R} D( a( \omega_{j, n}), 4^{-1}R_n \lambda(\omega_{j, n}))) = 0 \end{align} $$
for any sequence
![]() $R_n \to \infty $
.
$R_n \to \infty $
.
Each of the sequences
![]() $\{\omega _{j, n}\}_{n =1}^\infty $
for
$\{\omega _{j, n}\}_{n =1}^\infty $
for
![]() $j \in \{1, \dots , M\}$
satisfies the hypothesis of the Compactness Lemma 2.15 (noting that
$j \in \{1, \dots , M\}$
satisfies the hypothesis of the Compactness Lemma 2.15 (noting that
![]() $\mathcal T(\omega _{j, n}) = 0$
since
$\mathcal T(\omega _{j, n}) = 0$
since
![]() $\omega _{j, n}$
is harmonic), and passing to a (joint) subsequence, we can find non-negative integers
$\omega _{j, n}$
is harmonic), and passing to a (joint) subsequence, we can find non-negative integers
![]() $M_j$
, a sequence
$M_j$
, a sequence
![]() $\breve R_n \le \widetilde R_n$
with
$\breve R_n \le \widetilde R_n$
with
![]() $1 \ll \breve R_n \ll \xi _n \lambda _{\max , n}^{-1}$
, harmonic maps
$1 \ll \breve R_n \ll \xi _n \lambda _{\max , n}^{-1}$
, harmonic maps
![]() $\omega _{j, 0}$
(possibly constant), nontrivial harmonic maps
$\omega _{j, 0}$
(possibly constant), nontrivial harmonic maps
![]() $\theta _{j, k}$
, scales
$\theta _{j, k}$
, scales
![]() $\mu _{j, k, n} \ll \lambda (\omega _{j, n})$
and centers
$\mu _{j, k, n} \ll \lambda (\omega _{j, n})$
and centers
![]() $b_{j, k, n}\in D(a(\omega _{ j, n}),C \lambda (\omega _{ j, n}))$
for each j and where
$b_{j, k, n}\in D(a(\omega _{ j, n}),C \lambda (\omega _{ j, n}))$
for each j and where
![]() $k \in \{1, \dots , M_j\}$
, satisfying (2.65), (2.66), and so that
$k \in \{1, \dots , M_j\}$
, satisfying (2.65), (2.66), and so that
 $$ \begin{align} &\lim_{n \to \infty} \Bigg[E\Big( \omega_{ j, n} - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda(\omega_{j, n})}\Big)- \sum_{k =1}^{M_j} \big(\theta_{j, k}\Big( \frac{ \cdot - b_{j, k, n}}{ \mu_{j, k, n}} \Big) - \theta_{j, k}( \infty)\big); D_{j,n} \Big) \nonumber \\&\quad + \Big\| \omega_{ j, n} - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda(\omega_{j, n})}\Big)- \sum_{k =1}^{M_j} \big(\theta_{j, k}\Big( \frac{ \cdot - b_{j, k, n}}{ \mu_{j, k, n}} \Big) - \theta_{j, k}( \infty)\big)\Big\|_{L^\infty( D_{j,n})} \nonumber \\&\quad + \sum_{k \neq k'} \Big( \frac{ \mu_{ j, k, n}}{\mu_{j, k', n}} + \frac{ \mu_{ j, k', n}}{\mu_{ j, k, n}} + \frac{| b_{ j, k, n} - b_{ j, k', n} |^{2}}{\mu_{ j, k, n} \mu_{j, k', n}} \Big)^{-1} + \sum_{k =1}^{M_j} \frac{ \mu_{j, k, n}}{\operatorname{dist}( b_{j, k, n}, \partial D(a(\omega_{ j, n}),C \lambda(\omega_{ j, n}))} \Bigg]= 0, \end{align} $$
$$ \begin{align} &\lim_{n \to \infty} \Bigg[E\Big( \omega_{ j, n} - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda(\omega_{j, n})}\Big)- \sum_{k =1}^{M_j} \big(\theta_{j, k}\Big( \frac{ \cdot - b_{j, k, n}}{ \mu_{j, k, n}} \Big) - \theta_{j, k}( \infty)\big); D_{j,n} \Big) \nonumber \\&\quad + \Big\| \omega_{ j, n} - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda(\omega_{j, n})}\Big)- \sum_{k =1}^{M_j} \big(\theta_{j, k}\Big( \frac{ \cdot - b_{j, k, n}}{ \mu_{j, k, n}} \Big) - \theta_{j, k}( \infty)\big)\Big\|_{L^\infty( D_{j,n})} \nonumber \\&\quad + \sum_{k \neq k'} \Big( \frac{ \mu_{ j, k, n}}{\mu_{j, k', n}} + \frac{ \mu_{ j, k', n}}{\mu_{ j, k, n}} + \frac{| b_{ j, k, n} - b_{ j, k', n} |^{2}}{\mu_{ j, k, n} \mu_{j, k', n}} \Big)^{-1} + \sum_{k =1}^{M_j} \frac{ \mu_{j, k, n}}{\operatorname{dist}( b_{j, k, n}, \partial D(a(\omega_{ j, n}),C \lambda(\omega_{ j, n}))} \Bigg]= 0, \end{align} $$
where
![]() $D_{j,n}:=D(a(\omega _{ j, n}), 4 R_n \lambda (\omega _{ j, n}))$
,
$D_{j,n}:=D(a(\omega _{ j, n}), 4 R_n \lambda (\omega _{ j, n}))$
,
![]() $C>0$
is some finite constant, and
$C>0$
is some finite constant, and
![]() $R_n$
is a sequence, to be fixed below, such that
$R_n$
is a sequence, to be fixed below, such that
![]() $1 \ll R_n \le \breve R_n$
. In this decomposition, we distinguish the (possibly constant) harmonic maps
$1 \ll R_n \le \breve R_n$
. In this decomposition, we distinguish the (possibly constant) harmonic maps
![]() $\omega _{j, 0}$
, which arise as the weak limits
$\omega _{j, 0}$
, which arise as the weak limits
![]() $\omega _{j, n}\big ( \lambda (\omega _{j, n})( \cdot + a( \omega _{j, n}))\big ) \rightharpoonup \omega _{j, 0}$
, and we call these the body maps associated to the sequence
$\omega _{j, n}\big ( \lambda (\omega _{j, n})( \cdot + a( \omega _{j, n}))\big ) \rightharpoonup \omega _{j, 0}$
, and we call these the body maps associated to the sequence
![]() $\mathfrak {h}_j = \{\omega _{j, n}\}_{n =1}^\infty $
.
$\mathfrak {h}_j = \{\omega _{j, n}\}_{n =1}^\infty $
.
Define the set of indices
 $$ \begin{align} \mathcal J_{\max}:= \Big\{ j \in \{1, \dots, M\} \mid C_j^{-1} \le \frac{\lambda_{\max, n}}{\lambda( \omega_{j, n})} \le C_j, \,\, \textrm{for each}\,\, n\, \, \textrm{for some} \, \, C_j>1\Big\} \end{align} $$
$$ \begin{align} \mathcal J_{\max}:= \Big\{ j \in \{1, \dots, M\} \mid C_j^{-1} \le \frac{\lambda_{\max, n}}{\lambda( \omega_{j, n})} \le C_j, \,\, \textrm{for each}\,\, n\, \, \textrm{for some} \, \, C_j>1\Big\} \end{align} $$
and let
 $$ \begin{align} 4 \pi K_0 := \sum_{j \in \mathcal J_{\max}} E( \omega_{j, 0}). \end{align} $$
$$ \begin{align} 4 \pi K_0 := \sum_{j \in \mathcal J_{\max}} E( \omega_{j, 0}). \end{align} $$
That is,
![]() $4 \pi K_0$
is the sum of the energies of the body maps associated to the
$4 \pi K_0$
is the sum of the energies of the body maps associated to the
![]() $\omega _{j, n}$
arising from indices
$\omega _{j, n}$
arising from indices
![]() $j \in \mathcal J_{\max }$
. Note that
$j \in \mathcal J_{\max }$
. Note that
![]() $\mathcal J_{\max }$
is a (possibly strict) subset of the set of indices
$\mathcal J_{\max }$
is a (possibly strict) subset of the set of indices
![]() $\mathcal R$
associated to the roots.
$\mathcal R$
associated to the roots.
Case 1: First suppose that
![]() $K_0 = K$
, which means that
$K_0 = K$
, which means that
![]() $\mathcal J_{\max } = \mathcal R = \{1, \dots , M\}$
and all of the energy in
$\mathcal J_{\max } = \mathcal R = \{1, \dots , M\}$
and all of the energy in
![]() $D( y_n, \rho _n)$
is captured by the body maps. In this case, the sequences
$D( y_n, \rho _n)$
is captured by the body maps. In this case, the sequences
![]() $\{\omega _{j, n}\}$
have no concentrating bubbles – that is,
$\{\omega _{j, n}\}$
have no concentrating bubbles – that is,
![]() $M_j = 0$
for each j, and we have
$M_j = 0$
for each j, and we have
 $$ \begin{align} \lim_{n \to \infty} E\Big( \omega_{ j, n} - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda(\omega_{j, n})}\Big); D(a(\omega_{ j, n}), 4R_n \lambda(\omega_{j, n}))\Big) = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( \omega_{ j, n} - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda(\omega_{j, n})}\Big); D(a(\omega_{ j, n}), 4R_n \lambda(\omega_{j, n}))\Big) = 0 \end{align} $$
and
 $$ \begin{align} \lim_{n \to \infty} \Big\| \omega_{j, n} - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda_{\max, n}}\Big)\Big\|_{L^{\infty}( D(a(\omega_{j, n}), 4R_n \lambda_{\max, n}))} = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \Big\| \omega_{j, n} - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda_{\max, n}}\Big)\Big\|_{L^{\infty}( D(a(\omega_{j, n}), 4R_n \lambda_{\max, n}))} = 0 \end{align} $$
for each
![]() $j \in \{1, \dots , M\}$
. Using (3.24), the fact that
$j \in \{1, \dots , M\}$
. Using (3.24), the fact that
![]() $\lambda ( \omega _{j, n}) \simeq \lambda _{\max , n}$
for each
$\lambda ( \omega _{j, n}) \simeq \lambda _{\max , n}$
for each
![]() $j \in \{1, \dots , M\}$
, and the above, we can now fix (for Case 1) a sequence
$j \in \{1, \dots , M\}$
, and the above, we can now fix (for Case 1) a sequence
![]() $R_n \le \breve R_n$
so that
$R_n \le \breve R_n$
so that
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(s_n) - \omega_{j, 0}\big( \frac{ \cdot - a( \omega_{j, n})}{\lambda(\omega_{j, n})}\big); D( a(\omega_{j, n}), 4 R_n \lambda_{\max, n})\Big) = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(s_n) - \omega_{j, 0}\big( \frac{ \cdot - a( \omega_{j, n})}{\lambda(\omega_{j, n})}\big); D( a(\omega_{j, n}), 4 R_n \lambda_{\max, n})\Big) = 0 \end{align} $$
and
 $$ \begin{align} \lim_{n \to \infty} \Big\| u(s_n) - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda_{\max, n}}\Big)\Big\|_{L^{\infty}( D(a(\omega_{j, n}), 4 R_n \lambda_{\max, n}))} = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \Big\| u(s_n) - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda_{\max, n}}\Big)\Big\|_{L^{\infty}( D(a(\omega_{j, n}), 4 R_n \lambda_{\max, n}))} = 0 \end{align} $$
for each
![]() $j \in \{1, \dots , M\}$
(i.e., we need to additionally ensure that
$j \in \{1, \dots , M\}$
(i.e., we need to additionally ensure that
![]() $4R_n \lambda _{\max , n} \le \min \{ \nu _{j, n}\}_{j =1}^M$
). Using Lemma 2.10 and Lemma 2.12 along with the fact that
$4R_n \lambda _{\max , n} \le \min \{ \nu _{j, n}\}_{j =1}^M$
). Using Lemma 2.10 and Lemma 2.12 along with the fact that
![]() $(t_n - s_n)^{\frac {1}{2}} \ll \lambda _{\max , n}$
, we can propagate these estimates to time
$(t_n - s_n)^{\frac {1}{2}} \ll \lambda _{\max , n}$
, we can propagate these estimates to time
![]() $t_n$
– that is,
$t_n$
– that is,
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n) - \omega_{j, 0}\big( \frac{ \cdot - a( \omega_{j, n})}{\lambda(\omega_{j, n})}\big); D( a(\omega_{j, n}), R_n \lambda_{\max, n})\Big) = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n) - \omega_{j, 0}\big( \frac{ \cdot - a( \omega_{j, n})}{\lambda(\omega_{j, n})}\big); D( a(\omega_{j, n}), R_n \lambda_{\max, n})\Big) = 0 \end{align} $$
and
 $$ \begin{align} \lim_{n \to \infty} \Big\| u(t_n) - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda_{\max, n}}\Big)\Big\|_{L^{\infty}( D(a(\omega_{j, n}), R_n \lambda_{\max, n}))} = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \Big\| u(t_n) - \omega_{j, 0}\Big( \frac{ \cdot - a( \omega_{j, n})}{\lambda_{\max, n}}\Big)\Big\|_{L^{\infty}( D(a(\omega_{j, n}), R_n \lambda_{\max, n}))} = 0 \end{align} $$
for each
![]() $j \in \{1, \dots , M\}$
. Using Lemma 2.9 and that
$j \in \{1, \dots , M\}$
. Using Lemma 2.9 and that
![]() $(t_n - s_n)^{\frac {1}{2}} \ll \lambda _{\max , n}$
, we can also propagate (3.27) to time
$(t_n - s_n)^{\frac {1}{2}} \ll \lambda _{\max , n}$
, we can also propagate (3.27) to time
![]() $t_n$
, deducing
$t_n$
, deducing
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D(y_n, \rho_n) \setminus \bigcup_{j =1}^M D( a(\omega_{j, n}); R_n \lambda_{\max, n})\Big) = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D(y_n, \rho_n) \setminus \bigcup_{j =1}^M D( a(\omega_{j, n}); R_n \lambda_{\max, n})\Big) = 0. \end{align} $$
Combining (3.35), (3.36), (3.37), the disjointness of the discs
![]() $D(a(\omega _{j, n}), R_n \lambda (\omega _{j, n}))$
, the asymptotic orthogonality of the triples
$D(a(\omega _{j, n}), R_n \lambda (\omega _{j, n}))$
, the asymptotic orthogonality of the triples
![]() $(\omega _{j, 0}, a(\omega _{j, n}), \lambda (\omega _{j, n}))$
, and Remark 3.2, we find that
$(\omega _{j, 0}, a(\omega _{j, n}), \lambda (\omega _{j, n}))$
, and Remark 3.2, we find that
which contradicts (3.23).
Case 2: Next, consider the case
![]() $K_0 < K$
. We show this case leads to a contradiction with the minimality of K. Again, we will need
$K_0 < K$
. We show this case leads to a contradiction with the minimality of K. Again, we will need
![]() $R_n \to \infty $
such that
$R_n \to \infty $
such that
![]() $4R_n \lambda _{\max , n} \le \min \{\nu _{j, n}\}_{j \in \mathcal J_{\max }} $
and
$4R_n \lambda _{\max , n} \le \min \{\nu _{j, n}\}_{j \in \mathcal J_{\max }} $
and
![]() $R_n \le \breve R_n$
.
$R_n \le \breve R_n$
.
We claim there exists an integer
![]() $L \ge 1$
, sequences
$L \ge 1$
, sequences
![]() $\{ x_{\ell , n} \}_{\ell =1}^L$
with
$\{ x_{\ell , n} \}_{\ell =1}^L$
with
![]() $x_{\ell , n} \in D(y_n, \xi _n)$
for each n and each
$x_{\ell , n} \in D(y_n, \xi _n)$
for each n and each
![]() $\ell \in \{1, \dots , L\}$
, and a sequence
$\ell \in \{1, \dots , L\}$
, and a sequence
![]() $r_n$
such that
$r_n$
such that
such that the discs
![]() $D(x_{\ell , n}, r_n)$
are disjoint for
$D(x_{\ell , n}, r_n)$
are disjoint for
![]() $\ell \in \{1, \dots , L\}$
and satisfy
$\ell \in \{1, \dots , L\}$
and satisfy
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(s_n); \bigcup_{\ell =1}^L D( x_{ \ell, n}, r_n)\Big) = 4\pi K - 4 \pi K_0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(s_n); \bigcup_{\ell =1}^L D( x_{ \ell, n}, r_n)\Big) = 4\pi K - 4 \pi K_0 \end{align} $$
as well as
for
![]() $\ell \neq \ell '$
, and finally such that there exist sequences
$\ell \neq \ell '$
, and finally such that there exist sequences
![]() $\alpha _n \to 0, \beta _n \to \infty $
so that
$\alpha _n \to 0, \beta _n \to \infty $
so that
 $$ \begin{align} \lim_{n \to \infty} \sum_{ \ell = 1}^L E( u(s_n); D( x_{ \ell, n}, \beta_n r_n) \setminus D( x_{ \ell, n}, \alpha_n r_n)) = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \sum_{ \ell = 1}^L E( u(s_n); D( x_{ \ell, n}, \beta_n r_n) \setminus D( x_{ \ell, n}, \alpha_n r_n)) = 0 \end{align} $$
and a sequence
![]() $\breve \xi _n$
so that
$\breve \xi _n$
so that
We construct a set of sequences
![]() $\mathcal P:=\{ \{x_{\ell ,n}\}\: :\:1\le \ell \le L \}$
and the radii
$\mathcal P:=\{ \{x_{\ell ,n}\}\: :\:1\le \ell \le L \}$
and the radii
![]() $\{r_n\}$
as follows. Any root
$\{r_n\}$
as follows. Any root
![]() $\mathfrak {h}_j$
with
$\mathfrak {h}_j$
with
![]() $j\in \mathcal J_{\max }$
we call a dominant root. For any dominant root
$j\in \mathcal J_{\max }$
we call a dominant root. For any dominant root
![]() $\mathfrak {h}_{j_0}$
, we define
$\mathfrak {h}_{j_0}$
, we define
![]() $\mathcal T(j_0)=\{ \mathfrak {h}_j\preceq \mathfrak {h}_{j_0} \}$
as the bubble tree with root
$\mathcal T(j_0)=\{ \mathfrak {h}_j\preceq \mathfrak {h}_{j_0} \}$
as the bubble tree with root
![]() $\mathfrak {h}_{j_0}$
, and
$\mathfrak {h}_{j_0}$
, and
![]() $\mathcal D(j_0)$
as the maximal elements of the pruned tree
$\mathcal D(j_0)$
as the maximal elements of the pruned tree
![]() $\mathcal T(j_0)\setminus \{ \mathfrak {h}_{j_0} \}$
.
$\mathcal T(j_0)\setminus \{ \mathfrak {h}_{j_0} \}$
.
We define
![]() $\mathcal P_0$
as the points
$\mathcal P_0$
as the points
![]() $y_{ \ell , n}$
for
$y_{ \ell , n}$
for
![]() $\ell \in \{1, \dots , L'\}$
as an enumeration of all (i)
$\ell \in \{1, \dots , L'\}$
as an enumeration of all (i)
![]() $a(\omega _{ j, n})$
with
$a(\omega _{ j, n})$
with
![]() $\mathfrak {h}_j \in \mathcal R \setminus \mathcal J_{\max }$
(i.e., the centers of the roots that are not dominant), (ii)
$\mathfrak {h}_j \in \mathcal R \setminus \mathcal J_{\max }$
(i.e., the centers of the roots that are not dominant), (ii)
![]() $a(\omega _{ j, n})$
with
$a(\omega _{ j, n})$
with
![]() $\mathfrak {h}_j \in \mathcal D(j_0)$
for some
$\mathfrak {h}_j \in \mathcal D(j_0)$
for some
![]() $j_0 \in \mathcal J_{\max , n}$
and (iii) sequences
$j_0 \in \mathcal J_{\max , n}$
and (iii) sequences
![]() $b_{ j_0, k, n}$
associated to harmonic maps
$b_{ j_0, k, n}$
associated to harmonic maps
![]() $\theta _{j_0, k} \big ( \frac { \cdot - b_{j_0, k, n}}{\mu _{ j_0, k, n}}\big )$
for some
$\theta _{j_0, k} \big ( \frac { \cdot - b_{j_0, k, n}}{\mu _{ j_0, k, n}}\big )$
for some
![]() $j_0 \in \mathcal J_{\max , n}$
that are
$j_0 \in \mathcal J_{\max , n}$
that are
-
• asymptotically orthogonal to every
 $\mathfrak {h}_j \in \mathcal D(j_0)$
$\mathfrak {h}_j \in \mathcal D(j_0)$
-
• not descendants of any
 $\mathfrak {h}_j \in \mathcal D(j_0)$
.
$\mathfrak {h}_j \in \mathcal D(j_0)$
.
Passing to a joint subsequence, we can assume that the limits
 $$ \begin{align} \lim_{n \to \infty} \frac{(t_n - s_n)^{\frac{1}{2}}}{ \operatorname{dist}( y_{\ell', n}, y_{ \ell, n})} \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \frac{(t_n - s_n)^{\frac{1}{2}}}{ \operatorname{dist}( y_{\ell', n}, y_{ \ell, n})} \end{align} $$
exist in
![]() $[0, \infty ]$
for all
$[0, \infty ]$
for all
![]() $\ell \neq \ell ' \in \{1, \dots , L'\}$
. We define
$\ell \neq \ell ' \in \{1, \dots , L'\}$
. We define
![]() $\mathcal P$
by means of
$\mathcal P$
by means of
![]() $\mathcal P_0$
by the following algorithm: we include the sequence
$\mathcal P_0$
by the following algorithm: we include the sequence
![]() $y_{ \ell _0, n}\in \mathcal P_0$
in the set
$y_{ \ell _0, n}\in \mathcal P_0$
in the set
![]() $\mathcal P$
if
$\mathcal P$
if
 $$ \begin{align} \lim_{n \to \infty} \frac{(t_n - s_n)^{\frac{1}{2}}}{ \operatorname{dist}( y_{ \ell_0, n}, y_{ \ell, n})} = 0, \quad \forall \ell \in \{1, \dots, L')\}\setminus \ell_0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \frac{(t_n - s_n)^{\frac{1}{2}}}{ \operatorname{dist}( y_{ \ell_0, n}, y_{ \ell, n})} = 0, \quad \forall \ell \in \{1, \dots, L')\}\setminus \ell_0. \end{align} $$
For those
![]() $y_{\ell _0, n}\in \mathcal P_0$
for which the above does not hold, we define the sets
$y_{\ell _0, n}\in \mathcal P_0$
for which the above does not hold, we define the sets
 $$ \begin{align} \mathcal B(\ell_0) := \Big\{ \ell_0 \, \, \textrm{and any}\, \, \ell \, \, \textrm{for which } \, \, \lim_{n \to \infty} \frac{(t_n - s_n)^{\frac{1}{2}}}{ \operatorname{dist}( y_{ \ell_0, n}, y_{ \ell, n})} \neq0\Big\}. \end{align} $$
$$ \begin{align} \mathcal B(\ell_0) := \Big\{ \ell_0 \, \, \textrm{and any}\, \, \ell \, \, \textrm{for which } \, \, \lim_{n \to \infty} \frac{(t_n - s_n)^{\frac{1}{2}}}{ \operatorname{dist}( y_{ \ell_0, n}, y_{ \ell, n})} \neq0\Big\}. \end{align} $$
An index
![]() $\ell $
can be in at most one set
$\ell $
can be in at most one set
![]() $\mathcal B(\ell _0)$
(i.e., the sets
$\mathcal B(\ell _0)$
(i.e., the sets
![]() $\mathcal B(\ell ) = \mathcal B(\ell ')$
if
$\mathcal B(\ell ) = \mathcal B(\ell ')$
if
![]() $\ell ' \in \mathcal B(\ell )$
). For each of the sets
$\ell ' \in \mathcal B(\ell )$
). For each of the sets
![]() $\mathcal B(\ell _0)$
, we let, for each n,
$\mathcal B(\ell _0)$
, we let, for each n,
![]() $x_{ \ell _0, n}$
denote the barycenter of the points
$x_{ \ell _0, n}$
denote the barycenter of the points
![]() $y_{ \ell , n}$
associated to indices
$y_{ \ell , n}$
associated to indices
![]() $\ell \in \mathcal B(\ell _0)$
. We include the points
$\ell \in \mathcal B(\ell _0)$
. We include the points
![]() $x_{ \ell _0, n}$
in the set
$x_{ \ell _0, n}$
in the set
![]() $\mathcal P$
. This completes the construction of the set
$\mathcal P$
. This completes the construction of the set
![]() $\mathcal P$
, which consists of finitely many (say
$\mathcal P$
, which consists of finitely many (say
![]() $L \in \mathbb {N}$
) sequences
$L \in \mathbb {N}$
) sequences
![]() $\{x_{ \ell , n}\} \subset D(y_n, \xi _n)$
for
$\{x_{ \ell , n}\} \subset D(y_n, \xi _n)$
for
![]() $\ell \in \{1, \dots , L\}$
.
$\ell \in \{1, \dots , L\}$
.
We choose
![]() $r_n$
to be any sequence such that
$r_n$
to be any sequence such that
 $$ \begin{align} (t_n - s_n)^{\frac{1}{2}} &\ll r_n \ll \lambda_{\max, n}, \nonumber\\ R_n\lambda( \omega_{j, n}) &\ll r_n \quad \forall\, j \not \in \mathcal J_{\max}, \\ \max(\mu_{j, k, n},\xi_{j,n}) &\ll r_n \quad \forall \, j \in \mathcal J_{\max}, \forall \, k \in \{1, \dots, M_j\}, \nonumber \end{align} $$
$$ \begin{align} (t_n - s_n)^{\frac{1}{2}} &\ll r_n \ll \lambda_{\max, n}, \nonumber\\ R_n\lambda( \omega_{j, n}) &\ll r_n \quad \forall\, j \not \in \mathcal J_{\max}, \\ \max(\mu_{j, k, n},\xi_{j,n}) &\ll r_n \quad \forall \, j \in \mathcal J_{\max}, \forall \, k \in \{1, \dots, M_j\}, \nonumber \end{align} $$
and such that the discs
![]() $D(x_{ \ell , n}, r_n)$
satisfy (3.41). In view of the definition of
$D(x_{ \ell , n}, r_n)$
satisfy (3.41). In view of the definition of
![]() $j_0\in \mathcal J_{\max }$
,
$j_0\in \mathcal J_{\max }$
,
for all
![]() $j\in \mathcal R \setminus \mathcal J_{\max }$
. This ensures that for any
$j\in \mathcal R \setminus \mathcal J_{\max }$
. This ensures that for any
![]() $x_{ \ell , n}$
, which is one of the sequences
$x_{ \ell , n}$
, which is one of the sequences
![]() $a(\omega _{ j, n})$
for
$a(\omega _{ j, n})$
for
![]() $j \in \mathcal R \setminus \mathcal J_{\max }$
, the disc
$j \in \mathcal R \setminus \mathcal J_{\max }$
, the disc
![]() $D(x_{\ell , n}, r_n)$
is separated from any of the discs
$D(x_{\ell , n}, r_n)$
is separated from any of the discs
![]() $D(a(\omega _{ j_0, n}),R_n \lambda _{\max , n})$
for
$D(a(\omega _{ j_0, n}),R_n \lambda _{\max , n})$
for
![]() $j_0 \in \mathcal J_{\max }$
by an amount
$j_0 \in \mathcal J_{\max }$
by an amount
![]() $\gg r_n$
(we are free to take
$\gg r_n$
(we are free to take
![]() $R_n \to \infty $
to be diverging as slowly as needed).
$R_n \to \infty $
to be diverging as slowly as needed).
We claim that the sequences of discs
![]() $D(x_{\ell , n}, r_n)$
with
$D(x_{\ell , n}, r_n)$
with
![]() $x_{ \ell , n} \in \mathcal P$
satisfy (3.40). To see this, first note that for any
$x_{ \ell , n} \in \mathcal P$
satisfy (3.40). To see this, first note that for any
![]() $j_0 \in \mathcal J_{\max }$
,
$j_0 \in \mathcal J_{\max }$
,
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(s_n) - \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big); D( a(\omega_{j_0, n}), 4R_n \lambda_{\max, n}) \setminus \bigcup_{\ell=1}^{L} D( x_{ \ell,n}, r_n)\Big) = 0, \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(s_n) - \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big); D( a(\omega_{j_0, n}), 4R_n \lambda_{\max, n}) \setminus \bigcup_{\ell=1}^{L} D( x_{ \ell,n}, r_n)\Big) = 0, \end{align} $$
which follows from the construction of the set
![]() $\{x_{\ell , n}\}_{\ell = 1}^L$
, the limit in (3.28) and the choice of
$\{x_{\ell , n}\}_{\ell = 1}^L$
, the limit in (3.28) and the choice of
![]() $r_n$
. Note also that
$r_n$
. Note also that
![]() $r_n \ll \lambda _{\max , n}$
means that
$r_n \ll \lambda _{\max , n}$
means that
 $$ \begin{align} \lim_{n \to \infty} E\Big( \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big); \bigcup_{\ell=1}^{L} D( x_{ \ell, n}, r_n)\Big) = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big); \bigcup_{\ell=1}^{L} D( x_{ \ell, n}, r_n)\Big) = 0. \end{align} $$
We can conclude from the above, (3.48), (3.30) and (3.27) that
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(s_n); D(y_n, \rho_n) \setminus \bigcup_{\ell=1}^{L} D( x_{\ell,n}, r_n)\Big) = 4 \pi K_0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(s_n); D(y_n, \rho_n) \setminus \bigcup_{\ell=1}^{L} D( x_{\ell,n}, r_n)\Big) = 4 \pi K_0. \end{align} $$
The condition (3.40) follows then from above and the disjointness of the discs
![]() $D(x_{\ell ,n}, r_n)$
. The condition (3.42) and the existence of the sequence
$D(x_{\ell ,n}, r_n)$
. The condition (3.42) and the existence of the sequence
![]() $\breve \xi _n$
as in (3.43) follows from the construction of the set
$\breve \xi _n$
as in (3.43) follows from the construction of the set
![]() $\mathcal P$
and the choice of
$\mathcal P$
and the choice of
![]() $r_n$
.
$r_n$
.
We claim that there must exist
![]() $\ell _1 \in \{1, \dots , L\}$
,
$\ell _1 \in \{1, \dots , L\}$
,
![]() $ \eta _1>0$
so that, up to passing to a subsequence in n, we have
$ \eta _1>0$
so that, up to passing to a subsequence in n, we have
To see this, we argue by contradiction. If (3.51) fails, then we would have
We will use the above to show that
which contradicts (3.23). To start,
![]() $(t_n - s_n)^{\frac {1}{2}} \ll r_n$
means we can use Lemma 2.9 and (3.42) to propagate (3.40), (3.50) and (3.48) to time
$(t_n - s_n)^{\frac {1}{2}} \ll r_n$
means we can use Lemma 2.9 and (3.42) to propagate (3.40), (3.50) and (3.48) to time
![]() $t_n$
, giving
$t_n$
, giving
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); \bigcup_{\ell =1}^L D( x_{ \ell, n}, r_n)\Big) &= 4\pi K - 4 \pi K_0, \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); \bigcup_{\ell =1}^L D( x_{ \ell, n}, r_n)\Big) &= 4\pi K - 4 \pi K_0, \end{align} $$
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D(y_n, \rho_n) \setminus \bigcup_{\ell=1}^{L} D( x_{\ell,n}, r_n)\Big) &= 4 \pi K_0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D(y_n, \rho_n) \setminus \bigcup_{\ell=1}^{L} D( x_{\ell,n}, r_n)\Big) &= 4 \pi K_0 \end{align} $$
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n) - \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big); D( a(\omega_{j_0, n}), R_n \lambda_{\max, n}) \setminus \bigcup_{\ell=1}^{L} D( x_{ \ell,n}, r_n)\Big) &= 0, \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n) - \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big); D( a(\omega_{j_0, n}), R_n \lambda_{\max, n}) \setminus \bigcup_{\ell=1}^{L} D( x_{ \ell,n}, r_n)\Big) &= 0, \end{align} $$
for all
![]() $ j_0 \in \mathcal J_{\max }$
, where in the last line we remark that for each
$ j_0 \in \mathcal J_{\max }$
, where in the last line we remark that for each
![]() $\ell \in \{1, \dots , L\}$
, either the disc
$\ell \in \{1, \dots , L\}$
, either the disc
![]() $D(x_{\ell , n}; r_n)$
is completely contained in
$D(x_{\ell , n}; r_n)$
is completely contained in
![]() $D( a(\omega _{j_0, n}), R_n \lambda _{\max , n})$
or disjoint from it.
$D( a(\omega _{j_0, n}), R_n \lambda _{\max , n})$
or disjoint from it.
Next, using
![]() $\lambda _{\max , n} R_n \le \min \{\nu _{j, n}\}_{j \in \mathcal J_{\max }}$
and
$\lambda _{\max , n} R_n \le \min \{\nu _{j, n}\}_{j \in \mathcal J_{\max }}$
and
![]() $ \max (\mu _{j, k, n},\xi _{j,n}) \ll r_n \quad \forall \, j \in \mathcal J_{\max }, \forall \, k \in \{1, \dots , M_j\}$
, we see that (3.24) can be combined with the middle line of (3.28) to yield
$ \max (\mu _{j, k, n},\xi _{j,n}) \ll r_n \quad \forall \, j \in \mathcal J_{\max }, \forall \, k \in \{1, \dots , M_j\}$
, we see that (3.24) can be combined with the middle line of (3.28) to yield
 $$ \begin{align} \lim_{n \to \infty} \Big\| u(s_n) - \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big) \Big\|_{L^\infty( D( a(\omega_{j_0, n}), 4R_n \lambda_{\max, n}) \setminus \bigcup_{\ell=1}^{L} D( x_{ \ell,n}, 4^{-1}r_n))} = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \Big\| u(s_n) - \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big) \Big\|_{L^\infty( D( a(\omega_{j_0, n}), 4R_n \lambda_{\max, n}) \setminus \bigcup_{\ell=1}^{L} D( x_{ \ell,n}, 4^{-1}r_n))} = 0 \end{align} $$
for all
![]() $j_0 \in \mathcal J_{\max }$
. Since
$j_0 \in \mathcal J_{\max }$
. Since
![]() $(t_n - s_n)^{\frac {1}{2}} \ll r_n$
, Lemmas 2.12, (3.48) and (3.42) allow us to propagate the above to time
$(t_n - s_n)^{\frac {1}{2}} \ll r_n$
, Lemmas 2.12, (3.48) and (3.42) allow us to propagate the above to time
![]() $t_n$
, yielding
$t_n$
, yielding
 $$ \begin{align} \lim_{n \to \infty} \Big\| u(t_n) - \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big) \Big\|_{L^\infty( D( a(\omega_{j_0, n}), R_n \lambda_{\max, n}) \setminus \bigcup_{\ell=1}^{L} D( x_{ \ell,n}, r_n))} = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \Big\| u(t_n) - \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big) \Big\|_{L^\infty( D( a(\omega_{j_0, n}), R_n \lambda_{\max, n}) \setminus \bigcup_{\ell=1}^{L} D( x_{ \ell,n}, r_n))} = 0. \end{align} $$
Using again Lemma 2.10 and (3.27), the construction of the sequences
![]() $\{ x_{\ell , n}\}$
and the choice of
$\{ x_{\ell , n}\}$
and the choice of
![]() $\lambda _{\max , n} \gg r_n \gg (t_n - s_n)^{\frac {1}{2}}$
as well as
$\lambda _{\max , n} \gg r_n \gg (t_n - s_n)^{\frac {1}{2}}$
as well as
![]() $r_n\gg R_n\lambda (\omega _{j,n})$
for all
$r_n\gg R_n\lambda (\omega _{j,n})$
for all
![]() $j\not \in \mathcal J_{\max }$
, we have
$j\not \in \mathcal J_{\max }$
, we have
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D( y_n, \rho_n) \setminus \Big[ \bigcup_{j \in \mathcal J_{\max}} D( a(\omega_{j, n}), R_n \lambda_{\max, n}) \cup \bigcup_{ \ell =1}^L D( x_{\ell, n}; r_n) \Big] \Big) = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D( y_n, \rho_n) \setminus \Big[ \bigcup_{j \in \mathcal J_{\max}} D( a(\omega_{j, n}), R_n \lambda_{\max, n}) \cup \bigcup_{ \ell =1}^L D( x_{\ell, n}; r_n) \Big] \Big) = 0. \end{align} $$
Now, by (3.52), after passing to a joint subsequence in n, for each
![]() $\ell \in \{1, \dots , L\}$
, we can find an integer
$\ell \in \{1, \dots , L\}$
, we can find an integer
![]() $\widetilde M_\ell \ge 0$
, a sequence of
$\widetilde M_\ell \ge 0$
, a sequence of
![]() $\widetilde M_{\ell }$
-bubble configurations
$\widetilde M_{\ell }$
-bubble configurations
![]() $\mathcal Q(\boldsymbol {\Omega }_{\ell , n})$
, and sequences of vectors
$\mathcal Q(\boldsymbol {\Omega }_{\ell , n})$
, and sequences of vectors
![]() $\vec \nu _{\ell , n} = (\nu _{\ell , n}, \nu _{ \ell ,1, n}, \dots , \nu _{\ell , \widetilde M_{\ell }, n})$
and
$\vec \nu _{\ell , n} = (\nu _{\ell , n}, \nu _{ \ell ,1, n}, \dots , \nu _{\ell , \widetilde M_{\ell }, n})$
and
![]() $\vec \xi _{\ell , n} = ( \xi _{\ell , n}, \xi _{ \ell ,1, n}, \dots , \xi _{\ell , \widetilde M_{\ell }, n})$
so that
$\vec \xi _{\ell , n} = ( \xi _{\ell , n}, \xi _{ \ell ,1, n}, \dots , \xi _{\ell , \widetilde M_{\ell }, n})$
so that
Here,
![]() $\boldsymbol {\Omega }_{\ell , n}=(\Omega _{\ell , n},\Omega _{\ell ,1, n},\ldots ,\Omega _{\ell , \widetilde M_{\ell }, n})$
. Dropping the constants
$\boldsymbol {\Omega }_{\ell , n}=(\Omega _{\ell , n},\Omega _{\ell ,1, n},\ldots ,\Omega _{\ell , \widetilde M_{\ell }, n})$
. Dropping the constants
![]() $\Omega _{ \ell ,n} \in \mathbb {S}^2$
in the
$\Omega _{ \ell ,n} \in \mathbb {S}^2$
in the
![]() $\widetilde M_{\ell }$
-bubble configurations, consider finally the sequence (in n) of multi-bubbles formed by the constant
$\widetilde M_{\ell }$
-bubble configurations, consider finally the sequence (in n) of multi-bubbles formed by the constant
![]() $\omega \in \mathbb {S}^2$
and the harmonic maps
$\omega \in \mathbb {S}^2$
and the harmonic maps
 $$ \begin{align} \{ \Omega_{\ell, k, n}\}_{\ell =1, k =1}^{\ell = L, k = \widetilde M_{\ell}}, \, \{\omega_{j, 0, n}\}_{j \in \mathcal J_{\max}}:= \Big\{ \omega_{j, 0}( \frac{\cdot - a(\omega_{j, n})}{ \lambda( \omega_{j, n})}) \Big\}_{j \in \mathcal J_{\max}}. \end{align} $$
$$ \begin{align} \{ \Omega_{\ell, k, n}\}_{\ell =1, k =1}^{\ell = L, k = \widetilde M_{\ell}}, \, \{\omega_{j, 0, n}\}_{j \in \mathcal J_{\max}}:= \Big\{ \omega_{j, 0}( \frac{\cdot - a(\omega_{j, n})}{ \lambda( \omega_{j, n})}) \Big\}_{j \in \mathcal J_{\max}}. \end{align} $$
For each
![]() $j \in \mathcal J_{\max }$
, we define
$j \in \mathcal J_{\max }$
, we define
![]() $\nu _{j, n} := R_n$
and
$\nu _{j, n} := R_n$
and
![]() $\xi _{j, n} = r_n$
, and then defining
$\xi _{j, n} = r_n$
, and then defining
we claim that
which would yield (3.53). Indeed, by (3.60) and since all of the
![]() $D( x_{\ell , n}, r_n)$
are disjoint and satisfy (3.41), any distinct triples
$D( x_{\ell , n}, r_n)$
are disjoint and satisfy (3.41), any distinct triples
![]() $( \Omega _{\ell , k, n}, a( \Omega _{\ell , k, n}), \lambda ( \Omega _{\ell , k, n}))$
and
$( \Omega _{\ell , k, n}, a( \Omega _{\ell , k, n}), \lambda ( \Omega _{\ell , k, n}))$
and
![]() $( \Omega _{\ell ', k', n}, a( \Omega _{\ell ', k', n}), \lambda ( \Omega _{\ell ', k', n}))$
are asymptotically orthogonal for
$( \Omega _{\ell ', k', n}, a( \Omega _{\ell ', k', n}), \lambda ( \Omega _{\ell ', k', n}))$
are asymptotically orthogonal for
![]() $(\ell , k) \neq ( \ell ', k')$
. Moreover, for any
$(\ell , k) \neq ( \ell ', k')$
. Moreover, for any
![]() $\ell $
and
$\ell $
and
![]() $j_0 \in \mathcal J_{\max }$
for which
$j_0 \in \mathcal J_{\max }$
for which
![]() $D( x_{\ell , n}, r_n) \subset D( a(\omega _{j_0, n}), R_n \lambda (\omega _{j_0, n}))$
, the triples
$D( x_{\ell , n}, r_n) \subset D( a(\omega _{j_0, n}), R_n \lambda (\omega _{j_0, n}))$
, the triples
 $$ \begin{align*}( \Omega_{\ell, k, n}, a( \Omega_{\ell, k, n}), \lambda( \Omega_{\ell, k, n})) \ \ \ \text{and}\ \ \ \Big(\omega_{j_0, 0}( \frac{\cdot - a(\omega_{j_0, n})}{ \lambda( \omega_{j_0, n})}),a(\omega_{j_0, n}), \lambda( \omega_{j_0, n})\Big)\end{align*} $$
$$ \begin{align*}( \Omega_{\ell, k, n}, a( \Omega_{\ell, k, n}), \lambda( \Omega_{\ell, k, n})) \ \ \ \text{and}\ \ \ \Big(\omega_{j_0, 0}( \frac{\cdot - a(\omega_{j_0, n})}{ \lambda( \omega_{j_0, n})}),a(\omega_{j_0, n}), \lambda( \omega_{j_0, n})\Big)\end{align*} $$
are asymptotically orthogonal since
![]() $r_n \ll \lambda _{\max , n}$
. Indeed,
$r_n \ll \lambda _{\max , n}$
. Indeed,
 $$ \begin{align} \lim_{n \to \infty} E\Big( \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big); D( x_{\ell, n}, r_n)\Big) = 0 , \quad \forall j_0 \in \mathcal J_{\max}, \quad \forall \ell\in \{1, \dots, L\} \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( \omega_{j_0, 0}\big( \frac{ \cdot - a( \omega_{j_0, n})}{\lambda(\omega_{j_0, n})}\big); D( x_{\ell, n}, r_n)\Big) = 0 , \quad \forall j_0 \in \mathcal J_{\max}, \quad \forall \ell\in \{1, \dots, L\} \end{align} $$
and
These observations, together with (3.56), (3.58), the estimate (3.59) and Remark 3.2 (using now
![]() $\breve \xi _n$
instead of
$\breve \xi _n$
instead of
![]() $\xi _n$
), yield (3.62). This completes the proof of (3.51).
$\xi _n$
), yield (3.62). This completes the proof of (3.51).
Having established (3.51), we claim that there exist times
![]() $\widetilde \sigma _n < t_n$
so that
$\widetilde \sigma _n < t_n$
so that
If not, we could find
![]() $c, c_1>0$
and a subsequence of the
$c, c_1>0$
and a subsequence of the
![]() $t_n$
for which
$t_n$
for which
But then we would have
 $$ \begin{align} \sum_n \int_{t_n - c r_n^2}^{t_n} \| \mathcal T( u(t)) \|_{L^2}^2 \, \mathrm{d} t \ge c_1 \sum_n \int_{t_n - c r_n^2}^{t_n} r_n^{-2} \, \mathrm{d} t \ge c c_1 \sum_n 1 = \infty, \end{align} $$
$$ \begin{align} \sum_n \int_{t_n - c r_n^2}^{t_n} \| \mathcal T( u(t)) \|_{L^2}^2 \, \mathrm{d} t \ge c_1 \sum_n \int_{t_n - c r_n^2}^{t_n} r_n^{-2} \, \mathrm{d} t \ge c c_1 \sum_n 1 = \infty, \end{align} $$
which contradicts (2.12). Given the sequence
![]() $\widetilde \sigma _n$
as in (3.65), we can apply the Compactness Lemma 2.15, so that after passing to a subsequence in n (still denoted by
$\widetilde \sigma _n$
as in (3.65), we can apply the Compactness Lemma 2.15, so that after passing to a subsequence in n (still denoted by
![]() $\widetilde \sigma _n, t_n$
), we have a bubble decomposition as in (2.64) for some sequence
$\widetilde \sigma _n, t_n$
), we have a bubble decomposition as in (2.64) for some sequence
![]() $\hat R_n \to \infty $
. The estimate (3.42) can be propagated to time
$\hat R_n \to \infty $
. The estimate (3.42) can be propagated to time
![]() $\widetilde \sigma _n$
using Lemma 2.9, which gives
$\widetilde \sigma _n$
using Lemma 2.9, which gives
The above ensures that the harmonic map in (2.64) at scale
![]() $r_n$
must be constant, which we denote by
$r_n$
must be constant, which we denote by
![]() $\widetilde \omega \in \mathbb {S}^2$
, and so we can conclude that in fact,
$\widetilde \omega \in \mathbb {S}^2$
, and so we can conclude that in fact,
By (2.67), we can find an integer
![]() $K_1 \ge 0$
so that
$K_1 \ge 0$
so that
Because of (3.51), we must have
![]() $K_1 \ge 1$
(since
$K_1 \ge 1$
(since
![]() $t_n -\widetilde \sigma _n \ll r_n^2$
).
$t_n -\widetilde \sigma _n \ll r_n^2$
).
Consider the time intervals
![]() $[\widetilde \sigma _n, t_n]$
and the discs
$[\widetilde \sigma _n, t_n]$
and the discs
![]() $D(x_{\ell _1, n}; r_n)$
. Property (1) from Definition 3.1 is given by the first line in (3.69). Property (2) is given by (3.51). Property (3) is satisfied because of the first estimate in (3.65), and property (4) because of (3.70).
$D(x_{\ell _1, n}; r_n)$
. Property (1) from Definition 3.1 is given by the first line in (3.69). Property (2) is given by (3.51). Property (3) is satisfied because of the first estimate in (3.65), and property (4) because of (3.70).
Lastly, we claim that
![]() $K_1 < K$
. This is clear if
$K_1 < K$
. This is clear if
![]() $K_0>0$
since in that case, some energy lies at the scale
$K_0>0$
since in that case, some energy lies at the scale
![]() $\simeq \lambda _{\max , n} \gg r_n$
. If
$\simeq \lambda _{\max , n} \gg r_n$
. If
![]() $K_0=0$
and
$K_0=0$
and
![]() $K_1 = K$
, then all of the energy in the larger discs
$K_1 = K$
, then all of the energy in the larger discs
![]() $D(y_n, \rho _n)$
would be captured within the sequence of discs
$D(y_n, \rho _n)$
would be captured within the sequence of discs
![]() $D(x_{\ell _1, n}, r_n)$
. However, recall that there is at least one index
$D(x_{\ell _1, n}, r_n)$
. However, recall that there is at least one index
![]() $j_0$
such that
$j_0$
such that
![]() $\lambda (\omega _{j_0, n}) = \lambda _{\max , n}$
, and we have chosen
$\lambda (\omega _{j_0, n}) = \lambda _{\max , n}$
, and we have chosen
![]() $r_n$
so that
$r_n$
so that
![]() $r_n \ll \lambda _{\max , n}= \lambda (\omega _{j_0, n})$
, which (by Definition 1.3) implies at least
$r_n \ll \lambda _{\max , n}= \lambda (\omega _{j_0, n})$
, which (by Definition 1.3) implies at least
![]() $3\pi $
in energy concentrates outside the discs
$3\pi $
in energy concentrates outside the discs
![]() $D(x_{\ell _1, n}, r_n)$
, a contradiction.
$D(x_{\ell _1, n}, r_n)$
, a contradiction.
We conclude that
![]() $K_1< K$
and that
$K_1< K$
and that
![]() $[\widetilde \sigma _n, t_n] \in \mathcal C_{K_1}( x_{\ell _1, n}, r_n, \epsilon _{1, n}, \eta _1)$
for some sequence
$[\widetilde \sigma _n, t_n] \in \mathcal C_{K_1}( x_{\ell _1, n}, r_n, \epsilon _{1, n}, \eta _1)$
for some sequence
![]() $\epsilon _{1, n} \to 0$
, contradicting the minimality of K. This completes the proof.
$\epsilon _{1, n} \to 0$
, contradicting the minimality of K. This completes the proof.
Proof of Corollary 3.5.
Let
![]() $\eta _0$
be as in Lemma 3.4 and fix an
$\eta _0$
be as in Lemma 3.4 and fix an
![]() $\eta \in (0, \eta _0]$
. Let
$\eta \in (0, \eta _0]$
. Let
![]() $\epsilon>0$
be given by Lemma 3.4 and define
$\epsilon>0$
be given by Lemma 3.4 and define
![]() $s_n$
by
$s_n$
by
which is well-defined for all sufficiently large n. Then
![]() $\boldsymbol {\delta }( u(s_n); D(y_n, \rho _n)) = \epsilon $
. Define
$\boldsymbol {\delta }( u(s_n); D(y_n, \rho _n)) = \epsilon $
. Define
![]() $\lambda _{\max }(s_n)$
as in the statement of the result. By Lemma 3.4, it follows that
$\lambda _{\max }(s_n)$
as in the statement of the result. By Lemma 3.4, it follows that
![]() $s_n +c_0 \lambda _{\max }(s_n)^2 \le \tau _n$
for all sufficiently large n. The remaining claims hold by the choice of
$s_n +c_0 \lambda _{\max }(s_n)^2 \le \tau _n$
for all sufficiently large n. The remaining claims hold by the choice of
![]() $s_n$
.
$s_n$
.
3.3. Proof of Theorem 1.8
Proof of Theorem 1.8.
Assume the theorem is false. Let
![]() $K \ge 1$
and fix collision intervals
$K \ge 1$
and fix collision intervals
![]() $[\sigma _n, \tau _n]\in \mathcal C_K( y_n, \rho _n, \epsilon _n, \eta )$
as in Definition 3.1 and Lemma 3.3. We assume that
$[\sigma _n, \tau _n]\in \mathcal C_K( y_n, \rho _n, \epsilon _n, \eta )$
as in Definition 3.1 and Lemma 3.3. We assume that
![]() $\eta>0$
is sufficiently small as in Lemma 3.4 and let
$\eta>0$
is sufficiently small as in Lemma 3.4 and let
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $s_n$
be given by Corollary 3.5, so we have
$s_n$
be given by Corollary 3.5, so we have
Let
![]() $M_n$
be a sequence of non-negative integers,
$M_n$
be a sequence of non-negative integers,
![]() $\mathcal Q( \boldsymbol {\omega }_n)$
a sequence of
$\mathcal Q( \boldsymbol {\omega }_n)$
a sequence of
![]() $M_n$
-bubble configurations, and
$M_n$
-bubble configurations, and
![]() $\vec \nu _n \in (0, \infty )^{M_n+1}$
,
$\vec \nu _n \in (0, \infty )^{M_n+1}$
,
![]() $\vec \xi _n \in (0, \infty )^{M_n+1}$
sequences so that
$\vec \xi _n \in (0, \infty )^{M_n+1}$
sequences so that
We fix a choice of
![]() $\xi _n, \nu _n$
(the first components of the vectors
$\xi _n, \nu _n$
(the first components of the vectors
![]() $\vec \xi _n, \vec \nu _n$
) as in Remark 3.2 so that (3.2) and (3.3) hold. Defining
$\vec \xi _n, \vec \nu _n$
) as in Remark 3.2 so that (3.2) and (3.3) hold. Defining
![]() $\lambda _{\max , n} = \lambda _{\max }(s_n)$
as in Corollary 3.5, we have that
$\lambda _{\max , n} = \lambda _{\max }(s_n)$
as in Corollary 3.5, we have that
![]() $[s_n, s_n + c_0 \lambda _{\max , n}^2] \subset [\sigma _n, \tau _n]$
and moreover that
$[s_n, s_n + c_0 \lambda _{\max , n}^2] \subset [\sigma _n, \tau _n]$
and moreover that
for all n sufficiently large. Since
![]() $\sup _{t < T_+}E(u(t)) < \infty $
we can, after passing to a subsequence, assume
$\sup _{t < T_+}E(u(t)) < \infty $
we can, after passing to a subsequence, assume
![]() $M_n = M$
for some fixed integer M and that the constant
$M_n = M$
for some fixed integer M and that the constant
![]() $\omega _{n} \in \mathbb {S}^2$
in the M-bubble configuration
$\omega _{n} \in \mathbb {S}^2$
in the M-bubble configuration
![]() $\mathcal Q(\boldsymbol {\omega }_n)$
are fixed (i.e.,
$\mathcal Q(\boldsymbol {\omega }_n)$
are fixed (i.e.,
![]() $\omega _n = \omega \in \mathbb {S}^2$
).
$\omega _n = \omega \in \mathbb {S}^2$
).
We claim there exists
![]() $c_1>0$
such that for all
$c_1>0$
such that for all
![]() $n \ge n_0$
,
$n \ge n_0$
,
If not, we could find a sequence
![]() $t_n \in [s_n, s_n + c_0 \lambda _{\max ,n }^2] \subset [ \sigma _n, \tau _n]$
such that
$t_n \in [s_n, s_n + c_0 \lambda _{\max ,n }^2] \subset [ \sigma _n, \tau _n]$
such that
By the Compactness Lemma 2.15, for all
![]() $x_n \in \mathbb {R}^2$
, there exists a subsequence of the
$x_n \in \mathbb {R}^2$
, there exists a subsequence of the
![]() $u(t_n)$
and a sequence
$u(t_n)$
and a sequence
![]() $R_n(x_n) \to \infty $
, such that, for any sequence
$R_n(x_n) \to \infty $
, such that, for any sequence
![]() $1 \ll \breve {R}_n \ll R_n(x_n)$
,
$1 \ll \breve {R}_n \ll R_n(x_n)$
,
By Lemma 2.9, we also have that
where here we have used that
![]() $|[\sigma _n, \tau _n]| \ll \rho _n^2$
to propagate Property (4) from Definition 3.1 from time
$|[\sigma _n, \tau _n]| \ll \rho _n^2$
to propagate Property (4) from Definition 3.1 from time
![]() $\sigma _n$
to time
$\sigma _n$
to time
![]() $t_n$
. Note also that
$t_n$
. Note also that
![]() $\rho _n^2 \gg \xi _n^2 \gg \tau _n - \sigma _n$
and Corollary 3.5 ensure that
$\rho _n^2 \gg \xi _n^2 \gg \tau _n - \sigma _n$
and Corollary 3.5 ensure that
![]() $\xi _n \gg \lambda _{\max , n}$
.
$\xi _n \gg \lambda _{\max , n}$
.
We claim that after passing to a subsequence, there exists an integer
![]() $L>0$
, sequences
$L>0$
, sequences
![]() $x_{\ell , n}$
for each
$x_{\ell , n}$
for each
![]() $\ell \in \{1, \dots , L\}$
, a number
$\ell \in \{1, \dots , L\}$
, a number
![]() $R \ge 2$
, and a sequence
$R \ge 2$
, and a sequence
![]() $1 \ll \widetilde R_n \ll \lambda _{\max , n}^{-1} \xi _n$
so that
$1 \ll \widetilde R_n \ll \lambda _{\max , n}^{-1} \xi _n$
so that
 $$ \begin{align} E\Big(u(s_n); D( y_n, \rho_n) \setminus \bigcup_{\ell =1}^L D( x_{\ell, n}, R \lambda_{\max, n}\Big) \le \frac{\pi}{2}, \end{align} $$
$$ \begin{align} E\Big(u(s_n); D( y_n, \rho_n) \setminus \bigcup_{\ell =1}^L D( x_{\ell, n}, R \lambda_{\max, n}\Big) \le \frac{\pi}{2}, \end{align} $$
and
for any
![]() $\ell \neq \ell '$
. We find the points
$\ell \neq \ell '$
. We find the points
![]() $x_{\ell , n}$
as follows. Passing to a subsequence, we can assume the existence of the limits
$x_{\ell , n}$
as follows. Passing to a subsequence, we can assume the existence of the limits
 $$ \begin{align} \lim_{n \to \infty} \frac{|a(\omega_{j, n}) - a(\omega_{k, n})|}{\lambda_{\max, n}} \in [0, \infty] \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \frac{|a(\omega_{j, n}) - a(\omega_{k, n})|}{\lambda_{\max, n}} \in [0, \infty] \end{align} $$
for each
![]() $j \neq k$
. We define the index sets
$j \neq k$
. We define the index sets
 $$ \begin{align} \mathcal L(j):= \Big\{ j \, \, \textrm{and any index} \, \, k \in \{1, \dots, M\}\, \, \textrm{such that} \lim_{n \to \infty} \frac{|a(\omega_{j, n}) - a(\omega_{k, n})|}{\lambda_{\max, n}} < \infty \Big\} \end{align} $$
$$ \begin{align} \mathcal L(j):= \Big\{ j \, \, \textrm{and any index} \, \, k \in \{1, \dots, M\}\, \, \textrm{such that} \lim_{n \to \infty} \frac{|a(\omega_{j, n}) - a(\omega_{k, n})|}{\lambda_{\max, n}} < \infty \Big\} \end{align} $$
and note that for any distinct indices
![]() $j, j'$
either
$j, j'$
either
![]() $\mathcal L(j) = \mathcal L(j')$
or they are disjoint. For each n and for each of the sets
$\mathcal L(j) = \mathcal L(j')$
or they are disjoint. For each n and for each of the sets
![]() $\mathcal L(j)$
, we let
$\mathcal L(j)$
, we let
![]() $x_{\mathcal L(j), n}$
denote the barycenter of the points
$x_{\mathcal L(j), n}$
denote the barycenter of the points
![]() $a(\omega _{j_1, n}), \dots , a(\omega _{j_{\#\mathcal L(j)}, n})$
where each
$a(\omega _{j_1, n}), \dots , a(\omega _{j_{\#\mathcal L(j)}, n})$
where each
![]() $j_k \in \mathcal L(j)$
. There are
$j_k \in \mathcal L(j)$
. There are
![]() $L \le M$
many distinct index sets
$L \le M$
many distinct index sets
![]() $\mathcal L(j)$
, and we let
$\mathcal L(j)$
, and we let
![]() $\{x_{\ell , n}\}_{\ell =1}^L$
be an enumeration of the distinct
$\{x_{\ell , n}\}_{\ell =1}^L$
be an enumeration of the distinct
![]() $x_{\mathcal L(j), n}$
.
$x_{\mathcal L(j), n}$
.
Next, from (3.73), Lemma 2.4 and the definitions of
![]() $\mathbf {d}$
and
$\mathbf {d}$
and
![]() $\lambda _{\max , n}$
we can find
$\lambda _{\max , n}$
we can find
![]() $R_1\ge 2$
so that
$R_1\ge 2$
so that
 $$ \begin{align} E\Big( u(s_n); D( y_n, \rho_n) \setminus \bigcup_{j =1}^M D( a( \omega_{j, n}), R_1 \lambda_{\max, n})\Big) \le \frac{\pi}{2} \end{align} $$
$$ \begin{align} E\Big( u(s_n); D( y_n, \rho_n) \setminus \bigcup_{j =1}^M D( a( \omega_{j, n}), R_1 \lambda_{\max, n})\Big) \le \frac{\pi}{2} \end{align} $$
for all sufficiently large n. From the above and the definition of the
![]() $x_{\ell , n}$
, we can find
$x_{\ell , n}$
, we can find
![]() $R\ge R_1$
so that (3.79) holds. The existence of a sequence
$R\ge R_1$
so that (3.79) holds. The existence of a sequence
![]() $1 \ll \widetilde R_n \ll \lambda _{\max , n}^{-1} \xi _n$
so that (3.80) holds follows from definition of the
$1 \ll \widetilde R_n \ll \lambda _{\max , n}^{-1} \xi _n$
so that (3.80) holds follows from definition of the
![]() $x_{\ell , n}$
.
$x_{\ell , n}$
.
Consider each of the sequences
![]() $x_{\ell , n}$
as the
$x_{\ell , n}$
as the
![]() $x_n$
in (3.77) and find corresponding sequences
$x_n$
in (3.77) and find corresponding sequences
![]() $R_{\ell , n}$
so that for any sequence
$R_{\ell , n}$
so that for any sequence
![]() $\breve R_n \le R_{\ell , n}$
,
$\breve R_n \le R_{\ell , n}$
,
Enlarge the sequence
![]() $\xi _n$
to a sequence
$\xi _n$
to a sequence
![]() $\widetilde \xi _n$
as in Remark (3.2) (i.e., so that
$\widetilde \xi _n$
as in Remark (3.2) (i.e., so that
![]() $\xi _n \ll \widetilde \xi _n \ll \rho _n$
). Then, since all of the
$\xi _n \ll \widetilde \xi _n \ll \rho _n$
). Then, since all of the
![]() $x_{\ell ,n} \in D( y_n, \xi _n)$
and
$x_{\ell ,n} \in D( y_n, \xi _n)$
and
![]() $\lambda _{\max , n} \ll \xi _n$
, we have
$\lambda _{\max , n} \ll \xi _n$
, we have
 $$ \begin{align} \lim_{n \to \infty} \frac{ \lambda_{\max, n}}{\operatorname{dist}( x_{\ell, n}, \partial D(y_n, \widetilde \xi_n))} = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \frac{ \lambda_{\max, n}}{\operatorname{dist}( x_{\ell, n}, \partial D(y_n, \widetilde \xi_n))} = 0 \end{align} $$
for each
![]() $\ell $
. We can thus find a sequence
$\ell $
. We can thus find a sequence
![]() $R_n \le \min \{ \widetilde R_n, R_{\ell , n}\}_{\ell = 1, \dots , L}$
such that
$R_n \le \min \{ \widetilde R_n, R_{\ell , n}\}_{\ell = 1, \dots , L}$
such that
![]() $D(x_{\ell , n}, R_n \lambda _{\max , n}) \subset D(y_n, \widetilde \xi _n)$
for each
$D(x_{\ell , n}, R_n \lambda _{\max , n}) \subset D(y_n, \widetilde \xi _n)$
for each
![]() $\ell $
.
$\ell $
.
Enlarging the excised discs (replacing R by
![]() $R_n$
) in (3.79), we obtain
$R_n$
) in (3.79), we obtain
 $$ \begin{align} E \Big(u(s_n); D( y_n, \rho_n) \setminus \bigcup_{\ell =1}^L D( x_{\ell, n}, R_n \lambda_{\max, n}\Big) \le \frac{\pi}{2}. \end{align} $$
$$ \begin{align} E \Big(u(s_n); D( y_n, \rho_n) \setminus \bigcup_{\ell =1}^L D( x_{\ell, n}, R_n \lambda_{\max, n}\Big) \le \frac{\pi}{2}. \end{align} $$
We use Lemma 2.9 to propagate this bound forward to time
![]() $t_n$
, giving
$t_n$
, giving
 $$ \begin{align} E\Big(u(t_n); D( y_n, \rho_n) \setminus \bigcup_{\ell =1}^L D( x_{\ell, n}, R_n \lambda_{\max, n}\Big) \le \pi. \end{align} $$
$$ \begin{align} E\Big(u(t_n); D( y_n, \rho_n) \setminus \bigcup_{\ell =1}^L D( x_{\ell, n}, R_n \lambda_{\max, n}\Big) \le \pi. \end{align} $$
However, by (3.84) (replacing
![]() $R_{1, n}$
by
$R_{1, n}$
by
![]() $R_n$
), we can find integers
$R_n$
), we can find integers
![]() $K_{\ell }$
so that
$K_{\ell }$
so that
for each
![]() $\ell \in \{1, \dots , L\}$
. Combining the above with (3.78), we see that
$\ell \in \{1, \dots , L\}$
. Combining the above with (3.78), we see that
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D(y_n, \rho_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell, n}, R_{ n} \lambda_{\max, n})\Big) = 4 K \pi - \sum_{\ell=1}^L 4 K_{\ell} \pi. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D(y_n, \rho_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell, n}, R_{ n} \lambda_{\max, n})\Big) = 4 K \pi - \sum_{\ell=1}^L 4 K_{\ell} \pi. \end{align} $$
Comparing the above with (3.87), it follows that
![]() $\sum _{\ell } 4 K_{\ell } \pi = 4 K \pi $
, and thus,
$\sum _{\ell } 4 K_{\ell } \pi = 4 K \pi $
, and thus,
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D(y_n, \rho_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell, n}, R_{ n} \lambda_{\max, n})\Big) = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D(y_n, \rho_n) \setminus \bigcup_{\ell =1}^L D(x_{\ell, n}, R_{ n} \lambda_{\max, n})\Big) = 0. \end{align} $$
From (3.84) and the definition of
![]() $R_n$
, we have
$R_n$
, we have
 $$ \begin{align} \lim_{n \to \infty} \sum_{\ell =1}^L \boldsymbol{\delta}( u(t_n); D( x_{\ell, n}, R_n \lambda_{\max, n})) = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \sum_{\ell =1}^L \boldsymbol{\delta}( u(t_n); D( x_{\ell, n}, R_n \lambda_{\max, n})) = 0 \end{align} $$
and moreover that the discs
![]() $D( x_{\ell , n}, R_n \lambda _{\max , n})$
are disjoint by (3.80) and the choice of
$D( x_{\ell , n}, R_n \lambda _{\max , n})$
are disjoint by (3.80) and the choice of
![]() $R_n \le \widetilde R_n$
. Combining (3.91), (3.85), the disjointness of the discs
$R_n \le \widetilde R_n$
. Combining (3.91), (3.85), the disjointness of the discs
![]() $D( x_{\ell , n}, R_n \lambda _{\max , n})$
, (3.90), and Remark 3.2, we conclude that
$D( x_{\ell , n}, R_n \lambda _{\max , n})$
, (3.90), and Remark 3.2, we conclude that
which contradicts (3.74), proving (3.75).
By (3.75), we have
 $$ \begin{align*} \sum_n \int_{s_n}^{s_n + c_0 \lambda_{\max}(s_n)^2} \| \mathcal T(u(t)) \|_{L^2}^2 \, \mathrm{d} t \ge c_1 \sum_n \int_{s_n}^{s_n + c_0 \lambda_{\max}(s_n)^2} \lambda_{\max}(s_n)^{-2} \, \mathrm{d} t \ge c_0c_1 \sum_{n}1 = \infty. \end{align*} $$
$$ \begin{align*} \sum_n \int_{s_n}^{s_n + c_0 \lambda_{\max}(s_n)^2} \| \mathcal T(u(t)) \|_{L^2}^2 \, \mathrm{d} t \ge c_1 \sum_n \int_{s_n}^{s_n + c_0 \lambda_{\max}(s_n)^2} \lambda_{\max}(s_n)^{-2} \, \mathrm{d} t \ge c_0c_1 \sum_{n}1 = \infty. \end{align*} $$
However, since the intervals
![]() $[\sigma _n, \tau _n]$
are disjoint, the above contradicts the bound (2.12) – that is,
$[\sigma _n, \tau _n]$
are disjoint, the above contradicts the bound (2.12) – that is,
 $$ \begin{align} \sum_n \int_{s_n}^{s_n + c_0 \lambda_{\max}(s_n)^2} \| \mathcal T(u(t)) \|_{L^2}^2 \, \mathrm{d} t \le \int_0^{T_+} \| \mathcal T(u(t) \|_{L^2}^2 \, \mathrm{d} t < \infty, \end{align} $$
$$ \begin{align} \sum_n \int_{s_n}^{s_n + c_0 \lambda_{\max}(s_n)^2} \| \mathcal T(u(t)) \|_{L^2}^2 \, \mathrm{d} t \le \int_0^{T_+} \| \mathcal T(u(t) \|_{L^2}^2 \, \mathrm{d} t < \infty, \end{align} $$
which completes the proof.
3.4. Proof of Theorem 1.1
In this section, we prove Theorem 1.1 using Theorem 1.8 as a main ingredient in the proof.
Proof of Theorem 1.1.
We consider the case of finite time blow-up (i.e.,
![]() $T_+ < \infty $
), noting that the analysis for the global case is similar.
$T_+ < \infty $
), noting that the analysis for the global case is similar.
Let
![]() $L \ge 1$
and
$L \ge 1$
and
![]() $\{x_\ell \}_{\ell =1}^L$
be the bubbling points given by the local theory of Struwe in Theorem 2.7. Let
$\{x_\ell \}_{\ell =1}^L$
be the bubbling points given by the local theory of Struwe in Theorem 2.7. Let
![]() $\rho _0>0$
be sufficiently small so that
$\rho _0>0$
be sufficiently small so that
![]() $D(x_\ell; 2\rho _0) \cap D(x_m; 2\rho _0) = \emptyset $
for each
$D(x_\ell; 2\rho _0) \cap D(x_m; 2\rho _0) = \emptyset $
for each
![]() $\ell \neq m$
. By Theorem 2.7, we have that
$\ell \neq m$
. By Theorem 2.7, we have that
 $$ \begin{align} \lim_{ t\to T_+} E\Big( u(t) - u^*; \mathbb{R}^2 \setminus \bigcup_{\ell =1}^LD(x_\ell; \rho_0) \Big) = 0. \end{align} $$
$$ \begin{align} \lim_{ t\to T_+} E\Big( u(t) - u^*; \mathbb{R}^2 \setminus \bigcup_{\ell =1}^LD(x_\ell; \rho_0) \Big) = 0. \end{align} $$
By Lemma 2.13, we know that for each
![]() $\ell $
,
$\ell $
,
and since
![]() $u^* \in \mathcal {E}$
,
$u^* \in \mathcal {E}$
,
for each
![]() $\ell \in \{1, \dots , L\}$
. Hence, it suffices to examine the solution
$\ell \in \{1, \dots , L\}$
. Hence, it suffices to examine the solution
![]() $u(t)$
in the discs
$u(t)$
in the discs
![]() $D( x_\ell; \sqrt {T_+- t})$
for each
$D( x_\ell; \sqrt {T_+- t})$
for each
![]() $\ell \in \{1, \dots , L\}$
. Fix an
$\ell \in \{1, \dots , L\}$
. Fix an
![]() $\ell $
and, to ease notation, we write
$\ell $
and, to ease notation, we write
![]() $y = x_\ell $
below. By Theorem 1.8, we know that for
$y = x_\ell $
below. By Theorem 1.8, we know that for
![]() $\rho (t):= \sqrt {T_+-t}$
, we have,
$\rho (t):= \sqrt {T_+-t}$
, we have,
Now, let
![]() $t_n \to T_+$
be any sequence of times. By the above, we can find a sequence
$t_n \to T_+$
be any sequence of times. By the above, we can find a sequence
![]() $1 \le M_n \le (4 \pi )^{-1} E( u_0)$
, a sequence of
$1 \le M_n \le (4 \pi )^{-1} E( u_0)$
, a sequence of
![]() $M_n$
-bubble configurations
$M_n$
-bubble configurations
![]() $\mathcal Q(\boldsymbol {\omega }_n)$
, and sequences
$\mathcal Q(\boldsymbol {\omega }_n)$
, and sequences
![]() $\vec \nu _{n} = (\nu _n, \nu _{1, n}, \dots , \nu _{M_n, n})$
,
$\vec \nu _{n} = (\nu _n, \nu _{1, n}, \dots , \nu _{M_n, n})$
,
![]() $\vec \xi _{n} = ( \xi _n, \xi _{1, n}, \dots , \xi _{M_n, n})$
such that
$\vec \xi _{n} = ( \xi _n, \xi _{1, n}, \dots , \xi _{M_n, n})$
such that
Passing to a subsequence of the
![]() $t_n$
, we may assume that
$t_n$
, we may assume that
![]() $M_n = M$
is a fixed integer and that the constants
$M_n = M$
is a fixed integer and that the constants
![]() $\omega _{ n}\in \mathbb {S}^2$
in the M-bubble configurations
$\omega _{ n}\in \mathbb {S}^2$
in the M-bubble configurations
![]() $\mathcal Q(\boldsymbol {\omega }_n)$
are fixed (i.e.,
$\mathcal Q(\boldsymbol {\omega }_n)$
are fixed (i.e.,
![]() $\omega _n = \omega \in \mathbb {S}^2$
). This proves the estimate (1.10).
$\omega _n = \omega \in \mathbb {S}^2$
). This proves the estimate (1.10).
Since each of the
![]() $\omega _{j, n}$
is a harmonic map (and thus
$\omega _{j, n}$
is a harmonic map (and thus
![]() $\mathcal T(\omega _{j,n}) = 0)$
, these sequences satisfy the hypothesis of the Compactness Lemma 2.15. Therefore, after passing to a joint subsequence, for each
$\mathcal T(\omega _{j,n}) = 0)$
, these sequences satisfy the hypothesis of the Compactness Lemma 2.15. Therefore, after passing to a joint subsequence, for each
![]() $j \in \{1, \dots , M\}$
, we can find integers
$j \in \{1, \dots , M\}$
, we can find integers
![]() $M_j \ge 0$
, harmonic maps
$M_j \ge 0$
, harmonic maps
![]() $\theta _{j, 0}, \theta _{ j, 1}, \dots \theta _{j, M_j}$
(where only
$\theta _{j, 0}, \theta _{ j, 1}, \dots \theta _{j, M_j}$
(where only
![]() $\theta _{j, 0}$
is possibly constant), along with sequences of vectors
$\theta _{j, 0}$
is possibly constant), along with sequences of vectors
![]() $b_{j, k, n} \in D(a(\omega _{ j, n}), C_j \lambda (\omega _{ j, n}))$
and scales
$b_{j, k, n} \in D(a(\omega _{ j, n}), C_j \lambda (\omega _{ j, n}))$
and scales
![]() $\mu _{ j, k, n} \ll \lambda (\omega _{ j, n})$
satisfying (2.65), (2.66) and so that
$\mu _{ j, k, n} \ll \lambda (\omega _{ j, n})$
satisfying (2.65), (2.66) and so that
 $$ \begin{align} \lim_{n \to \infty} &\Bigg[ E \Big( \omega_{j, n}- \theta_{j, 0}\big( \frac{ \cdot - a( \omega_{ j, })}{\lambda(\omega_{ j, n})}\big) - \sum_{k =1}^{M_j}\Big( \theta_{j, k} \big( \frac{\cdot - b_{ j, k, n}}{\mu_{ j, k, n}} \big) - \theta_{j, k}( \infty)\Big); D_{j,n} \Big) \nonumber\\ & + \Big\| \omega_{j, n}- \theta_{j, 0}\big( \frac{ \cdot - a( \omega_{ j, })}{\lambda(\omega_{ j, n})}\big) - \sum_{k =1}^{M_j}\Big( \theta_{j, k} \big( \frac{\cdot - b_{ j, k, n}}{\mu_{ j, k, n}} \big) - \theta_{j, k}( \infty)\Big)\Big\|_{L^\infty( D_{j,n})} \Bigg] = 0, \end{align} $$
$$ \begin{align} \lim_{n \to \infty} &\Bigg[ E \Big( \omega_{j, n}- \theta_{j, 0}\big( \frac{ \cdot - a( \omega_{ j, })}{\lambda(\omega_{ j, n})}\big) - \sum_{k =1}^{M_j}\Big( \theta_{j, k} \big( \frac{\cdot - b_{ j, k, n}}{\mu_{ j, k, n}} \big) - \theta_{j, k}( \infty)\Big); D_{j,n} \Big) \nonumber\\ & + \Big\| \omega_{j, n}- \theta_{j, 0}\big( \frac{ \cdot - a( \omega_{ j, })}{\lambda(\omega_{ j, n})}\big) - \sum_{k =1}^{M_j}\Big( \theta_{j, k} \big( \frac{\cdot - b_{ j, k, n}}{\mu_{ j, k, n}} \big) - \theta_{j, k}( \infty)\Big)\Big\|_{L^\infty( D_{j,n})} \Bigg] = 0, \end{align} $$
where
![]() $D_{j,n}:=D( a(\omega _{j, n}), R_{n} \lambda (\omega _{ j, n}))$
for some sequence
$D_{j,n}:=D( a(\omega _{j, n}), R_{n} \lambda (\omega _{ j, n}))$
for some sequence
![]() $R_n \to \infty $
, and where for each fixed j,
$R_n \to \infty $
, and where for each fixed j,
 $$ \begin{align} \lim_{n \to \infty} \sum_{k \neq k'} \Big( \frac{ \mu_{ j, k, n}}{\mu_{j, k', n}} + \frac{ \mu_{ j, k', n}}{\mu_{ j, k, n}} + \frac{| b_{ j, k, n} - b_{ j, k', n} |^{2}}{\mu_{ j, k, n} \mu_{j, k', n}} \Big)^{-1} = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \sum_{k \neq k'} \Big( \frac{ \mu_{ j, k, n}}{\mu_{j, k', n}} + \frac{ \mu_{ j, k', n}}{\mu_{ j, k, n}} + \frac{| b_{ j, k, n} - b_{ j, k', n} |^{2}}{\mu_{ j, k, n} \mu_{j, k', n}} \Big)^{-1} = 0. \end{align} $$
To make the notation for the scales and centers of the harmonic maps above more uniform, we also introduce the notation
Our goal is to find a collection of asymptotically orthogonal triples
![]() $(\omega _j, a_{j, n}, \lambda _{j, n})$
as in the statement of Theorem 1.1. The sequences
$(\omega _j, a_{j, n}, \lambda _{j, n})$
as in the statement of Theorem 1.1. The sequences
![]() $\{(\theta _{j, k}, b_{ j, k, n}, \mu _{ j, k, n})\}_{j =1, k =0}^{j = M, k = M_j}$
are not guaranteed to be such a collection. While (3.100) holds for each fixed j, the triples
$\{(\theta _{j, k}, b_{ j, k, n}, \mu _{ j, k, n})\}_{j =1, k =0}^{j = M, k = M_j}$
are not guaranteed to be such a collection. While (3.100) holds for each fixed j, the triples
![]() $(\theta _{j, k}, b_{j, k, n}, \mu _{ j, k, n})$
and
$(\theta _{j, k}, b_{j, k, n}, \mu _{ j, k, n})$
and
![]() $(\theta _{j', k'}, b_{ j', k', n}, \mu _{ j', k', n})$
with
$(\theta _{j', k'}, b_{ j', k', n}, \mu _{ j', k', n})$
with
![]() $j \neq j'$
might not be asymptotically orthogonal. As in Definition 3.7 and the proof of Lemma 3.4, we define the set of indices
$j \neq j'$
might not be asymptotically orthogonal. As in Definition 3.7 and the proof of Lemma 3.4, we define the set of indices
![]() $\mathcal R$
to be those associated to the roots (i.e., the maximal elements of the sequences
$\mathcal R$
to be those associated to the roots (i.e., the maximal elements of the sequences
![]() $\mathfrak {h}_j=\{\omega _{j,n}\}$
of harmonic maps under the partial order
$\mathfrak {h}_j=\{\omega _{j,n}\}$
of harmonic maps under the partial order
![]() $\preceq $
). For each root
$\preceq $
). For each root
![]() $\mathfrak {h}_{j_0}$
, we define the bubble tree
$\mathfrak {h}_{j_0}$
, we define the bubble tree
Let
![]() $C_0>0$
be large enough so that
$C_0>0$
be large enough so that
![]() $\mathfrak {h}_j\prec \mathfrak {h}_{j_0}$
implies
$\mathfrak {h}_j\prec \mathfrak {h}_{j_0}$
implies
![]() $ D(a(\omega _{j, n}), \lambda (\omega _{ j, n})) \subset D(a(\omega _{ j_0, n}), C_0\lambda (\omega _{ j_0, n})) $
for all n. The collection of all harmonic maps, together with scales and centers, concentrating inside the discs
$ D(a(\omega _{j, n}), \lambda (\omega _{ j, n})) \subset D(a(\omega _{ j_0, n}), C_0\lambda (\omega _{ j_0, n})) $
for all n. The collection of all harmonic maps, together with scales and centers, concentrating inside the discs
![]() $D(a(\omega _{ j_0,n}), C_0\lambda (\omega _{ j_0,n}))$
equals
$D(a(\omega _{ j_0,n}), C_0\lambda (\omega _{ j_0,n}))$
equals
 $$ \begin{align} \bigcup_{\mathfrak{h}_j \in \mathcal T(j_0)}\{ (\theta_{j, k}, b_{ j, k, n}, \mu_{ j, k, n})\}_{k =0}^{M_{j}}. \end{align} $$
$$ \begin{align} \bigcup_{\mathfrak{h}_j \in \mathcal T(j_0)}\{ (\theta_{j, k}, b_{ j, k, n}, \mu_{ j, k, n})\}_{k =0}^{M_{j}}. \end{align} $$
We let
 $$ \begin{align} \mathcal K(j, k):= \big\{ (j, k)& \, \, \textrm{and any} \, \, (j', k') \, \, \textrm{associated to a triple} \, \, (\omega_{j', k'}, b_{j', k', n}, \mu_{ j', k', n}) \nonumber\\ &\textrm{not asymptotically orthogonal to} \, \, (\omega_{j, k}, b_{ j, k, n}, \mu_{ j, k, n})\big\} \end{align} $$
$$ \begin{align} \mathcal K(j, k):= \big\{ (j, k)& \, \, \textrm{and any} \, \, (j', k') \, \, \textrm{associated to a triple} \, \, (\omega_{j', k'}, b_{j', k', n}, \mu_{ j', k', n}) \nonumber\\ &\textrm{not asymptotically orthogonal to} \, \, (\omega_{j, k}, b_{ j, k, n}, \mu_{ j, k, n})\big\} \end{align} $$
If
![]() $\#\mathcal K(j, k) = 1$
, we keep the triple
$\#\mathcal K(j, k) = 1$
, we keep the triple
![]() $ (\theta _{j, k}, b_{ j, k, n}, \mu _{ j, k, n})$
in our final collection – note that (1.9) and (1.14) will be consequences of (3.98) (3.99), and (2.65) (2.66). Now consider a set of indices
$ (\theta _{j, k}, b_{ j, k, n}, \mu _{ j, k, n})$
in our final collection – note that (1.9) and (1.14) will be consequences of (3.98) (3.99), and (2.65) (2.66). Now consider a set of indices
![]() $(j_1, k_1)$
with
$(j_1, k_1)$
with
![]() $\mathfrak {h}_{j_1} \in \mathcal T(j_0)$
and such that
$\mathfrak {h}_{j_1} \in \mathcal T(j_0)$
and such that
![]() $\#\mathcal K(j_1, k_1) \ge 2$
. After performing a fixed (in n) rescaling and translation of each harmonic map
$\#\mathcal K(j_1, k_1) \ge 2$
. After performing a fixed (in n) rescaling and translation of each harmonic map
![]() $\theta _{j, k}$
associated to an index
$\theta _{j, k}$
associated to an index
![]() $(j, k) \in \mathcal K(j_1, k_1)$
, we may assume that
$(j, k) \in \mathcal K(j_1, k_1)$
, we may assume that
and to simplify notation below, we simply write
![]() $b_n = b_{ j_1, k_1, n}$
and
$b_n = b_{ j_1, k_1, n}$
and
![]() $\mu _n = \mu _{ j_1, k_1, n}$
. By (3.98) and (3.99), we can also find
$\mu _n = \mu _{ j_1, k_1, n}$
. By (3.98) and (3.99), we can also find
![]() $r_n \to \infty $
a number
$r_n \to \infty $
a number
![]() $C_1>0$
, an integer
$C_1>0$
, an integer
![]() $L_1 \ge 0$
, and a finite number of sequences of discs
$L_1 \ge 0$
, and a finite number of sequences of discs
![]() $D(c_{ \ell , n}, \rho _{n, \ell }) \subset D( b_n, C_1 \mu _n)$
for
$D(c_{ \ell , n}, \rho _{n, \ell }) \subset D( b_n, C_1 \mu _n)$
for
![]() $\ell \in \{1, \dots , L_1\}$
and with
$\ell \in \{1, \dots , L_1\}$
and with
so that
and
and
 $$ \begin{align} \!\!\!\!\!\!\lim_{n \to \infty} E\Big( u(t_n) - \!\!\!\!\!\!\sum_{(j, k) \in \mathcal K(j_1, k_1)}\!\!\!\Big( \theta_{j, k}( \frac{\cdot - b_n}{ \mu_n}) - \theta_{j, k}( \infty) \Big); D( b_n, r_n\mu_n) \setminus \bigcup_{\ell =1}^{L_1} D(c_{n, \ell}, \rho_{n, \ell})\Big) = 0. \end{align} $$
$$ \begin{align} \!\!\!\!\!\!\lim_{n \to \infty} E\Big( u(t_n) - \!\!\!\!\!\!\sum_{(j, k) \in \mathcal K(j_1, k_1)}\!\!\!\Big( \theta_{j, k}( \frac{\cdot - b_n}{ \mu_n}) - \theta_{j, k}( \infty) \Big); D( b_n, r_n\mu_n) \setminus \bigcup_{\ell =1}^{L_1} D(c_{n, \ell}, \rho_{n, \ell})\Big) = 0. \end{align} $$
By Theorem 1.8 and (3.107), we know that,
This means that, after passing to a subsequence, we can find an integer
![]() $M_{j_1, k_1}$
, a sequence of
$M_{j_1, k_1}$
, a sequence of
![]() $M_{j_1, k_1}$
-bubble configurations
$M_{j_1, k_1}$
-bubble configurations
![]() $\mathcal Q(\boldsymbol {\Omega }_n)$
, with the nontrivial harmonic maps denoted by
$\mathcal Q(\boldsymbol {\Omega }_n)$
, with the nontrivial harmonic maps denoted by
![]() $\Omega _{m, n}$
for
$\Omega _{m, n}$
for
![]() $m \in \{1, \dots , M_{j_1, k_1}\}$
, sequences
$m \in \{1, \dots , M_{j_1, k_1}\}$
, sequences
![]() $\vec { \widetilde \nu }_n = (\widetilde \nu _n, \widetilde \nu _{1, n}, \dots , \widetilde \nu _{M_{j_1, k_1}, n})$
and
$\vec { \widetilde \nu }_n = (\widetilde \nu _n, \widetilde \nu _{1, n}, \dots , \widetilde \nu _{M_{j_1, k_1}, n})$
and
![]() $\vec { \widetilde \xi }_n = (\widetilde \xi _n, \widetilde \xi _{1, n}, \dots , \widetilde \xi _{M_{j_1, k_1}, n})$
, so that
$\vec { \widetilde \xi }_n = (\widetilde \xi _n, \widetilde \xi _{1, n}, \dots , \widetilde \xi _{M_{j_1, k_1}, n})$
, so that
Consider the centers and scales
![]() $a(\Omega _{m,n}), \lambda (\Omega _{m,n})$
associated to the harmonic maps
$a(\Omega _{m,n}), \lambda (\Omega _{m,n})$
associated to the harmonic maps
![]() $\Omega _{m, n}$
. Using (3.105), (3.106) (3.107) and (3.108), we see that there are only two possible cases.
$\Omega _{m, n}$
. Using (3.105), (3.106) (3.107) and (3.108), we see that there are only two possible cases.
Case 1: All of the harmonic maps
![]() $\Omega _{n, m}$
concentrate within the discs
$\Omega _{n, m}$
concentrate within the discs
![]() $\bigcup _{ \ell = 1}^{L_1}D( c_{ \ell , n}, \rho _{ \ell , n})$
(i.e., for each
$\bigcup _{ \ell = 1}^{L_1}D( c_{ \ell , n}, \rho _{ \ell , n})$
(i.e., for each
![]() $m \in \{1, \dots , M_{j_1, k_1}\}$
, we have
$m \in \{1, \dots , M_{j_1, k_1}\}$
, we have
![]() $D( a( \Omega _{ m, n}), \lambda (\Omega _{ m, n})) \subset D( c_{\ell , n}, \rho _{ \ell , n})$
for some
$D( a( \Omega _{ m, n}), \lambda (\Omega _{ m, n})) \subset D( c_{\ell , n}, \rho _{ \ell , n})$
for some
![]() $\ell \in \{1, \dots , L_1\}$
). This means that
$\ell \in \{1, \dots , L_1\}$
). This means that
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D( b_n, r_n\mu_n) \setminus \bigcup_{\ell =1}^{L_1} D(c_{\ell, n}, \rho_{ \ell, n})\Big) = 0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n); D( b_n, r_n\mu_n) \setminus \bigcup_{\ell =1}^{L_1} D(c_{\ell, n}, \rho_{ \ell, n})\Big) = 0. \end{align} $$
In fact, comparing the above with (3.108), one can deduce that the harmonic maps
 $$ \begin{align*}\sum_{(j, k) \in \mathcal K(j_1, k_1)} ( \theta_{j, k}(x) - \theta_{j, k}( \infty) ) = \textrm{constant} \in \mathbb{R}^3.\end{align*} $$
$$ \begin{align*}\sum_{(j, k) \in \mathcal K(j_1, k_1)} ( \theta_{j, k}(x) - \theta_{j, k}( \infty) ) = \textrm{constant} \in \mathbb{R}^3.\end{align*} $$
In this case, we discard all of the harmonic maps with indices
![]() $(j, k) \in \mathcal K(j_1, k_1)$
from the final collection.
$(j, k) \in \mathcal K(j_1, k_1)$
from the final collection.
Case 2: Exactly one of the harmonic maps
![]() $\Omega _{m_1, n}$
has scale
$\Omega _{m_1, n}$
has scale
![]() $\lambda ( \Omega _{m_1, n}) \simeq \mu _n$
and center
$\lambda ( \Omega _{m_1, n}) \simeq \mu _n$
and center
![]() $|a(\Omega _{ m_1, n}) - b_n| \lesssim \mu _n$
, and the rest concentrate within the discs
$|a(\Omega _{ m_1, n}) - b_n| \lesssim \mu _n$
, and the rest concentrate within the discs
![]() $\bigcup _{ \ell = 1}^{L_1}D( c_{ \ell , n}, \rho _{\ell , n})$
. We then have
$\bigcup _{ \ell = 1}^{L_1}D( c_{ \ell , n}, \rho _{\ell , n})$
. We then have
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n) - \Omega_{ m_1, n}; D( b_n, r_n\mu_n) \setminus \bigcup_{\ell =1}^{L_1} D(c_{ \ell, n}, \rho_{ \ell, n})\Big) = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n) - \Omega_{ m_1, n}; D( b_n, r_n\mu_n) \setminus \bigcup_{\ell =1}^{L_1} D(c_{ \ell, n}, \rho_{ \ell, n})\Big) = 0 \end{align} $$
and
By another application of the Compactness Lemma 2.15, we can find a nontrivial harmonic map, which we label
![]() $\Theta _{ j_1, k_1}$
, a non-negative integer P, scales
$\Theta _{ j_1, k_1}$
, a non-negative integer P, scales
![]() $\nu _{ p, n} \ll \mu _n$
, centers
$\nu _{ p, n} \ll \mu _n$
, centers
![]() $d_{ p, n}$
, and nontrivial harmonic maps
$d_{ p, n}$
, and nontrivial harmonic maps
![]() $\Theta _{p}$
, satisfying (2.65) and (2.66), and so that
$\Theta _{p}$
, satisfying (2.65) and (2.66), and so that
 $$ \begin{align} \lim_{n \to \infty} &\Bigg[E\Big( \Omega_{ m_1, n} - \Theta_{ j_1, k_1}\big( \frac{\cdot - b_n}{\mu_n}\big) - \sum_{p=1}^{P} \big(\Theta_p\big(\frac{ \cdot - d_{ p, n}}{\nu_{ p, n}} \big) - \Theta_p(\infty)\big); D( b_n, r_n\mu_n)\Big) \nonumber\\ & + \Big\| \Omega_{ m_1, n} - \Theta_{ j_1, k_1}\big( \frac{\cdot - b_n}{\mu_n}\big) - \sum_{p=1}^{P} \big(\Theta_p\big(\frac{ \cdot - d_{ p, n}}{\nu_{ p, n}} \big) - \Theta_p(\infty)\big)\Big\|_{L^\infty( D( b_n, r_n\mu_n)) } \Bigg]= 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} &\Bigg[E\Big( \Omega_{ m_1, n} - \Theta_{ j_1, k_1}\big( \frac{\cdot - b_n}{\mu_n}\big) - \sum_{p=1}^{P} \big(\Theta_p\big(\frac{ \cdot - d_{ p, n}}{\nu_{ p, n}} \big) - \Theta_p(\infty)\big); D( b_n, r_n\mu_n)\Big) \nonumber\\ & + \Big\| \Omega_{ m_1, n} - \Theta_{ j_1, k_1}\big( \frac{\cdot - b_n}{\mu_n}\big) - \sum_{p=1}^{P} \big(\Theta_p\big(\frac{ \cdot - d_{ p, n}}{\nu_{ p, n}} \big) - \Theta_p(\infty)\big)\Big\|_{L^\infty( D( b_n, r_n\mu_n)) } \Bigg]= 0 \end{align} $$
We know that the harmonic map
![]() $\Theta _{j_1, k_1}$
must be nontrivial because of (3.112) together with (3.108), where the latter ensures that energy cannot concentrate within the region
$\Theta _{j_1, k_1}$
must be nontrivial because of (3.112) together with (3.108), where the latter ensures that energy cannot concentrate within the region
 $$ \begin{align*}D(b_n, r_n \mu_n) \setminus \bigcup_{\ell =1}^{L_1} D(c_{\ell, n}, \rho_{ \ell, n})\end{align*} $$
$$ \begin{align*}D(b_n, r_n \mu_n) \setminus \bigcup_{\ell =1}^{L_1} D(c_{\ell, n}, \rho_{ \ell, n})\end{align*} $$
at scales smaller than
![]() $\mu _n$
. Indeed, by (3.108), the scales and centers of the nontrivial harmonic maps
$\mu _n$
. Indeed, by (3.108), the scales and centers of the nontrivial harmonic maps
![]() $\Theta _p$
must all concentrate within the discs
$\Theta _p$
must all concentrate within the discs
![]() $\bigcup _{\ell =1}^{L_1}D(c_{ \ell , n}, \rho _{\ell , n})$
, and we can conclude that
$\bigcup _{\ell =1}^{L_1}D(c_{ \ell , n}, \rho _{\ell , n})$
, and we can conclude that
 $$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n) - \Theta_{ j_1, k_1}( \frac{\cdot - b_n}{\mu_n}); D( b_n, r_n\mu_n) \setminus \bigcup_{\ell =1}^{L_1} D(c_{ \ell, n}, \rho_{ \ell, n})\Big) = 0 \end{align} $$
$$ \begin{align} \lim_{n \to \infty} E\Big( u(t_n) - \Theta_{ j_1, k_1}( \frac{\cdot - b_n}{\mu_n}); D( b_n, r_n\mu_n) \setminus \bigcup_{\ell =1}^{L_1} D(c_{ \ell, n}, \rho_{ \ell, n})\Big) = 0 \end{align} $$
and
In this case, we discard all the triples
![]() $(\theta _{j, k}, b_{ j, k, n}, \mu _{ j, k, n})$
with indices
$(\theta _{j, k}, b_{ j, k, n}, \mu _{ j, k, n})$
with indices
![]() $(j, k) \in \mathcal K(j_1, k_1)$
from the final collection and replace them with the triple
$(j, k) \in \mathcal K(j_1, k_1)$
from the final collection and replace them with the triple
![]() $(\Theta _{ j_1, k_1}, b_{j_1, k_1, n}, \mu _{ j_1, k_1, n})$
.
$(\Theta _{ j_1, k_1}, b_{j_1, k_1, n}, \mu _{ j_1, k_1, n})$
.
To summarize, we keep for the final decomposition any triples
![]() $(\theta _{j, k}, b_{ j, k, n}, \mu _{j, k, n})$
with
$(\theta _{j, k}, b_{ j, k, n}, \mu _{j, k, n})$
with
![]() $\mathfrak {h}_j \in \mathcal T(j_0)$
if
$\mathfrak {h}_j \in \mathcal T(j_0)$
if
![]() $\#\mathcal K(j, k) = 1$
. If
$\#\mathcal K(j, k) = 1$
. If
![]() $\#\mathcal K(j, k)>1$
, we discard all of the triples
$\#\mathcal K(j, k)>1$
, we discard all of the triples
![]() $( \theta _{j', k'}, b_{ j', k', n}, \mu _{ j', k', n})$
with indices
$( \theta _{j', k'}, b_{ j', k', n}, \mu _{ j', k', n})$
with indices
![]() $j' \in \mathcal K(j, k)$
and, in the event of Case
$j' \in \mathcal K(j, k)$
and, in the event of Case
![]() $2$
above, we replace them with
$2$
above, we replace them with
![]() $ \Theta _{j, k}, b_{ j, k, n}, \mu _{ j, k,n}$
. We perform this analysis for each index
$ \Theta _{j, k}, b_{ j, k, n}, \mu _{ j, k,n}$
. We perform this analysis for each index
![]() $j_0 \in \mathcal R$
, resulting in a final collection of triples that are mutually asymptotically orthogonal and satisfy the conclusions of the theorem.
$j_0 \in \mathcal R$
, resulting in a final collection of triples that are mutually asymptotically orthogonal and satisfy the conclusions of the theorem.
Funding statement
J. Jendrej is supported by ANR-18-CE40-0028 project ESSED. A. Lawrie is supported by NSF grant DMS-1954455 and the Solomon Buchsbaum Research Fund. W. Schlag is supported by NSF grant DMS-1902691.
Competing interests
The authors have no competing interest to declare.