Published online by Cambridge University Press: 13 March 2019
We prove a lower bound on the difference between the spectral radius of the Cayley graph of a group 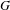 $G$ and the spectral radius of the Schreier graph
$G$ and the spectral radius of the Schreier graph  $H\backslash G$ for any subgroup
$H\backslash G$ for any subgroup 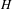 $H$ . As an application, we extend Kesten’s theorem on spectral radii to uniformly recurrent subgroups and give a short proof that the result of Lyons and Peres on cycle density in Ramanujan graphs [Lyons and Peres. Cycle density in infinite Ramanujan graphs. Ann. Probab.43(6) (2015), 3337–3358, Theorem 1.2] holds on average. More precisely, we show that if
$H$ . As an application, we extend Kesten’s theorem on spectral radii to uniformly recurrent subgroups and give a short proof that the result of Lyons and Peres on cycle density in Ramanujan graphs [Lyons and Peres. Cycle density in infinite Ramanujan graphs. Ann. Probab.43(6) (2015), 3337–3358, Theorem 1.2] holds on average. More precisely, we show that if 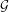 ${\mathcal{G}}$ is an infinite deterministic Ramanujan graph then the time spent in short cycles by a random trajectory of length
${\mathcal{G}}$ is an infinite deterministic Ramanujan graph then the time spent in short cycles by a random trajectory of length  $n$ is
$n$ is 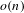 $o(n)$ .
$o(n)$ .