Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-10T22:22:43.753Z Has data issue: false hasContentIssue false
  • English
  • Français

Hausdorff dimension of divergent diagonal geodesics on product of finite-volume hyperbolic spaces

Published online by Cambridge University Press:  25 September 2017

LEI YANG
LEI YANG*
Affiliation:
Mathematical Sciences Research Institute, Berkeley, CA 94720, USA email yang.lei@mail.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the product space of several non-compact finite-volume hyperbolic spaces, 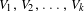$V_{1},V_{2},\ldots ,V_{k}$ of dimension $n$. Let 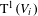$\text{T}^{1}(V_{i})$ denote the unit tangent bundle of 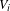$V_{i}$ and 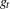$g_{t}$ denote the geodesic flow on 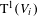$\text{T}^{1}(V_{i})$ for each 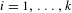$i=1,\ldots ,k$. We define

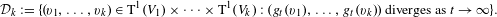$$\begin{eqnarray}{\mathcal{D}}_{k}:=\{(v_{1},\ldots ,v_{k})\,\in \,\text{T}^{1}(V_{1})\times \cdots \times \text{T}^{1}(V_{k})\,:\,(g_{t}(v_{1}),\ldots ,g_{t}(v_{k}))\text{ diverges as }t\rightarrow \infty \}.\end{eqnarray}$$
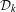We will prove that the Hausdorff dimension of ${\mathcal{D}}_{k}$ is equal to 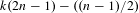$k(2n-1)-((n-1)/2)$. This extends a result of Cheung.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 5 , May 2019 , pp. 1401 - 1439
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Apanasov, B.. Infinite index subgroups and finiteness properties of intersections of geometrically finite groups. Topology Appl. 154(7) (2007), 1245–1253.Google Scholar
Bowditch, B. H.. Geometrical finiteness for hyperbolic groups. J. Funct. Anal. 113(2) (1993), 245–317.Google Scholar
Cheung, Y. and Chevallier, N.. Hausdorff dimension of singular vectors. Duke Math. J. 165(12) (2016), 2273–2329.Google Scholar
Cheung, Y.. Hausdorff dimension of the set of nonergodic directions. Ann. of Math. (2) 158 (2003), 661–678.Google Scholar
Cheung, Y.. Hausdorff dimension of the set of points on divergent trajectories of a homogeneous flow on a product space. Ergod. Th. & Dynam. Sys. 27(01) (2007), 65–85.Google Scholar
Cheung, Y.. Hausdorff dimension of the set of singular pairs. Ann. of Math. (2) 173(01) (2011), 127–167.Google Scholar
Cheung, Y., Hubert, P. and Masur, H.. Dichotomy for the Hausdorff dimension of the set of nonergodic directions. Invent. Math. 183(2) (2011), 337–383.Google Scholar
Dani, S. G.. Divergent trajectories of flows on homogeneous spaces and diophantine approximation. J. Reine Angew. Math. 359 (1985), 55–89.Google Scholar
Einsiedler, M., Kadyrov, S. and Pohl, A.. Escape of mass and entropy for diagonal flows in real rank one situations. Israel J. Math. 210(1) (2015), 245–295.Google Scholar
Falconer, K. J.. The Geometry of Fractal Sets. Cambridge University Press, Cambridge, 1986.Google Scholar
Garland, H. and Raghunathan, M. S.. Fundamental domains for lattices in rank one semisimple lie groups. Proc. Natl. Acad. Sci. 62(2) (1969), 309–313.Google Scholar
Gorodnik, A. and Shah, N. A.. Khinchin’s theorem for approximation by integral points on quadratic varieties. Math. Ann. 350(2) (2011), 357–380.Google Scholar
Kleinbock, D. Y. and Margulis, G. A.. Bounded orbits of nonquasiunipotent flows on homogeneous spaces. Amer. Math. Soc. Trans. 171 (1996), 141–172.Google Scholar
Marstrand, J. M.. The Dimension of Cartesian Product Sets (Mathematical Proceedings of the Cambridge Philosophical Society, 50) . Cambridge University Press, Cambridge, 1954, pp. 198–202.Google Scholar
Margulis, G. A.. On Some Aspects of the Theory of Anosov Systems. Springer, Berlin, 2004.Google Scholar
Masur, H.. Hausdorff dimension of the set of nonergodic foliations of a quadratic differential. Duke Math. J. 66(3) (1992), 387–442.Google Scholar
McMullen, C.. Area and Hausdorff dimension of Julia sets of entire functions. Trans. Amer. Math. Soc. 300(1) (1987), 329–342.Google Scholar
Moore, C. C.. Ergodicity of flows on homogeneous spaces. Amer. J. Math. 88(1) (1966), 154–178.Google Scholar
Masur, H. and Smillie, J.. Hausdorff dimension of sets of nonergodic measured foliations. Ann. of Math. (2) 134 (1991), 455–543.Google Scholar
Patterson, S. J.. Lectures on measures on limit sets of Kleinian groups. Analytical and Geometric Aspects of Hyperbolic Space (Coventry/Durham, 1984). Vol. 111. Durham, Warwick, 1987, pp. 281–323.Google Scholar
Sullivan, D.. The density at infinity of a discrete group of hyperbolic motions. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 171–202.Google Scholar
Sullivan, D.. Entropy, Hausdorff measures old and new, and limit sets of geometrically finite Kleinian groups. Acta Math. 153(1) (1984), 259–277.Google Scholar
Urbanski, M.. The Hausdorff dimension of the set of points with nondense orbit under a hyperbolic dynamical system. Nonlinearity 4(2) (1991), 385–397.Google Scholar